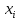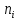Лаб 3 Садртдинов Тимур Отчет. В течение 5 ч регистрировалось прибытие автомашин к бензоколонке. Результаты представлены в таблице
 Скачать 19.03 Kb. Скачать 19.03 Kb.
|
|
Задание 7. В течение 5 ч регистрировалось прибытие автомашин к бензоколонке. Результаты представлены в таблице.
С помощью критерия Пирсона проверить гипотезу о равномерном распределении на отрезке (8;13) времени прибытия машин при a= 0,01. Задание 8. Для заданного интервального выборочного ряда (начальное значение 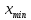 , шаг h) проверить гипотезу: закон распределения генеральной совокупности является нормальным при уровне значимости , шаг h) проверить гипотезу: закон распределения генеральной совокупности является нормальным при уровне значимости 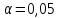 . .
Объем выборки n=431. Будем считать вариантами середины частичных интервалов: 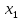 = -2,25, = -2,25, 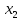 = -0,95, …, = -0,95, …, 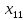 = 9,45. = 9,45.В итоге получим эмпирическое распределение равностоящих вариант.
Для нахождения 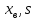 произведем некоторые дополнительные вычисления. произведем некоторые дополнительные вычисления.
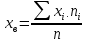 = 3,809 = 3,809D = 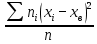 = 4,503 = 4,503S = 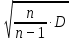 = 2,1246 = 2,1246Вычислим вероятности 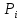 попадания значений рассматриваемой случайной величины X с функцией распределения F(x) в i-й частичный интервал и теоретические частоты попадания значений рассматриваемой случайной величины X с функцией распределения F(x) в i-й частичный интервал и теоретические частоты 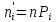 . Значение функции Ф(х) возьмем из таблицы значений функции Лапласа. . Значение функции Ф(х) возьмем из таблицы значений функции Лапласа.
Из таблицы получаем 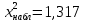 Найдем 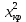 по таблице критических точек распределения Пирсона при уровне значимости по таблице критических точек распределения Пирсона при уровне значимости 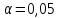 и числу степеней свободы k = 10 – 3 = 078. и числу степеней свободы k = 10 – 3 = 078.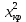 (0,05;7) = 14,1 (0,05;7) = 14,1Так как 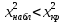 , то гипотеза о нормальном распределении принимается. , то гипотеза о нормальном распределении принимается. Задание 9. Для заданного интервального выборочного ряда (начальное значение 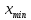 , шаг h) проверить гипотезу: закон распределения генеральной совокупности является показательным при уровне значимости , шаг h) проверить гипотезу: закон распределения генеральной совокупности является показательным при уровне значимости 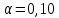 . .
Объем выборки n=358. Будем считать вариантами середины частичных интервалов: 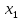 = 0,1, = 0,1, 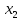 = 0,3, …, = 0,3, …, 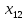 = 2,1. = 2,1.Для нахождения 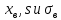 произведем некоторые дополнительные вычисления. произведем некоторые дополнительные вычисления.
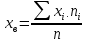 = 0,259 = 0,259D = 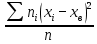 = 0,0616 = 0,0616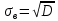 = 0,248372248366483 = 0,248372248366483S = 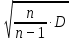 = 0,248 = 0,248Вычислим теоретические частоты в предположении о показательном распределении генеральной совокупности при 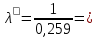 3,857 3,857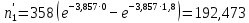 Аналогично вычислим остальные результаты в таблице:
Наблюдаемое значение критерия 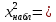 12,87 12,87Критическая точка 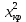 (0,10;8) = 13,362 (0,10;8) = 13,362Так как 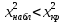 , то гипотеза о нормальном распределении принимается. , то гипотеза о нормальном распределении принимается. Задание 10. Для заданного интервального выборочного ряда (начальное значение 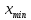 , шаг h) проверить гипотезу: закон распределения генеральной совокупности является равномерным при уровне значимости , шаг h) проверить гипотезу: закон распределения генеральной совокупности является равномерным при уровне значимости 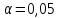 . .
Объем выборки n=375. Будем считать вариантами середины частичных интервалов: 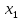 = 9,5, = 9,5, 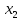 = 11,7, …, = 11,7, …, 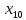 = 29,3. = 29,3.В итоге получим эмпирическое распределение равностоящих вариант.
Для нахождения 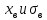 произведем некоторые дополнительные вычисления. произведем некоторые дополнительные вычисления.
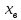 = 18,951. = 18,951.D = 36,450. 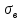 = = 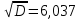 . .Следовательно, 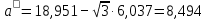 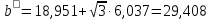 Найдем дифференциальную функцию предполагаемого равномерного распределения: 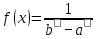 = = 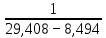 = 0,048 = 0,048Найдем теоретические частоты: 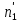 = = 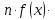 - - 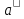 ) = 18,036 ) = 18,036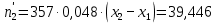 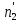 = … = = … = 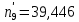 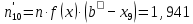 Сравним эмпирические и теоретические частоты. Для этого составим расчётную таблицу.
Из таблицы получаем 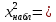 276,72 276,72Найдем 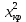 по таблице критических точек распределения Пирсона при уровне значимости по таблице критических точек распределения Пирсона при уровне значимости 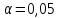 и числу степеней свободы k = n – 3 = 7. и числу степеней свободы k = n – 3 = 7.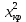 (0,05;7) = 14,1. (0,05;7) = 14,1.Так как 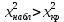 , то гипотеза о нормальном распределении отклоняется. , то гипотеза о нормальном распределении отклоняется. |