|
|
СР по геометрии. С-47 Векторы. Вариант 1 Изобразите параллелепипед abcda1B1C1 Постройте на рисунке векторы, равные 1 2
Вариант 1
1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные:
1)  ; 2) ; 2)  . .
2. ABCDA1B1C1D1 – параллелепипед, отрезки АC и BD пересекаются в точке М. Разложите вектор
 по векторам по векторам 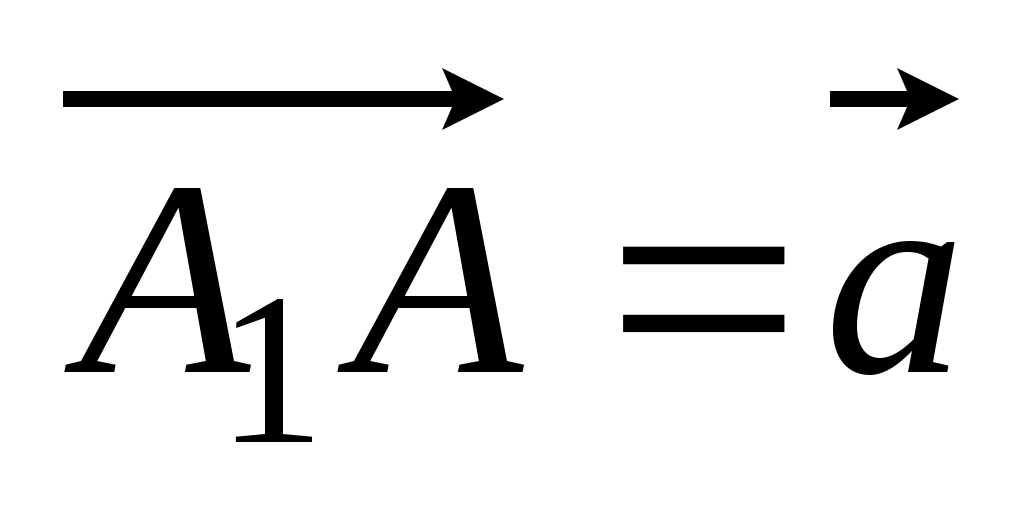 , ,  , ,  . .
3. В тетраэдре DABC точка М – точка пересечения медиан грани DBC, Е – середина АС. Разложите вектор
 по векторам по векторам  , , 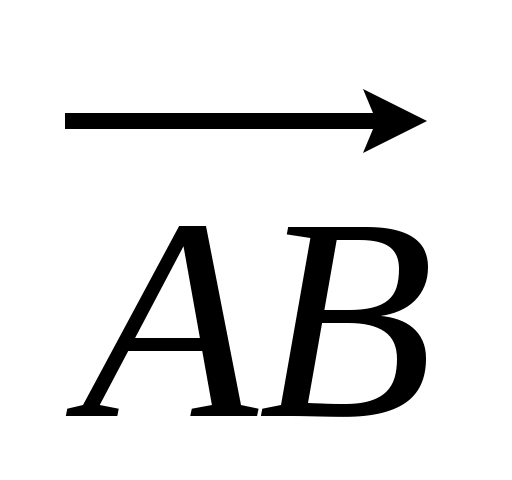 и и  . .
4. DABC – тетраэдр, О – точка пересечения медиан АВС, точка F лежит на AD, причем AF : FD = 3 : 1. Разложите вектор  по векторам по векторам 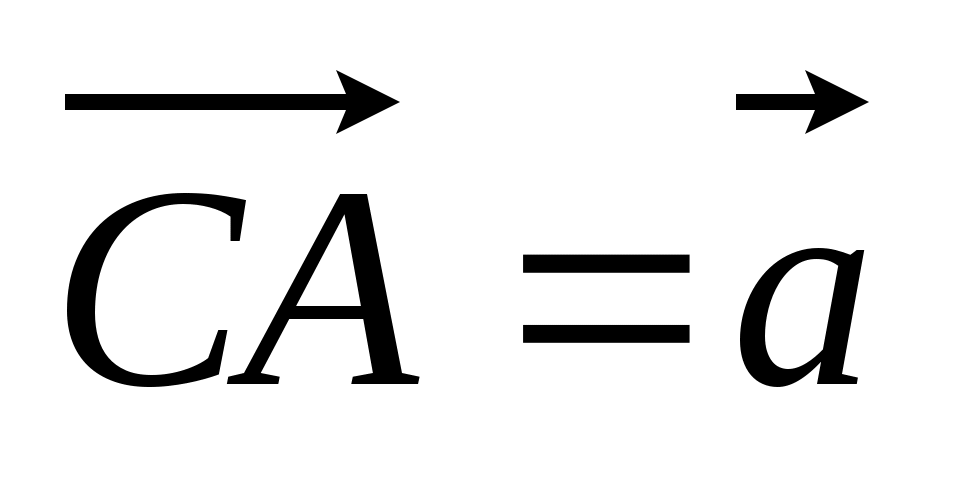 , , 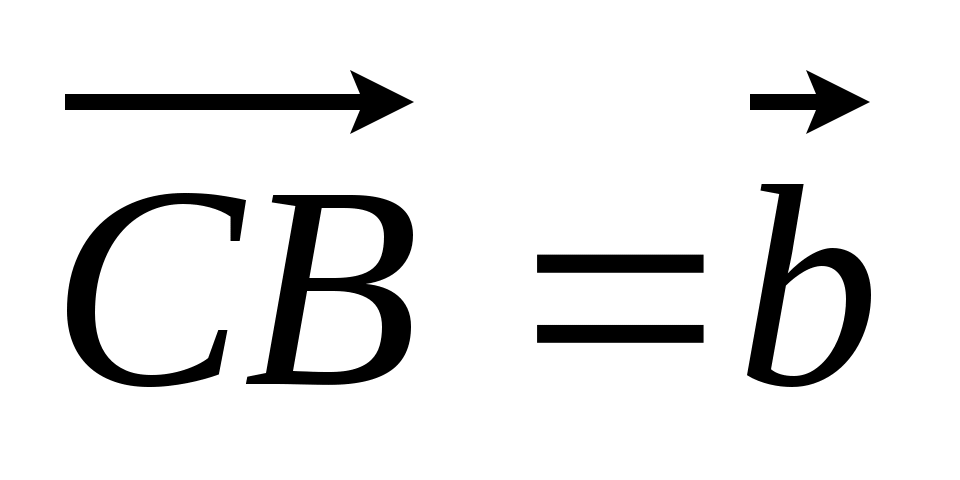 , , 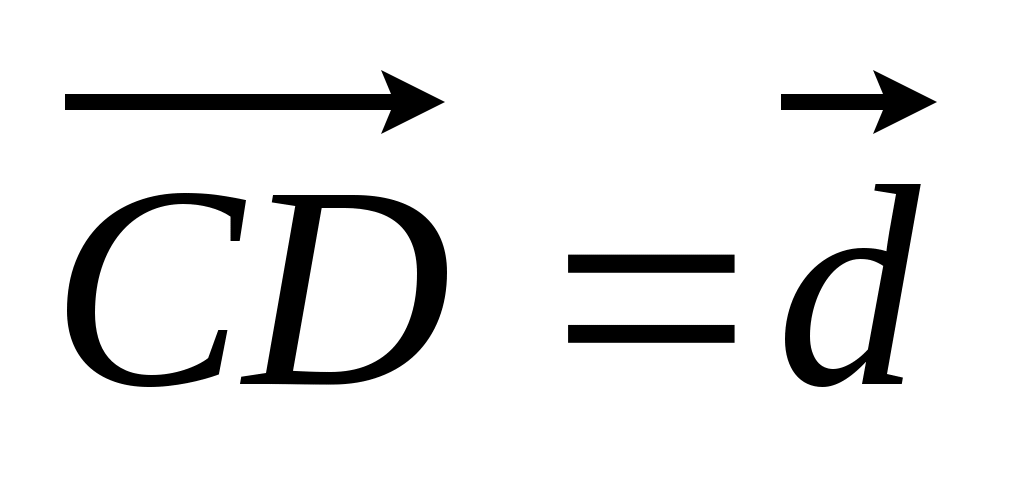 . .
|
Вариант 2
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный:
1) 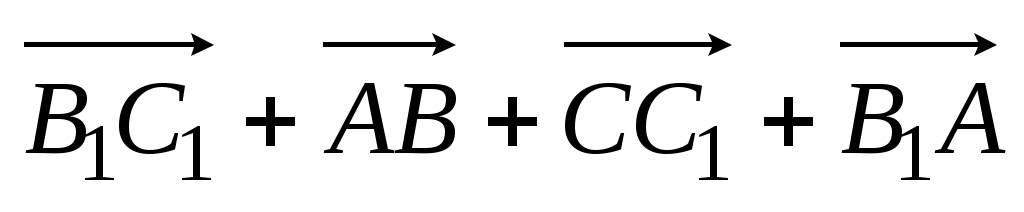 ; 2) ; 2) 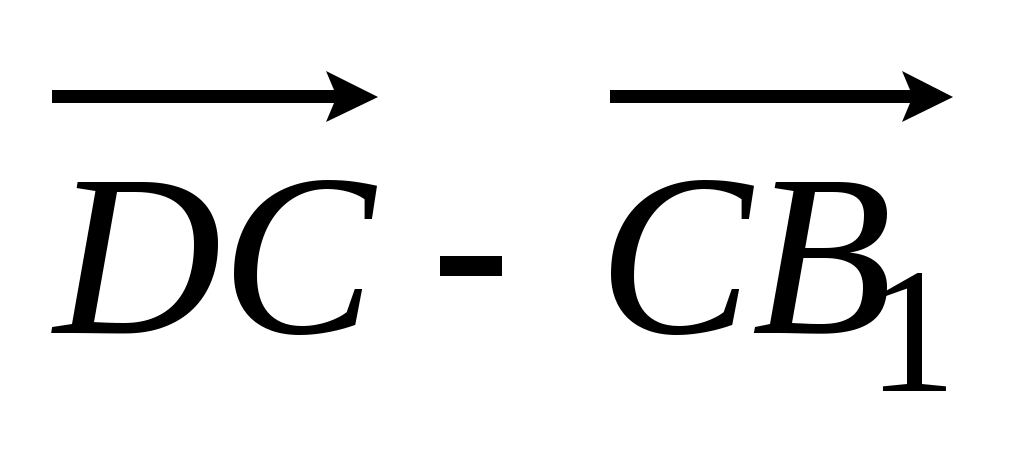 . .
2. В параллелепипеде ABCDA1B1C1D1 диагонали грани АВCD пересекаются в точке О. Разложите вектор
 по векторам, по векторам, 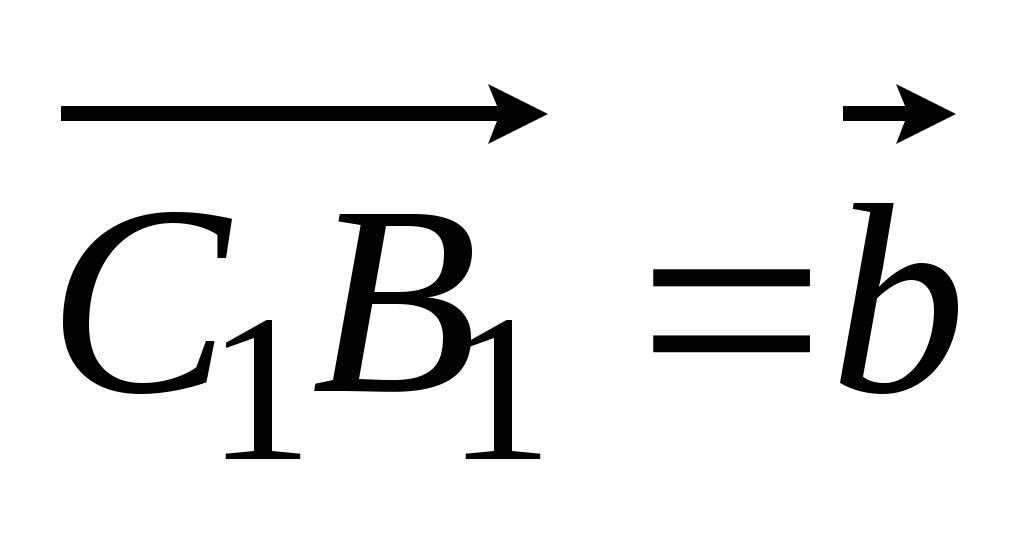 , , 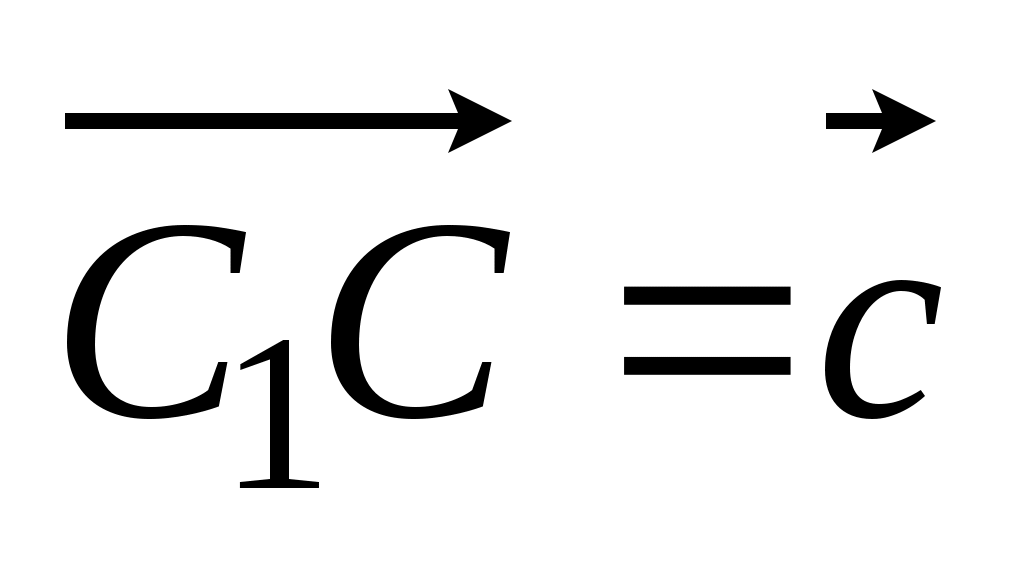 , , 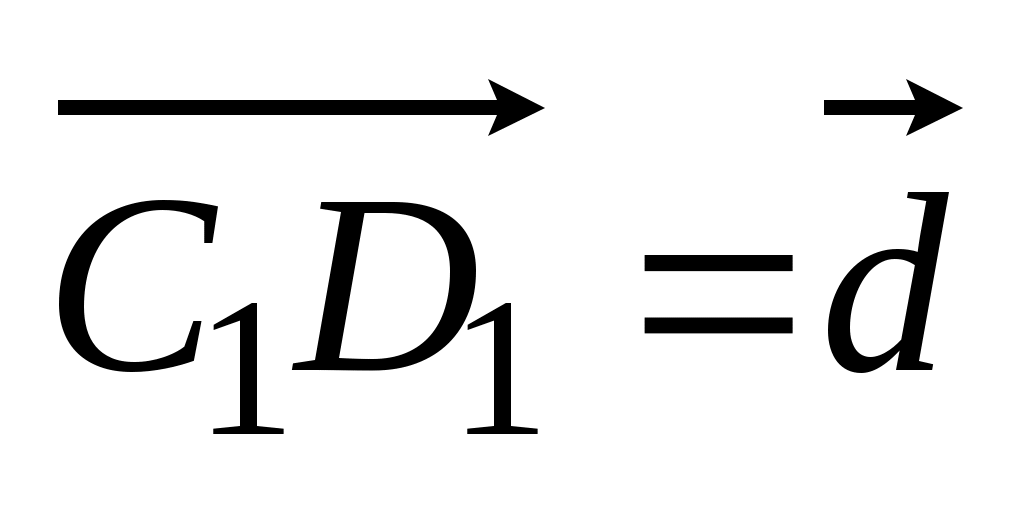 . .
3. DABC – тетраэдр, точка Е – середина ребра АD, а точка М – точка пересечения медиан грани BDC. Разложите вектор  по векторам по векторам 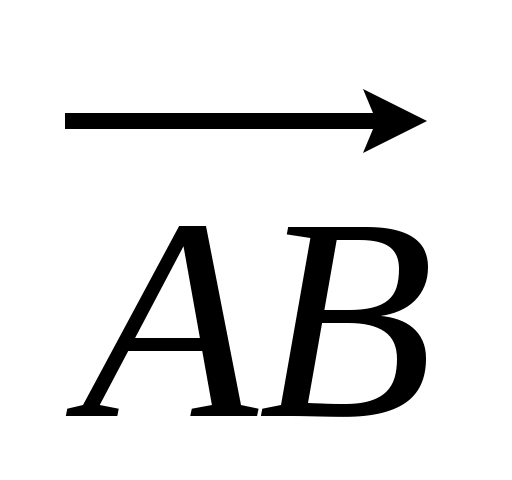 , ,  и и  . .
4. Дан тетраэдр DABC. Медианы грани АВС пересекаются в точке М,  , причем DN : NC = 5 : 1. Разложите вектор , причем DN : NC = 5 : 1. Разложите вектор  по векторам по векторам 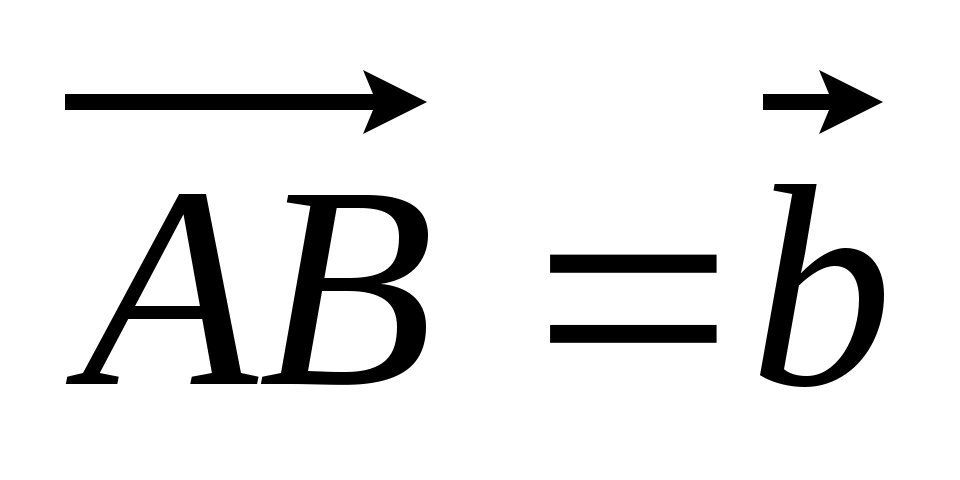 , , 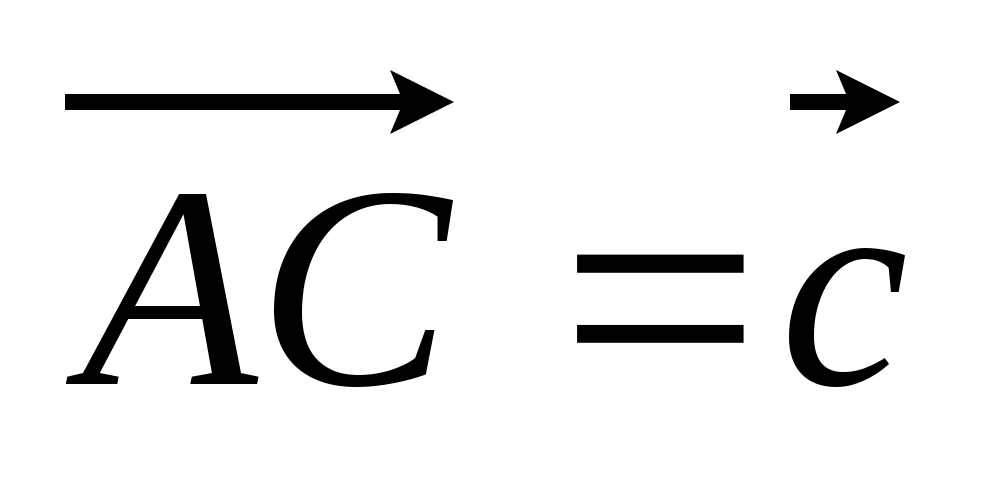 , , 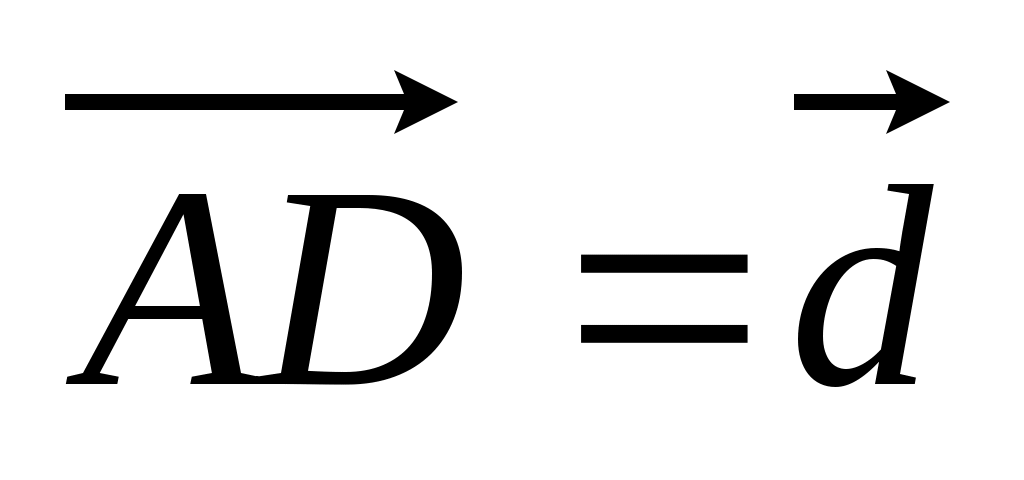 . .
|
Вариант 3
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный:
1) 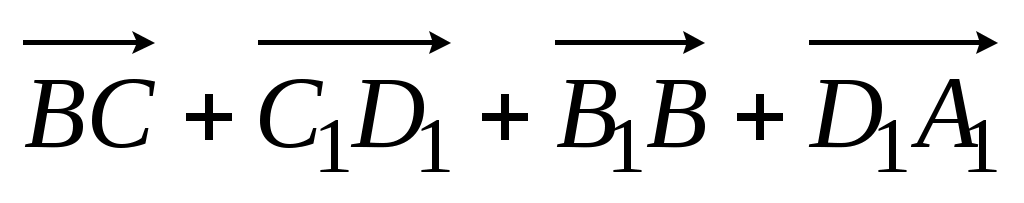 ; 2) ; 2) 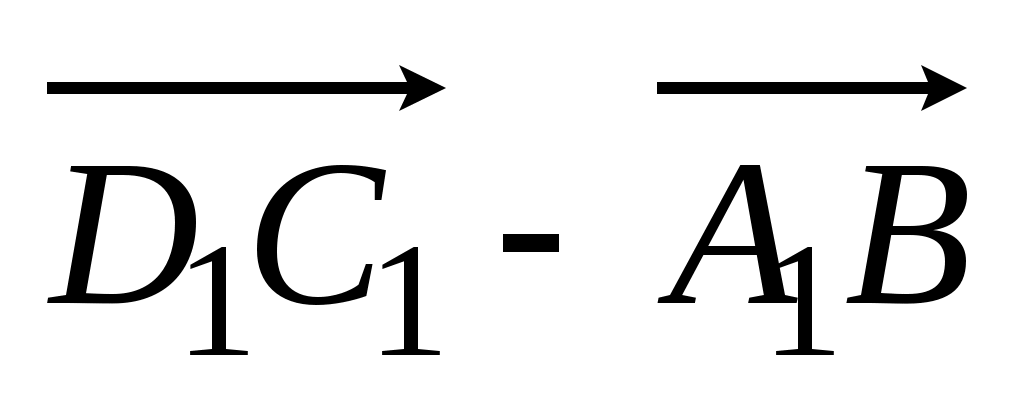 . .
2. К – точка пересечения диагоналей В1D1 и А1C1 параллелепипедаABCDA1B1C1D1. Разложите вектор
 по векторам по векторам 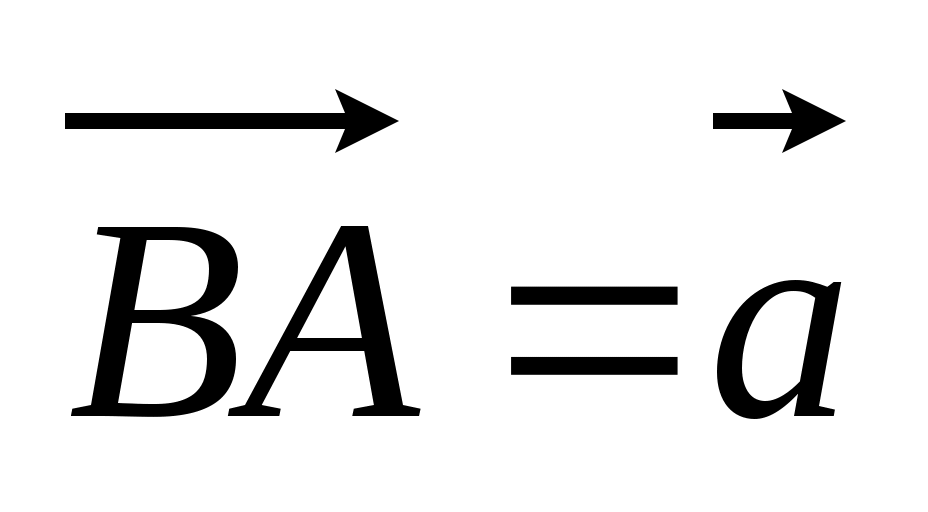 , , 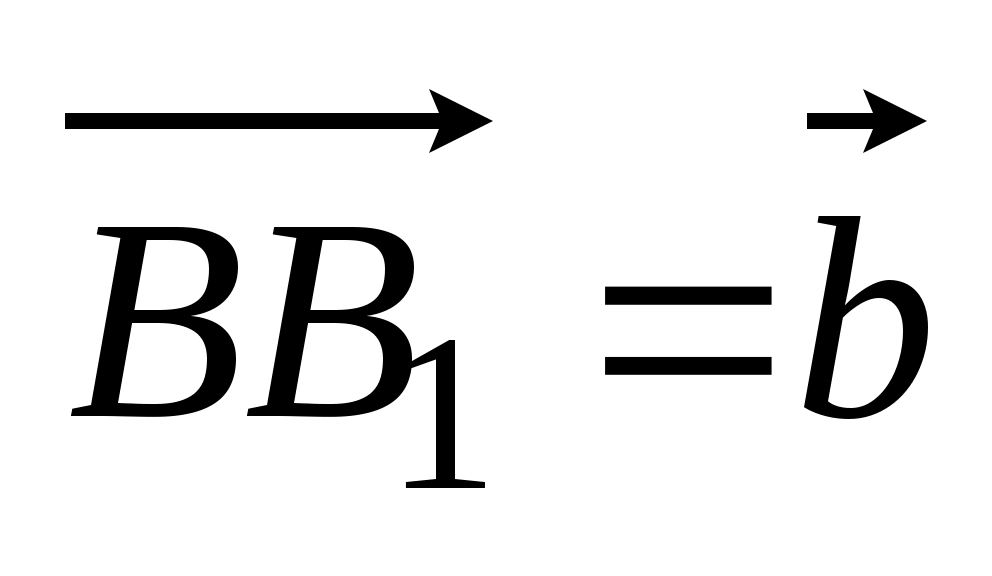 , ,  . .
3. DABC – тетраэдр, точка Е – середина ребра DВ, а точка М – точка пересечения медиан грани АBC. Разложите вектор
 по векторам по векторам  , ,  и и  . .
4. В тетраэдре DABC R – точка пересечения медиан грани DВС,  , причем AK : KB = 2 : 7. Разложите вектор , причем AK : KB = 2 : 7. Разложите вектор
 по векторам по векторам 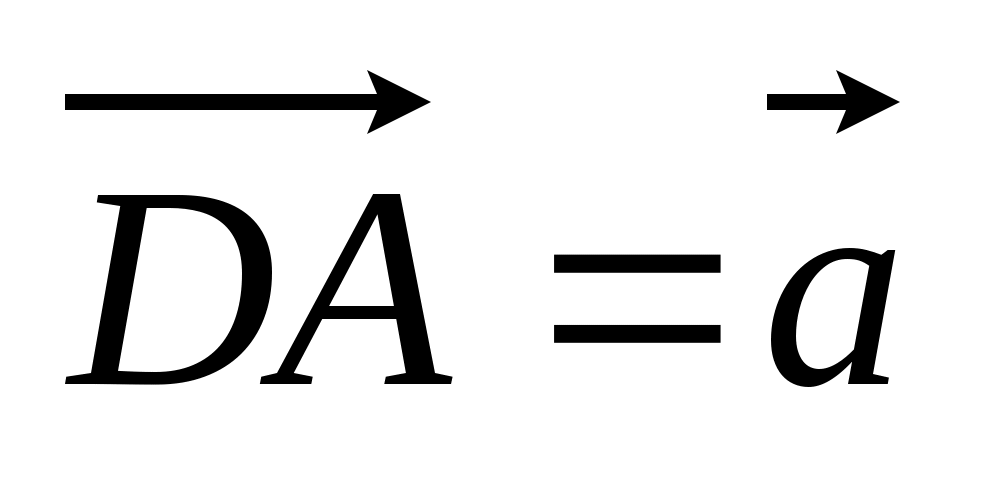 , ,  , ,  . .
|
Вариант 4
1. Укажите вектор с началом и концом в вершинах параллелепипедаABCDA1B1C1D1, равный:
1)  ; 2) ; 2) 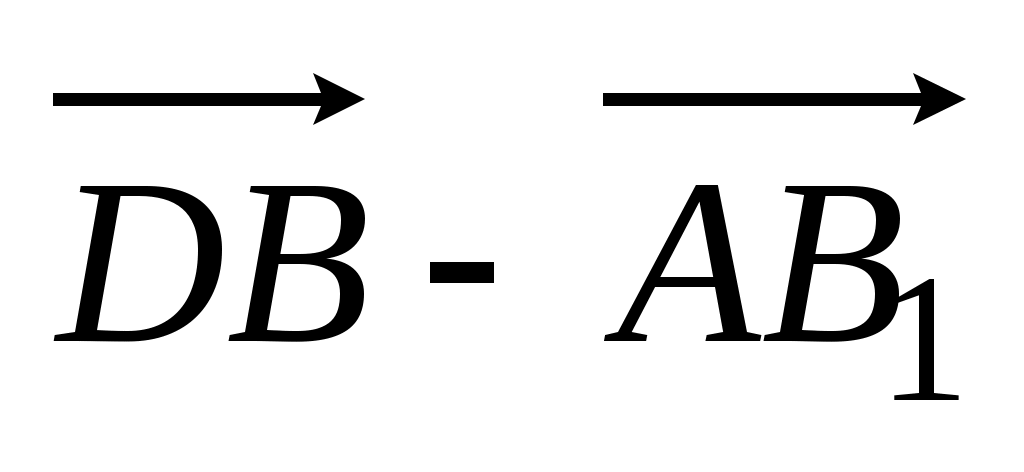 . .
2. ABCDA1B1C1D1 – параллелепипед, N – точка пересечения отрезков АC и ВD. Разложите вектор
 по векторам по векторам 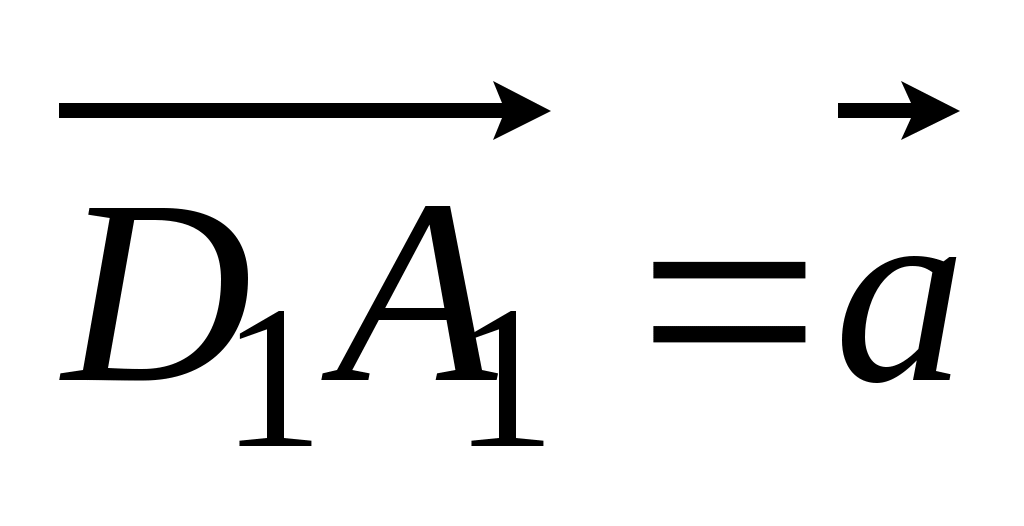 , , 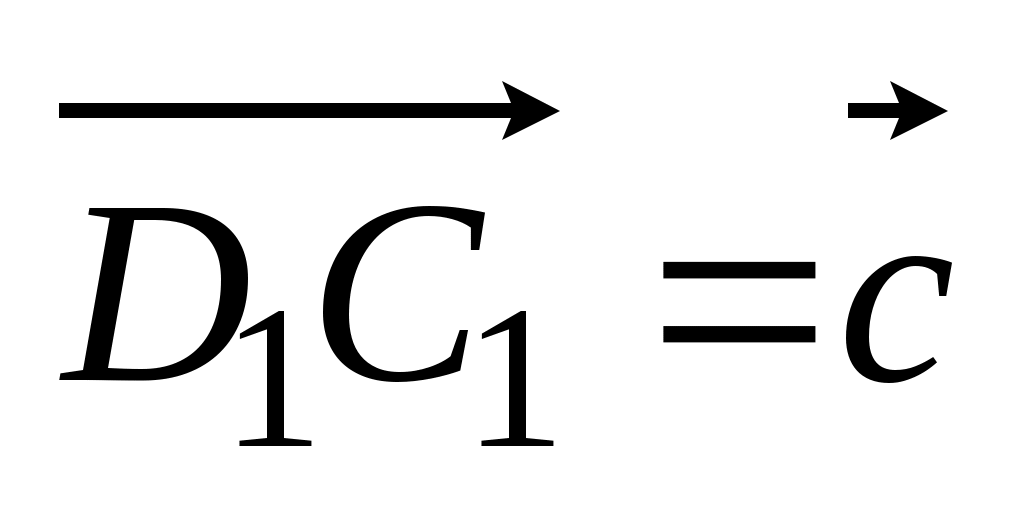 , , 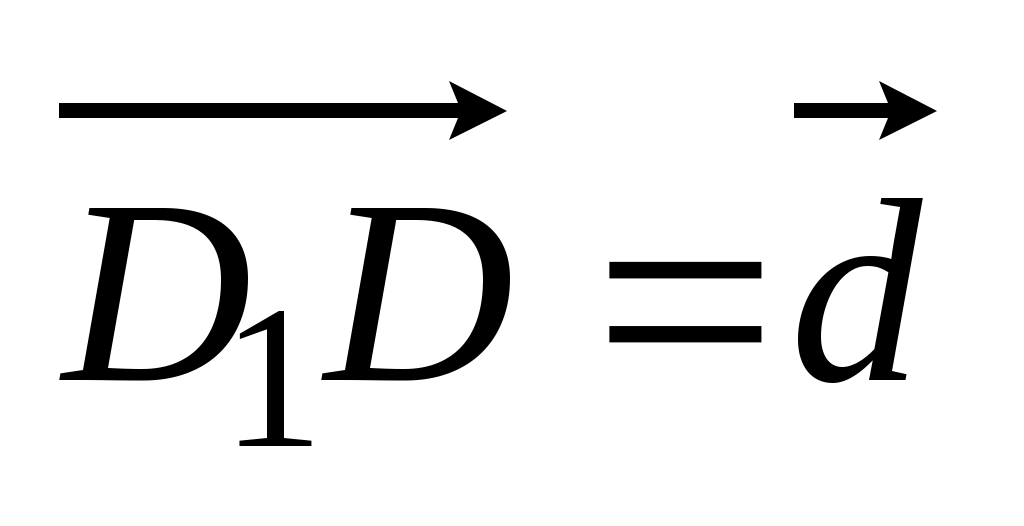 . .
3. Медианы грани ACD тетраэдра DABC пересекаются в точке М, а точка К – середина ребра АВ. Разложите вектор
 по векторам по векторам  , ,  и и  . .
4. DABC – тетраэдр, M – точка пересечения медиан АВС, точка К лежит на DC так, что DK : KC = 3 : 2. Разложите вектор 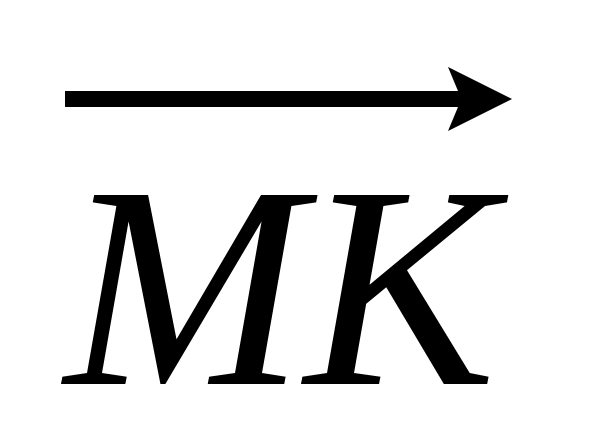 по векторам по векторам 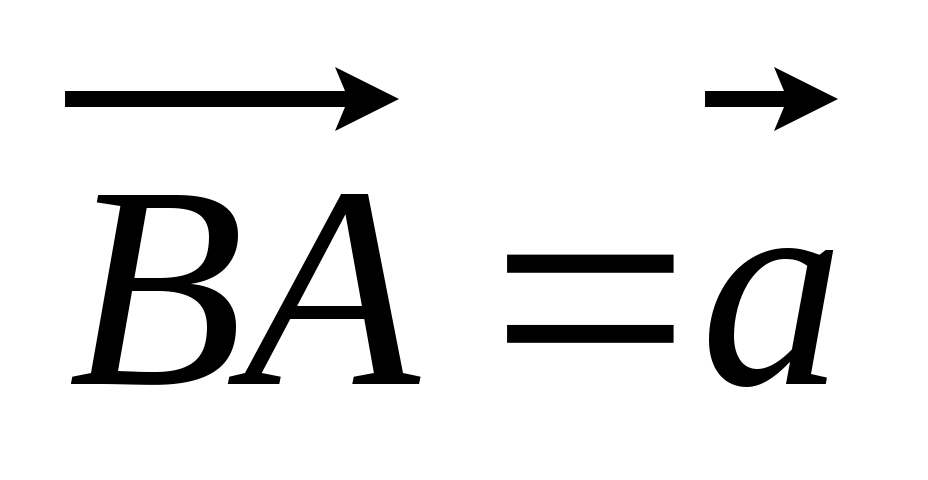 , , 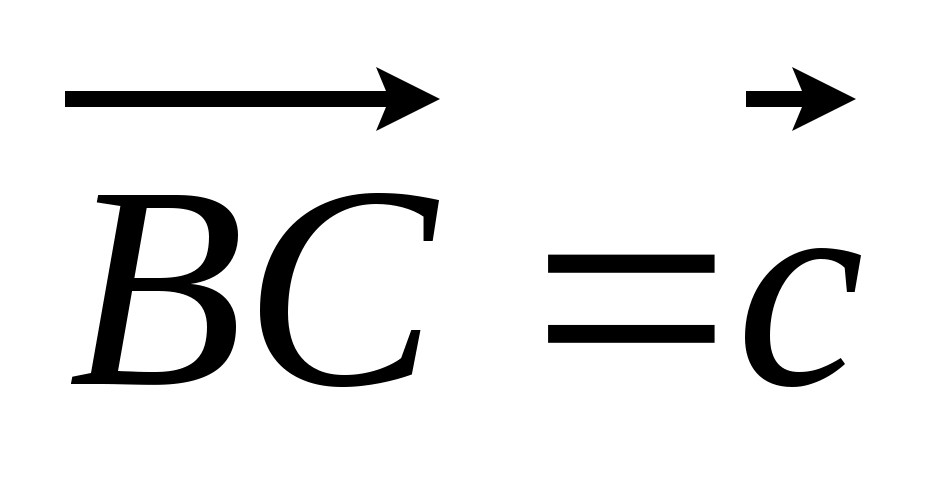 , , 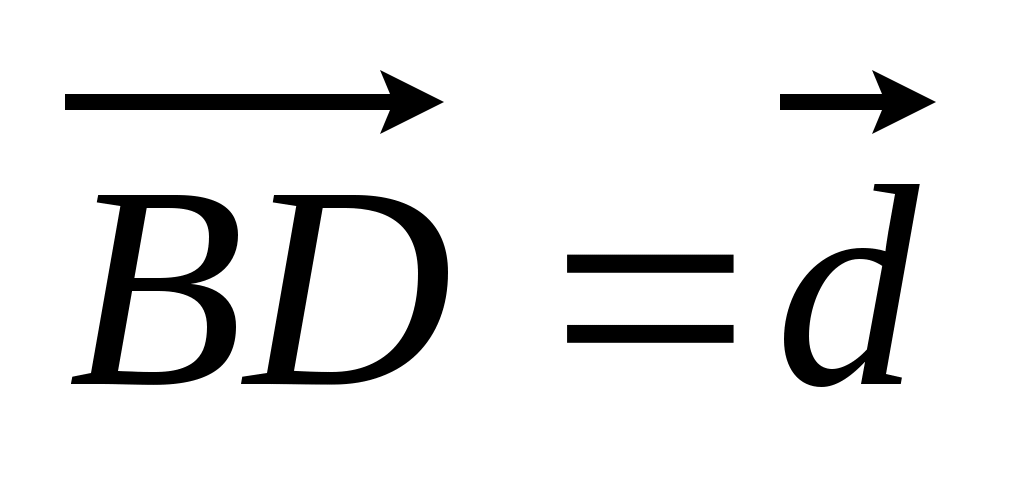 . .
|
Вариант 5
1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные:
1) 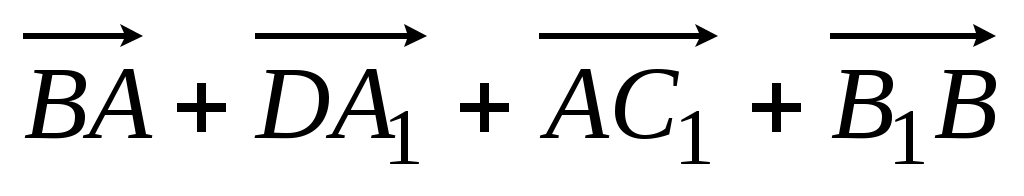 ; 2) ; 2)  . .
2. В параллелепипедеABCDA1B1C1D1 точка P – точка пересечения отрезков АC и BD. Разложите вектор
 по векторам по векторам 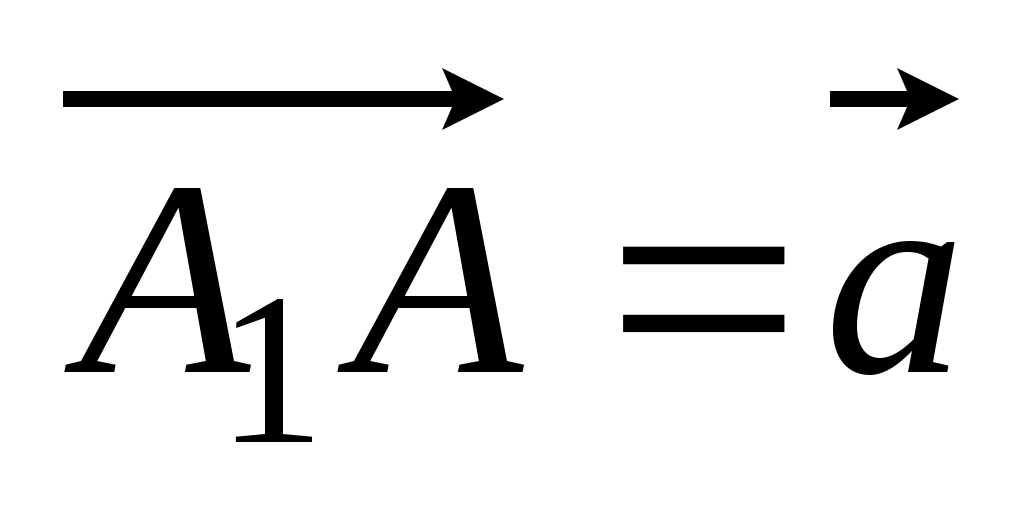 , ,  , ,  . .
3. В тетраэдре DABC медианы грани DBC пересекаются в
точке М, середина ребра АС – точка Е. Разложите вектор
 по векторам по векторам  , , 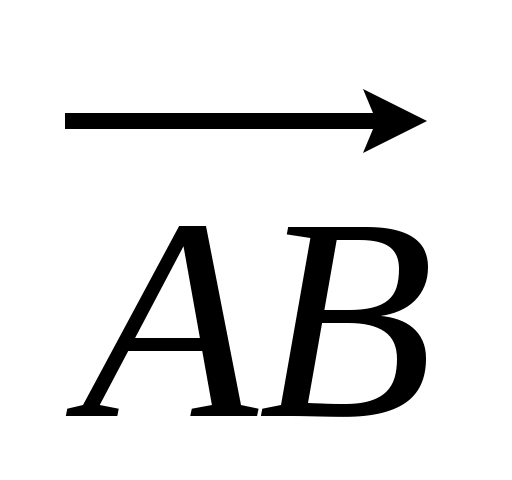 и и  . .
4. Дан тетраэдр DABC. M – точка пересечения медиан АВС,  , причем DH : HA = 1 : 3. Разложите вектор , причем DH : HA = 1 : 3. Разложите вектор
 по векторам по векторам 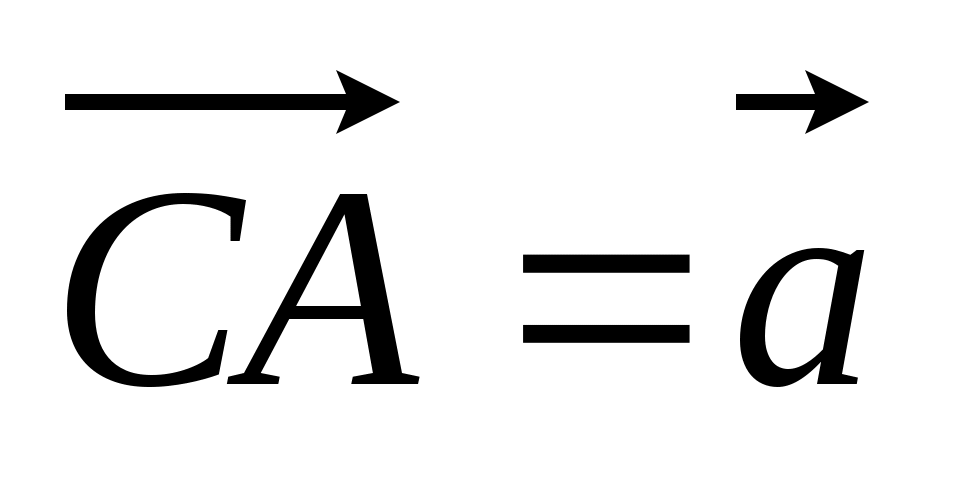 , , 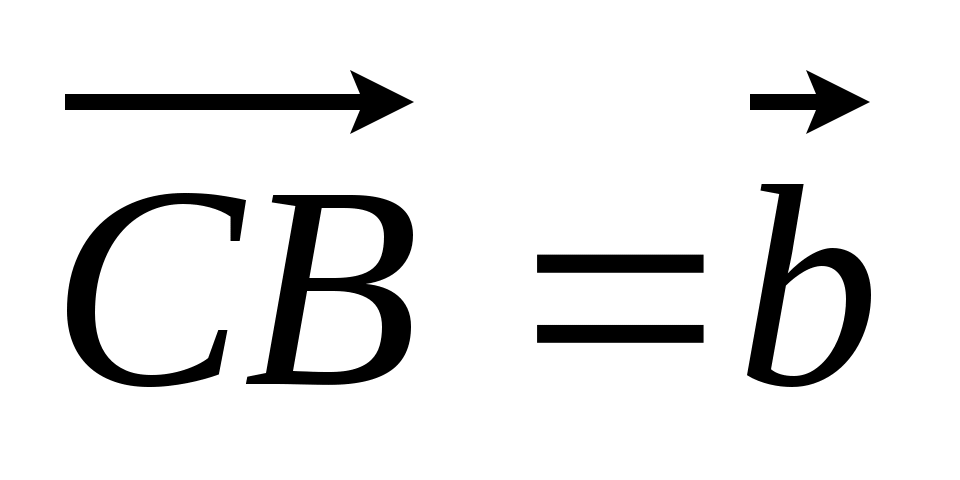 , , 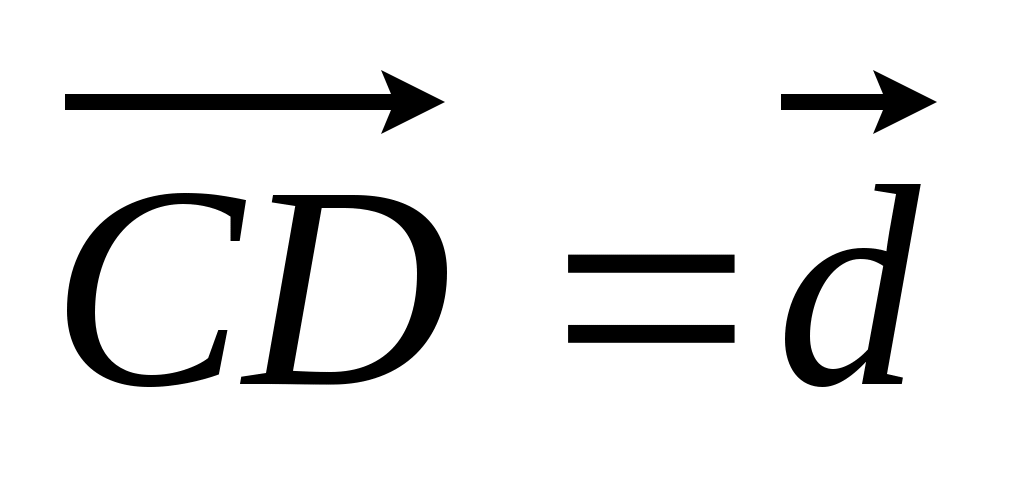 . .
|
Вариант 6
1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные:
1) 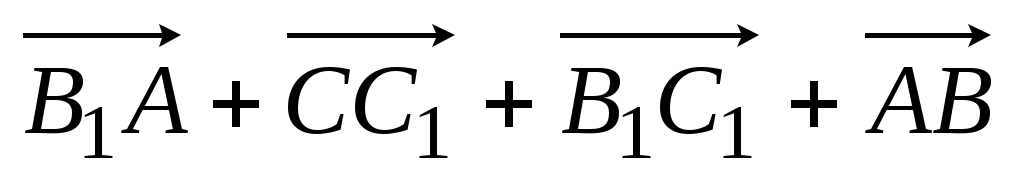 ; 2) ; 2) 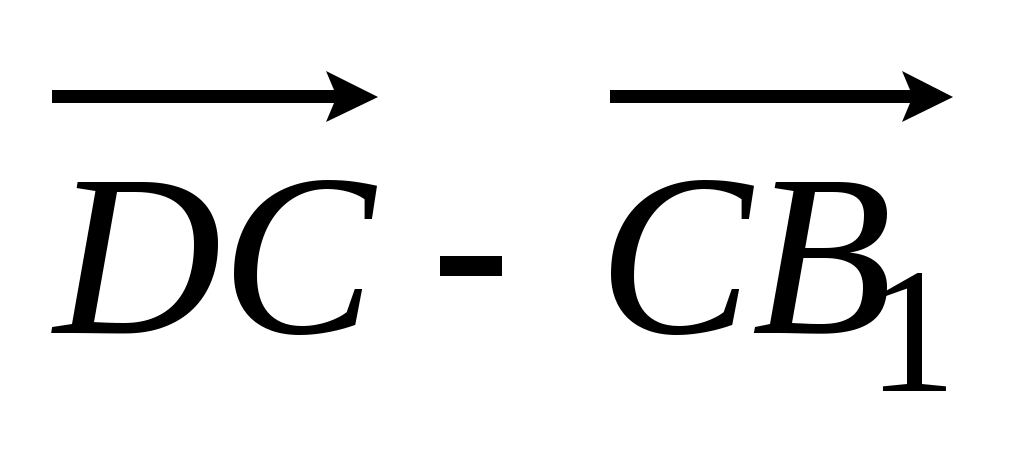 . .
2. Дан параллелепипедABCDA1B1C1D1. Диагонали его грани АВCD пересекаются в точке К. Разложите вектор
 по векторам, по векторам, 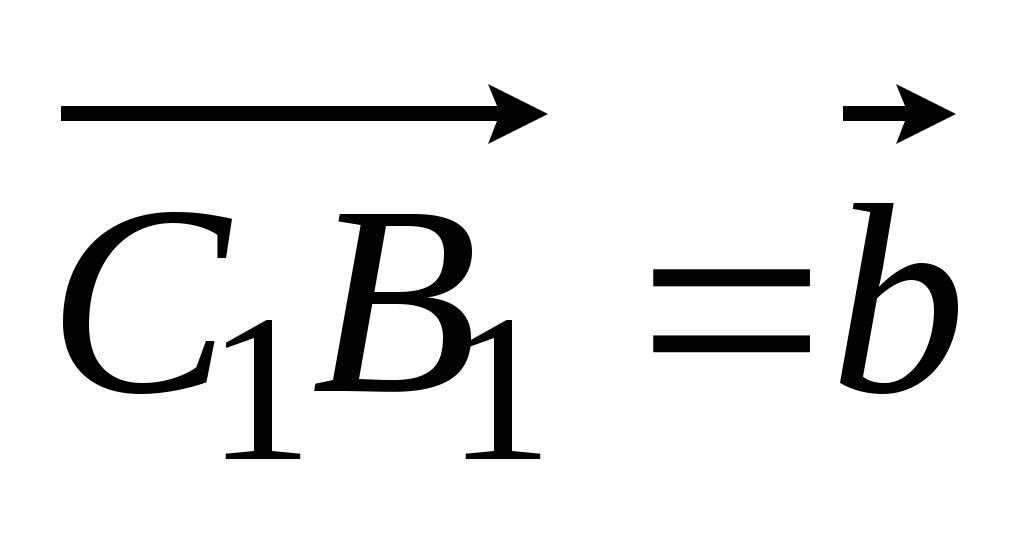 , , 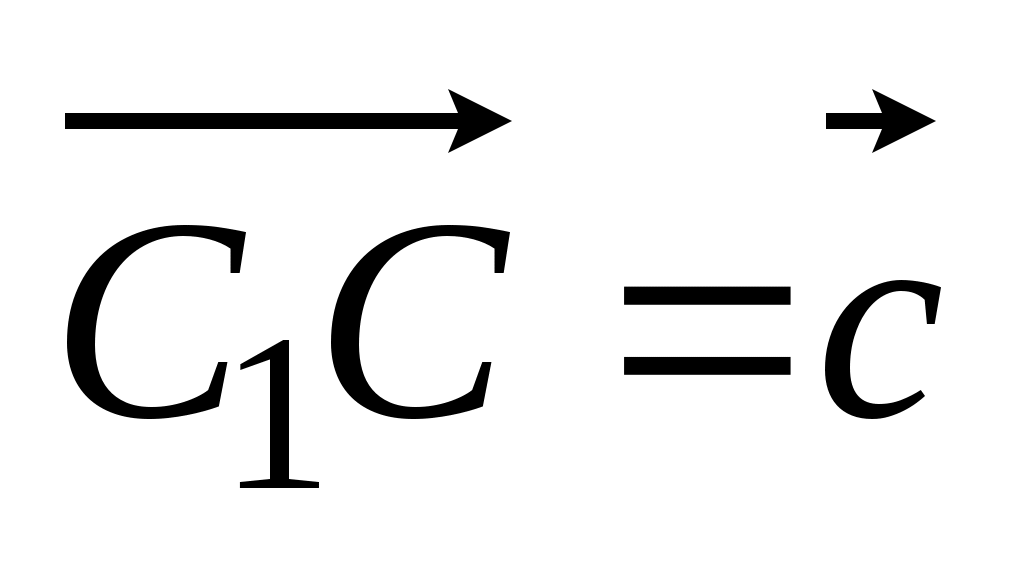 , , 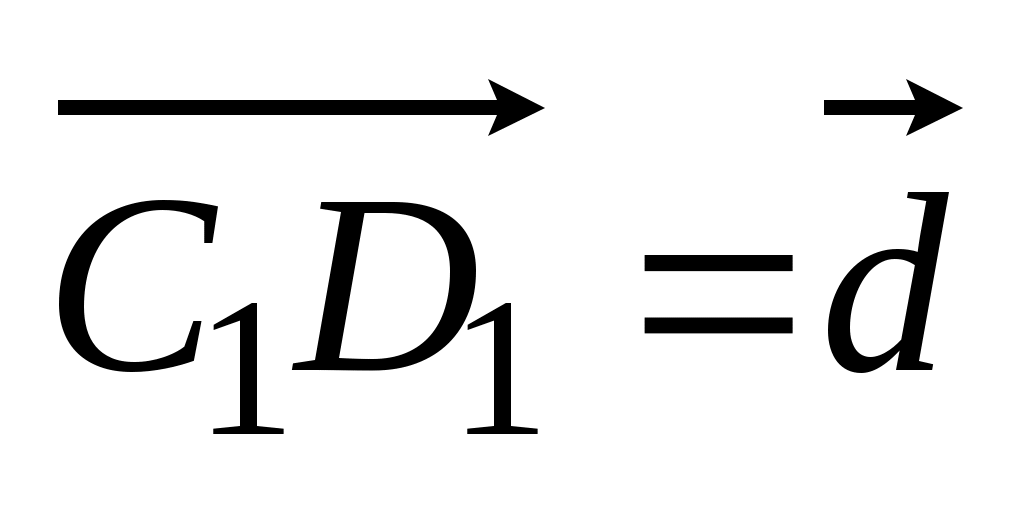 . .
3. В тетраэдреDABC точка Е – середина ребра АD, а точка М – точка пересечения медиан грани BDC. Разложите вектор
 по векторам по векторам 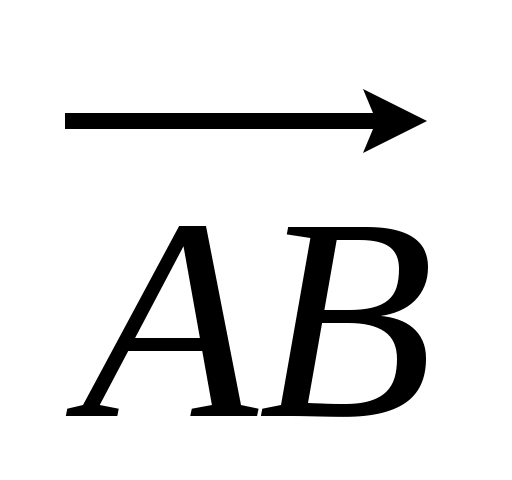 , ,  и и  . .
4. DABC – тетраэдр, медианы треугольника АВС пересекаются в точке К, а 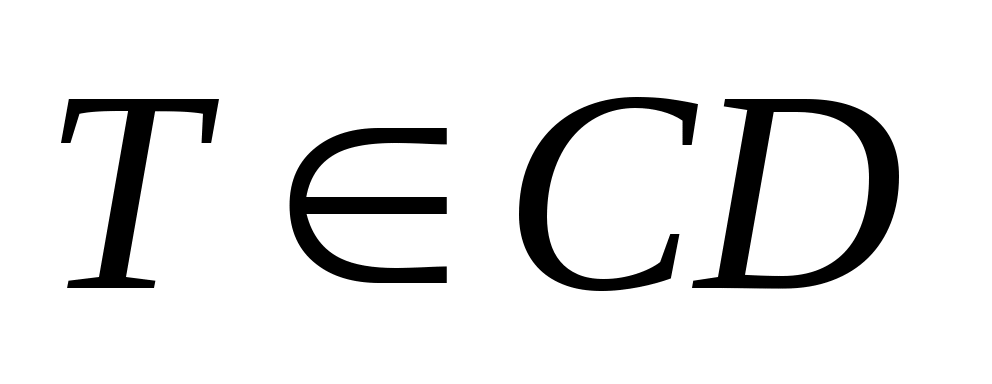 так, что CT : TD = 1 : 5. Разложите вектор так, что CT : TD = 1 : 5. Разложите вектор  по векторам по векторам 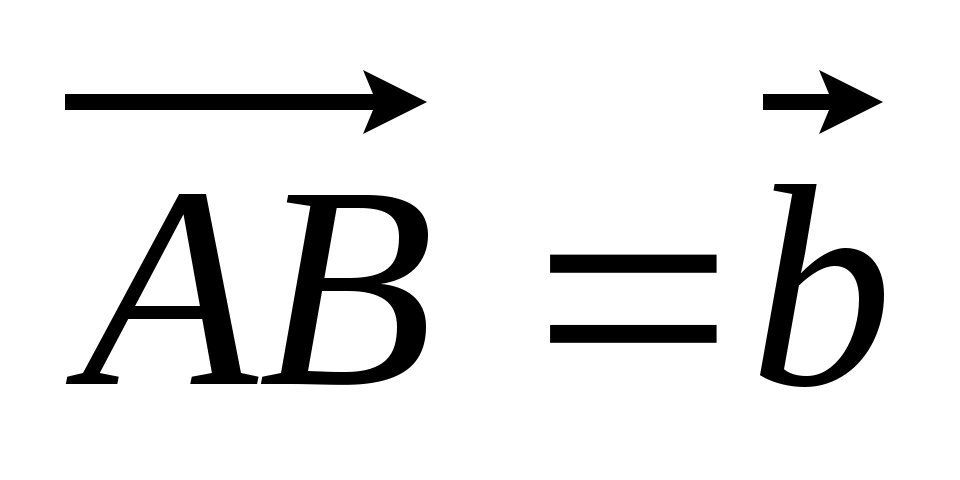 , , 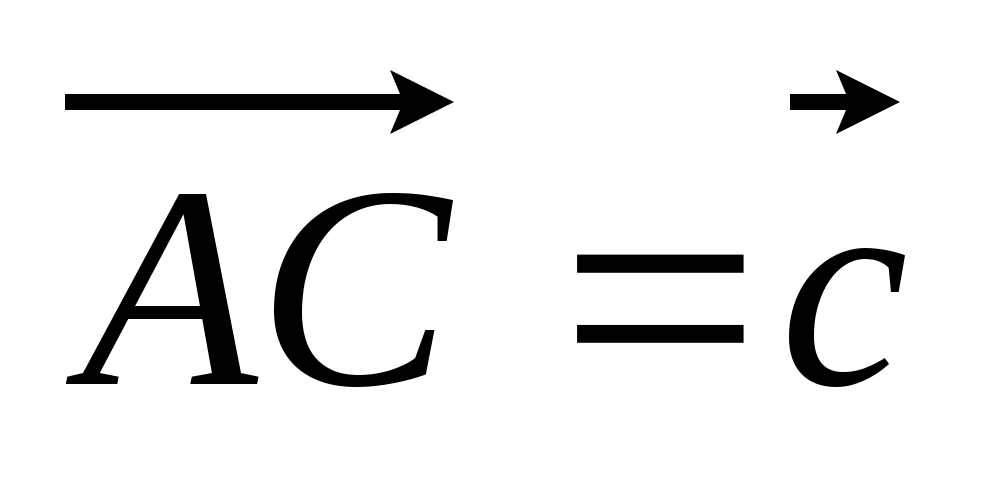 , , 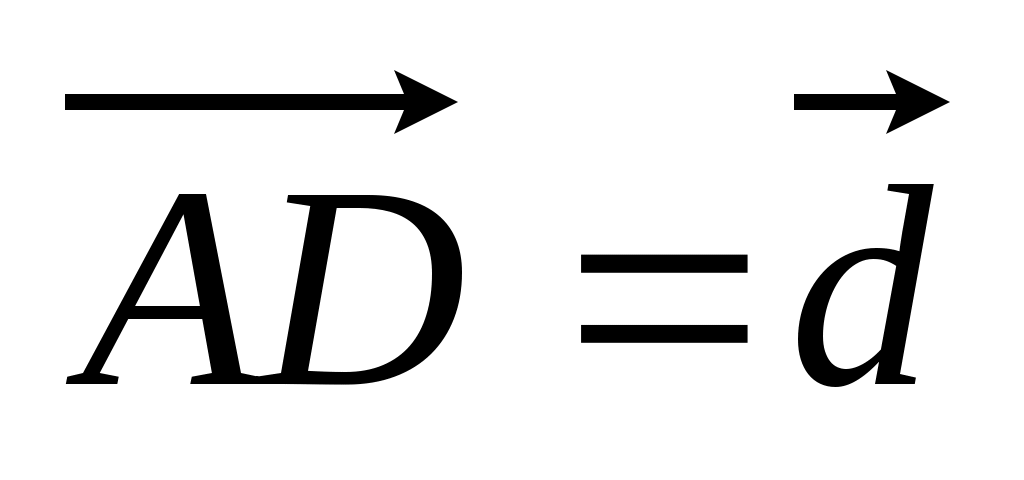 . .
|
Вариант 7
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный:
1) 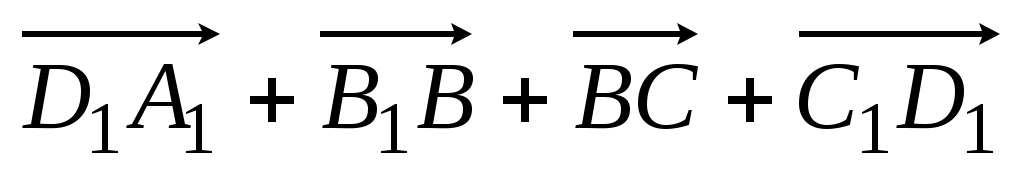 ; 2) ; 2) 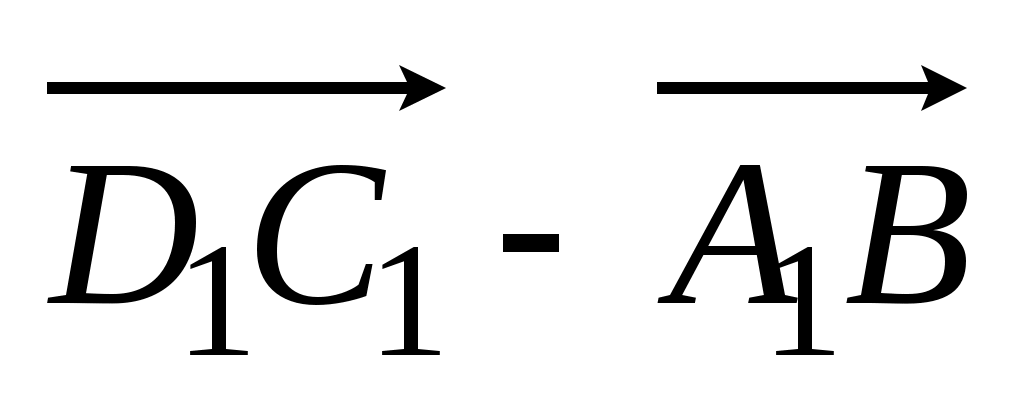 . .
2. ABCDA1B1C1D1 – параллелепипед, точка R – точка пересечения В1D1 и А1C1. Разложите вектор
 по векторам по векторам 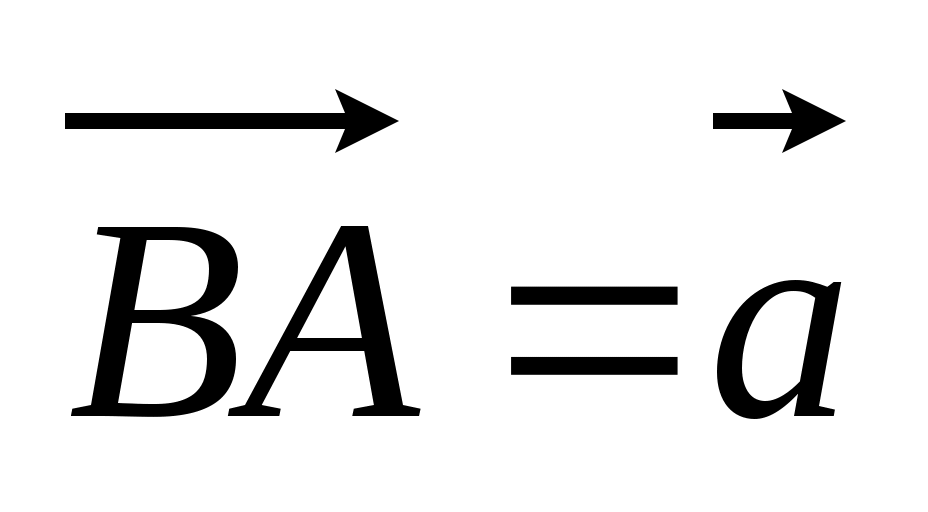 , , 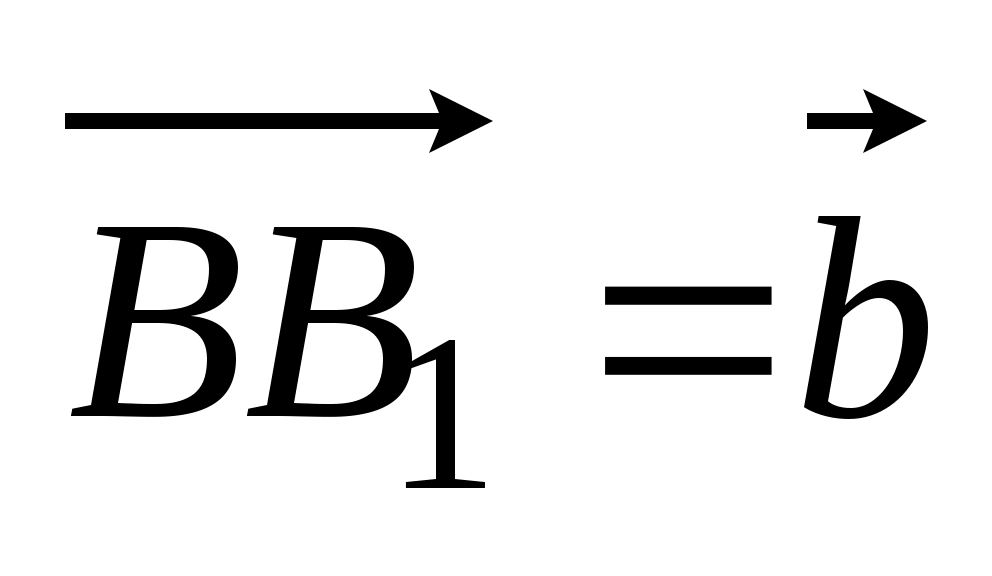 , ,  . .
3. Точка Е – середина ребра DВ тетраэдра DABC, а точка М – точка пересечение медиан грани АBC. Разложите вектор  по векторам по векторам  , ,  и и  . .
4. DABC – тетраэдр, P – точка пересечения медиан грани DВС, а точка М лежит на ВА, причем BM : MA = 7 : 2. Разложите вектор  по векторам по векторам 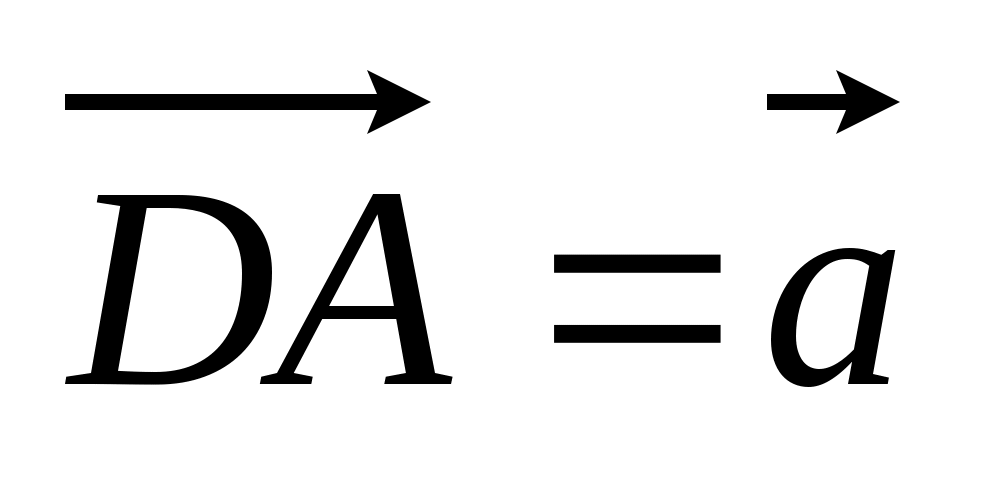 , ,  , ,  . .
|
Вариант 8
1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные:
1)  ; 2) ; 2) 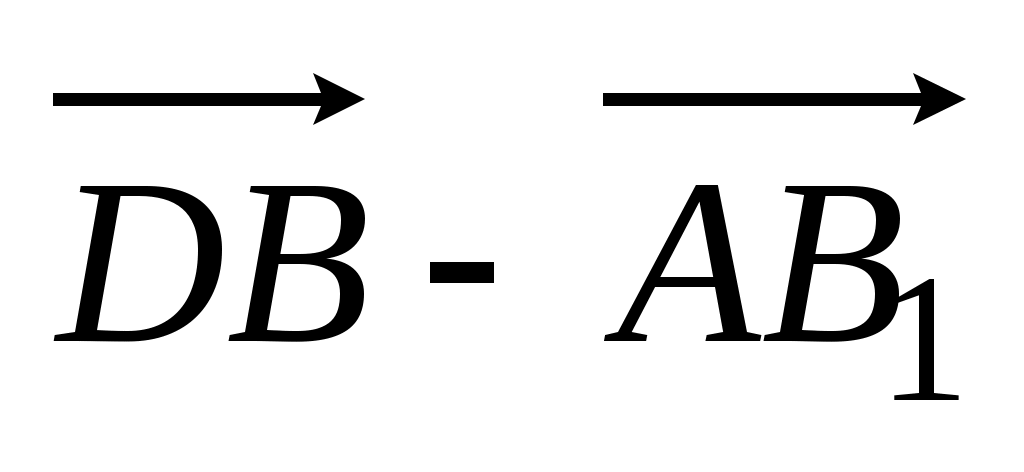 . .
2. Дан параллелепипед ABCDA1B1C1D1. Точка T – точка пересечения отрезков АC и ВD. Разложите вектор
 по векторам по векторам 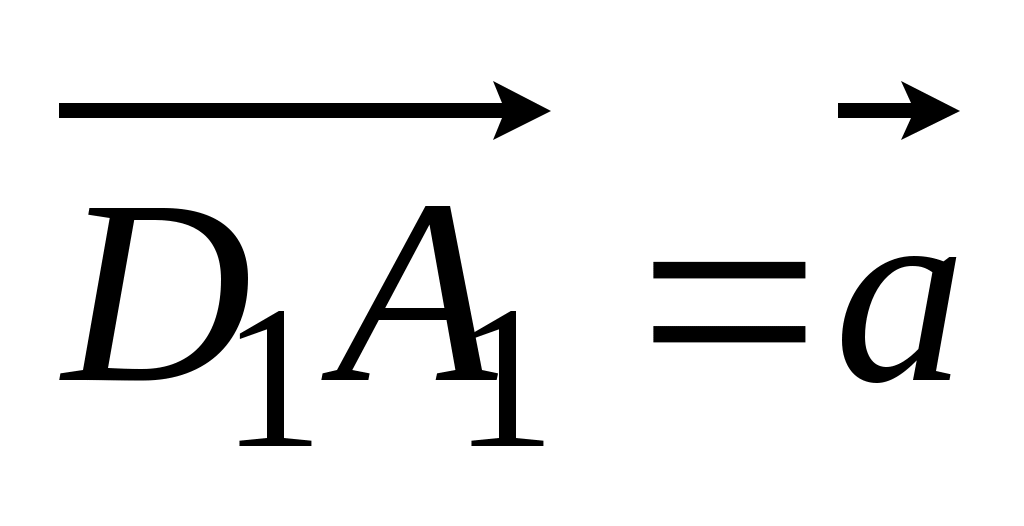 , , 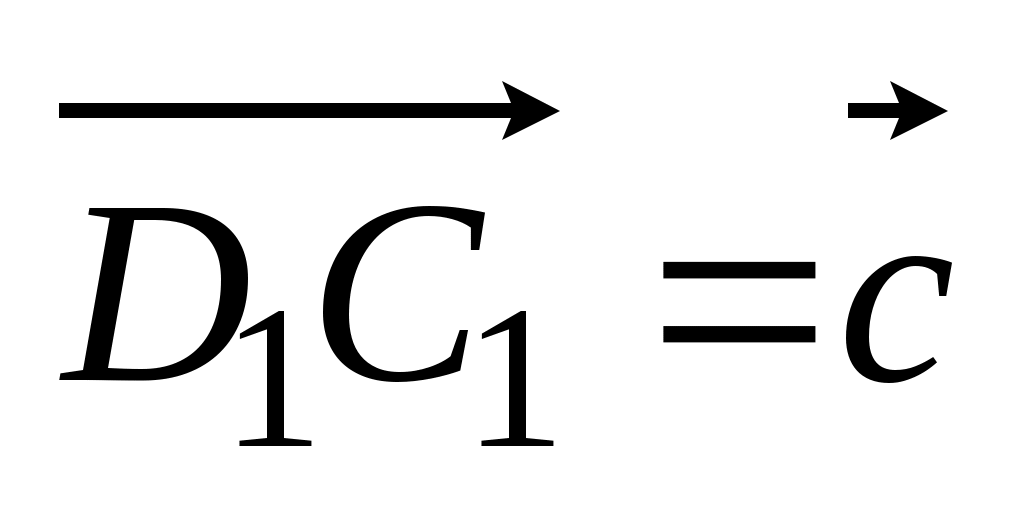 , , 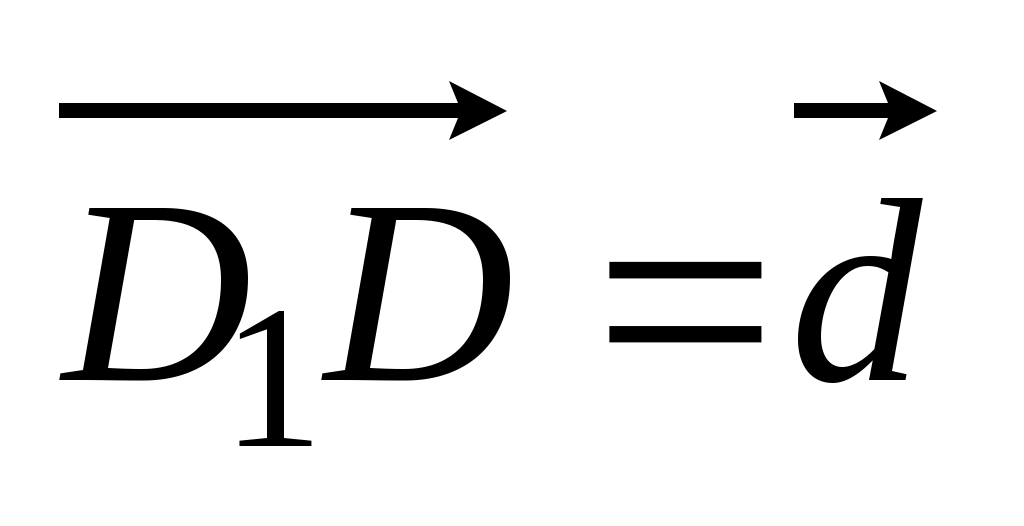 . .
3. В тетраэдре DABC точка М – точка пересечения медиан грани ACD, а точка К – середина ребра АВ. Разложите вектор  по векторам по векторам  , ,  и и  . .
4. Медианы грани АВС тетраэдра DABC пересекаются в точке О, на ребре CD лежит N так, что CN : ND = 2 : 3. Разложите вектор  по векторам по векторам 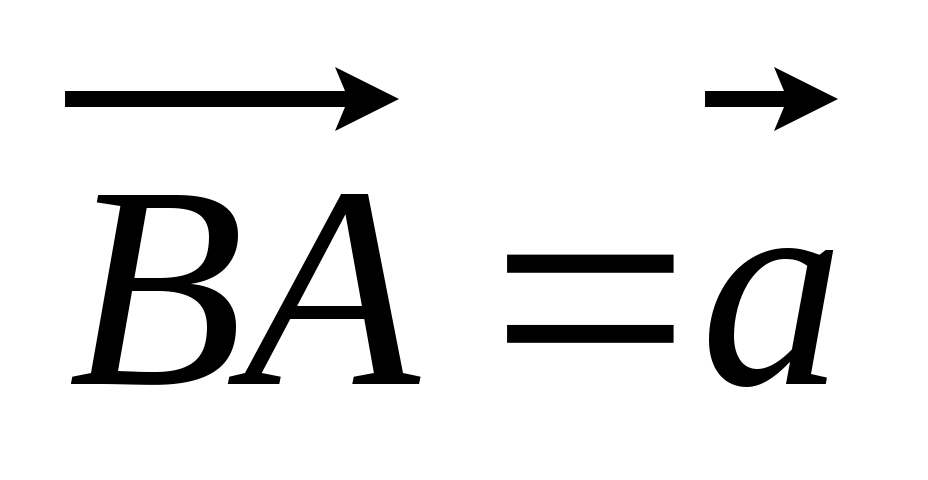 , , 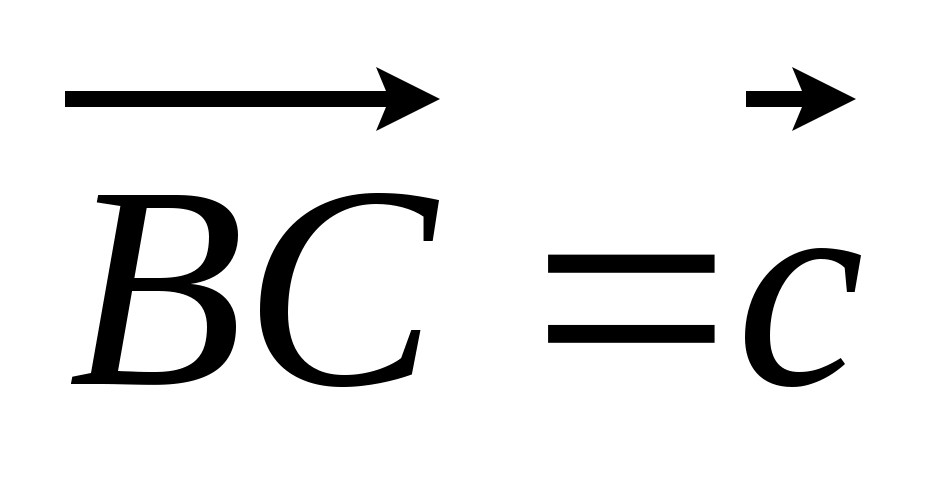 , , 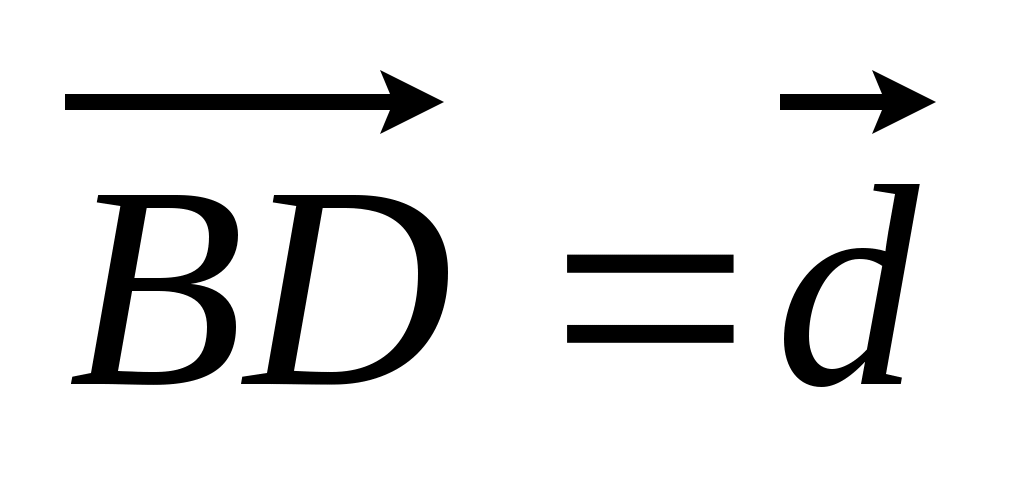 . .
| |
|
|
 Скачать 243.5 Kb.
Скачать 243.5 Kb.