алг 7. Вариант 1 При каких значениях переменной имеет смысл выражение 4(х 3) Сократите дробь Выполните вычитание Упростите выражение
 Скачать 125.4 Kb. Скачать 125.4 Kb.
|
|
Вариант 1 При каких значениях переменной имеет смысл выражение 4/(х – 3) ? Сократите дробь: 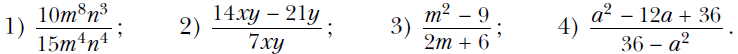 Выполните вычитание: 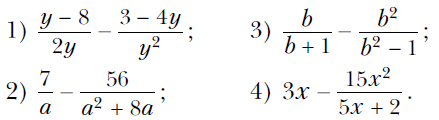 Упростите выражение: ----------------------------------------------------------------------------------------------------------------------------- Вариант 2 При каких значениях переменной имеет смысл выражение 5/(x – 7) ? Сократите дробь: 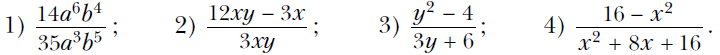 Выполните вычитание: 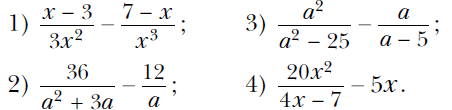 Упростите выражение: ------------------------------------------------------------------------------------------------------------------------------------------ Вариант 3 При каких значениях переменной имеет смысл выражение 3/(y + 7) ? Сократите дробь: 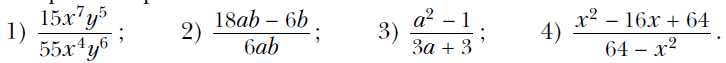 Выполните вычитание: 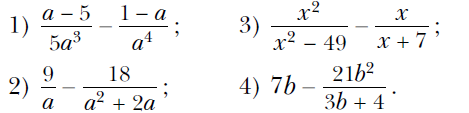 Упростите выражение: 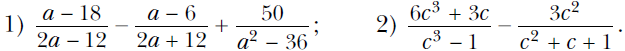 Вариант 1 При каких значениях переменной имеет смысл выражение 4/(х – 3) ? Сократите дробь: 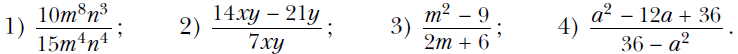 Выполните вычитание: 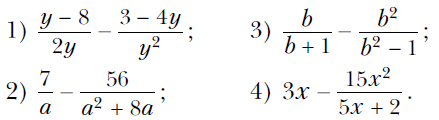 Упростите выражение: ------------------------------------------------------------------------------------------------------------------------------------ Вариант 2 При каких значениях переменной имеет смысл выражение 5/(x – 7) ? Сократите дробь: 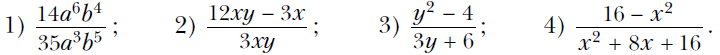 Выполните вычитание: 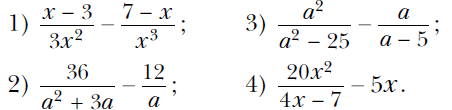 Упростите выражение: ------------------------------------------------------------------------------------------------------------------------------------------ Вариант 3 При каких значениях переменной имеет смысл выражение 3/(y + 7) ? Сократите дробь: 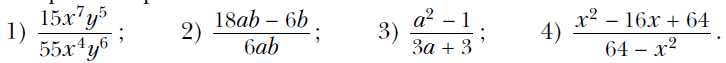 Выполните вычитание: 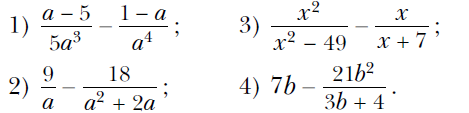 Упростите выражение: 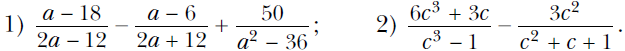 Вариант 4 При каких значениях переменной имеет смысл выражение 5/(x – 2) ? Сократите дробь: 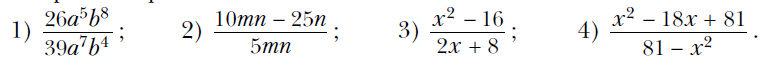 Выполните вычитание: 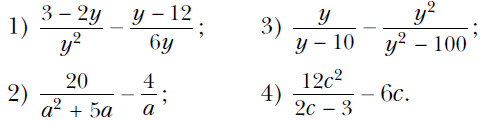 Упростите выражение: 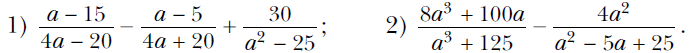 Известно, что (k – 2p)/p = 3. Найдите значение выражения: 1) p/k; 2) (6p – 7k)/p. Постройте график функции у = (x2 – 36)/(x + 6) – (3x2 + 2x)/x. Алгебра. Мерзляк 8 класс Контрольная 1 Ответы на контрольную работу Ответы на Вариант 1 # 1. Выражение имеет смысл при любом х, кроме х = 3. # 2. 1) 2m4/3n; 2) (2x – 3)/x; 3) (m – 3)/2; 4) (6 – a)/(6 + a). # 3. 1) (y2 – 6)/2y2; 2) 7/(a + 8); 3) b/(1 – b2); 4) 6x/(5x + 2). # 4. 1) 1/(a2 – 9); 2) 2b/(b – 2). # 5. 1) a/b = 7; 2) 4 5/7. # 6. y = 3x – 1; x ≠ 0; x ≠ –2. Смотреть РЕШЕНИЕ задачи № 6 в тетради Ответы на Вариант 2 № 1). Выражение имеет смысл при любом x, кроме х = 7. № 2). 1) 2a3/5b; 2) (4y – 1)/y; 3) (y – 2)/3; 4) (4 – x)/(4 + x). № 3). 1) (x2 – 21)/3x3; 2) –12/(a + 3); 3) 5a/(25 – a2); 4) 35x/(4x – 7). № 4). 1) 3/(a2 – 16); 2) 4a/(a + 3). № 5). 1) y/x = 1/3; 2) 10. № 6). y = –x – 1; x ≠ 0; x ≠ 5. Смотреть РЕШЕНИЕ задачи № 6 в тетради Ответы на Вариант 3 № 1. Выражение имеет смысл при любом y, кроме у = –7. № 2. 1) 3x3/11y; 2) (3a – 1)/a; 3) (a – 1)/3; 4) (8 – x)/(8 + x). № 3. 1) (a2 – 5)/5a4; 2) 9/(a + 2); 3) 7x/(x2 – 49); 4) 28b/(3b + 4). № 4. 1) 22/(36 – a2); 2) 3c/(c – 1). № 5. 1) m/n = –1; 2) 6. № 6. y = x + 2; x ≠ 0; x ≠ 3. Смотреть РЕШЕНИЕ задачи № 6 в тетради Ответы на Вариант 4 № 1. Выражение имеет смысл при любом x, кроме х = 2. № 2. 1) 2b4/3a2; 2) (2m – 5)/m; 3) (x – 4)/2; 4) (9 – x)/(9 + x). № 3. 1) (18 – y2)/6y2; 2) –4/(a + 5); 3) 10y/(y2 – 100); 4) 18c/(2c – 3). № 4. 1) 5/(a2 – 25); 2) 4a/(a + 5). № 5. 1) p/k = 1/5; 2) –29. № 6. y = –2x – 8; x ≠ 0; x ≠ –6. Смотреть РЕШЕНИЕ задачи № 6 в тетради Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ) |
