опксис. Вариант 12. Вариант 12 Исходные данные
 Скачать 0.67 Mb.
|
|
Вариант 12 Исходные данные: Найти маршруты наименьшей стоимости, связывающие все хосты сети друг с другом, используя алгоритм Флойда-Уоршелла. Стоимости канальных участков заданы в таблице 1. Трафик: речь Алгоритм: Флойда-Уоршелла Топология: 2  Рис.1 – Топология сети Таблица 1 Стоимости канальных участков 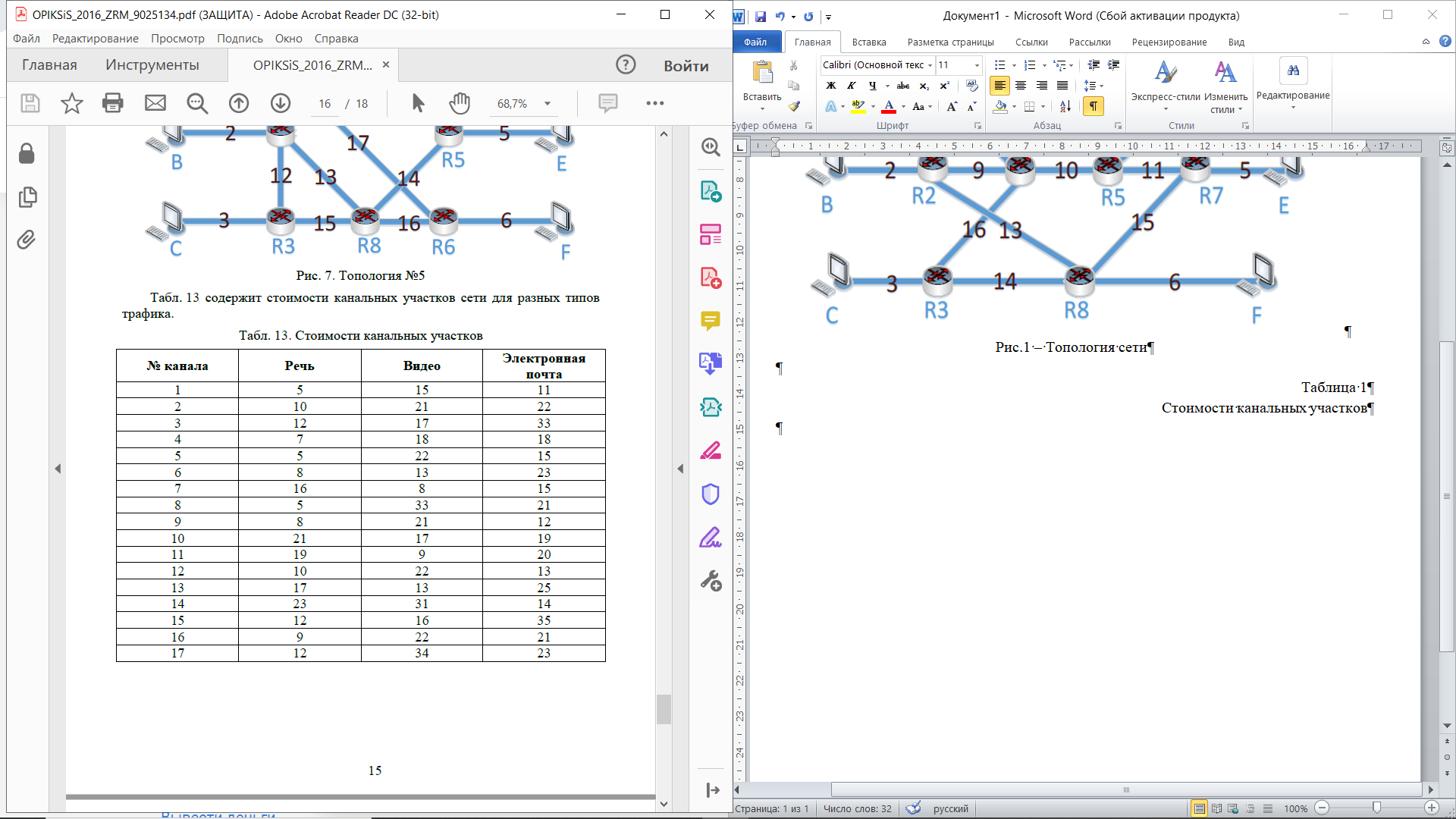 Теоретическое описание Маршрутизация — процесс определения маршрута данных в сетях связи. Алгоритм Флойда-Уоршелла Задача заключается в поиске таблицы расстояний для каждой пары вершин. Алгоритм Флойда-Уоршелла предполагает построение данной таблицы путем получения последовательностей:  где матрица кратчайших путей от узла i к узлу j, в которых промежуточные вершины не могут иметь номера превышающие k, N – количество узлов в сети. Последняя матрица 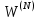 содержит длины всех кратчайших путей.Формальное описание алгоритма: N – множество узлов сети D – весовая матрица, dii=0, dij=∞, если нет звена между i-м и j-м узлами, dij>0, если есть звено между i-м и j-м узлами k – номер промежуточного узла на маршруте  – стоимость канала от узла i к узлу j, с учетом промежуточного узлаАлгоритм: Инициализация 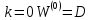 Модификация Для каждого последующего  определяются стоимости маршрутов между парами узлов следующим образом: Завершение Алгоритм завершается при k=N Выполнение работы Задача заключается в том, чтобы определить маршруты с наименьшей стоимостью для всех хостов сети (A, B, C, D, E, F). Поскольку каждый хост подключен к одному роутеру через единственный канал, имеет смысл сначала определить стоимости маршрутов для маршрутизаторов (R1, R2, R3, R4, R5, R6), а затем добавить к ним стоимости каналов к хостам. Будем использовать топологию на рис.2 с указанной стоимостью канальных участков из таблицы 1.  Рис.2 – Вспомогательная топология сети При нахождении маршрутов с наименьшей стоимостью будем использовать топологию, приведенную на рис.2. Весовая матрица содержит стоимости канальных участков между всеми парами узлов сети: 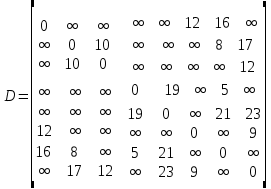 Таблицы 2-8 содержат итерации k=0, 1, 2, …, N алгоритма Флойда-Уоршелла при построении кратчайших путей для каждой пары узлов. При k=0 таблица стоимостей маршрутов полностью соответствует весовой матрице. Таблица 2 Маршруты 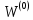 с промежуточным узлом k=0
Таблица 3 Маршруты 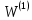 с промежуточным узлом k=1
|