Задачи по малекулярке. задачи малекулярка. Вариант 13. А. Законы идеальных газов
 Скачать 21.26 Kb. Скачать 21.26 Kb.
|
|
ВАРИАНТ 13. А. Законы идеальных газов. А 13. Какой объем Vзанимает при нормальных условиях смесь газов - азота массой т и гелия массой т2? Решение задачи:
V=V1+V2, V1= 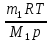 , V2= , V2=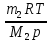 → →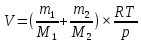  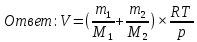 Б. Элементы статистической физики. Б 13. Найти изменение высоты h, соответствующее изменению давления на p, в двух случаях: 1) вблизи поверхности Земли, где температура Т1, давление p1; 2) на некоторой высоте, где температура Т2, давление p2.
P = P0e (- mgh/kT) Ln 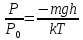 → (Ln → (Ln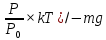 =h → =h →Ответ: 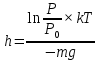 В. Физические основы термодинамики. В 13. Кислород массой m занимает объём V1 и находится под давлением P1. Газ был нагрет сначала при постоянном давлении до объёма V2, а затем при постоянном объёме до давления P2. Определить: 1) изменение внутренней энергии газа; 2) совершённую им работу; 3) количество теплоты,переданное газу.
1) ∆U= 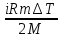 , Для нахождение , Для нахождение 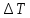 → pV=mRT/M→ → pV=mRT/M→T=pVM/mR→ ∆U= 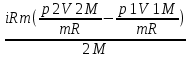 2) A= 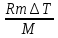 → A= → A=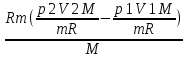 3) Q=∆U+A → Q= 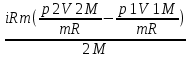 + +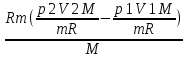 Г. Первое начало термодинамики. Циклы. Г 13. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причём наибольшее давление газа в два раза больше наименьшего, а наибольший объём в четыре раза больше наименьшего. Определить термический КПД цикла.
A=2P⋅3V−P⋅3V=3PV PV=nRT T1=PV/nR, T2=2PV/n, T3=2P⋅4V/nR, T4=P⋅4V/nR T2−T1=PV/nR, T3−T2=6PV/nR Изохорное нагревание: Q1=nCv(T2−T1)=CvPV/R Изобарное нагревание: Q2=nCp6PV/nR=6CpPV/R При изохоре: Cv=3R При изобаре: Cp=4R → Q=Q1+Q2=3PV+24PV=27PV→ η=A/Q=3PV/27PV=1/9 Д. Энтропия. Д 13. Найти изменение энтропии при изобарном расширении азота массой m от объема V1 до объема V2.
ΔS= 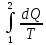 Cp=(i+2)R/i, dQ=(m/M)⋅Cp⋅dT → ΔS= 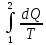 = =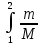 ⋅Cp⋅dT/T= ⋅Cp⋅dT/T=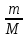 * *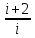 ⋅R⋅ ⋅R⋅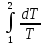 = =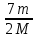 p=const, V1/T1=V2 /T2, T2 /T1=V2 /V1 ΔS= 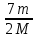 ⋅R⋅ln(V2/V1) ⋅R⋅ln(V2/V1)Ответ: ΔS= 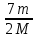 ⋅R⋅ln(V2/V1) ⋅R⋅ln(V2/V1) |
