Вариант №14 профильного ЕГЭ по математике 2023. Вариант 14 - 2023. Вариант 14 2023
 Скачать 227.79 Kb. Скачать 227.79 Kb.
|
|
Вариант №14 − 2023 1 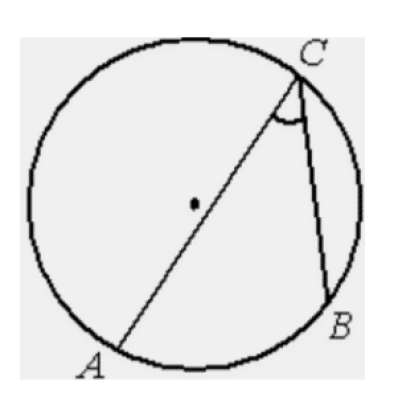 . На окружности отмечены точки . На окружности отмечены точки  , ,  и и  . Дуга окружности . Дуга окружности  , не содержащая точку , не содержащая точку  , составляет 200°. Дуга окружности , составляет 200°. Дуга окружности 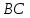 , не содержащая точку , не содержащая точку 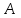 , составляет 80°. Найдите вписанный угол , составляет 80°. Найдите вписанный угол 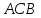 . Ответ дайте в градусах. . Ответ дайте в градусах.2  . Найдите объём многогранника, вершинами которого являются точки . Найдите объём многогранника, вершинами которого являются точки  , , 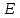 , , 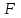 , , 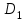 , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы 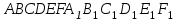 , площадь основания которой равна 8, а боковое ребро равно 9. , площадь основания которой равна 8, а боковое ребро равно 9.3. В классе 35 человек, среди них у шестерых в году пятерки по теории вероятностей, а у восьмерых в году пятерки по физике. При этом нет никого, у кого были бы пятерки по этим двум предметам. Найдите вероятность того, что случайно выбранный ученик класса имеет пятерку по одному из этих двух предметов. 4.В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,5. Найдите вероятность, что в случайный момент времени хотя бы один продавец окажется свободным (клиенты заходят в магазин независимо друг от друга). 5. Найдите корень уравнения. В ответе запишите наибольший отрицательный корень.  . .6 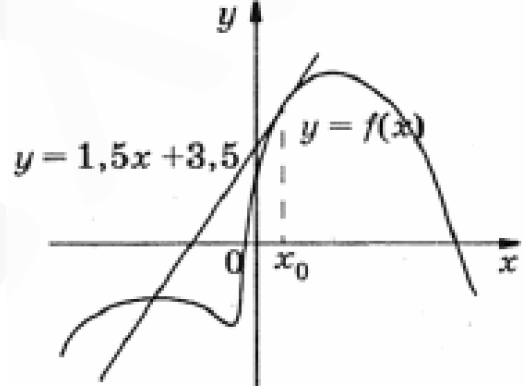 . Найдите значение выражения . Найдите значение выражения  . .7. На рисунке изображён график функции  и касательная к этому графику, проведённая в точке и касательная к этому графику, проведённая в точке  . Уравнение касательной дано на рисунке. Найдите значение производной функции . Уравнение касательной дано на рисунке. Найдите значение производной функции 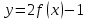 в точке в точке  . .8. Мяч бросили под углом  к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле 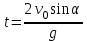 . При каком наименьшем значении угла . При каком наименьшем значении угла  (в градусах) время полёта будет не меньше 2,1 секунды, если мяч бросают с начальной скоростью (в градусах) время полёта будет не меньше 2,1 секунды, если мяч бросают с начальной скоростью  м/с? Считайте, что ускорение свободного падения м/с? Считайте, что ускорение свободного падения  м/с2. м/с2.9. Первый и второй насосы наполняют бассейн за 10 минут, второй и третий − за 14 минут, а первый и третий − за 15 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе? 1 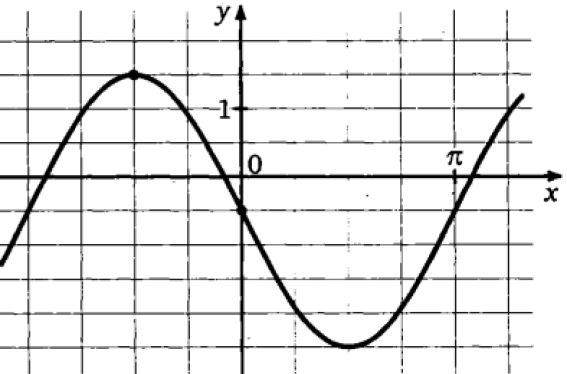 0. На рисунке изображён график функции 0. На рисунке изображён график функции  . Найдите значение выражения . Найдите значение выражения  . .11. Найдите наименьшее значение функции 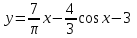 на отрезке на отрезке  . .========================================================== 12. а) Решите уравнение 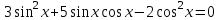 . .б) Найдите все корни этого уравнения, принадлежащие отрезку 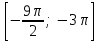 . .13. В основании правильной треугольной пирамиды  лежит треугольник лежит треугольник 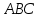 со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре  отмечена точка отмечена точка  так, что так, что 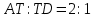 . Через точку . Через точку  параллельно прямым параллельно прямым  и и 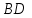 проведена плоскость. проведена плоскость.а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником. б) Найдите площадь сечения. 14. Решите неравенство  . .15.По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 125 миллионов, а за четыре года станет больше 200 миллионов рублей. 16. Диагонали трапеции перпендикулярны боковым сторонам. а) Докажите, что трапеция равнобедренная. б) Найдите площадь трапеции, если её основания равны 10 и 26. 17−(1). Найдите все значения 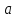 , при каждом из которых уравнение , при каждом из которых уравнение 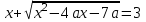 имеет хотя бы один корень. имеет хотя бы один корень.17−(2).Найдите все значения параметра 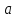 , при каждом из которых на интервале (1; 2) существует хотя бы одно число , при каждом из которых на интервале (1; 2) существует хотя бы одно число  , неудовлетворяющее неравенству , неудовлетворяющее неравенству  . .18. Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 792 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию? |
