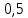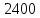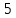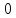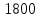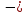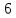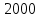Графическое решение задач линейного программирования. Заказ №2603 (07.01.2023) Вариант 5. Вариант 5 Задание 1
 Скачать 458.54 Kb. Скачать 458.54 Kb.
|
|
Вариант 5 Задание 1 Предприятие изготавливает два вида продукции – П1 и П2, которая поступает в оптовую продажу. Для производства продукции используют два вида сырья – 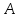 и и 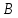 . Максимально возможные запасы сырья в сутки составляют . Максимально возможные запасы сырья в сутки составляют 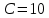 и и 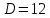 единиц соответственно. Расход сырья на единицу продукции вида П1 и П2 дан в таблице. единиц соответственно. Расход сырья на единицу продукции вида П1 и П2 дан в таблице.
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 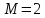 единицу. Кроме того, известно, что спрос на продукцию П2 никогда не превышает единицу. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 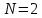 единиц в сутки. Оптовые цены единицы продукции равны: единиц в сутки. Оптовые цены единицы продукции равны: 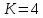 денежных единиц для П1 и денежных единиц для П1 и 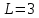 денежных единиц для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Определить предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение? На сколько можно снизить запас недефицитного ресурса при сохранении полученного оптимального решения? Какому из ресурсов следует отдать предпочтение при вложении дополнительных средств? Каков диапазон изменения цен на продукцию, при котором не происходит изменения оптимального решения? Решение провести графическим методом денежных единиц для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Определить предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение? На сколько можно снизить запас недефицитного ресурса при сохранении полученного оптимального решения? Какому из ресурсов следует отдать предпочтение при вложении дополнительных средств? Каков диапазон изменения цен на продукцию, при котором не происходит изменения оптимального решения? Решение провести графическим методомРешение: Введем переменные:  – объем производства продукции П1, ед. – объем производства продукции П1, ед.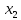 – объем производства продукции П2, ед. – объем производства продукции П2, ед.Целевая функция, отражающая доход предприятия, будет иметь вид: 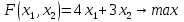 Ограничения: 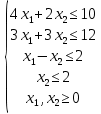 Изобразим область допустимых планов:           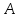 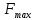 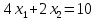 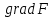 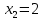 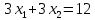 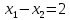 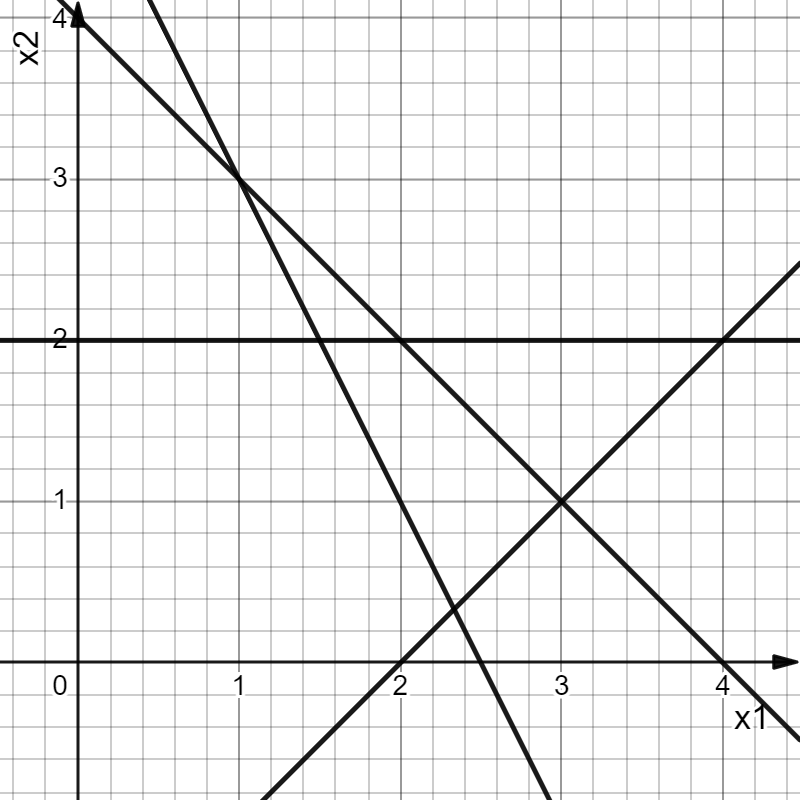 Построим линии уровня целевой функции 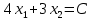 и будем смещать их в направлении градиента целевой функции, пока не достигнем границы области допустимых планов. и будем смещать их в направлении градиента целевой функции, пока не достигнем границы области допустимых планов.Найдем координаты точки 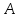 : :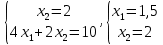 Получим оптимальный план и оптимум задачи: 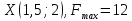 Определим допустимое увеличение запасов дефицитного ресурса 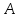 . Для этого сместим график линии, описывающей этот ресурс, так, чтобы значение целевой функции выросло: . Для этого сместим график линии, описывающей этот ресурс, так, чтобы значение целевой функции выросло:            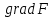 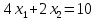 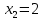 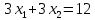 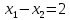 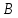 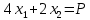 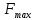  Новая линия будет проходить через точку 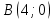 . Значит: . Значит: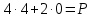 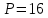 Получим, что запасы ресурса 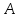 можно увеличить на 6 единиц, оптимальный план и оптимум при таком изменении составят: можно увеличить на 6 единиц, оптимальный план и оптимум при таком изменении составят: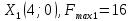 Определим, на сколько можно снизить запас недефицитного ресурса 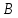 при сохранении полученного оптимального решения. Для этого сместим график линии, описывающей этот ресурс, так, чтобы он проходил через точку при сохранении полученного оптимального решения. Для этого сместим график линии, описывающей этот ресурс, так, чтобы он проходил через точку 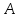 : :            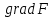 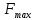 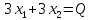 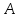 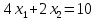 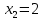 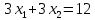 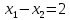  Новая линия будет проходить через точку 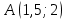 . Значит: . Значит: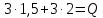  Получим, что запасы ресурса 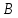 можно уменьшить на 1,5 единицы, оптимальный план и оптимум при таком изменении останутся прежними. можно уменьшить на 1,5 единицы, оптимальный план и оптимум при таком изменении останутся прежними.При вложении дополнительных средств необходимо отдать предпочтение дефицитному ресурсу 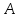 , так как при увеличении его запасов вырастет объем производства, а следовательно, и прибыль предприятия. , так как при увеличении его запасов вырастет объем производства, а следовательно, и прибыль предприятия.Определим диапазон изменения цен на продукцию, при котором не происходит изменения оптимального решения. Рассмотрим продукцию П1. При увеличении цены на продукт П1 крайнее положение будет достигаться тогда, когда линии уровня будут параллельны прямой 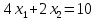 . Пусть . Пусть 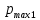 – верхняя граница цены на продукт П1. Тогда справедливо равенство: – верхняя граница цены на продукт П1. Тогда справедливо равенство: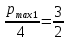 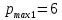 При уменьшении цены на продукт П1 крайнее положение будет достигаться тогда, когда линии уровня будут параллельны прямой 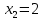 . Пусть . Пусть 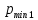 – нижняя граница цены на продукт П1. Тогда справедливо равенство: – нижняя граница цены на продукт П1. Тогда справедливо равенство: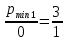 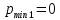 Получим, что цена на продукт П1 может меняться в диапазоне от 0 до 6 денежных единиц. Рассмотрим продукцию П2. При увеличении цены на продукт П2 крайнее положение будет достигаться тогда, когда линии уровня будут параллельны прямой 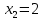 . Пусть . Пусть 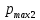 – верхняя граница цены на продукт П2. Тогда справедливо равенство: – верхняя граница цены на продукт П2. Тогда справедливо равенство: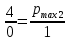 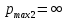 При уменьшении цены на продукт П2 крайнее положение будет достигаться тогда, когда линии уровня будут параллельны прямой 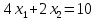 . Пусть . Пусть 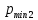 – нижняя граница цены на продукт П2. Тогда справедливо равенство: – нижняя граница цены на продукт П2. Тогда справедливо равенство: 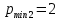 Получим, что цена на продукт П2 может меняться в диапазоне от 2 денежных единиц (верхней границы нет). Выводы: Для достижения максимальной прибыли от реализации продукции необходимо произвести 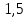 единицы продукта П1 и 2 единицы продукта П2. Прибыль при этом составит 12 денежных единиц. единицы продукта П1 и 2 единицы продукта П2. Прибыль при этом составит 12 денежных единиц.При увеличении запасов ресурса 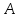 на 6 единиц, можно будет произвести 4 единицы продукции П1 и не производить продукцию П2. Прибыль при этом вырастет и составит 16 денежных единиц. на 6 единиц, можно будет произвести 4 единицы продукции П1 и не производить продукцию П2. Прибыль при этом вырастет и составит 16 денежных единиц.При уменьшении запасов ресурса 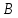 на 1,5 единицы план производства, а соответственно, и прибыль не изменятся на 1,5 единицы план производства, а соответственно, и прибыль не изменятсяПри установлении цены на единицу продукции П1 до 6 денежных единиц, а на единицу продукции П2 от 2 денежных единиц, план производства, а соответственно, и прибыль не изменятся. Задание 2 Решить с помощью MS Excel задачу. Для приготовления четырех видов продукции (A, B, C, D) используют три вида сырья. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице. Определить план выпуска продукции из условия максимизации его стоимости. Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов. Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения. Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно? На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции? На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли? Определите изменение стоимости продукции и количество выпускаемых изделий при увеличении второго вида сырья на 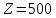 единиц. единиц. Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде в-строки  . . Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план. На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным? На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?
Решение: Введем переменные:  – объем произведенной продукции вида – объем произведенной продукции вида 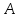 , ед. , ед.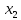 – объем произведенной продукции вида – объем произведенной продукции вида 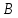 , ед. , ед.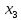 – объем произведенной продукции вида – объем произведенной продукции вида 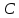 , ед. , ед.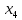 – объем произведенной продукции вида – объем произведенной продукции вида 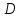 , ед. , ед.Целевая функция примет вид: 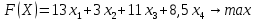 Ограничения: 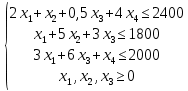 Отчет о результатаx: 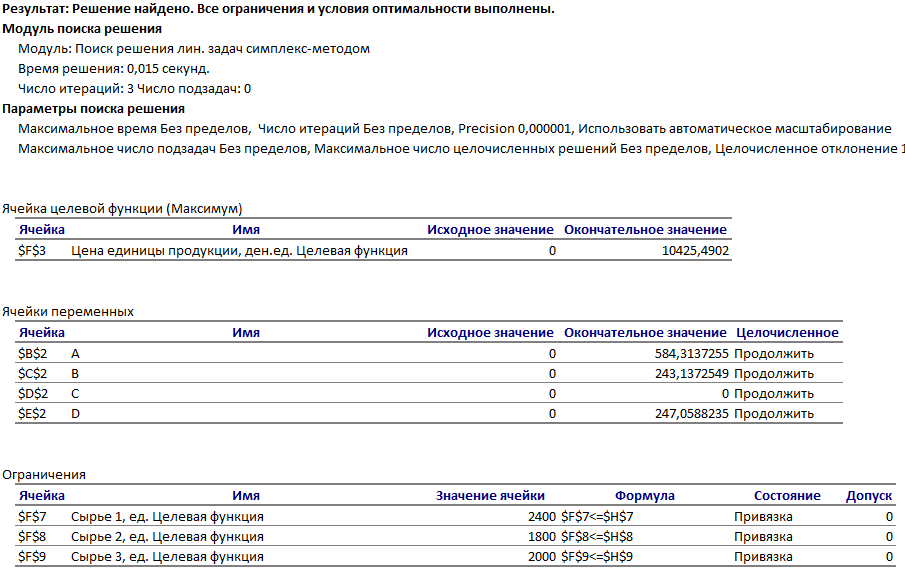 Отчет об устойчивости 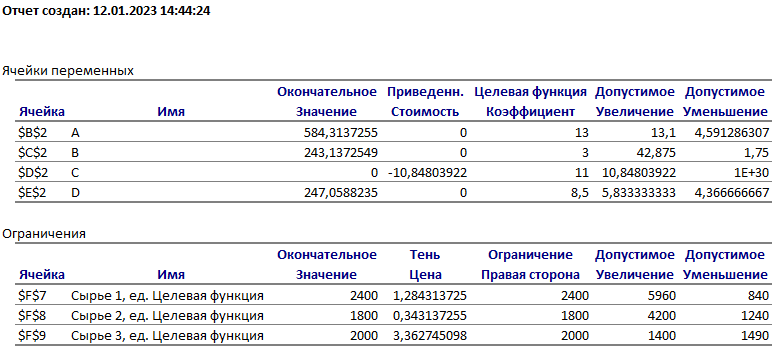 Отчет о пределах 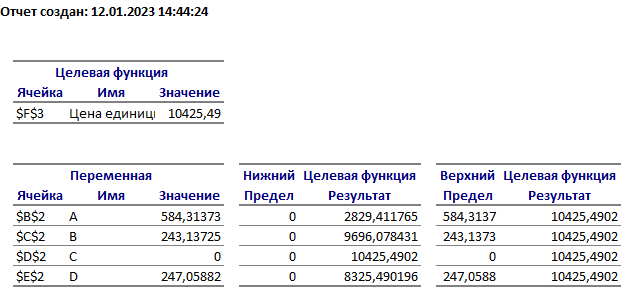 Определить план выпуска продукции из условия максимизации его стоимости. Получим, что для достижения максимальной прибыли, необходимо произвести 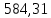 единиц продукции единиц продукции 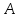 , , 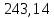 единиц продукции единиц продукции 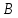 , продукцию типа , продукцию типа 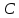 не производить вовсе и не производить вовсе и 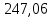 единиц продукции единиц продукции 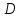 . Прибыль при таком производстве составит . Прибыль при таком производстве составит 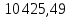 денежных единиц. денежных единиц.Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов. Исходя из отчета по результатам видим, что все ресурсы являются связными. Это значит, что все ресурсы были использованы, то есть все ресурсы являются дефицитными. Поэтому любое снижение запаса ресурса будет приводить к уменьшению прибыли. Теневая цена указывает на рост целевой функции при росте запасов сырья. Наиболее ценным является сырье 3, так как теневая цена у него наибольшая.  Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения. Максимальный интервал изменения запасов: 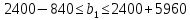 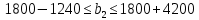 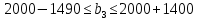 Получим: 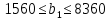 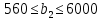 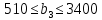 Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно? Найдем себестоимости продукта 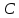 : :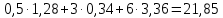 Так как себестоимость продукта 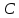 больше цены 11 на 10,85, то производство продукта больше цены 11 на 10,85, то производство продукта 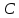 является нерентабельным. является нерентабельным.На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции? Нормированная стоимость по продукту 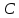 не равна нулю, значит, если мы будем принудительно выпускать единицу продукта не равна нулю, значит, если мы будем принудительно выпускать единицу продукта 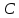 , то целевая функция уменьшится на 10,85. , то целевая функция уменьшится на 10,85.На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли? Снизить можно только запас недефицитного ресурса. Так как все ресурсы являются дефицитными, то любое снижение запаса ресурсов будет приводить к уменьшению прибыли, например, если уменьшить запас третьего ресурса на единицу, то прибыль уменьшится на 3,36 денежных единиц. Определите изменение стоимости продукции и количество выпускаемых изделий при увеличении второго вида сырья на 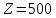 единиц. единиц.изменение стоимости продукции: Рассмотрим целевую функцию двойственной задачи с измененным количеством второго вида сырья: 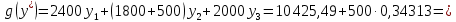 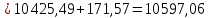 изменение количества выпускаемых изделий: Внесем изменения в исходную таблицу и перерешаем задачу: 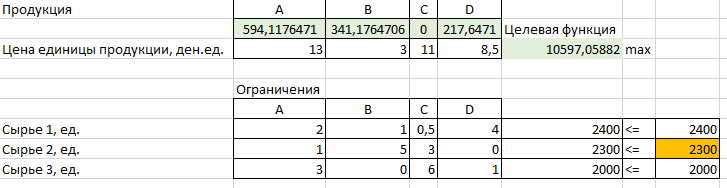 Отчет о результатах 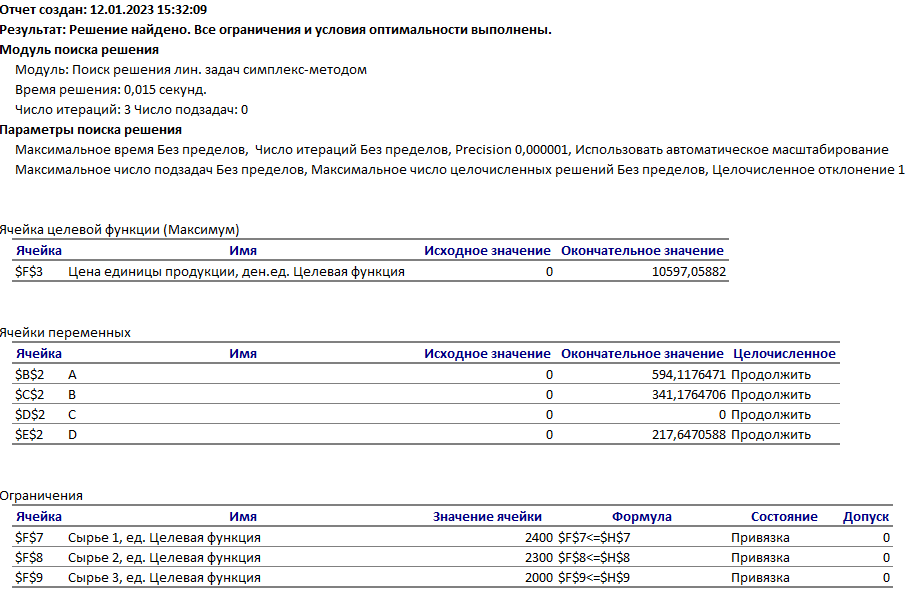 Отчет об устойчивости: 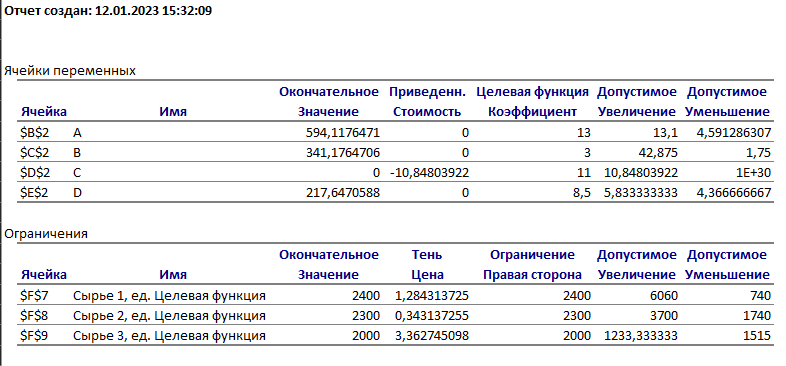 Отчет о пределах: 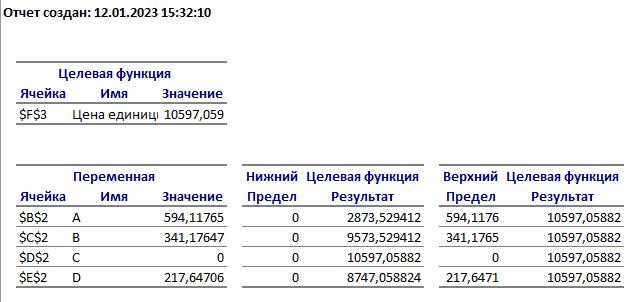 В итоге получим новый план выпуска: Продукция типа 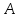 – 594,12 единиц, типа – 594,12 единиц, типа 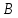 – 341,18 единиц, тип – 341,18 единиц, тип 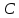 – не производить, тип – не производить, тип 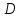 – 217,65 единиц. Прибыль при этом составит – 217,65 единиц. Прибыль при этом составит 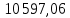 денежных единиц. денежных единиц.Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде в-строки  . . Так как 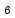 не входят в допустимые интервалы изменения запасов ресурсов, внесем изменения запасов ресурсов в таблицу и пересчитаем задачу: не входят в допустимые интервалы изменения запасов ресурсов, внесем изменения запасов ресурсов в таблицу и пересчитаем задачу: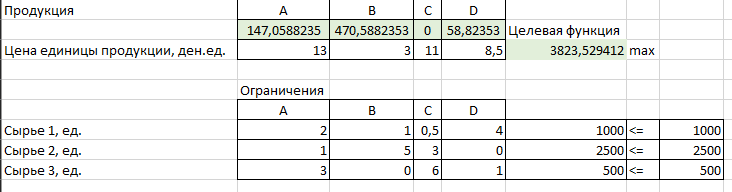 Отчет о результатах: 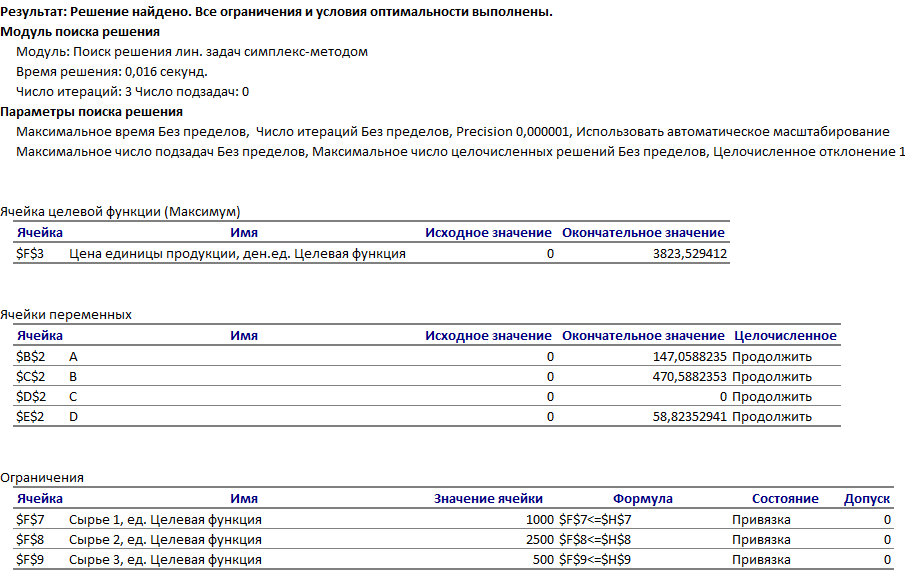 Отчет об устойчивости: 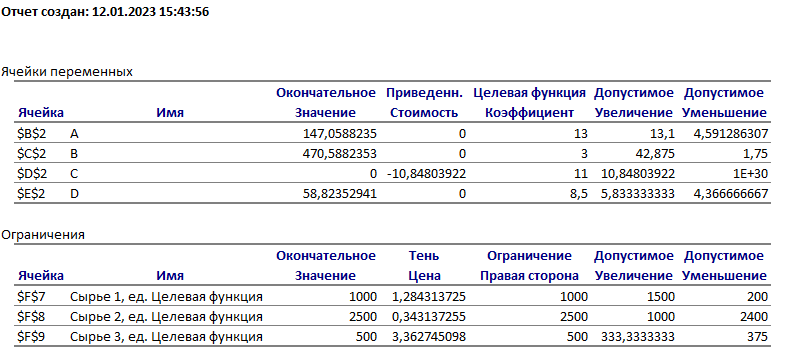 Отчет о пределах: 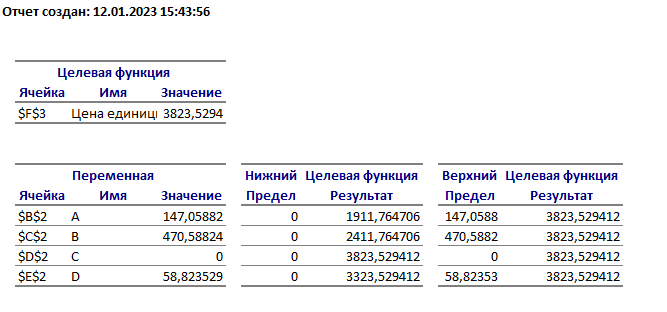 В итоге получим новый план выпуска: Продукция типа 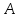 – 147,06 единиц, типа – 147,06 единиц, типа 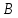 – 470,59 единиц, тип – 470,59 единиц, тип 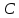 – не производить, тип – не производить, тип 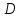 – 58,82 единиц. Прибыль при этом составит – 58,82 единиц. Прибыль при этом составит 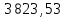 денежных единиц. денежных единиц.Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план. 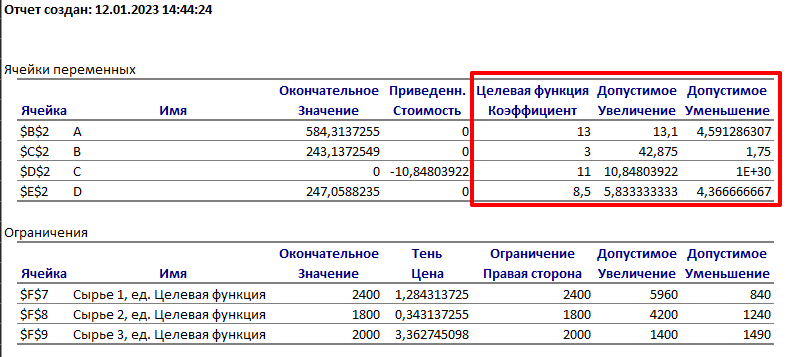 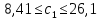 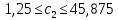 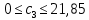 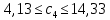 Так как продукт 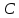 не производится, то уменьшение его цены не скажется на решении. Но если цена превысит не производится, то уменьшение его цены не скажется на решении. Но если цена превысит  денежных единиц, то он станет рентабельным. денежных единиц, то он станет рентабельным.На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным? В нашем случае нерентабельным является выпуск продукта 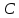 . .Продукт 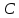 станет рентабельным, если его цена возрастет с 11 до 21,85. станет рентабельным, если его цена возрастет с 11 до 21,85.Продукт 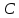 можно сделать рентабельным, снизив его себестоимость, что можно сделать, снизив затраты сырья на единицу продукции. можно сделать рентабельным, снизив его себестоимость, что можно сделать, снизив затраты сырья на единицу продукции.Ограничение по двойственной задаче по третьему ресурсу имеет вид: 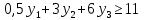 С учетом этого, уравнение рентабельности имеет вид: 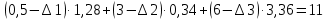 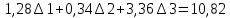 Найдем одно из возможных решений. Пусть 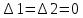 , тогда , тогда 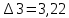 . .То есть если потребление третьего ресурса на единицу продукции 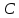 снизится на 3,22 единицы, то продукция снизится на 3,22 единицы, то продукция 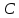 станет рентабельной. станет рентабельной.На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%? Общее изменение прибыли можно записать в виде: 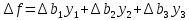 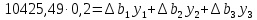 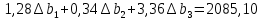 Полученное уравнение имеет множество решений. Пусть 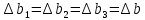 , тогда: , тогда: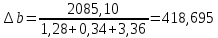 Получим, что для увеличения прибыли на 20% необходимо увеличить запас каждого ресурса на 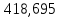 единиц. единиц. | |||||||||||||||||||||||||||||||||||||||||||||