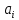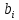Вариант 7 Задание Нечеткие технологии и системы. Задание 1
 Скачать 36.07 Kb.
|
|
Задания для выполнения РГР Вариант 7 Задание 1. Нечеткие технологии и системы. Задание 1. Основные этапы построенияCADT – модели. Задание 3. Фермер может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30 000 долл. чистого дохода, а урожай соевых бобов 10 000 у.е. Если цены останутся неизменными, фермер лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000 у.е. соответственно. a) Представьте данную задачу в виде дерева решений. b) Какую культуру следует выращивать Мак-Кою? Задание 4.Задача о замене оборудования: Руководство предприятия планирует свою деятельность на один год (четыре квартала). Установленное на предприятии оборудование в начале каждого квартала может быть продано по остаточной стоимости и заменено новы, приобретаемым по рыночной стоимости. прогнозируемая рыночная стоимость оборудования М усл. ден. ед.в зависимости от номера квартала (от 1 до 4) меняется следующим представленным в таблице образом:
К характеристикам оборудования относятся: Р производительность (усл. ед. продукции в квартал); Q-затраты на эксплуатацию (усл. ден.ед.в квартал); S-остаточная стоимость оборудования (усл. ден.ед.). Характеристики оборудования зависят от его наработки (под наработкой оборудования будем понимать число полных кварталов его эксплуатации).Данные зависимости представлены в следующей таблице:
Будем считать, что установленное на предприятии оборудование является быстро изнашивающимся и при наработке 4 квартала не подлежит дальнейшей эксплуатации. В начале года наработка установленного на предприятии оборудования равнялась 2 кварталам. Стоимость С однойусл. ед. продукции предприятия, выпускаемой на данном оборудовании. будем считать постоянной и равной 0,1 усл. ден. ед.Требуется определить оптимальную стратегию обновления оборудования на один год с целью достижения максимального суммарного экономического эффекта за весь год. Задание 5.Для данного конечного автомата, заданного таблично, со множеством внутренних состояний {1,2,3,4,5,6,7,8,9}, входным алфавитом {a, b} и выходным алфавитом {x, y}: 1. Выяснить, является ли автомат сильно связным. 2. Построить эквивалентный минимальный автомат. 3. Проверить работу исходного и минимального автоматов над словом «bbabaab»
Задание 6. 1.Написать таблицу состояний данного автомата. 2. Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом.
  Задание 7. Диспетчер управляет внутризаводским транспортом и имеет в своем распоряжении два грузовика. Заявки на перевозки поступают к диспетчеру каждые 5 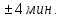 С вероятностью 0,5 диспетчер запрашивает по радио один из грузовиков и передает ему заявку, если тот свободен. В противном случае он запрашивает другой грузовик и таким образом продолжает сеансы связи, пока один из грузовиков не освободится.Каждый сеанс связи длится ровно 1 мин. Диспетчер допускает у себя накопление до пяти заявок, после чего вновь прибывшие заявки получают отказ.Грузовики выполняют заявки на перевозку за 12 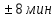 . Смоделировать работу внутризаводского транспорта в течение 10 час. Подсчитать число обслуженных и отклоненных заявок. Определить коэффициент загрузки грузовиков.Задание 8. Время между приходом клиентов в парикмахерскую является случайной величиной, изменяющейся по экспоненциальному закону с математическим ожиданием 15 мин. В парикмахерской работает один мастер, который выполняет мужскую стрижку от 10 до 15 мин., время стрижки имеет равномерное распределение на этом интервале. Клиенты обслуживаются в порядке очереди. Смоделировать работу парикмахерской по обслуживанию 20 клиентов. Требуется определить следующие параметры работы парикмахерской: 1) среднюю занятость парикмахера; 2) Среднее количество ожидающих клиентов; 3) Среднее время ожидания клиента в очереди. Задание 9. Имеются поквартальные данные по розничному товарообороту.
Постройте график временного ряда. Проведите предварительный анализ временного ряда.Постройте аддитивную и мультипликативную модели временного ряда. Оцените качество построенной модели через показатель доли объясненной дисперсии уровней ряда. Проверьте временной ряд на автокорреляцию и нормальность распределения ошибок. Найдите оптимальный тренд и рассчитайте точечный прогноз на следующиечетыре квартала. Задание 10. Банк разработал правила, согласно которым очередь в окно не должна быть длиннее двух человек. Если появляется третий клиент, то все трое сопровождаются в кабинет менеджера и обслуживаются по высшему разряду. Перед окном нет никакой очереди. Более того, вооруженный охранник на входе в банк не пропускает более одного клиента в минуту (именно столько времени требуется для тщательной проверки клиента). В результате длина очереди в окно определяется процессом Маркова, описывающим, что происходит в течение одной минуты: Если нет очереди, то с вероятностью ½ клиент появится в течение одной минуты и с вероятностью ½ не появится. Перед окном стоит один человек. С вероятностью 1/6 этого клиента обслужат, и он уйдет; с вероятностью 1/3 появится второй клиент и с вероятностью ½ ничего не изменится. Перед окном в очереди два человека. С вероятностью 1/6 одного клиента обслужат и, и он уйдет; с вероятностью 1/6 появится третий клиент, и все трое уйдут в кабинет менеджера, и с вероятностью 2/3 ничего не изменится. a) Постройте матрицу М преобразующую распределение вероятностей  в момент t в распределение вероятностей в момент (t+1).b) Когда банк открывается в 9 часов утра, 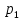 =1. Каково распределение вероятностей через три минуты.с) Получите собственные значения и собственные векторы матрицы М. d) Каково будет распределение вероятностей после многих часов работы банка? Оцените, через какое время вероятност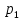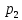и , и 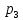 будут совпадать с предельными значениями с точностью до 0,001.е) Сколько в среднем посетителей обслуживается в течении одной минуты? Сколько клиентов приглашается в кабинет менеджера? Задание 11. Автозаправочная станция имеет две колонки, Площадка вокруг нее допускает одновременное ожидание не более 4 машин, Поток машин, прибывающий на станцию простейший с интенсивностью 1 машина в минуту, Время обслуживания автомашины распределено по показательному закону со средним значением 2 минуты.Найти для АЗС финальные вероятности состояния для 1, 2, 3 и 4-х машин, абсолютную пропускную способность и вероятность отказа в обслуживании. Задание 12.На железнодорожной станции расположена гостиница, в которой имеется 20 мест.Посетитель в случае занятости мест уходит в другую гостиницу.Среднее время снятия гостиницы составляет 8 часов.Интенсивность потока поступления клиентов составляет 5 человек в час. Определите вероятность отказа и абсолютную пропускную способность гостиницы Задание 13. Средний годовой спрос D=140 единиц за 300 рабочих дней, стоимость подачи заказов  =45 рублей/ заказ, издержки хранения одной единицы  =15 рублей/ год, годовая стоимость отсутствия запасов 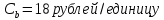 . Время поставки 4 дня.
Сколько нужно заказывать и когда, если цель – минимизировать общую стоимость запасов. Задание 14.Менеджер плавательного бассейна разрабатывает план подготовки к первой тренировке команды пловцов, Тренировку предполагается провести 1 сентября. Данныео подготовительных мероприятиях приведены в таблице (оценки времени указаны в днях).
1)Какова ожидаемая продолжительность проекта? 2) сколько и какие работы на критическом пути? 3)Если менеджер планирует начать проект 11 августа, то какова вероятность того, что программа тренировки пловцов будет завершена к1 сентября за16 рабочих дней? |
,1
,0
