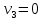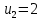Вариант 8. Вариант 8 Решите задачу графическим методом. Найти максимум и минимум функции при ограничениях Решение
 Скачать 77 Kb. Скачать 77 Kb.
|
|
Вариант 8 Решите задачу графическим методом. Найти максимум и минимум функции  при ограничениях при ограничениях 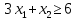 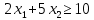 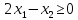 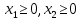 Решение: Решим задачу графическим методом. С учетом системы ограничений построим множество допустимых решений. Строим в системе координат  прямые: прямые:   Изобразим полуплоскости, определяемые системой ограничений. Находим множество допустимых решений как общую часть полученных полуплоскостей – неограниченная область 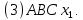 Вектор градиентного направления Вектор градиентного направления  Минимальное значение функции Чтобы найти минимальное значение целевой функции, перемещаем линию уровня в направлении вектору-градиенту до первого касания области допустимых решений  На отрезке прямой На отрезке прямой 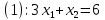 от точки от точки 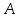 до точки до точки  целевая функция достигает минимума. целевая функция достигает минимума. Координаты точки 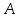 – точки пересечения – точки пересечения  и и  : :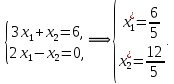 Координаты точки  – точки пересечения – точки пересечения  и и 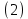 : : Значение целевой функции 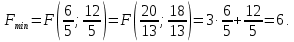 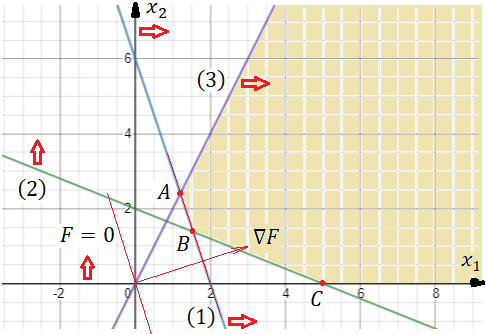 Максимальное значение функции Чтобы найти максимальное значение целевой функции, перемещаем линию уровня в направлении вектора-градиента до последнего касания области допустимых решений  Так область допустимых решений неограниченна справа, целевая функция также неограниченна сверху. Задача на максимум не имеет решения. Так область допустимых решений неограниченна справа, целевая функция также неограниченна сверху. Задача на максимум не имеет решения.Ответ: 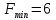 на отрезке прямой на отрезке прямой 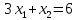 от точки от точки 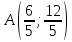 до точки до точки 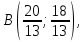 целевая функция неограниченна сверху. целевая функция неограниченна сверху. Решить задачу ЛП симплексным методом  при ограничениях  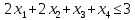 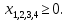 Решение: Решим задачу симплекс-методом. Преобразуем исходную модель. В ограничения типа  добавим дополнительные переменные добавим дополнительные переменные 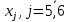 . Модель задачи будет выглядеть так: . Модель задачи будет выглядеть так: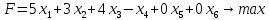 при условиях:  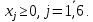 Стандартная форма записи модели: 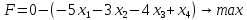 при условиях: 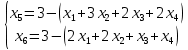 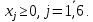 Заполним первую симплекс-таблицу.
В 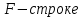 среди оценок среди оценок 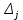 есть отрицательные значения, следовательно, план есть отрицательные значения, следовательно, план 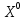 не является оптимальным. Среди значений не является оптимальным. Среди значений 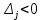 находим наибольшее по абсолютной величине находим наибольшее по абсолютной величине 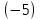 , столбец , столбец 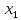 выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений 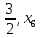 – ведущая строка. Элемент 2 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. Переходим к следующей симплексной таблице. – ведущая строка. Элемент 2 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. Переходим к следующей симплексной таблице.
В 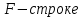 среди оценок среди оценок 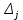 есть отрицательное значение, следовательно, план есть отрицательное значение, следовательно, план 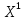 не является оптимальным. Столбец не является оптимальным. Столбец 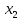 выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений выбираем в качестве ведущего. Для положительных элементов ведущего столбца находим наименьшее из симплексных отношений 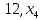 – ведущая строка. Элемент 5/2 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. Переходим к следующей симплексной таблице. – ведущая строка. Элемент 5/2 на пересечении ведущего столбца и ведущей строки – разрешающий элемент. Переходим к следующей симплексной таблице.
В 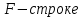 среди оценок среди оценок 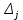 нет отрицательных, следовательно, план нет отрицательных, следовательно, план  является оптимальным. является оптимальным. 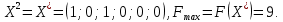 Возвращаясь к исходной задаче четырех переменных, запишем оптимальное решение:  Ответ: 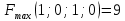 . .
Решение: Проверяем условие баланса: 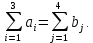 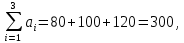  Так как  задача сбалансированная. задача сбалансированная. Строим начальный план методом «минимальной стоимости». Вписываем в ячейку  (имеет наименьший тариф 1) наименьшее из значений (имеет наименьший тариф 1) наименьшее из значений  и и 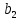 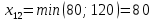 и исключаем из дальнейшего рассмотрения и исключаем из дальнейшего рассмотрения 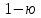 строку. Потребности второго потребителя уменьшаются на величину строку. Потребности второго потребителя уменьшаются на величину 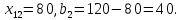 Далее в ячейку Далее в ячейку 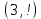 записываем наименьшее из значений записываем наименьшее из значений 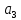 и и  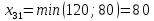 и исключаем из дальнейшего рассмотрения и исключаем из дальнейшего рассмотрения 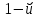 столбец. Запасы третьего поставщика уменьшаются на величину столбец. Запасы третьего поставщика уменьшаются на величину 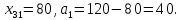 С оставшейся матрицей поступаем аналогично предыдущему: 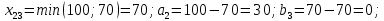 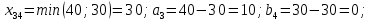 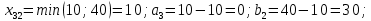 
Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок  равно равно 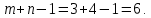 Определим полную стоимость перевозок по найденному опорному плану: Определим полную стоимость перевозок по найденному опорному плану: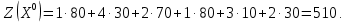 Проверим план, построенный методом «минимальной стоимости» на оптимальность. С помощью метода потенциалов вычислим потенциалы строк и столбцов по стоимости перевозок в загруженных клетках. Если известен  , то , то 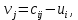 если известен если известен 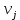 , то , то 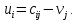 Положим, например, Положим, например, 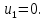 Тогда будут вычислены и остальные потенциалы строк и столбцов. Тогда будут вычислены и остальные потенциалы строк и столбцов.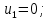 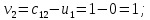 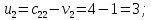 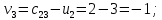 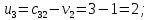  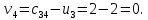
Для незагруженных клеток вычислим величины превышения стоимости 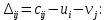 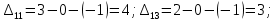   Полученный план не оптимален. Среди оценок 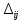 имеется отрицательное значение. Потенциальной является клетка имеется отрицательное значение. Потенциальной является клетка 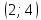 . От клетки . От клетки 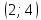 строим замкнутый контур: строим замкнутый контур: 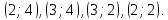 Начиная с клетки Начиная с клетки 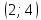 разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки 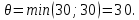 Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-». Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Определим полную стоимость перевозок по найденному опорному плану:  Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:  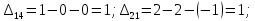 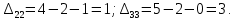 Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален. Ответ: оптимальный план перевозок, обеспечивающий минимальные затраты 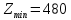 (усл.ед.): (усл.ед.):
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







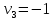
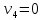
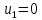
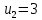
 - 4
- 4