Гидравлика и гидропневмопривод. Вариант 8 Задача 1
 Скачать 83.15 Kb. Скачать 83.15 Kb.
|
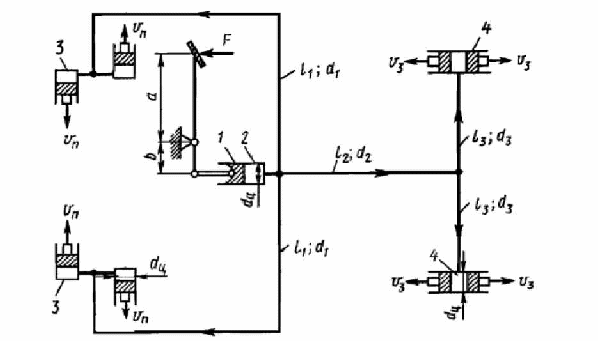 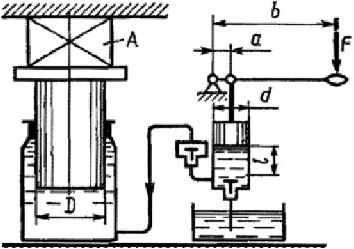 Вариант 8 Вариант 8Задача 1. Давление в цилиндре гидравлического пресса повышается в результате нагнетания в него жидкости ручным насосом и сжатия её в цилиндре. Определить число двойных ходов n поршня ручного насоса, необходимое для увеличения силы прессования детали A = 1,2 МПа, если диаметры поршней: D =600мм, d = 20мм; ход поршня ручного насоса l = 30мм; объёмный модуль упругости жидкости K = 1300мПа; объём жидкости в прессе V= 60 л. Чему равно максимальное усилие F на рукоятке насоса при ходе нагнетания, если b/a =8. Рис. 1 Схема гидропресса Дано: D =600мм, d = 10мм, A = 1,2 Мпа, l = 30мм, K = 1300мПа, V= 60 л. Найти: F, если b/a =10. Решение: Усилие прессования определяется по формуле: 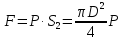 где 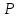 – давление жидкости; – давление жидкости;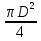 – площадь большого поршня; – площадь большого поршня;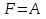 – усилие прессования. – усилие прессования.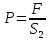 Определим давление под поршнем D: 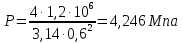 Определим уменьшение объема при упругом сжатии жидкости: 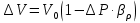 где 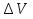 – уменьшение объема при сжатии; – уменьшение объема при сжатии;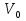 – начальный объем; – начальный объем;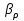 – объемный коэффициент сжатия равный 1/К; – объемный коэффициент сжатия равный 1/К;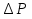 – увеличение давления. – увеличение давления.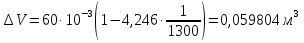 Определим на сколько уменьшился объем жидкости в прессе после упругого сжатия 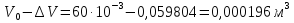 Определим объем жидкости в малом цилиндре за один ход поршня ручного насоса: 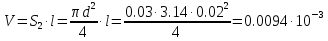 Определим число двойных ходов nпоршня ручного насоса: 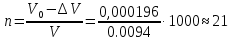 Определим силу давления на поршень ручного насоса: 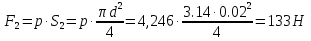 Определим усилие на рукоятку ручного насоса пресса: 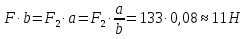 Задача 2. В кузов автомобиля - самосвала до уровня 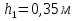 налит цементный раствор, плотностью налит цементный раствор, плотностью 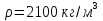 . Определить наименьший допустимый путь торможения самосвала от скорости . Определить наименьший допустимый путь торможения самосвала от скорости 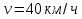 до остановки исходя из условия, чтобы раствор не выплеснулся из кузова. Определить силу давления раствора на передний борт при торможении. Для упрощения принять, что кузов самосвала имеет форму прямоугольной коробки размерами до остановки исходя из условия, чтобы раствор не выплеснулся из кузова. Определить силу давления раствора на передний борт при торможении. Для упрощения принять, что кузов самосвала имеет форму прямоугольной коробки размерами 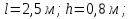 ширина кузова ширина кузова 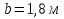 , а движение автомобиля прямолинейное, равнозамедленное. , а движение автомобиля прямолинейное, равнозамедленное.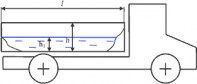 Рис. 2 Схема смещения груза при торможении Дано: 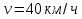 , , 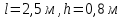 , , 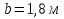 , , 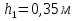 , , 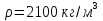 . .Решение: На раствор в кузове действуют две силы: тяжести G, направленная вниз и инерции F=m  a, направленная вправо при торможении автомобиля. Решая дифференциальное уравнение поверхности уровня получаем, при X=0, Y=0, Z=-g a, направленная вправо при торможении автомобиля. Решая дифференциальное уравнение поверхности уровня получаем, при X=0, Y=0, Z=-g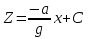 где - 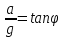 – тангенс угла наклона свободной поверхности жидкости к горизонту, значение которого в условиях данной задачи равно: – тангенс угла наклона свободной поверхности жидкости к горизонту, значение которого в условиях данной задачи равно: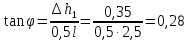 Следовательно, замедление автомобиля 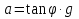 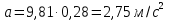 Длину торможения автомобиля найдем из уравнений равнозамедленного движения: 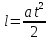 где 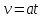 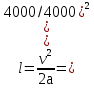 Определим силу давления раствора на передний борт автомобиля: 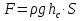 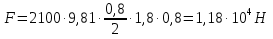 Задача 3. В гидротормозной системе автомобиля передача усилия F от ножной педали к тормозам колёс производится посредством жидкости, вытесняемой поршнем 1 из главного тормозного цилиндра 2 по трубопроводам в рабочие тормозные цилиндры передних 3 и задних 4 колёс. На первом этапе торможения за счёт хода поршней рабочих цилиндров выбирается зазор между тормозными колодками и барабанами. На втором этапе торможения происходит сжатие всего объёма жидкости V в системе, выравнивание давления и прижатие колодок к барабанам. Диаметры всех цилиндров одинаковы. Определить: 1) скорости перемещения поршней колёсных тормозных цилиндров для передних ( 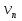 ) и задних ( ) и задних (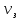 ); 2) ход педали, необходимый для упругого сжатия тормозной жидкости в системе. Плотность жидкости р, модуль объёмной упругости ); 2) ход педали, необходимый для упругого сжатия тормозной жидкости в системе. Плотность жидкости р, модуль объёмной упругости 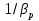 , жидкость - минеральное масло, вязкостью v. , жидкость - минеральное масло, вязкостью v.Рис. 4 Схема тормозной системы автомобиля Дано: 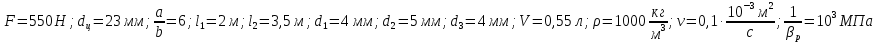 Решение: Для решения используем формулу сжимаемости жидкости: 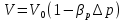 где 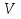 – конечный объем жидкости; – конечный объем жидкости; 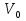 – начальный объем жидкости; – начальный объем жидкости;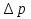 – увеличение давления; – увеличение давления; 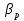 – коэффициент объемного сжатия. – коэффициент объемного сжатия.Задаёмся режимом течения, основываясь на роде жидкости – значении вязкости (вода, бензин, керосин – режим обычно турбулентный; масла – ламинарный). Потери напора в гидролиниях при ламинарном режиме определяют по закону Пуазейля: 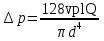 1. Определим силу давления 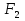 на шток поршня главного тормозного цилиндра. Составим уравнение момента относительно оси поворота педали: на шток поршня главного тормозного цилиндра. Составим уравнение момента относительно оси поворота педали: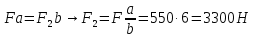 2. Определим давление в главном тормозном цилиндре по формуле: 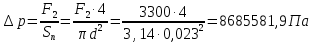 Это давление передается во всей гидролинии. 3. Определим расход в тормозном цилиндре передних колес, используя формулу Пуазейля: 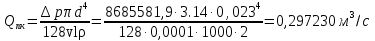 4. Определим расход в тормозном цилиндре передних колес разделив общий расход пополам: 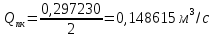 5. Определим скорость перемещения поршня в тормозном цилиндре передних колес: 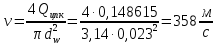 6. Определим расход 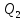 в общей линии задних колёс, используя формулу Пуазейля: в общей линии задних колёс, используя формулу Пуазейля: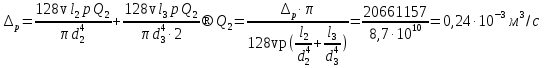 7. Определим расход 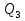 в линии задних колёс: в линии задних колёс: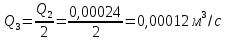 8. Определим расход 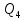 в тормозном цилиндре задних колёс: в тормозном цилиндре задних колёс: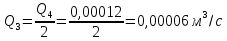 9. Определим скорость движения поршня в тормозном цилиндре задних колёс: 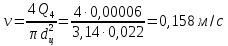 10. Определить суммарный расход масла в главном тормозном цилиндре: 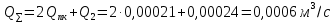 11. Определим изменение объёма масла в системе при упругом сжатии по формуле: 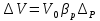 где: 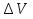 – изменение объёма = – изменение объёма = 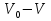 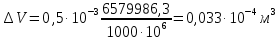 12. Определим ход педели: 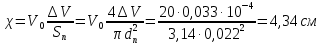 |
