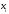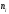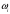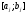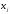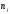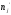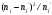Контрольная работа по математической статистике. контрольная работа Матстат вариант1. Вариант Считать максимальную дневную температуру в СанктПетербурге 23 февраля случайной величиной
 Скачать 147.97 Kb. Скачать 147.97 Kb.
|
|
Вариант 1. Считать максимальную дневную температуру в Санкт-Петербурге 23 февраля случайной величиной 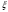 .Из генеральной совокупности - данных Гидрометеослужбы о такой температуре в разные годы сделана следующая выборка ( в градусах Цельсия): .Из генеральной совокупности - данных Гидрометеослужбы о такой температуре в разные годы сделана следующая выборка ( в градусах Цельсия):
Решить задачи 1-5. Задача 1. Вариационный ряд, построенный по данной выборке, извлеченный из генеральной совокупности, включает 19 вариант: -18, -14, -13, -12, -11, -10, -9, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4 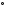 С. С.Выборочный закон распределения оказывается следующим:
Выборочное среднее равно: 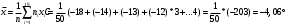 Найдем: 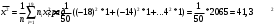 И получим выборочные дисперсии: 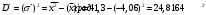 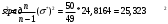 , где , где Заметим, что полученные результаты говорят о том, что 23 февраля в Санкт-Петербурге следует ожидать максимальную дневную температуру равную примерно 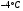 , с разбросом порядка , с разбросом порядка 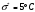 , т.е. примерно в 70% случаев температура должна падать в интервал (-9) – (+1) , т.е. примерно в 70% случаев температура должна падать в интервал (-9) – (+1) 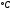 . .Задача 2. Будем считать, что рассматриваемая выборка достаточно велика 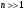 и применима формула: и применима формула: 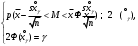 В которой учитываются полученные выше результаты: 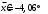 , , 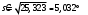 , а , а 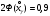 и и 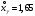 . .Тогда доверительный интервал для математического ожидания 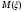 c надежностью (доверительной вероятностью) c надежностью (доверительной вероятностью) 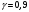 определяется следующим образом: определяется следующим образом: 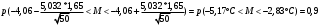 Это означает, что если нет тренда, то средний за все годы максимум температуры в Санкт-Петербурге 23 февраля с вероятностью 90% заключен в интервале -5,17 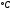 - (-2,83) - (-2,83) 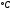 . .Задача 3. Квантили нормального распределения равны: 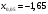 , ,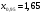 и для n=50, и для n=50, 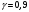 имеем: имеем: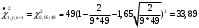 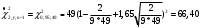 Таким образом, доверительный интервал для дисперсии случайной величины ( если предположить, что она имеет нормальное распределение) с надежностью (доверительной вероятность) 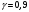 определяется следующим образом: определяется следующим образом: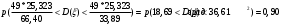 Иными словами, среднее квадратическое отклонение величины 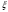 характеризующее ее разброс относительно характеризующее ее разброс относительно 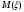 =-4,06 =-4,06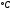 , с вероятностью 90% заключено в пределах от -6,05 до -4,32 , с вероятностью 90% заключено в пределах от -6,05 до -4,32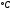 . . Задача 4. Построим группированную выборку, разбив интервал, в который попали все наши варианты на 8 подинтервалов (j=1,2…8).
Гистограмма частот для группированной выборки представлена на рис.1, где h=3 – ширина соответствующего интервала. 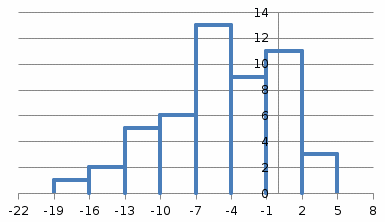  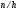 Применим критерий H. Теоретические частоты рассчитаем по формуле: 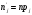 , где вероятности , где вероятности 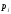 найдем из формулы: найдем из формулы: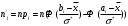 . .Тогда: 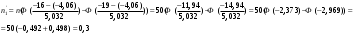 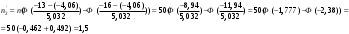 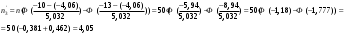 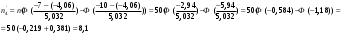 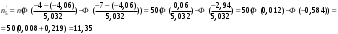 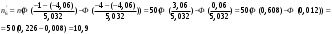 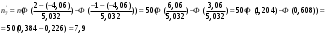 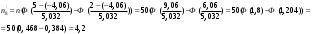 Результаты вычислений можно проверить просуммировав теоретические частоты. Очевидно, что сумма всех 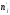 , приведенных в таблице ниже, должна примерно равняться числу вариант, т.е. 50. , приведенных в таблице ниже, должна примерно равняться числу вариант, т.е. 50.
В нашем случае сумма теоретических частот равна 48,3, что связано с недостаточным отличием нижнего интервала -19 от среднего значения -4,06. Эмпирическое значение критерия 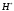 для данной группированной выборки вычисляется по формуле: для данной группированной выборки вычисляется по формуле: 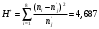 Построим правостороннюю критическую область, удовлетворяющую равенству: 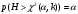 Критическая точка  равна квантили порядка равна квантили порядка 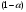 распределения хи-квадрат распределения хи-квадрат 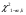 . Из приложения для уровня значимости . Из приложения для уровня значимости 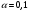 и k=s-3=5 имеем: и k=s-3=5 имеем: 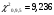 В силу того, что наблюдаемое значение критерия не попадает в критическую область 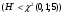 , можно принять гипотезу о нормальном распределении случайной величины при уровне значимости , можно принять гипотезу о нормальном распределении случайной величины при уровне значимости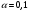 . . Задача 5. При равномерном законе плотность распределения вероятностей имеет параметры a и b. Оценим их, применяя метод моментов. Тогда параметры выражаются через характеристики выборки следующим образом: 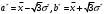 Используя найденные выше значения выборочного среднего и выборочной дисперсии, получим: 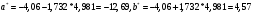 Применим критерий H. Используем группированную выборку, сделанную выше, и вычислим теоретические частоты. В результате получим:
Наблюдаемое (эмпирическое) значение критерия равно: 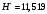 Рассмотрим правостороннюю критическую область. Критическая точка  равна квантили порядка равна квантили порядка 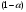 распределения хи-квадрат распределения хи-квадрат 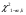 . Из приложения для уровня значимости . Из приложения для уровня значимости 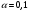 и k=s-3=5 имеем: и k=s-3=5 имеем: 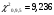 Поскольку эмпирическое значение критерия попадает в критическую область определяемую как 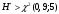 , то гипотеза о равномерном распределении данной случайной величины отвергается при уровне значимости , то гипотеза о равномерном распределении данной случайной величины отвергается при уровне значимости 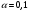 . . |