Отчет. Вариант Выборочное уравнение показательной зависимости
 Скачать 51.35 Kb.
|
|
Вариант 5. 1. Выборочное уравнение показательной зависимости
Рассчитаем показательную зависимость (регрессию) с помощью встроенного аналитического пакет в MS Excel. 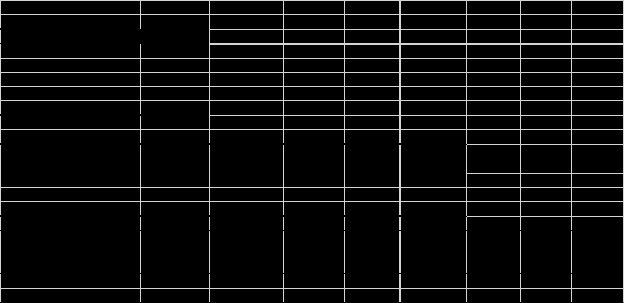 Исходя из полученных результатов можно сказать, что множественный коэффициент детерминации R-квадрат равен 0,98, это говорит о высокой точности аппроксимации (модель хорошо описывает явление). Проведем проверку полученных коэффициентов с помощью встроенных функций: =НАКЛОН(D3:D12;C3:C12) и =ОТРЕЗОК(D3:D12;C3:C12)  Проверка выполнена. 2.1. Выборочный коэффициент корреляции (сделайте выводы о тесноте связи)  Коэффициент корреляции найдем с помощью встроенной функции =КОРРЕЛ(C4:C13;D4:D13) Тесноту связи x относительно y определим с помощью встроенного аналитического пакет в MS Excel.  Таким образом, полученный коэффициент корреляции (0,991700469) близок к 1. Это означает что между показателями существует сильная прямая взаимосвязь. Проверим графическим методом полученный вывод, построив график зависимости x относительно y. 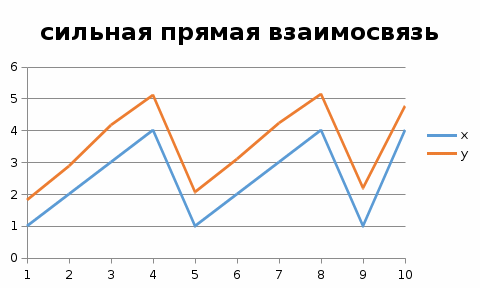 2.2. Выборочное уравнение линии регрессии имеет вид представленный на графике. 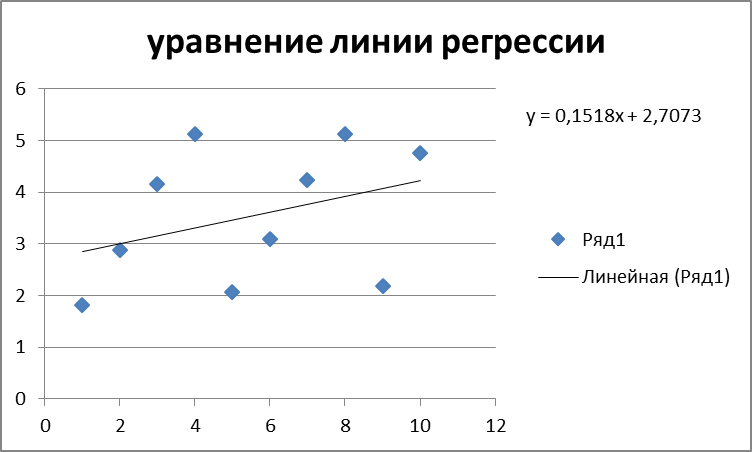 3. Выборочное уравнение равносторонней гиперболы Гиперболическая регрессия имеет вид: 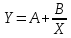 . 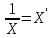Выполним замену переменных:  Тогда, уравнение регрессии запишется в виде: 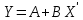 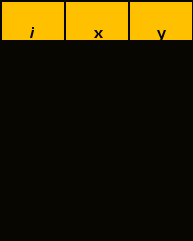 Вычислим 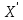 добавив новую колонку к таблице и применив формулу =1/C3. 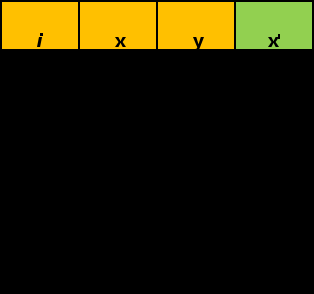 Используем метод наименьших квадратов для нахождения А и В. Для этого используем функцию =ЛИНЕЙН(D3:D12;E3:E12;1;1).  Вычислим гиперболическую регрессию подставив найденные коэффициенты A и B в формулу =$H$3+$G$3/C3 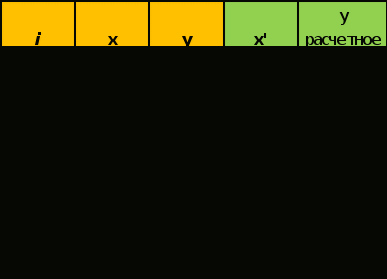 Проведем графическое решение задачи. 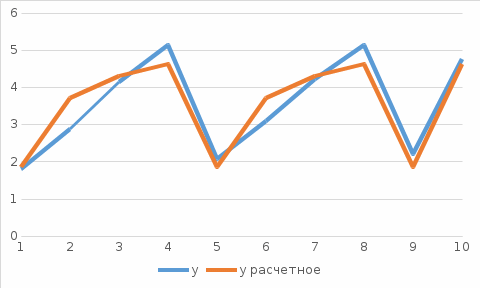 Таким образом, полученная регрессионная зависимость отражает соответствие исходным статистическим данным. |