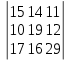Методы оптимальной решений. Задание 4. Методы оптимальных решений. Варианта Матрица доходности Вероятность P

• Название: Варианта Матрица доходности Вероятность P
• Анкор: Методы оптимальной решений
• Дата: 03.07.2020
• Размер: 20.28 Kb.
• Имя файла: Задание 4. Методы оптимальных решений.docx
• Тип: Документы; #133585

Исходные данные

№ варианта	Матрица доходности	Вероятность (P)
5		(0,3;0,4;0,3)

Решение: Необходимо по заданным условиям задачи найти все критерии оптимальности и выбрать оптимальный вариант для строительства. Какой из вариантов проектов (A_i) будет чаще всего повторяться, тот проект и будет оптимальным.

Матрица доходности имеет вид:

	Q1	Q2	Q3
A1	15	14	11
A2	10	19	12
A3	17	16	29

1. 
   Критерий Вальда (выбирается наибольший элемент матрицы доходности из её минимально возможных элементов)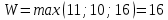
   

– этот вариант выбора соответствует проекту (А₃).

2. 
   Критерий оптимизма (выбирается наибольший элемент матрицы доходности из её максимально возможных элементов)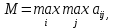
   

- этот вариант выбора соответствует проекту (А₃).

3. 
   Критерий пессимизма (выбирается наименьший элемент матрицы доходности из её минимально возможных элементов)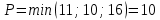
   

- этот вариант выбора соответствует проекту (А₂).

4. 
   Критерий Сэвиджа (предназначен для выбора максимального элемента матрицы рисков из её минимально возможных элементов)
   

Сначала необходимо построить матрицу рисков (r_ij)



Рассчитываем 1-й столбец матрицы рисков.

r₁₁ = 17 - 15 = 2; r₂₁ = 17 - 10 = 7; r₃₁ = 17 - 17 = 0;

Рассчитываем 2-й столбец матрицы рисков.

r₁₂ = 19 - 14 = 5; r₂₂ = 19 - 19 = 0; r₃₂ = 19 - 16 = 3;

Рассчитываем 3-й столбец матрицы рисков.

r₁₃ = 29 - 11 = 18; r₂₃ = 29 - 12 = 17; r₃₃ = 29 - 29 = 0;

Матрица рисков имеет следующий вид: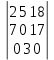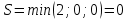



- этот вариант выбора соответствует проектам (А₂, А₃).

5. 
   Критерий Байеса (выбирается максимальный из ожидаемых элементов матрицы доходности при известной вероятности наступления возможных стратегий природы)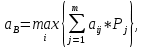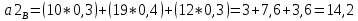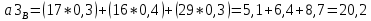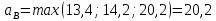
   

- этот вариант выбора соответствует проекту (А₃).