|
Формулы по векторной алгебре и геометрии. Векторная алгебра. Условие коллинеарности(параллельности) векторов и или, где. Орт
Векторная алгебра.
Условие коллинеарности(параллельности) векторов  и и 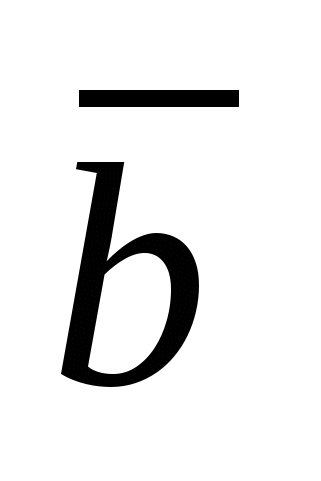 : : 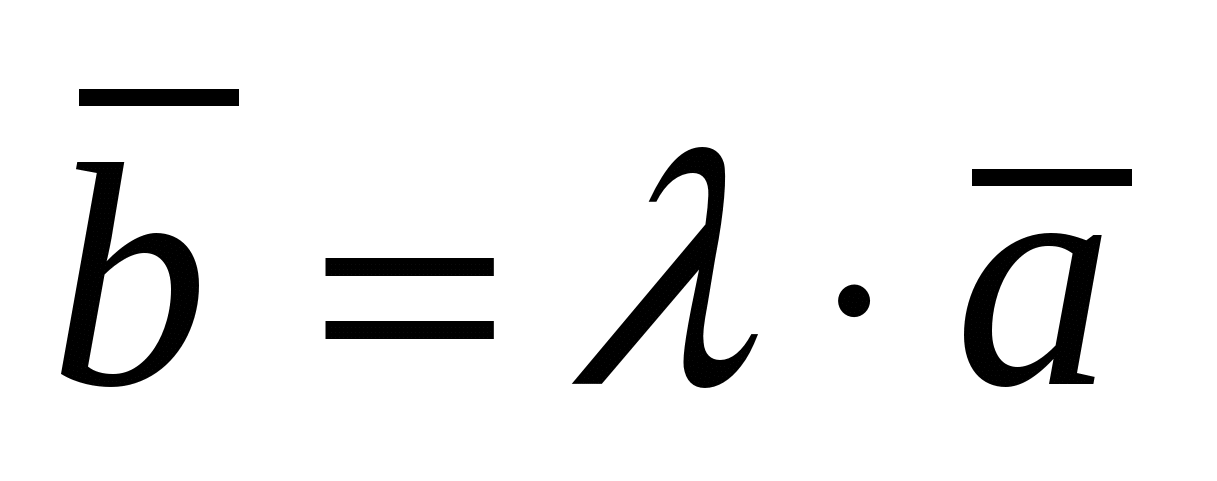 или или 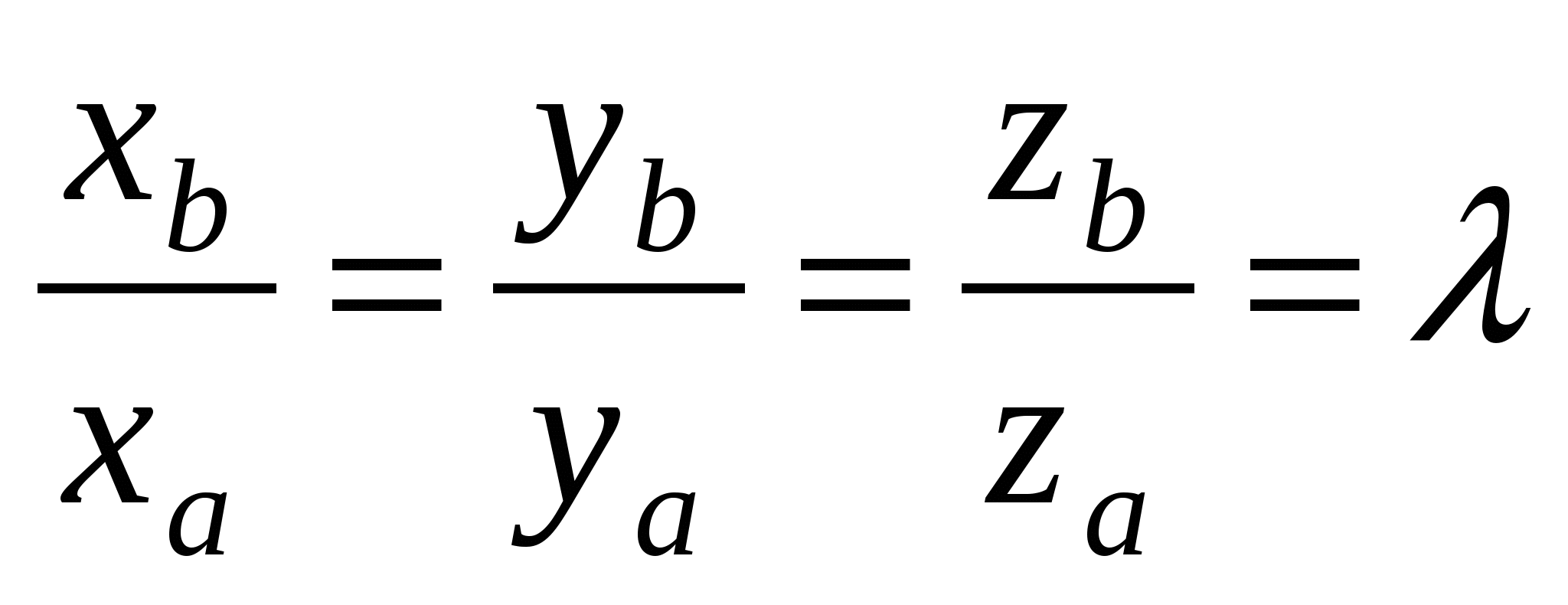 , где , где 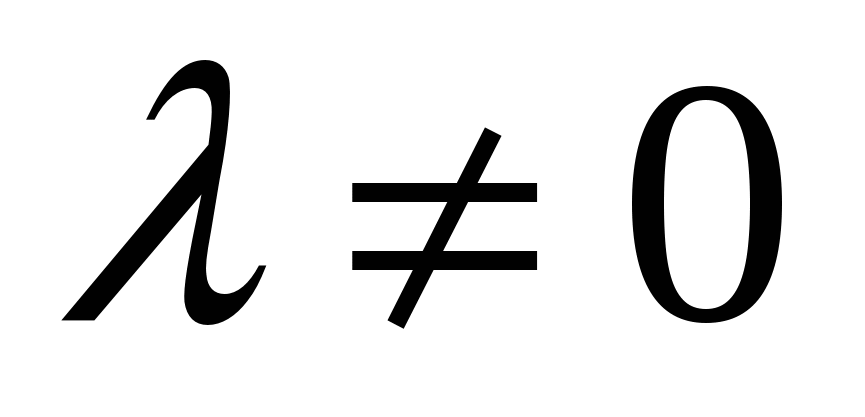 . .
Орт вектора 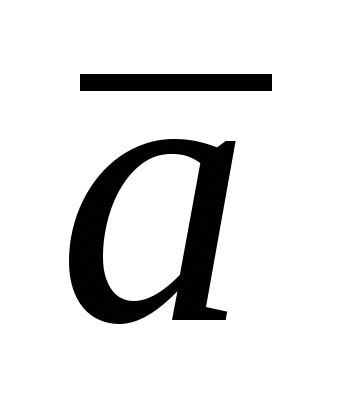 - вектор - вектор 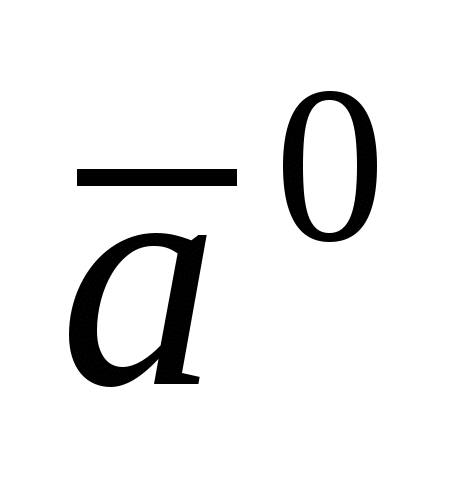 , имеющий единичную длину и направление вектора , имеющий единичную длину и направление вектора 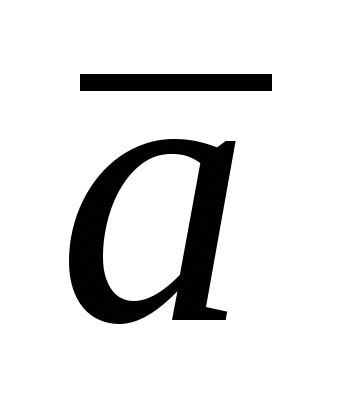 : : 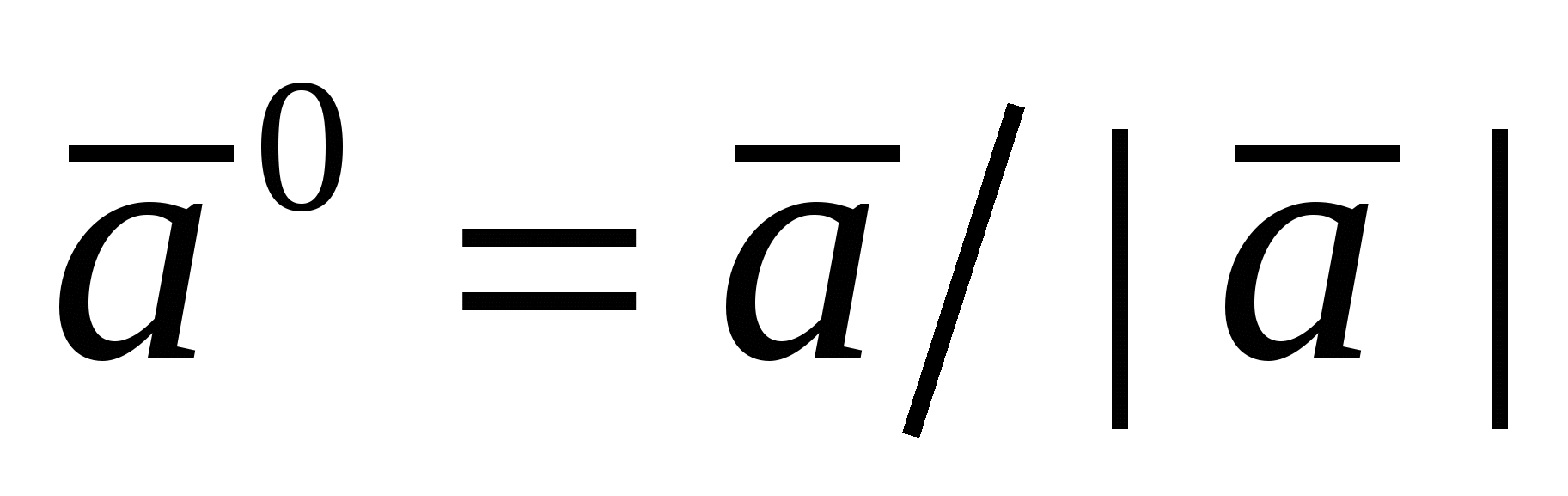 . .
Проекция вектора  на вектор на вектор 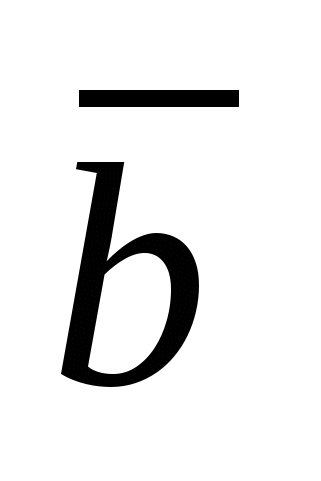 - число - число 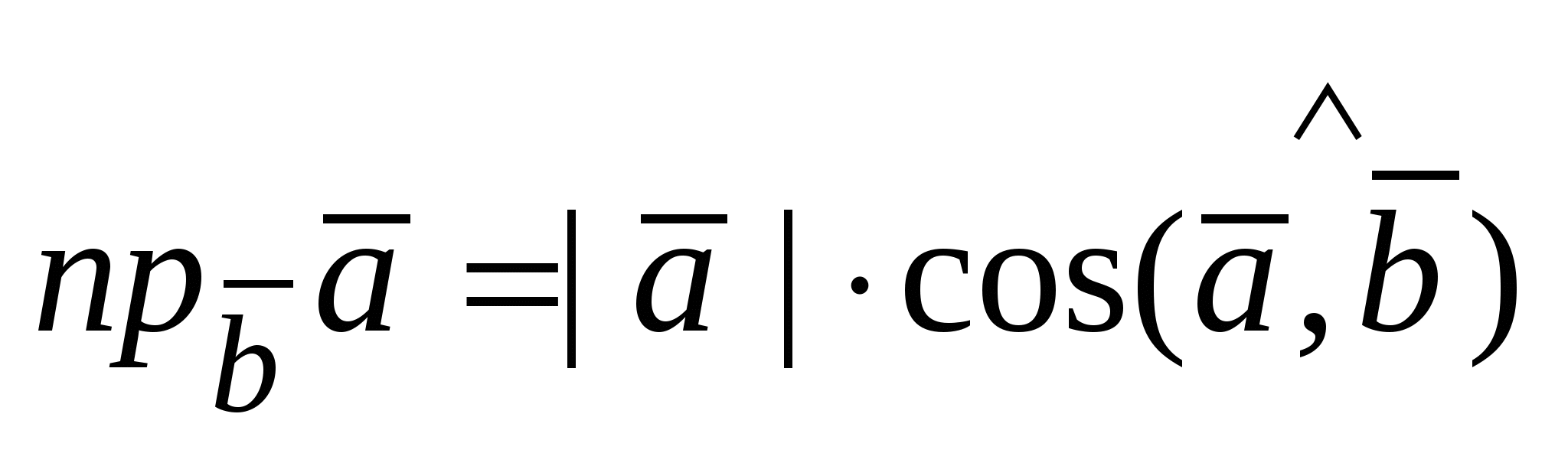 . .
Действия над векторами в координатной форме:
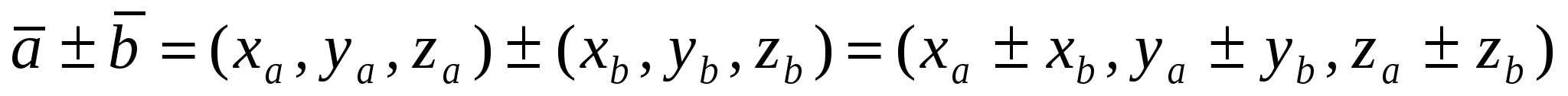 ; ; 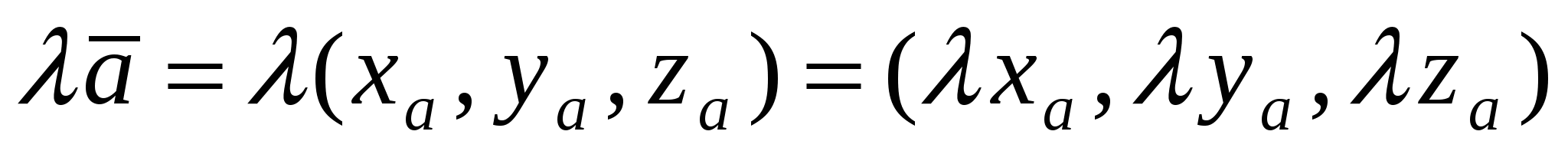 . .
Длина  вектора вектора 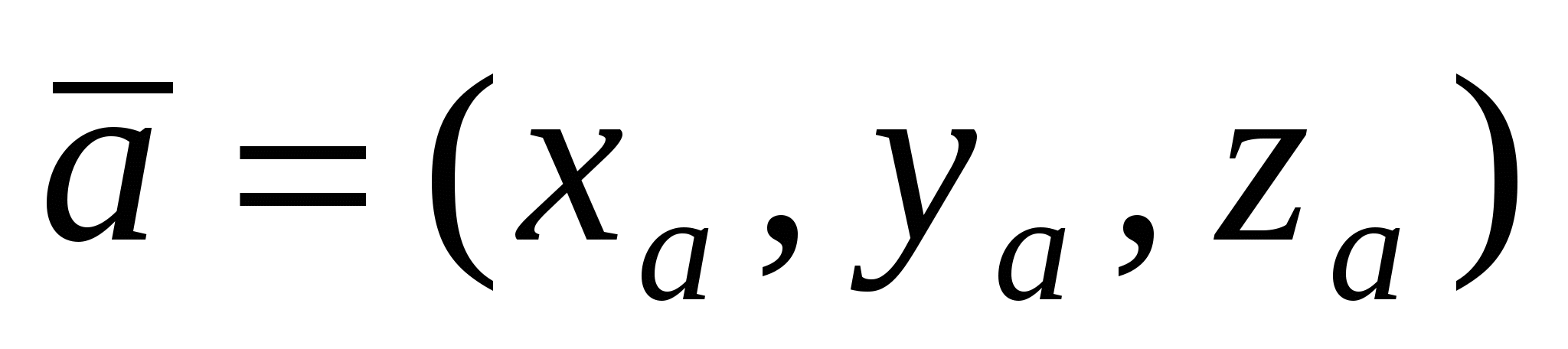 : : 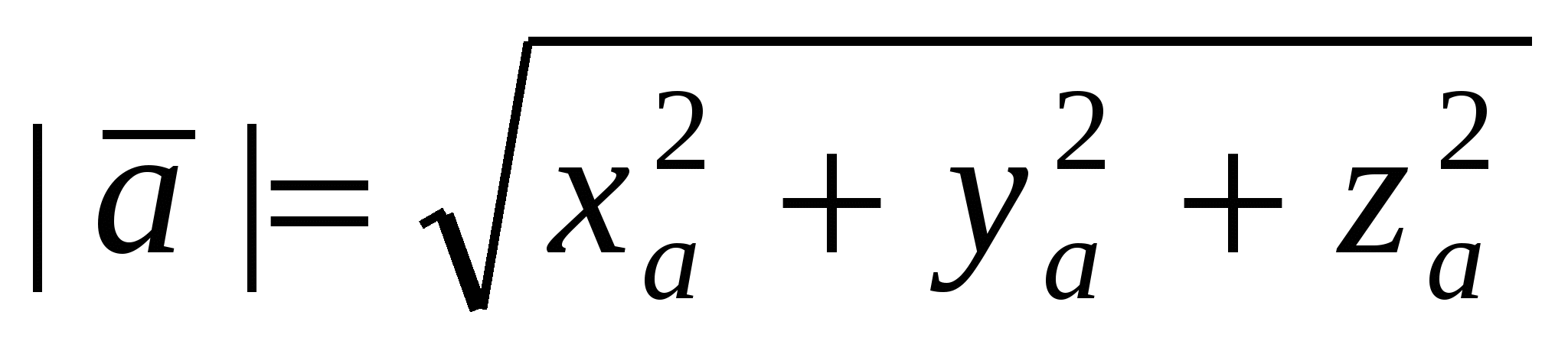 . .
Направляющие косинусывектора  - числа: - числа:
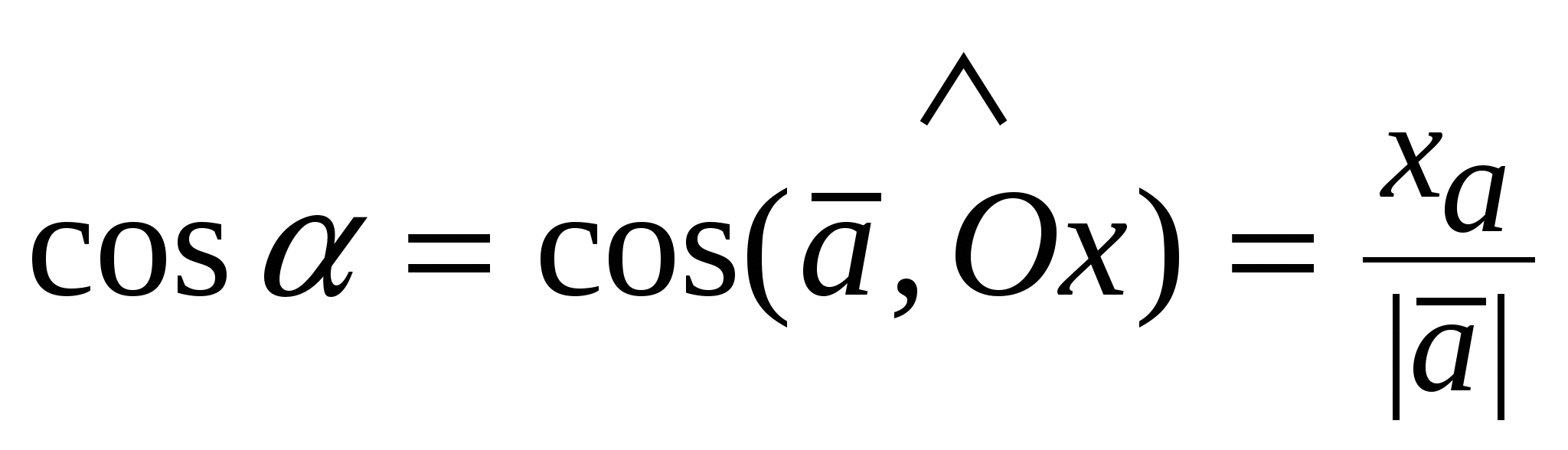 , , 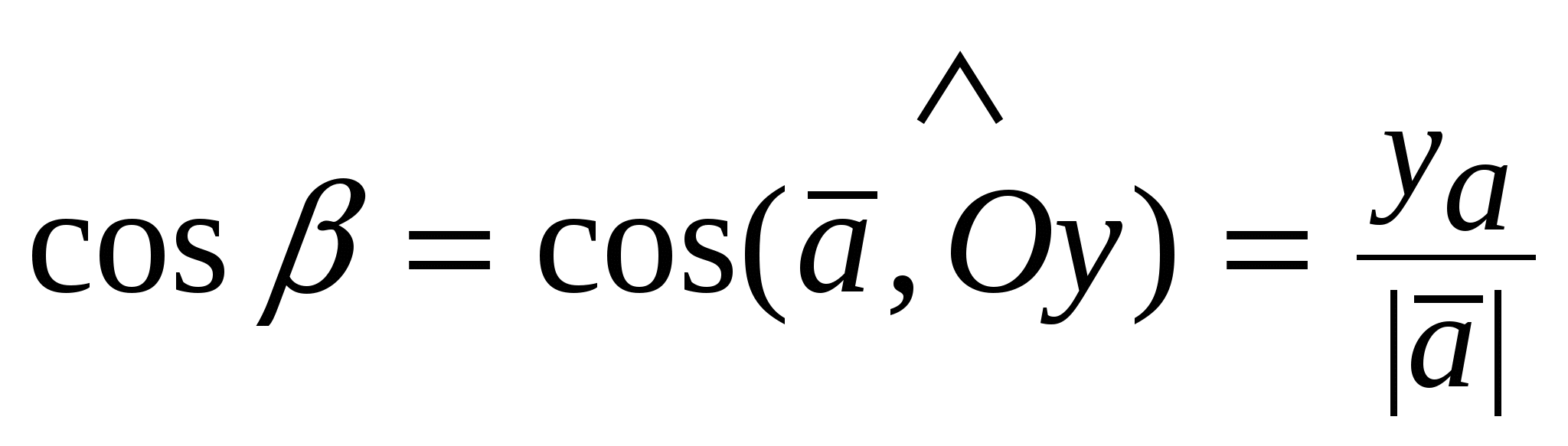 , , 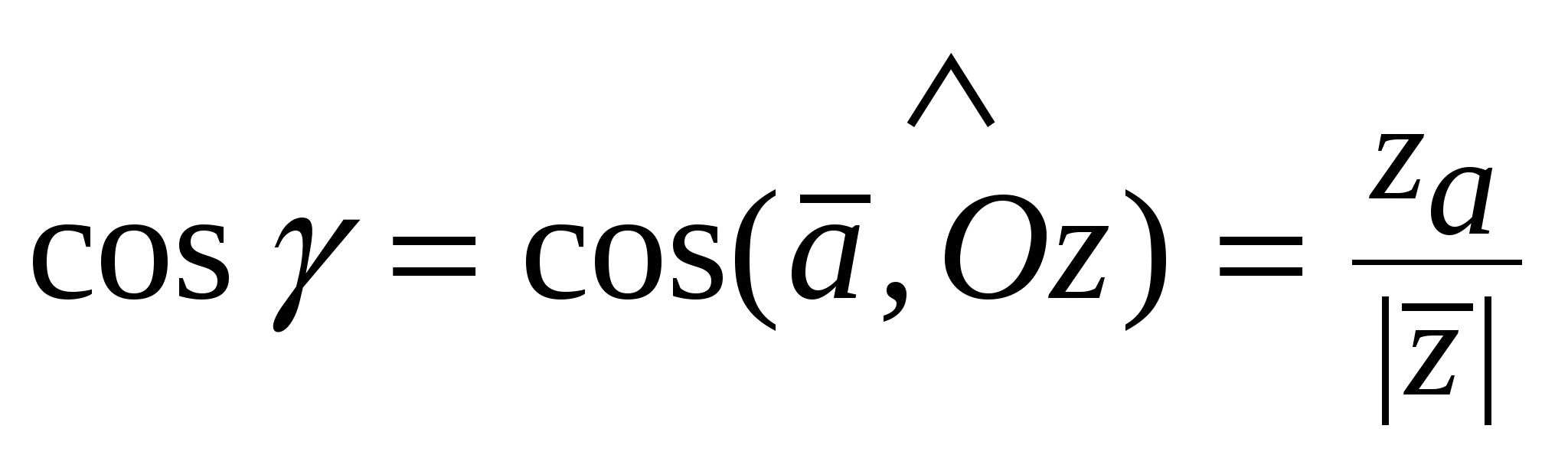 , при этом , при этом 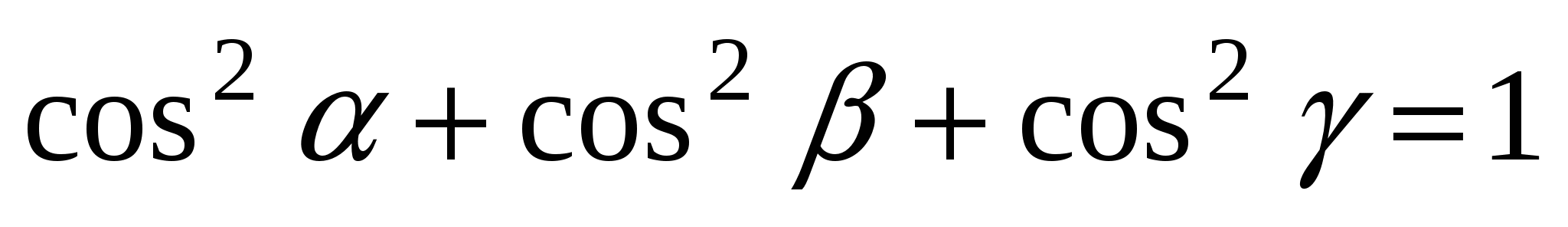 . .
Координаты вектора 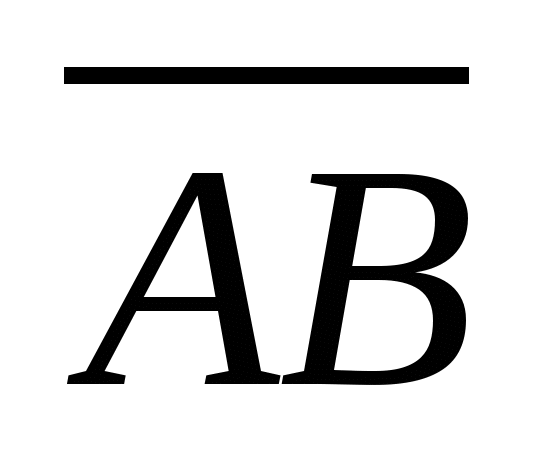 , заданного точками , заданного точками 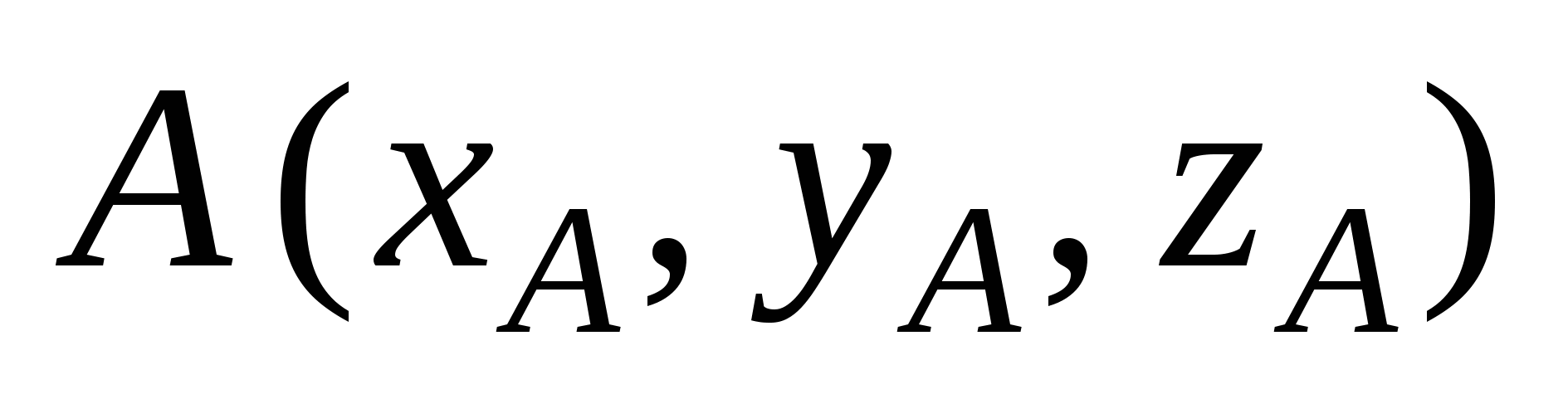 и и 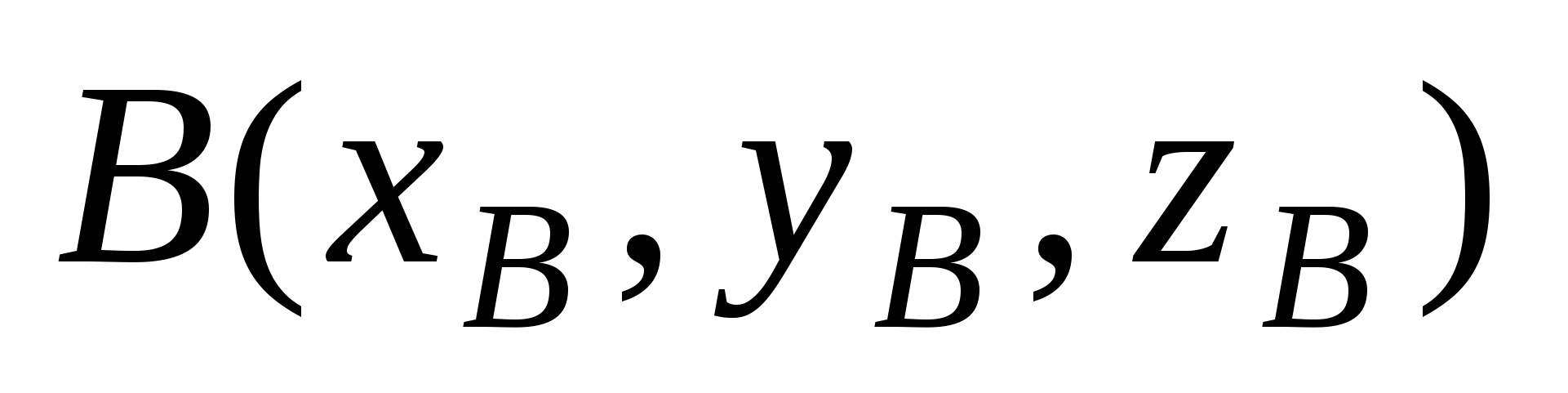 : : 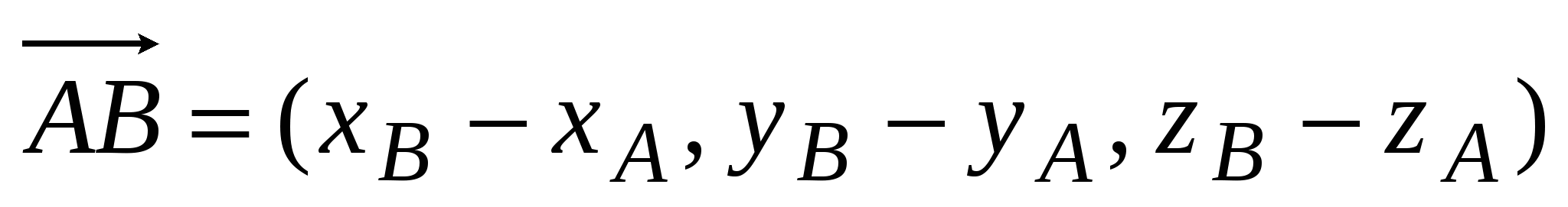 . .
Расстояние 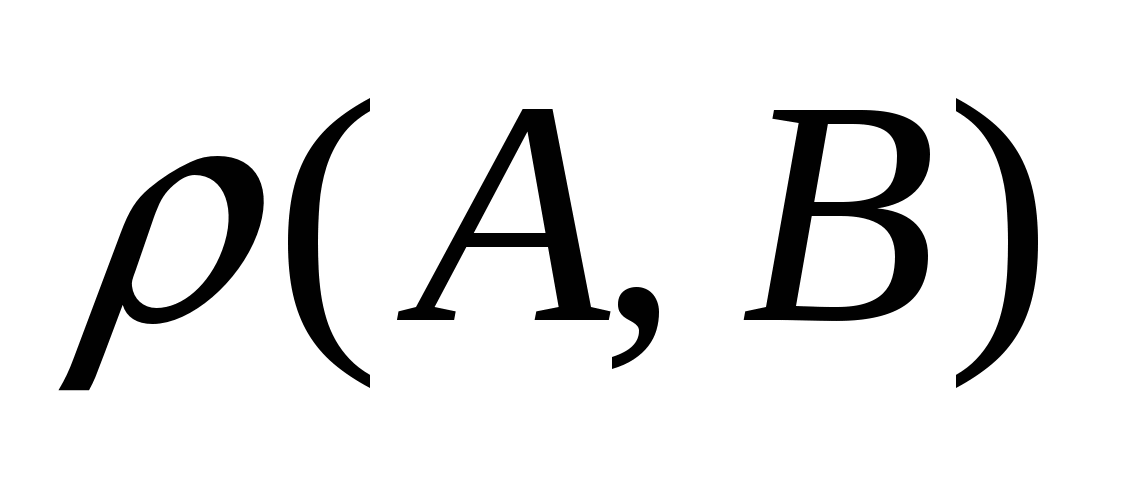 между точками между точками 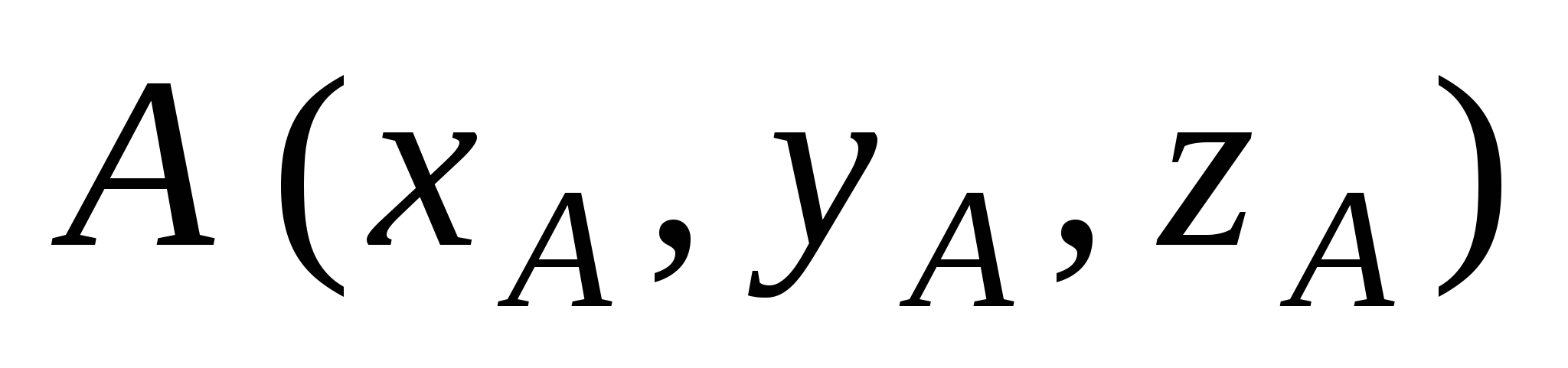 и и 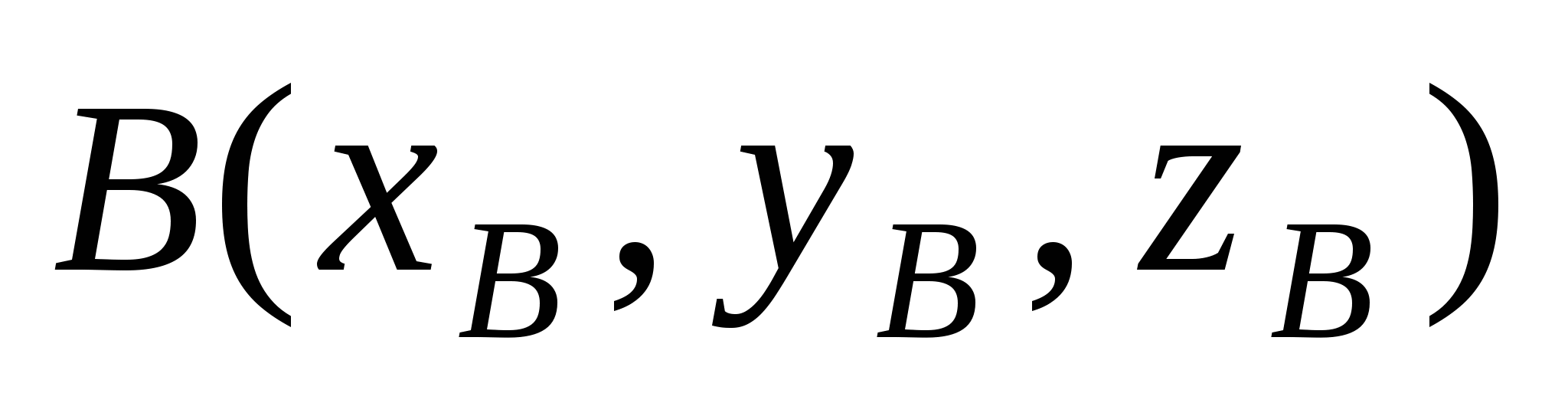 : :
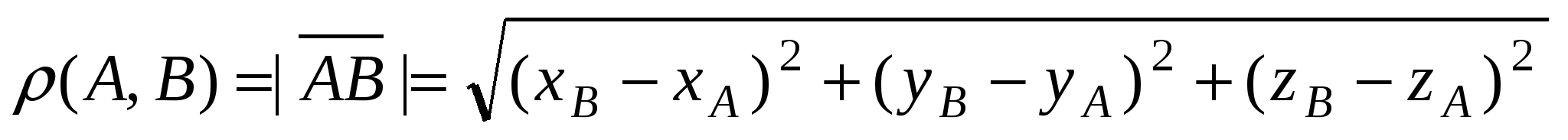 . .
Координаты точки 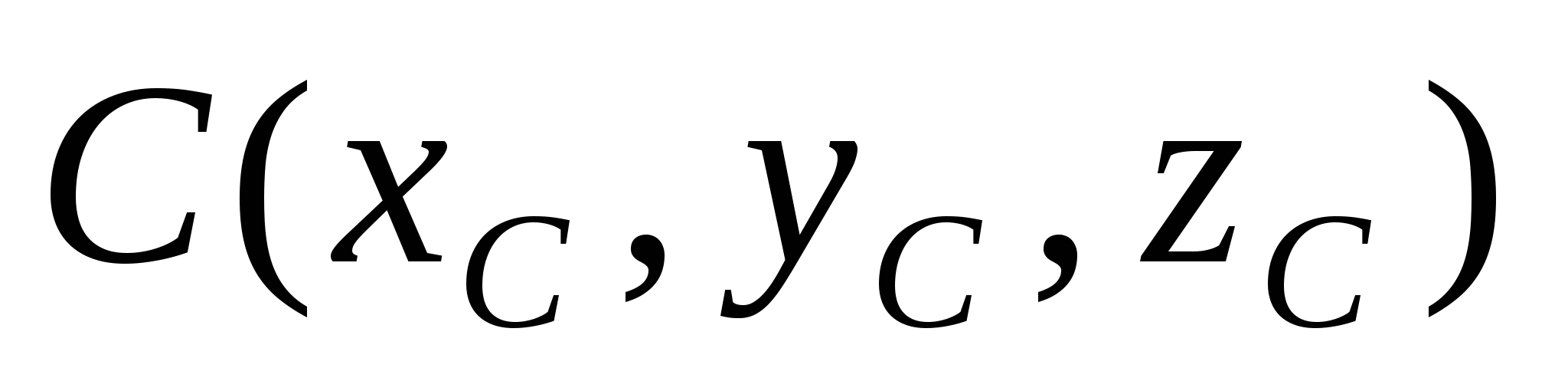 делящей отрезок делящей отрезок 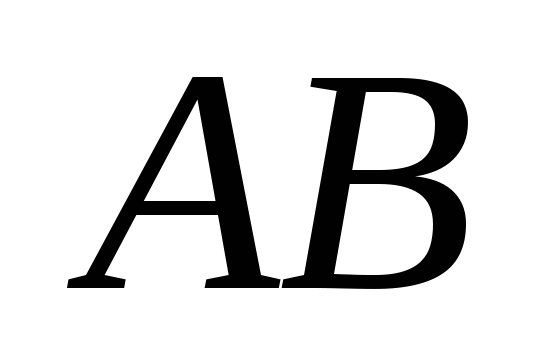 пополам: пополам: 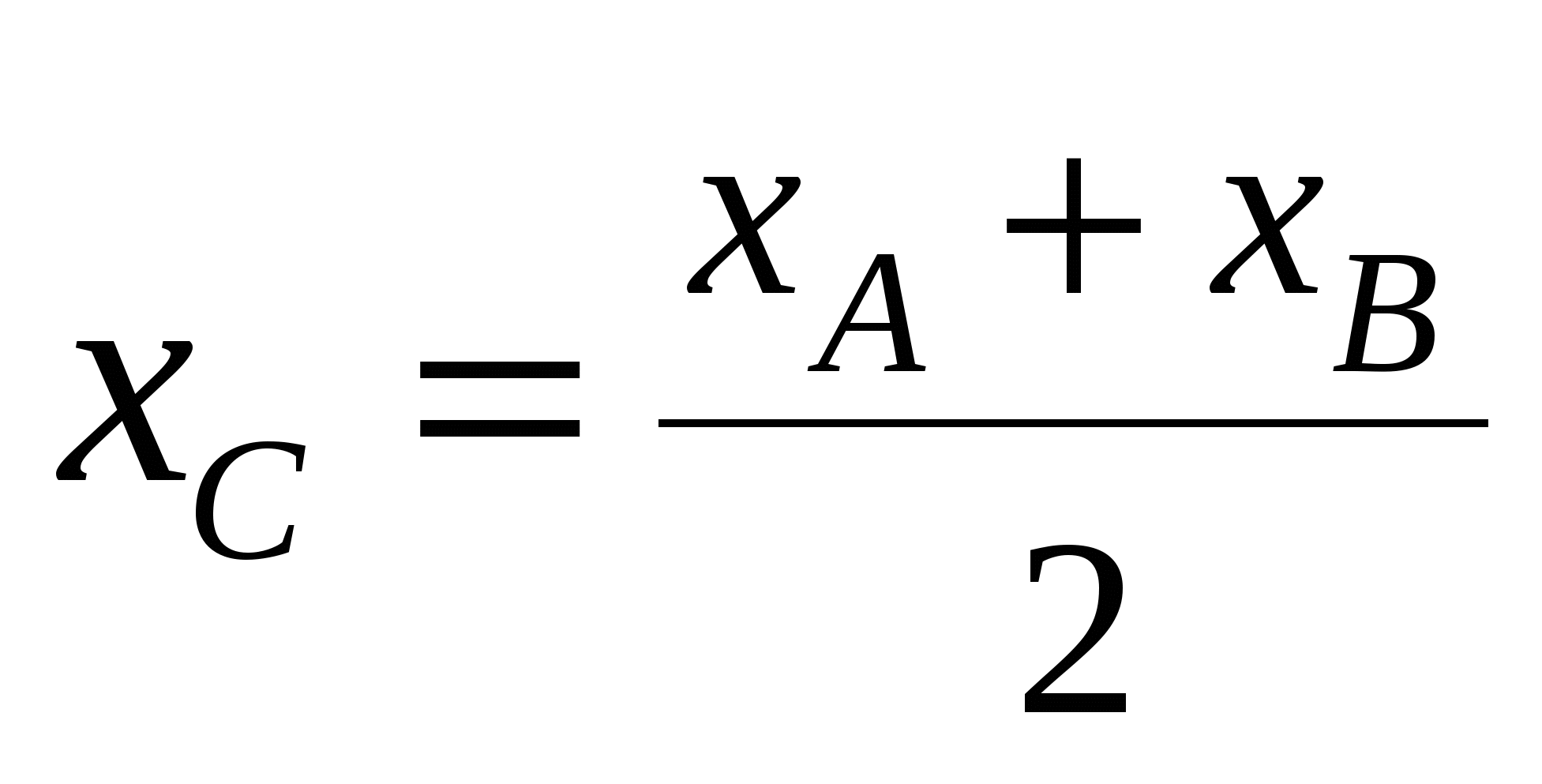 , , 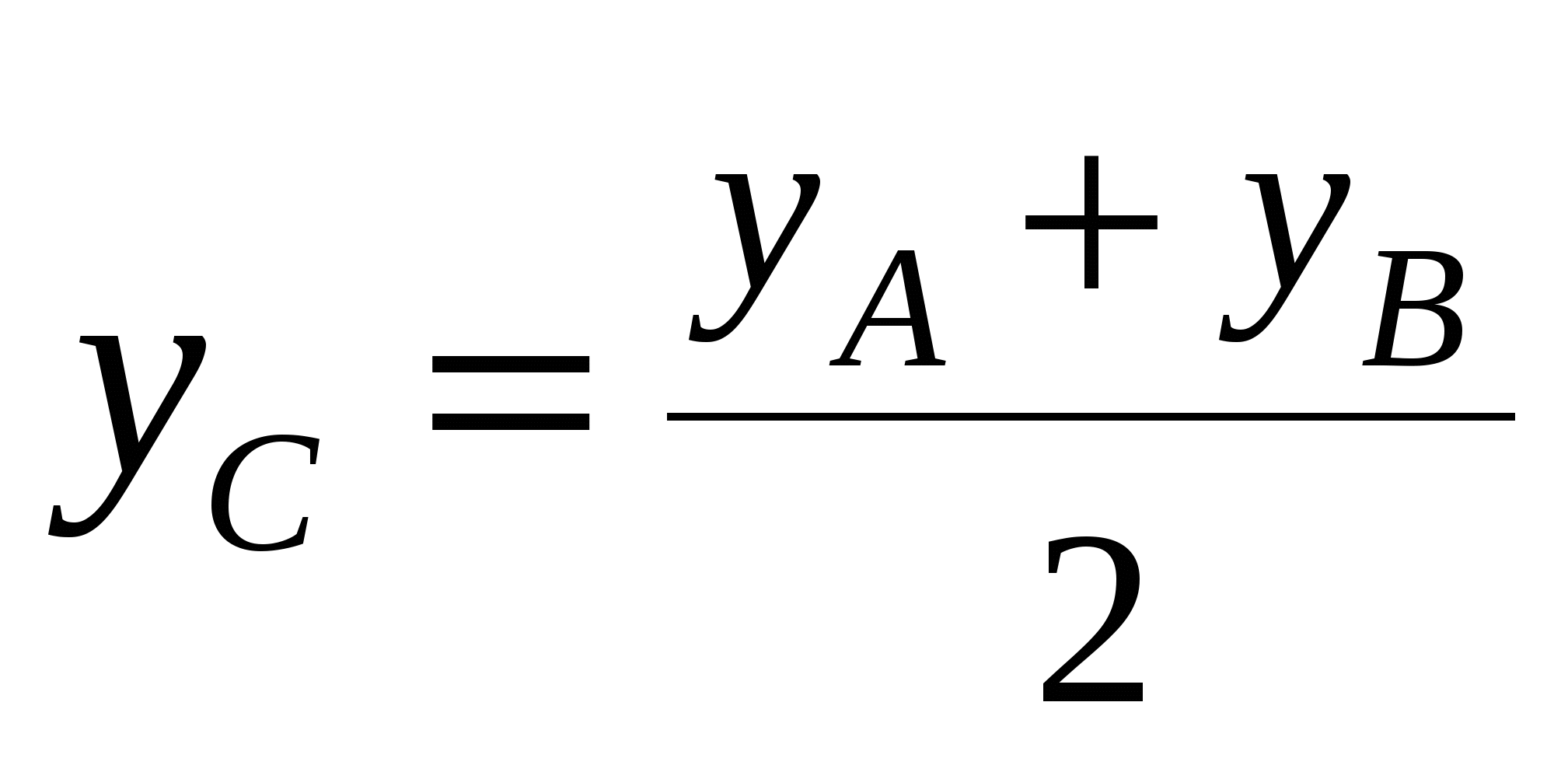 , , 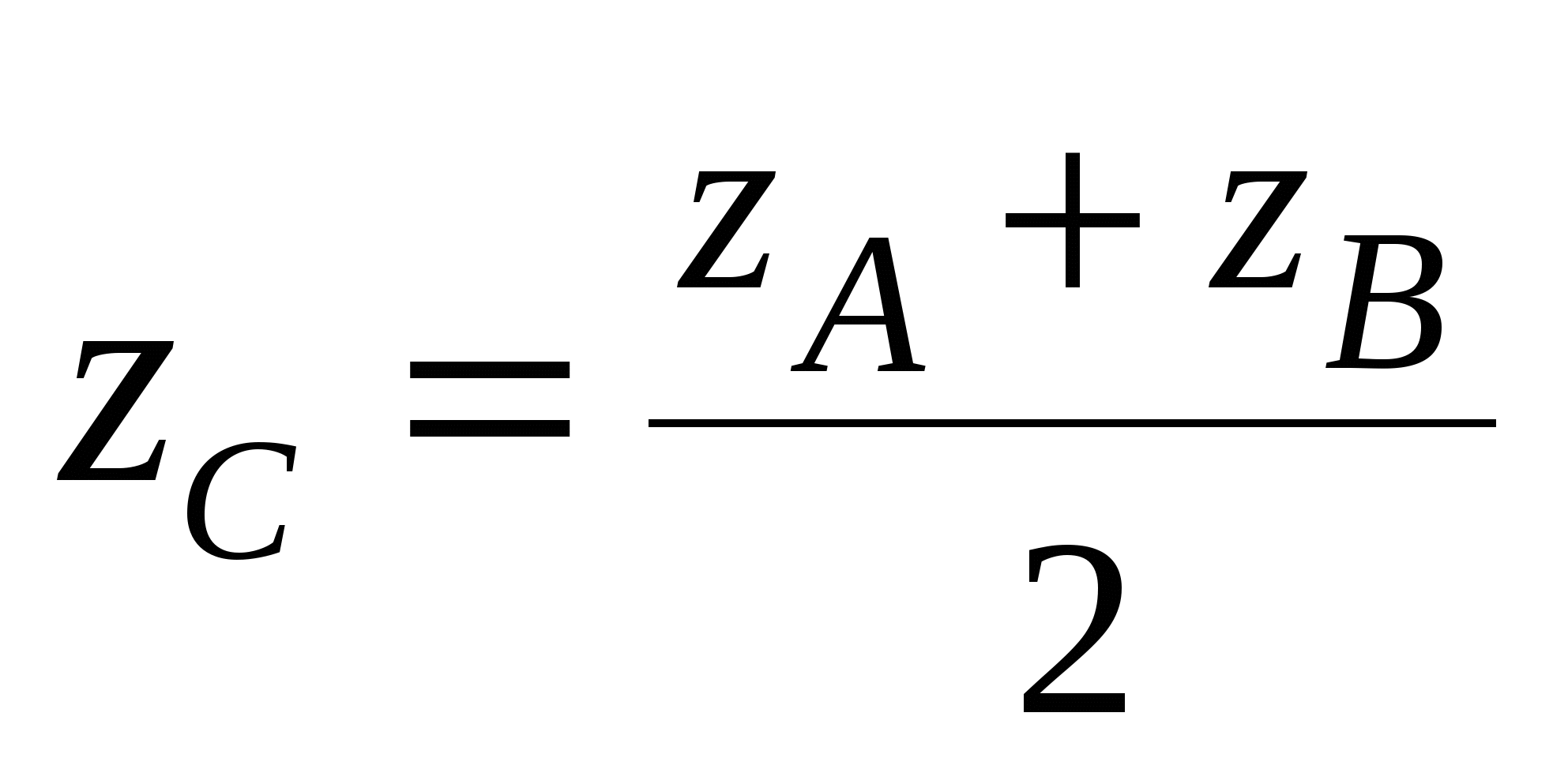 . .
Скалярное произведение векторов.
Скалярное произведение ненулевых векторов  и и 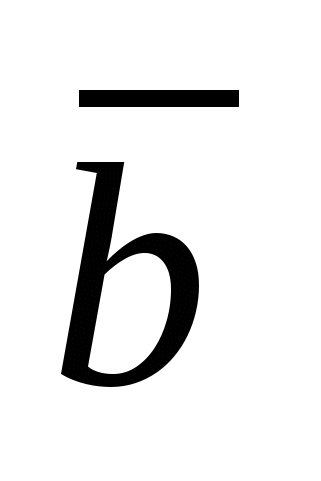 - число: - число: 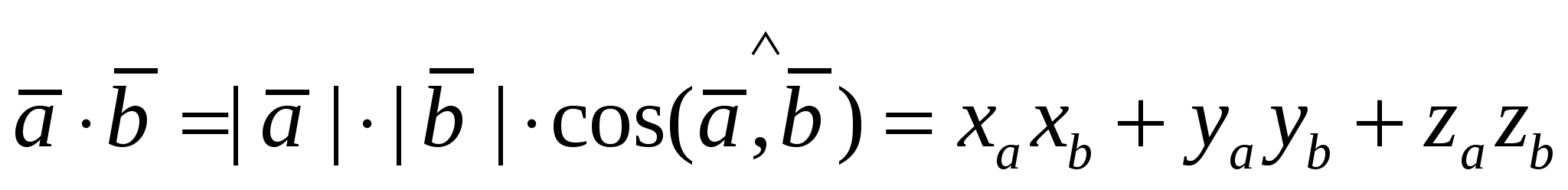 . .
Скалярное произведение обладает свойствами:
1) 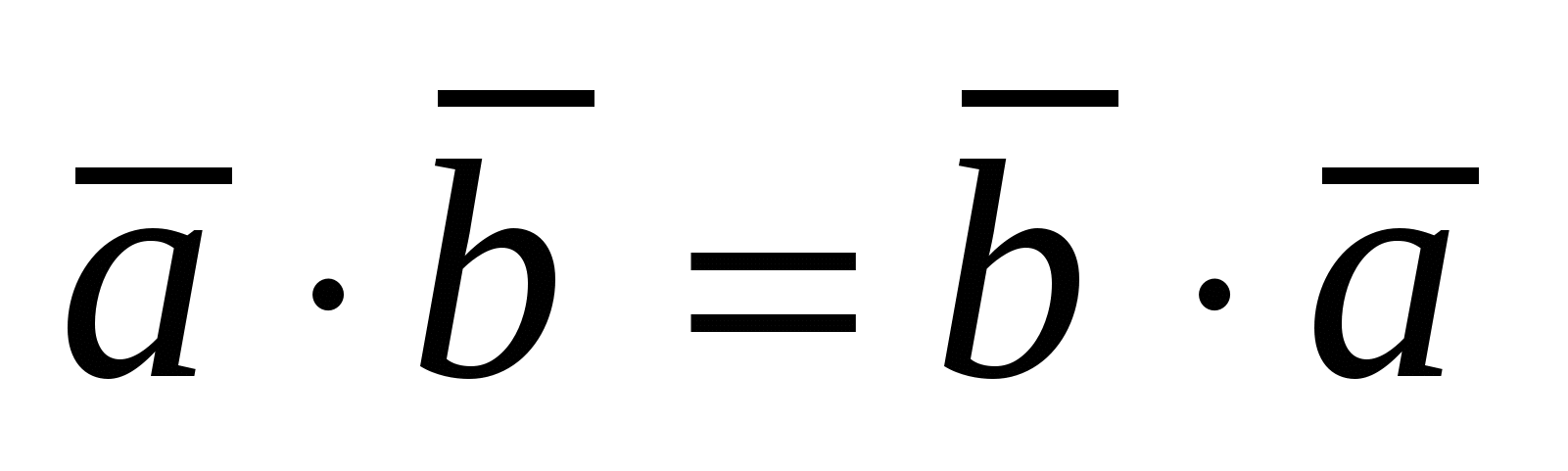 ; 2) ; 2) 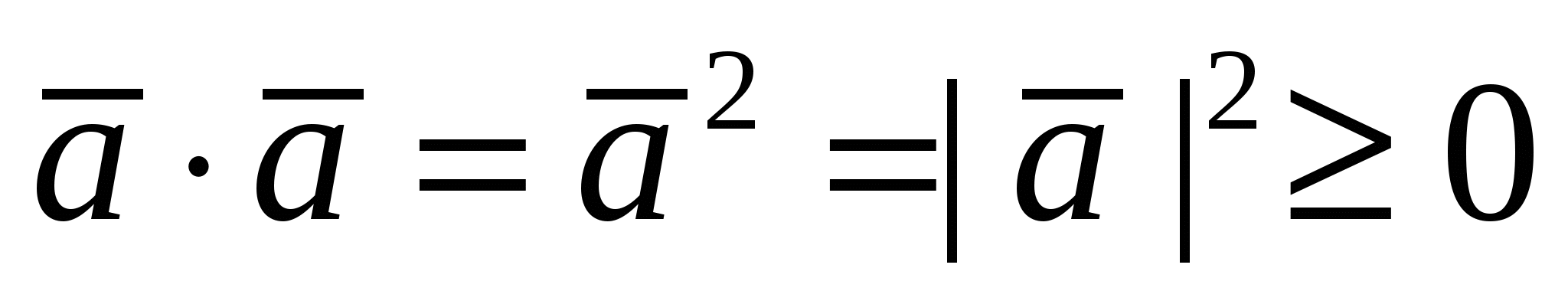 ; 3) ; 3) 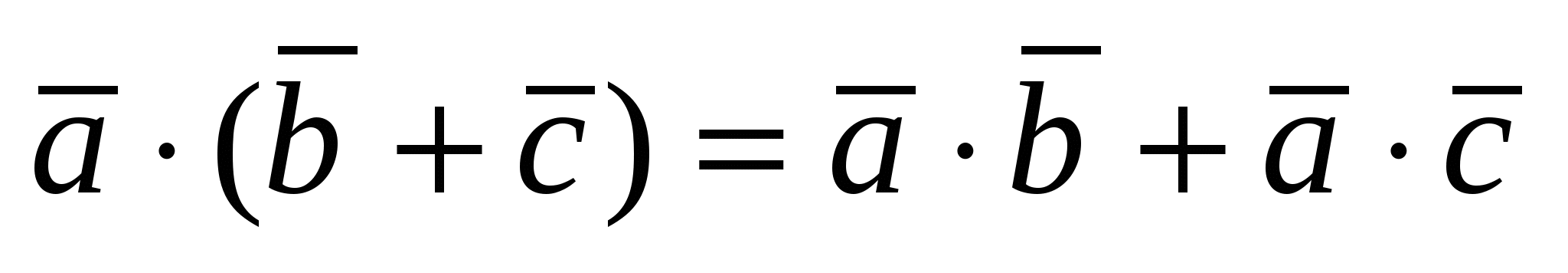 ; 4) ; 4) 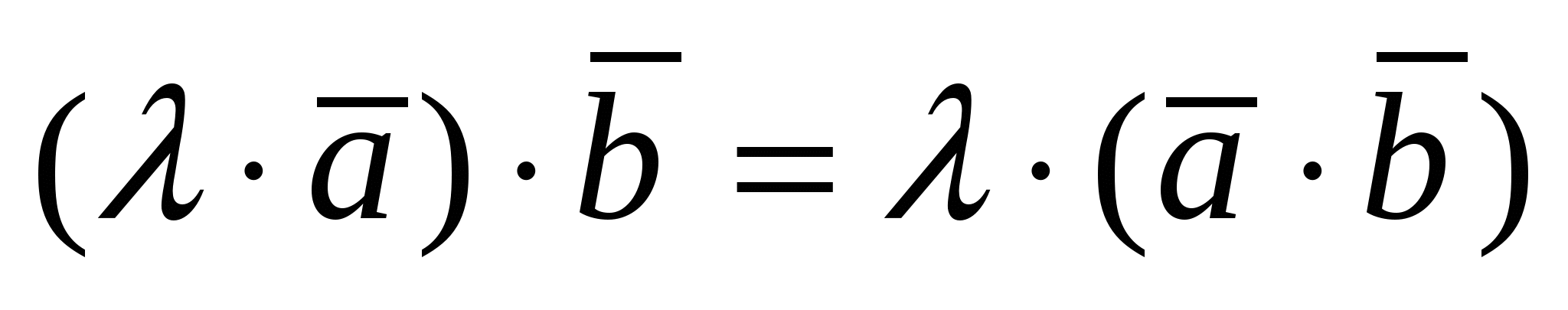 , где , где 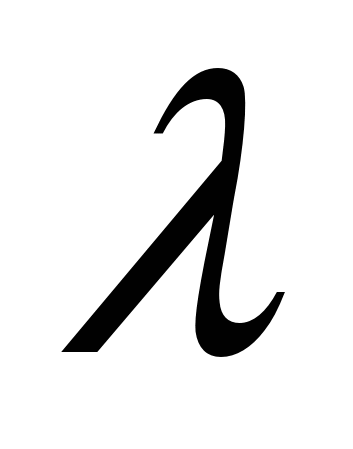 - число; - число;
Для векторов канонического базиса 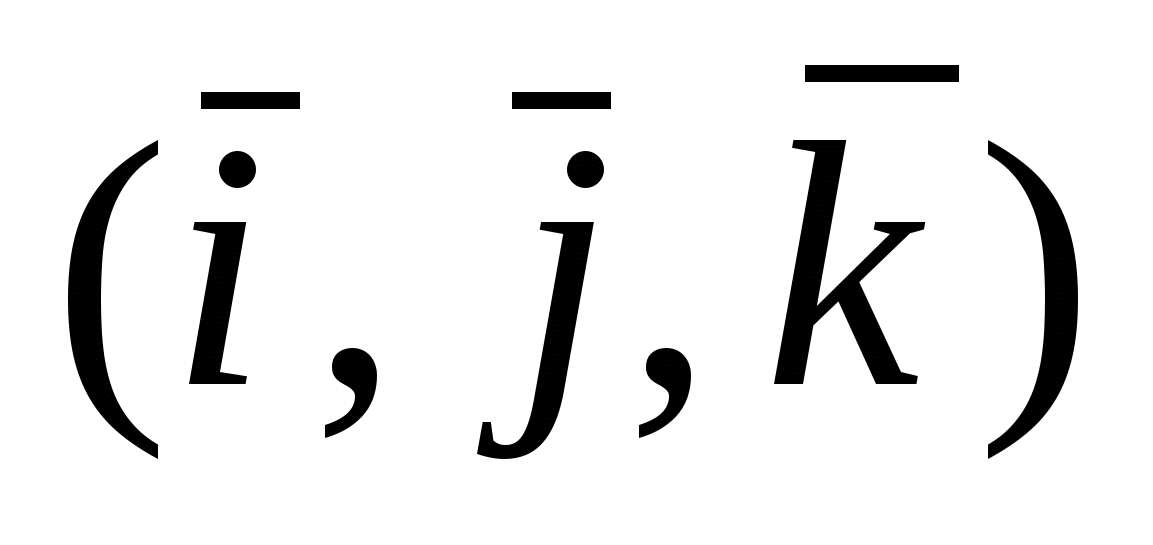 : : 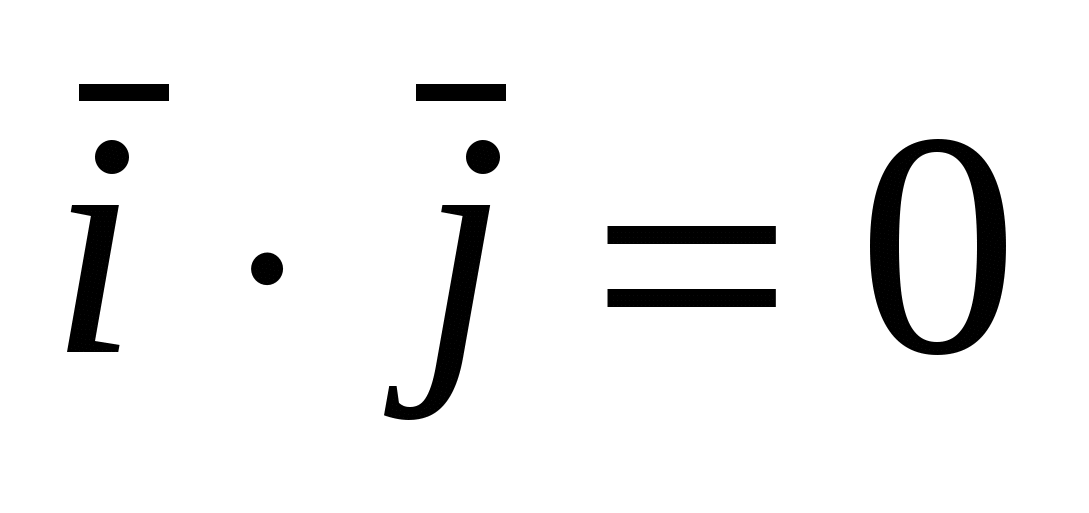 , , 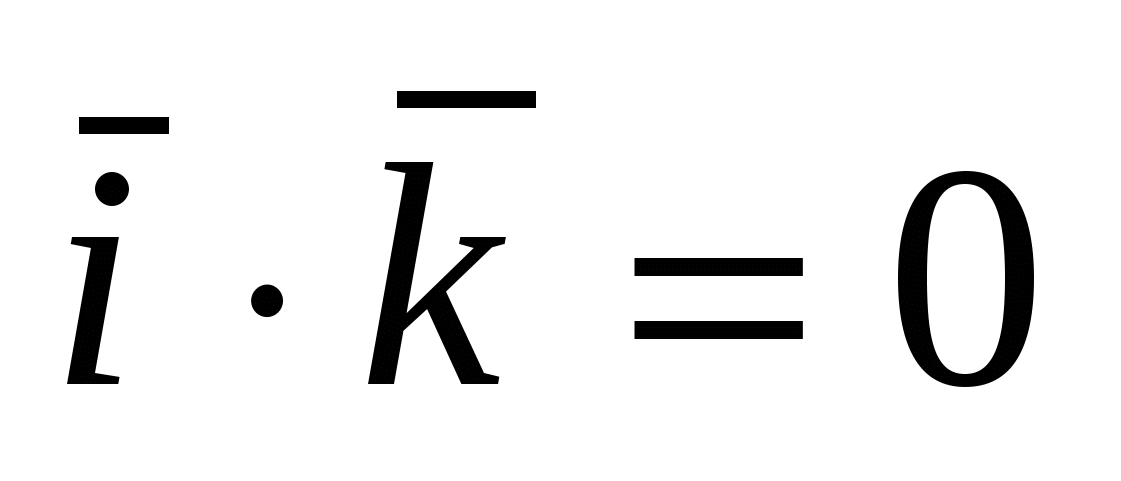 , , 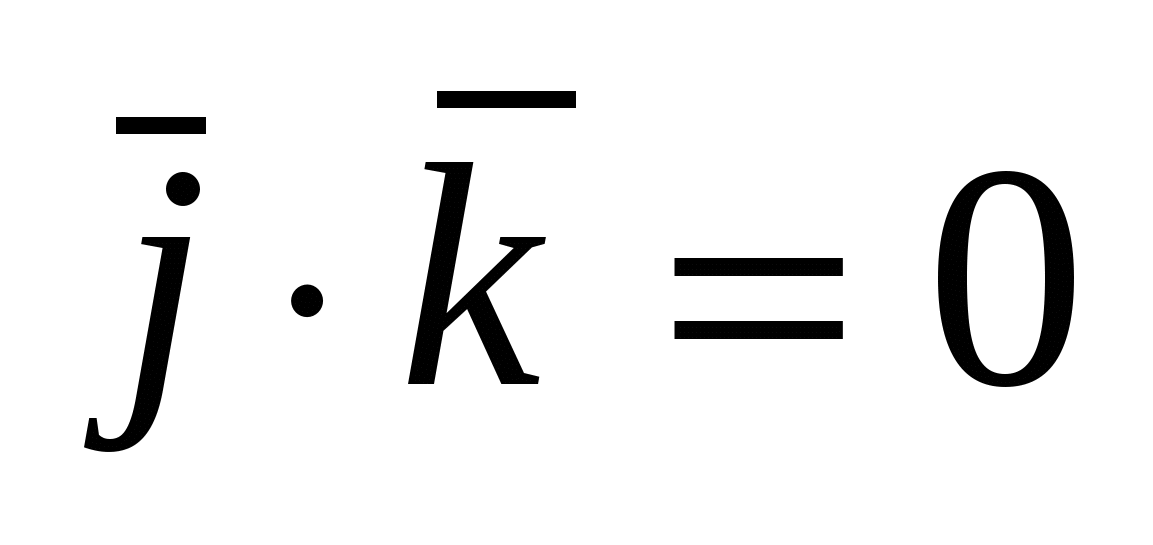 , , 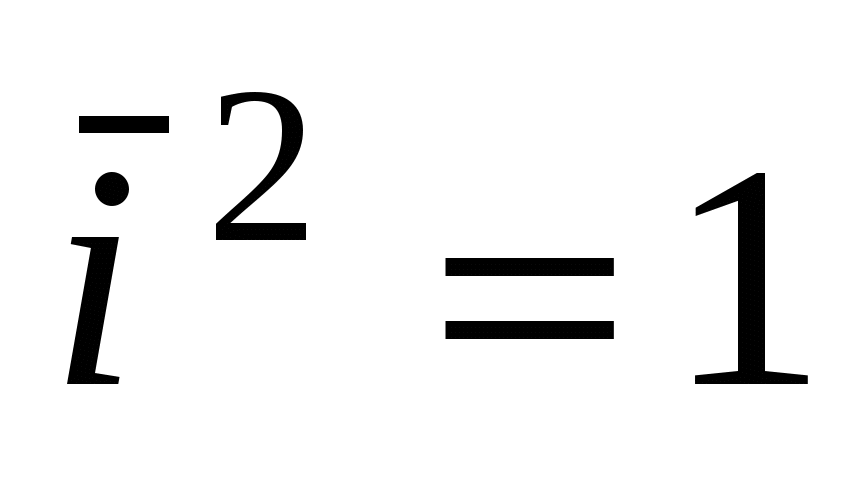 , , 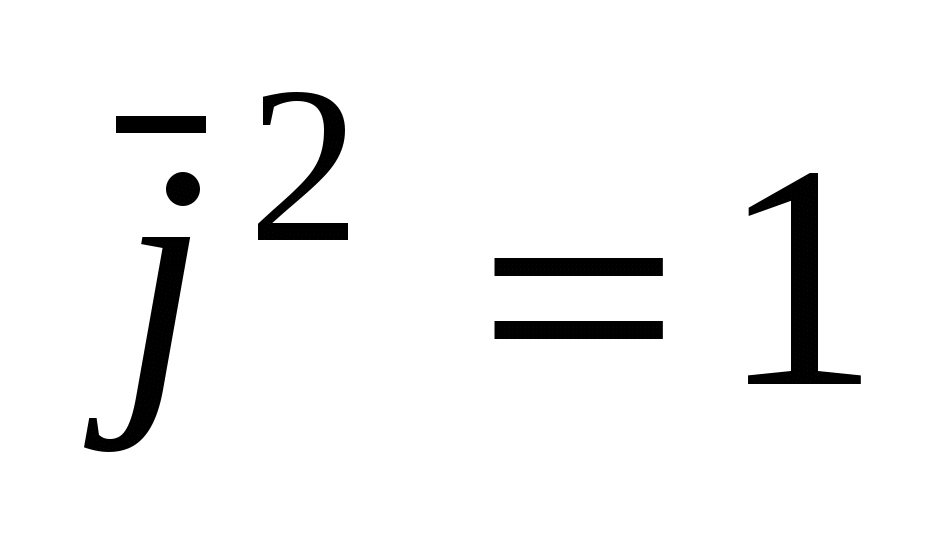 , , 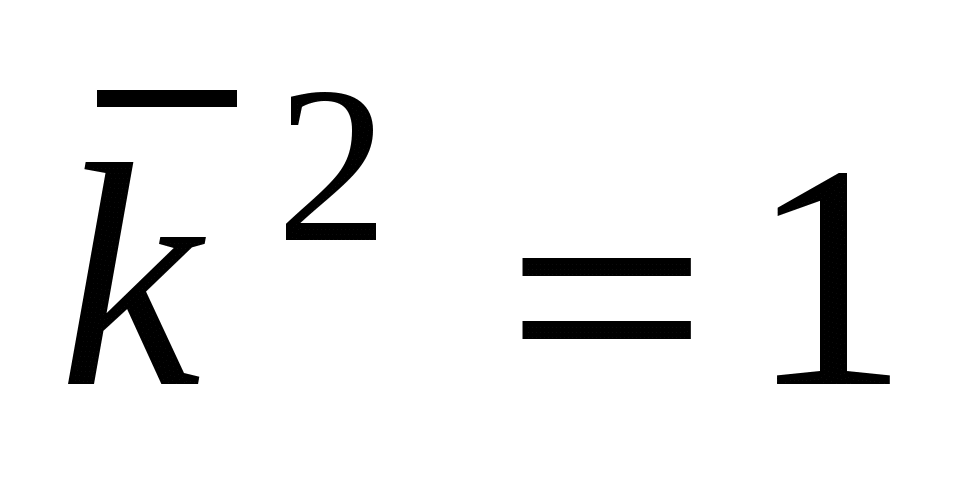 . .
Некоторые приложения скалярного произведения:
1) Вычисление угла между векторами  и и 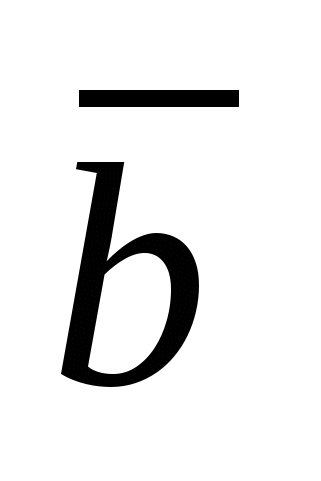 : : 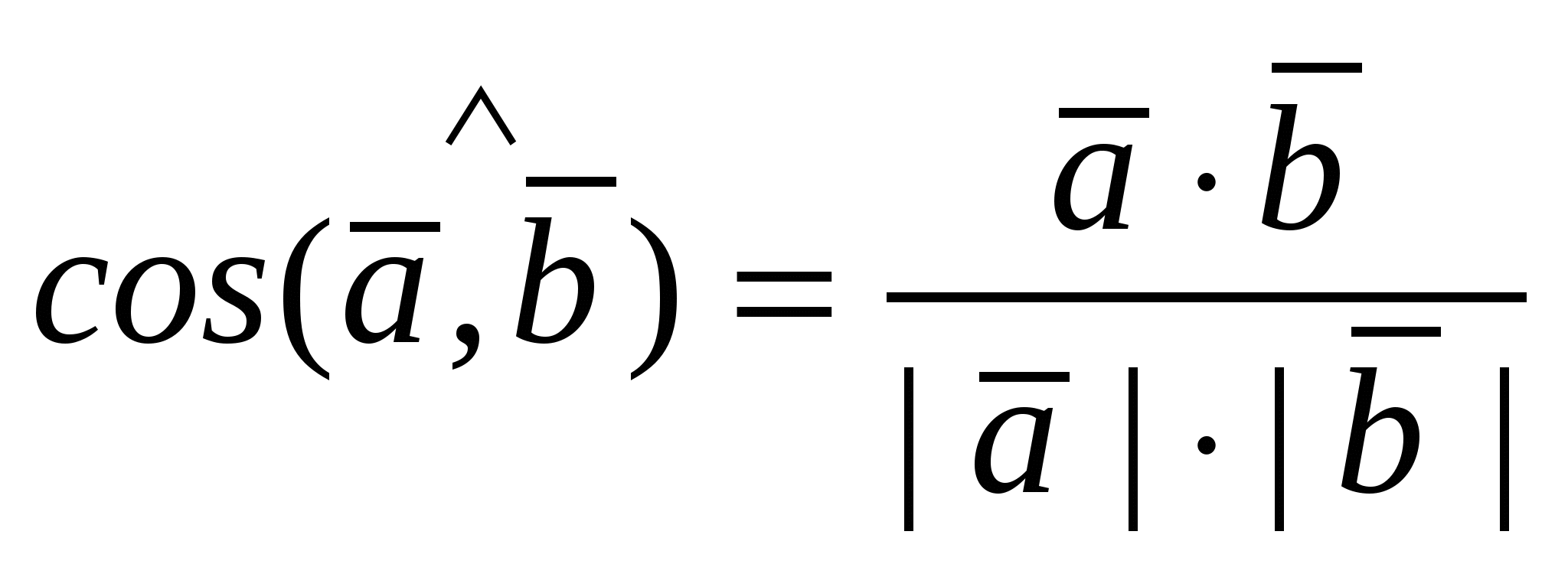 . .
2) Нахождение проекции вектора  на вектор на вектор 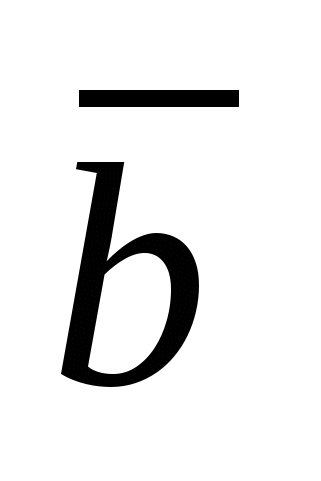 : : 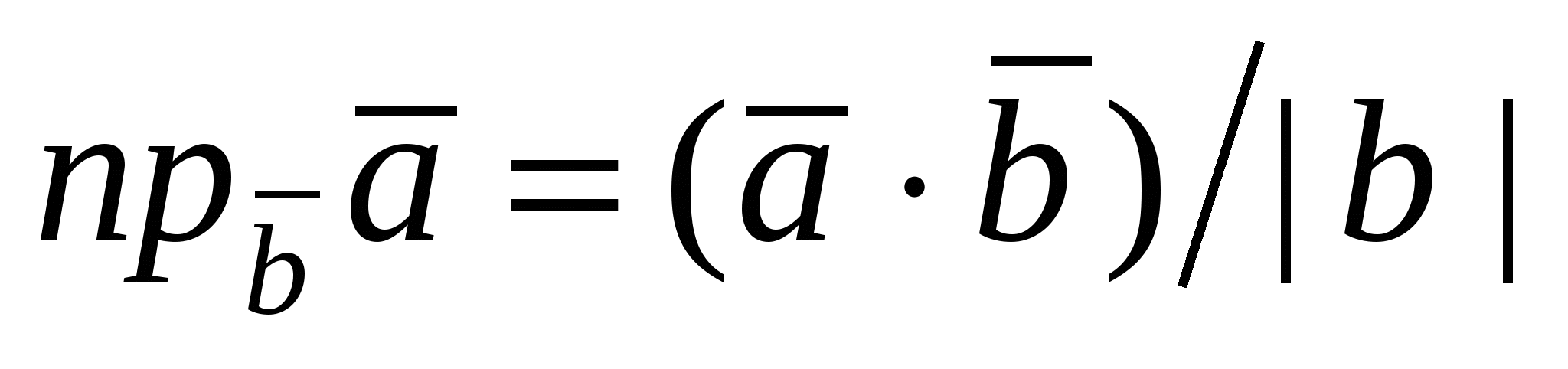 . .
3) Вычисление длины вектора 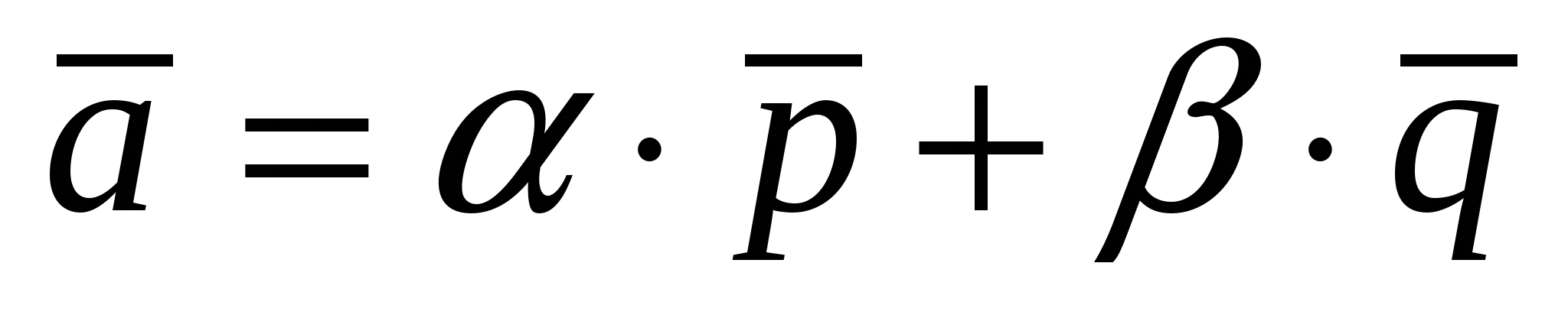 : : 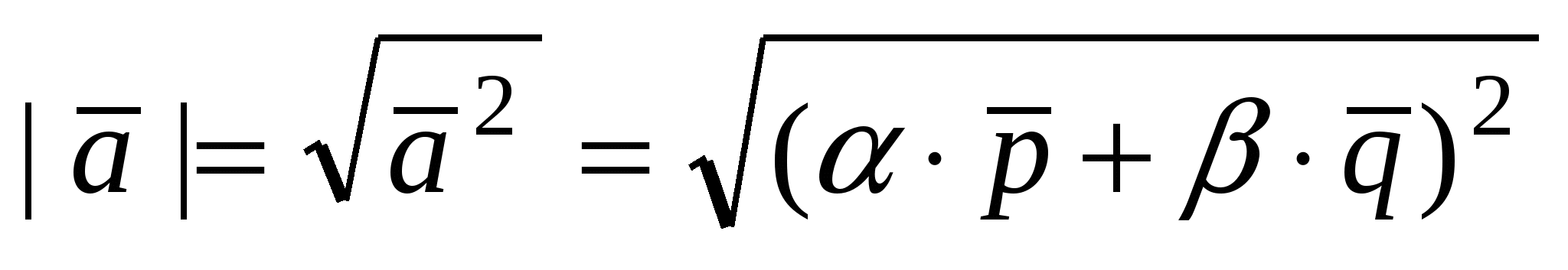
4) Установление перпендикулярности векторов  и и 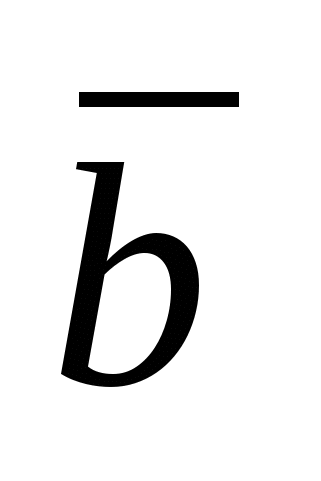 : : 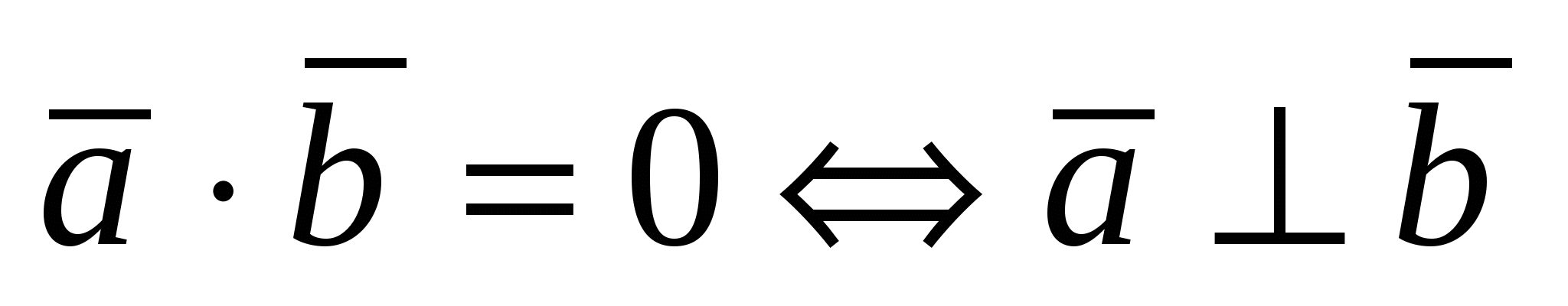 . .
Векторное произведение векторов.
Векторное произведение векторов  и и 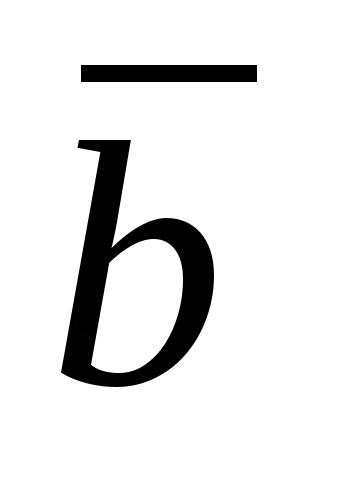 - вектор - вектор 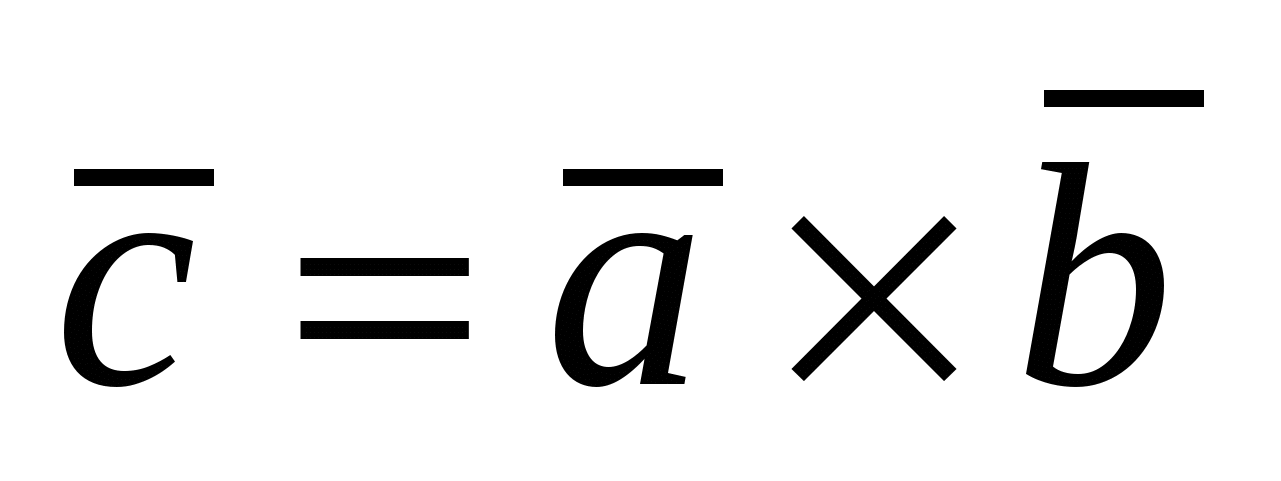 , определяемый условиями: , определяемый условиями:
1) 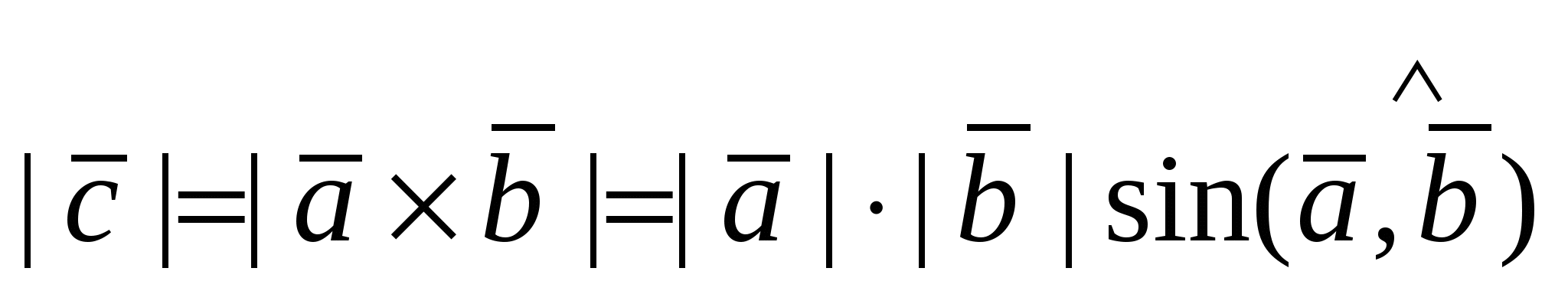 ; 2) ; 2) 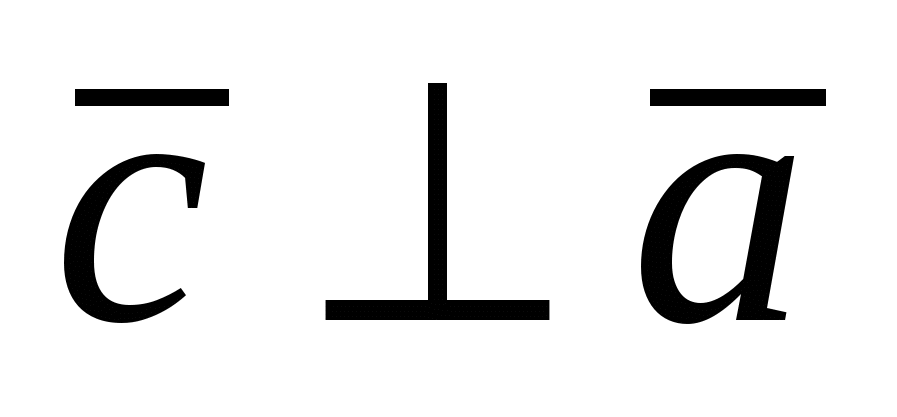 и и 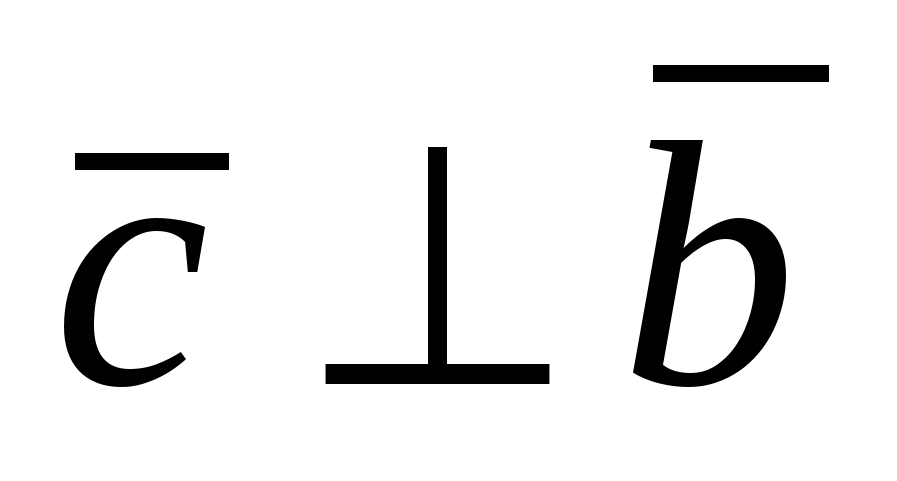 ; 3) ; 3)  - правая тройка векторов. - правая тройка векторов.
Векторное произведение обладает свойствами:
1) 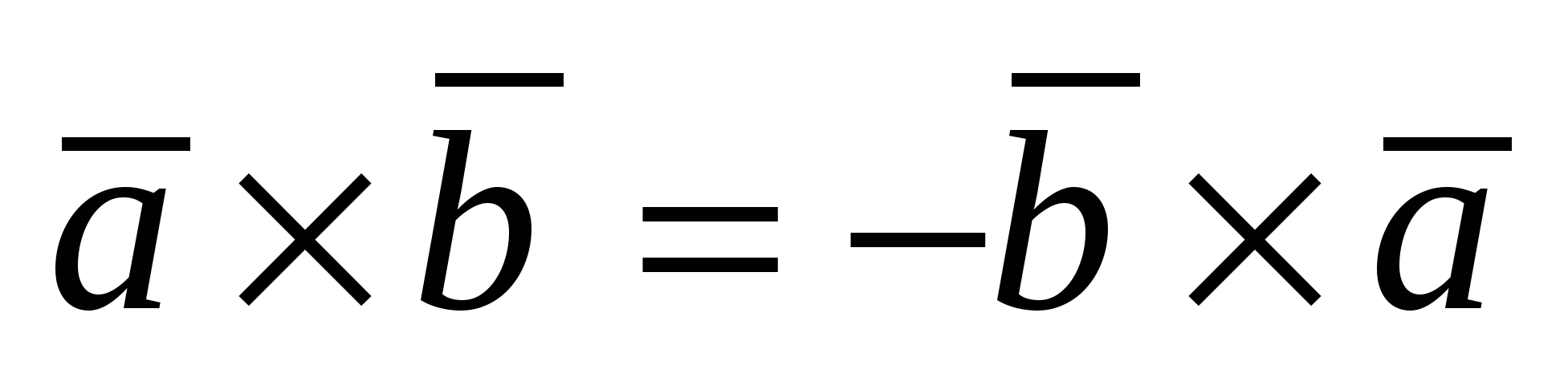 ; 2) ; 2) 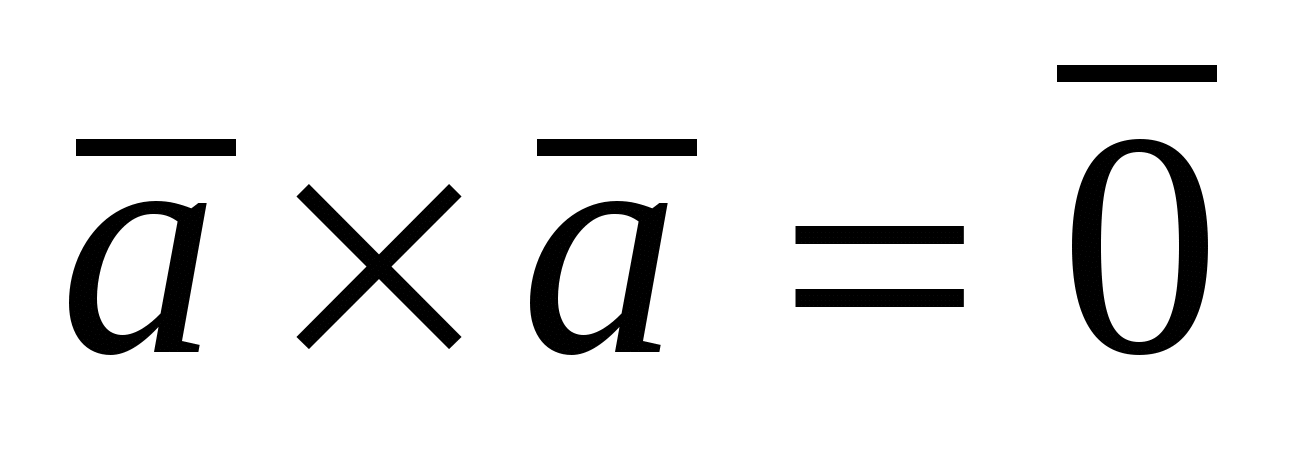 3) 3) 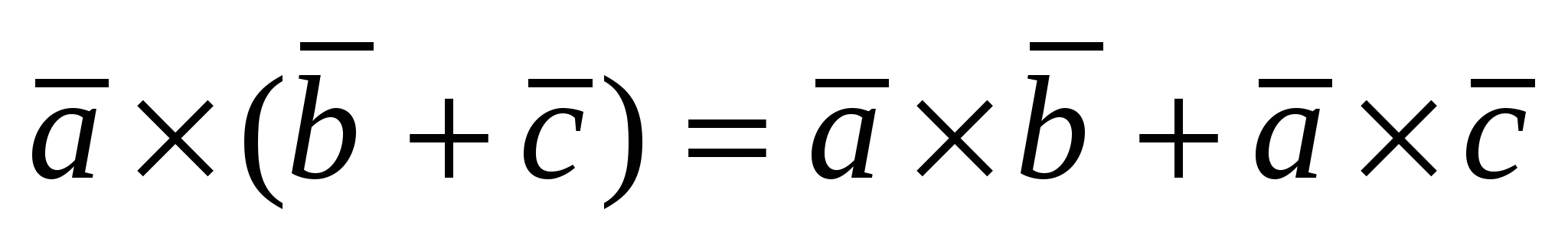 ; 4) ; 4) 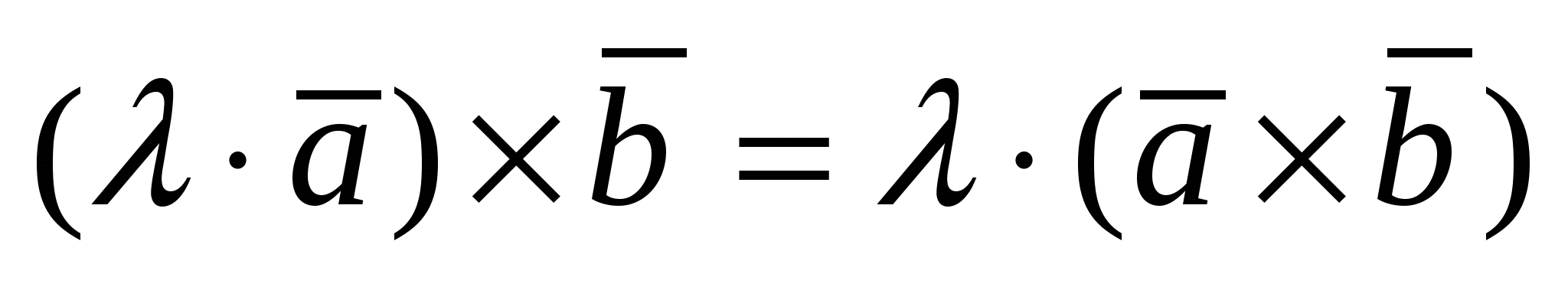 , где , где 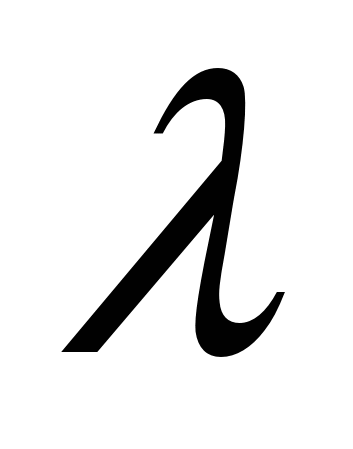 - число; - число;
Для векторов канонического базиса 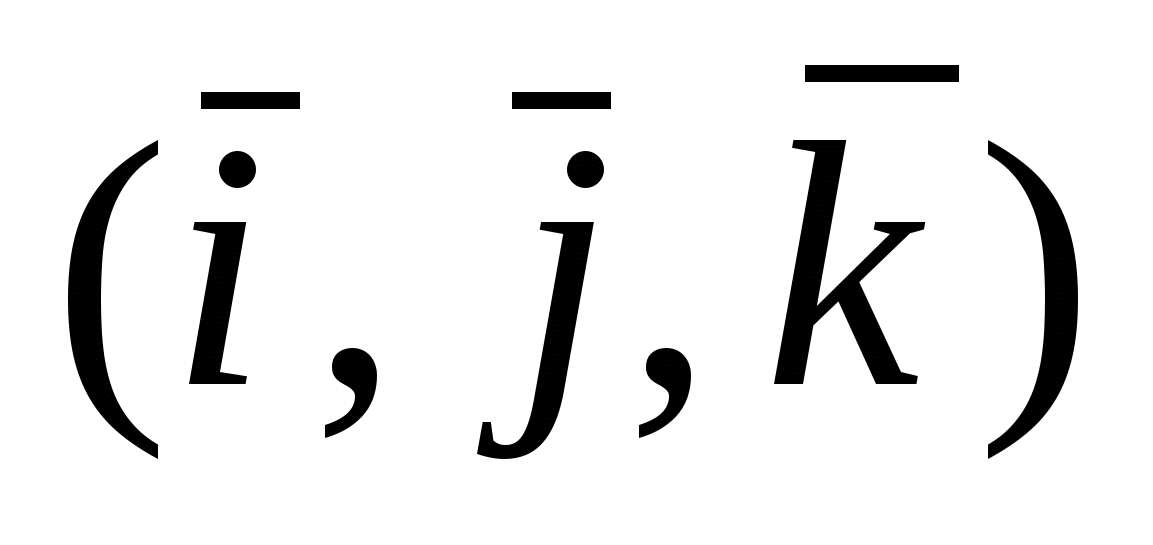 : : 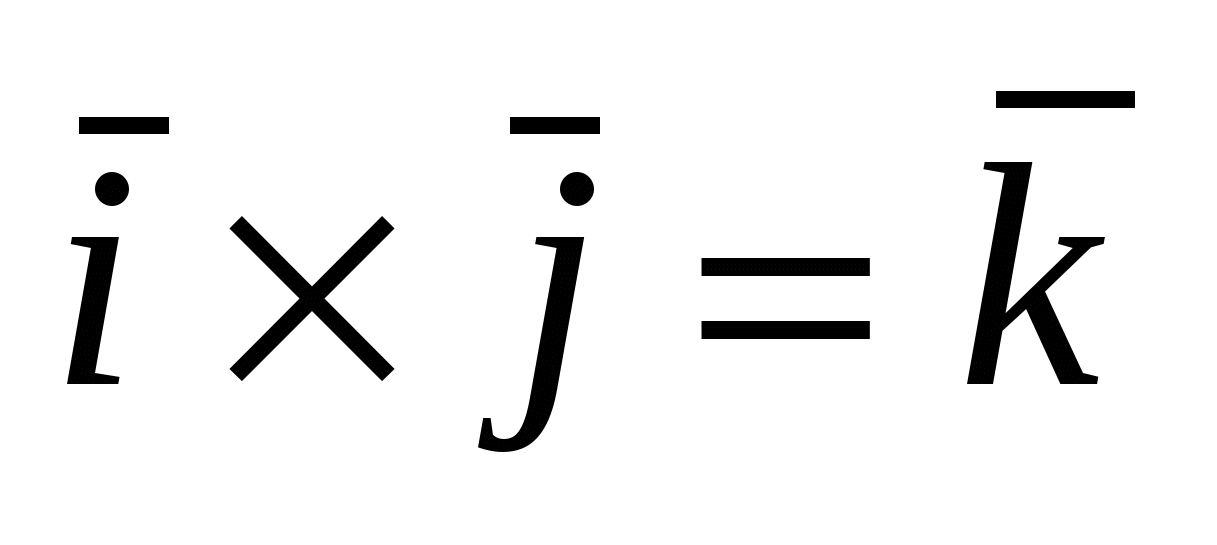 , , 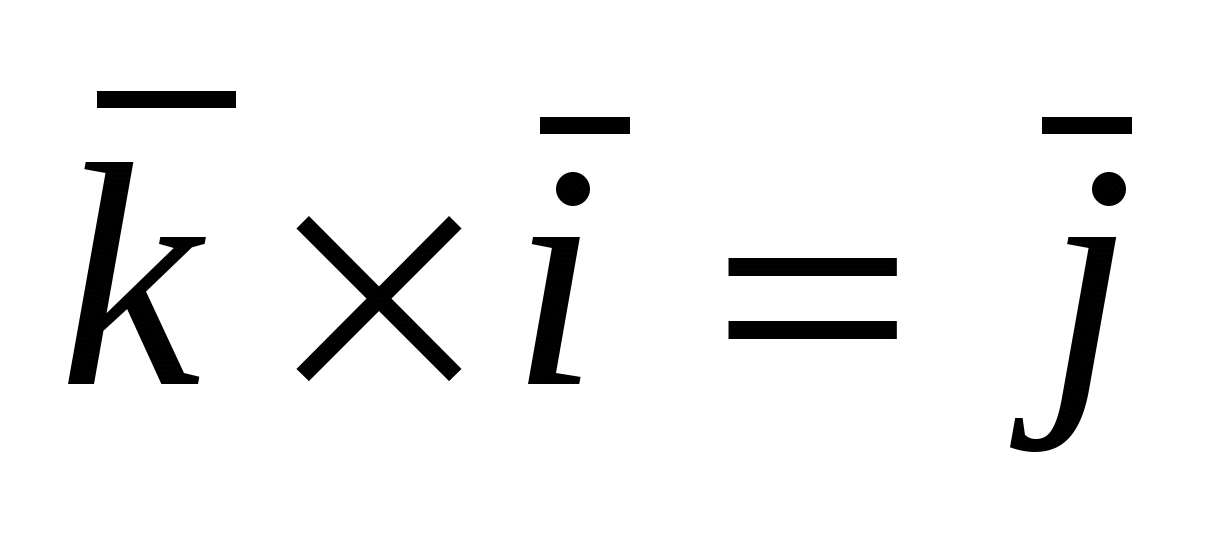 , , 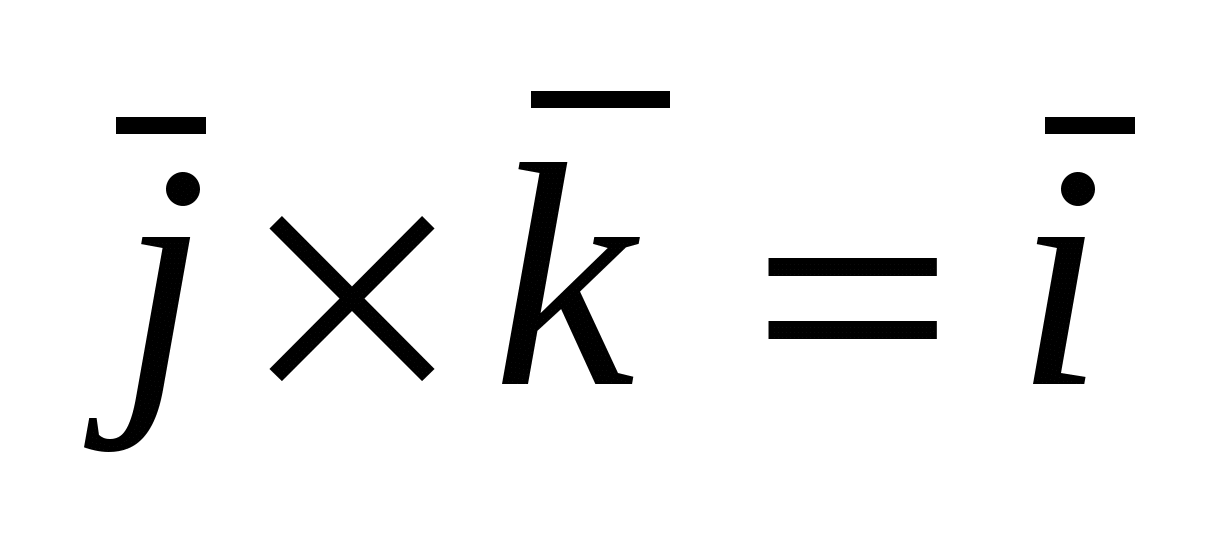 , , 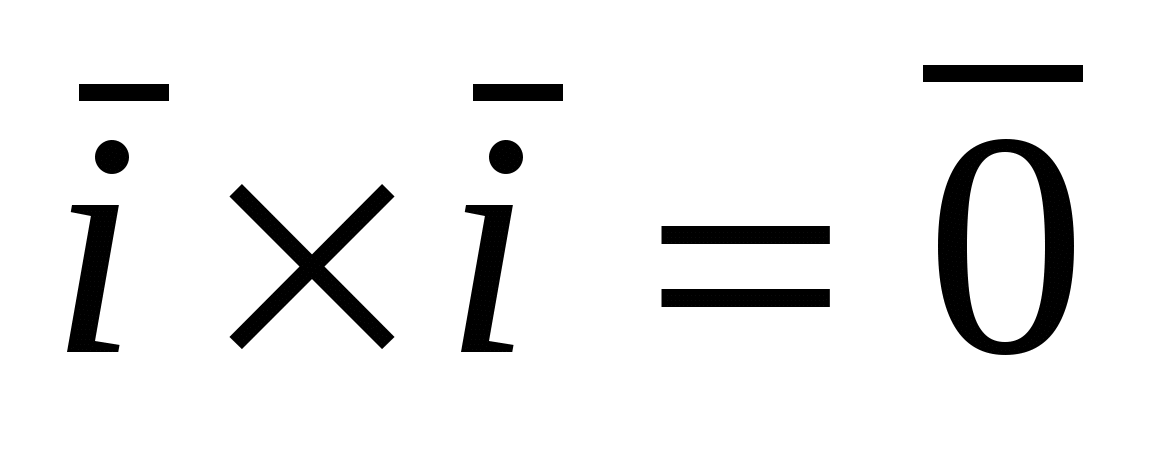 , , 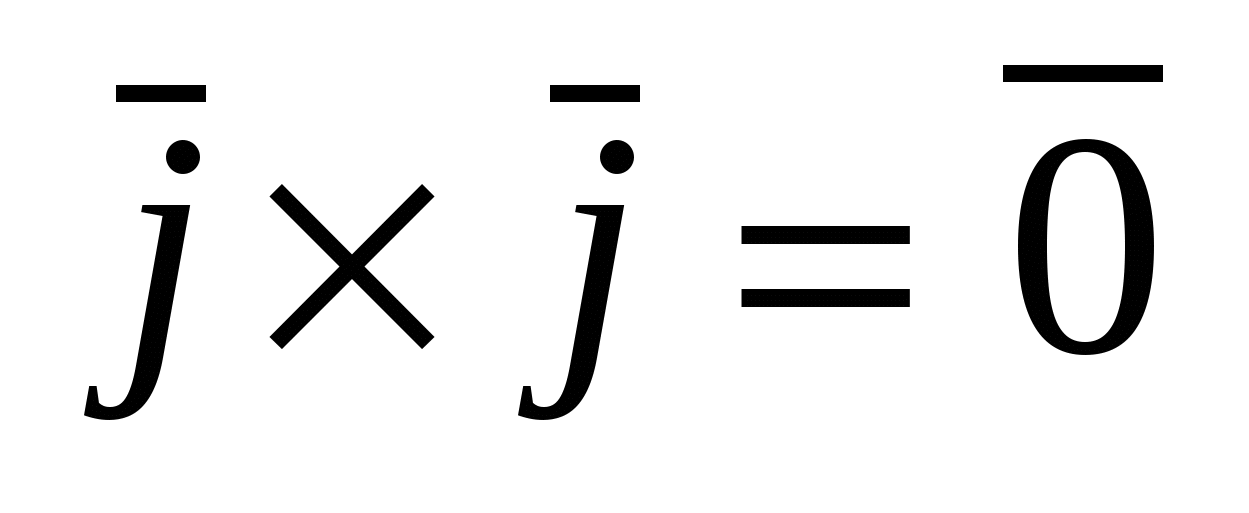 , , 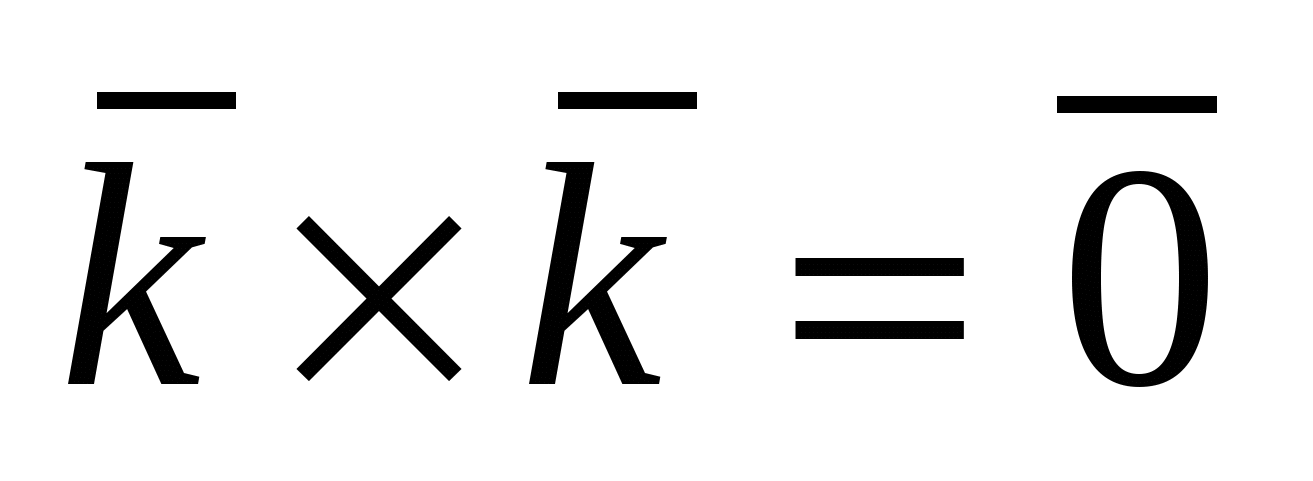 . .
Для векторов  и и 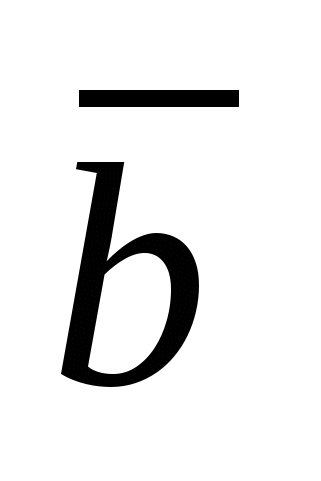 , заданных координатами , заданных координатами 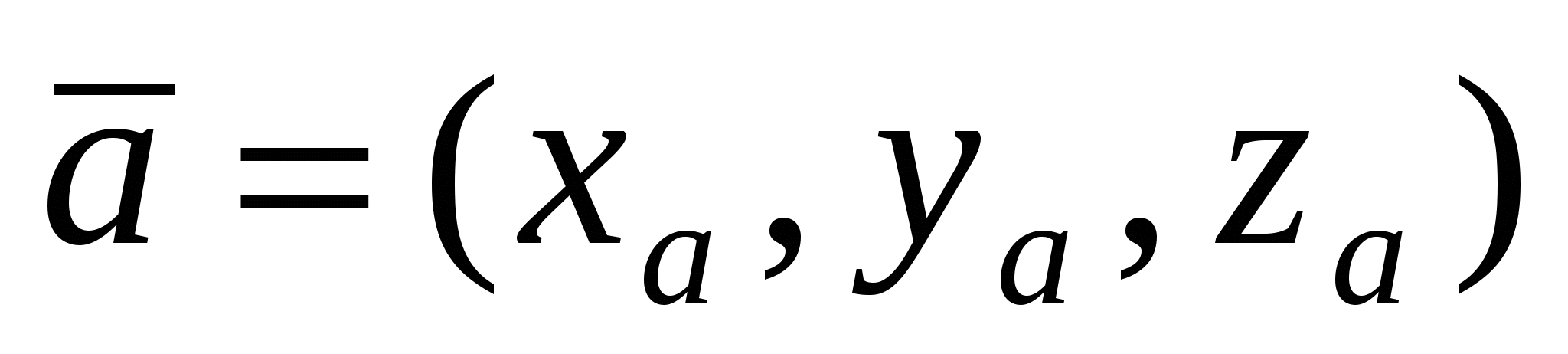 , , 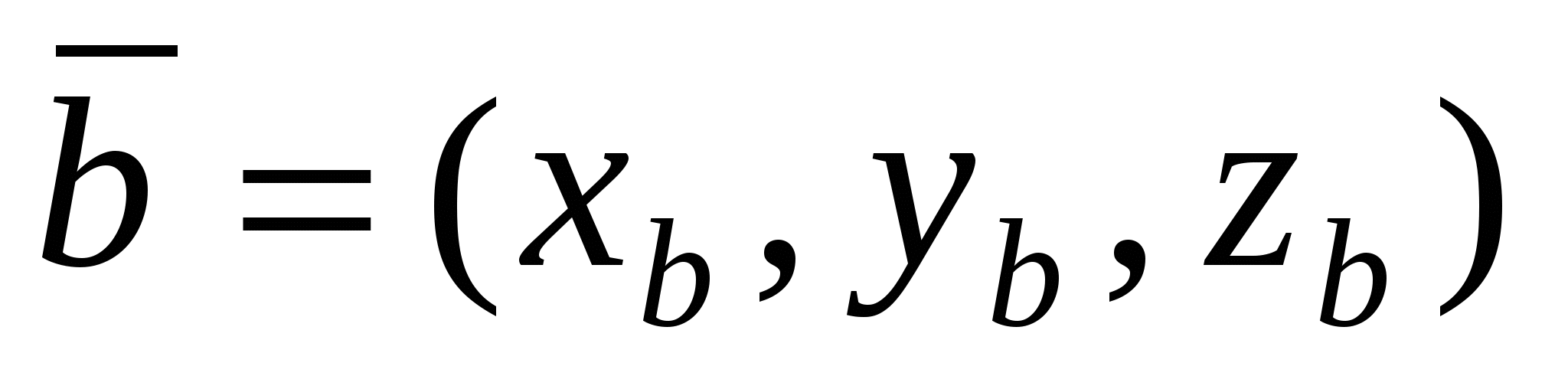 : : 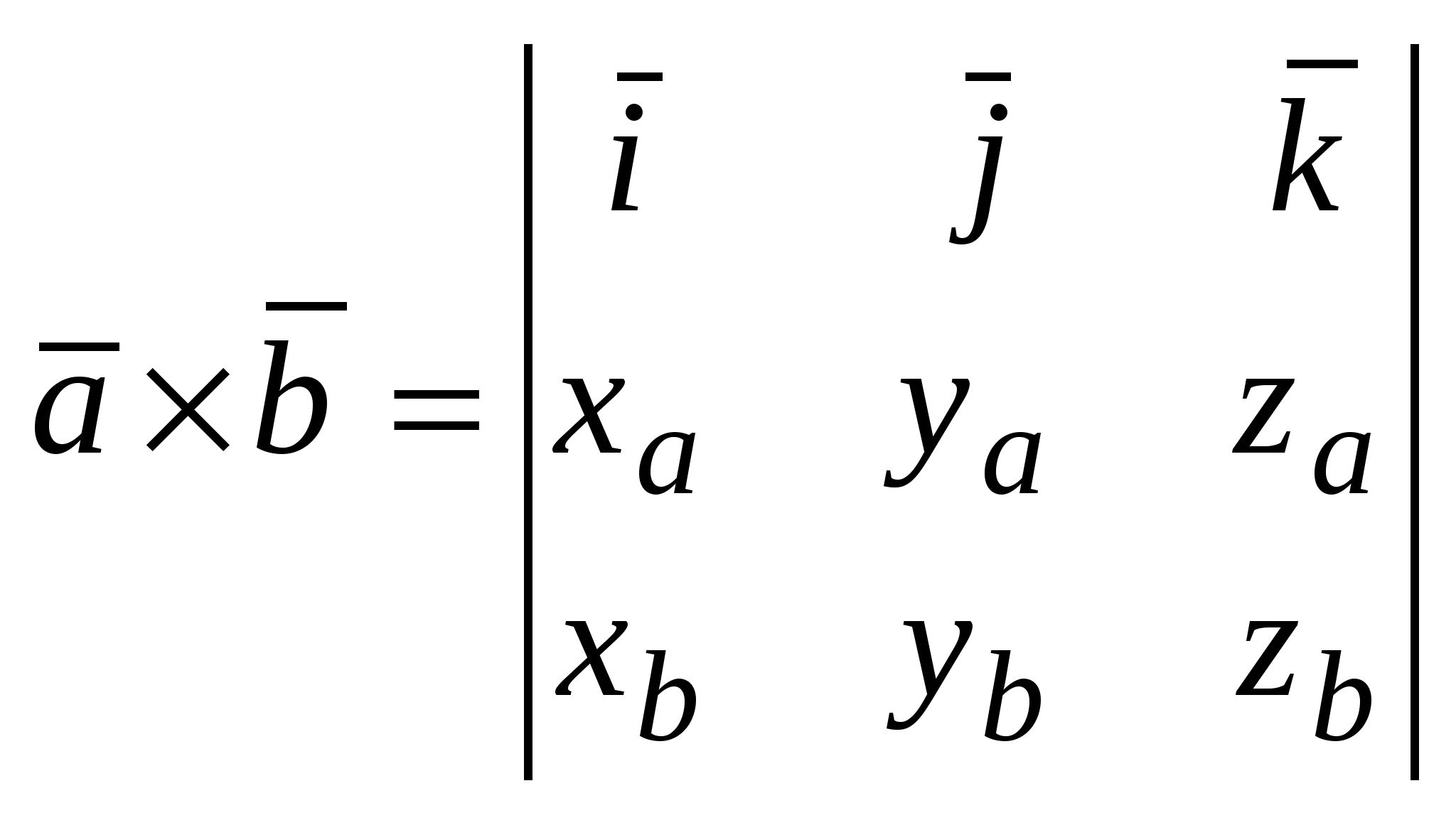
Некоторые приложения векторного произведения:
1) Вычисление площадей треугольника и параллелограмма: 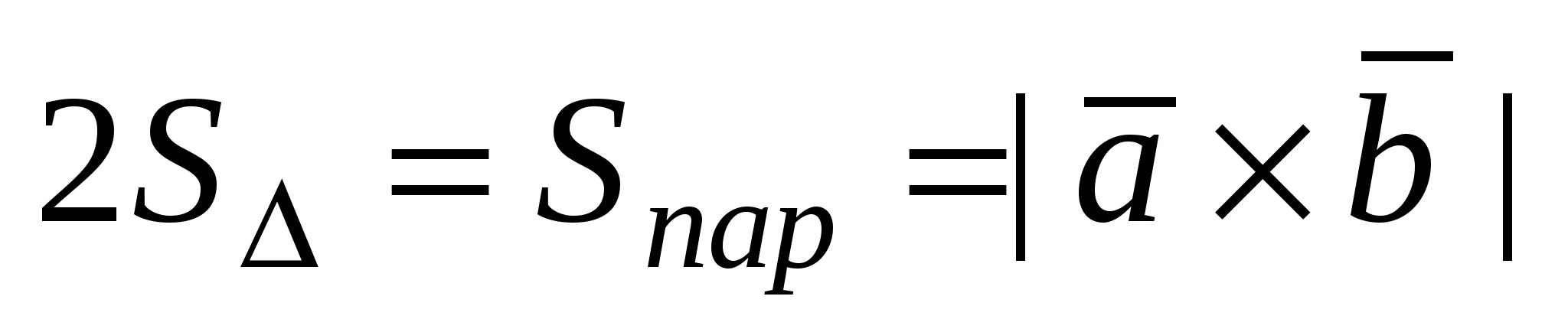 . .
2) Установление параллельности векторов  и и 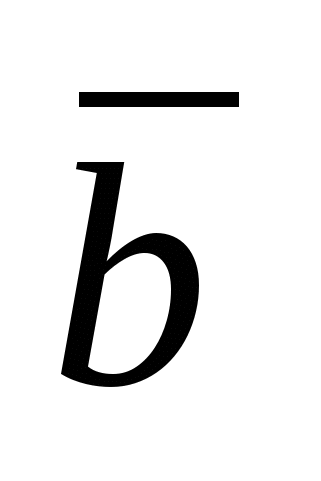 : : 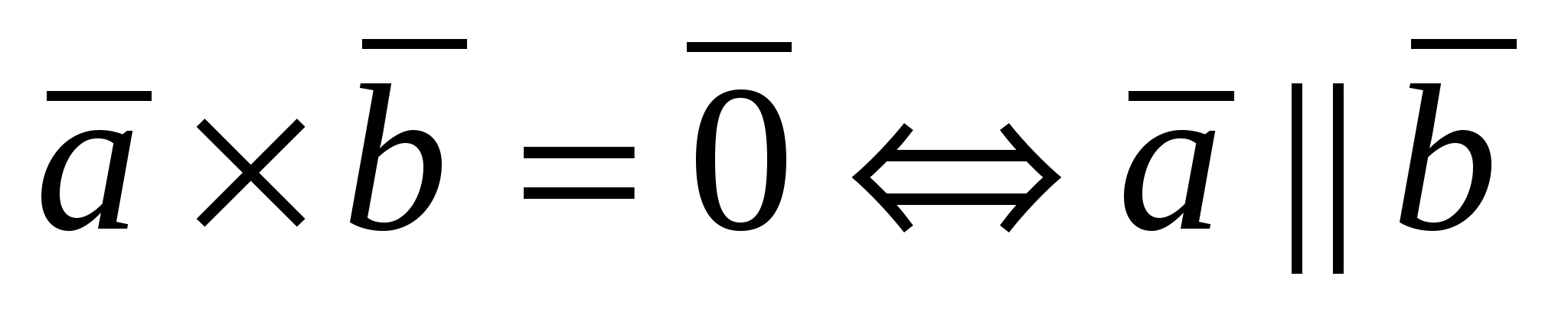 . .
Смешанное произведение векторов.
Смешанное произведение упорядоченной тройки векторов  , ,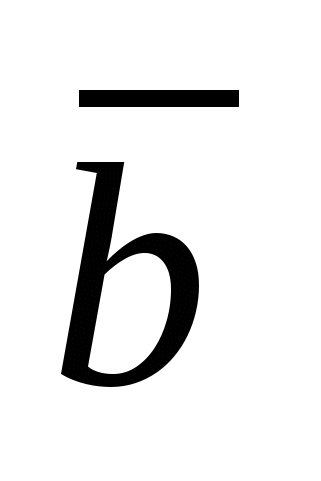 и и 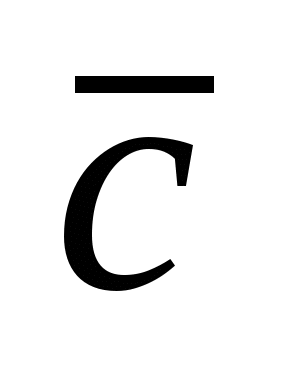 - число - число 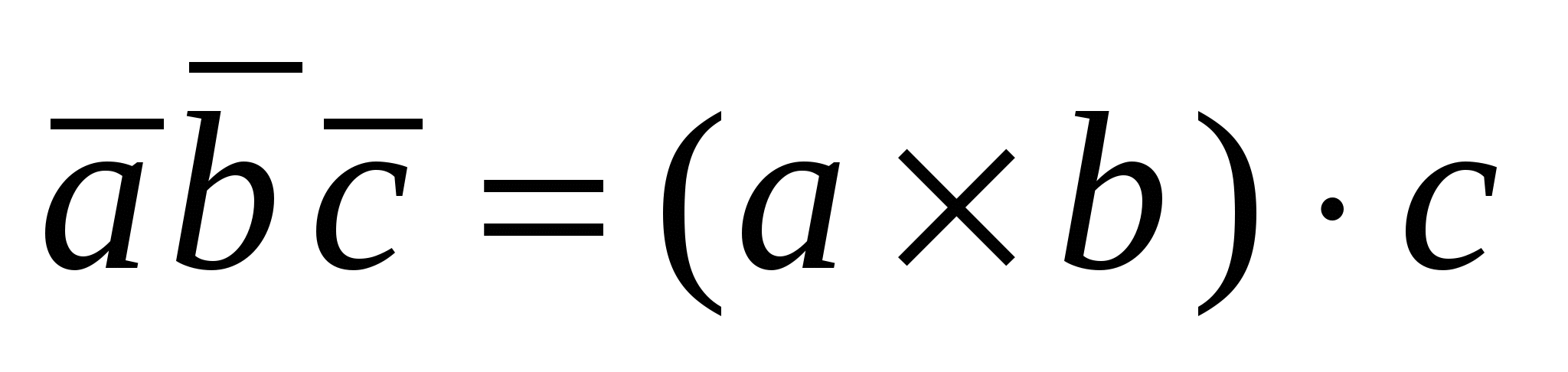 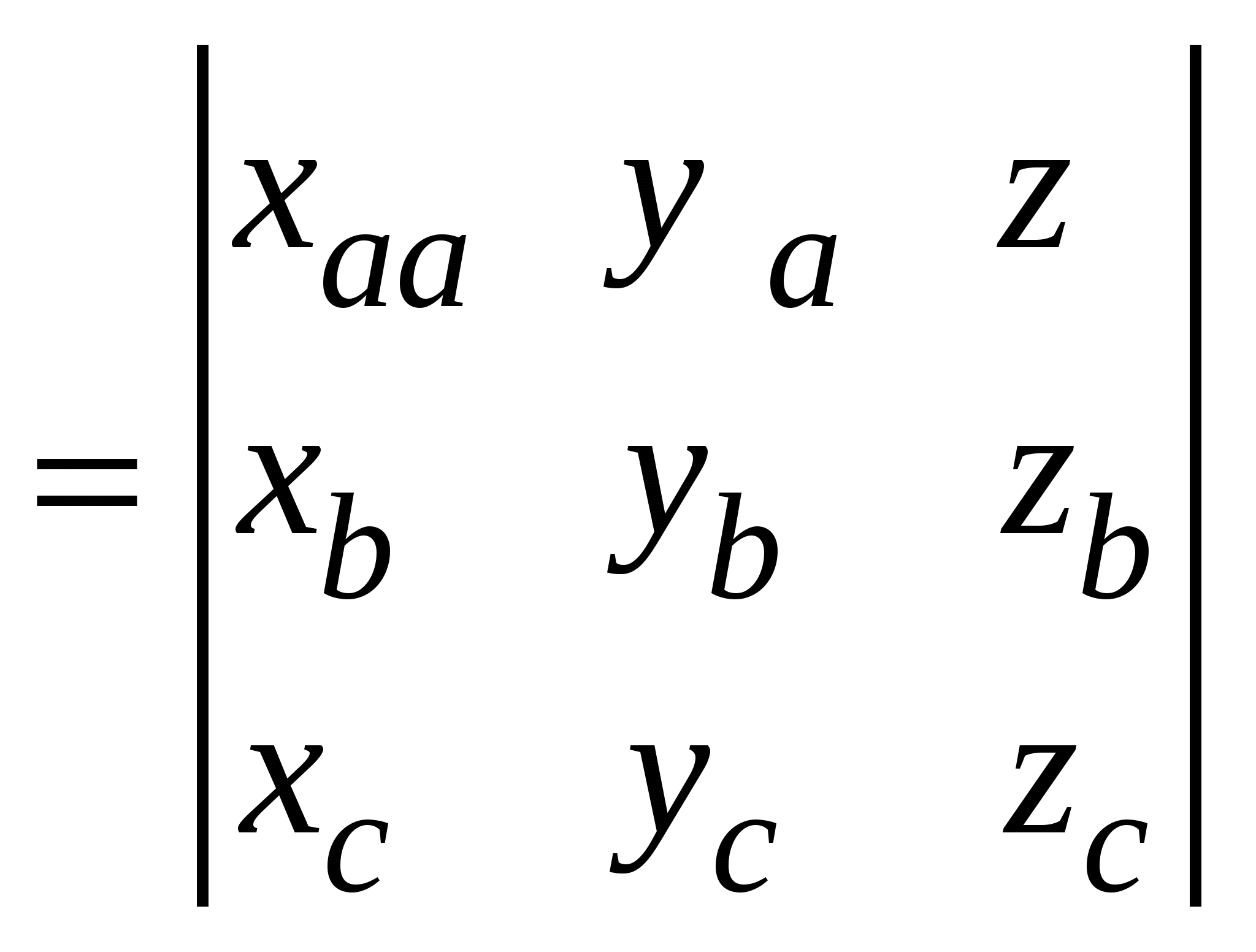 . Смешанное произведение обладает свойствами: . Смешанное произведение обладает свойствами:
1) 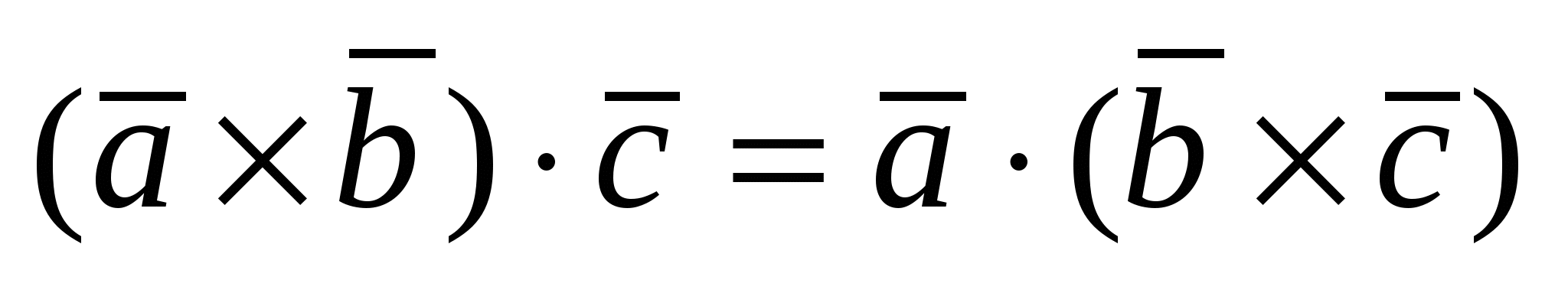 ; 2) ; 2) 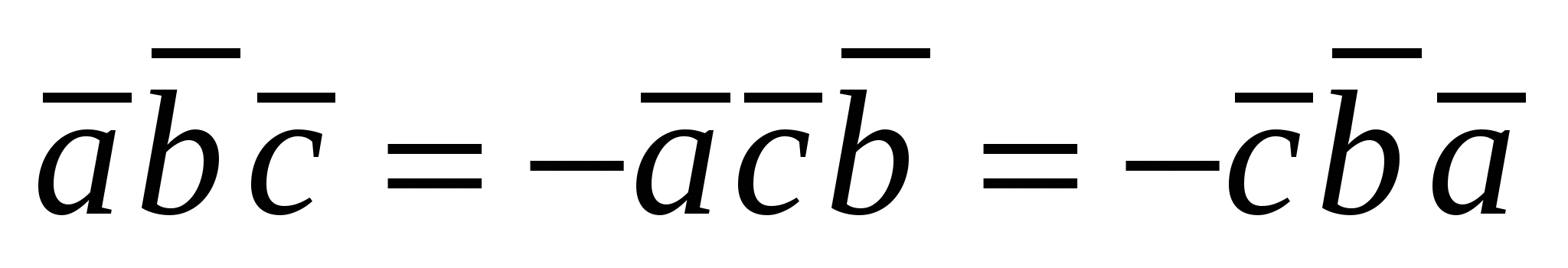 ; 3) ; 3) 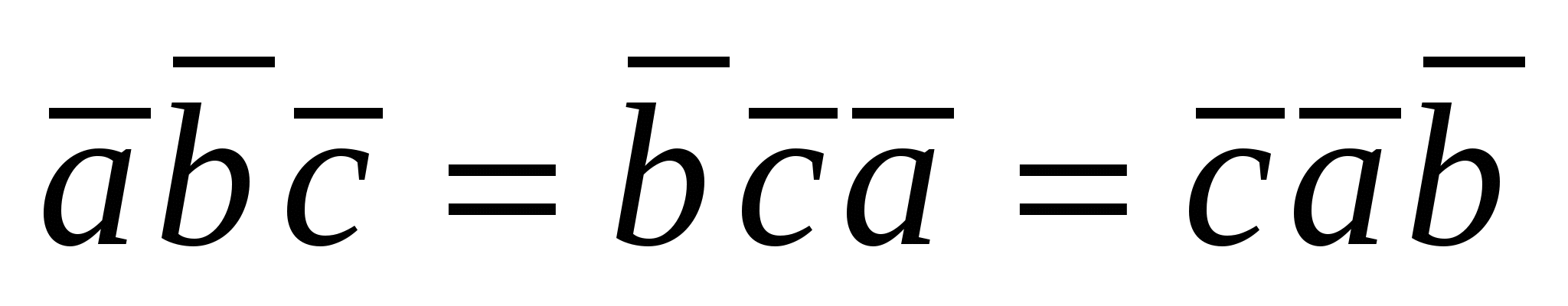 ; 4) ; 4) 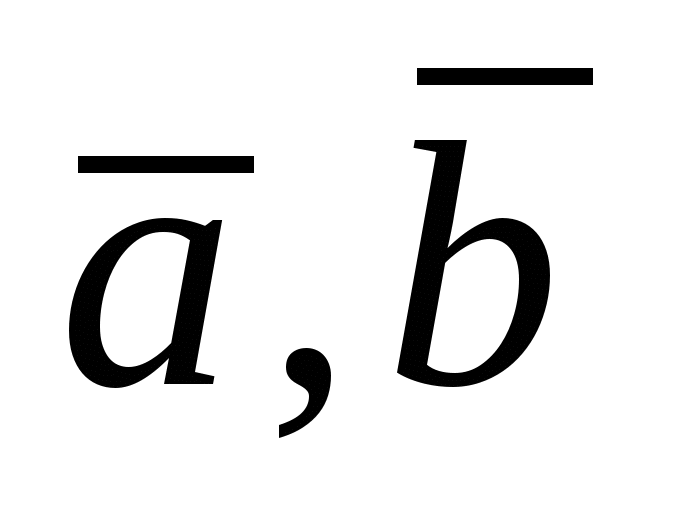 и и 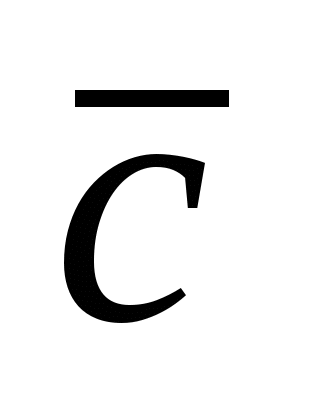 -компланарны -компланарны 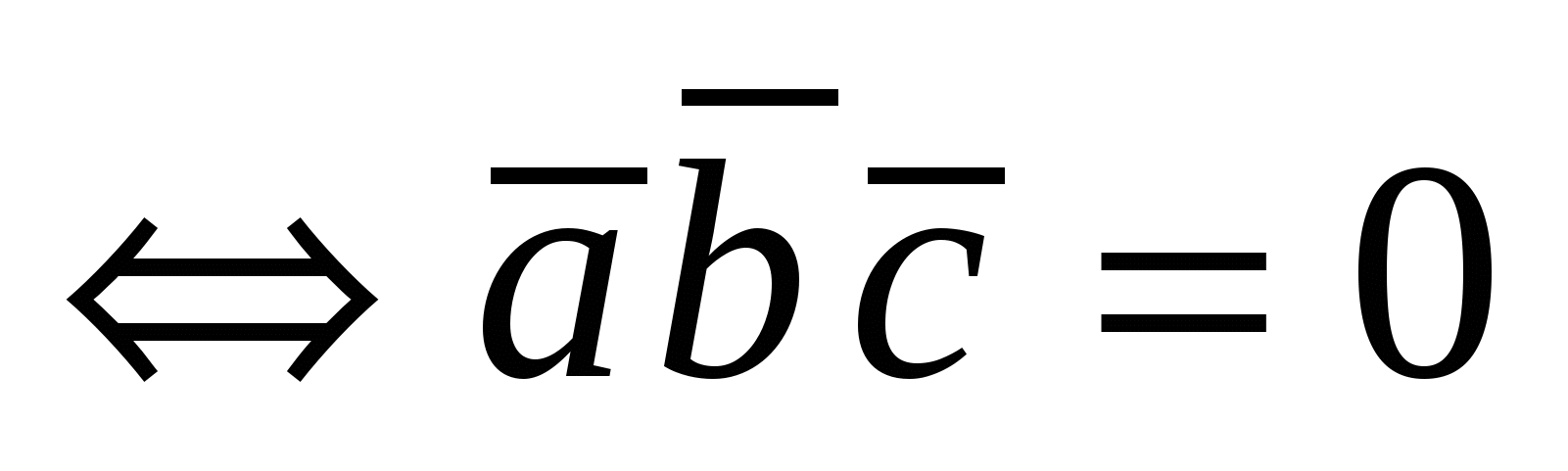 ; ;
Некоторые приложения смешанного произведения:
1) Вычисление объёмов тетраэдра и параллелепипеда: 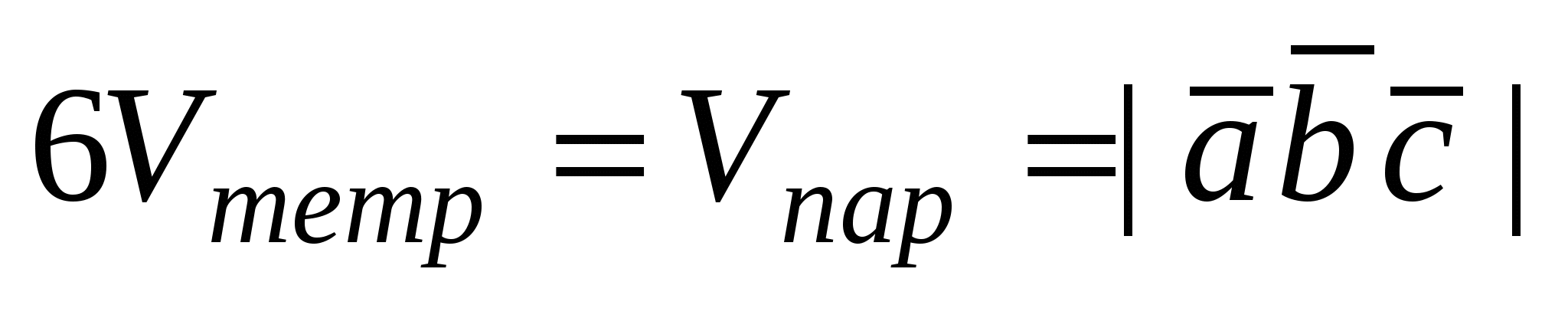 . .
2) Установление компланарности векторов  , ,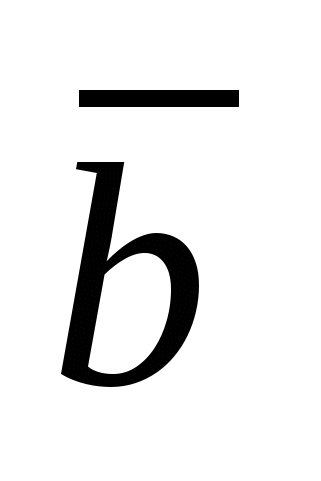 и и 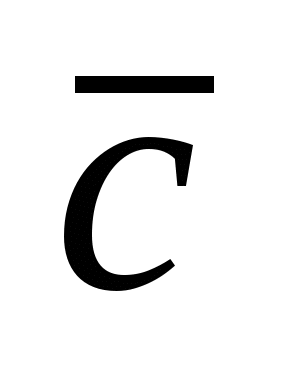 : : 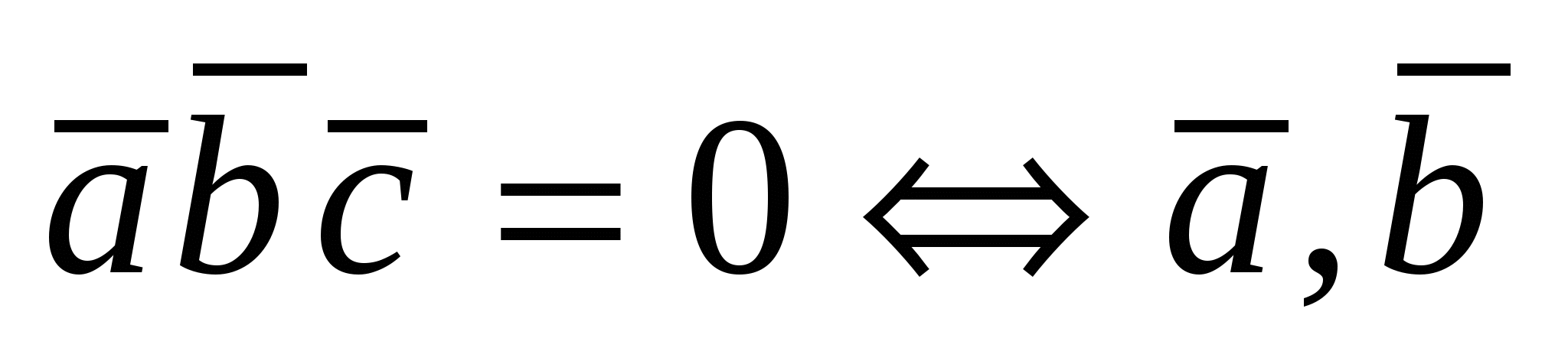 и и 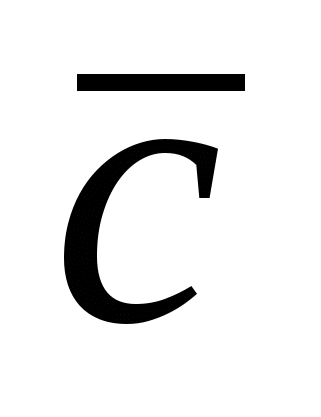 - компланарны. - компланарны.
3) Установление принадлежности четырёх точек 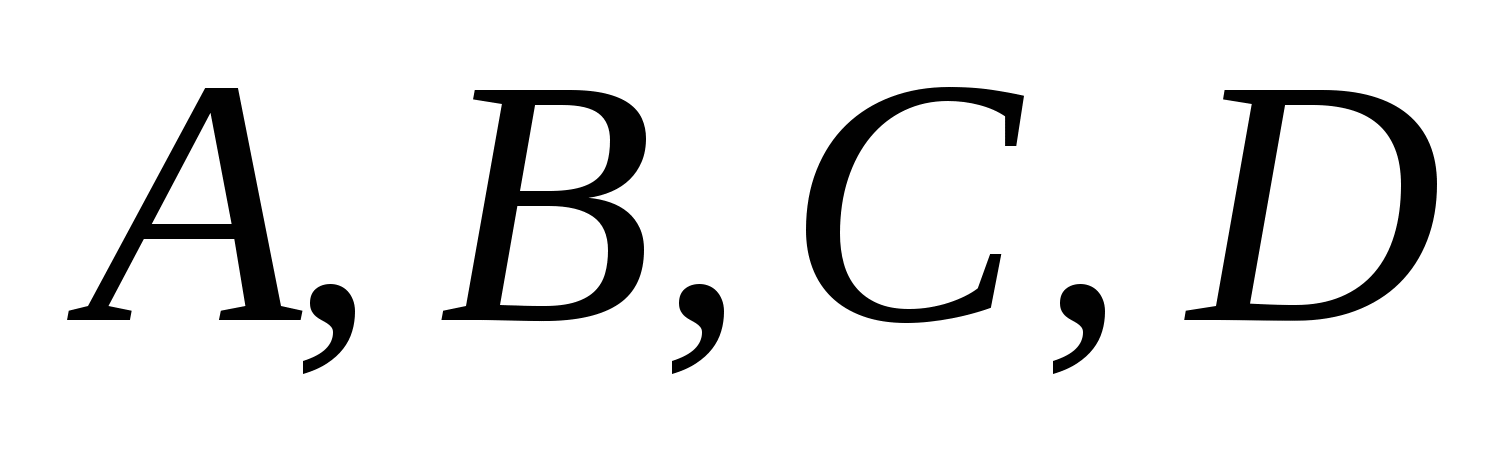 одной плоскости: одной плоскости: 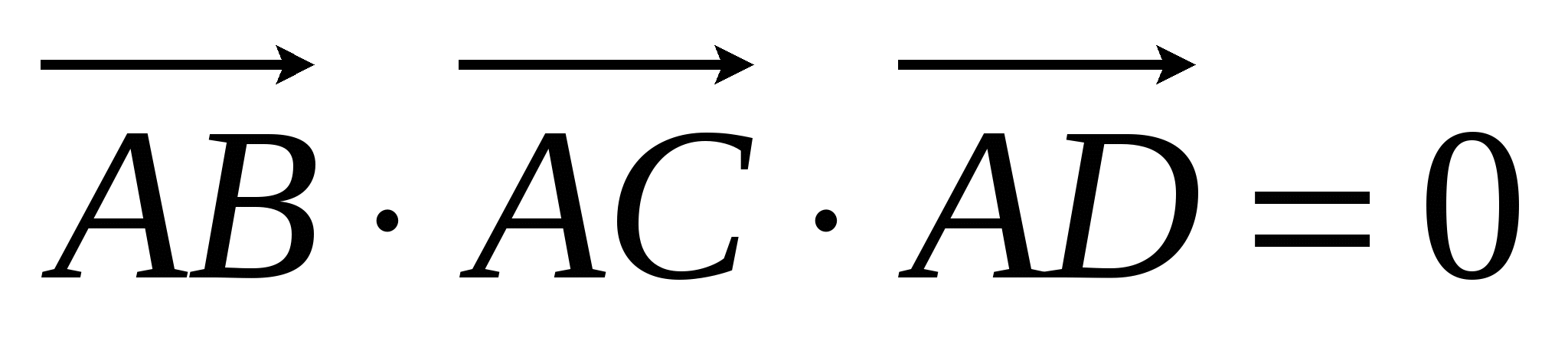
Прямая линия на плоскости.
1) 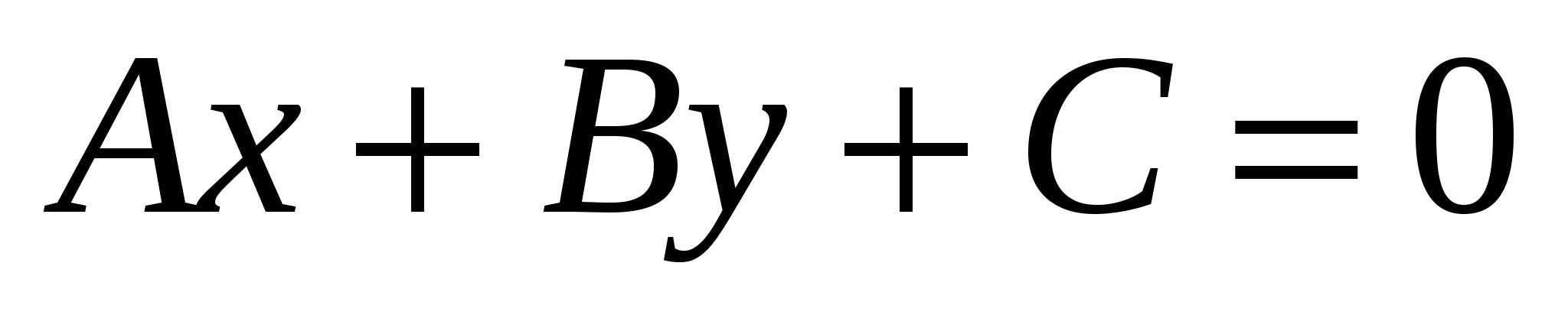 - общее уравнение прямой, где - общее уравнение прямой, где 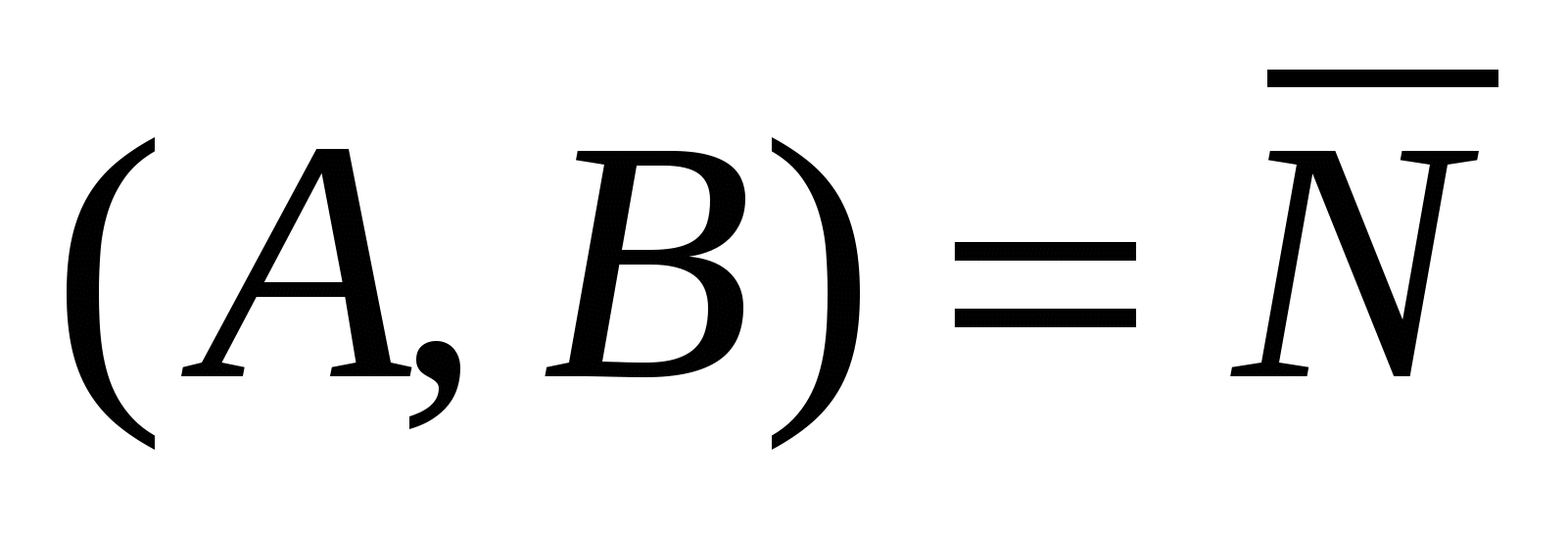 - нормальный вектор прямой; - нормальный вектор прямой;
2) 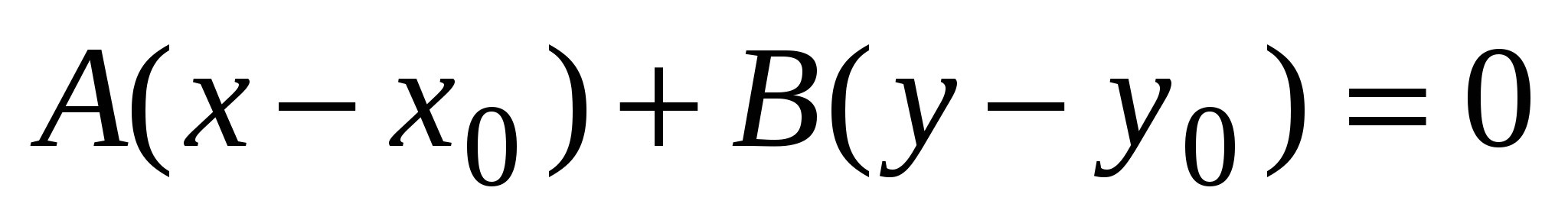 - уравнение прямой, проходящей через точку - уравнение прямой, проходящей через точку 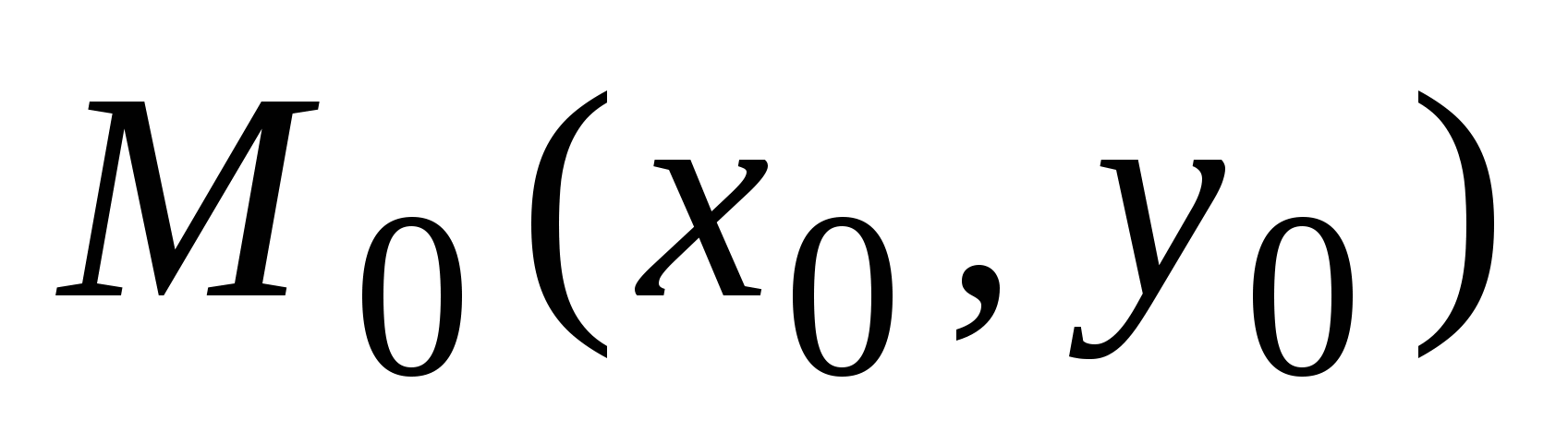 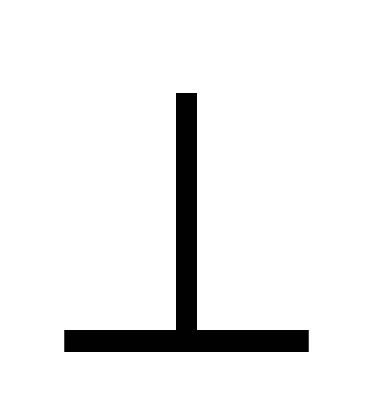 вектору вектору 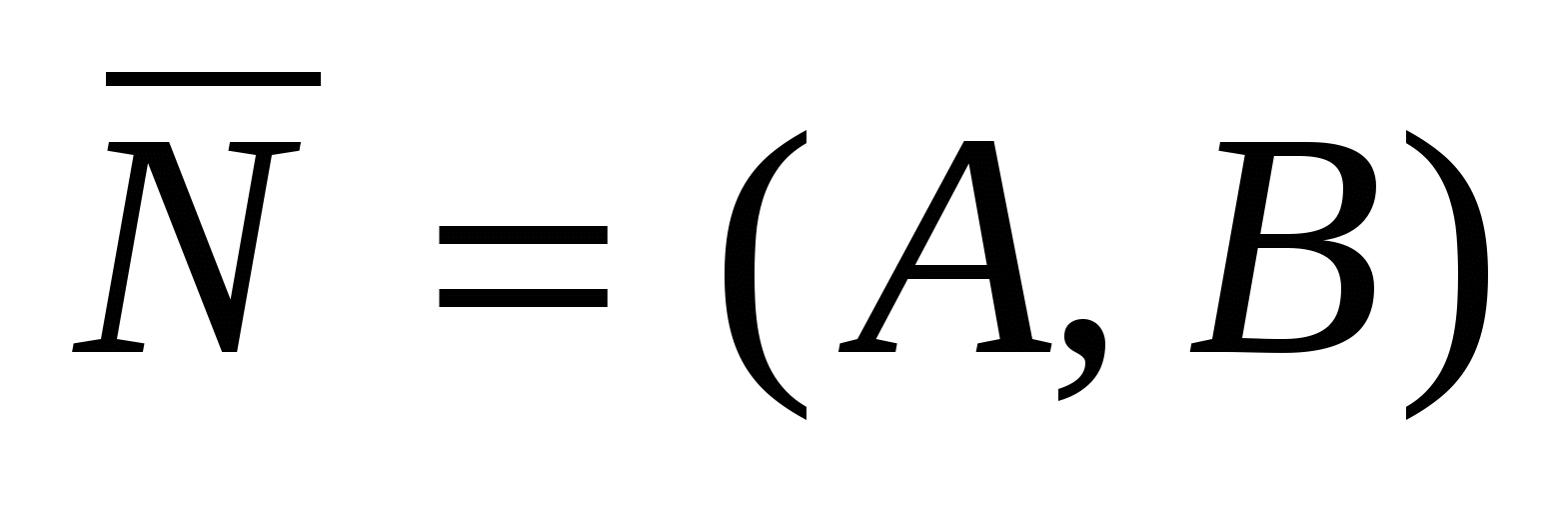 ; ;
3) 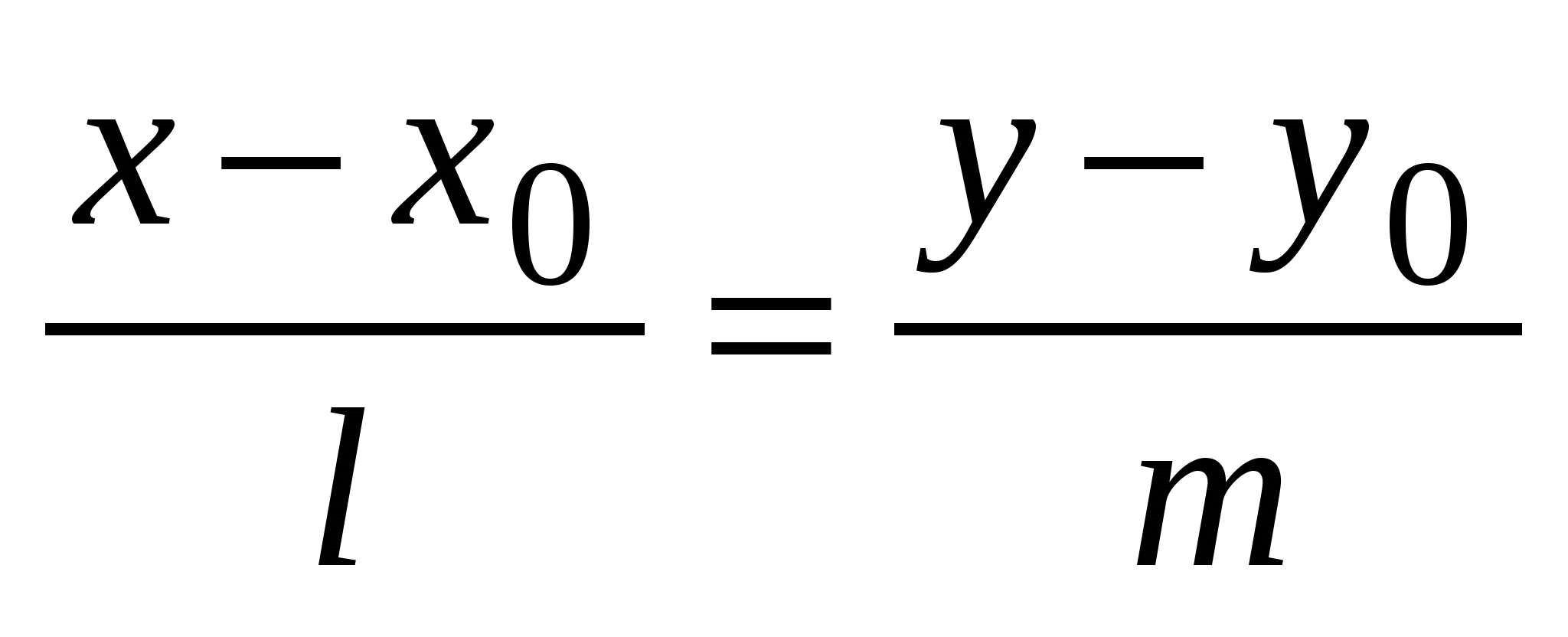 - уравнение прямой, проходящей через точку - уравнение прямой, проходящей через точку 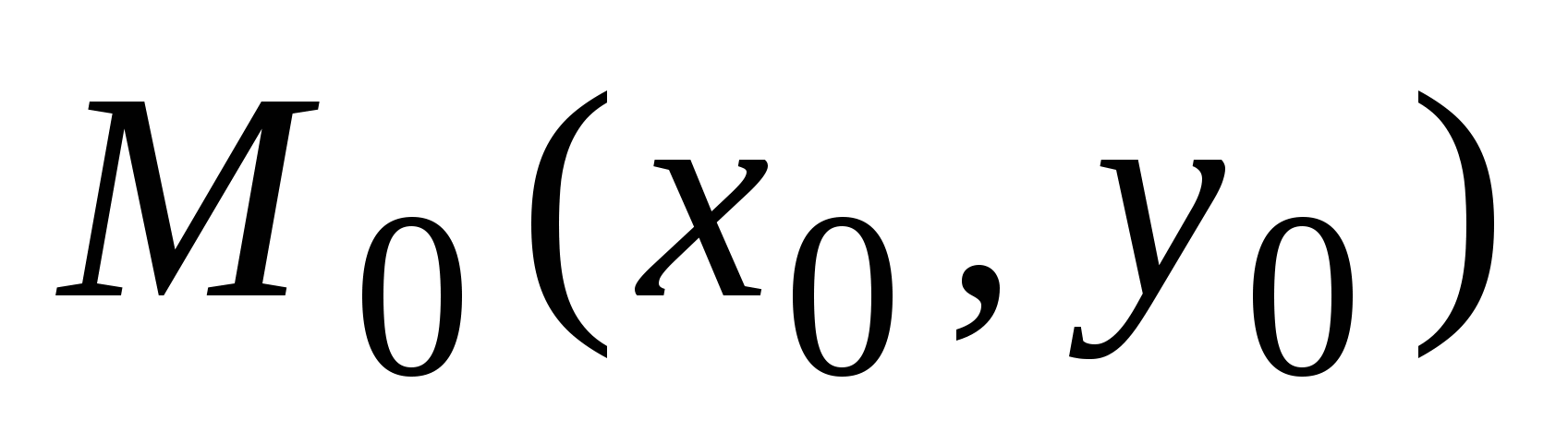 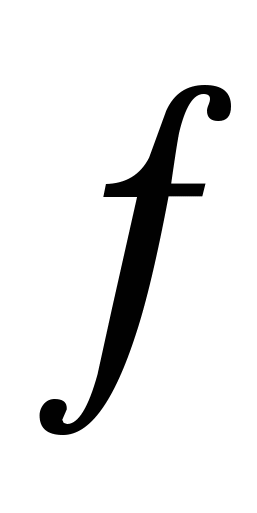 вектору вектору 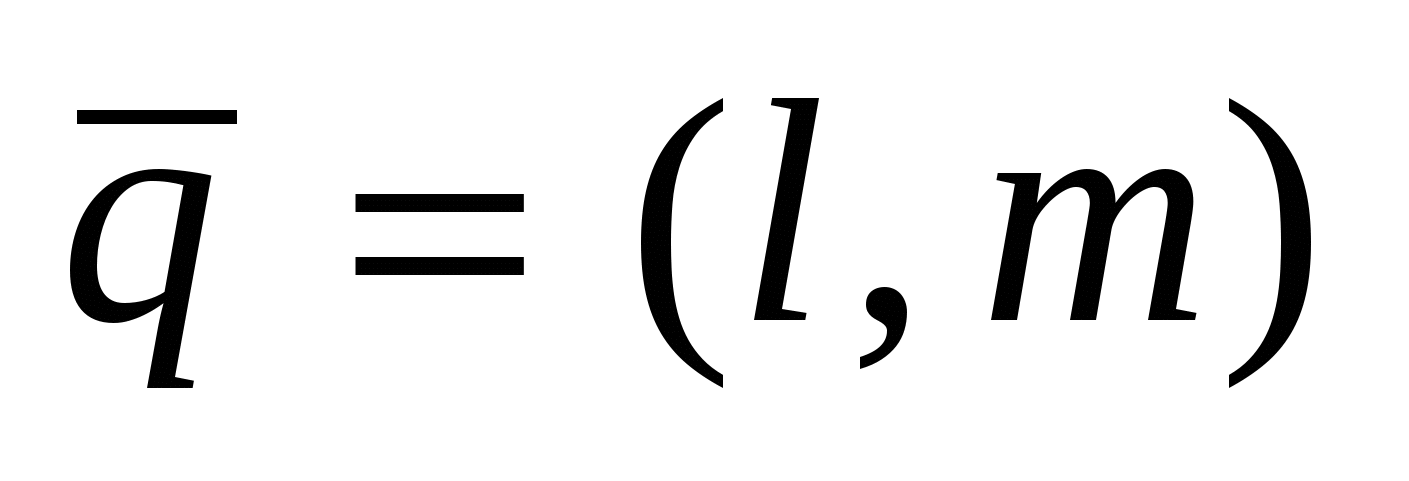 (каноническое уравнение); (каноническое уравнение);
4) 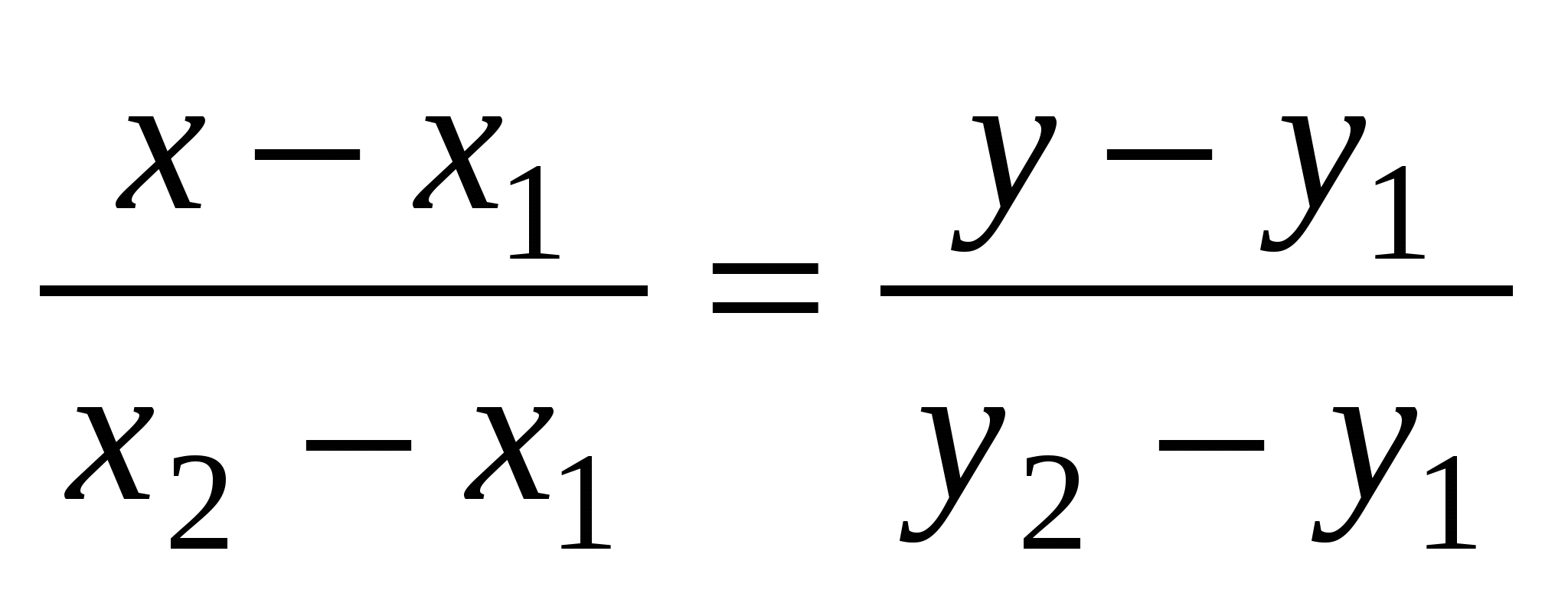 - уравнение прямой, проходящей через две данные точки - уравнение прямой, проходящей через две данные точки 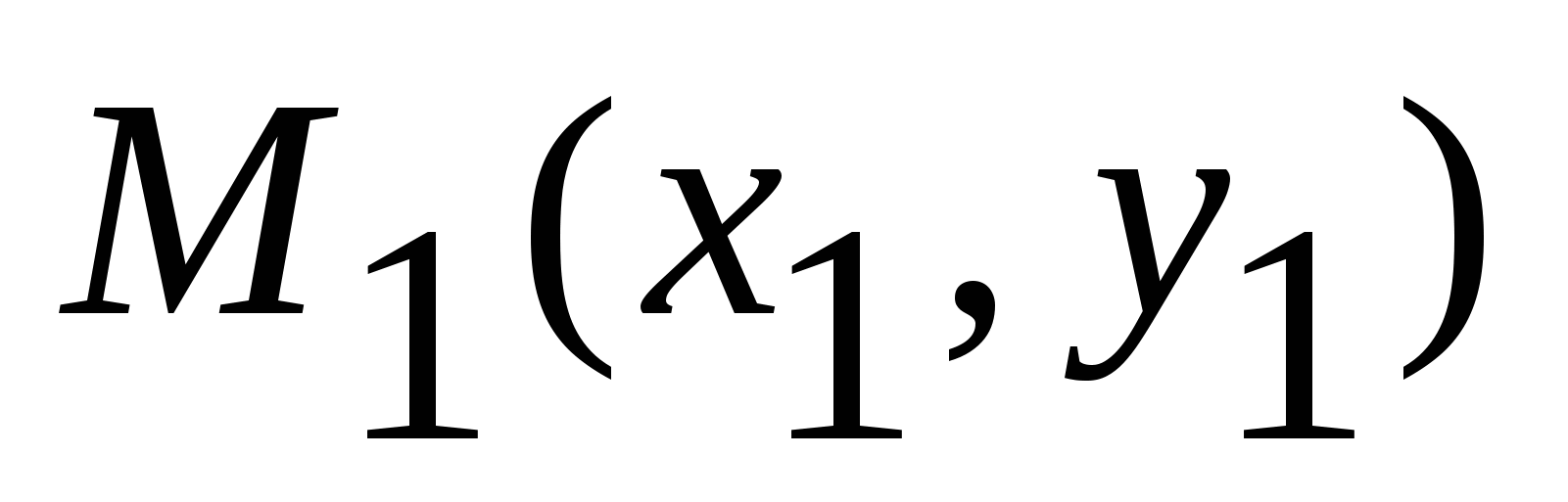 , , 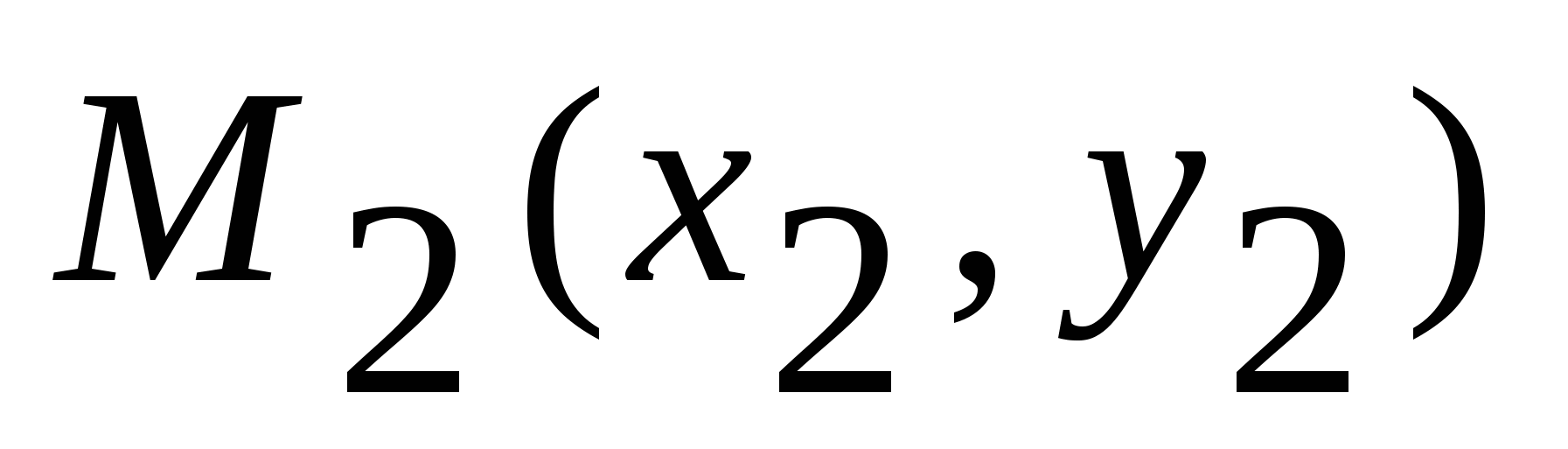 ; ;
5) 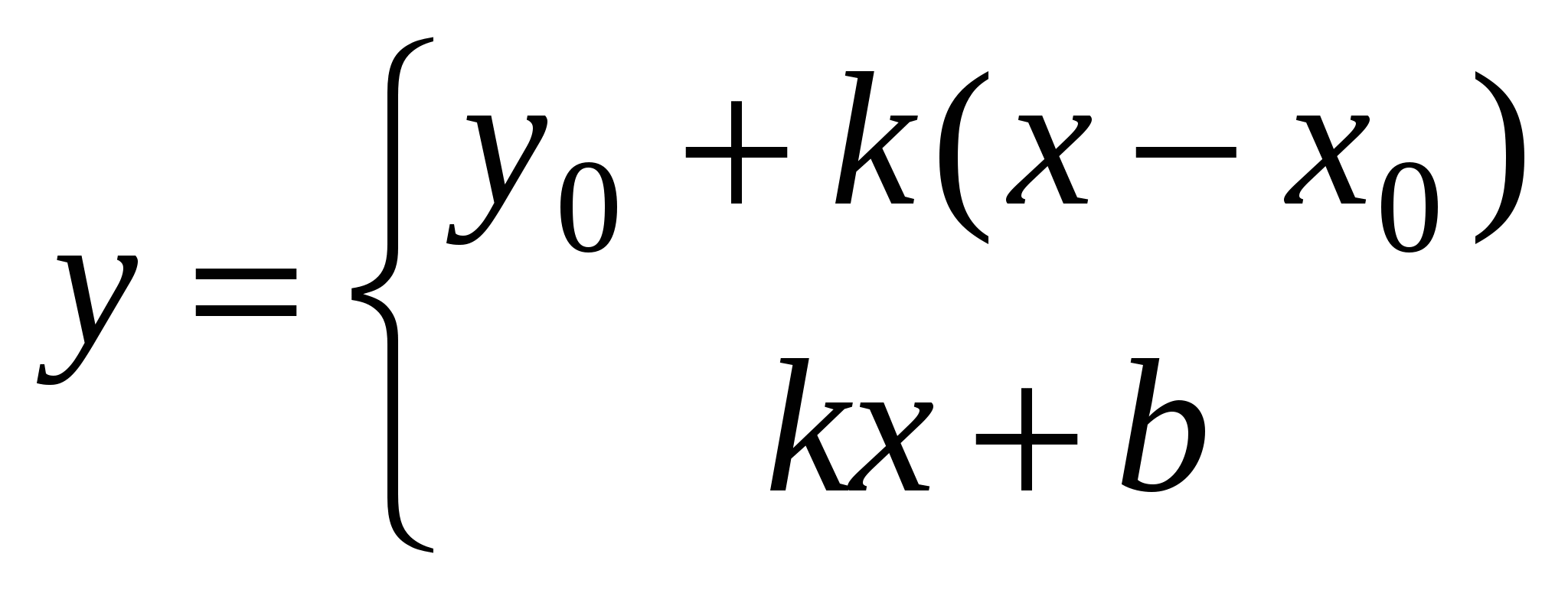 - уравнения прямой с угловым коэффициентом - уравнения прямой с угловым коэффициентом 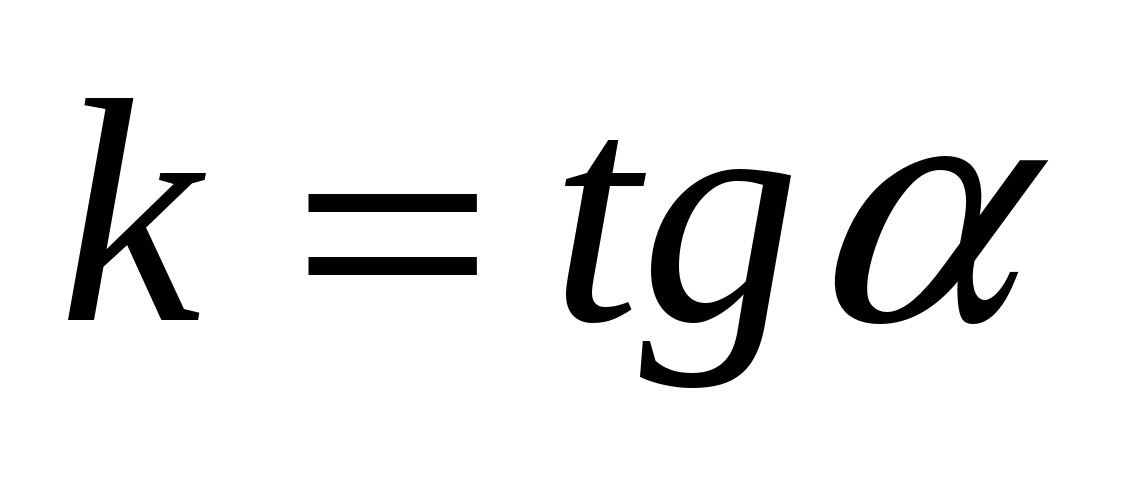 , где , где 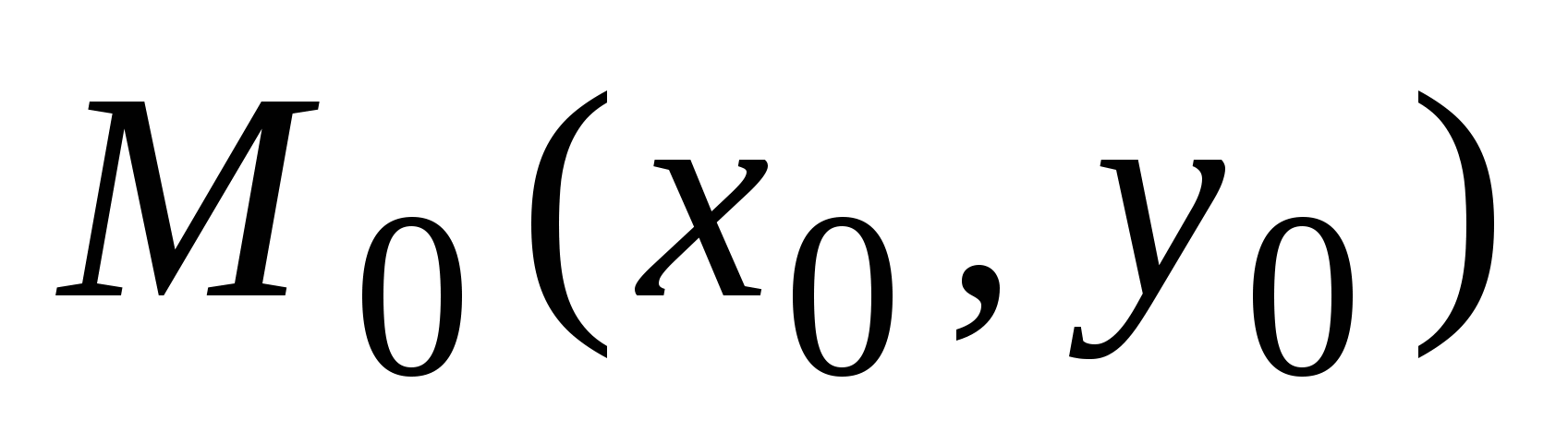 - точка через которую прямая проходит; - точка через которую прямая проходит;  ( (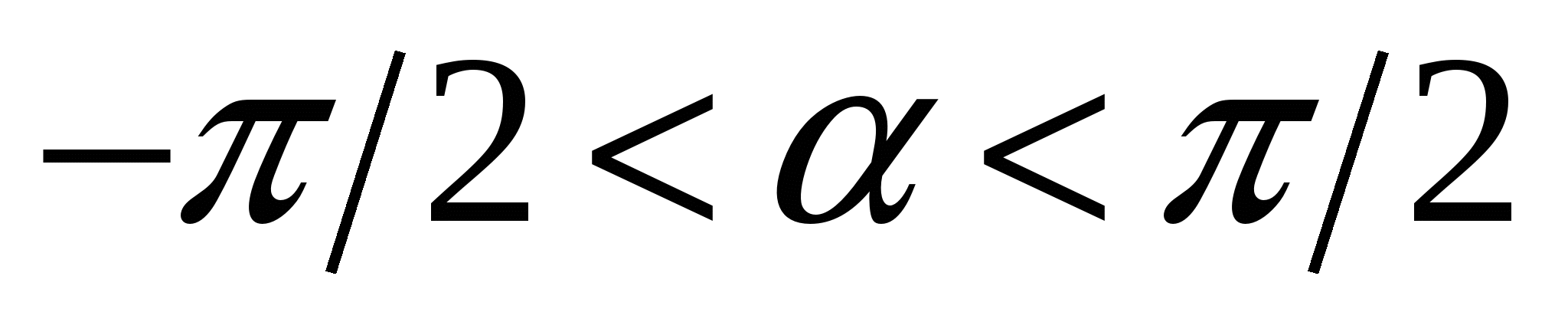 ) – угол прямой осью ) – угол прямой осью 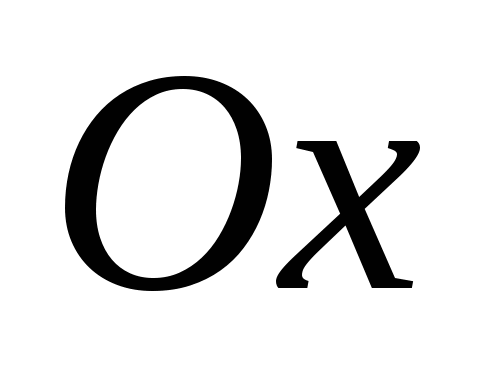 ; ; 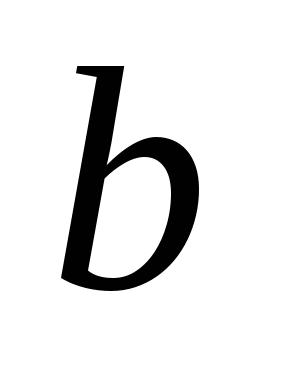 - длина отрезка (со знаком - длина отрезка (со знаком 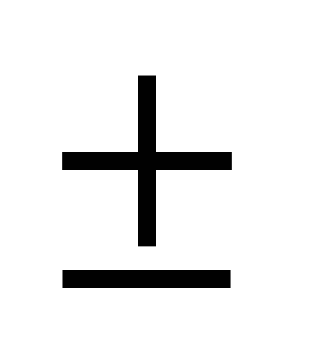 ), отсекаемого прямой на оси ), отсекаемого прямой на оси 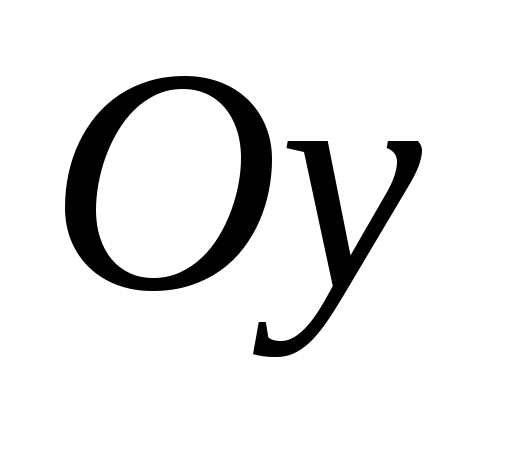 ( « ( «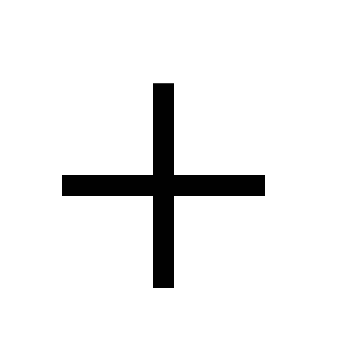 », если на положительной части оси и « », если на положительной части оси и « », если на отрицательной). », если на отрицательной).
6) 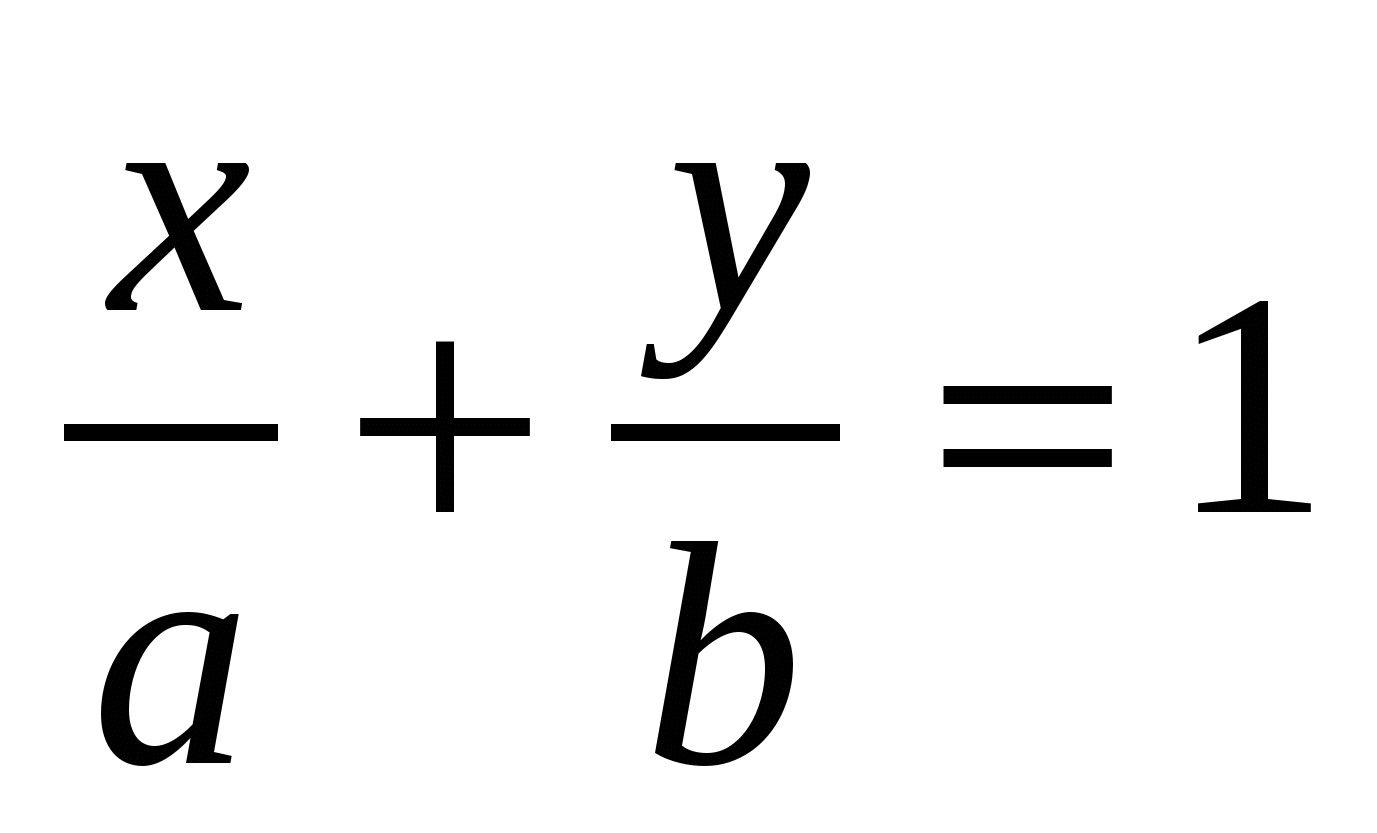 - уравнение прямой в отрезках, где - уравнение прямой в отрезках, где  и и 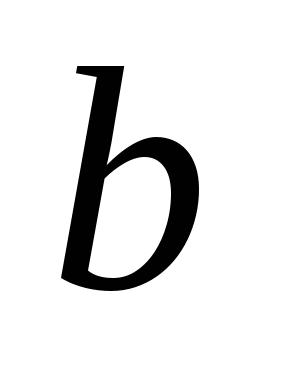 - длины отрезков (со знаком - длины отрезков (со знаком 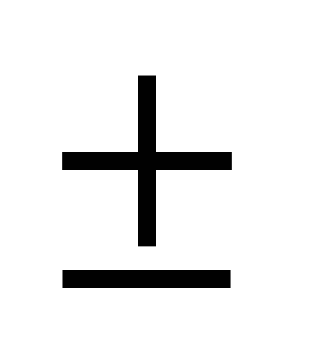 ), отсекаемых прямой на координатных осях ), отсекаемых прямой на координатных осях 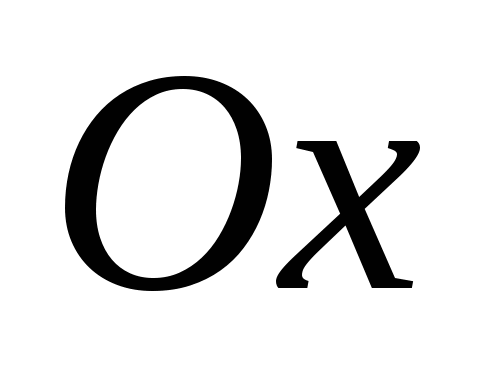 и и 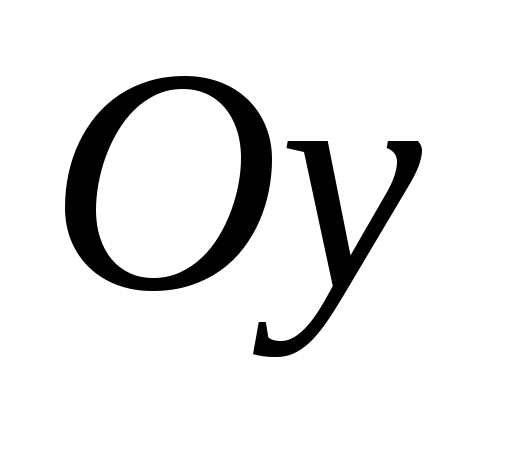 ( « ( «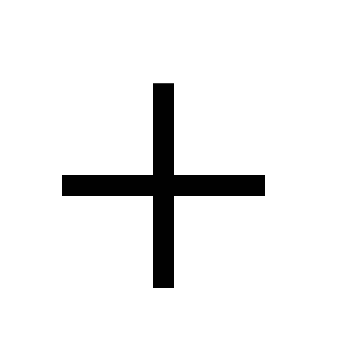 », если на положительной части оси и « », если на положительной части оси и « », если на отрицательной). », если на отрицательной).
Расстояние от точки 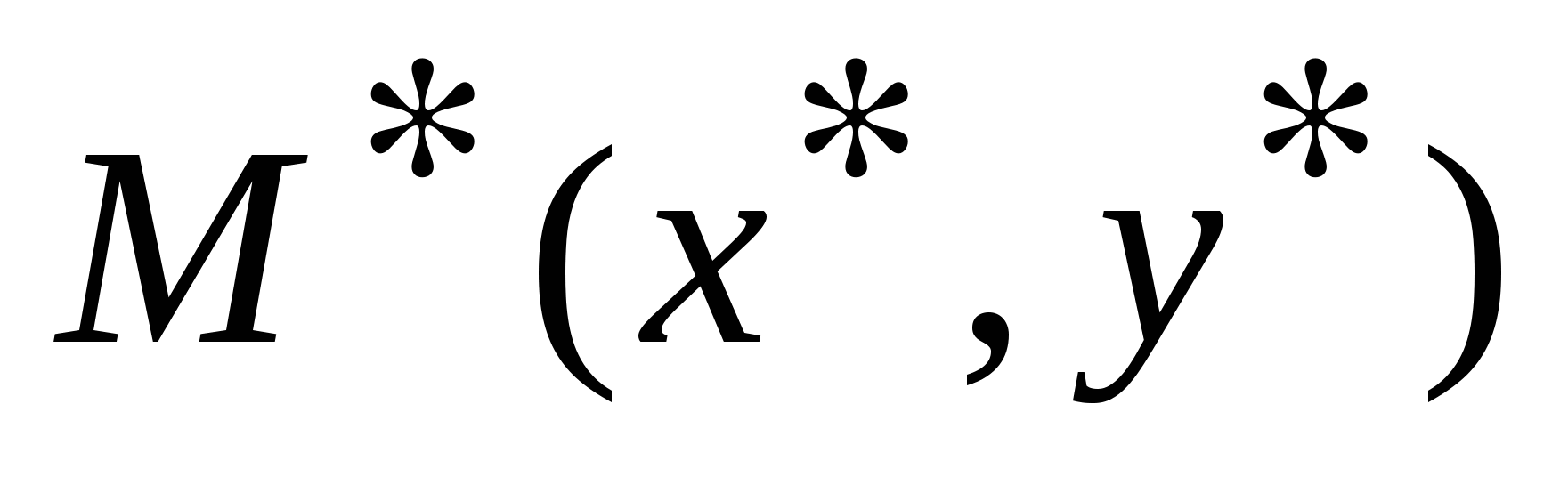 до прямой до прямой 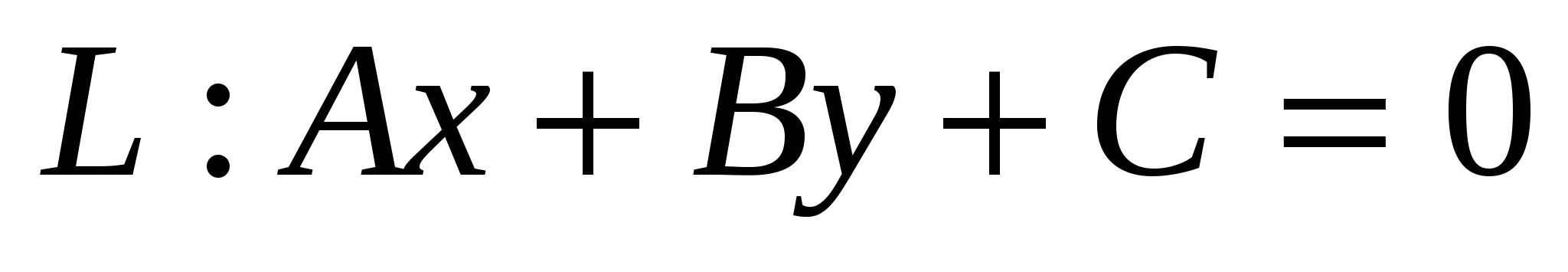 : :  . .
Угол 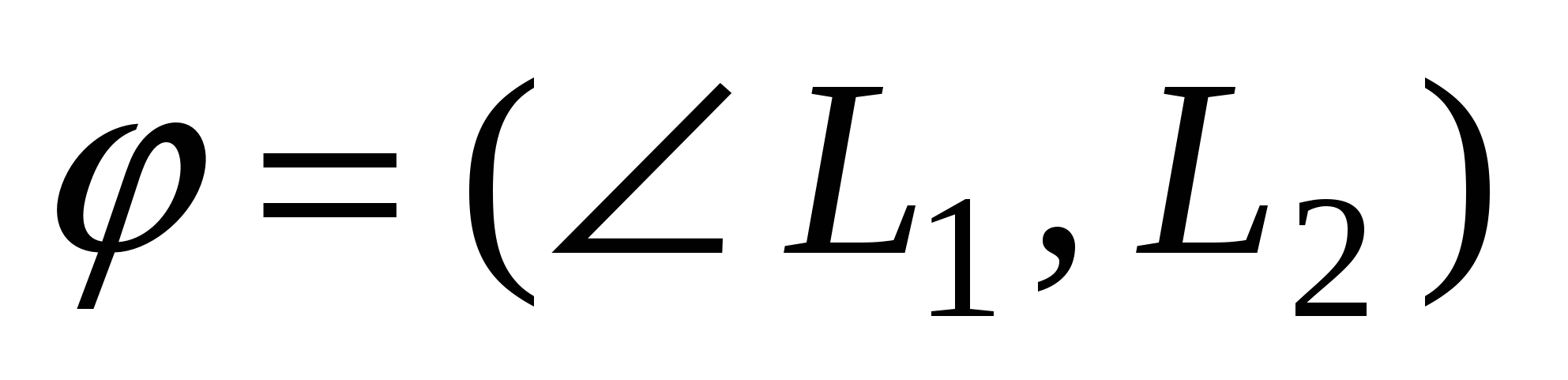 , ( , (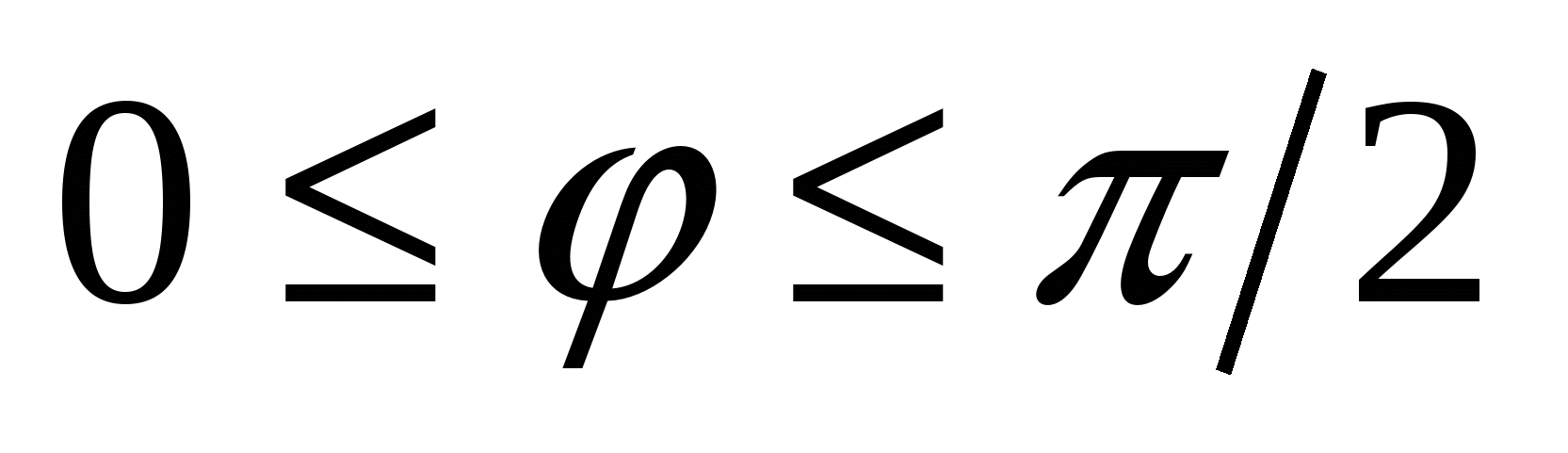 ) между прямыми ) между прямыми 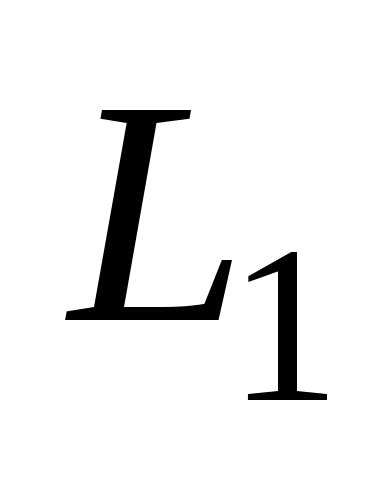 и и 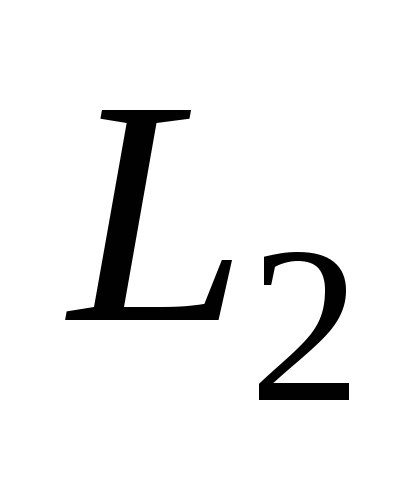 : : 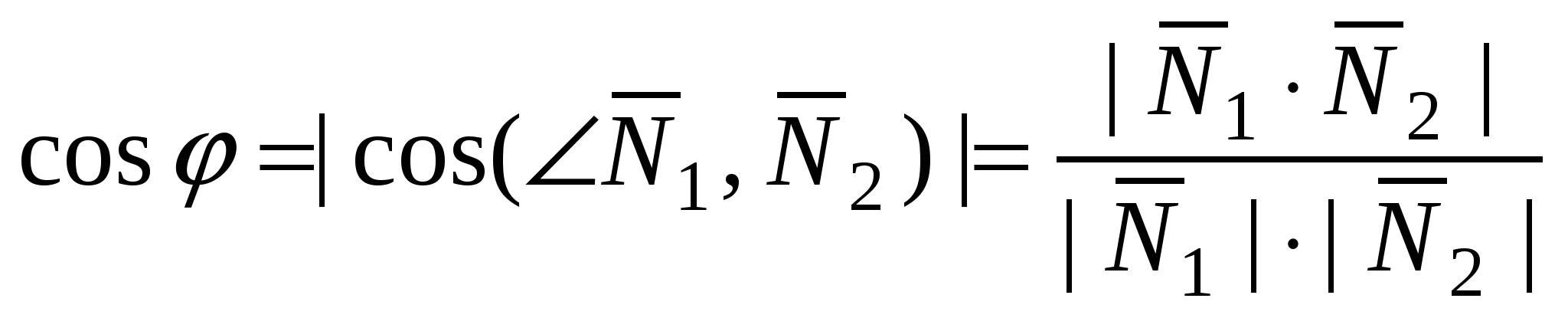 ; ; 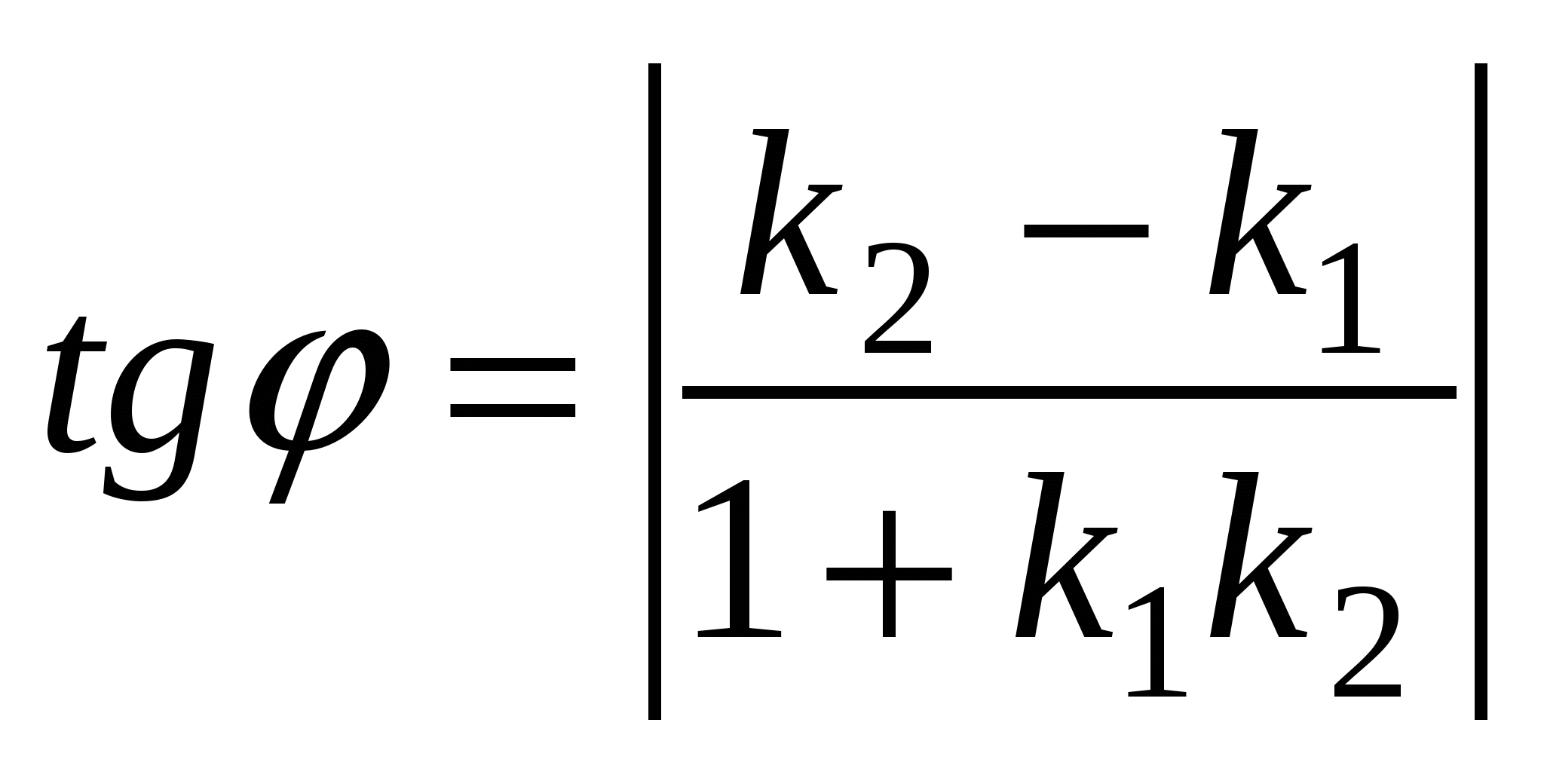 . .
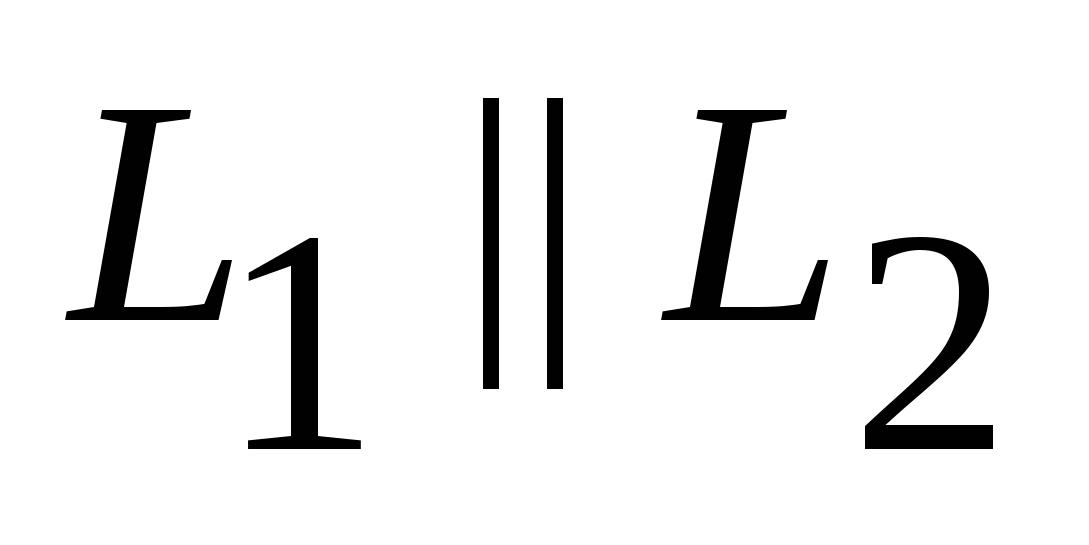 , если , если  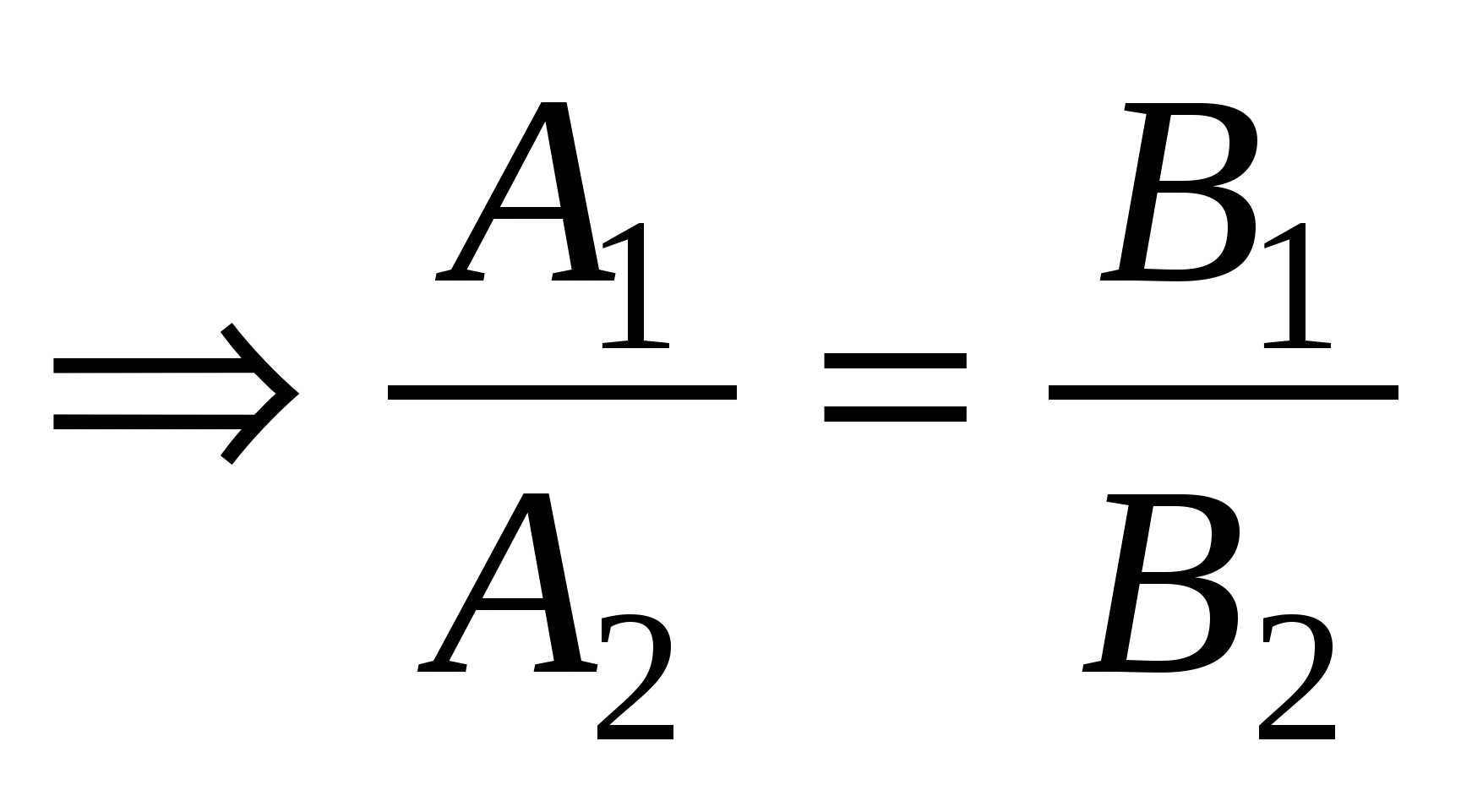 или или 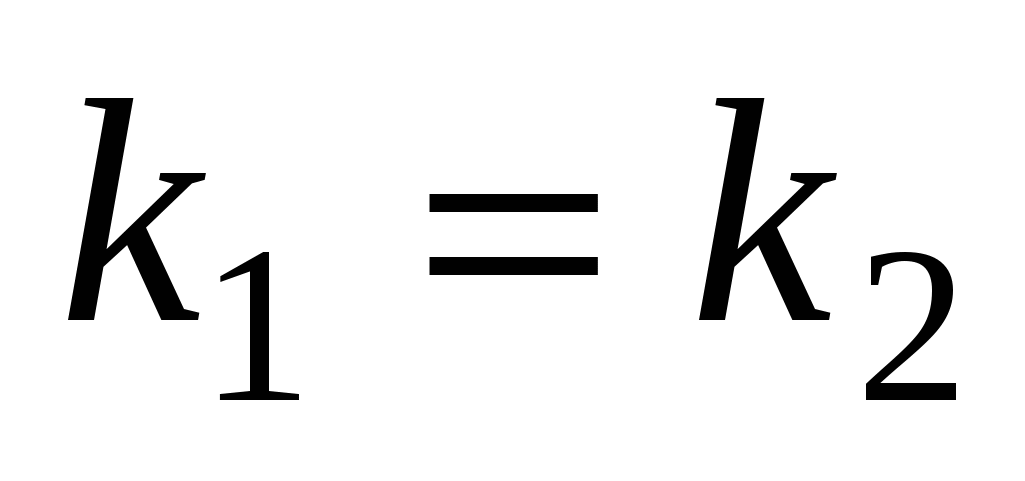 . .
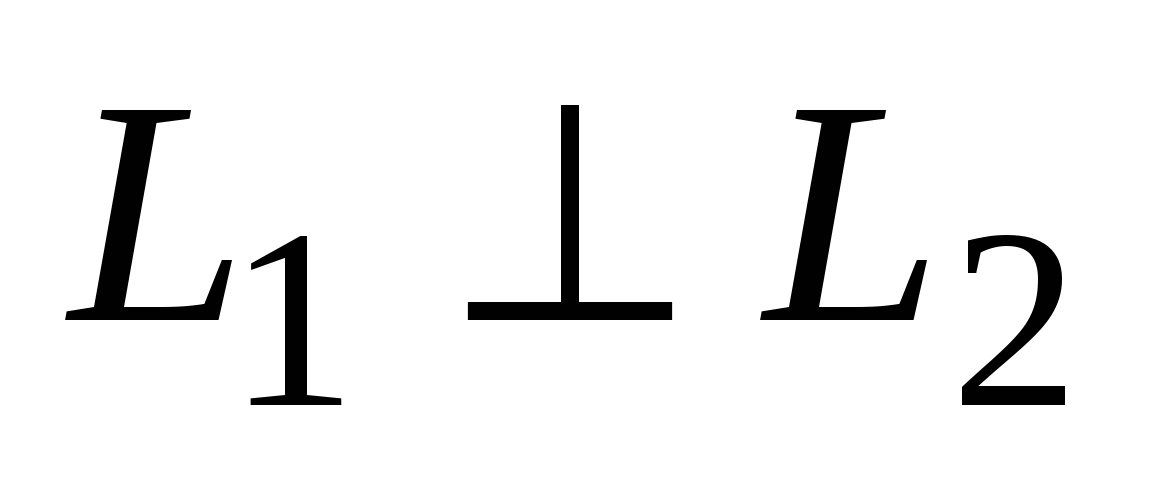 ,если ,если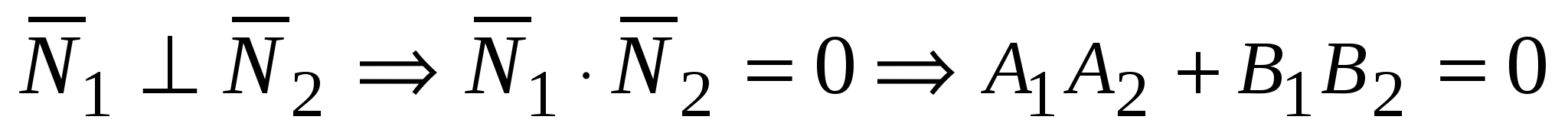 или или 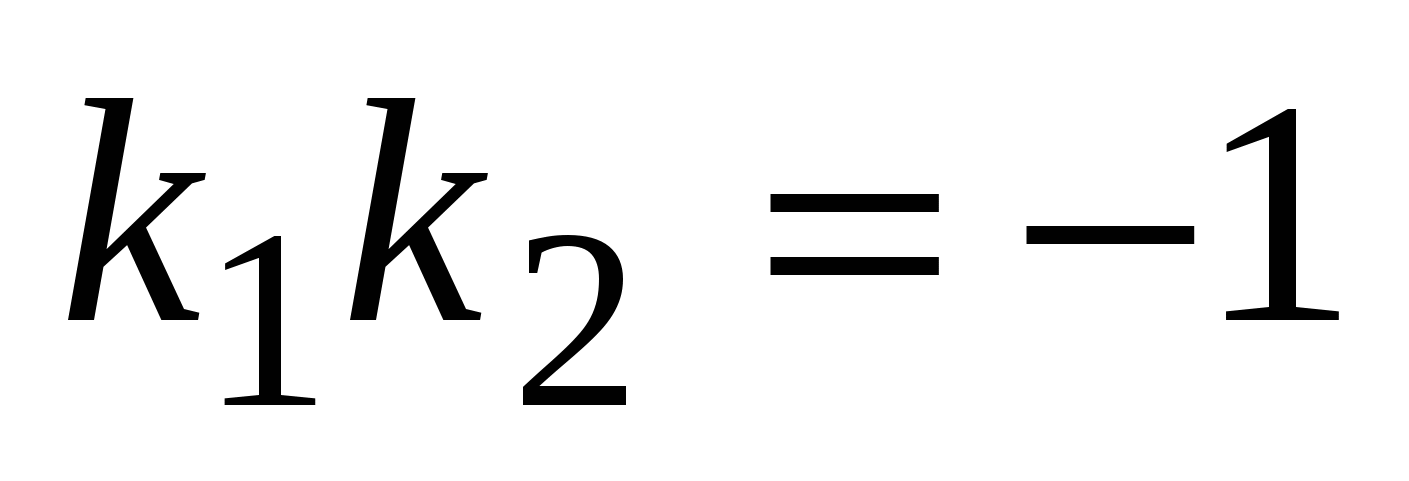
Координаты точки пересечения прямых 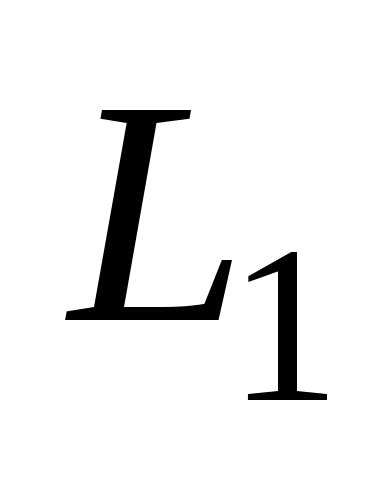 и и 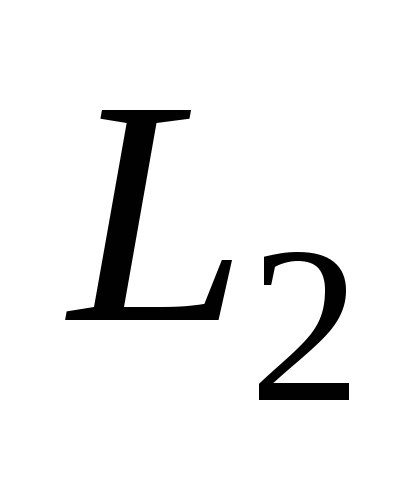 : : 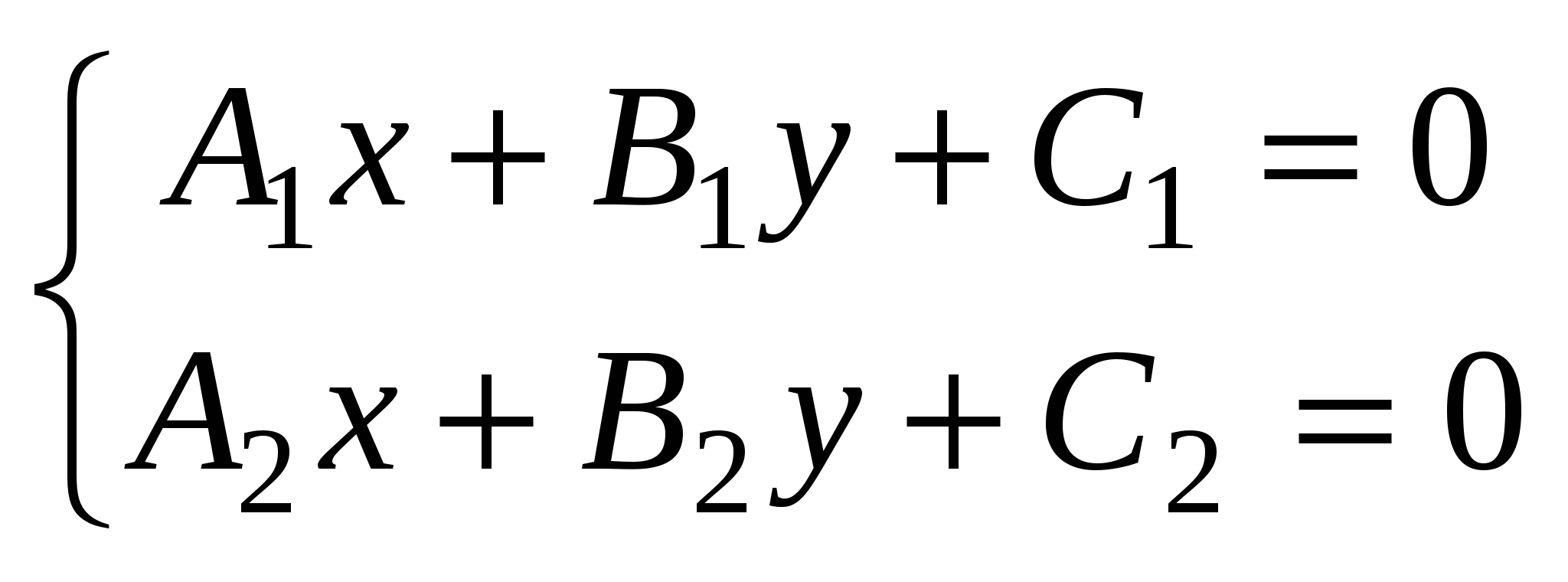 или или 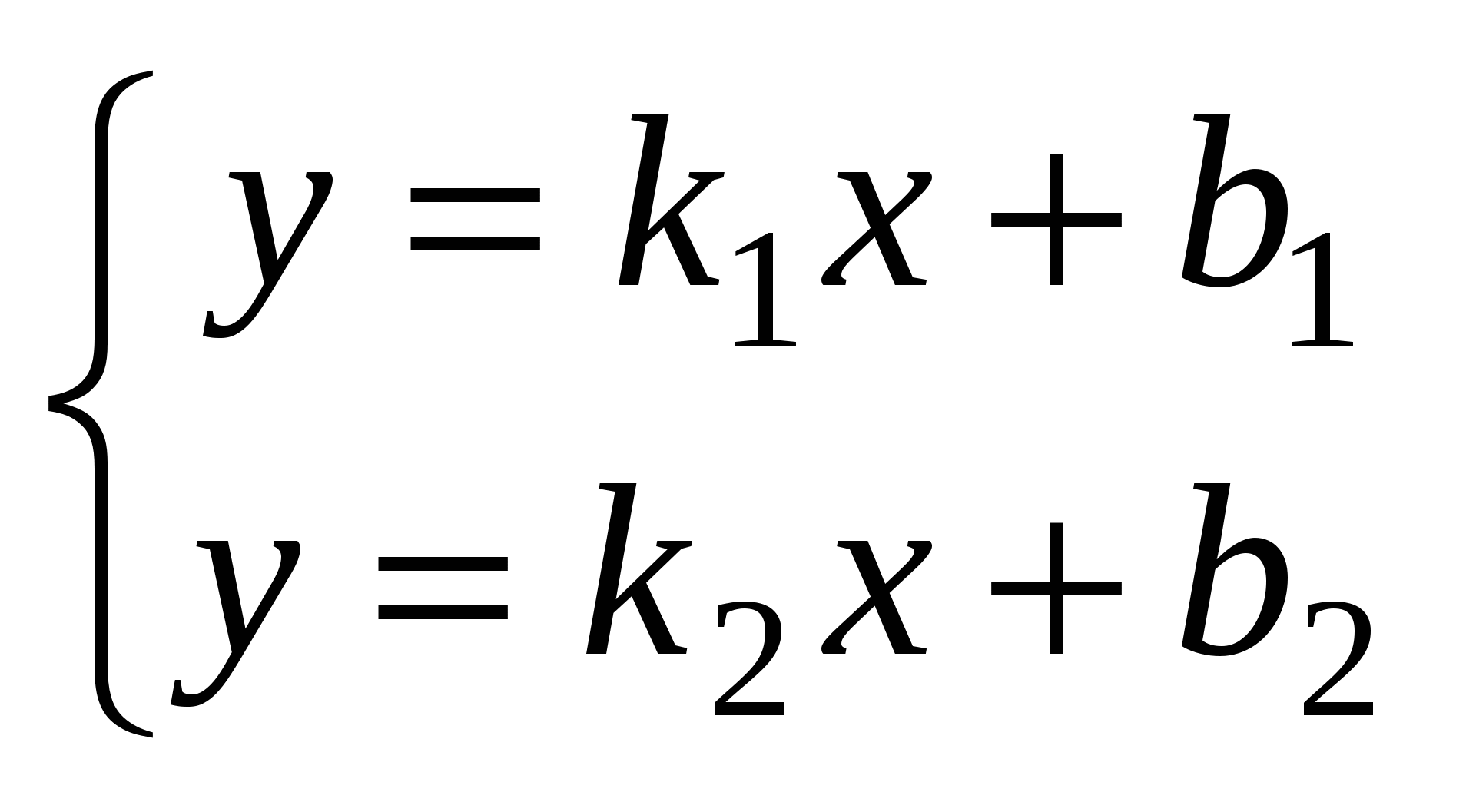 . .
Кривые на плоскости.
Алгебраическая кривая второго порядка: 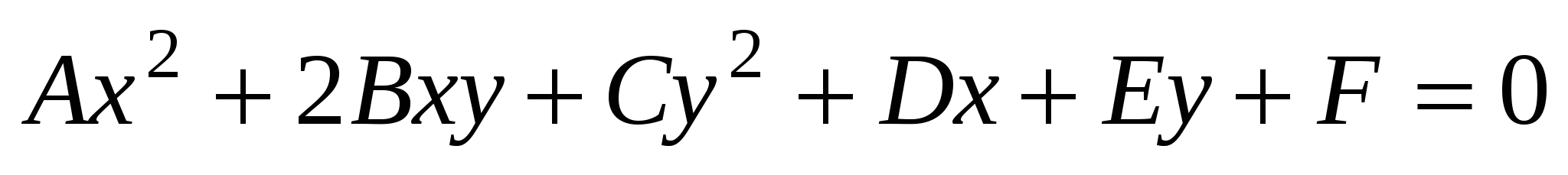 , где числа , где числа 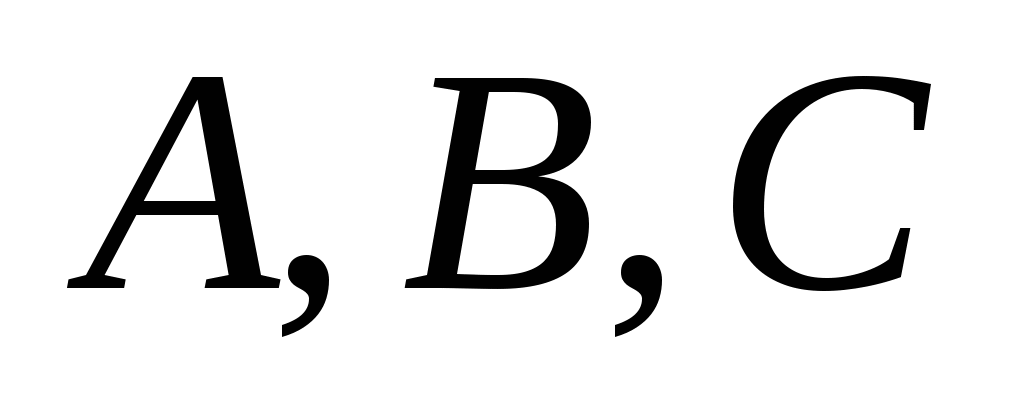 - не равны нулю одновременно. - не равны нулю одновременно.
Классификация кривых второго порядка:
1) если 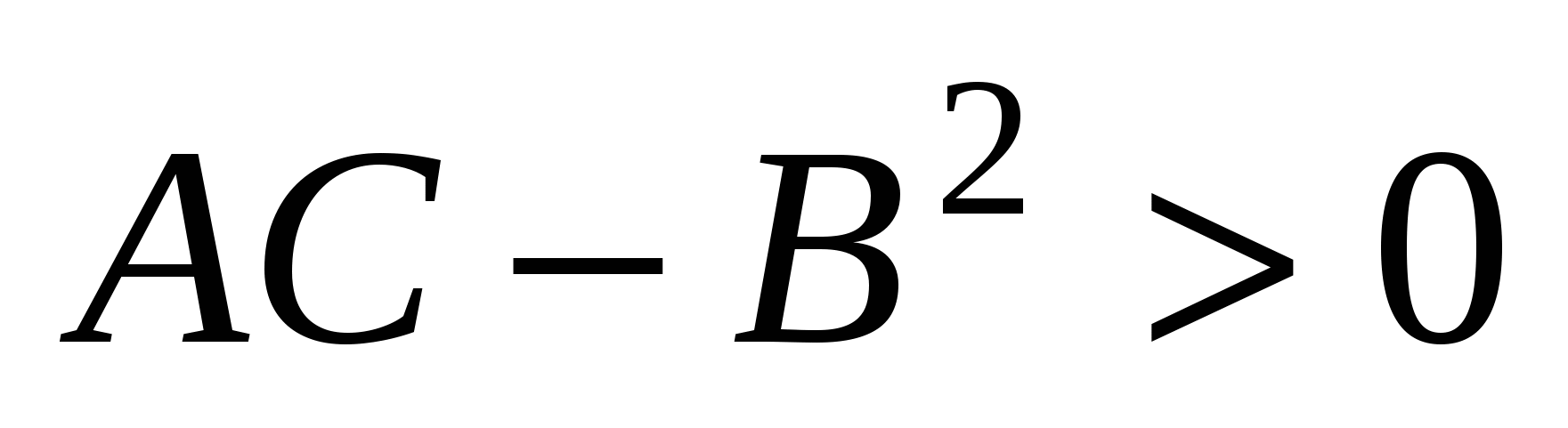 , то общее уравнение определяет кривую эллиптического типа (окружность (при , то общее уравнение определяет кривую эллиптического типа (окружность (при 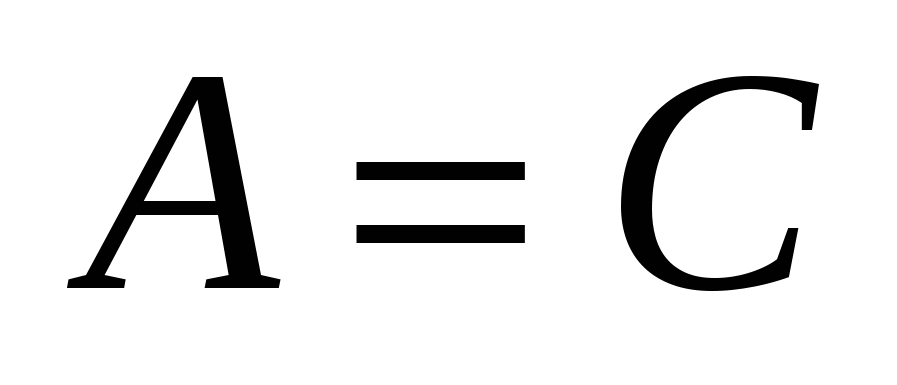 ), эллипс (при ), эллипс (при 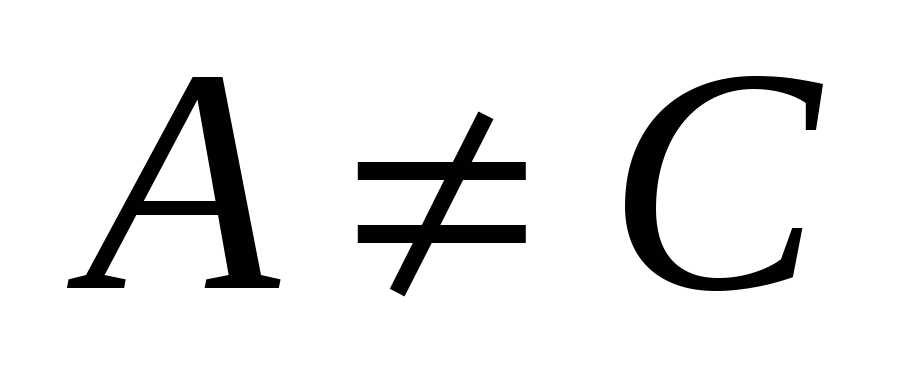 ), пустое множество, точку); ), пустое множество, точку);
2) если 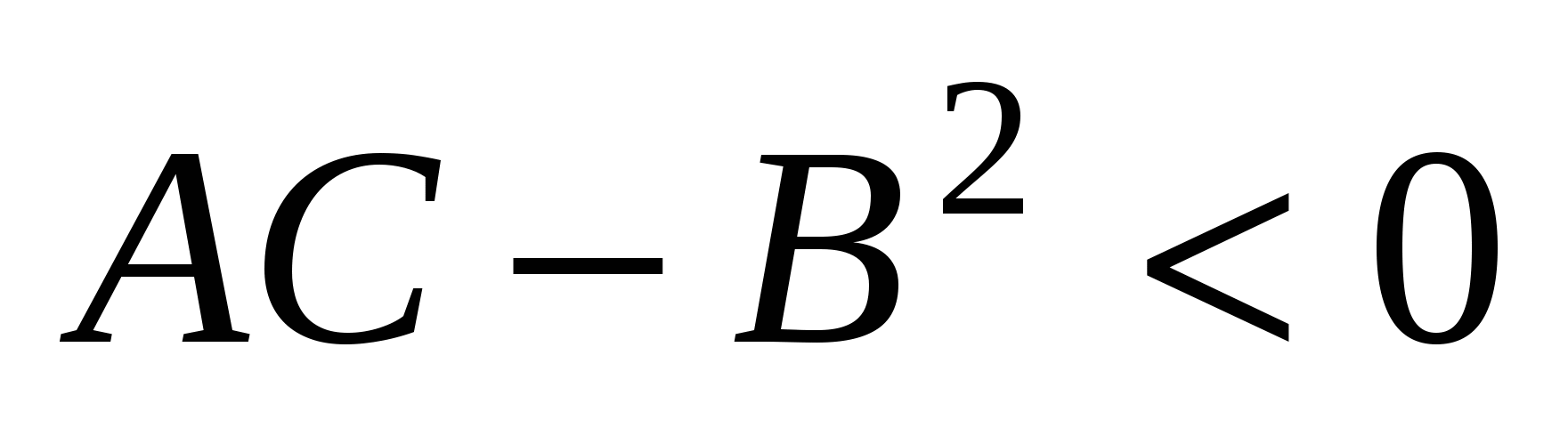 , то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); , то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых);
3) если 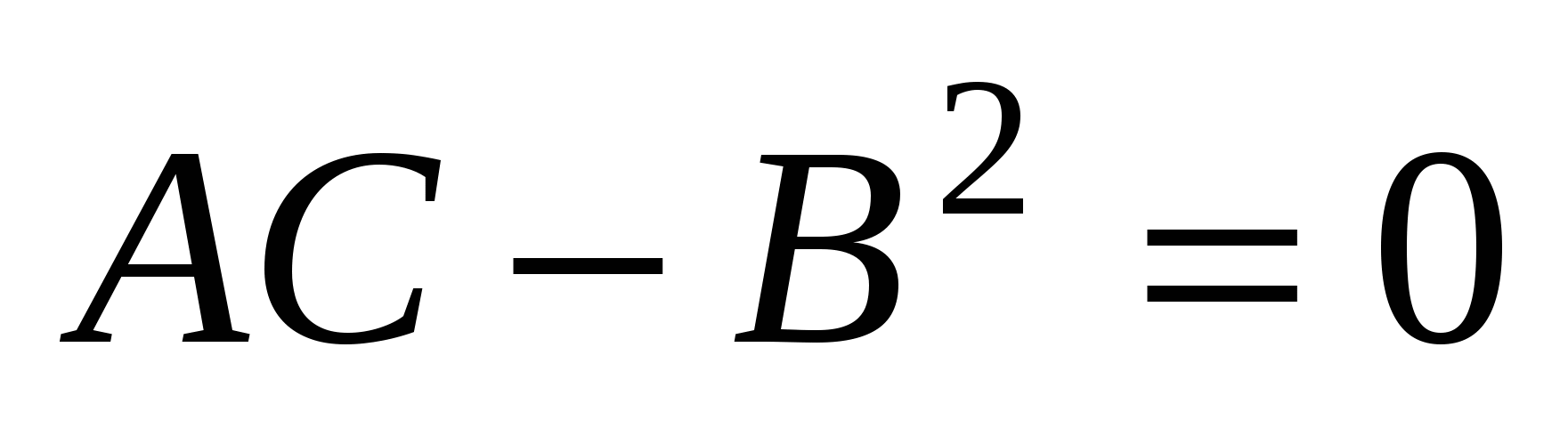 , то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых) . , то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых) .
Окружность, эллипс, гипербола и парабола являются невырожденными кривыми второго порядка.
Окружность.Каноническое уравнение окружности: 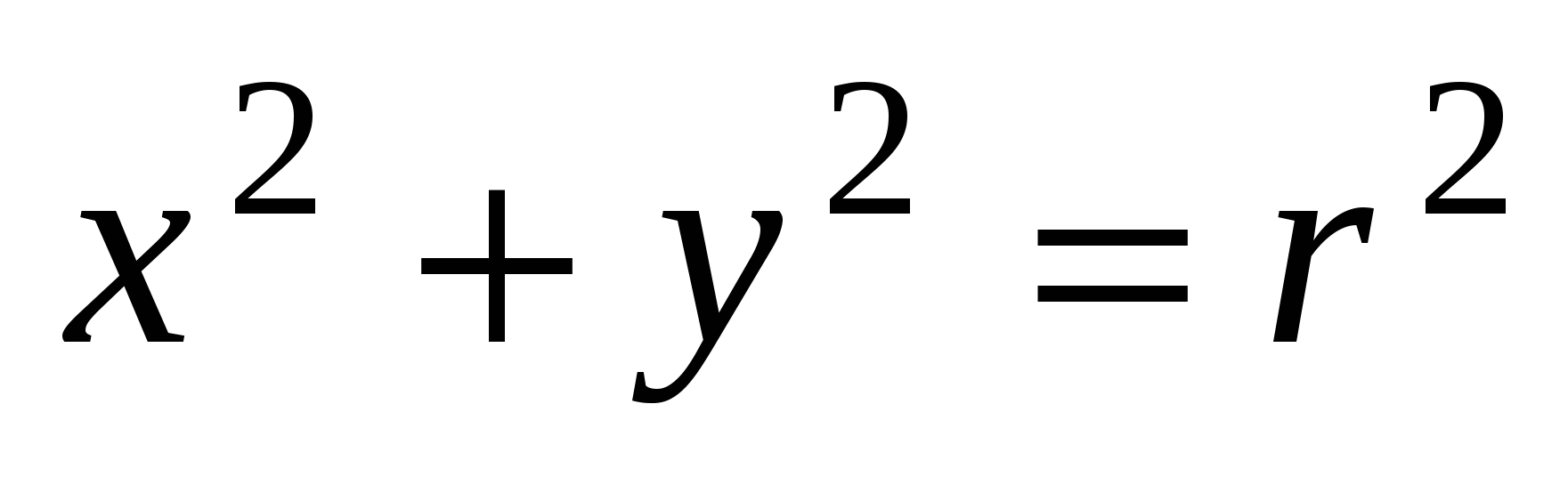 , где , где 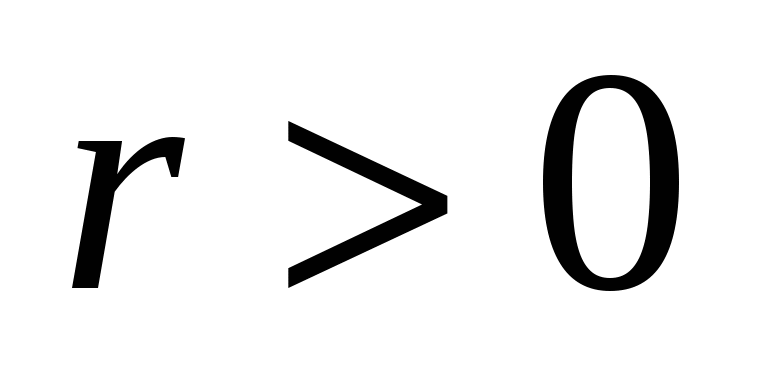 радиус окружности, точка радиус окружности, точка 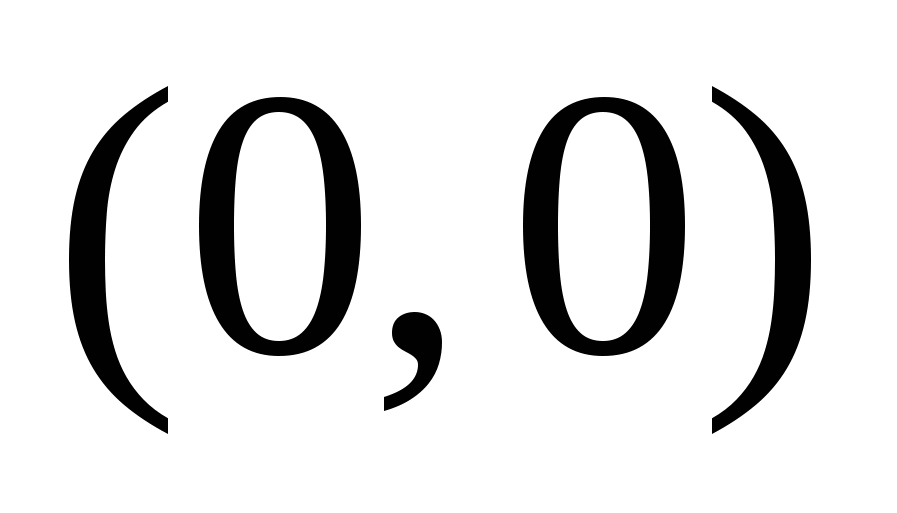 -центрокружности. -центрокружности.
Нормальное уравнение окружности: 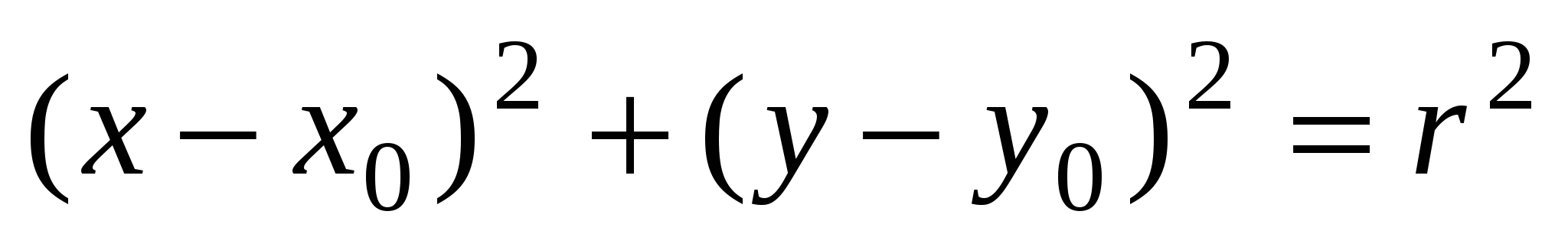 . Оно определяет окружность с центром в точке . Оно определяет окружность с центром в точке 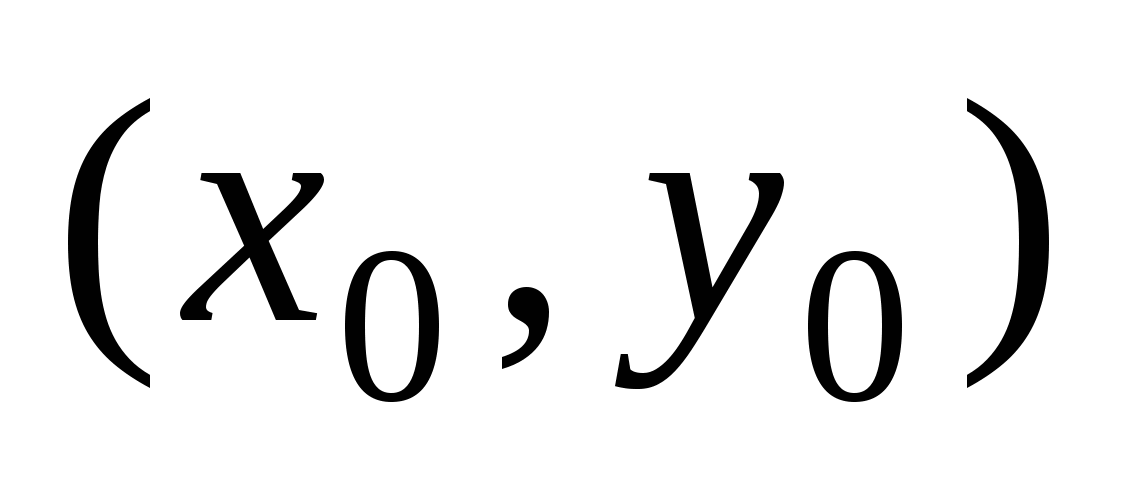 и радиусом и радиусом 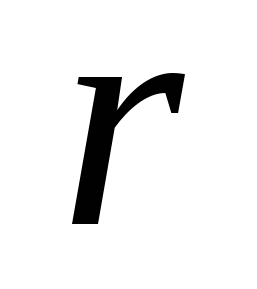 . .
Эллипс.Каноническое уравнение эллипса: 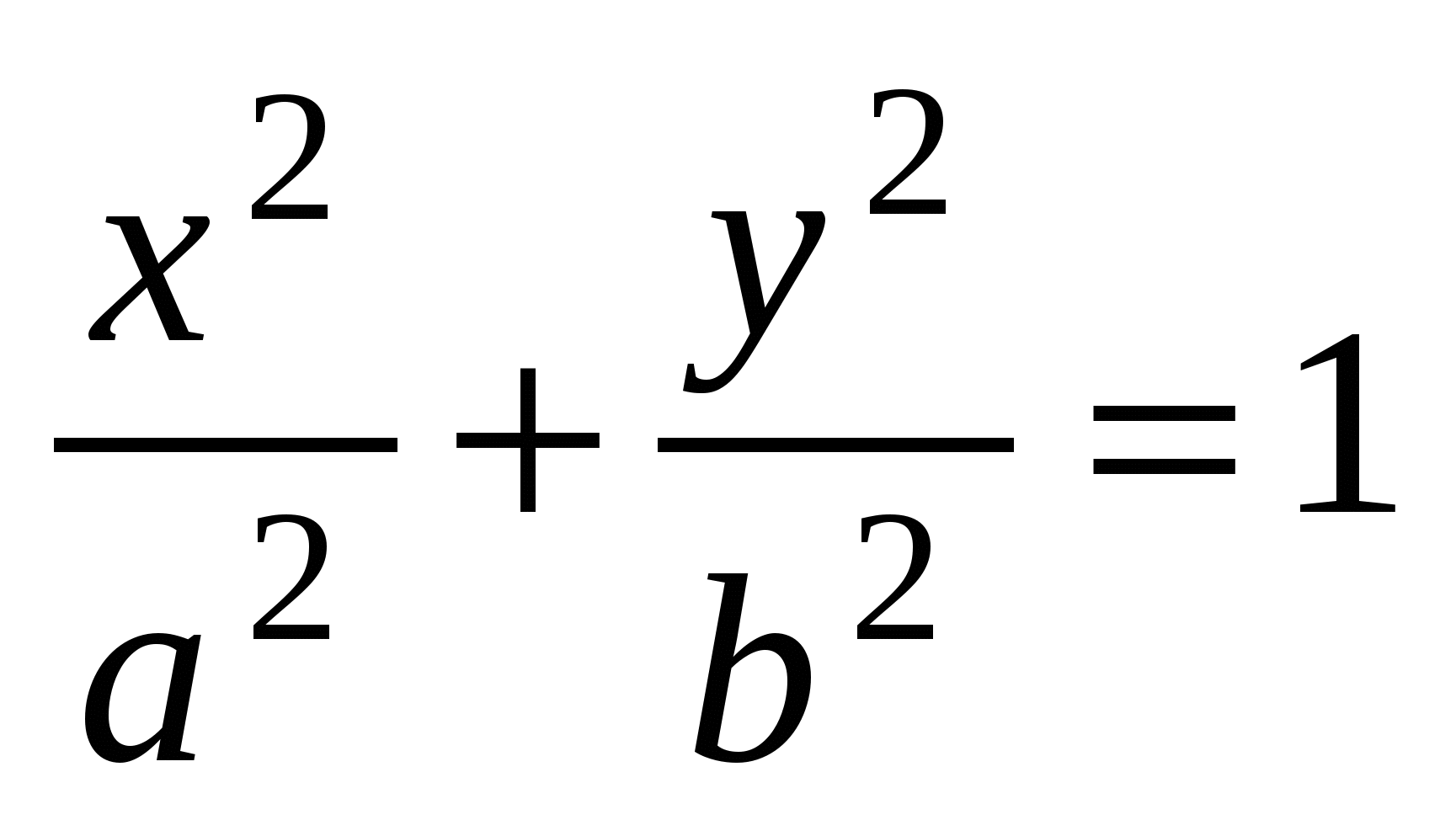 , , 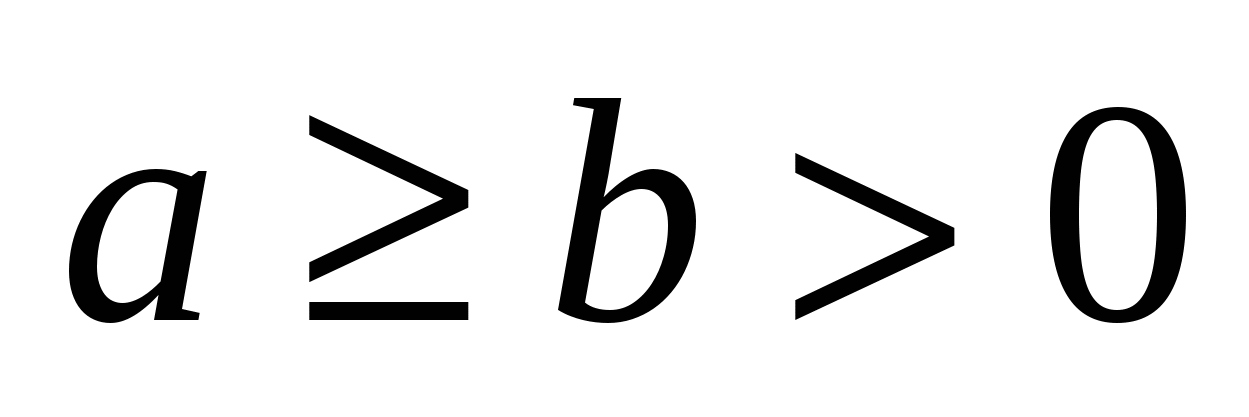 . .
Числа  и и 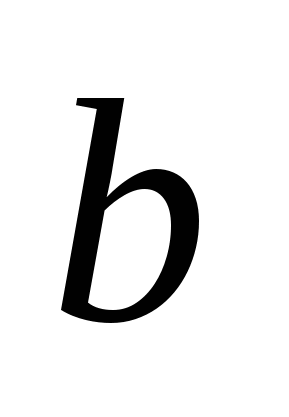 - большая и малая полуоси эллипса; точки - большая и малая полуоси эллипса; точки 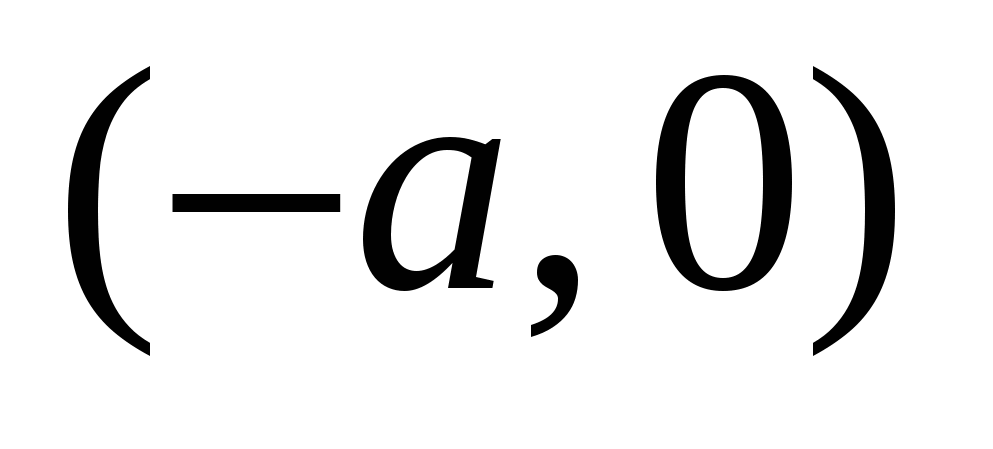 , , 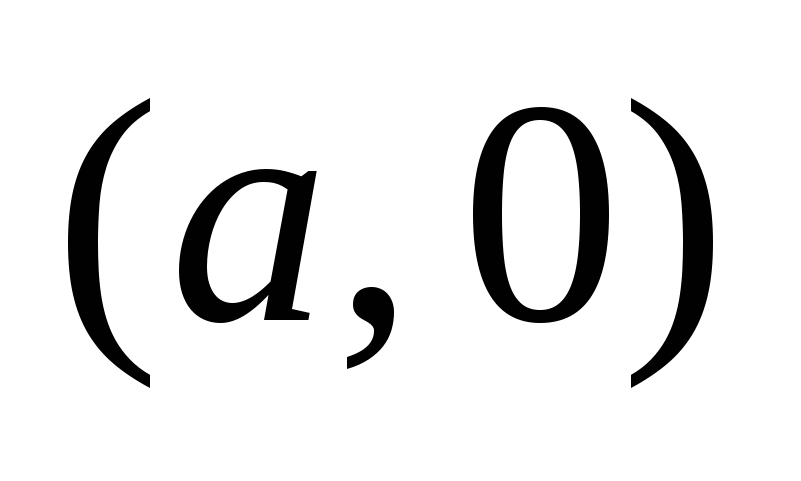 , , 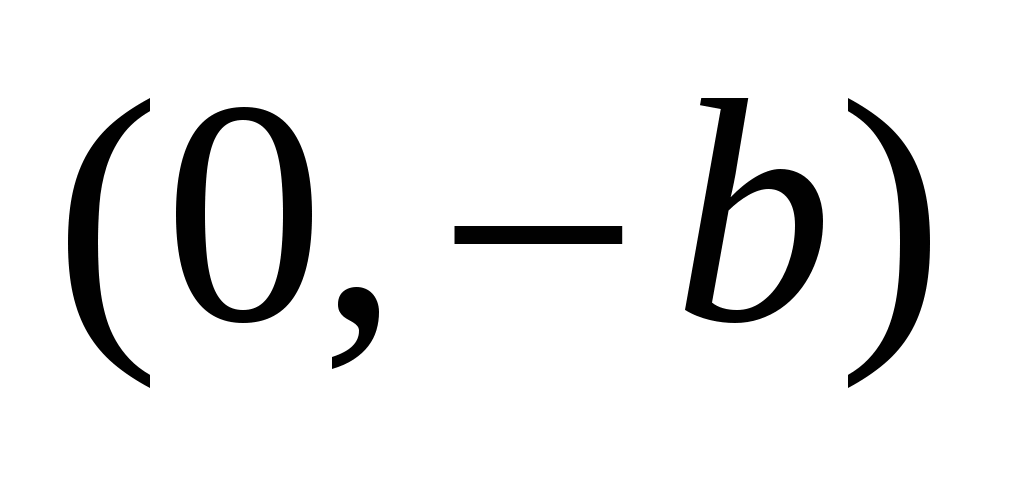 , , 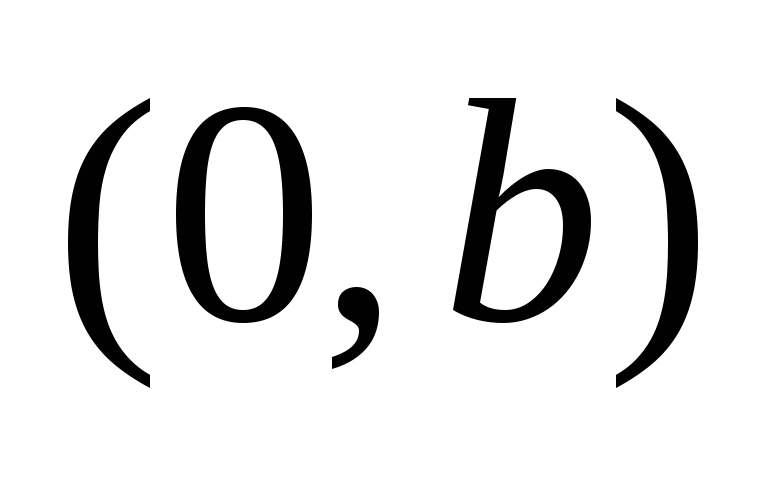 - вершины; оси - вершины; оси 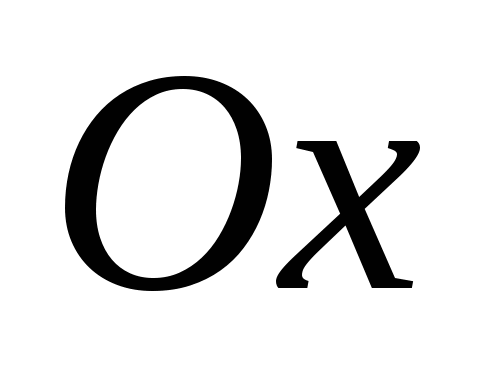 и и 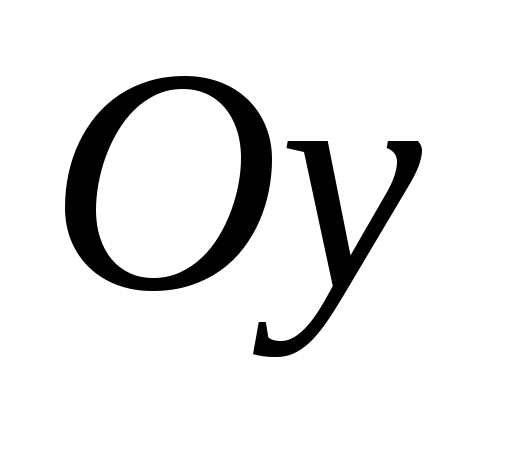 - главные оси симметрии; точка - главные оси симметрии; точка 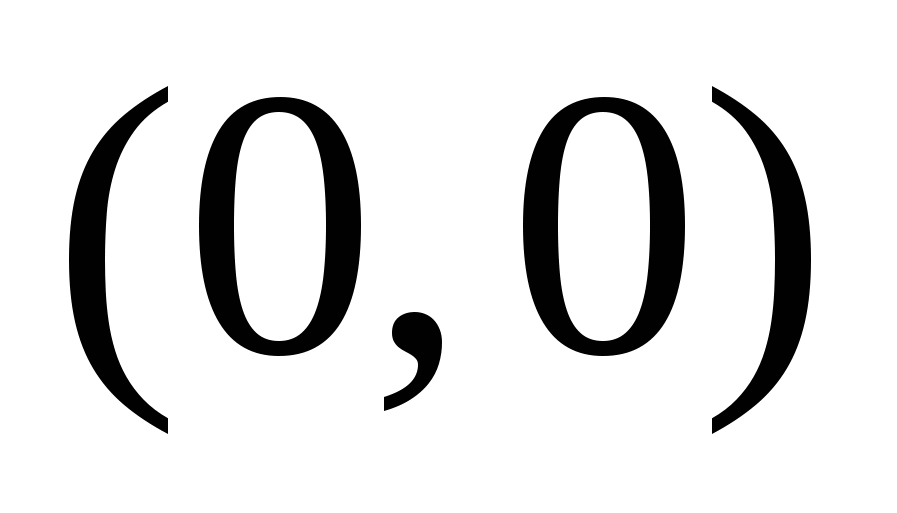 - центр симметрии (или просто центр) эллипса; прямоугольник со сторонами - центр симметрии (или просто центр) эллипса; прямоугольник со сторонами 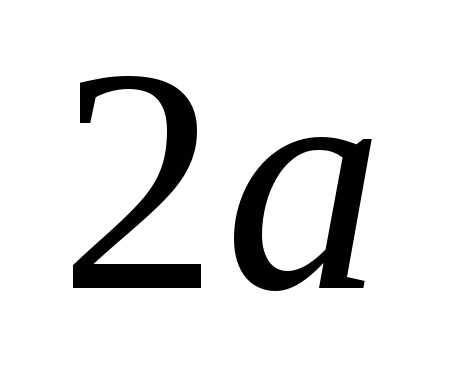 , , 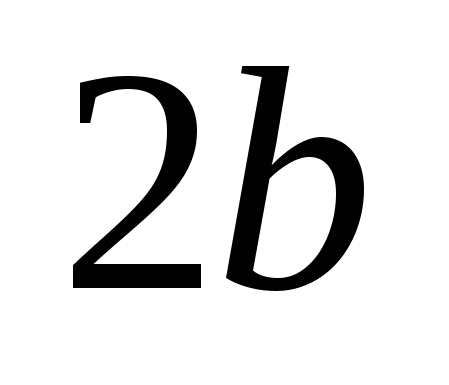 параллельными главным осям симметрии и центром в точке параллельными главным осям симметрии и центром в точке 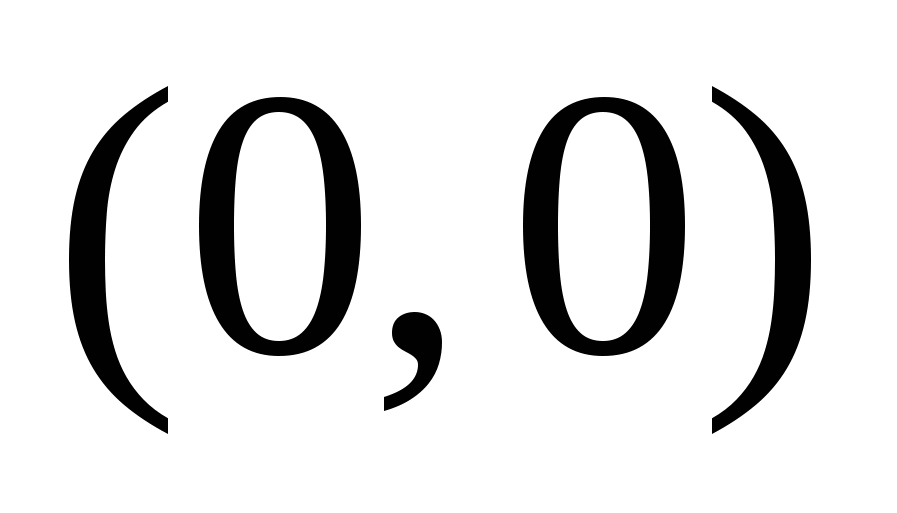 - основной прямоугольник эллипса; точки - основной прямоугольник эллипса; точки 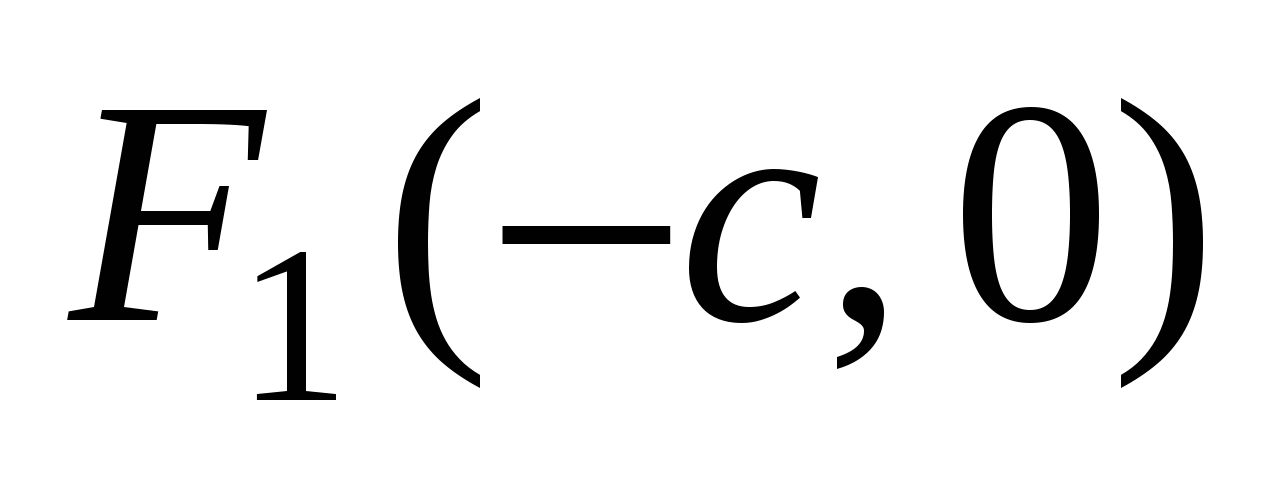 и и 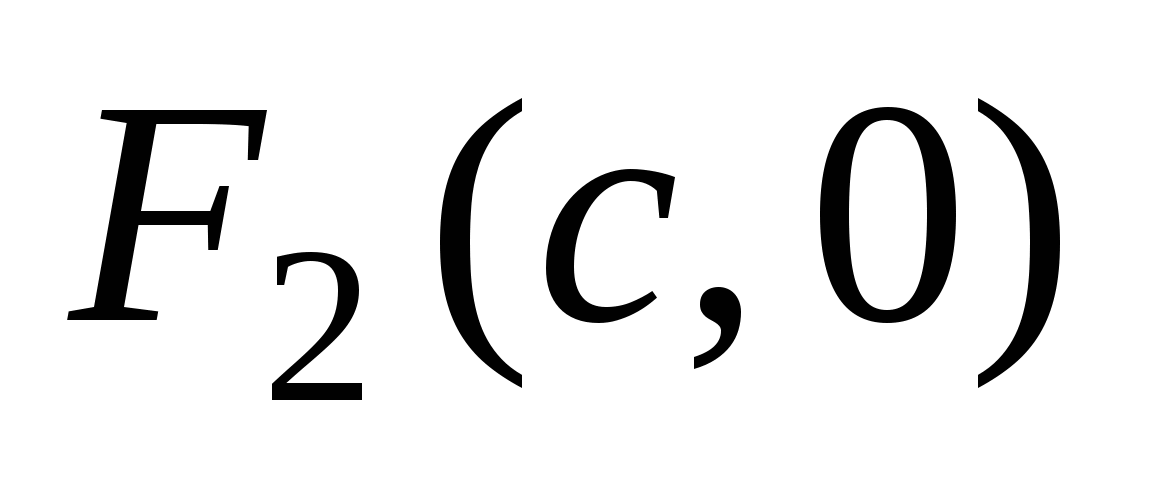 , где , где 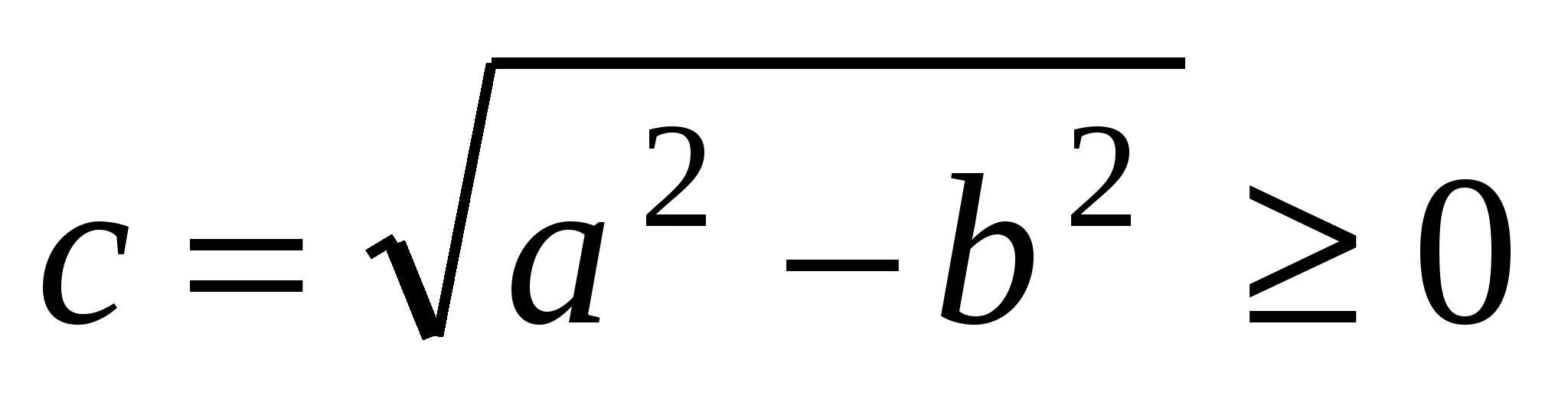 - фокусы эллипса; векторы - фокусы эллипса; векторы 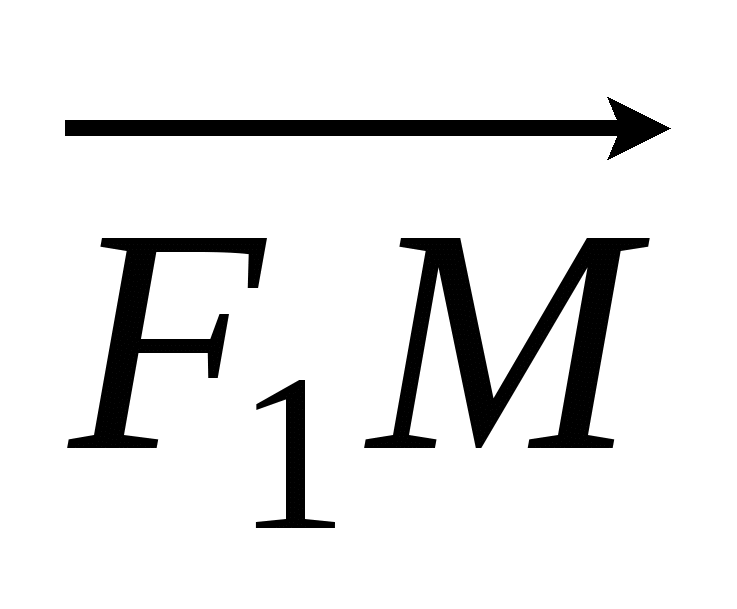 и и 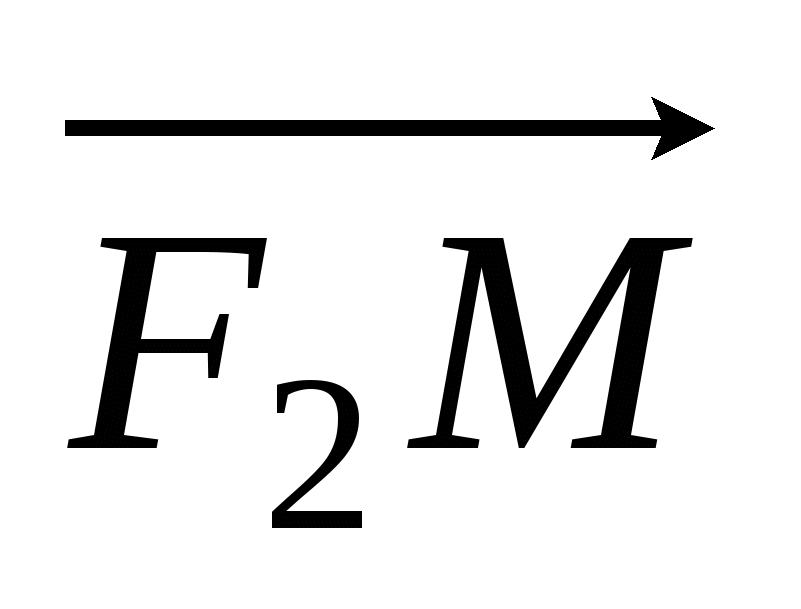 - фокальные радиус-векторы; числа - фокальные радиус-векторы; числа 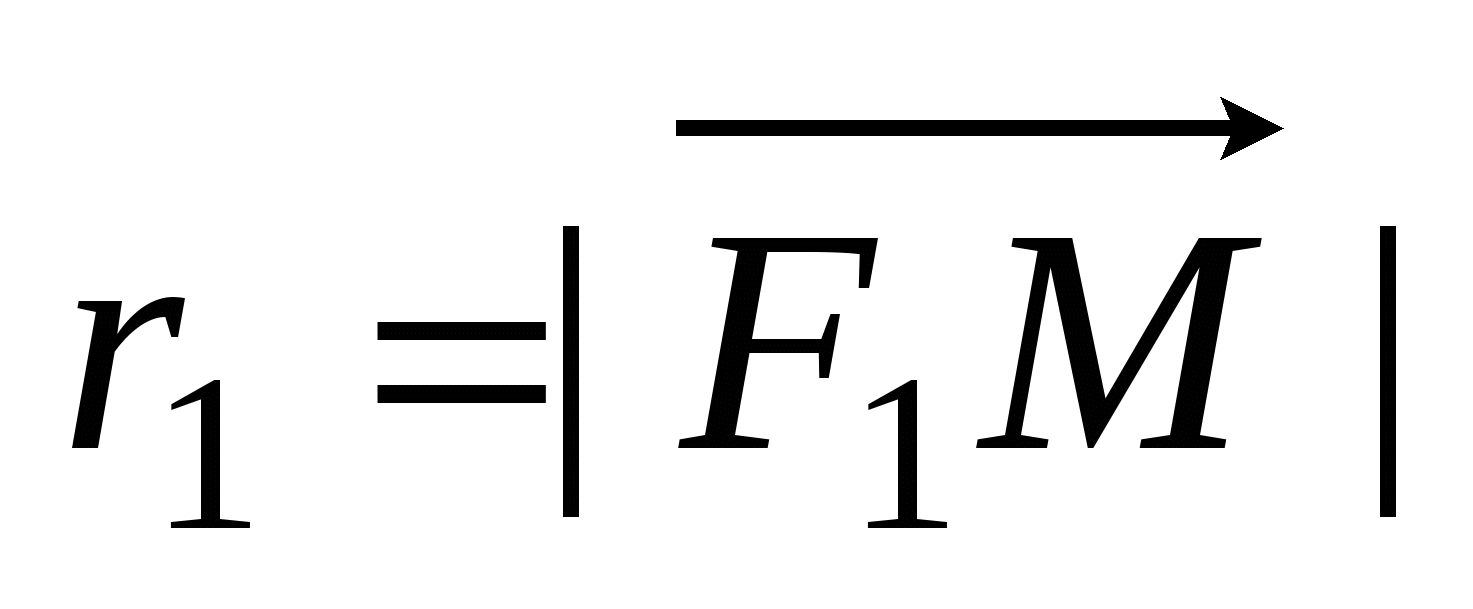 и и 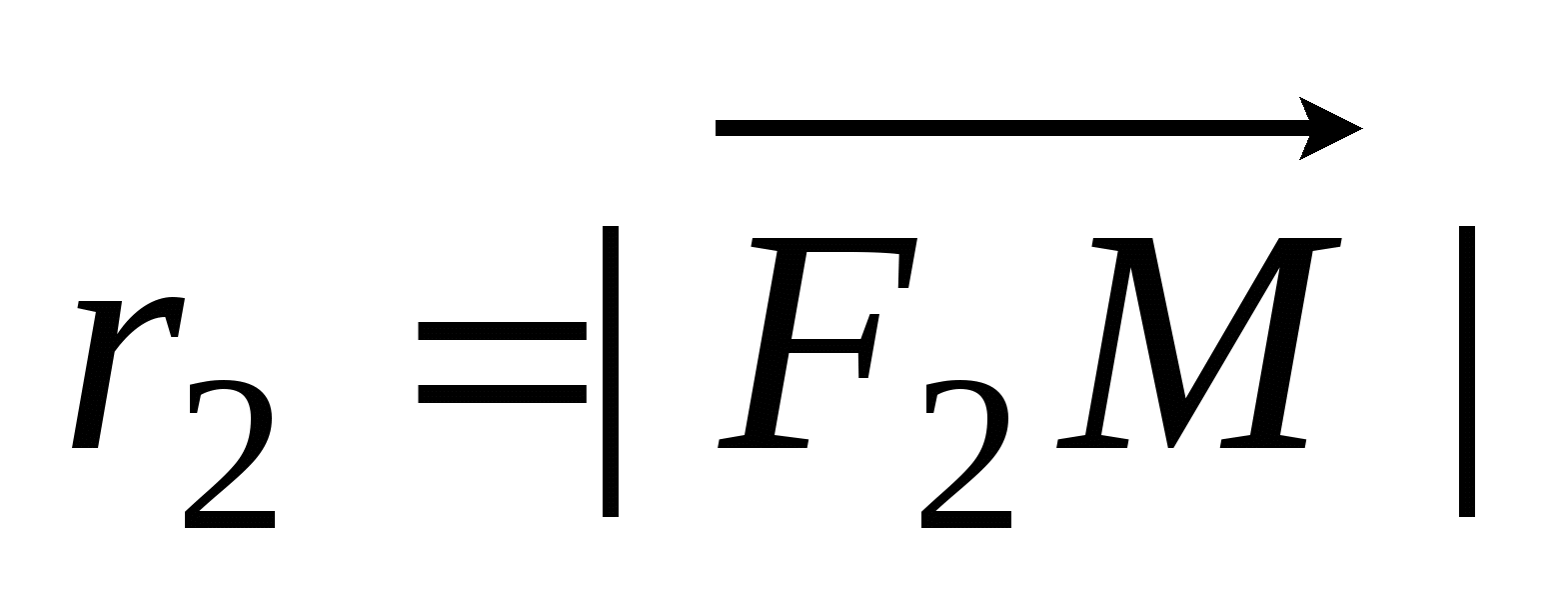 - фокальные радиусыточки - фокальные радиусыточки 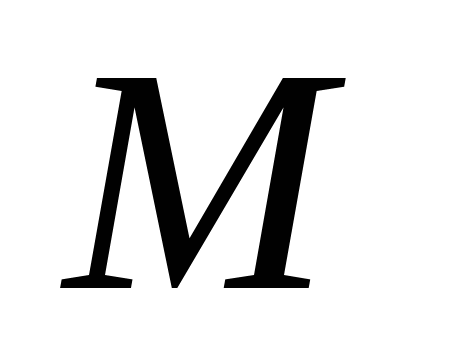 , принадлежащей эллипсу; число , принадлежащей эллипсу; число 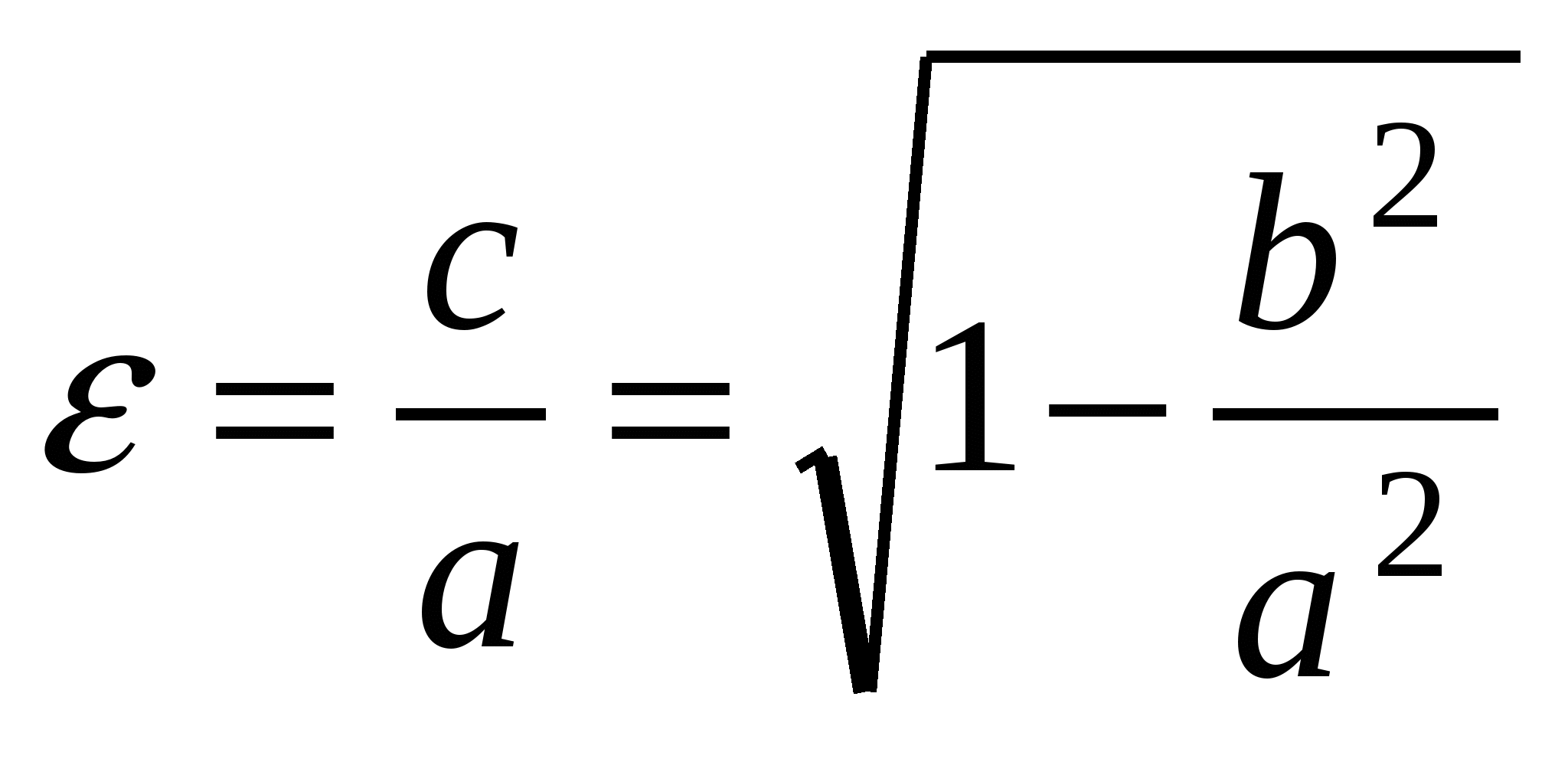 ( (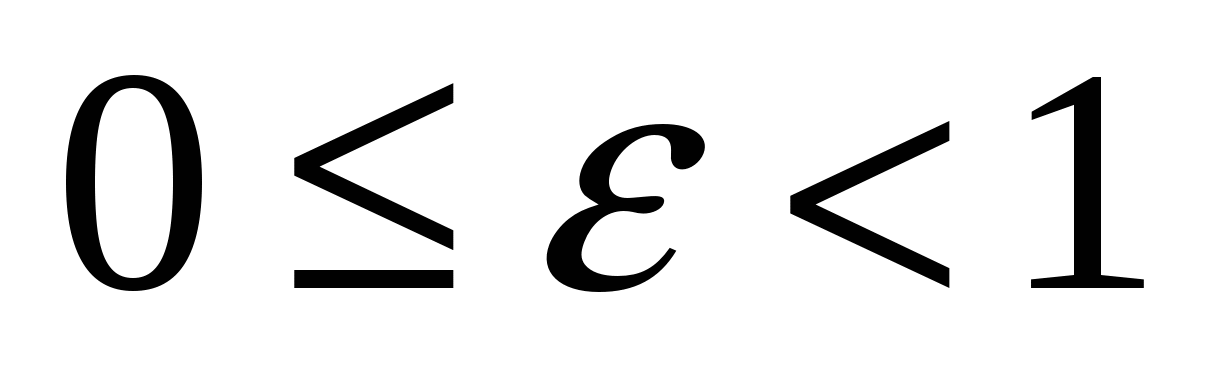 ) - эксцентриситет эллипса (при ) - эксцентриситет эллипса (при 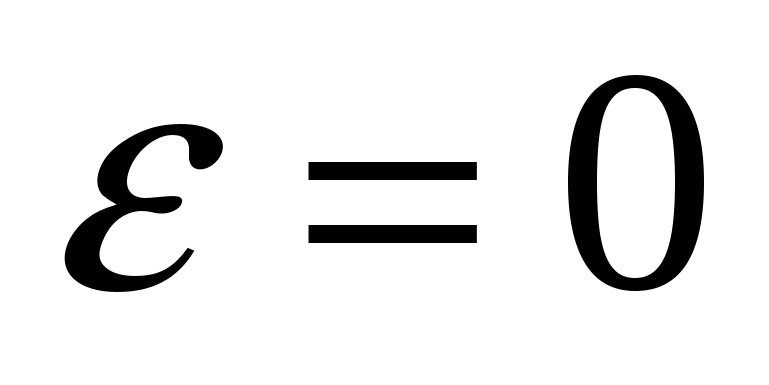 эллипс является окружностью); прямые эллипс является окружностью); прямые 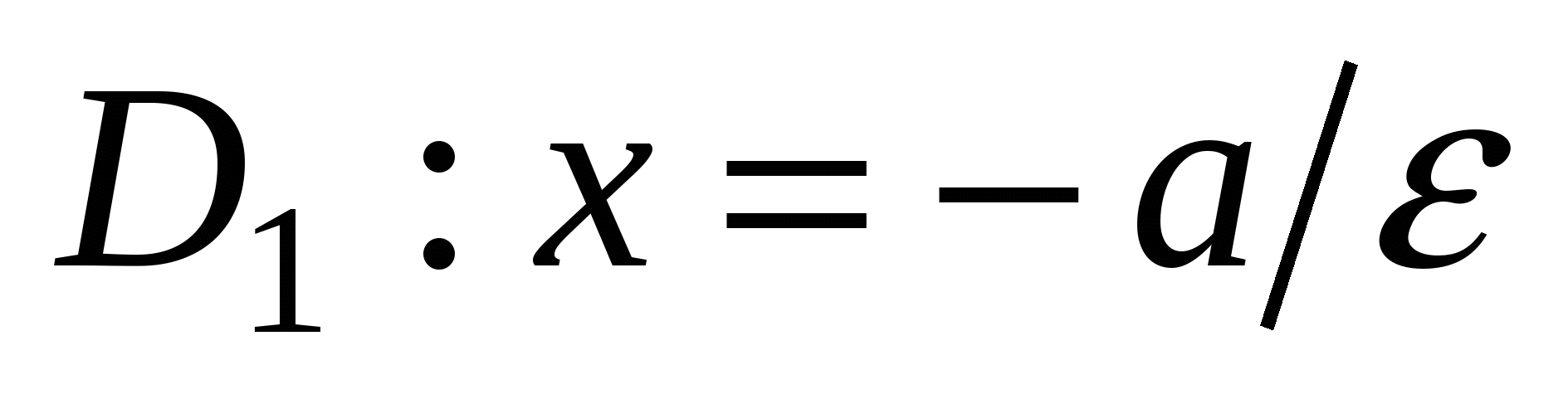 и и 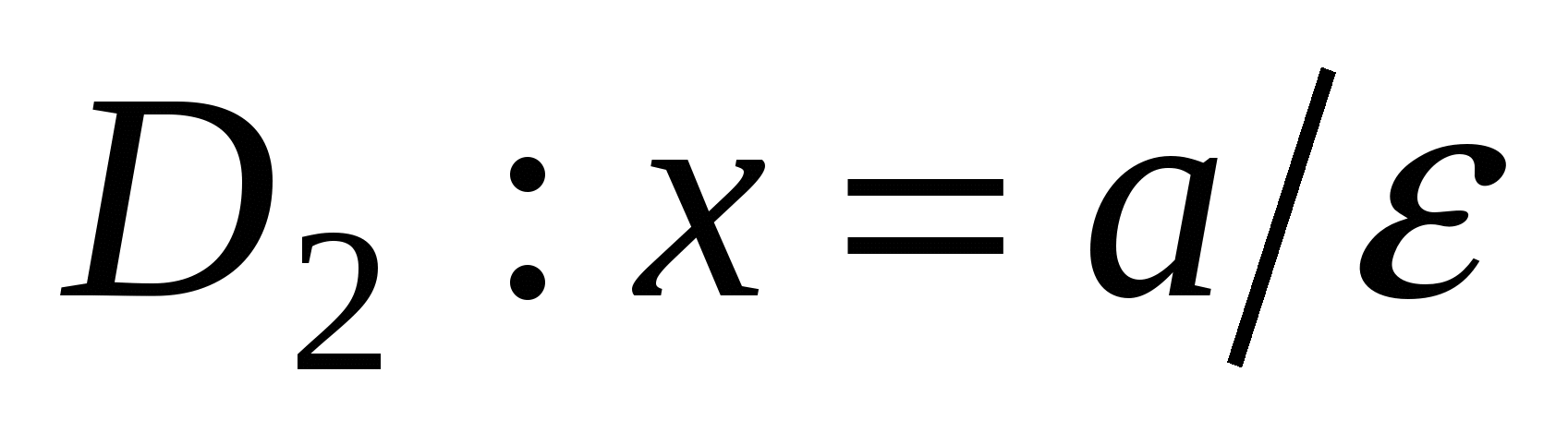 - директрисы эллипса. - директрисы эллипса.
Гипербола.Каноническое уравнение гиперболы 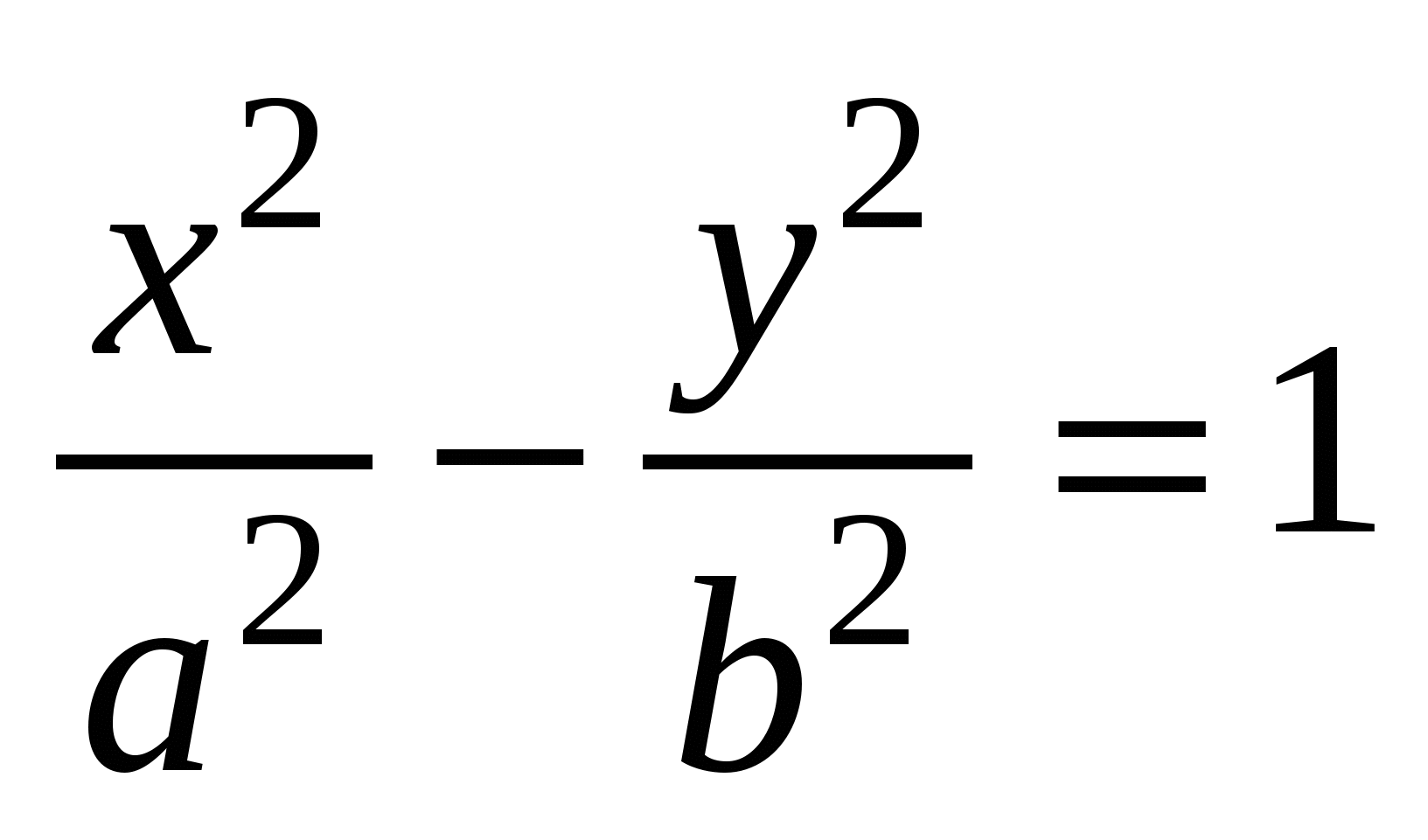 , , 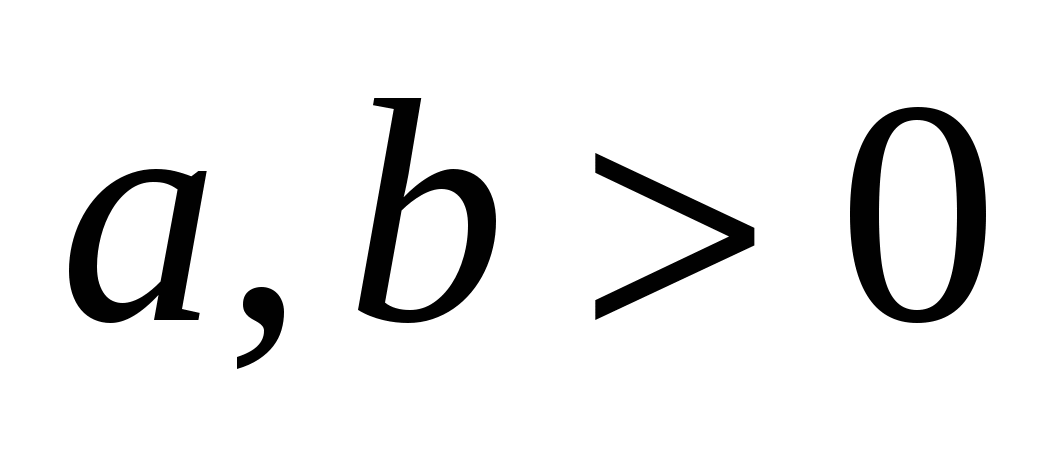 . .
Числа  и и 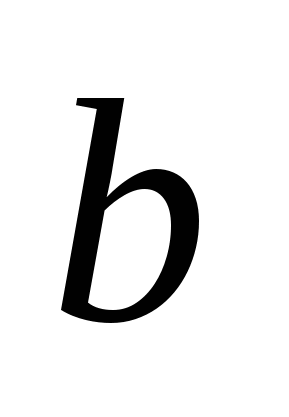 - действительная и мнимая полуоси гиперболы; точки - действительная и мнимая полуоси гиперболы; точки 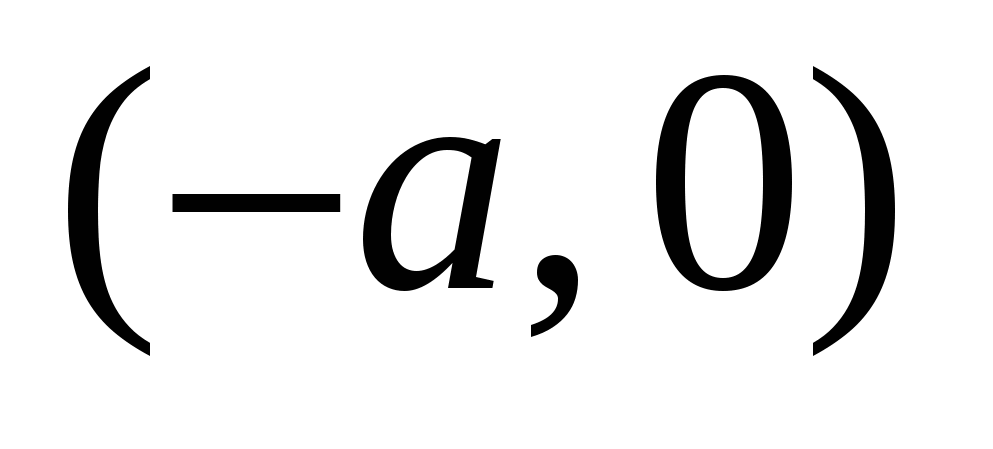 , , 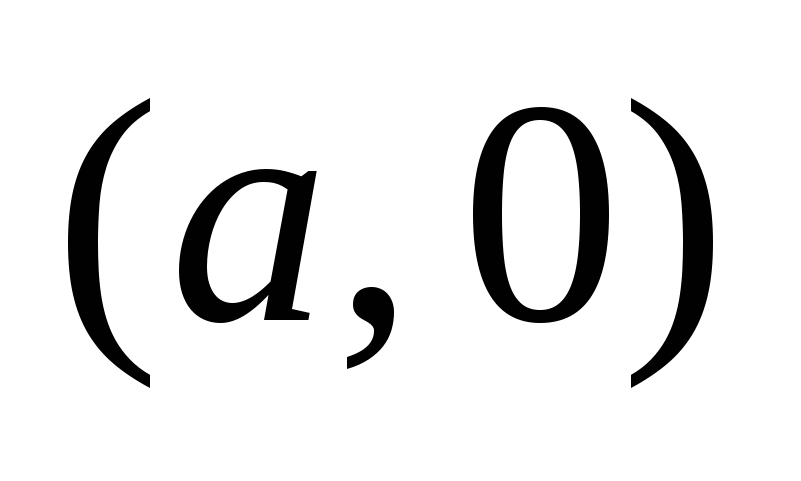 - вершинами; оси - вершинами; оси 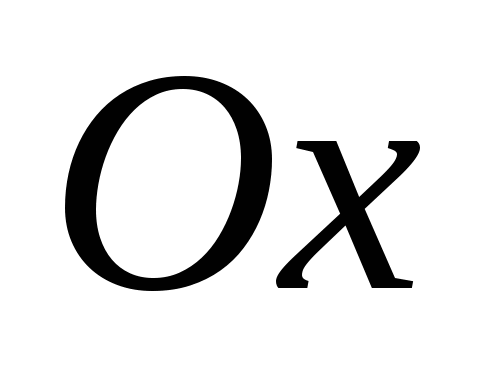 и и 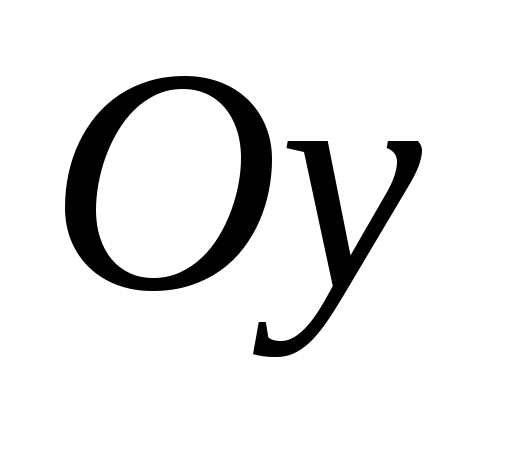 - главные оси симметрии; точка - главные оси симметрии; точка 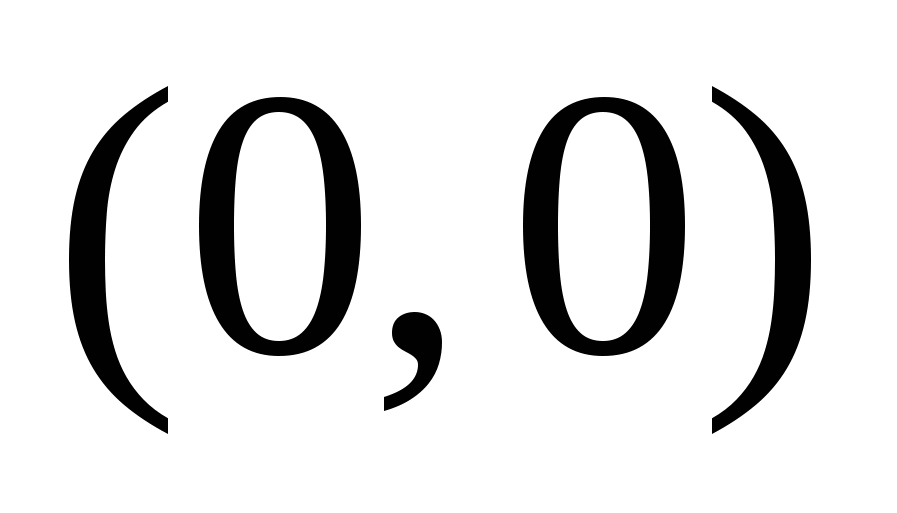 - центр симметрии (или просто центр) гиперболы; прямоугольник со сторонами - центр симметрии (или просто центр) гиперболы; прямоугольник со сторонами 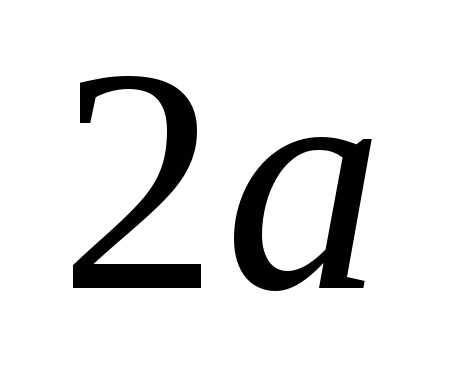 , , 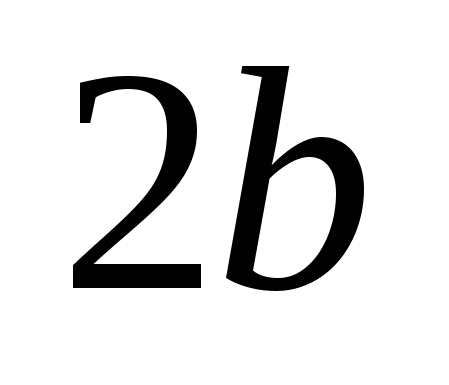 параллельными главным осям симметрии и центром в точке параллельными главным осям симметрии и центром в точке 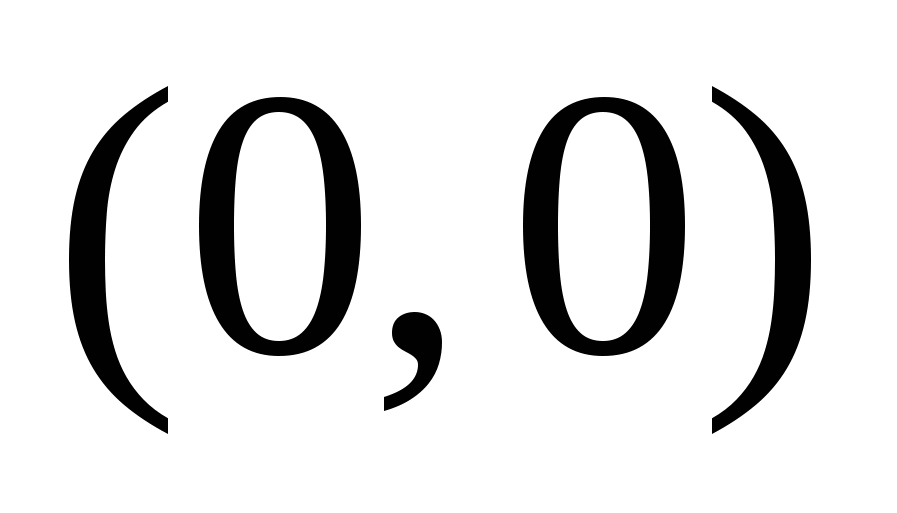 - основной прямоугольник гиперболы; точки - основной прямоугольник гиперболы; точки 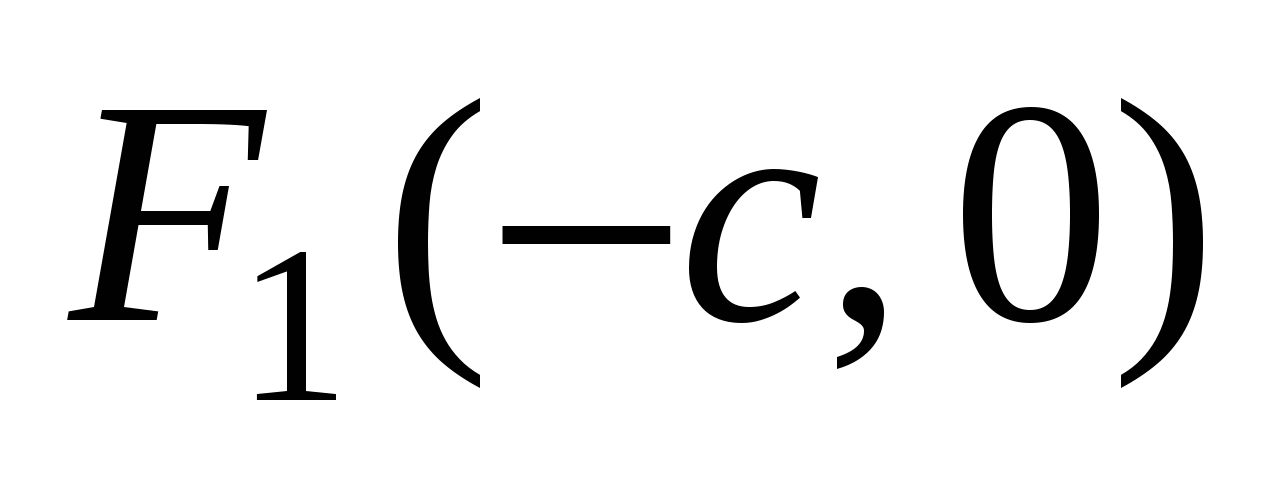 и и 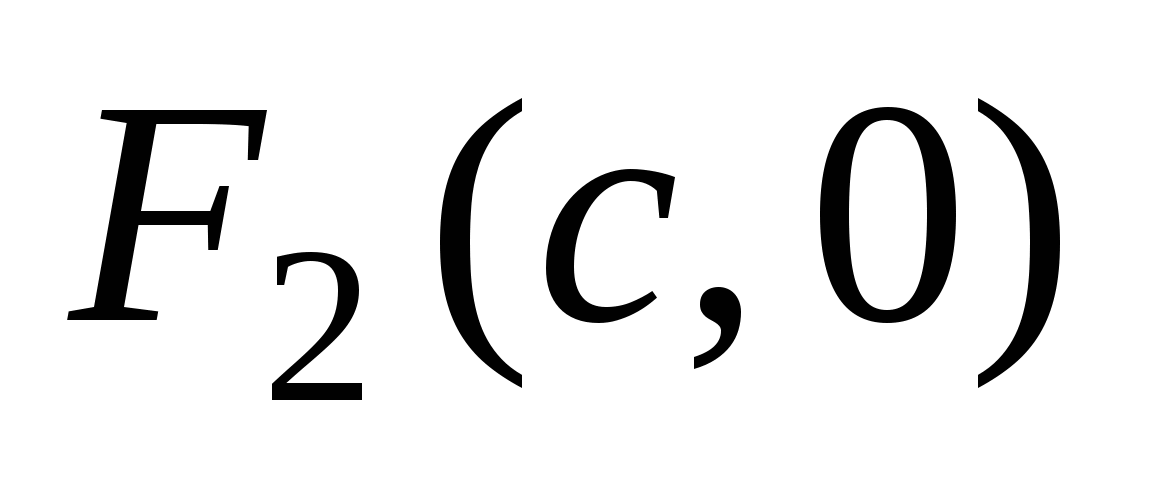 , где , где 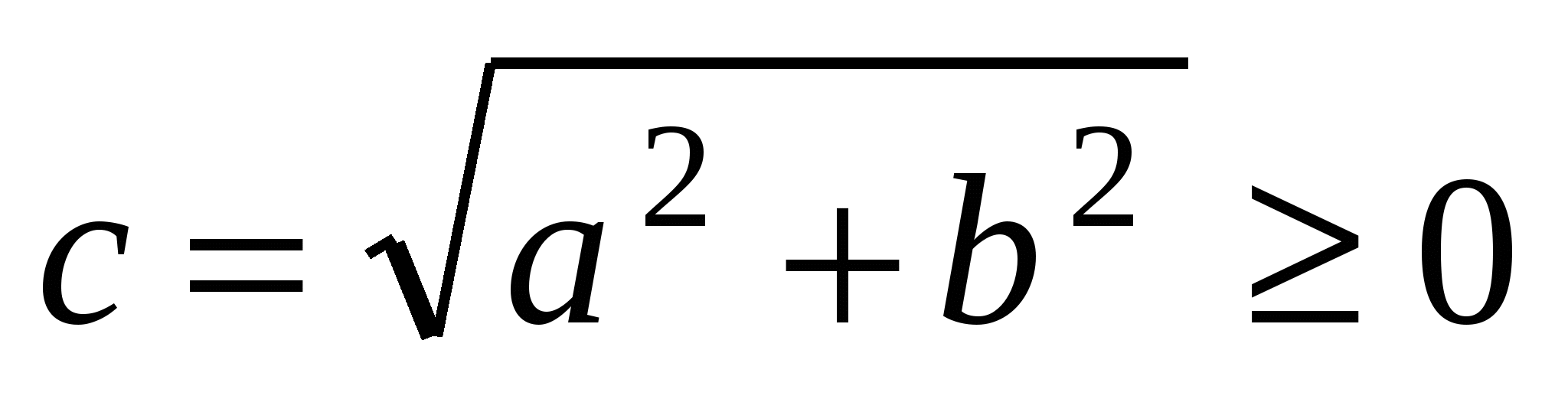 - фокусы гиперболы; векторы - фокусы гиперболы; векторы 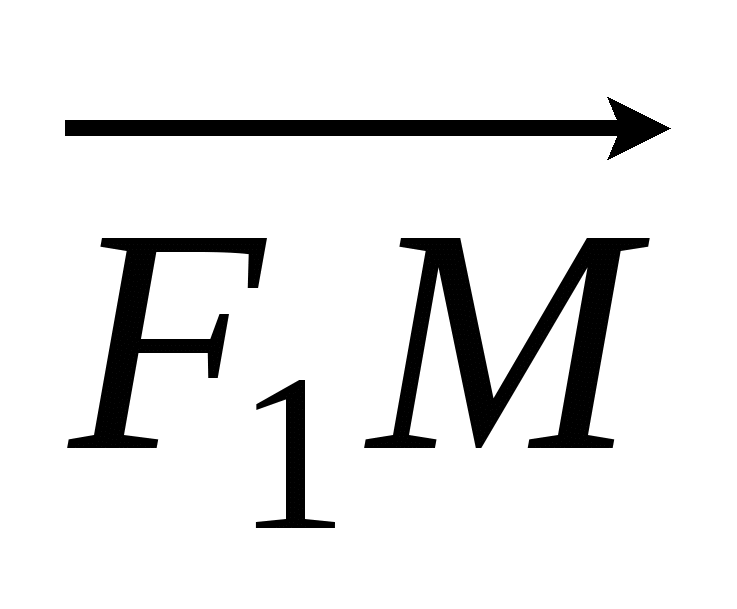 и и 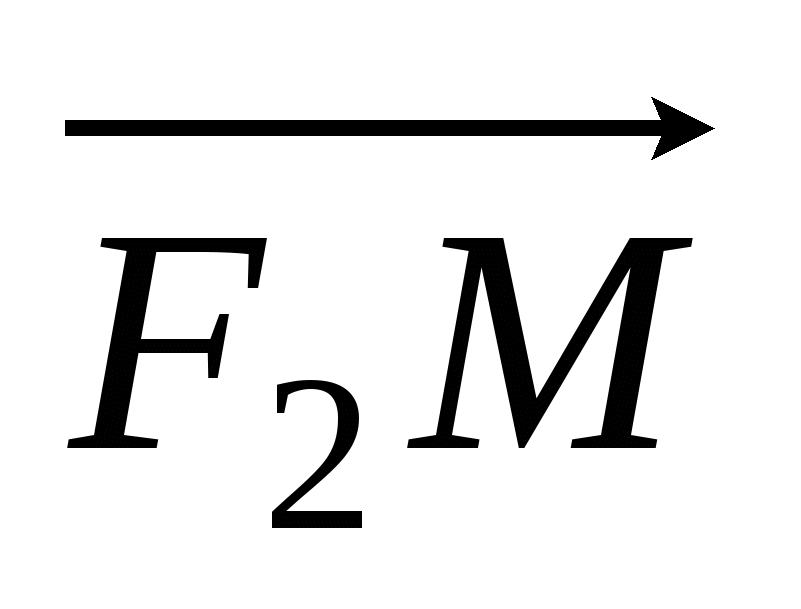 - фокальные радиус-векторы; числа - фокальные радиус-векторы; числа 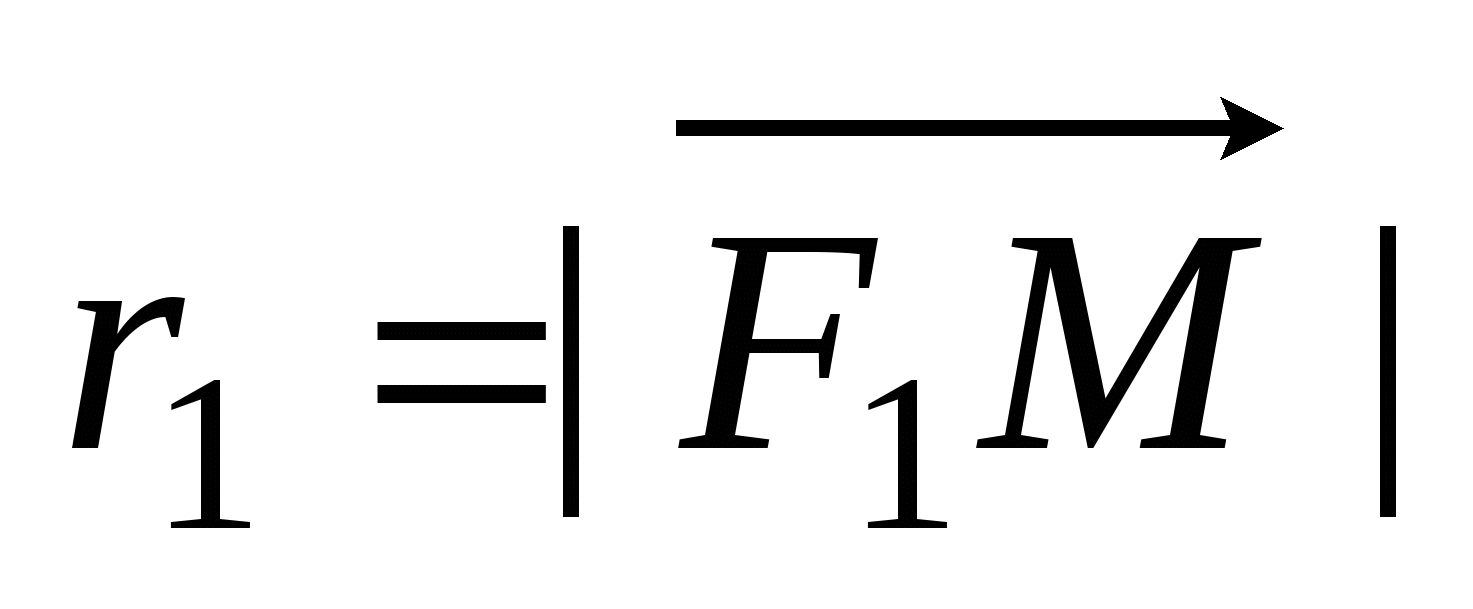 и и 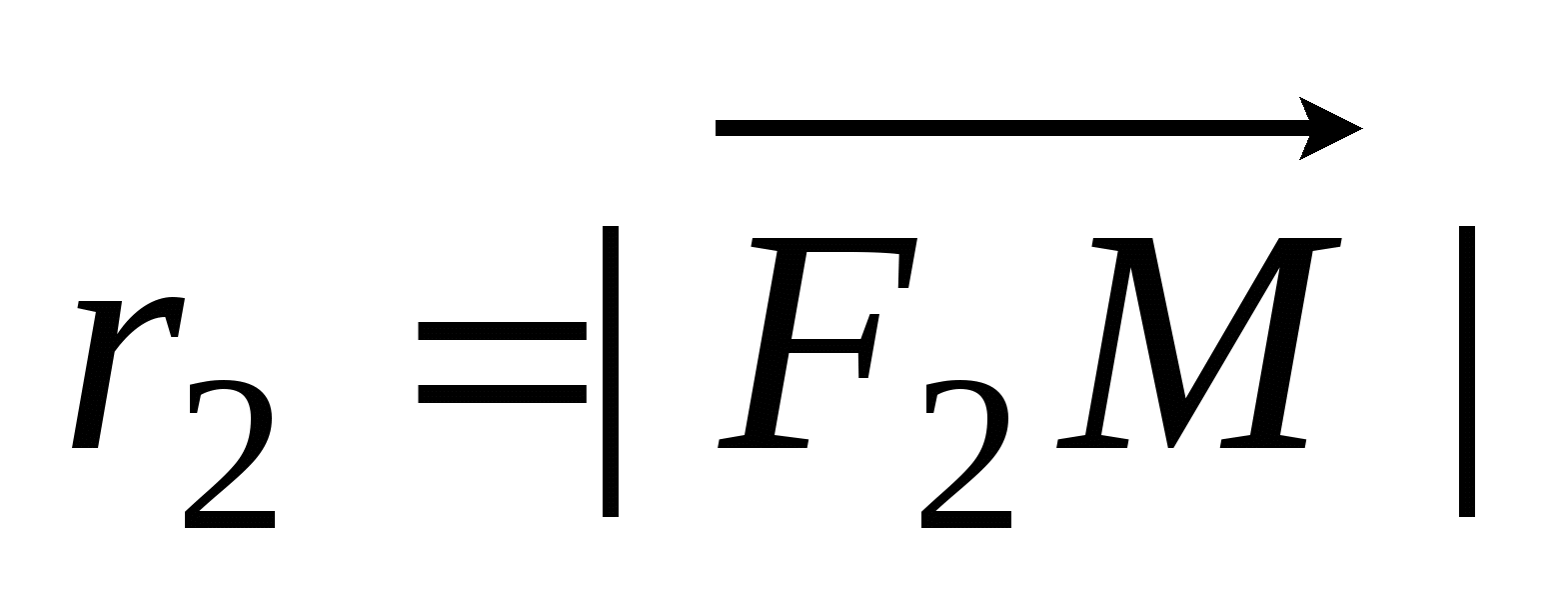 - фокальные радиусы точки - фокальные радиусы точки 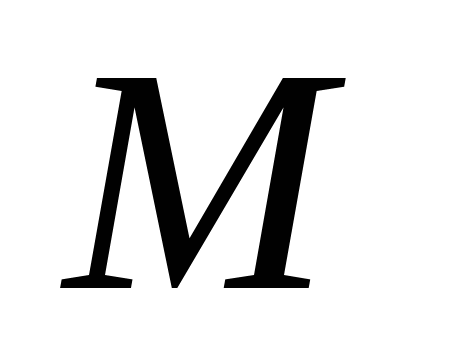 , принадлежащей гиперболе; число , принадлежащей гиперболе; число 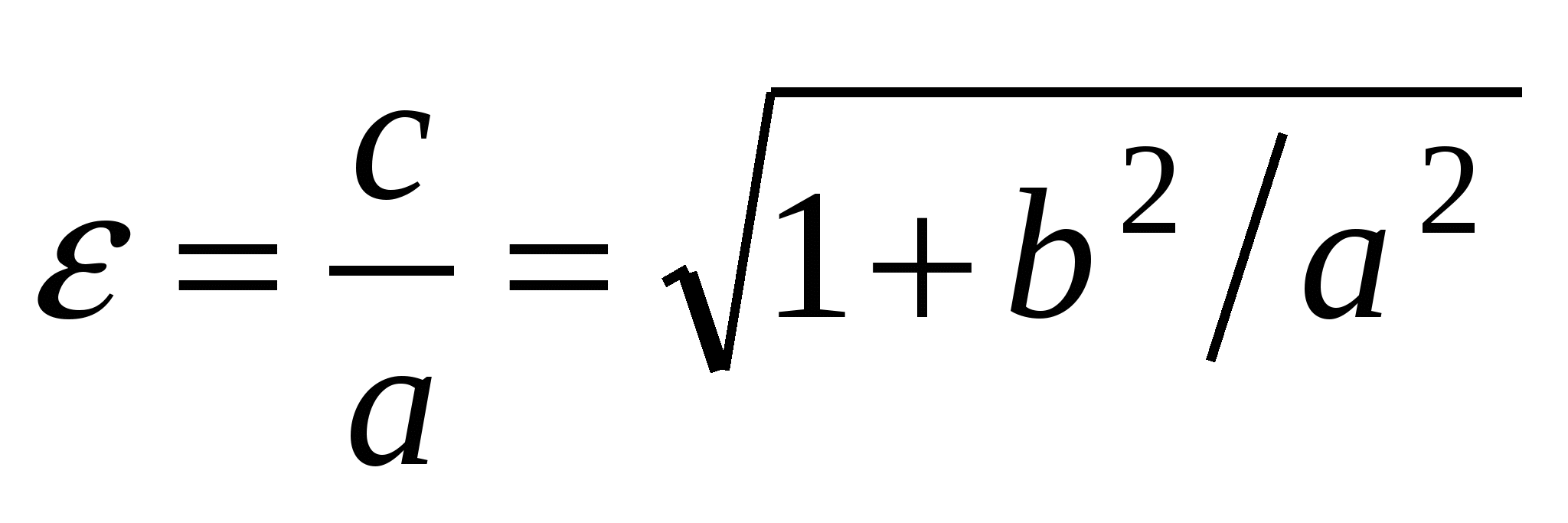 ( (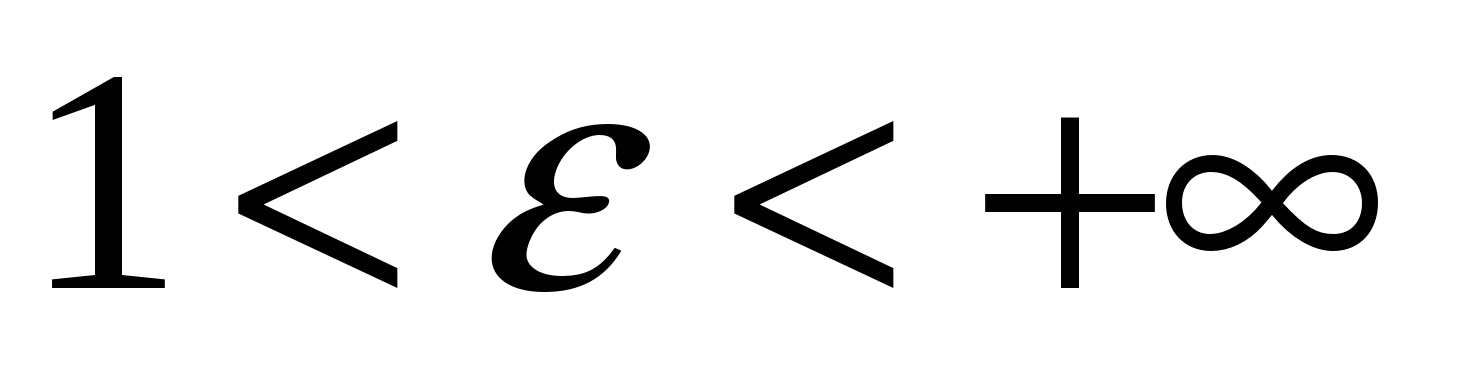 ) - эксцентриситетгиперболы; прямые ) - эксцентриситетгиперболы; прямые 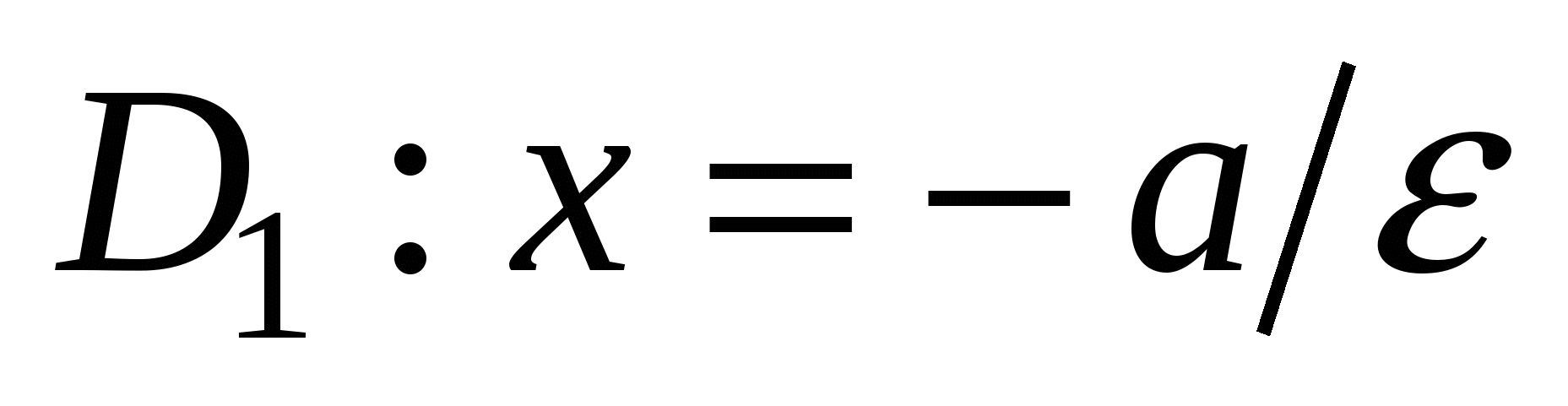 и и 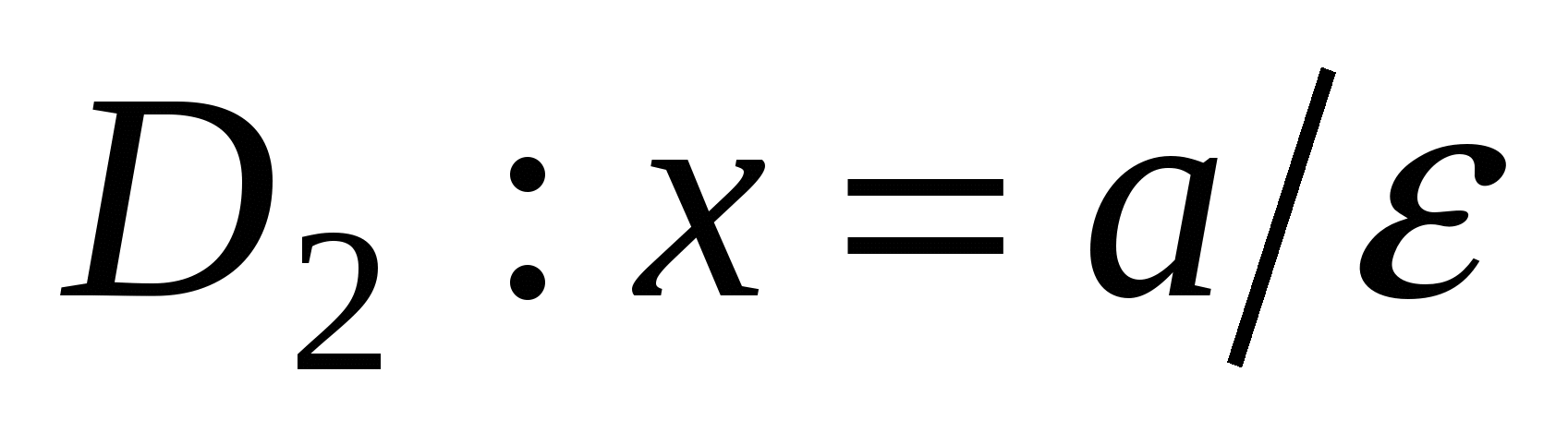 - директрисы гиперболы; прямые - директрисы гиперболы; прямые 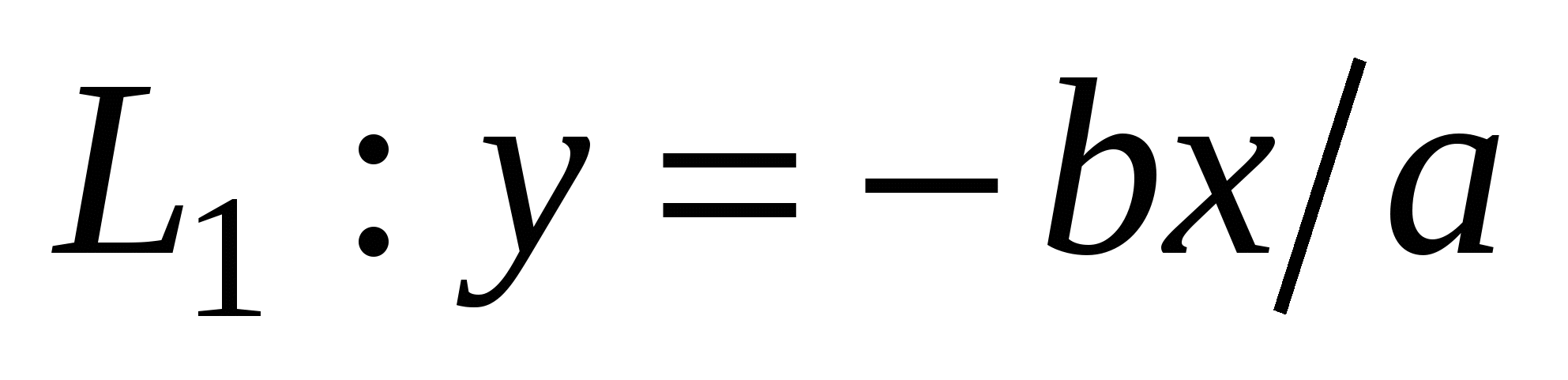 и и 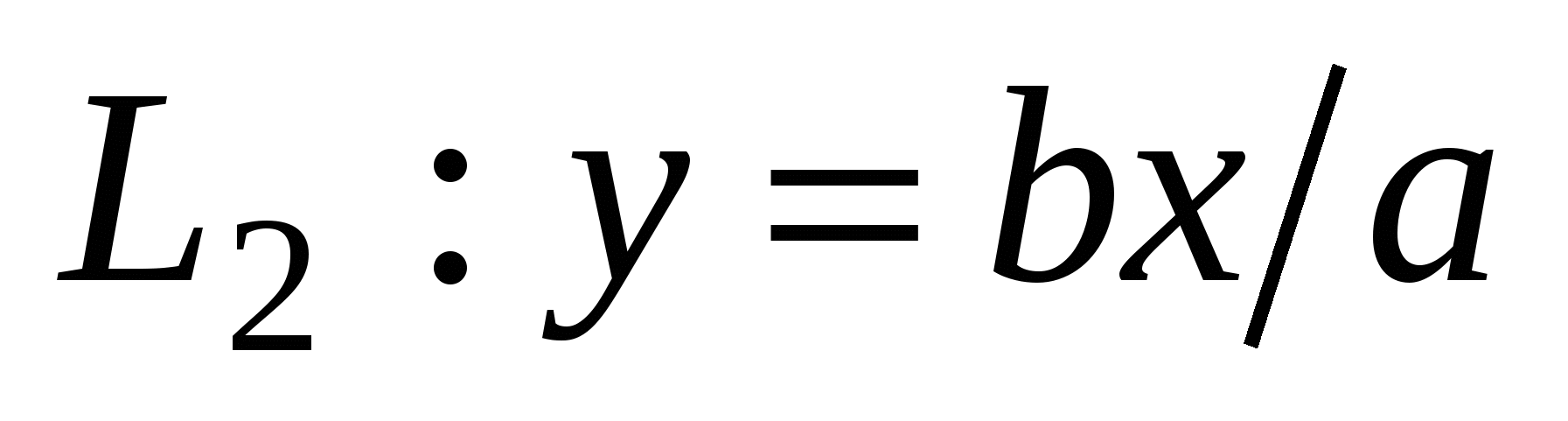 называются асимптотами гиперболы (они проходят через противоположные вершины основного прямоугольника гиперболы). называются асимптотами гиперболы (они проходят через противоположные вершины основного прямоугольника гиперболы).
Парабола.Каноническое уравнение параболы: 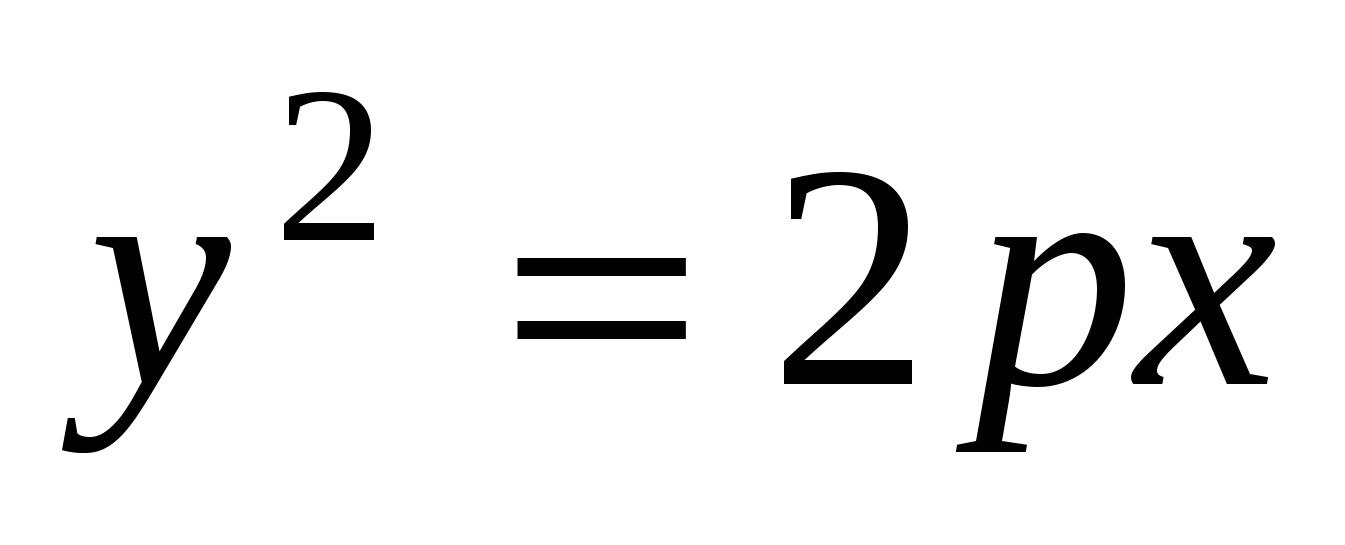 , , 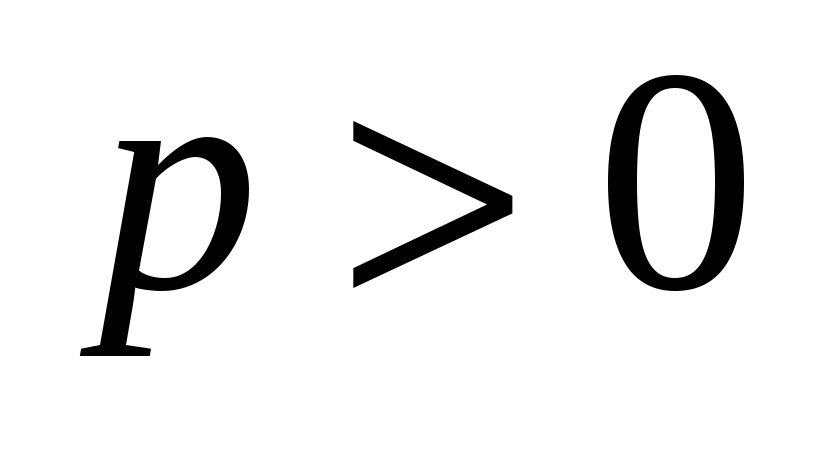 . .
Число 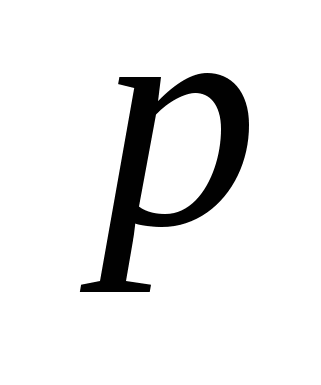 - параметр параболы; ось - параметр параболы; ось 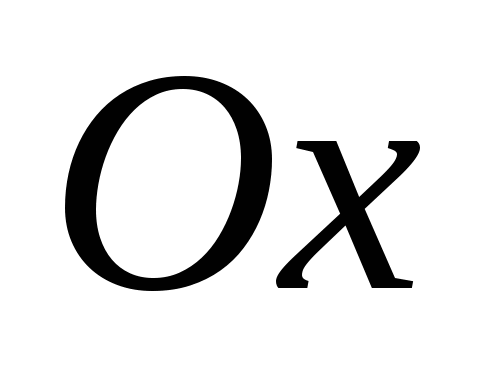 - ось симметрии; точка – вершина параболы; точка - ось симметрии; точка – вершина параболы; точка 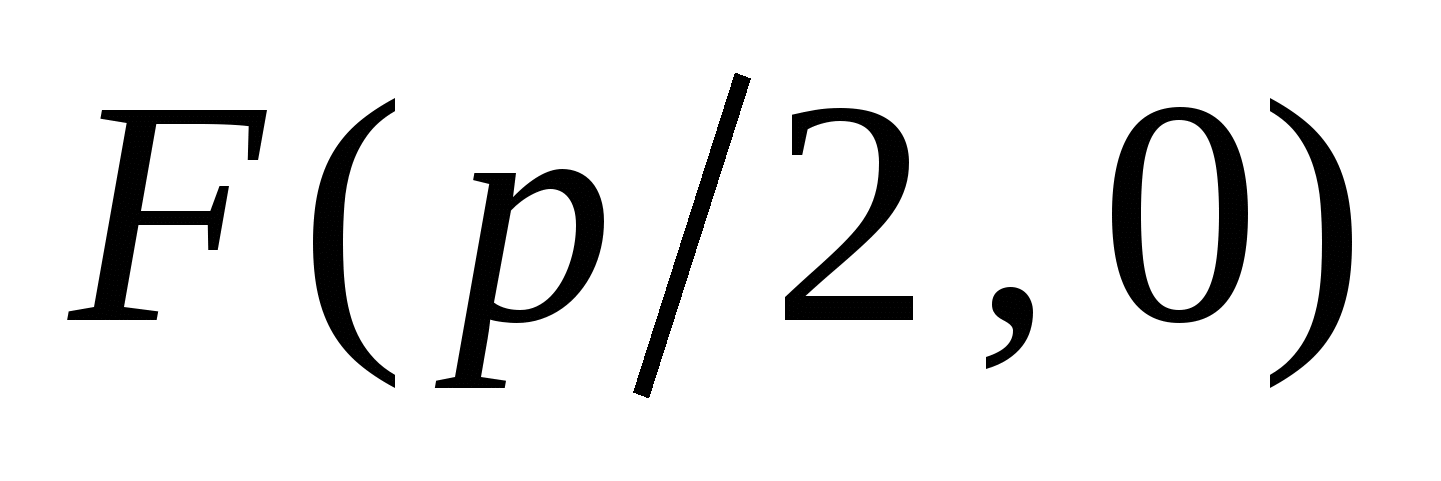 - фокус параболы; вектор - фокус параболы; вектор  - фокальный радиус-вектор; число - фокальный радиус-вектор; число 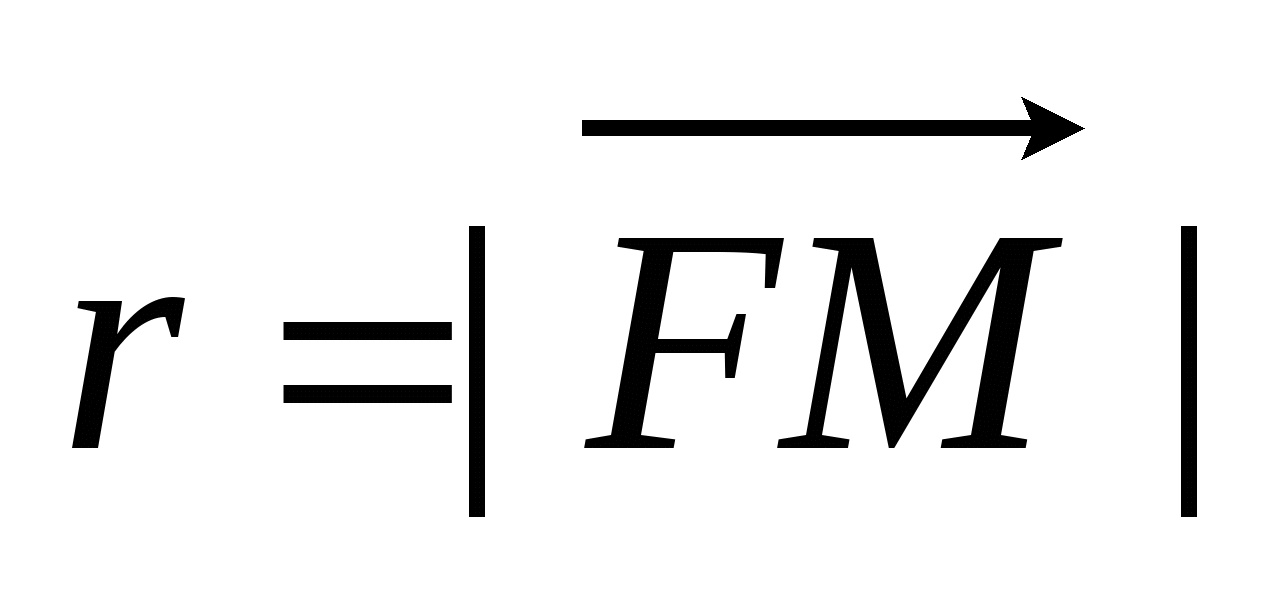 - фокальный радиус точки - фокальный радиус точки 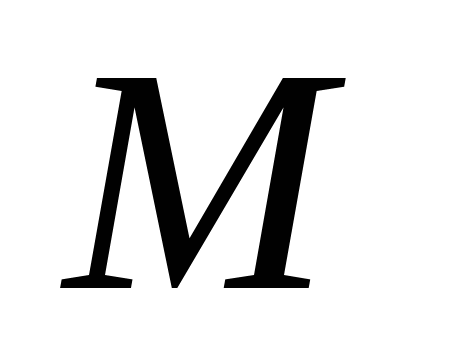 , принадлежащей параболе; прямая , принадлежащей параболе; прямая 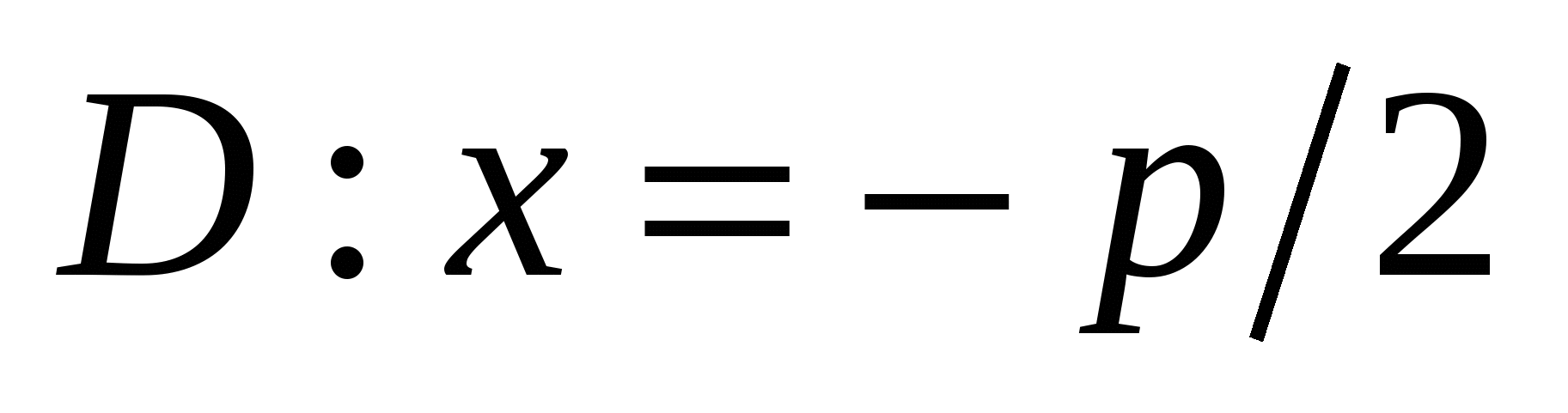 - директриса параболы. - директриса параболы.
Плоскость.
1) 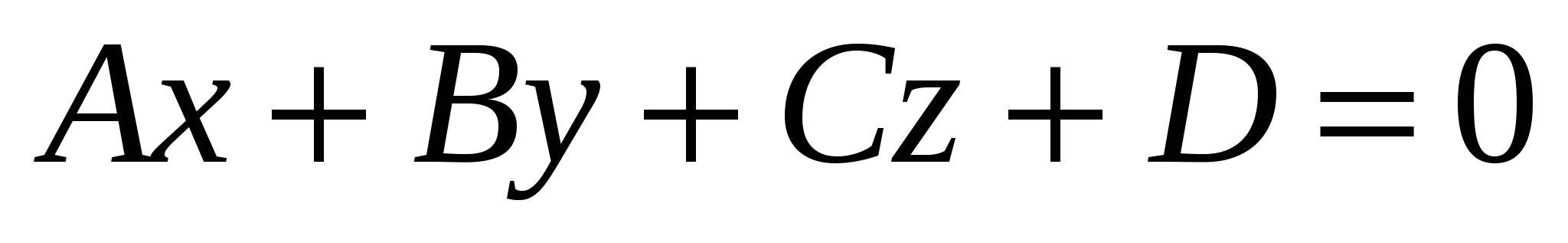 - общее уравнение плоскости, где - общее уравнение плоскости, где 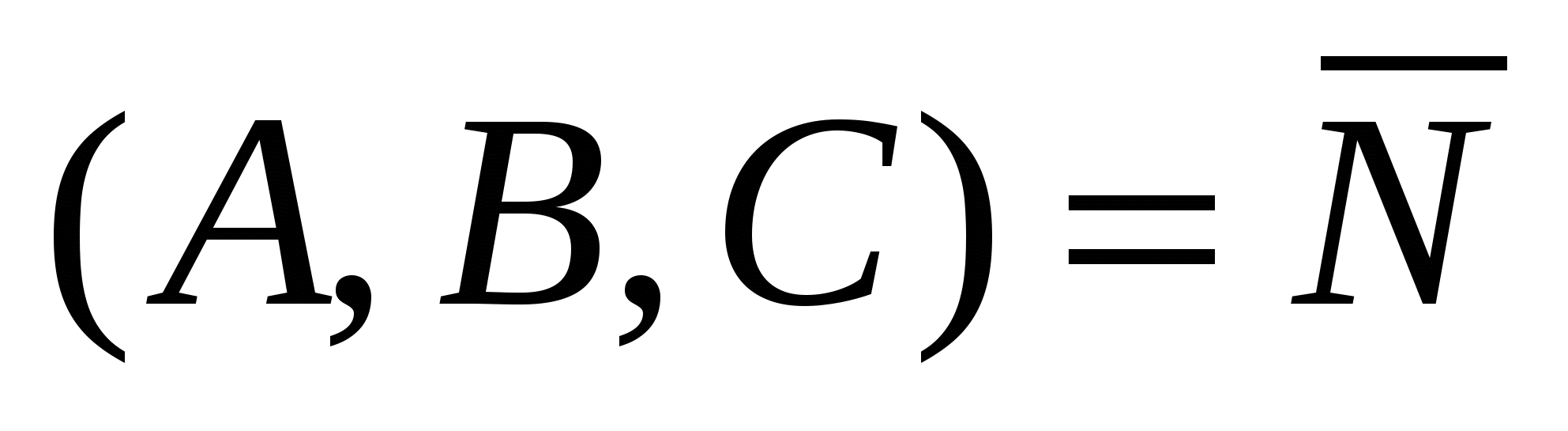 - нормальный вектор плоскости; - нормальный вектор плоскости;
2) 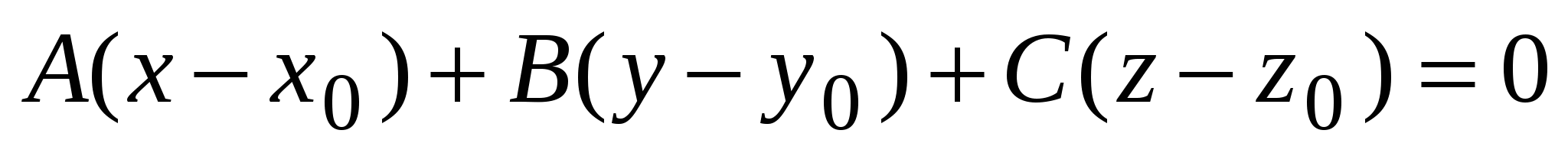 - уравнение плоскости, проходящей через точку - уравнение плоскости, проходящей через точку 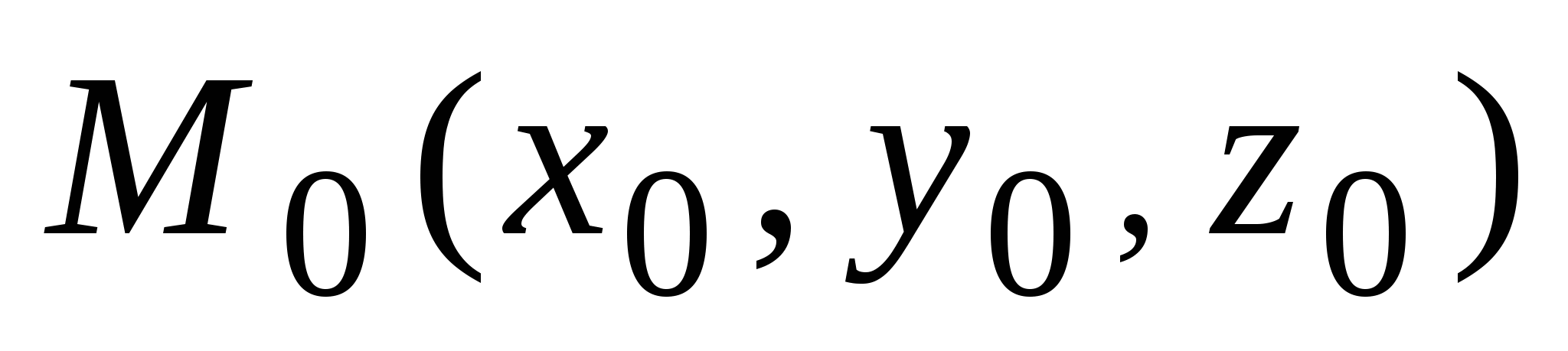 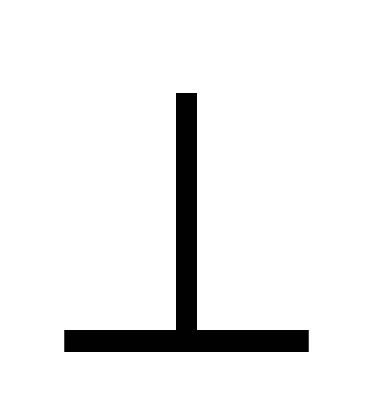 вектору вектору 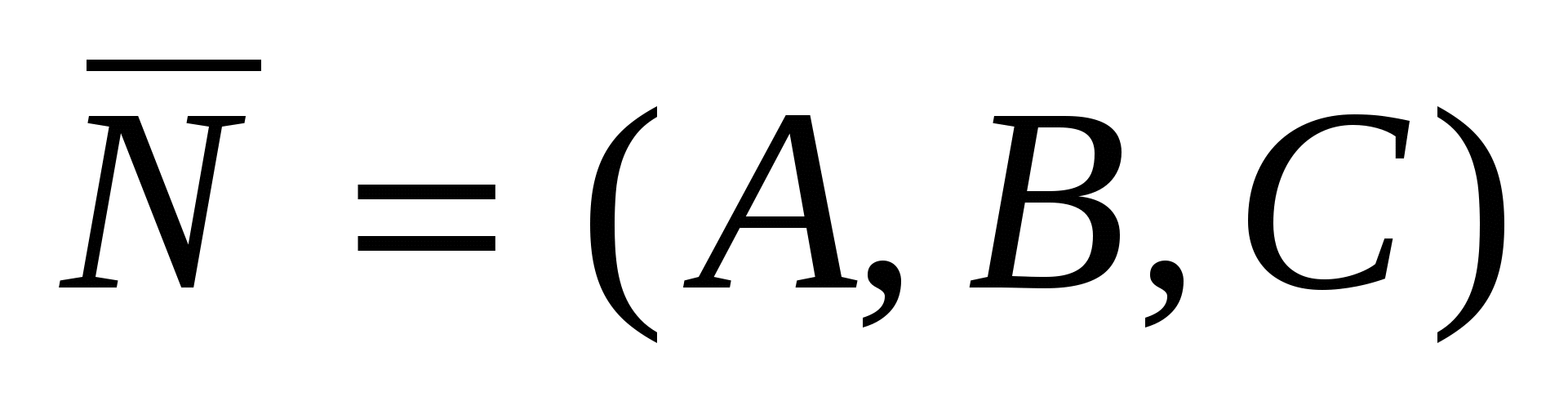 ; ;
3) 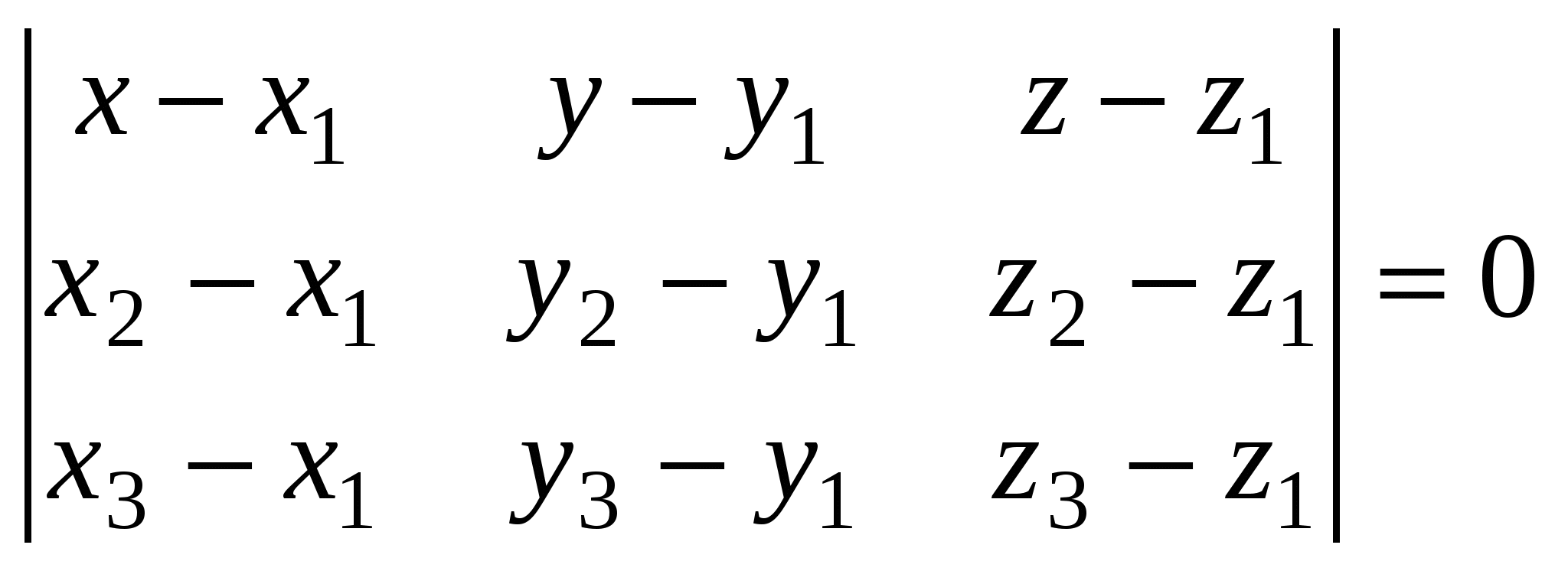 - уравнение плоскости, проходящей через три точки - уравнение плоскости, проходящей через три точки 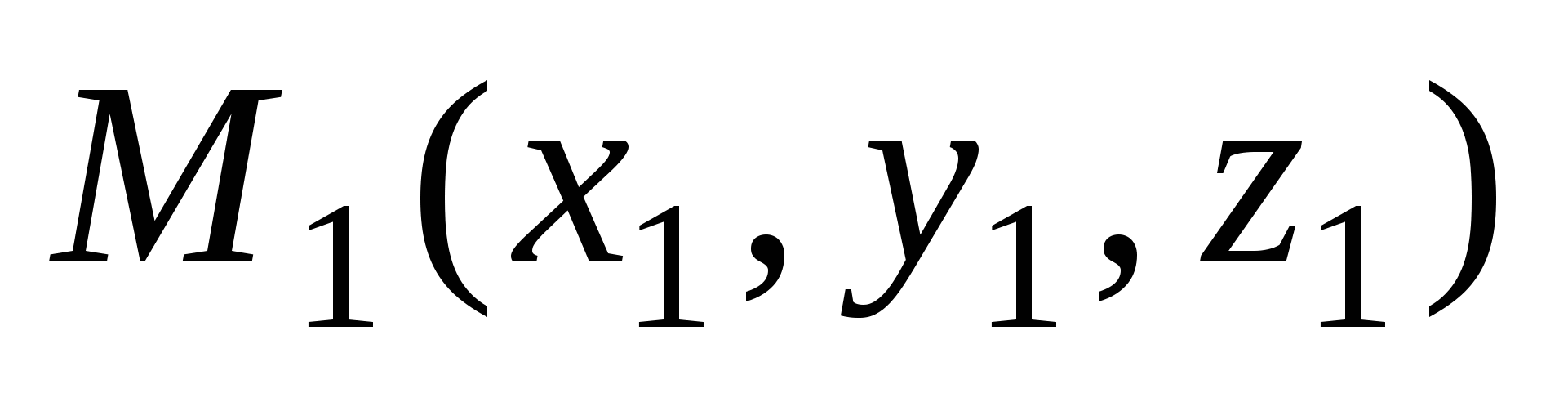 , , 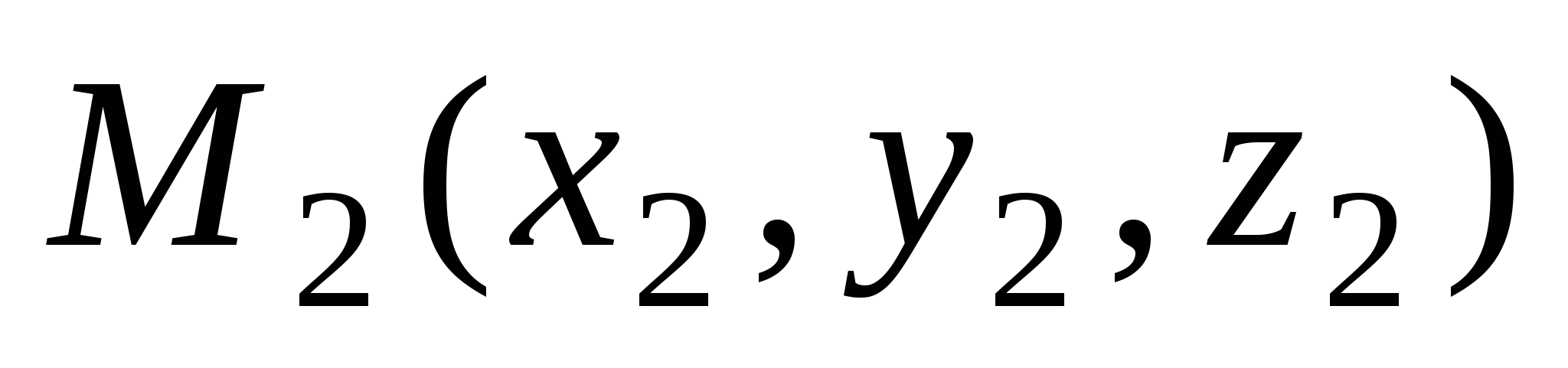 и и 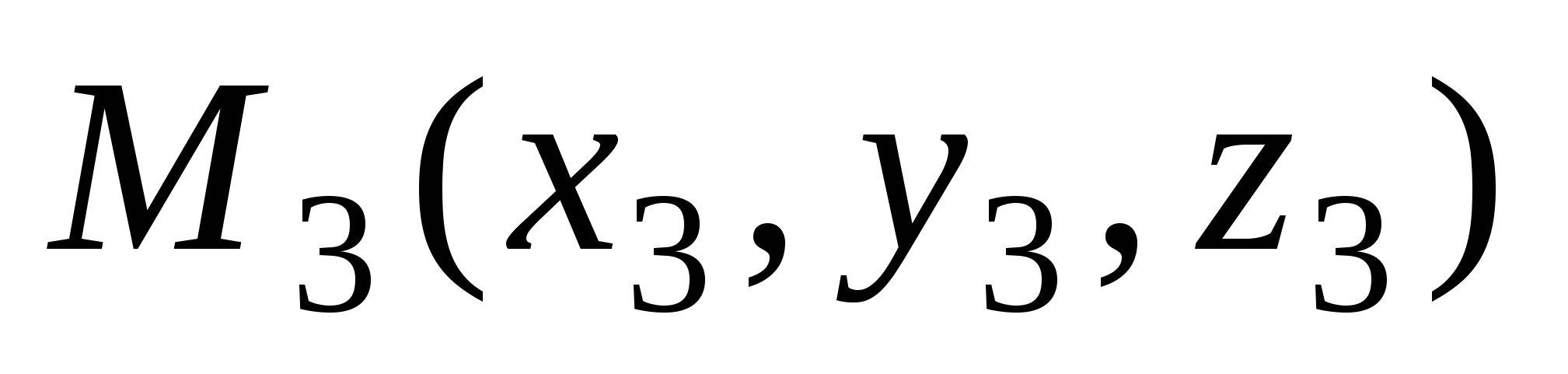 ; ;
4) 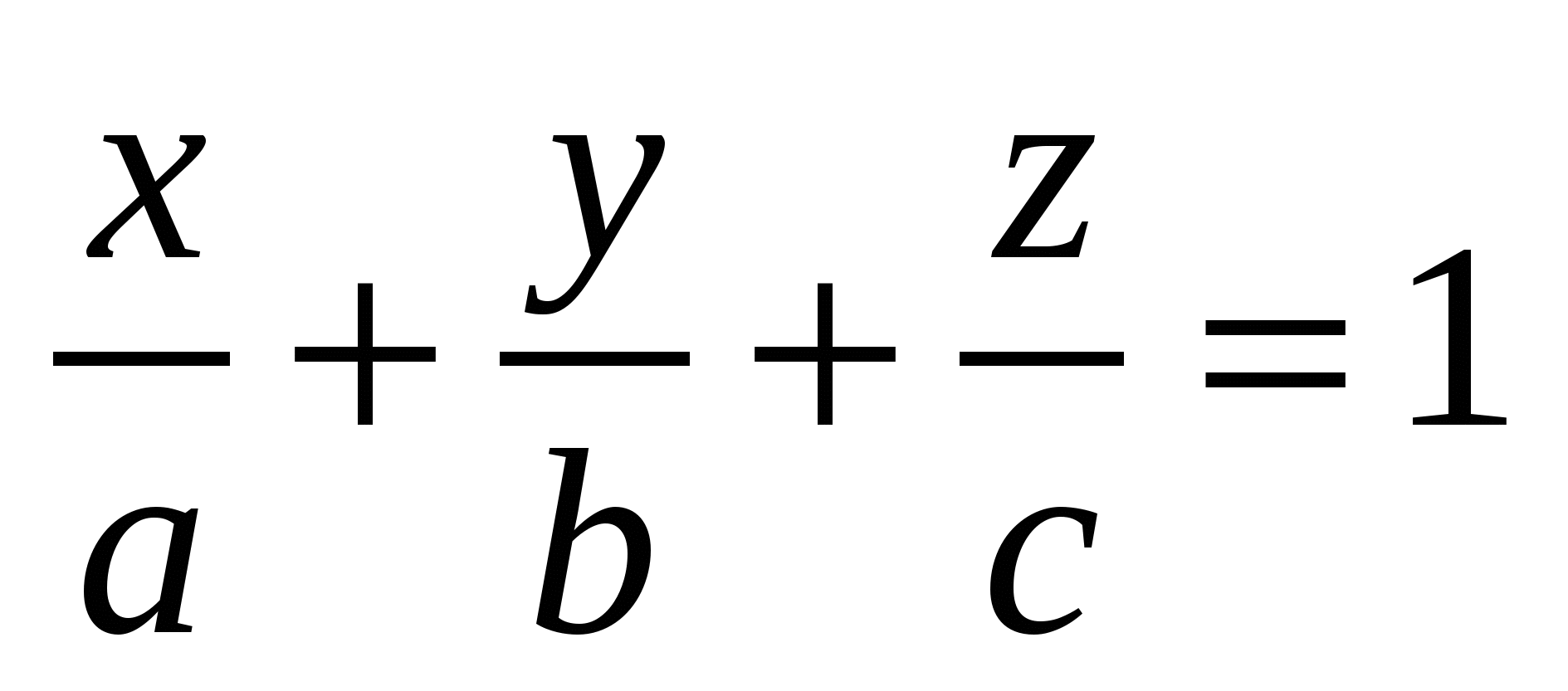 - уравнение плоскости в отрезках, где - уравнение плоскости в отрезках, где  , ,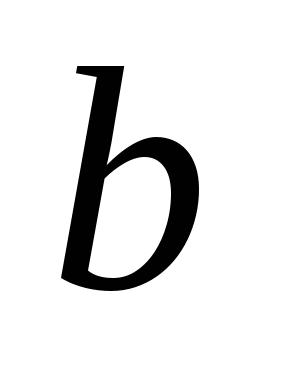 и и 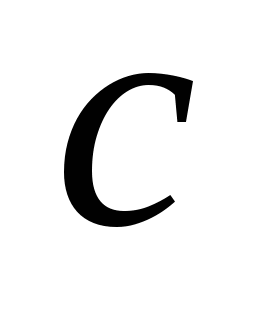 - дины отрезков (со знаком - дины отрезков (со знаком 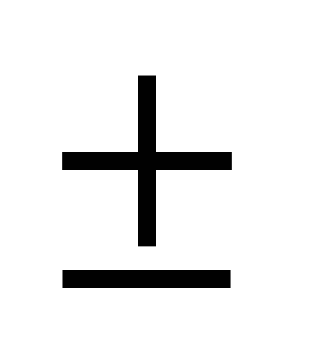 ), отсекаемых плоскостью на осях ), отсекаемых плоскостью на осях 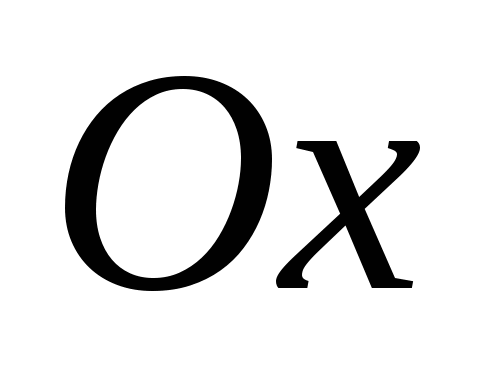 , ,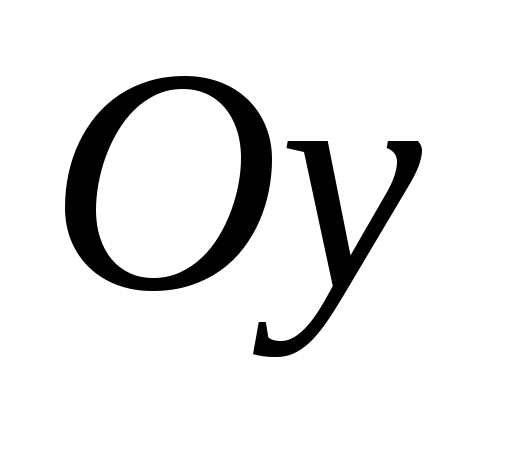 и и  ( « ( «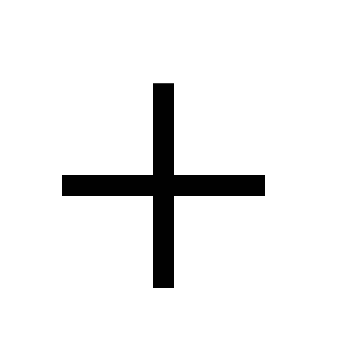 », если на положительной части оси и « », если на положительной части оси и « », если на отрицательной). », если на отрицательной).
Если 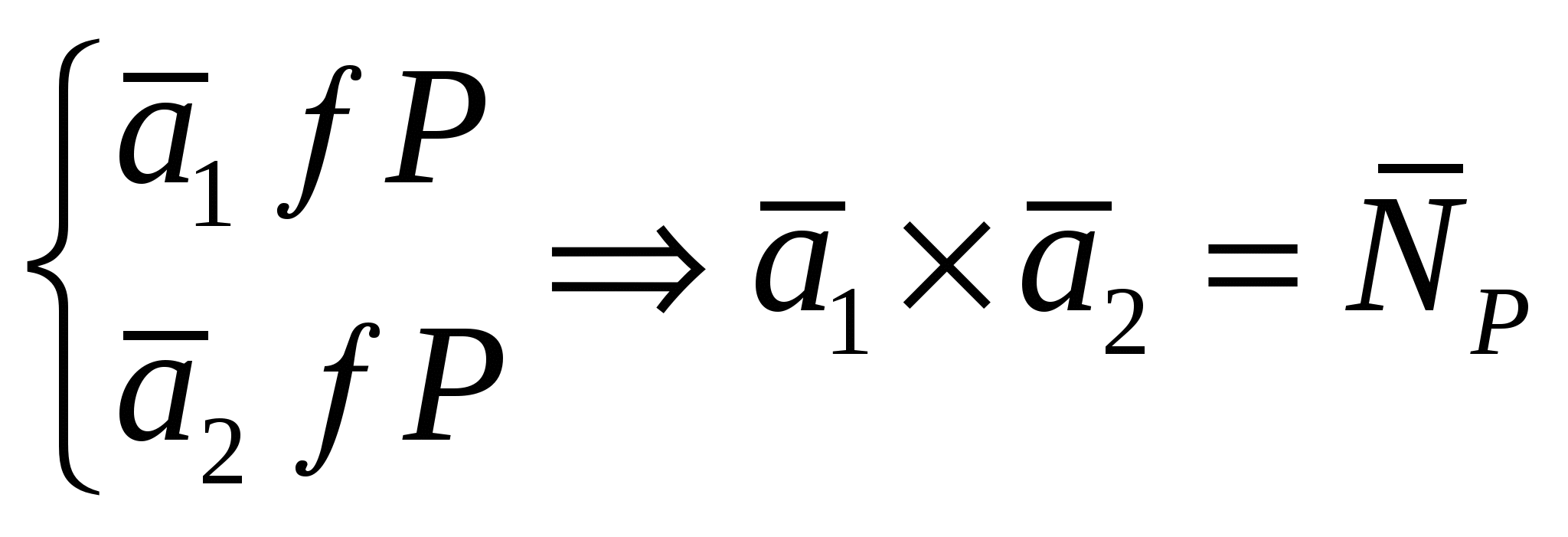 . .
Расстояние от точки 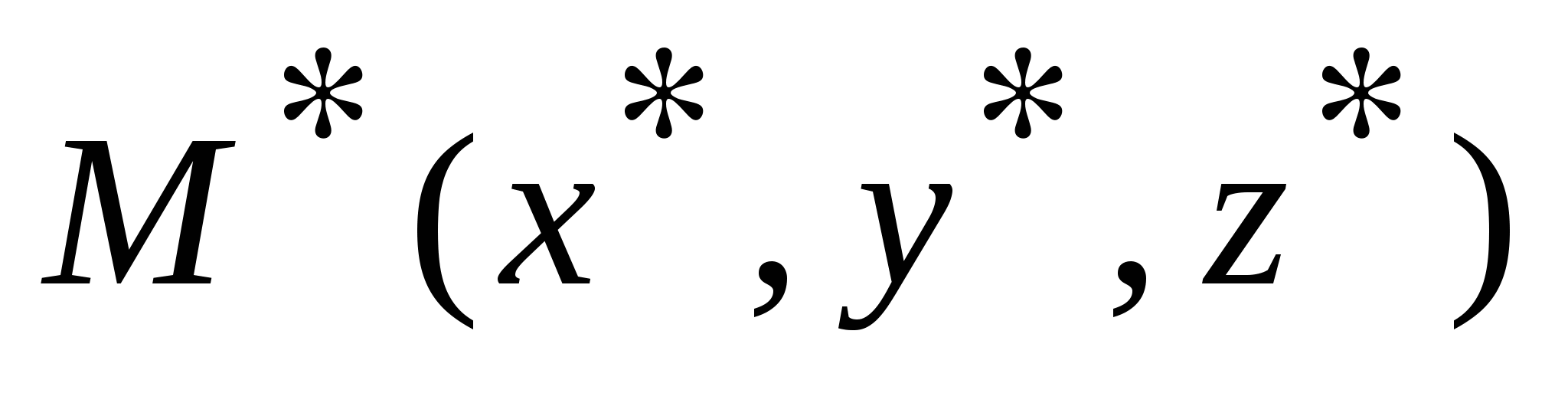 до плоскости до плоскости 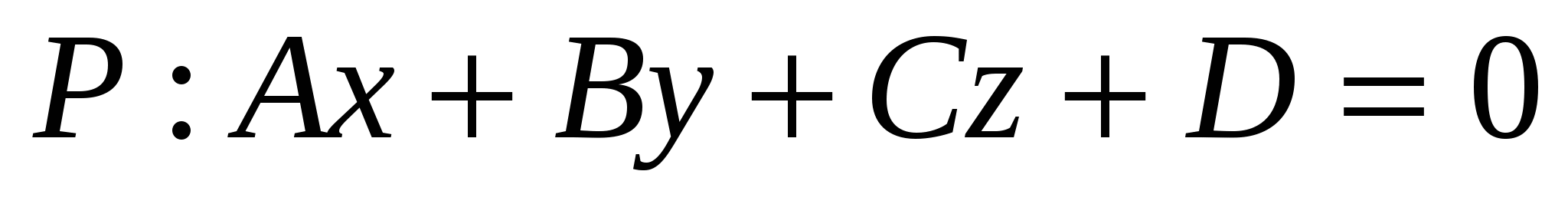 : : 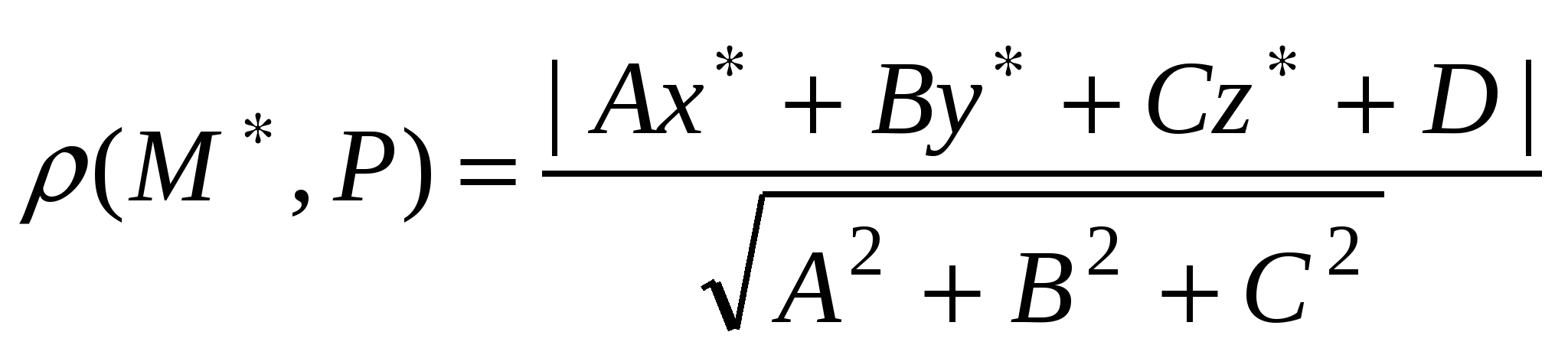 . .
Угол 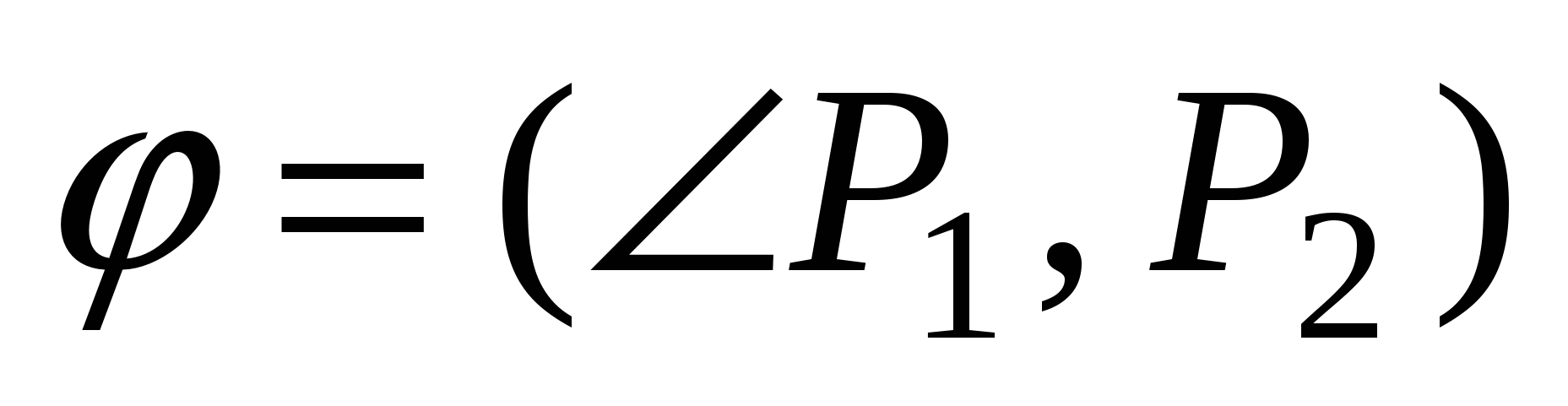 , ( , (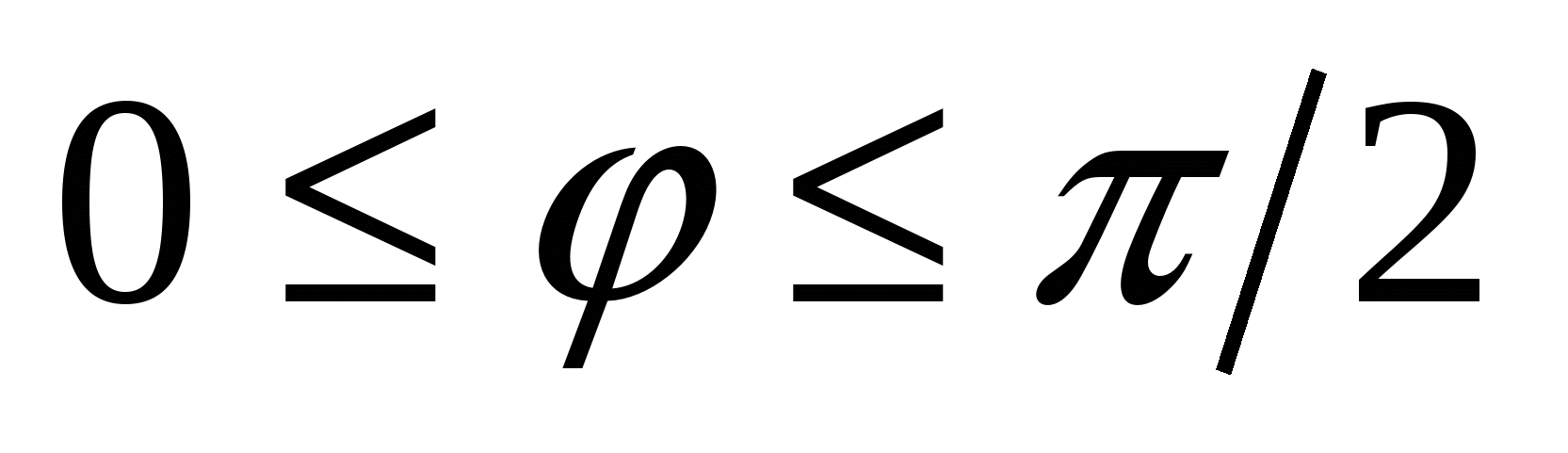 ) между плоскостями ) между плоскостями 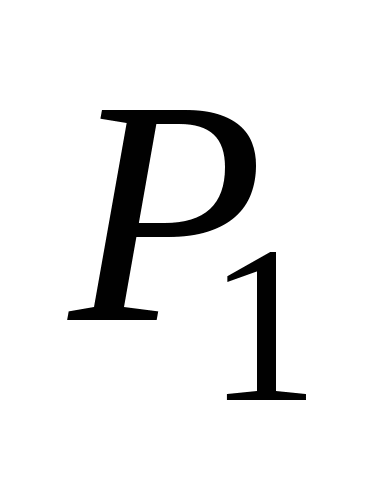 и и 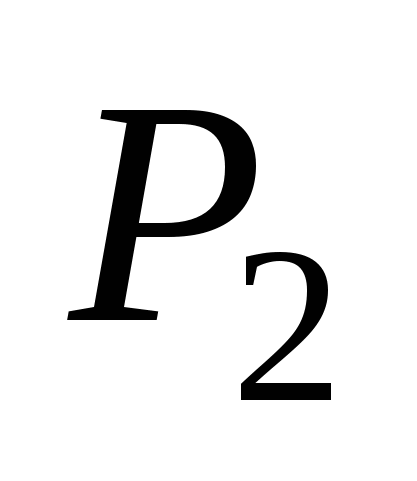 : : 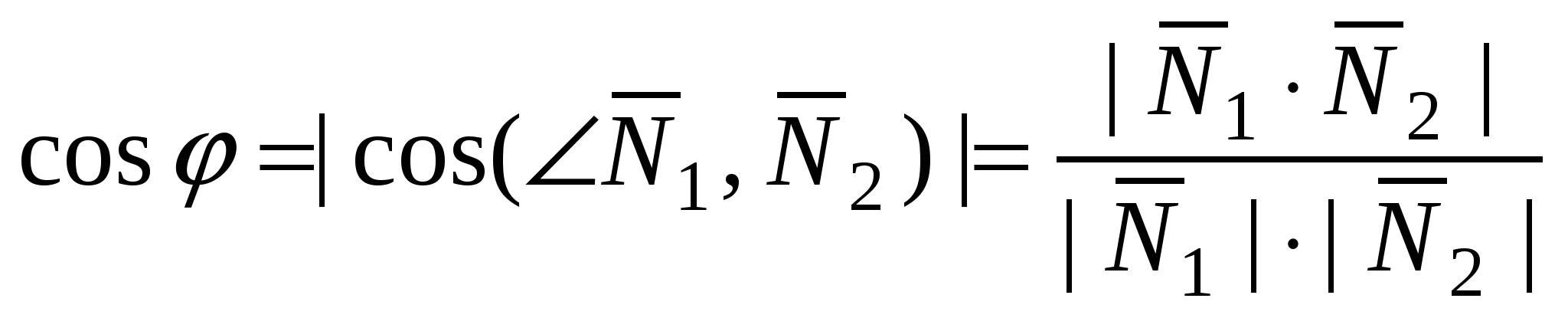 . .
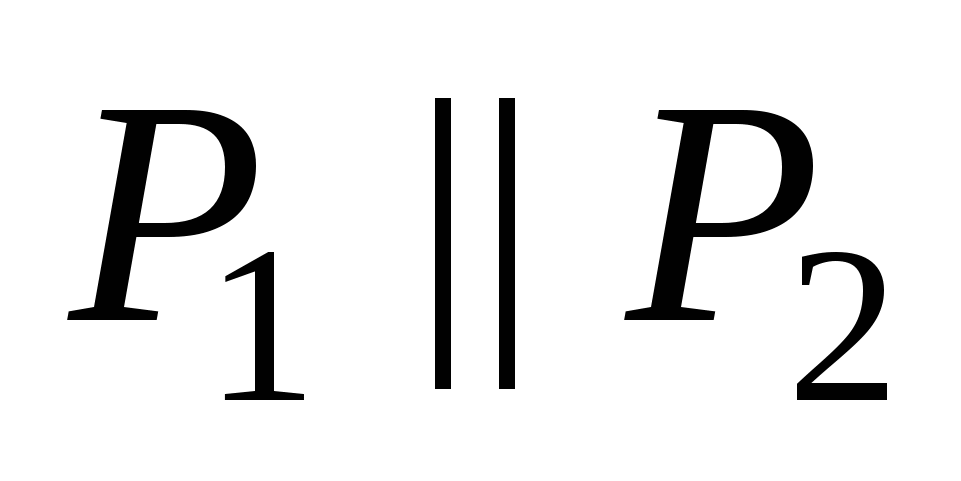 , если , если  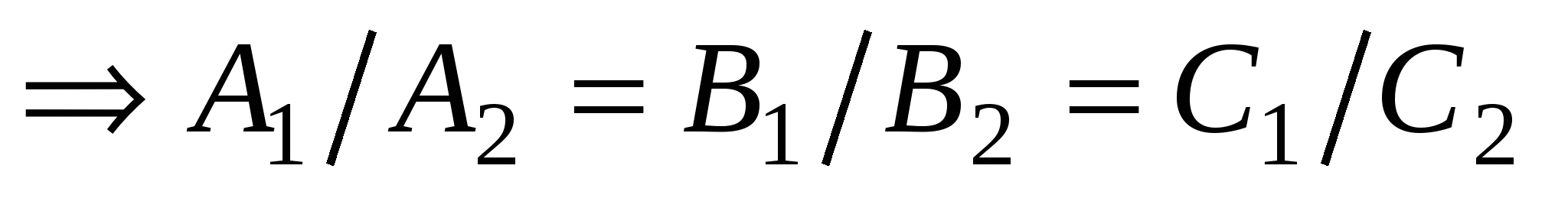
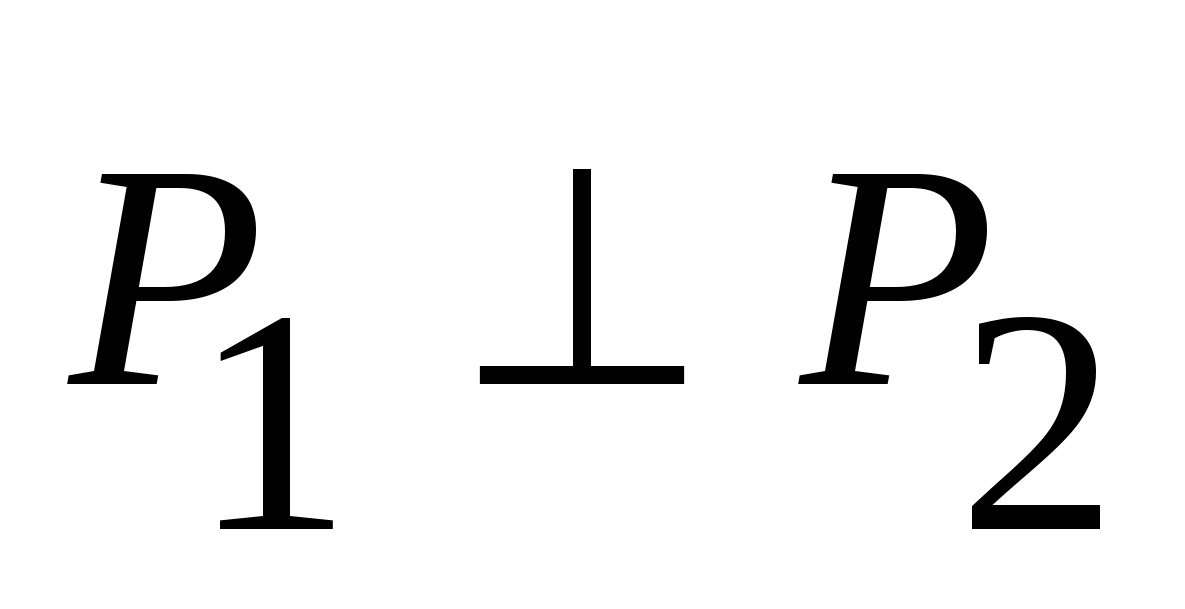 , если , если 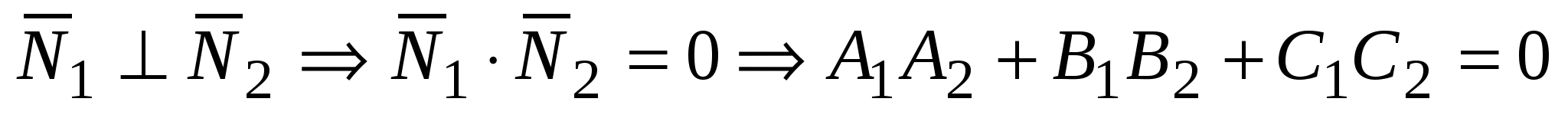 . .
Прямая в пространстве.
1) 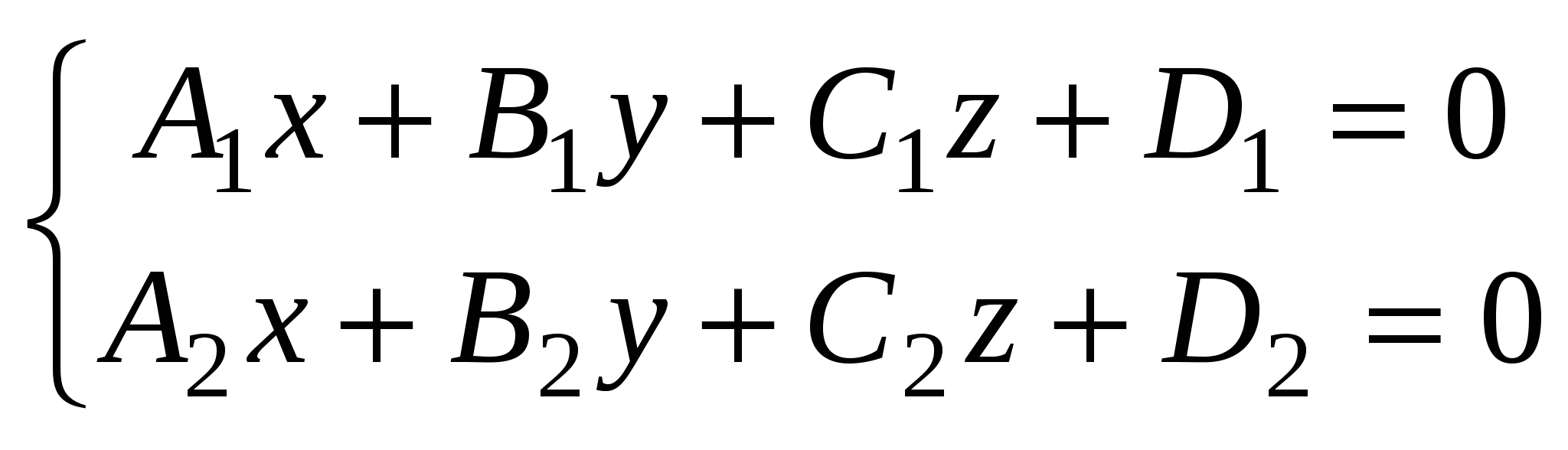 - общее уравнение прямой, как линии пересечения двух плоскостей, где - общее уравнение прямой, как линии пересечения двух плоскостей, где 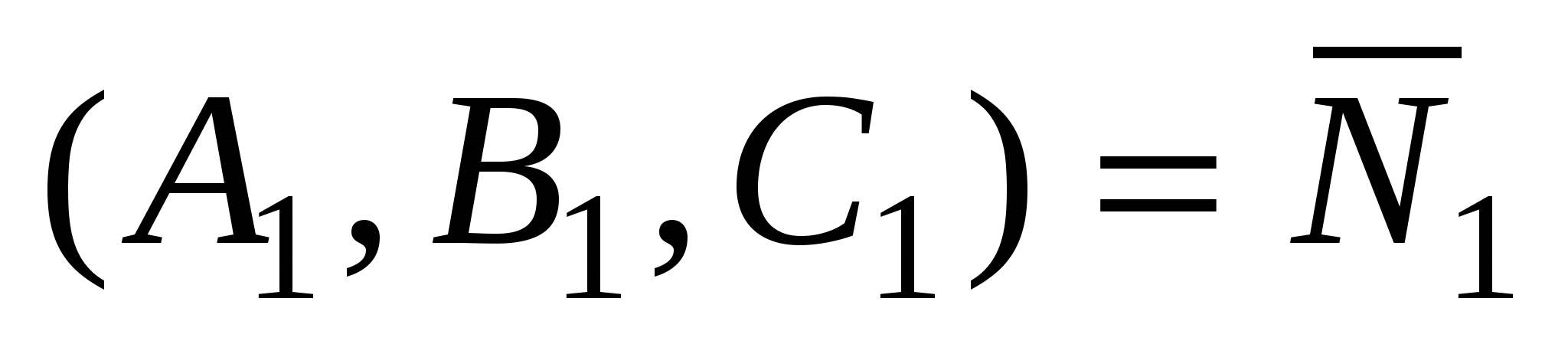 и и 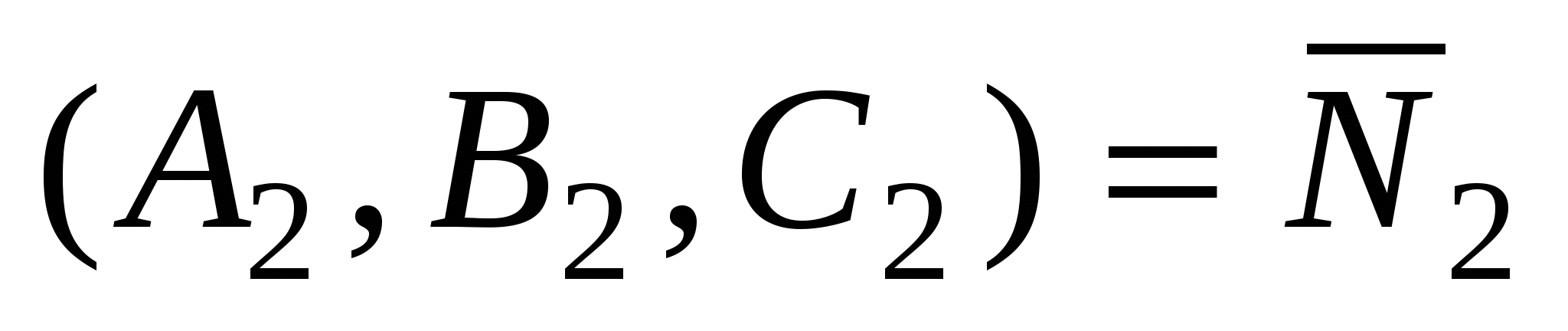 - нормальные векторы плоскостей - нормальные векторы плоскостей 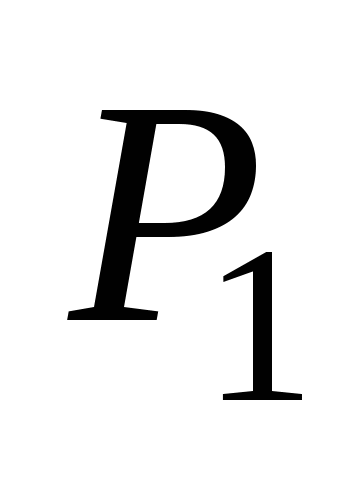 и и 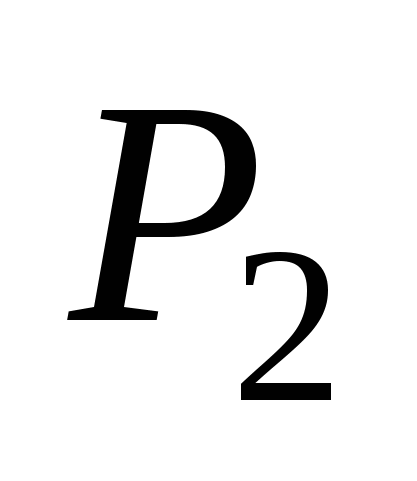 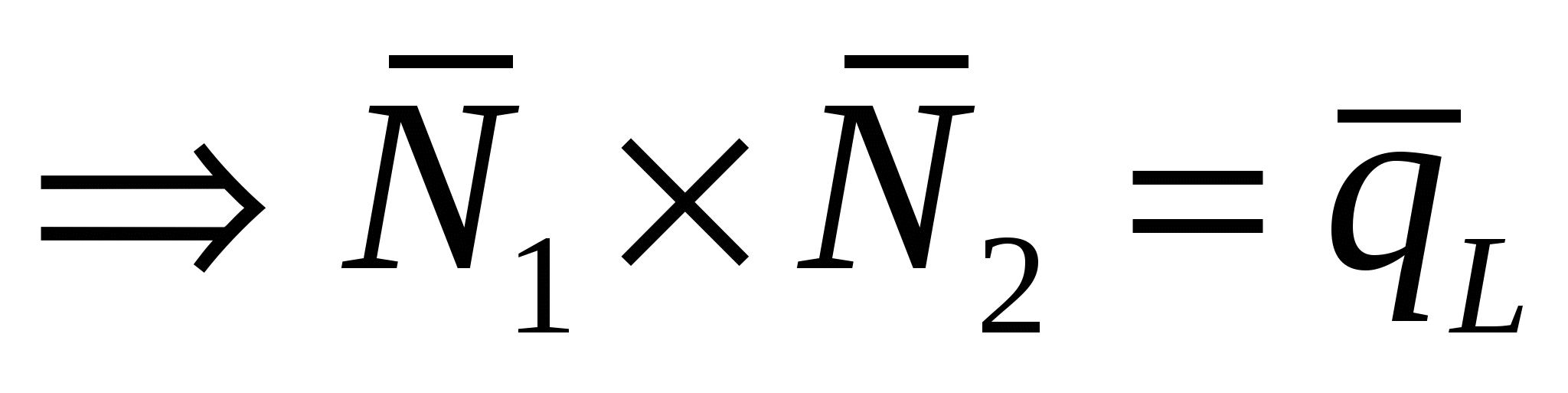 . .
2) 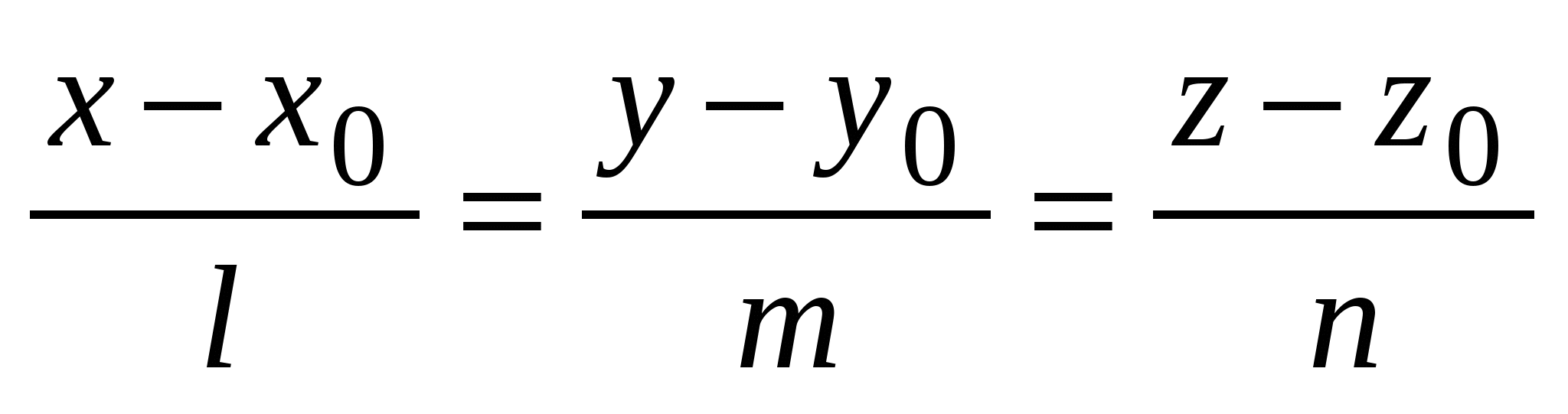 - уравнение прямой, проходящей через точку - уравнение прямой, проходящей через точку 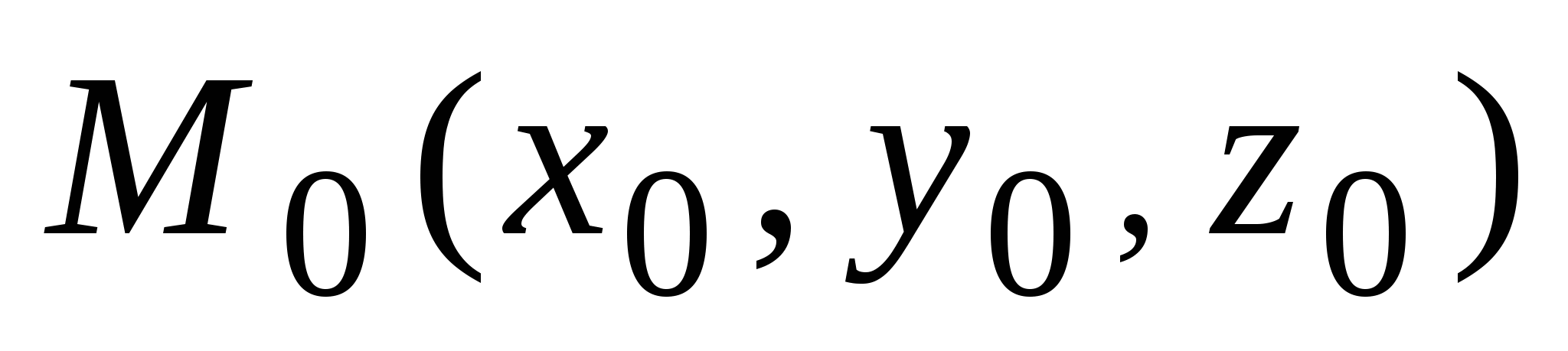 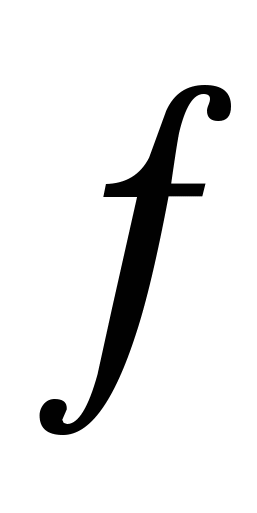 вектору вектору 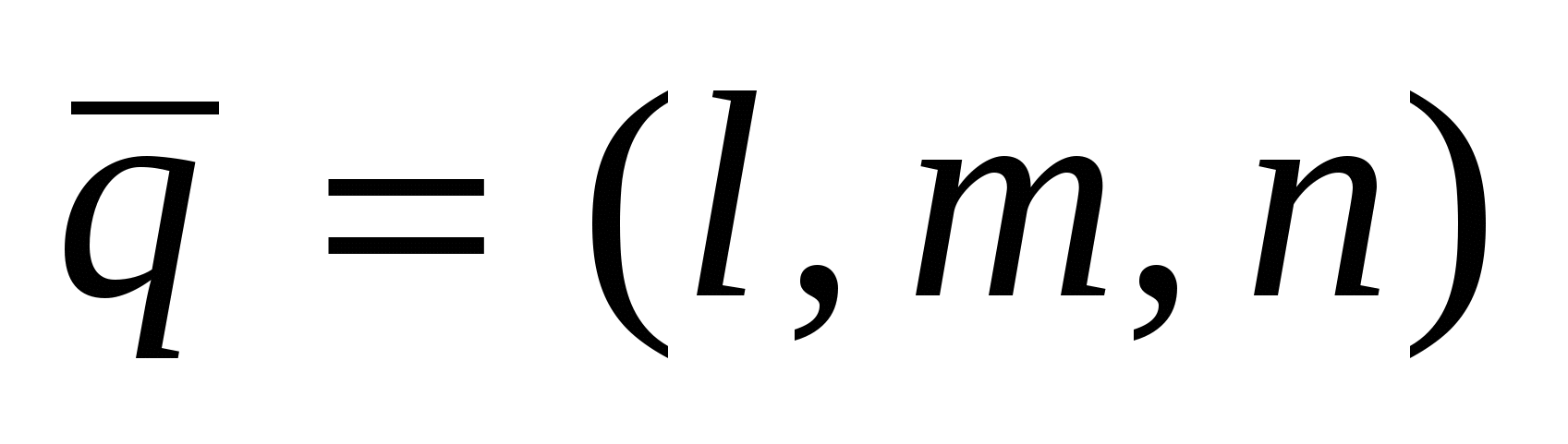 (каноническое уравнение); (каноническое уравнение);
3) 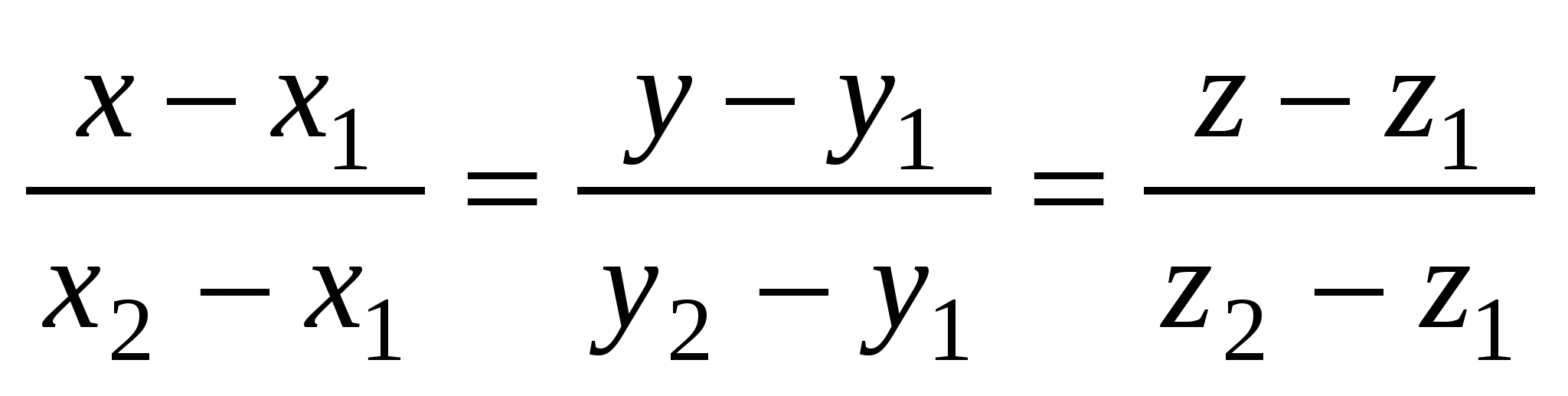 - уравнение прямой, проходящей через две точки - уравнение прямой, проходящей через две точки 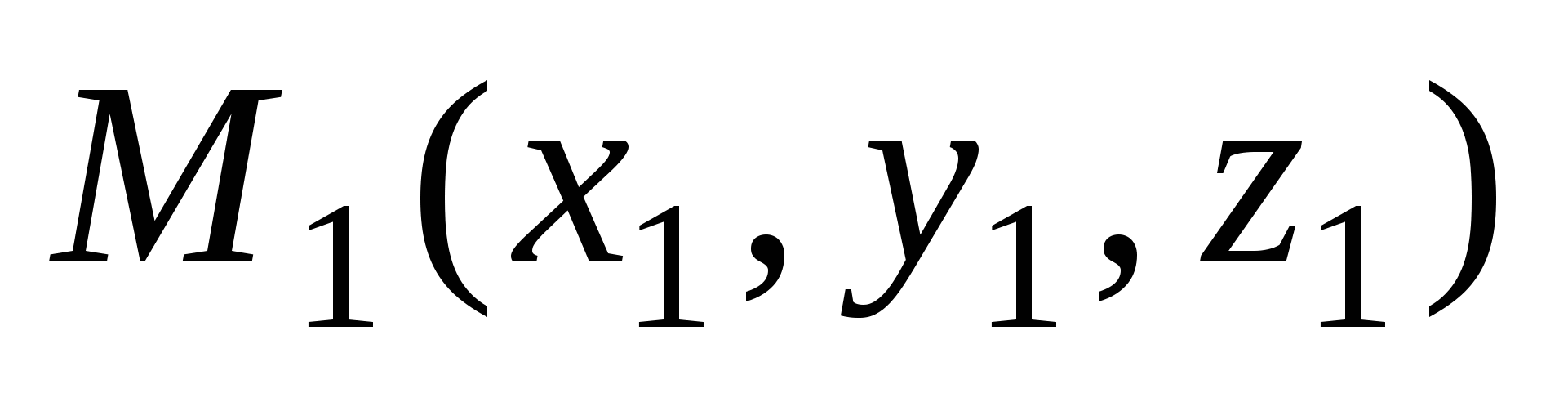 , , 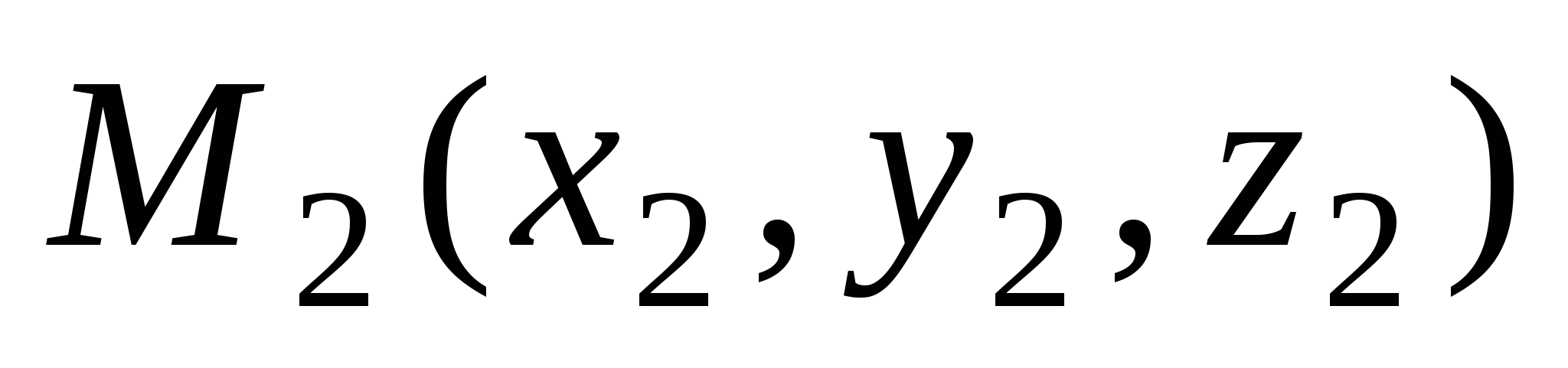 ; ;
4) 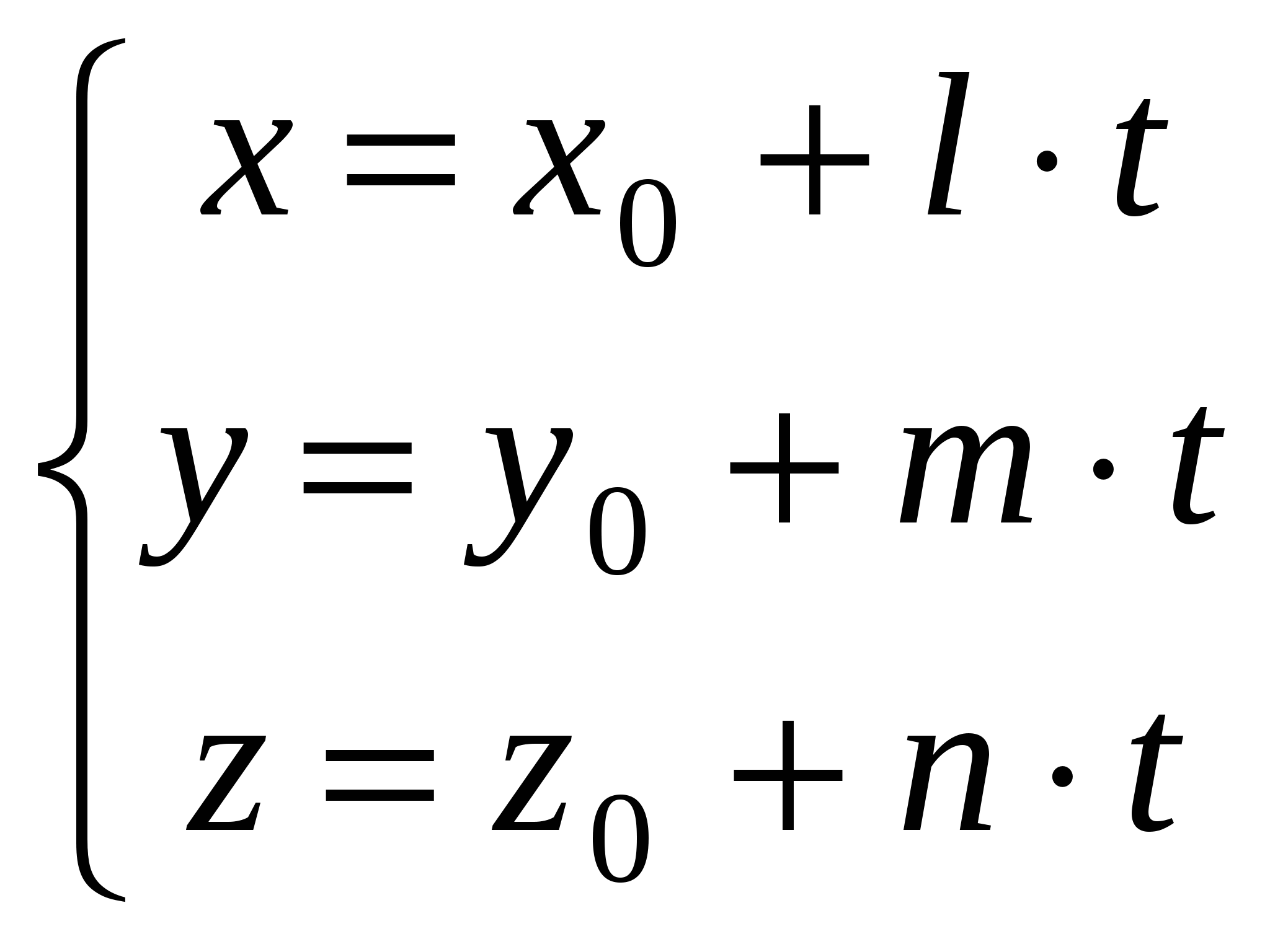 - уравнение прямой, проходящей через точку - уравнение прямой, проходящей через точку 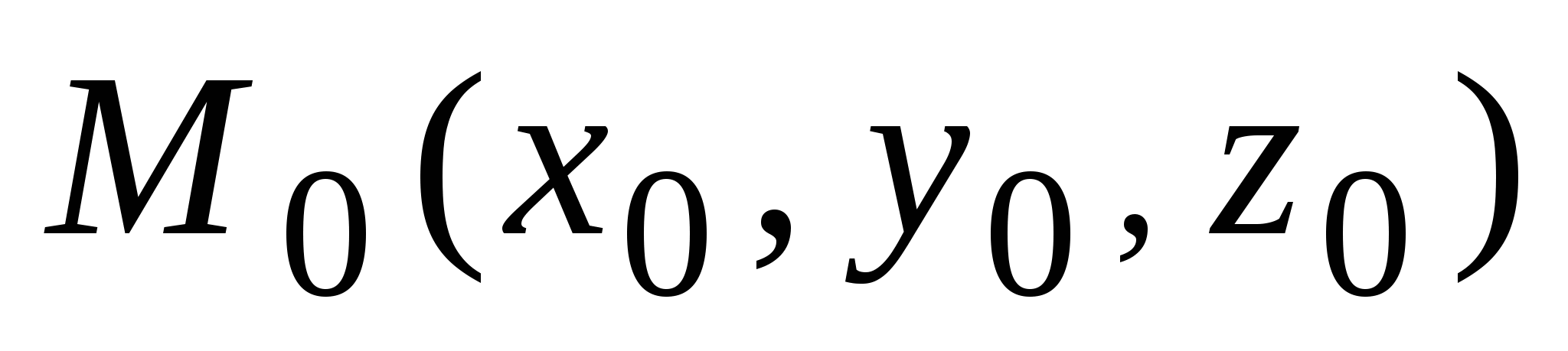 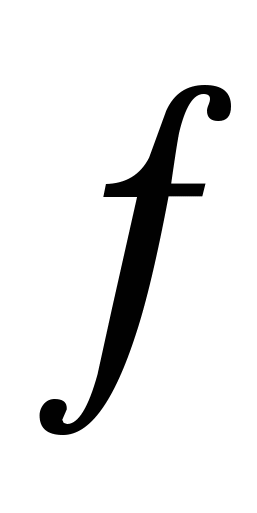 вектору вектору 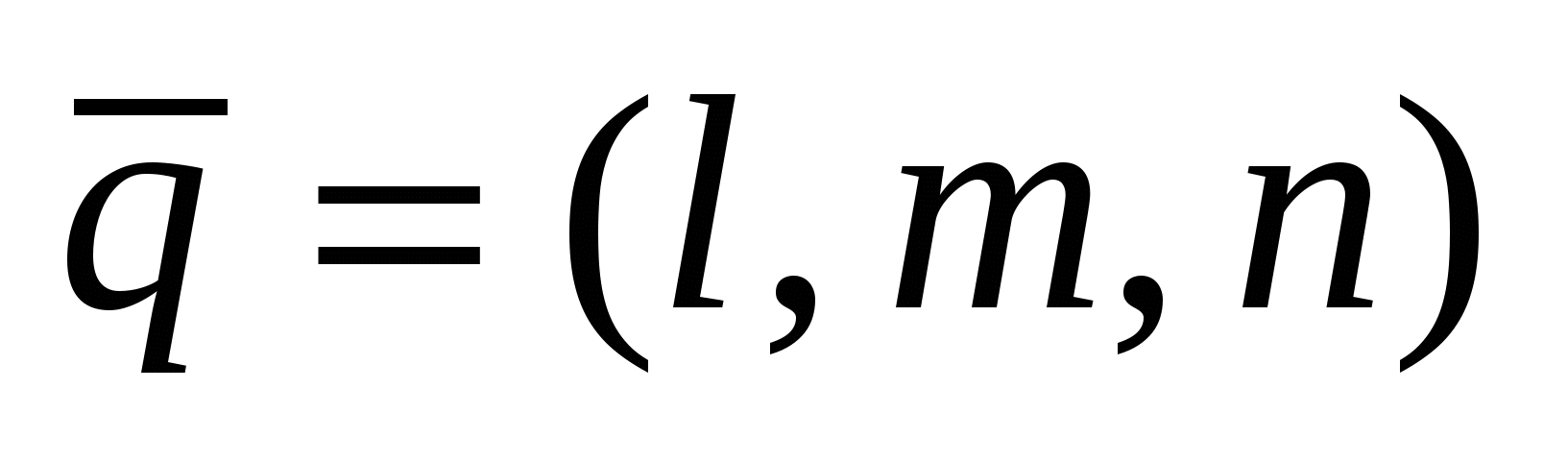 , , 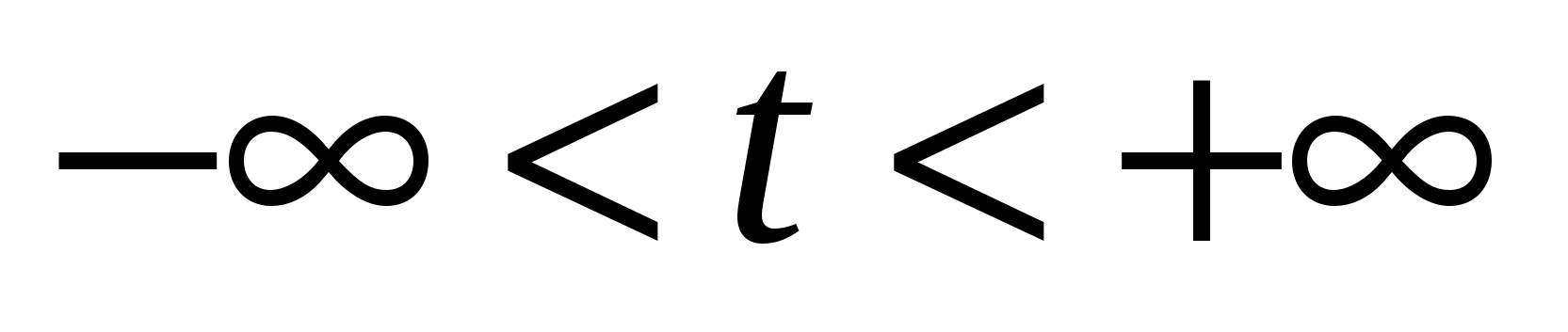 (параметрическое уравнение); (параметрическое уравнение);
Угол 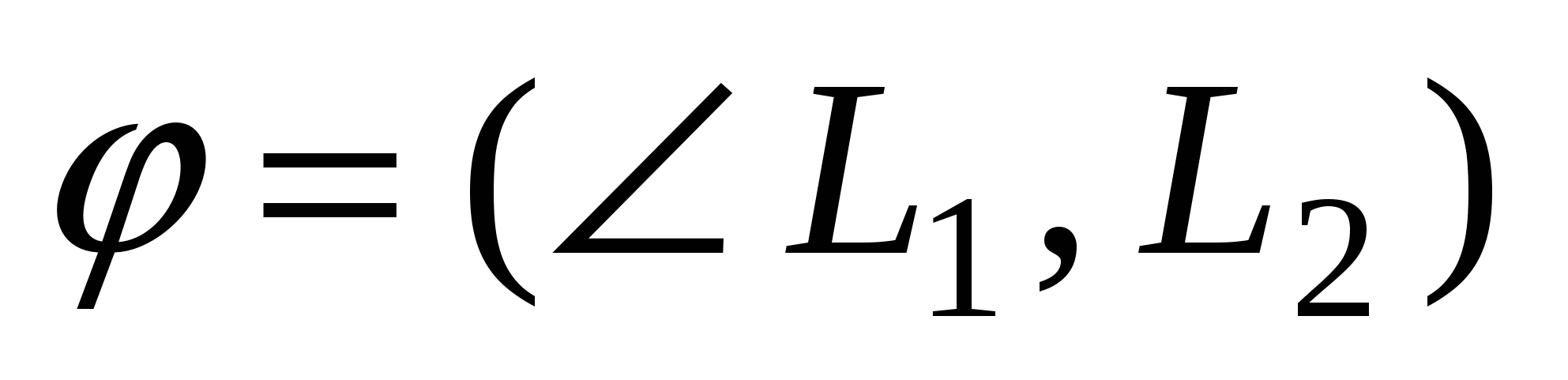 , ( , (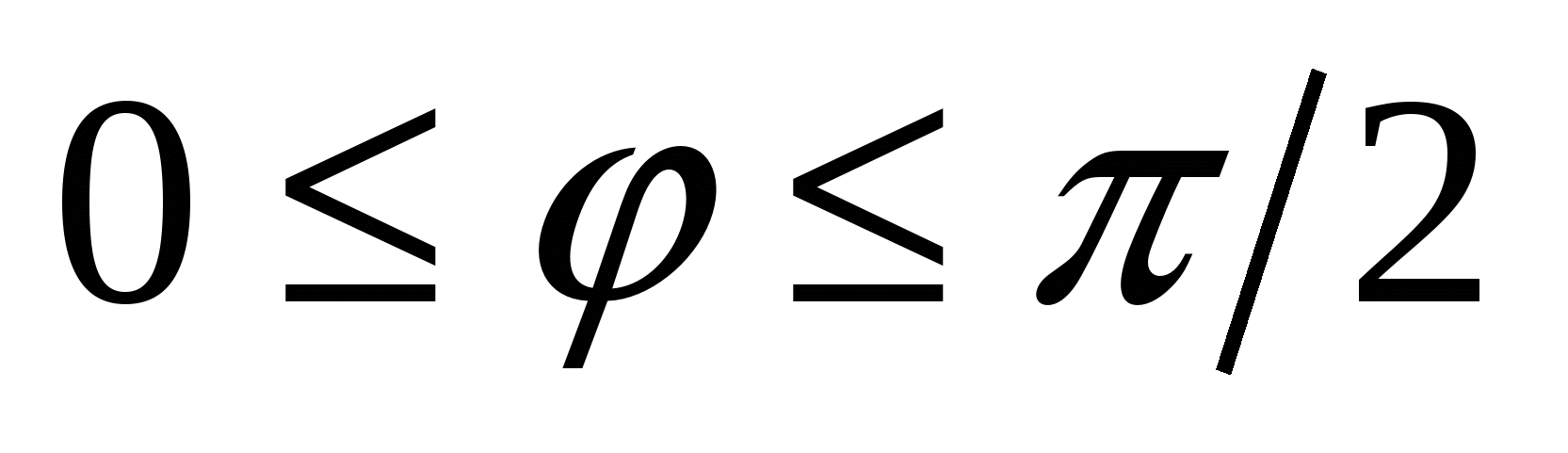 ) между прямыми ) между прямыми 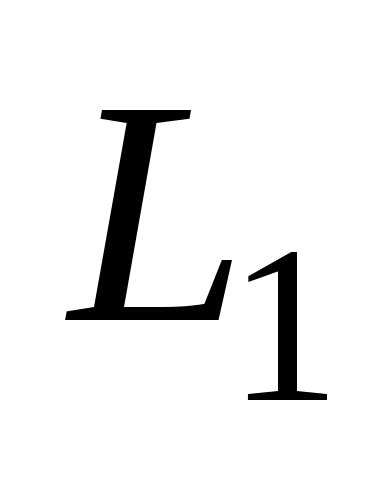 и и 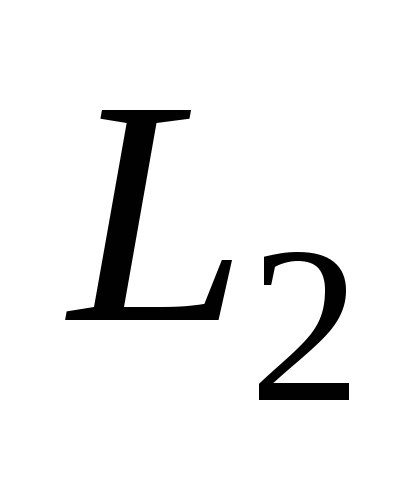 : : 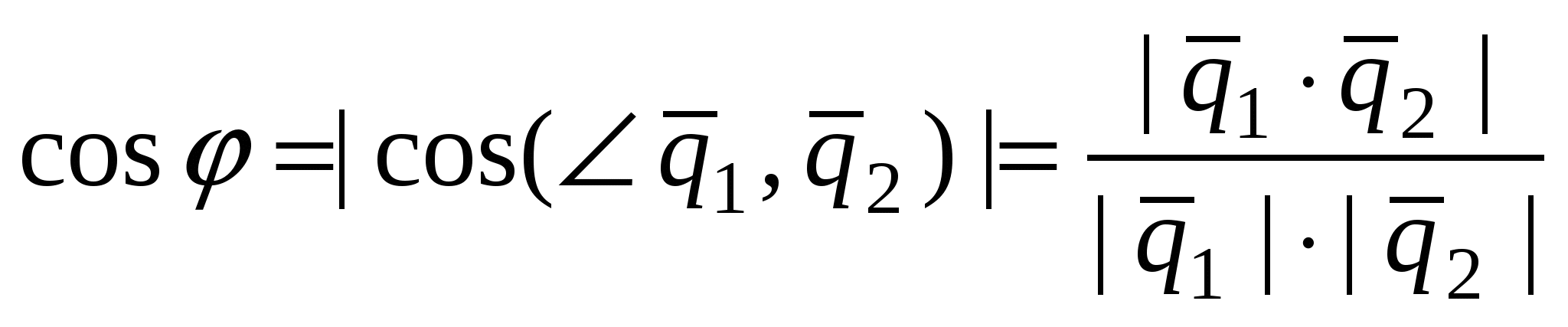 . .
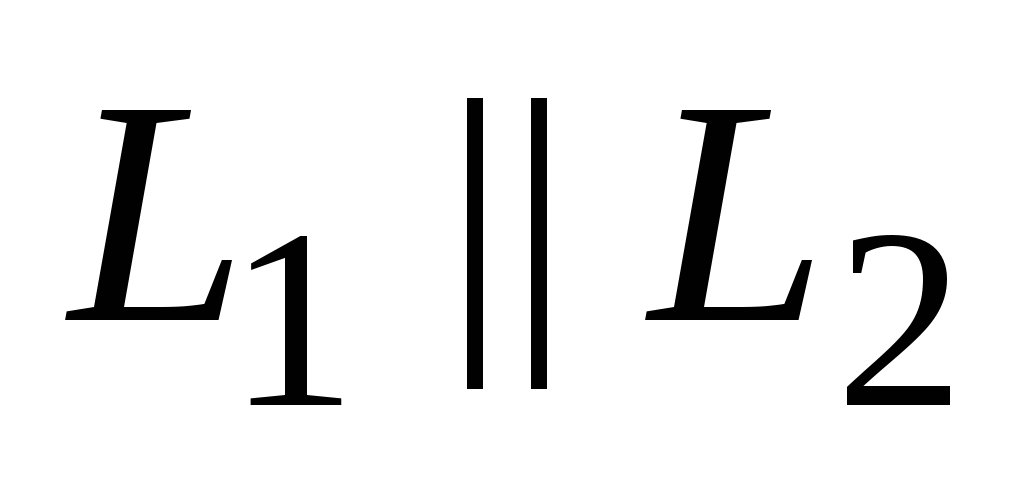 , если , если 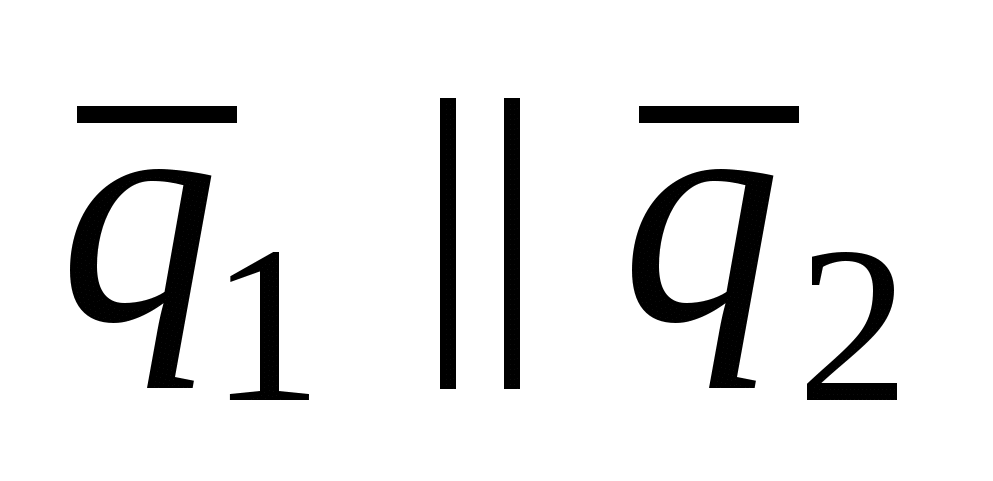  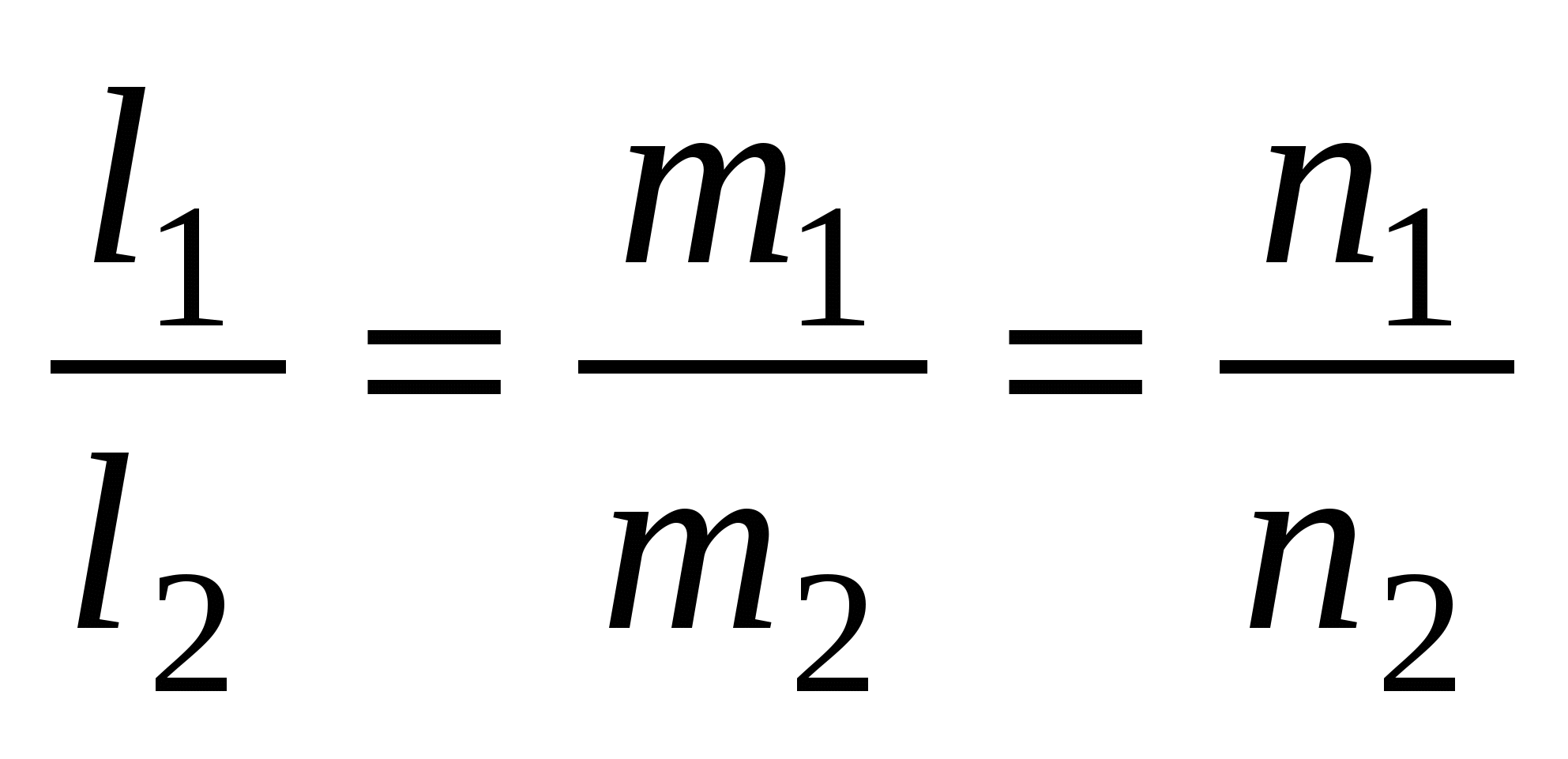 . . 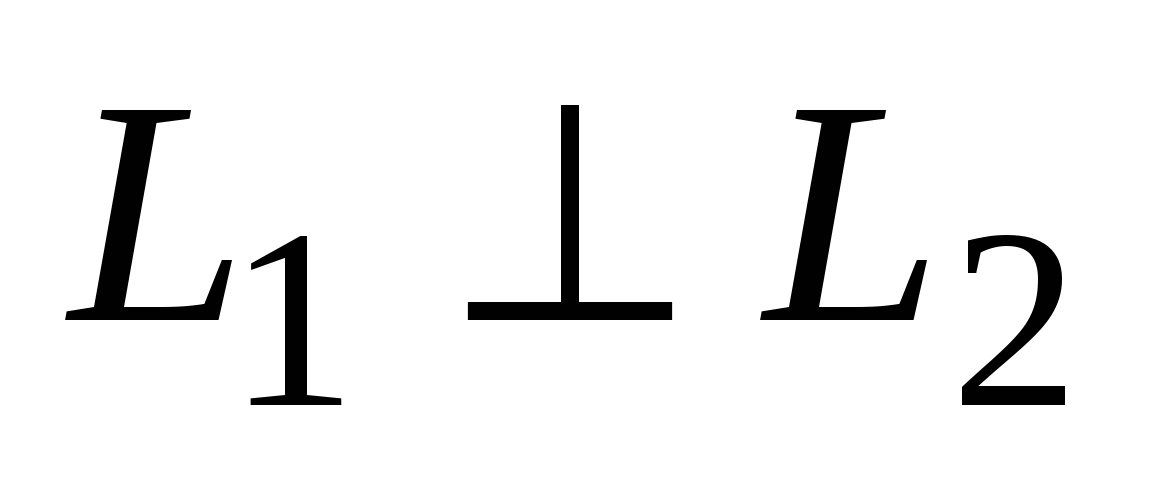 , если , если 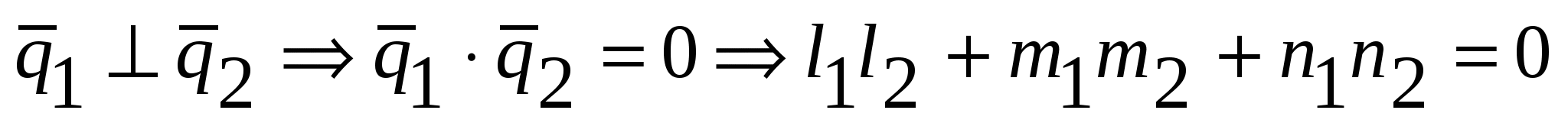 . .
Угол 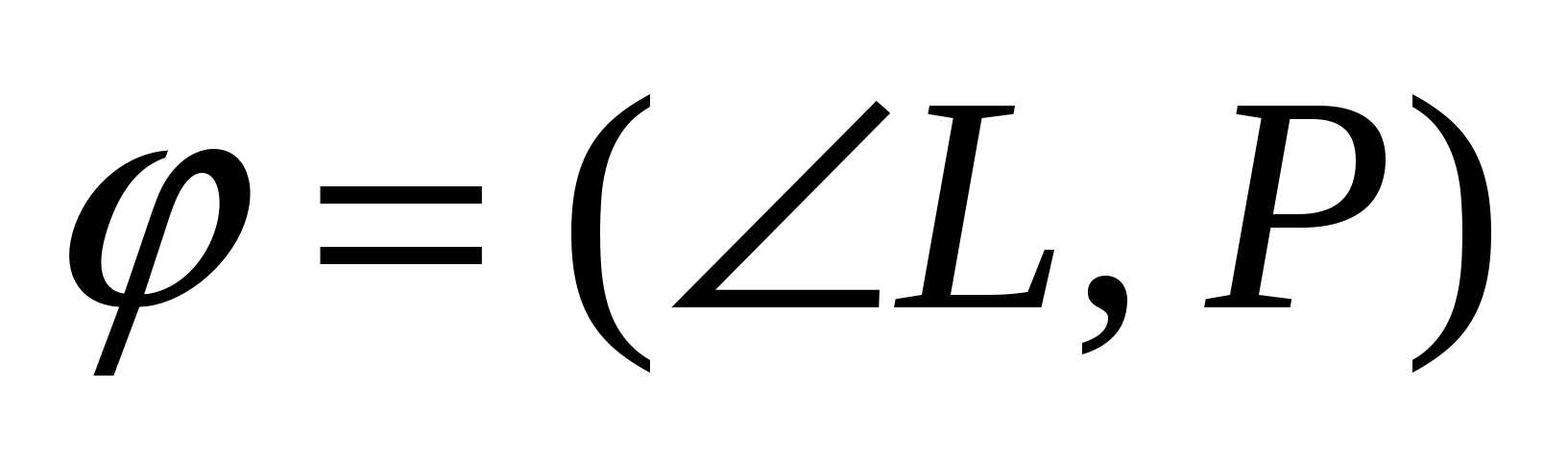 , ( , (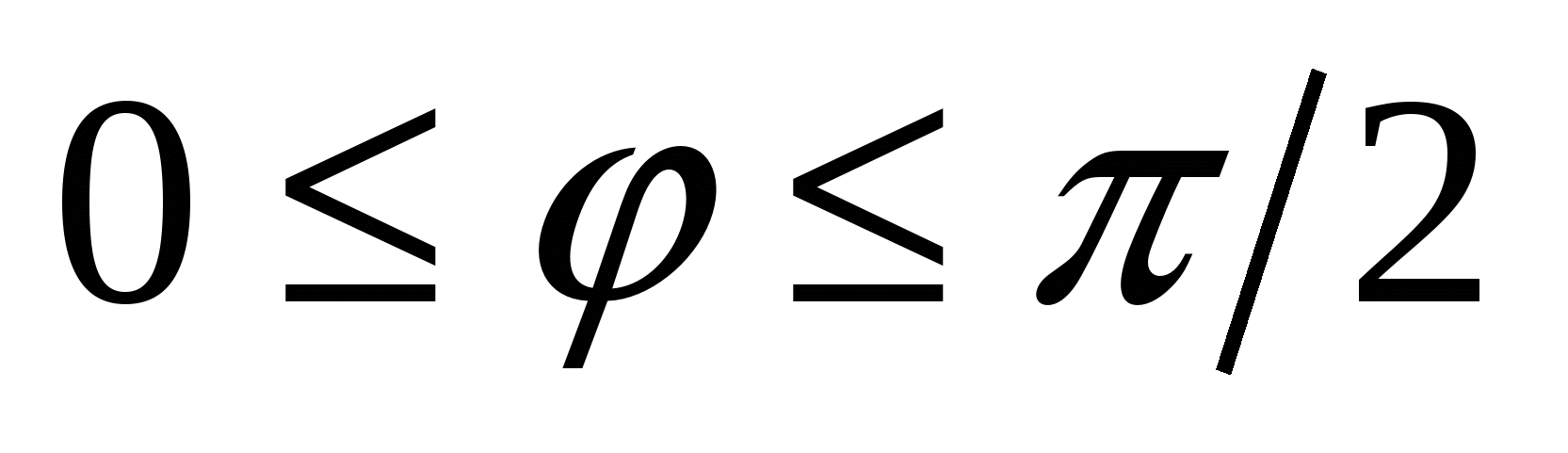 ) между прямой ) между прямой 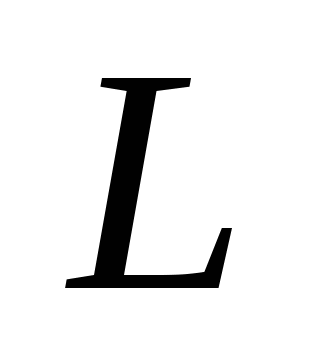 , заданной каноническим уравнением и плоскостью , заданной каноническим уравнением и плоскостью 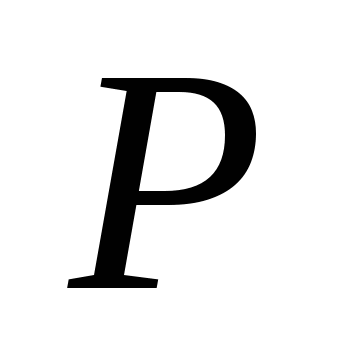 , заданной общим уравнением находится по формуле: , заданной общим уравнением находится по формуле: 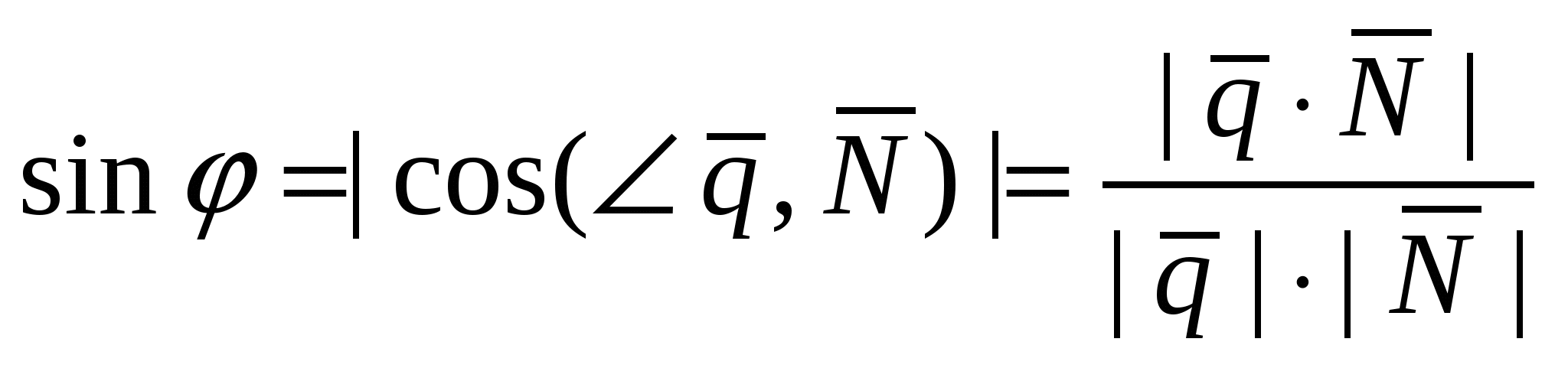 . .
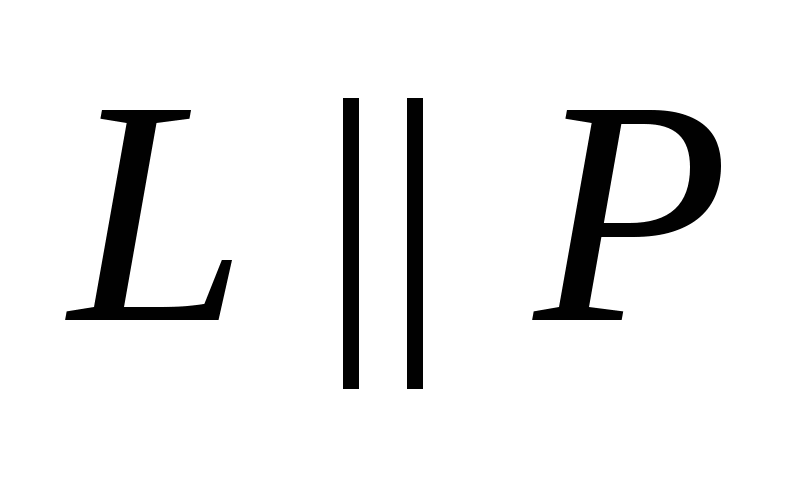 , если , если 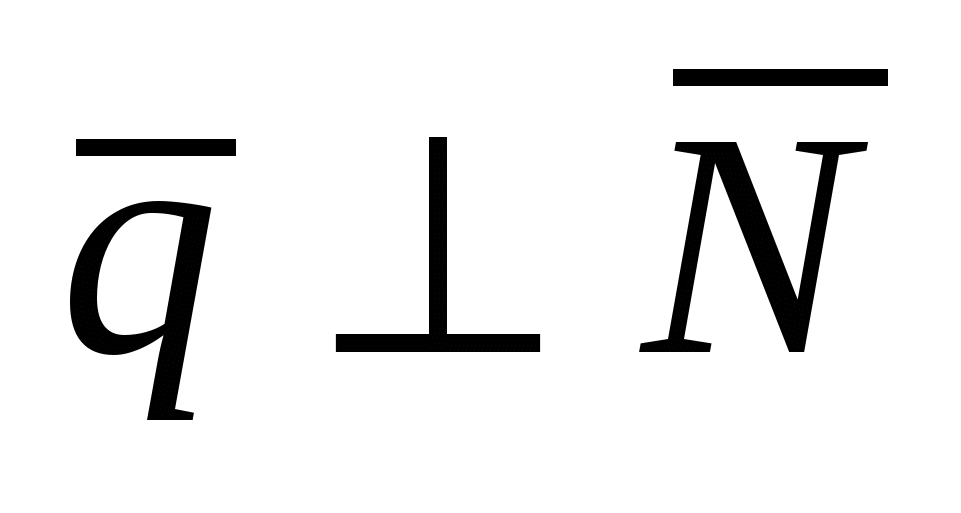  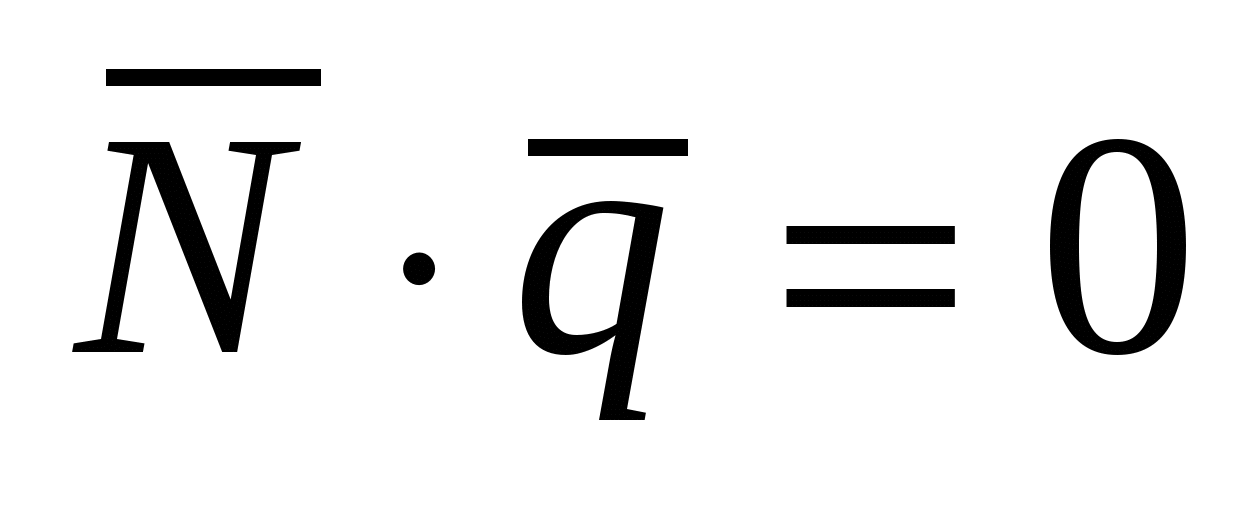  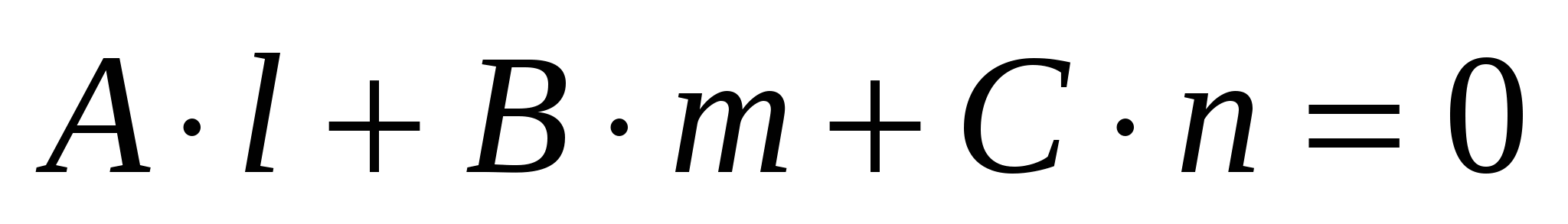 . .
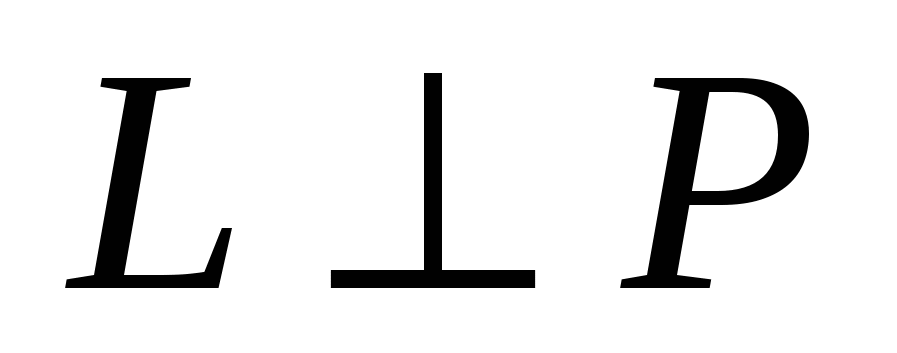 , если , если 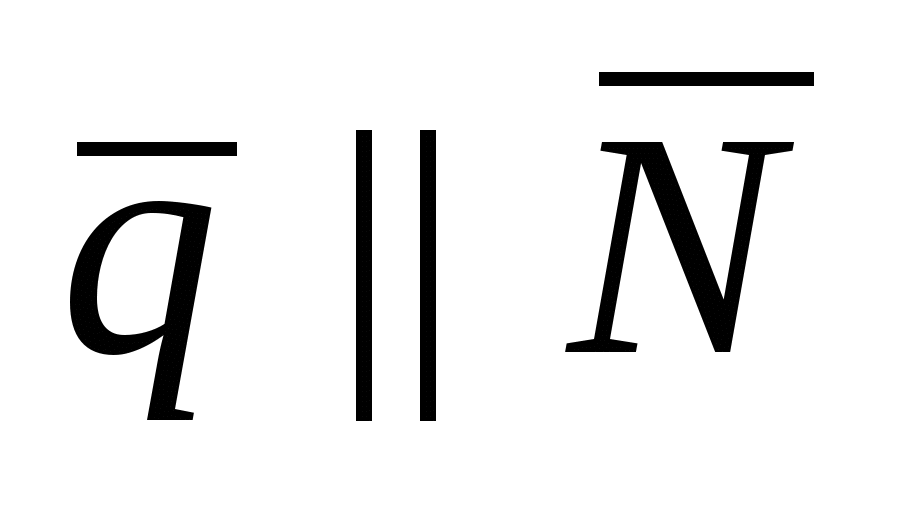  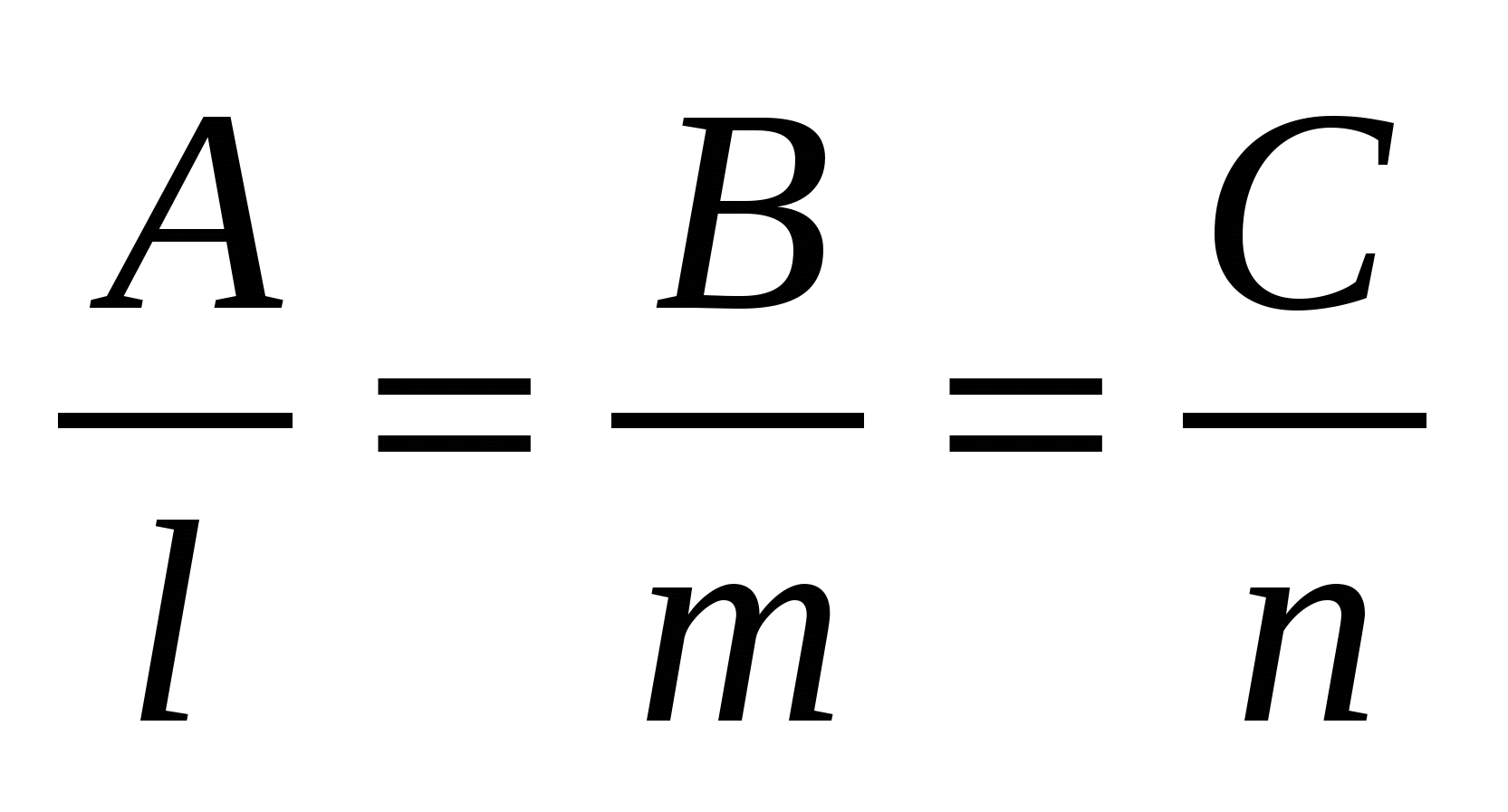 . .
Расстояние между параллельными прямыми 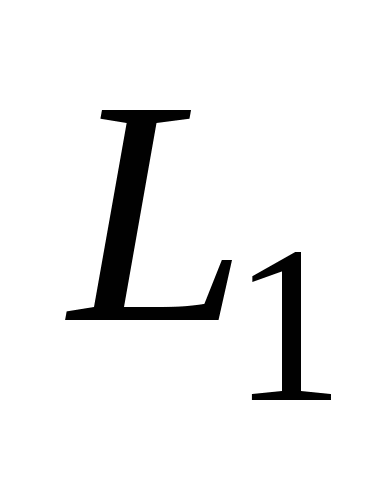 и и 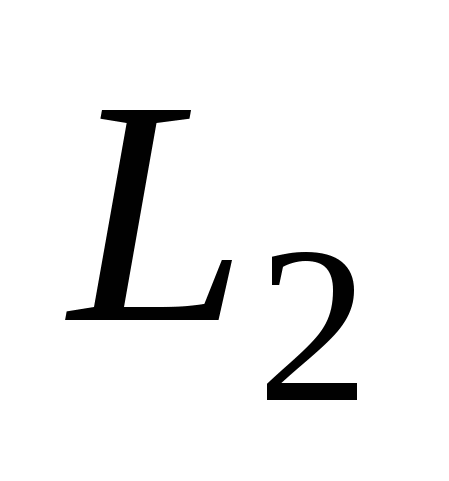 : : 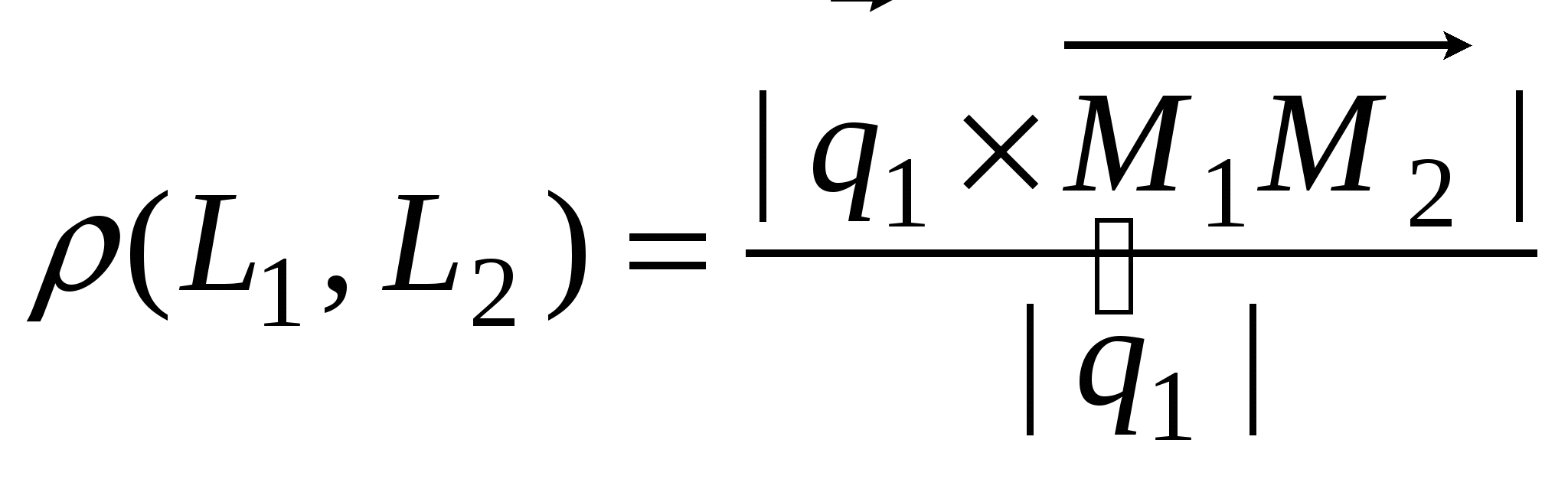 . .
Расстояние между скрещивающимися прямыми 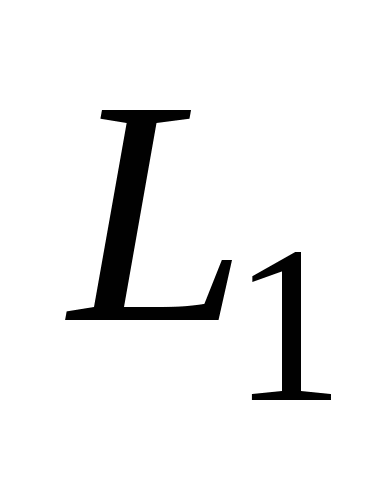 и и 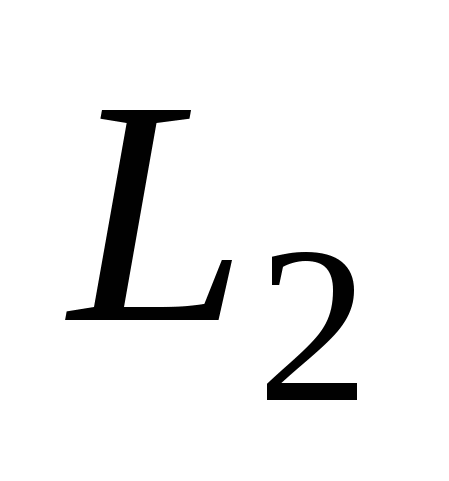 : : 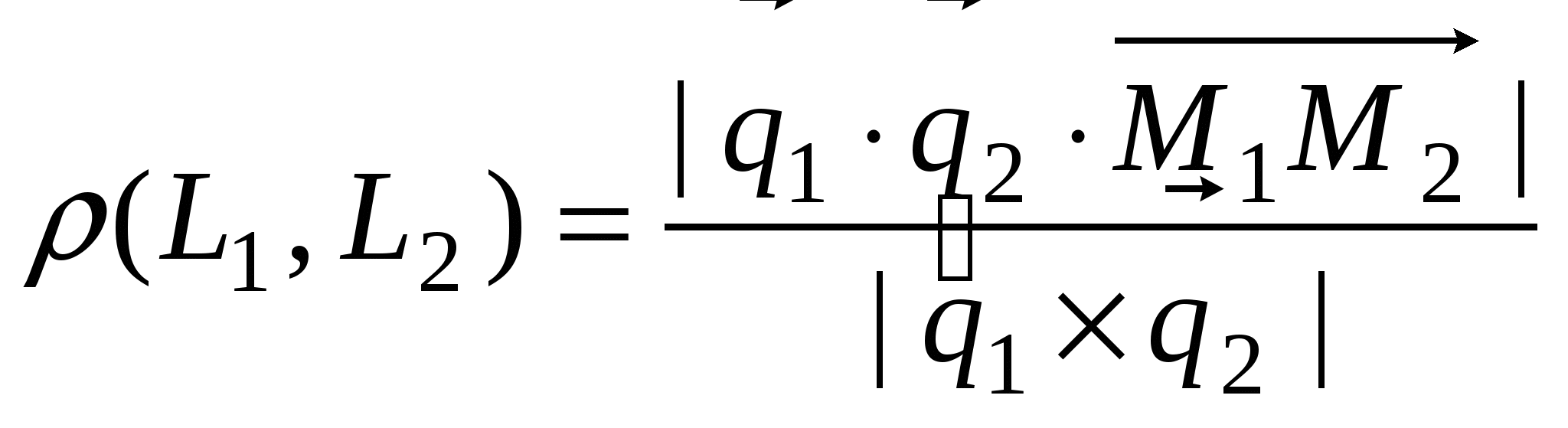 . .
Поверхности.
Алгебраическая поверхность второго порядка: 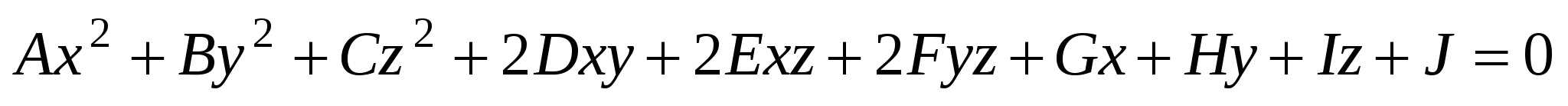 , где числа , где числа 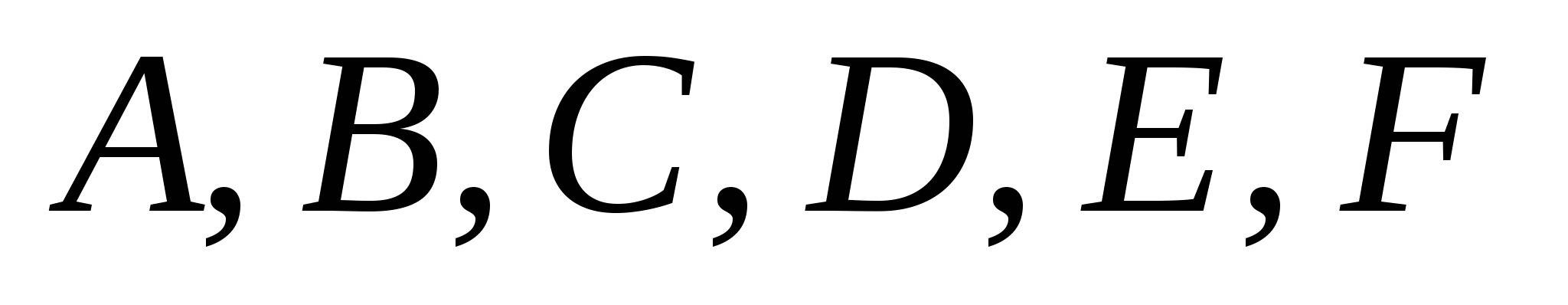 не равны нулю одновременно. не равны нулю одновременно.
Сфера.Каноническое уравнение сферы: 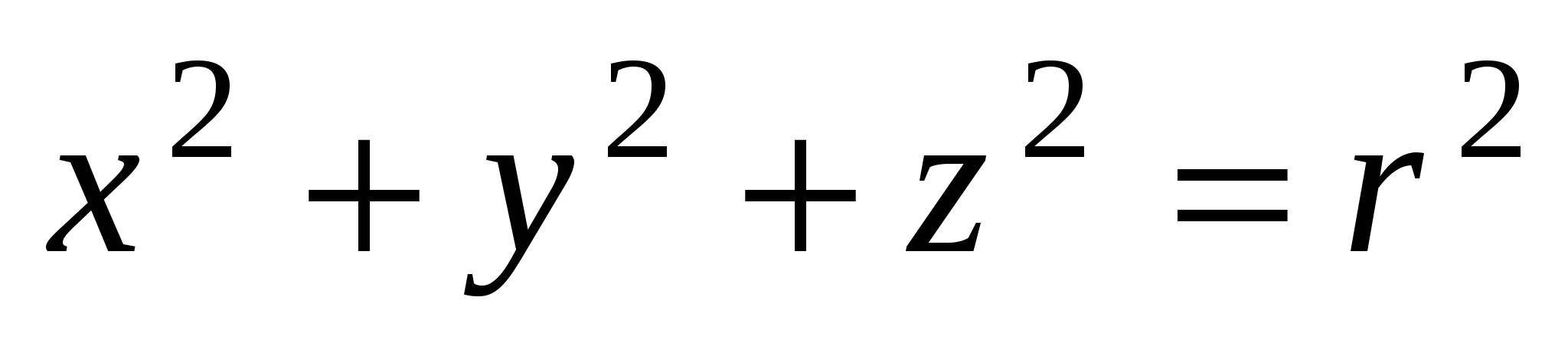 , где число , где число 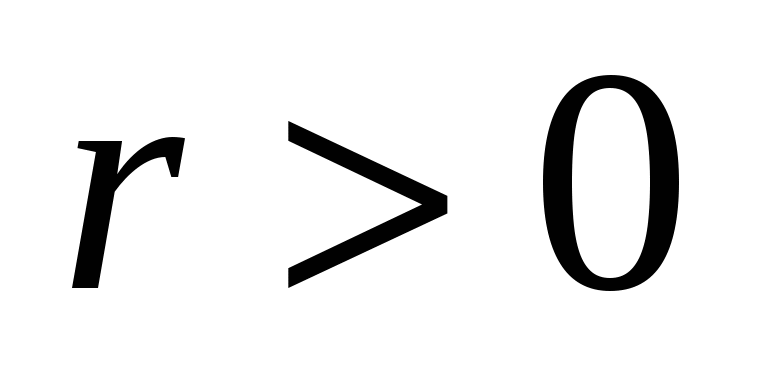 -радиус сферы, точка -радиус сферы, точка 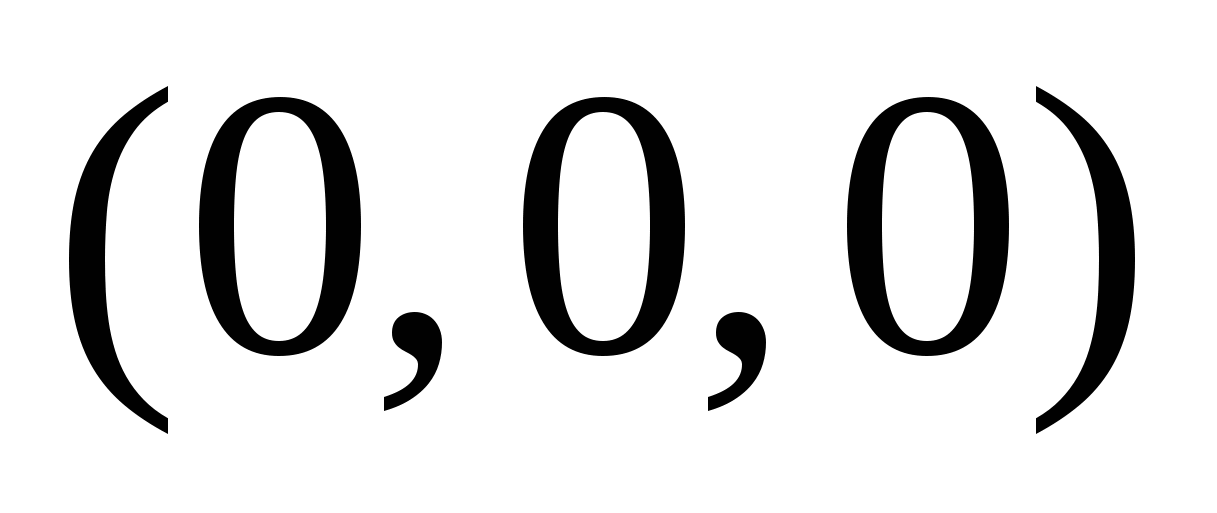 - центр сферы. - центр сферы.
Нормальное уравнение сферы: 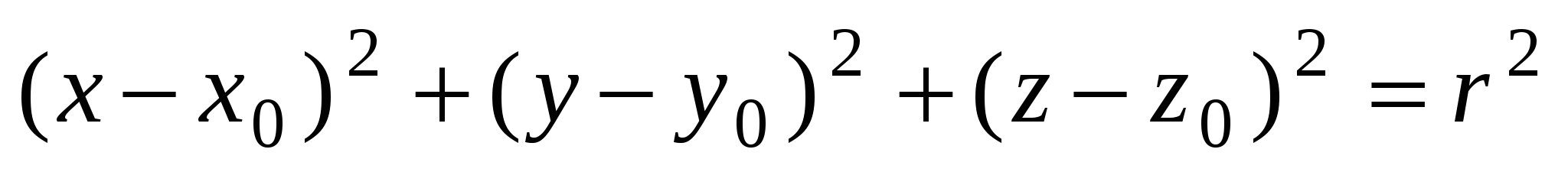 . Оно определяет сферу с центром в точке . Оно определяет сферу с центром в точке 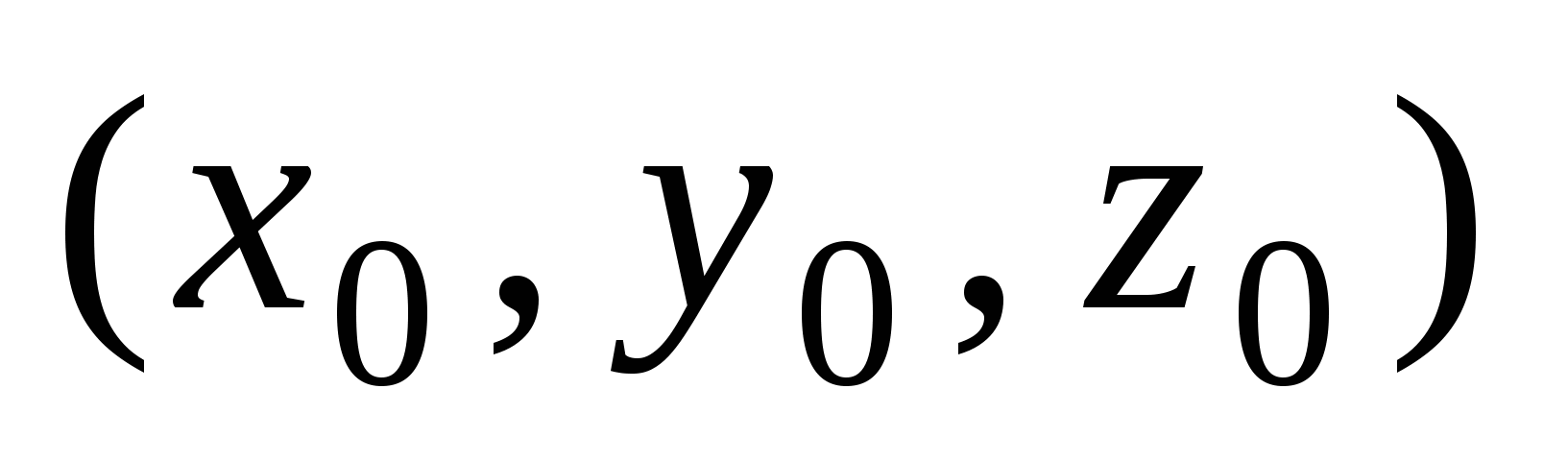 и радиусом и радиусом 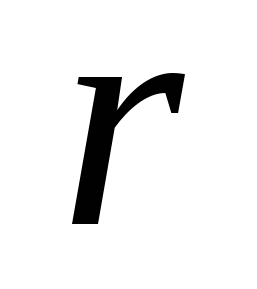 . . |
|
|
 Скачать 0.58 Mb.
Скачать 0.58 Mb.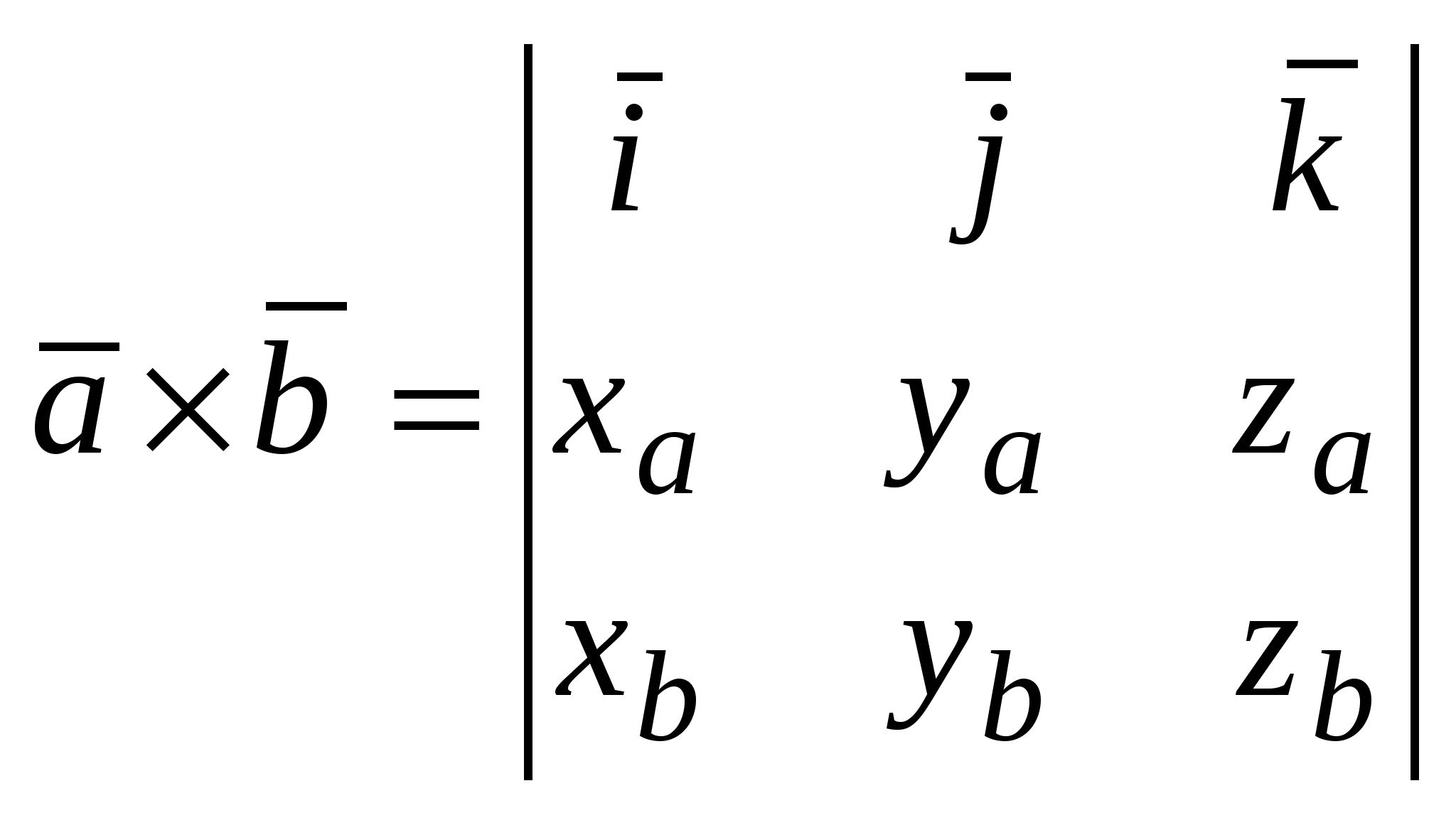
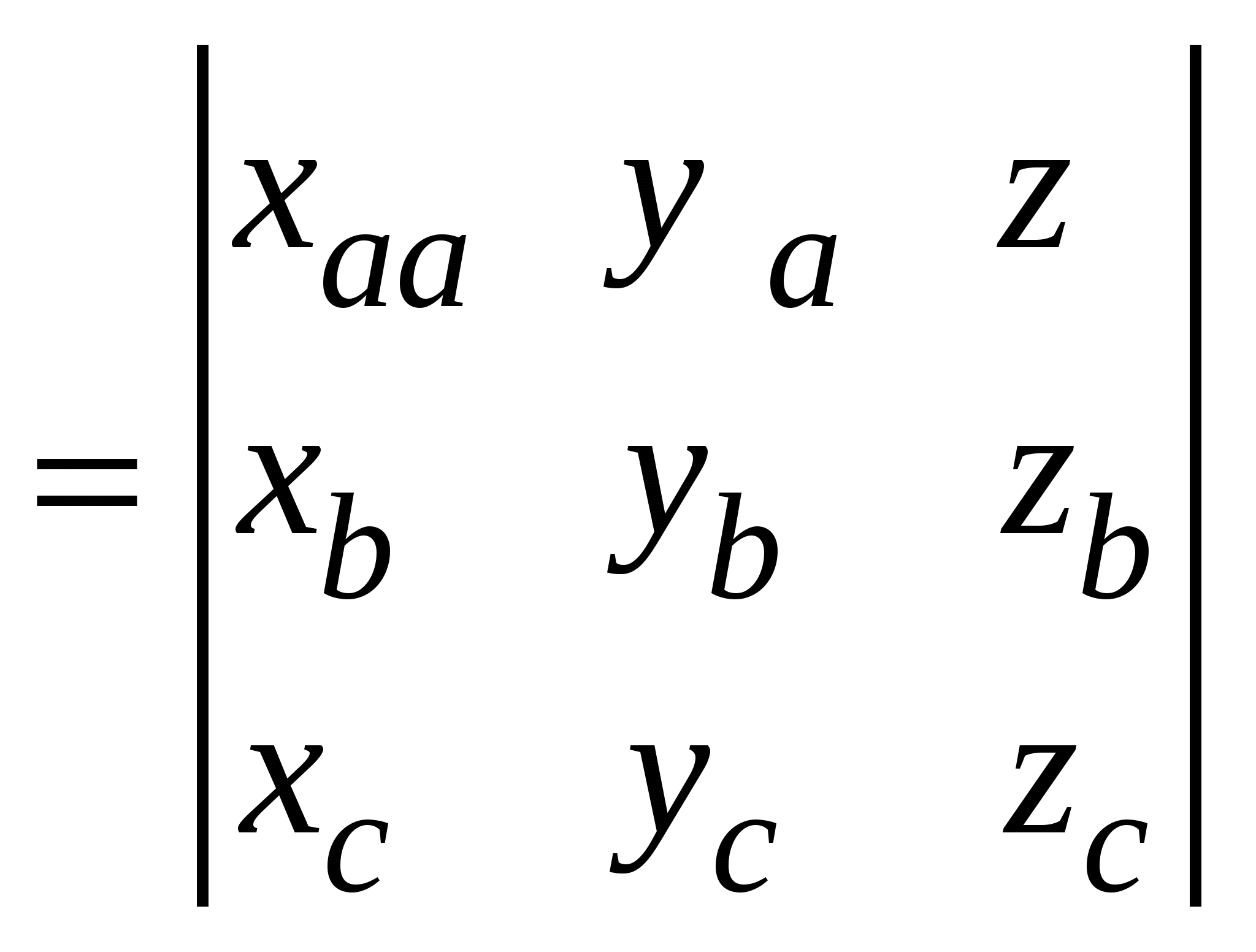 . Смешанное произведение обладает свойствами:
. Смешанное произведение обладает свойствами: 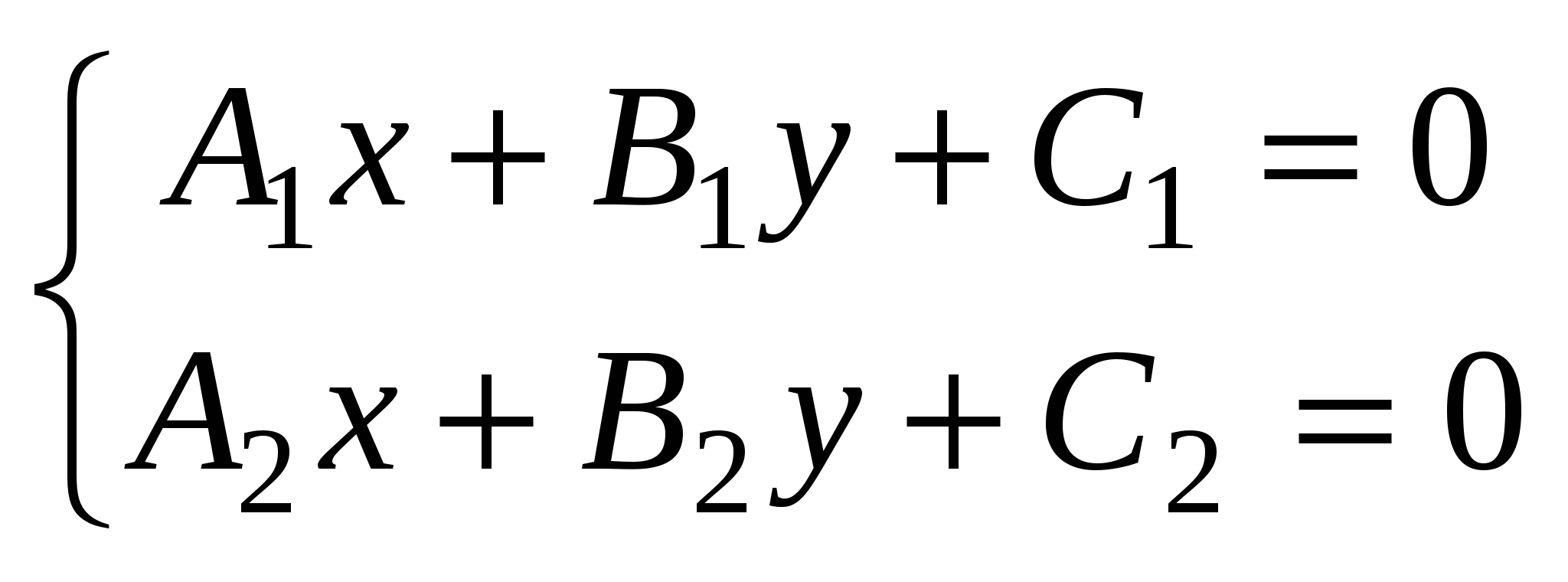 или
или 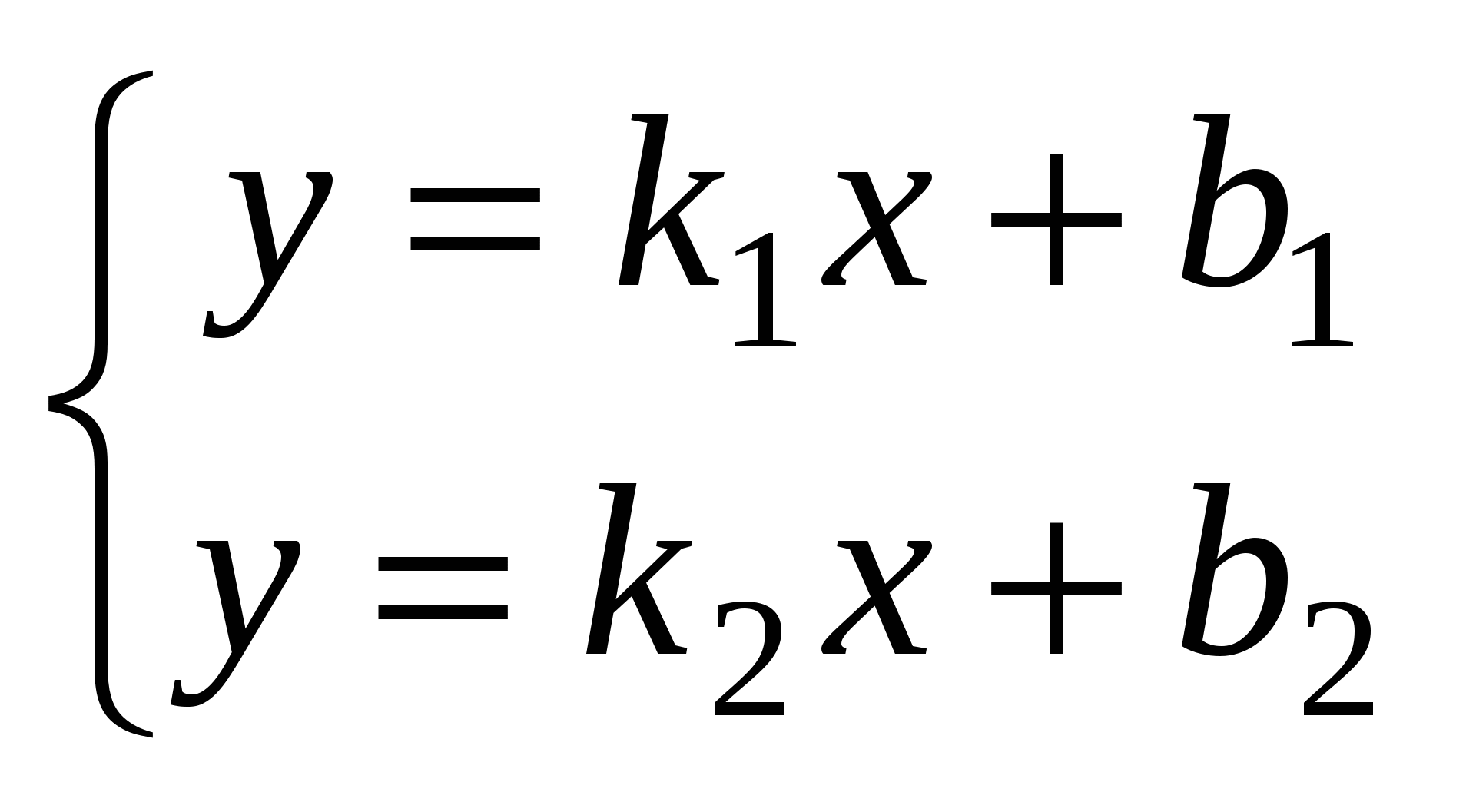 .
.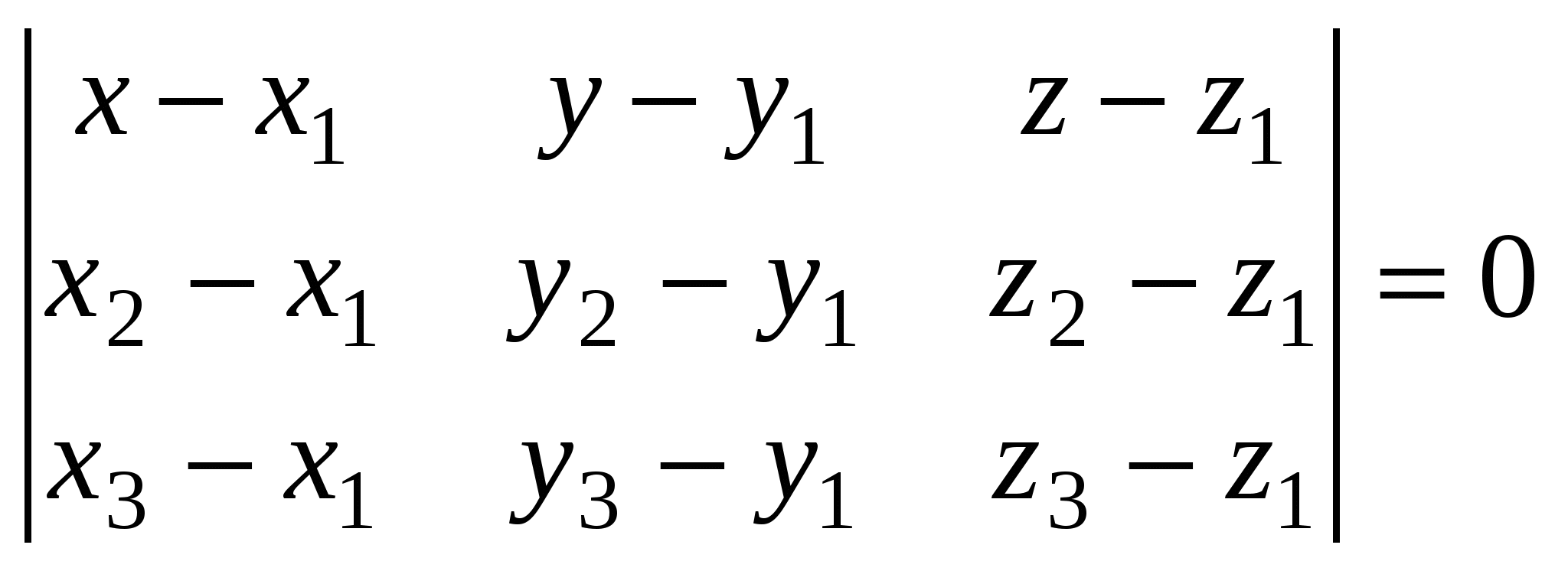 - уравнение плоскости, проходящей через три точки
- уравнение плоскости, проходящей через три точки 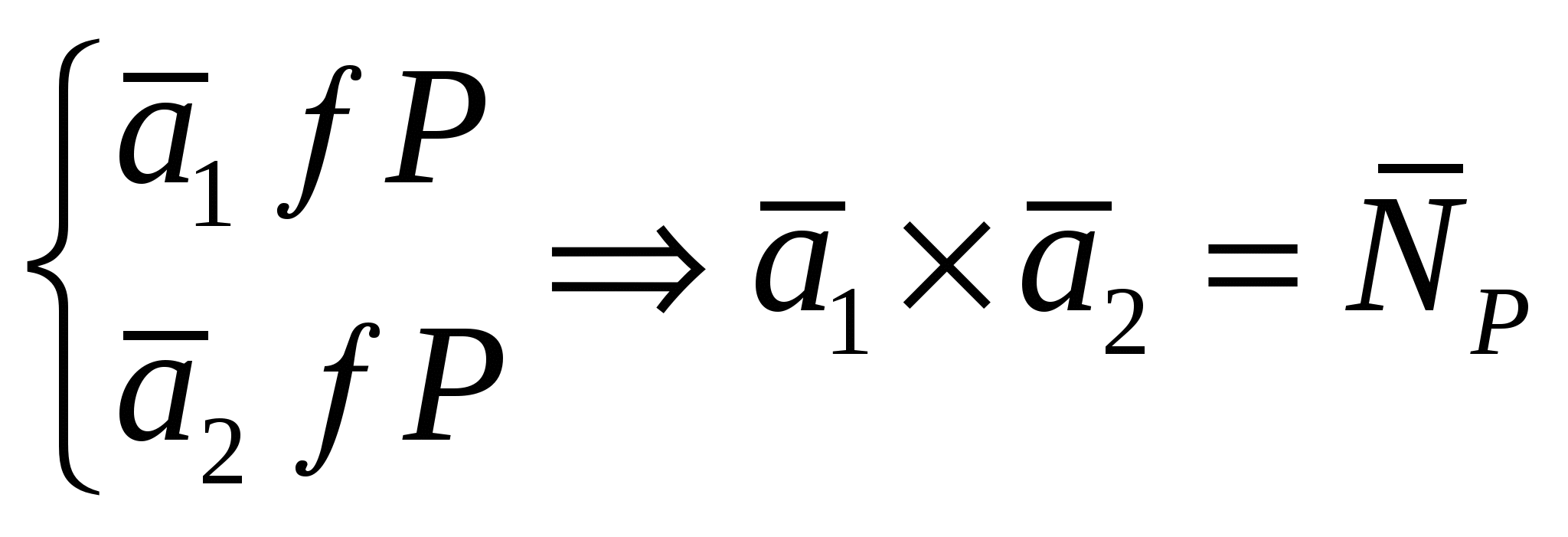 .
.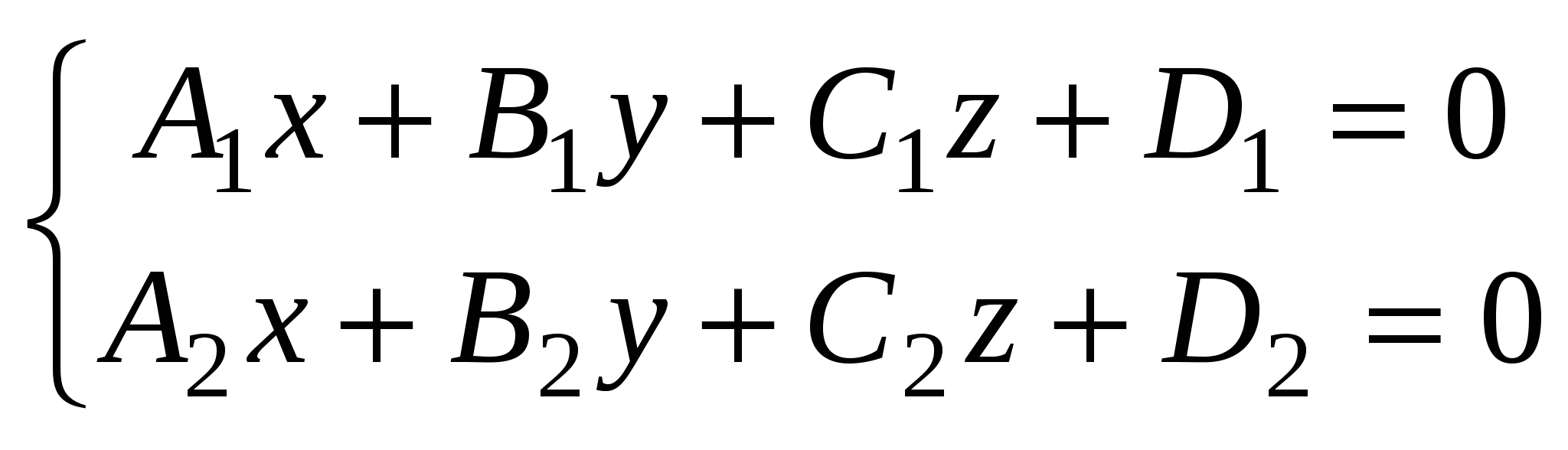 - общее уравнение прямой, как линии пересечения двух плоскостей, где
- общее уравнение прямой, как линии пересечения двух плоскостей, где 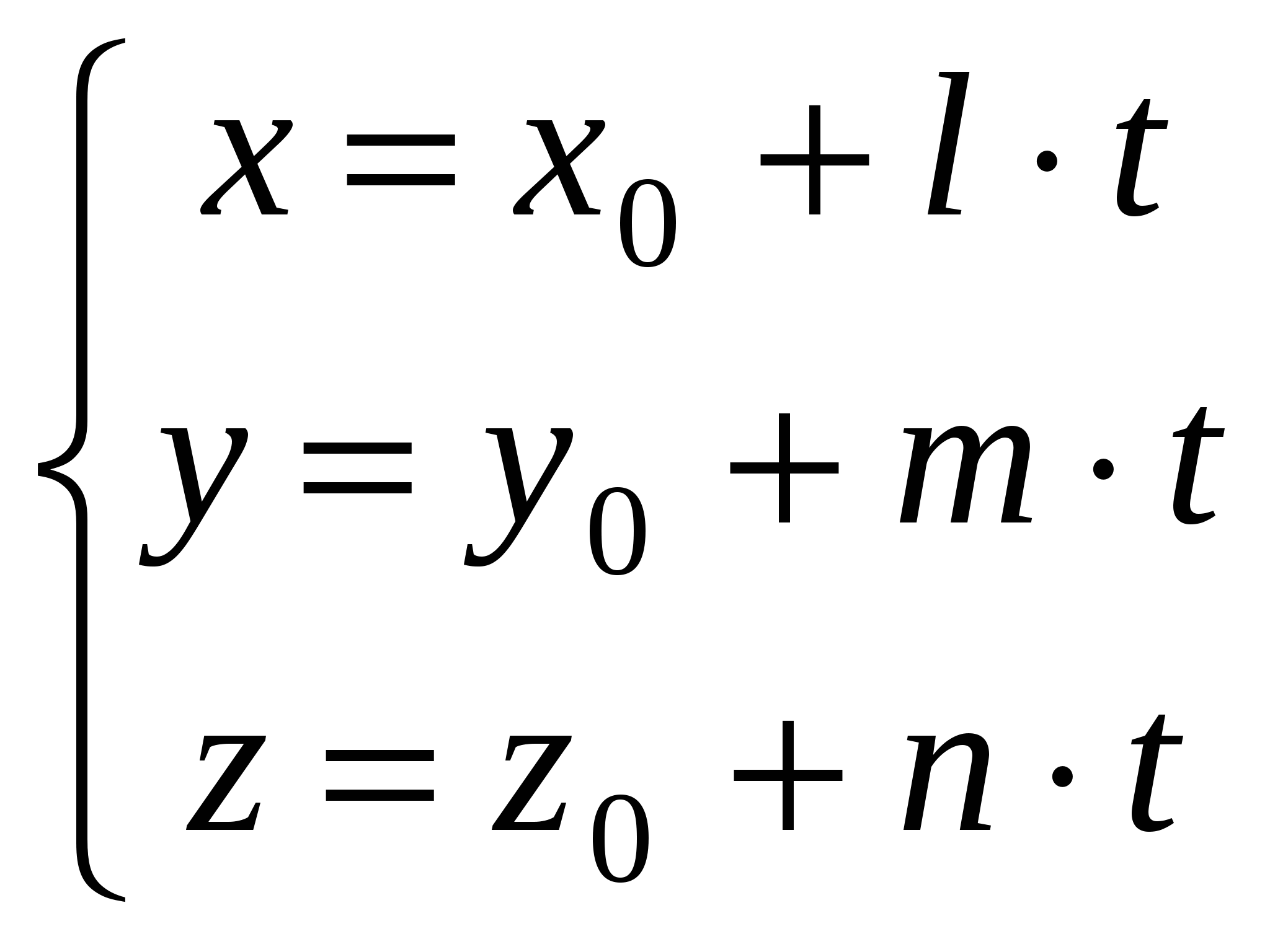 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 