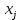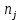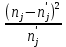Теория вероятности. ТВиМС Вариант 8 - 2021-09-30T142603.770. Входные данные
 Скачать 34.91 Kb. Скачать 34.91 Kb.
|
|
Входные данные: Считать максимальную дневную температуру в Санкт-Петербурге 1 октября случайной величиной 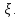 Из генеральной совокупности – данных Гидрометеослужбы о такой температуре в разные года сделана следующая выборка (в градусах Цельсия): Из генеральной совокупности – данных Гидрометеослужбы о такой температуре в разные года сделана следующая выборка (в градусах Цельсия):
Задача 1 Для приведенной выборки случайной величины 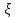 построить вариационный ряд и выборочный закон распределения построить вариационный ряд и выборочный закон распределения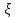 . Найти выборочное среднее . Найти выборочное среднее 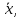 выборочную дисперсию выборочную дисперсию 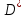 и исправленную выборочную дисперсию и исправленную выборочную дисперсию 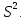 По имеющимся данным построим вариационный ряд (для этого упорядочим варианты случайной величины 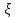 в порядке их возрастания): в порядке их возрастания):4, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 18, 18, 18, 18, 20, 20. Сосчитая частоты для каждого значения случайной величины 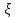 , составим выборочный закон распределения. Запишем его в виде таблицы: , составим выборочный закон распределения. Запишем его в виде таблицы:
Рассчитаем выборочное среднее по формуле: 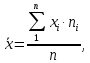 где n - объем выборки: 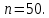 Получаем: 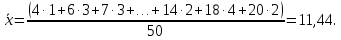 Найдем выборочную дисперсию 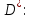 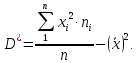 Получаем: 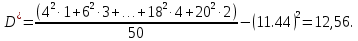 Вычисляем исправленную выборочную дисперсию 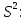 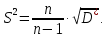 Получаем: 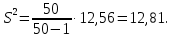 Полученные результаты говорят о том, что 1 октября в Санкт-Петербурге следует ожидать максимальную дневную температуру, равную примерно 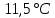 с разбросом порядка с разбросом порядка 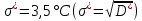 , т.е. примерно в 70% случаев температура должна попадать в интервал 8 – 15 , т.е. примерно в 70% случаев температура должна попадать в интервал 8 – 15 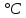 (в выборке в этот интервал попадает 74% значений). (в выборке в этот интервал попадает 74% значений).Задача 2 Построить с надежностью 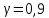 доверительный интервал для математического ожидания случайной величины доверительный интервал для математического ожидания случайной величины 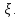 Интервальной оценкой (с доверительной вероятностью 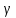 ) математического ожидания а нормально распределенной величины ) математического ожидания а нормально распределенной величины 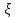 по среднему по среднему 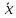 при известном среднеквадратическом отклонении при известном среднеквадратическом отклонении 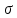 служит доверительный интервал служит доверительный интервал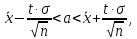 где 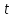 – значение аргумента функции Лапласа – значение аргумента функции Лапласа 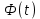 , при котором , при котором 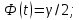 n – объем выборки. Среднеквадратическое отклонение 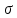 определяется как: определяется как: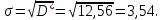 Находим значение аргумента 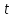 из соотношения: из соотношения: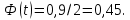 По таблице для интегральной функции Лапласа 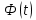 получим получим 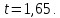 Находим искомый доверительный интервал: 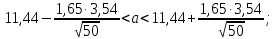 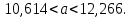 Этот означает, что если нет тренда, то средний за все годы максимум температуры в Санкт-Петербурге 1 октября с вероятностью 90% заключен в интервале 10,6 – 12,3 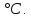 Задача 3 Построить с надежностью 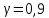 доверительный интервал для дисперсии доверительный интервал для дисперсии 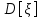 случайной величины случайной величины 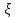 в предположении, что она имеет нормальное распределение. в предположении, что она имеет нормальное распределение.Интервальной оценкой дисперсии 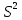 нормально распределенной величины Х по известной выборочной дисперсии нормально распределенной величины Х по известной выборочной дисперсии 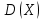 доверительный интервал доверительный интервал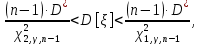 где 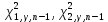 – критерия распределения Пирсона (определяются из таблицы). – критерия распределения Пирсона (определяются из таблицы).При больших значениях n (n 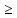 30) для вычисления квантилей используются асимптотические формулы: 30) для вычисления квантилей используются асимптотические формулы: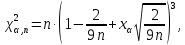 где 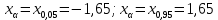 – квантили нормального распределения. Для – квантили нормального распределения. Для 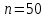 и и 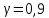 имеем: имеем: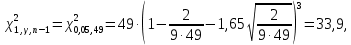 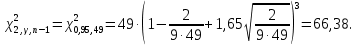 Находим доверительный интервал: 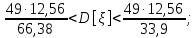 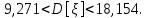 Другими словами, среднеквадратическое отклонение величины 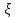 , характеризующее ее разброс относительно , характеризующее ее разброс относительно 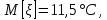 с вероятностью 90% заключено в пределах от 3 до 4,3 с вероятностью 90% заключено в пределах от 3 до 4,3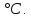 Задача 4 Используя критерий согласия Пирсона, проверить гипотезу о нормальном распределении случайной величины 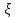 с уровнем значимости с уровнем значимости 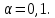 Проверим гипотезу о том, что случайная величина 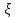 подчиняется нормальному закону распределения. подчиняется нормальному закону распределения.Имеем распределение:
Построим группированную выборку, разбив интервал, в который попали все наши варианты, на 6 подинтервалов:
Теоретические частоты рассчитаем по формуле 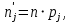 где вероятности где вероятности 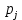 найдем по формуле: найдем по формуле: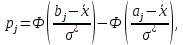 Тогда 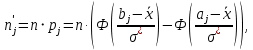 где 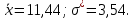 Рассчитаем все теоретические частоты: 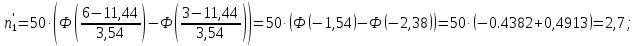 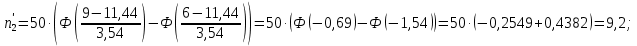 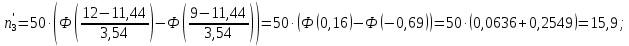 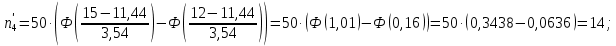 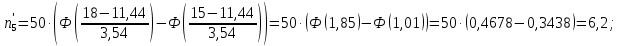 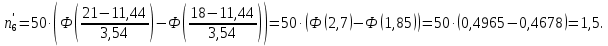 Результаты вычислений можно проверить, если просуммировать теоретические частоты. Очевидно, что сумма всех 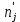 должна примерно равняться числу вариант, то есть 50. должна примерно равняться числу вариант, то есть 50.
В нашем случае сумма теоретических частот равна 49,5, следовательно, можно утверждать, что вычисления произведены верно. Для нахождения эмпирического значения критерия 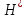 составим расчетную таблицу и рассчитаем его по формуле: составим расчетную таблицу и рассчитаем его по формуле: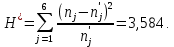 Построим правостороннюю критическую область, удовлетворяющую равенству 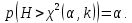 Критическая точка 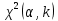 равна квантили порядка равна квантили порядка 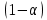 распределения распределения 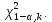 Тогда по уровню значимости Тогда по уровню значимости 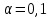 и числу степеней свободы и числу степеней свободы 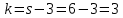 имеем: имеем: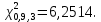 В силу того, что наблюдаемое значение критерия не попадает в критическую область 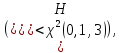 можно принять гипотезу о нормальном распределении случайной величины можно принять гипотезу о нормальном распределении случайной величины 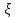 при уровне значимости при уровне значимости 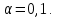 Задача 5 Используя критерий согласия Пирсона, проверить гипотезу о равномерном законе распределения случайной величины 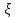 с уровнем значимости с уровнем значимости 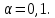 Найдем параметры a и b для равномерного закона распределения. Оценим их, применяя метод моментов. Тогда параметры можно выразить через характеристики выборки следующим образом: 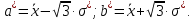 Используя найденные в задачах 1 и 2 значения выборочного среднего и среднеквадратического отклонения, получим: 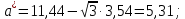 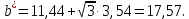 Рассчитаем теоретические частоты 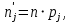 где вероятности где вероятности 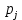 найдем по формуле: найдем по формуле: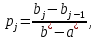 тогда получаем: 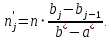 Рассчитаем все теоретические частоты: 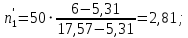 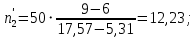 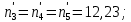 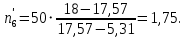 Найдем наблюдаемое значение критерия 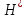 . Для этого используем группированную выборку, сделанную выше, и рассчитанные теоретические частоты. В результате получим: . Для этого используем группированную выборку, сделанную выше, и рассчитанные теоретические частоты. В результате получим:
Наблюдаемое (эмпирическое) значение критерия 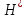 будет равно: будет равно: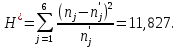 Находим критическую точку правосторонней области аналогично задаче 4. Критическая точка 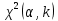 равна квантили порядка равна квантили порядка 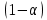 распределения распределения 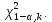 Тогда по уровню значимости Тогда по уровню значимости 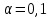 и числу степеней свободы и числу степеней свободы 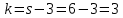 имеем: имеем: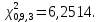 В силу того, что наблюдаемое значение критерия не попадает в критическую область 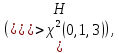 то отвергаем гипотезу о равномерном распределении случайной величины то отвергаем гипотезу о равномерном распределении случайной величины 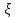 при уровне значимости при уровне значимости 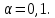 |

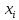
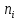
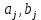 ]
]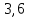 ]
]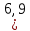 ]
]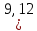 ]
]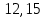 ]
] ]
] ]
]