VI. ряды теоретические вопросы Сходимость и сумма ряда. Необходимое условие сходимости ряда
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
|
Задача 5. Исследовать на сходимость ряд. 5.1. 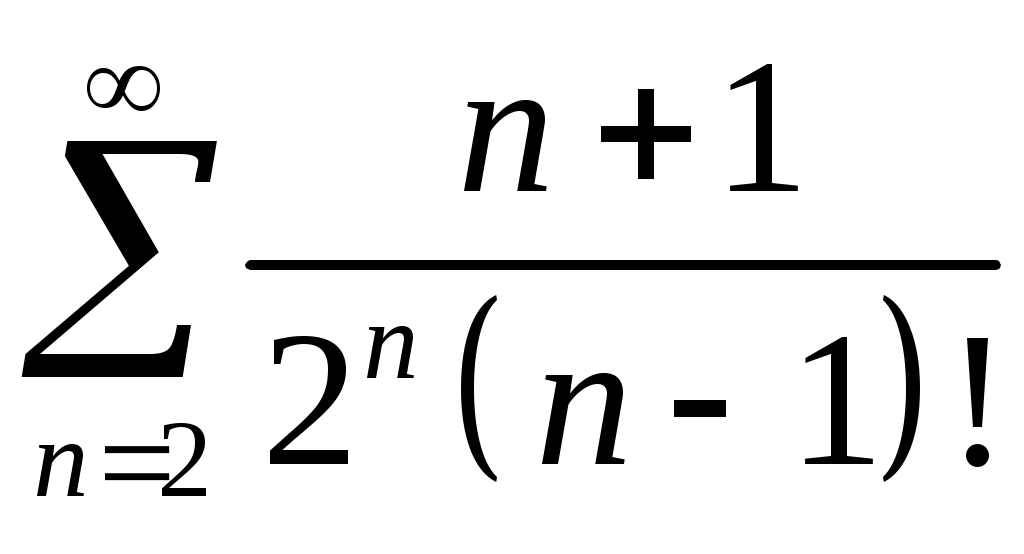 . 5.2. . 5.2. 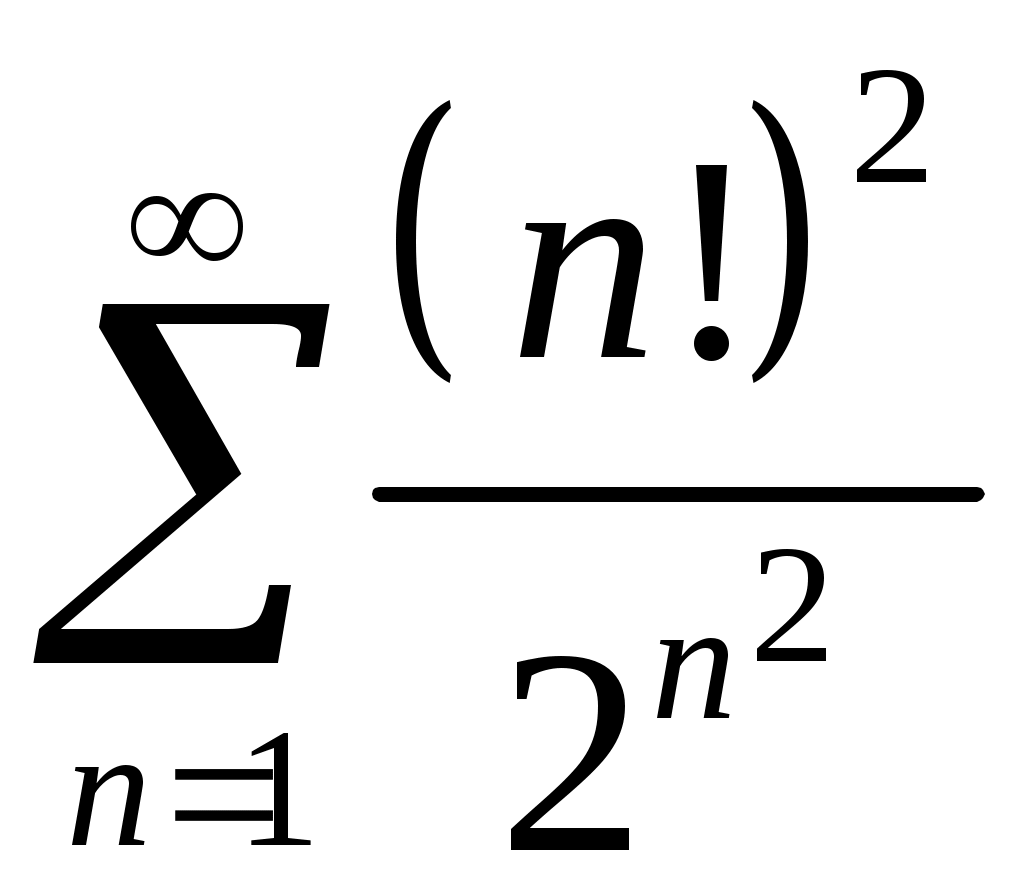 . .5.3. 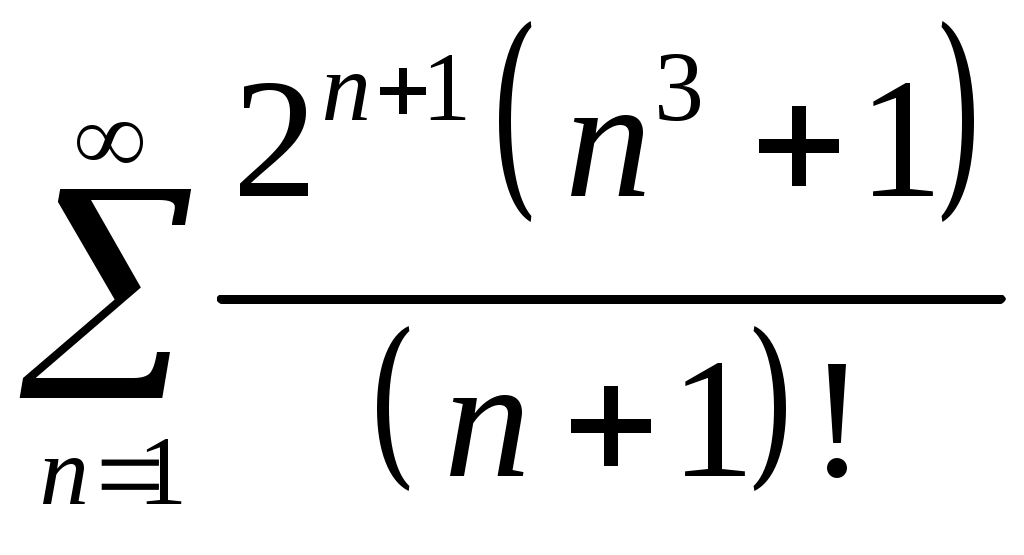 . 5.4. . 5.4. 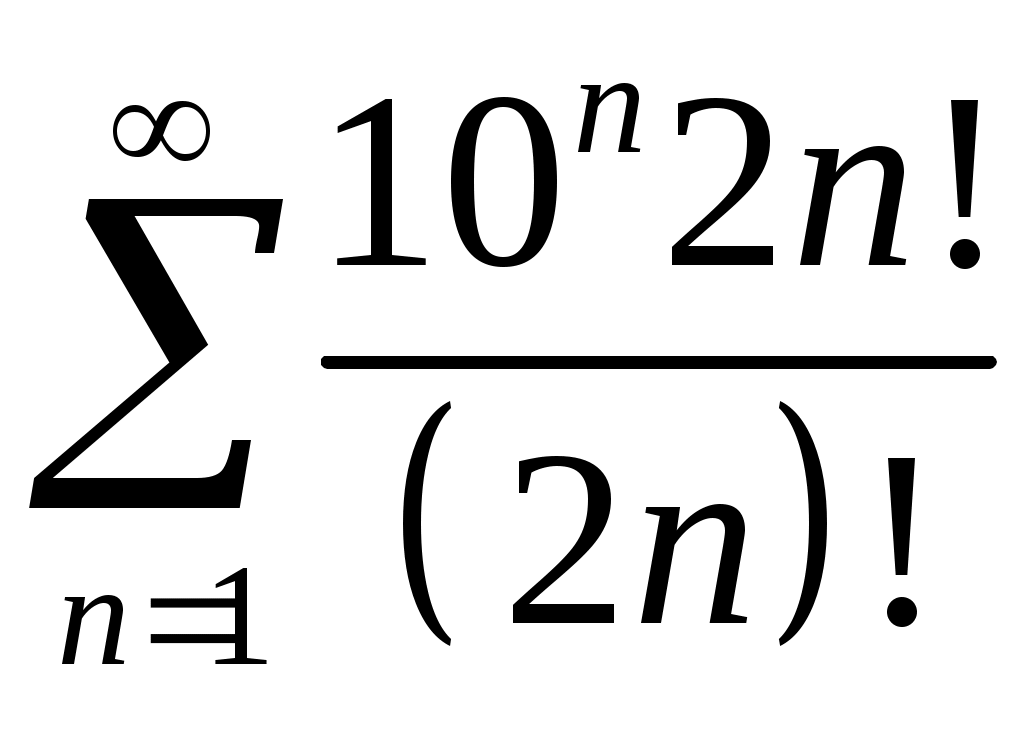 . .5.5. 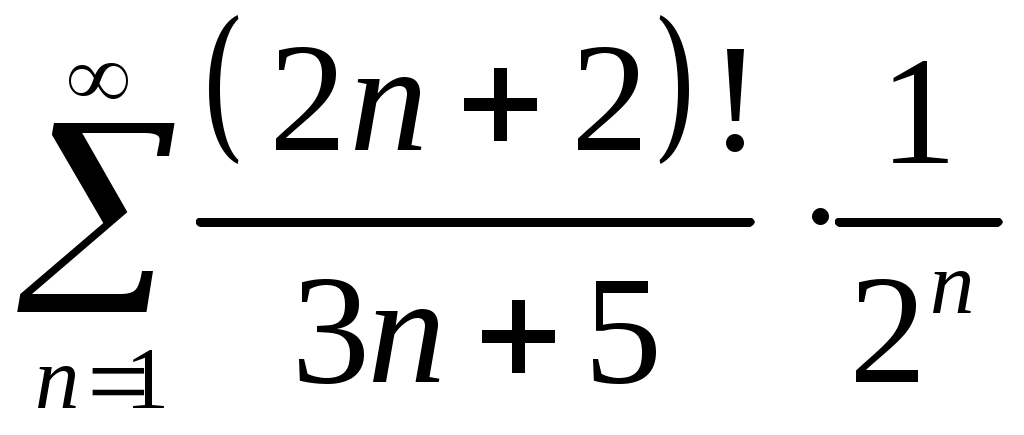 . 5.6. . 5.6. 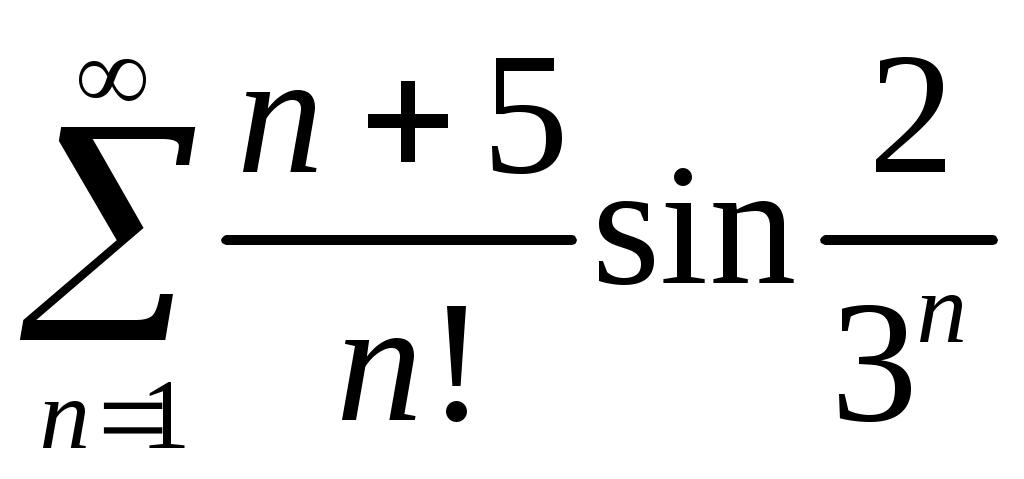 . .5.7. 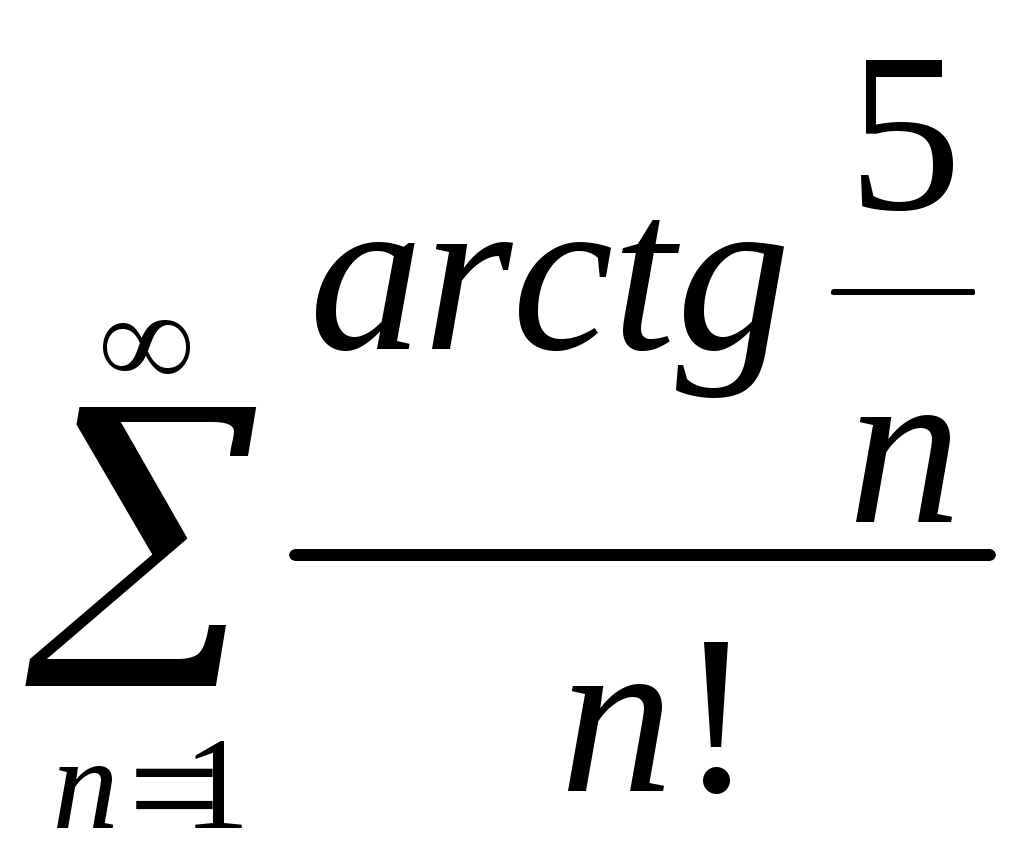 . 5.8. . 5.8. 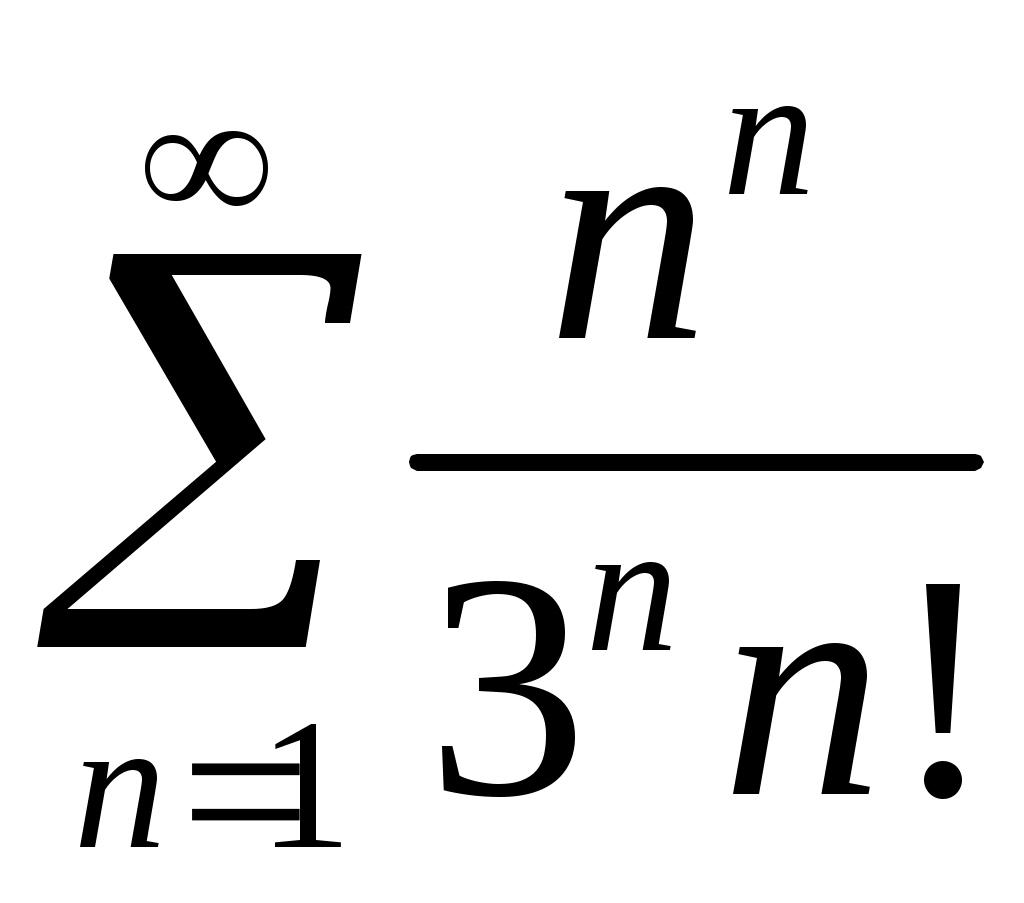 . .5.9. 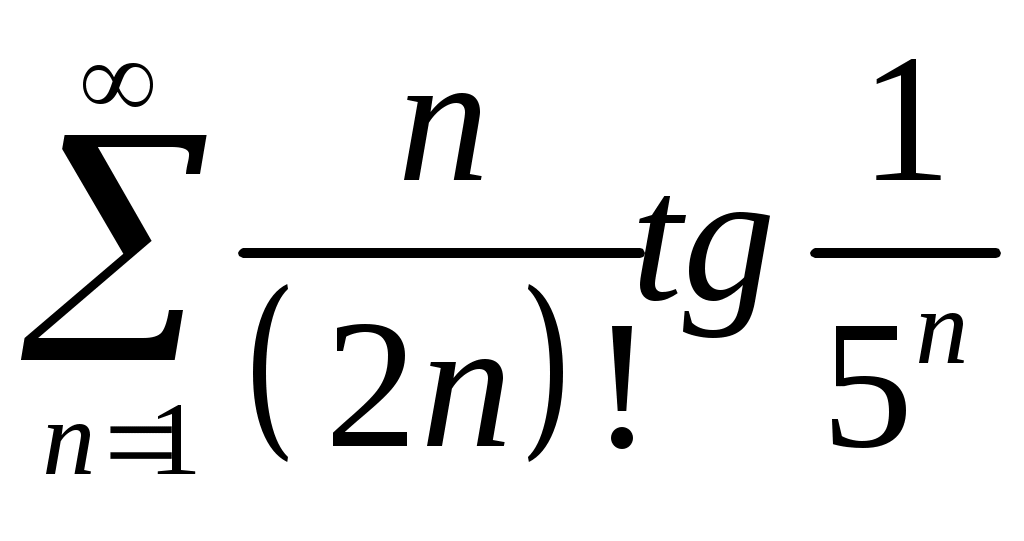 . 5.10. . 5.10. 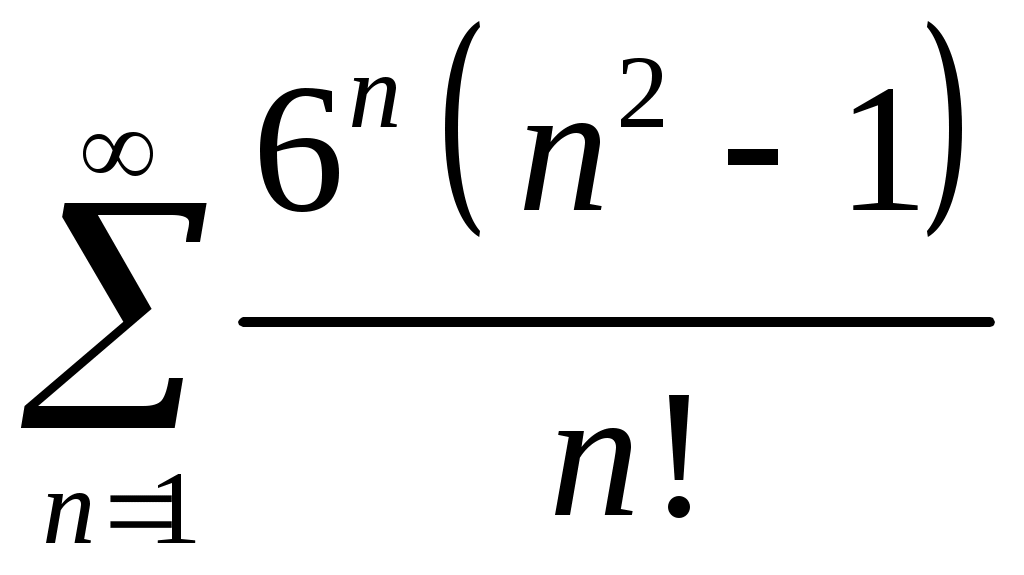 . .5.11. 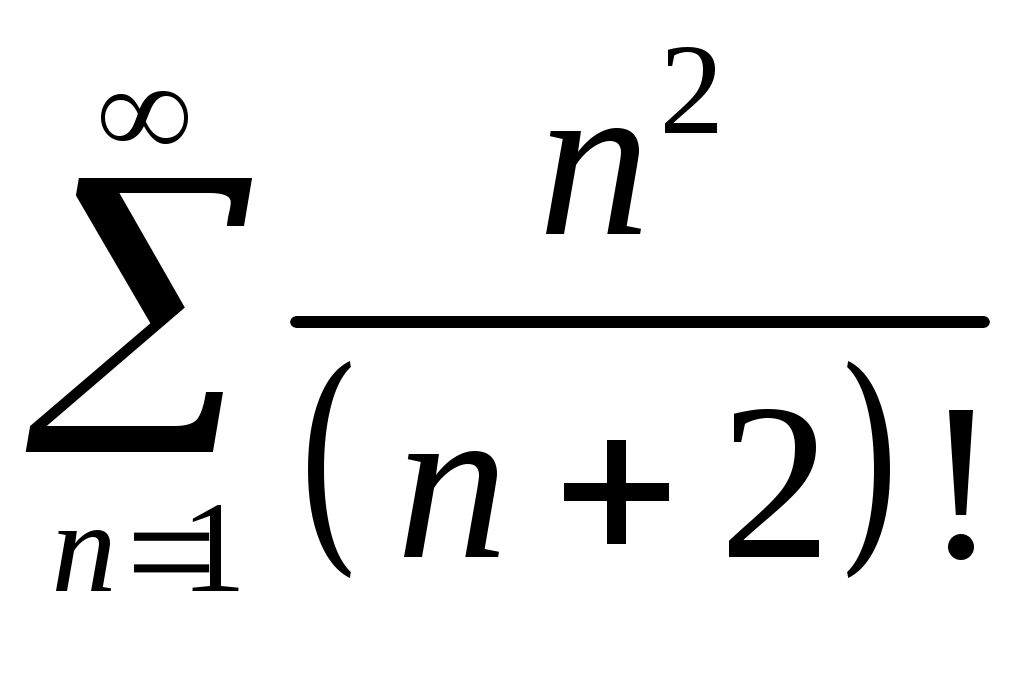 . 5.12. . 5.12. 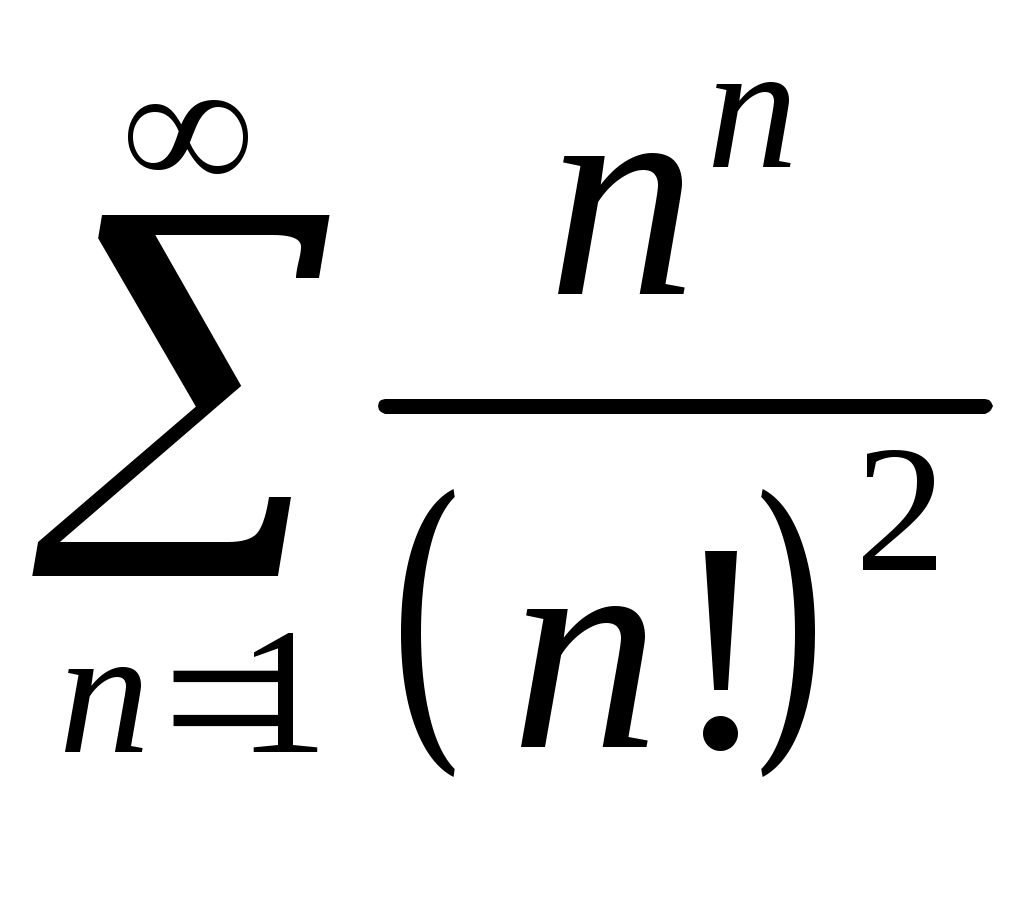 . .5.13. 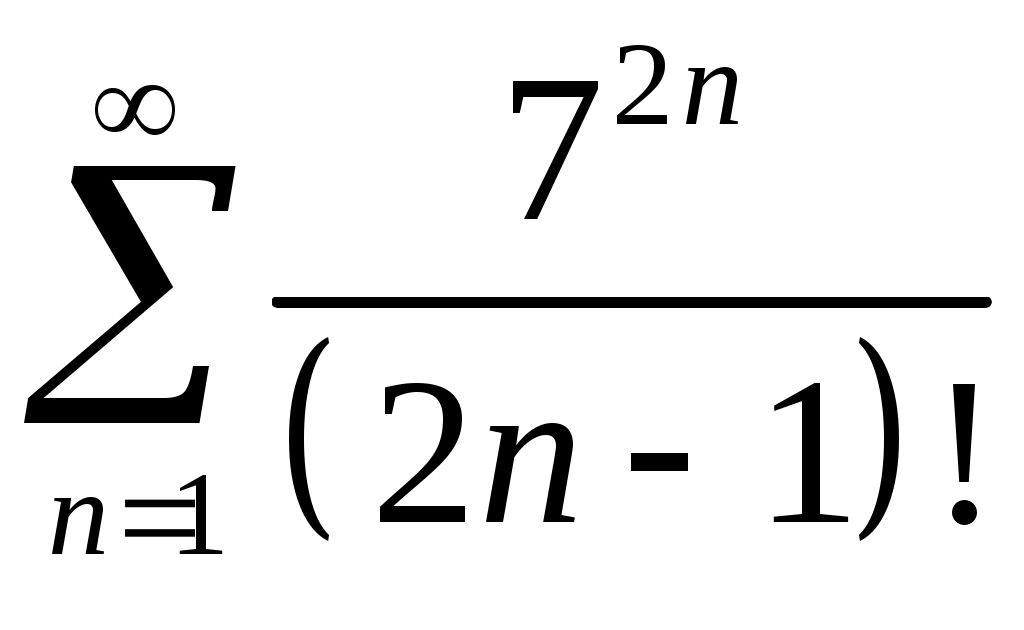 . 5.14. . 5.14. 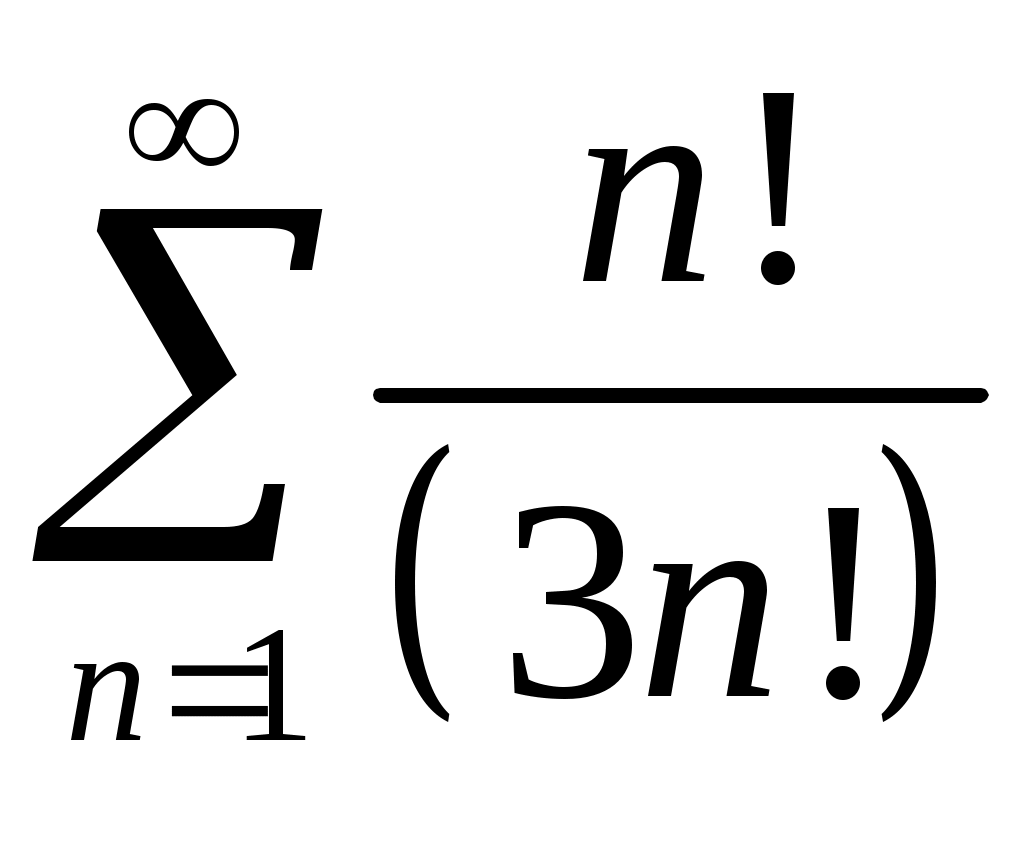 . .5.15. 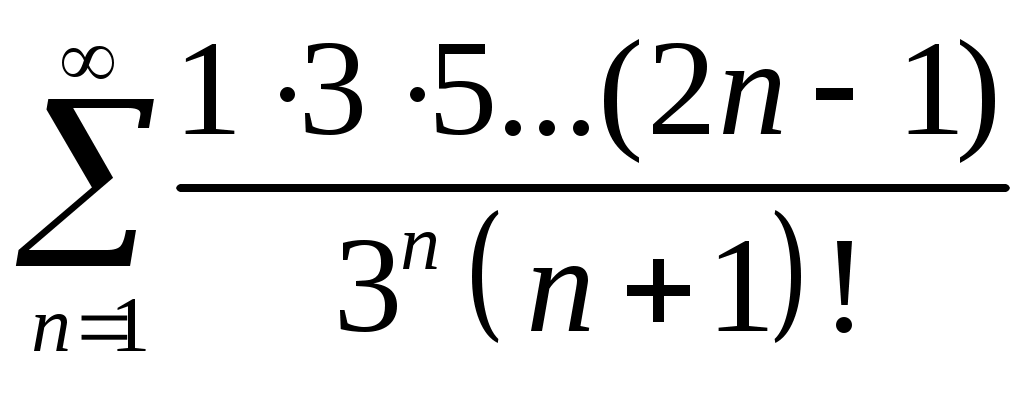 . 5.16. . 5.16. 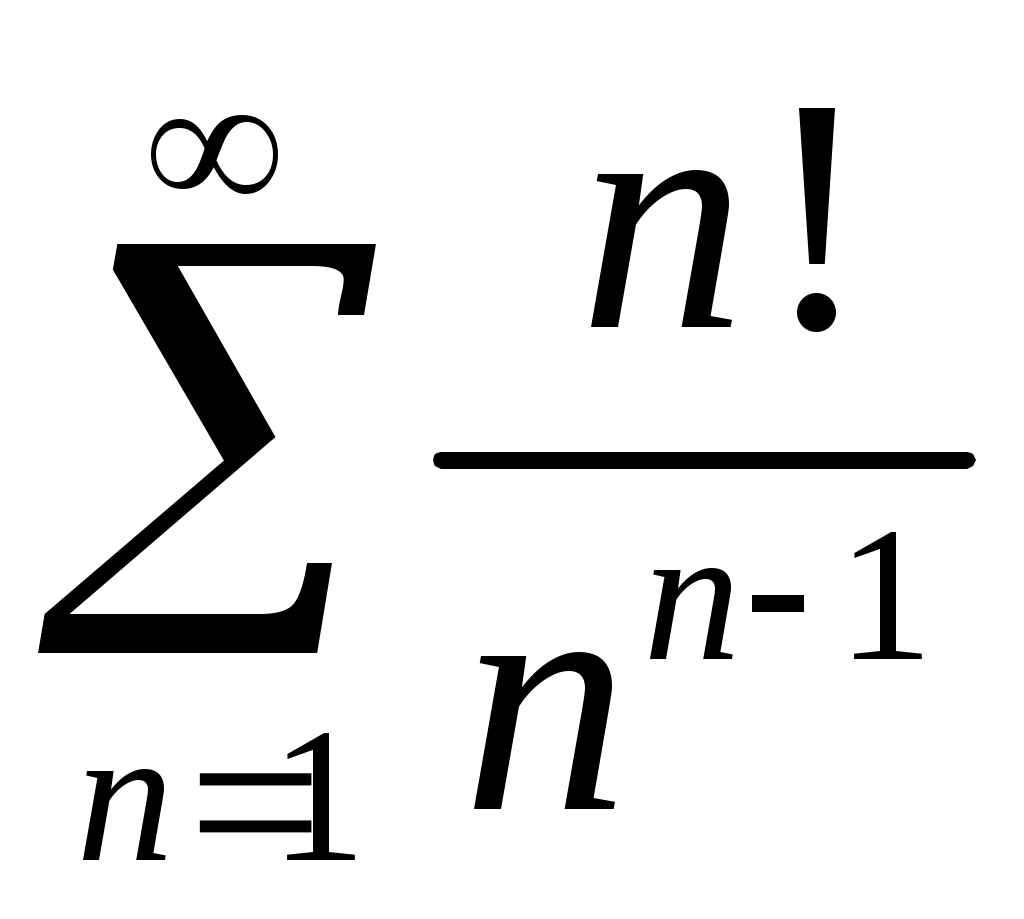 . ? . ?5.17. 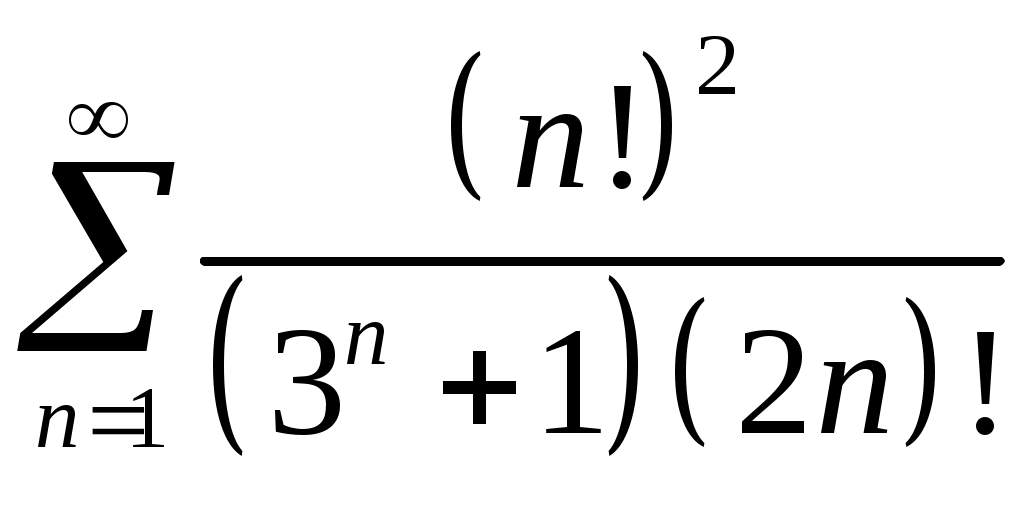 . 5.18. . 5.18. 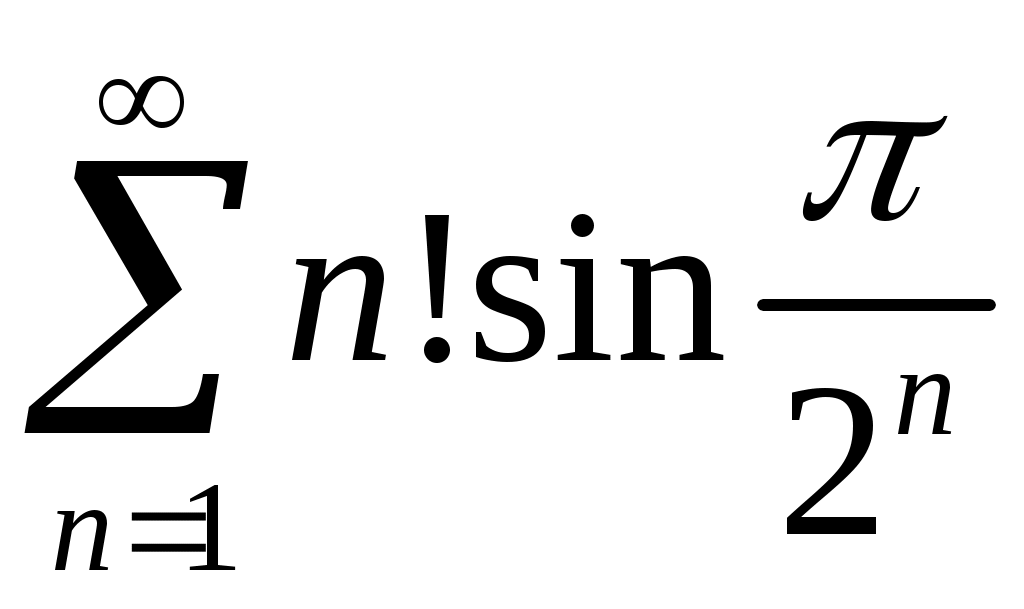 . .5.19. 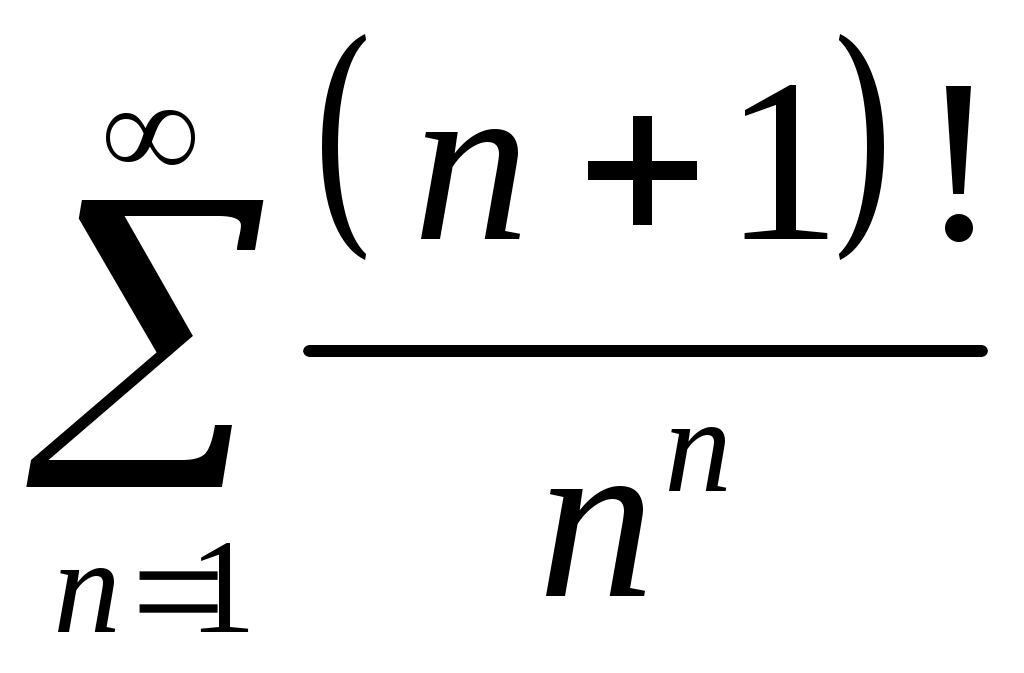 . 5.20. . 5.20. 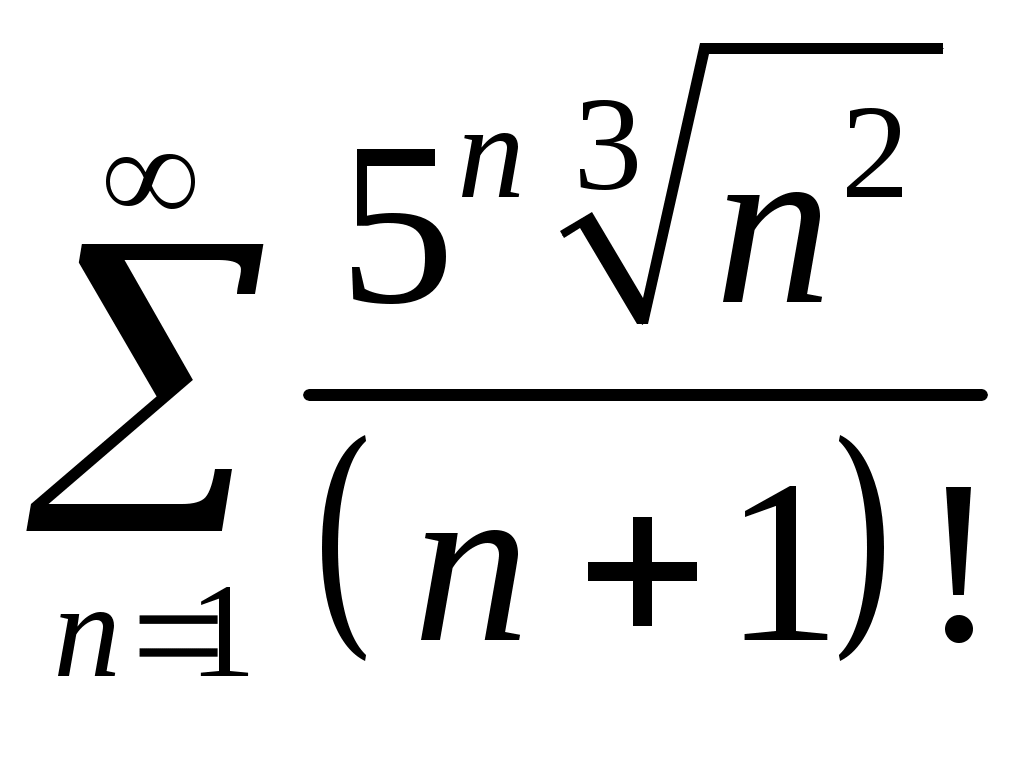 . .5.21. 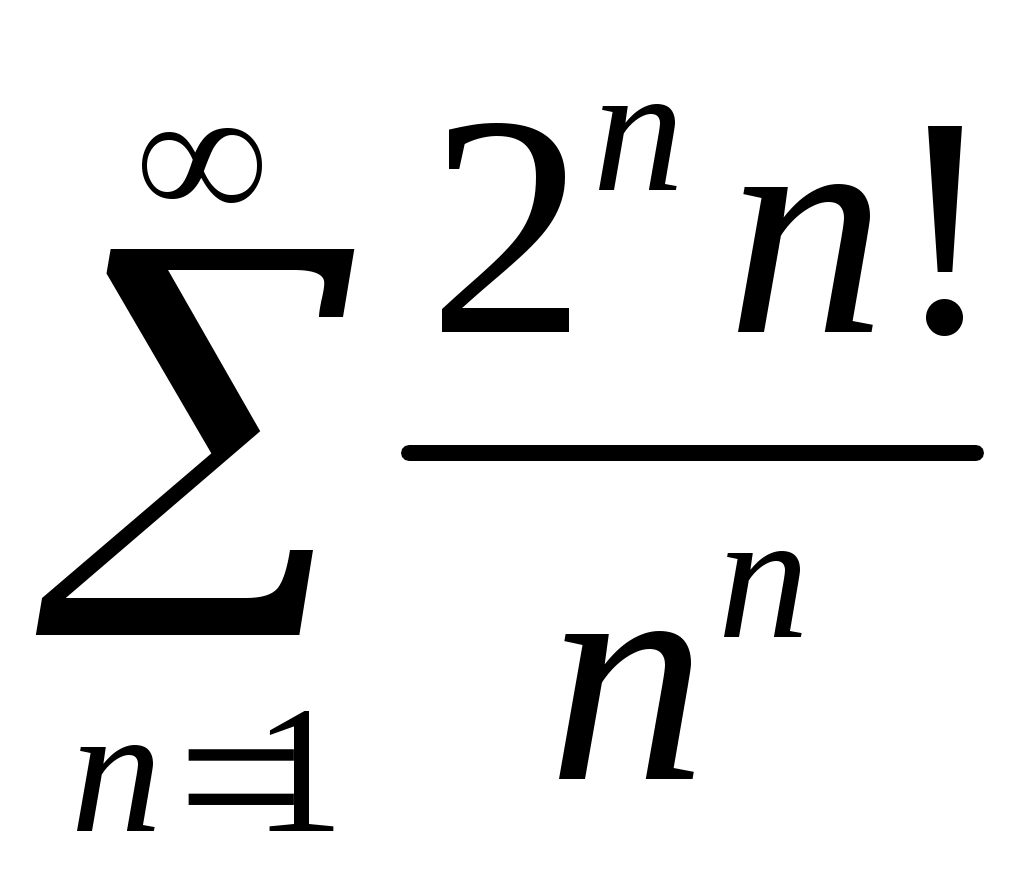 . 5.22. . 5.22. 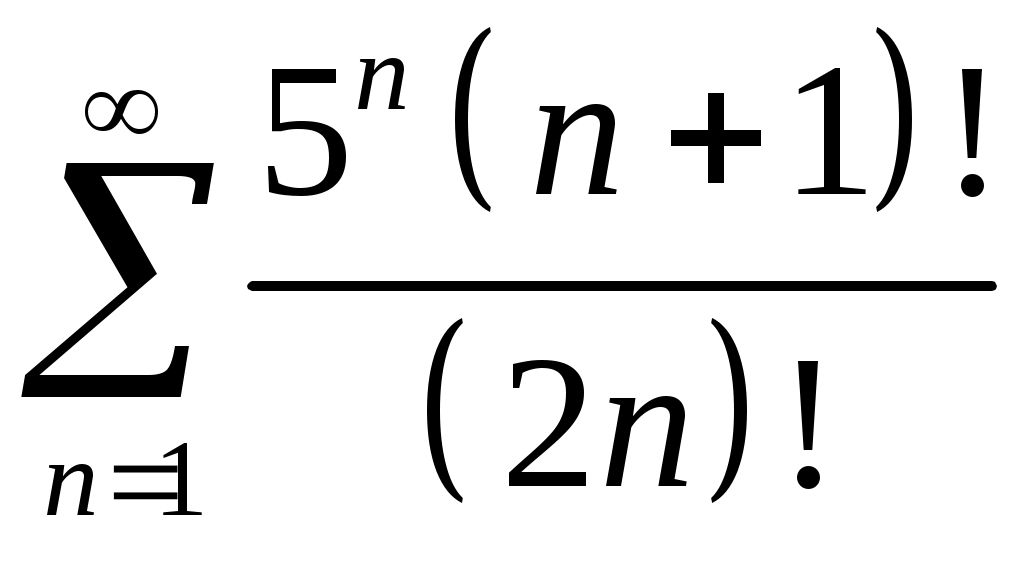 . .5.23. 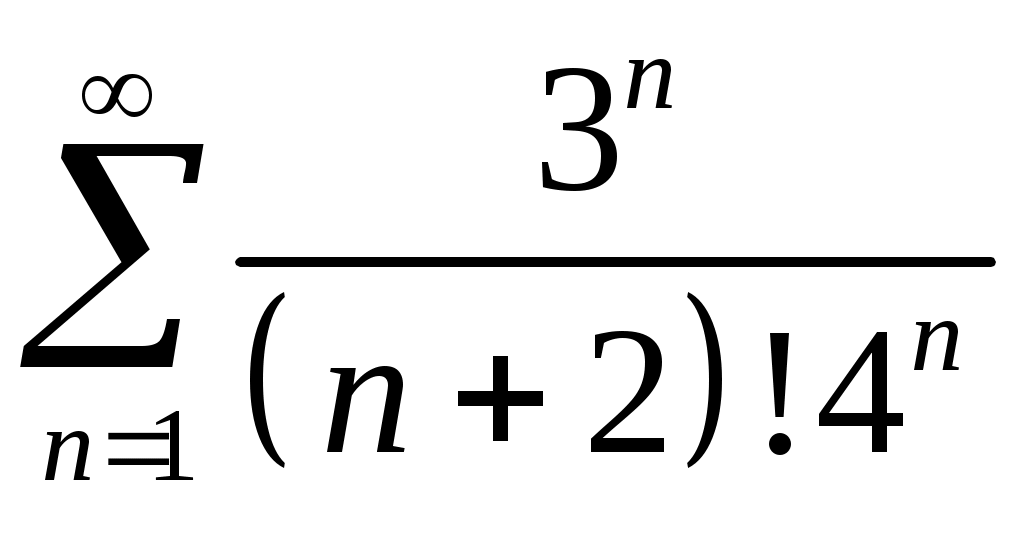 . 5.24. . 5.24. 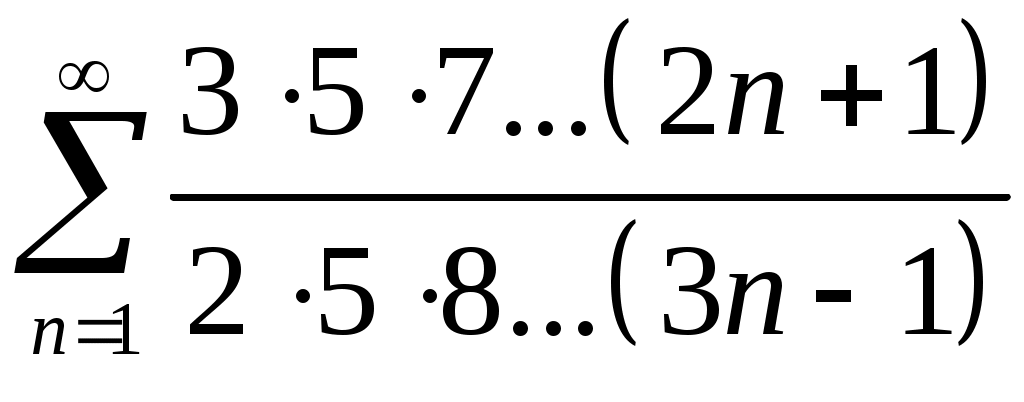 . .5.25. 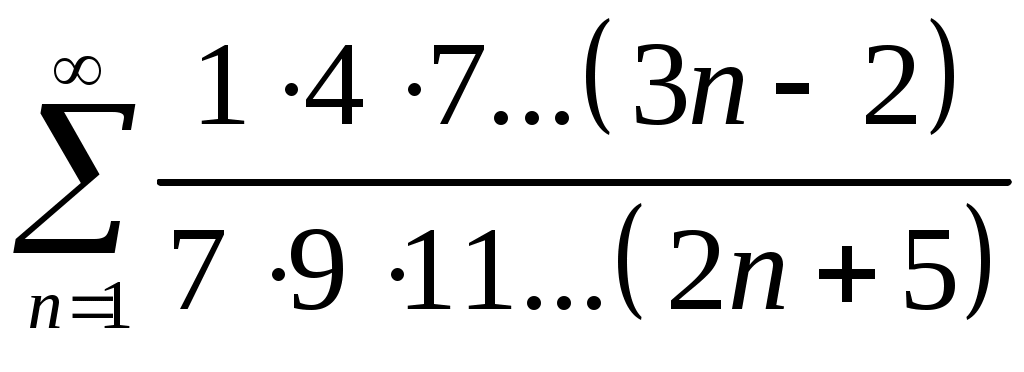 . 5.26. . 5.26. 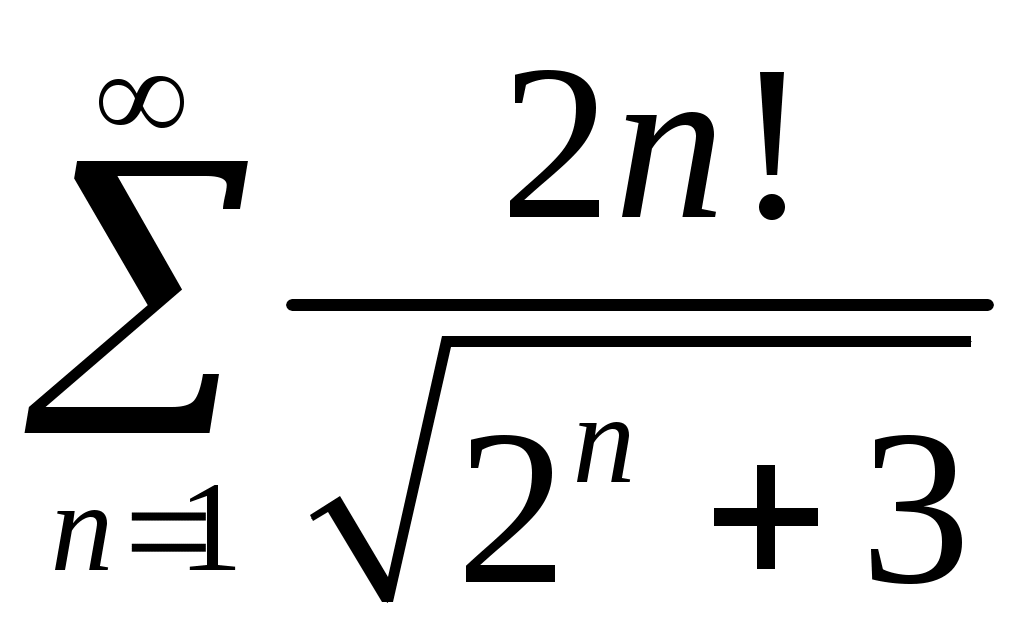 . .5.27. 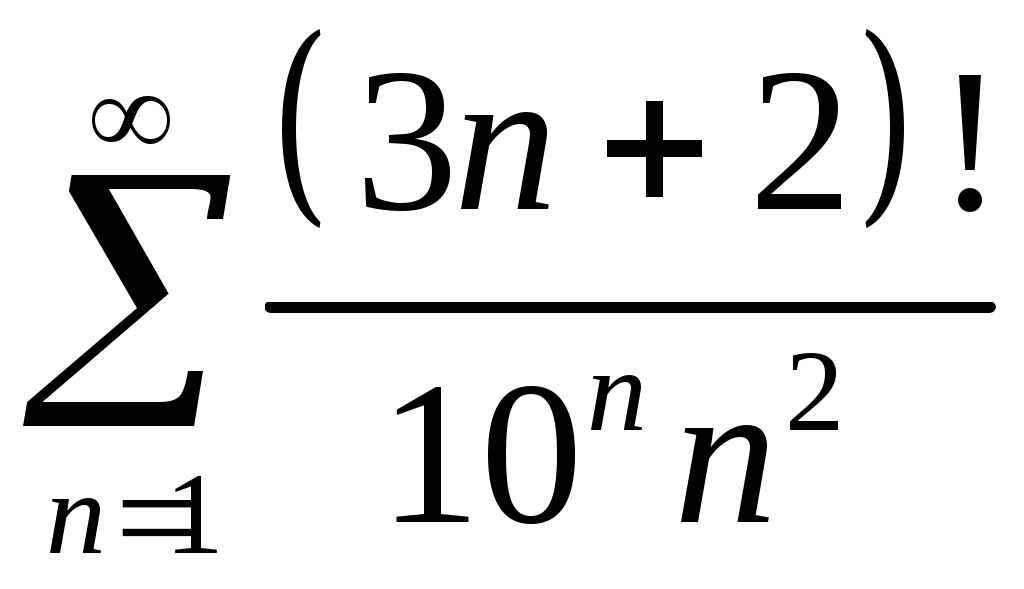 . 5.28. . 5.28. 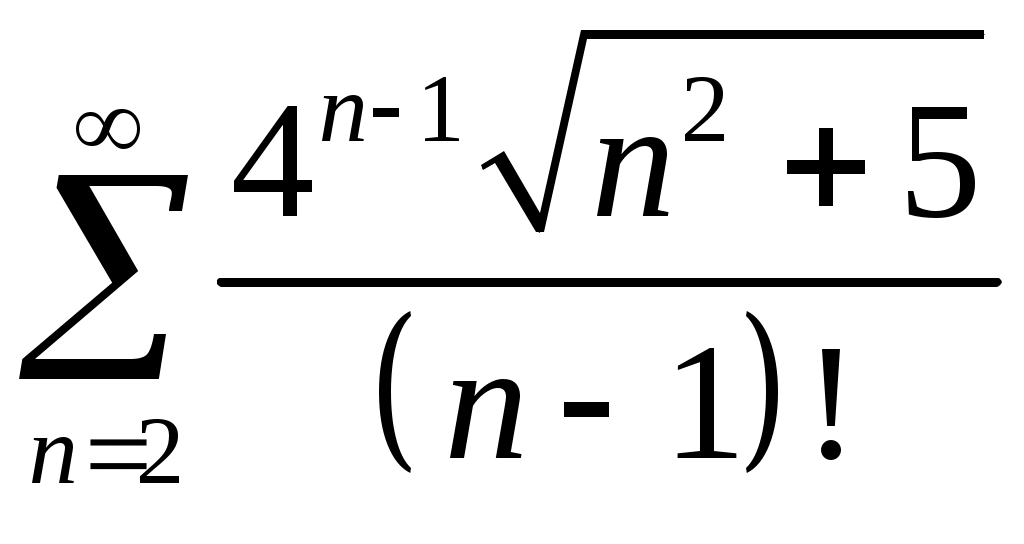 . .5.29. 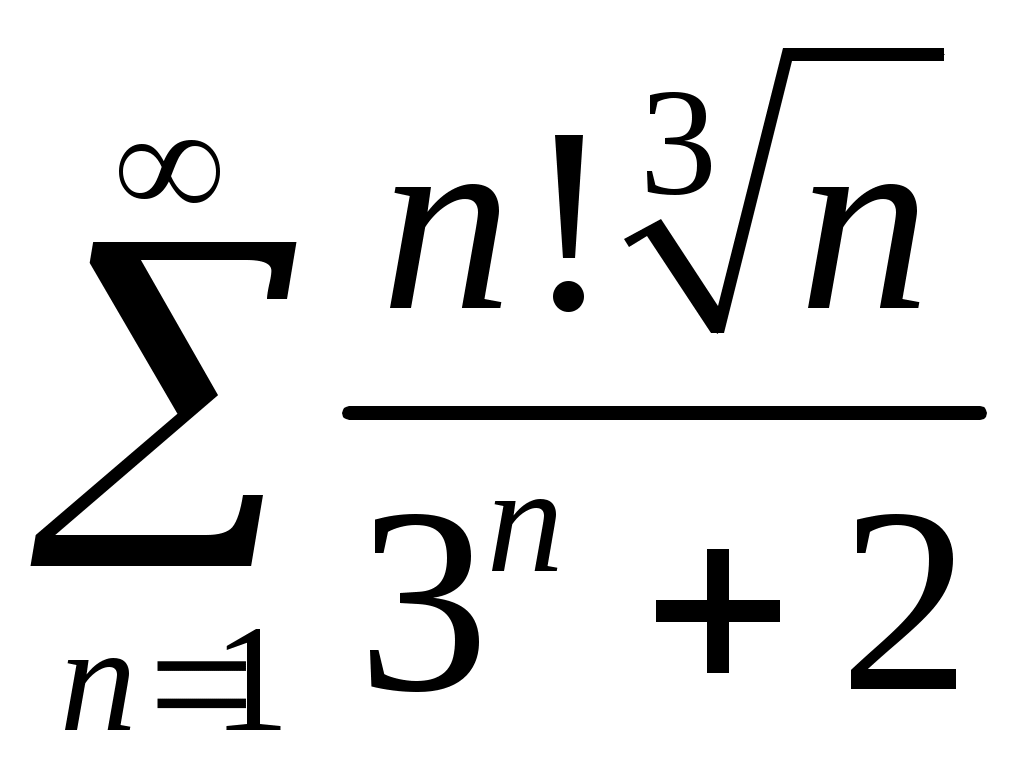 . 5.30. . 5.30. 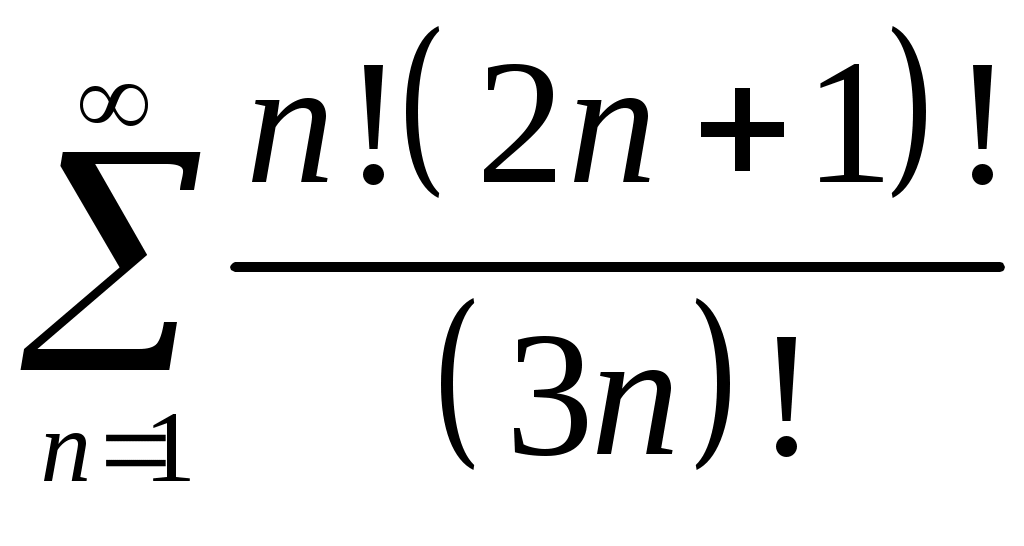 . .5.31. 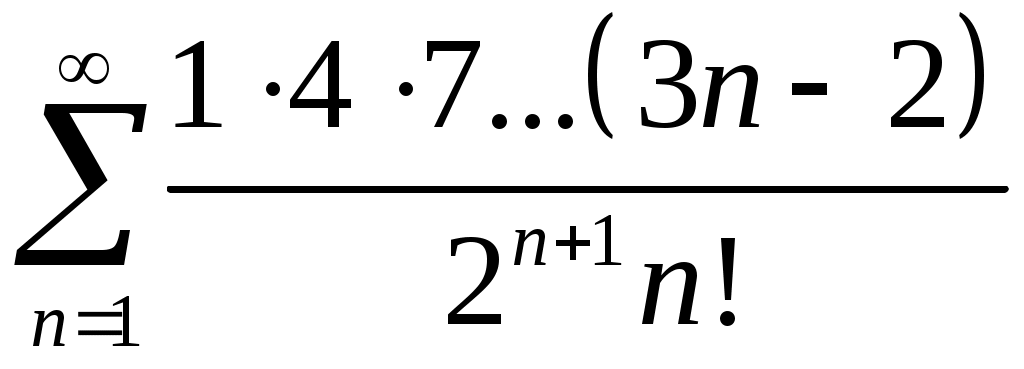 . .Задача 6. Исследовать на сходимость ряд. 6.1. 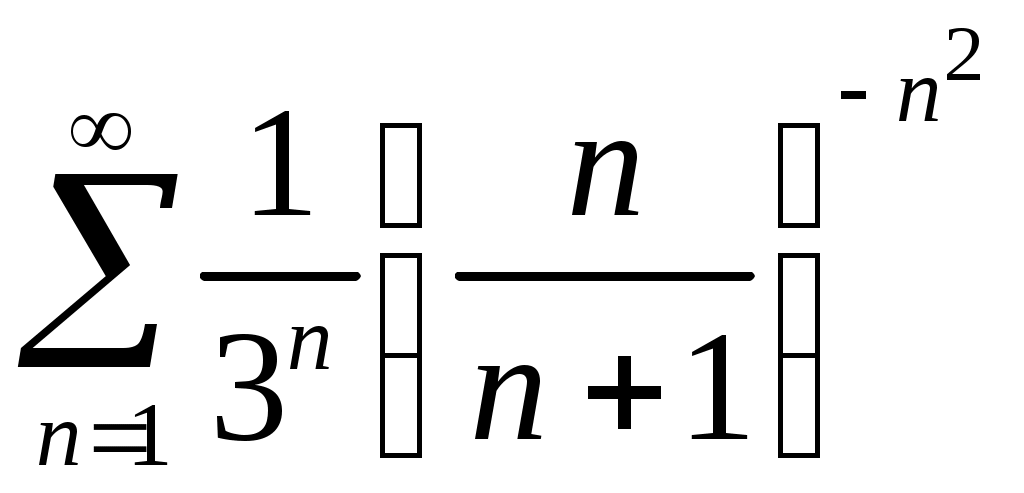 . 6.2. . 6.2. 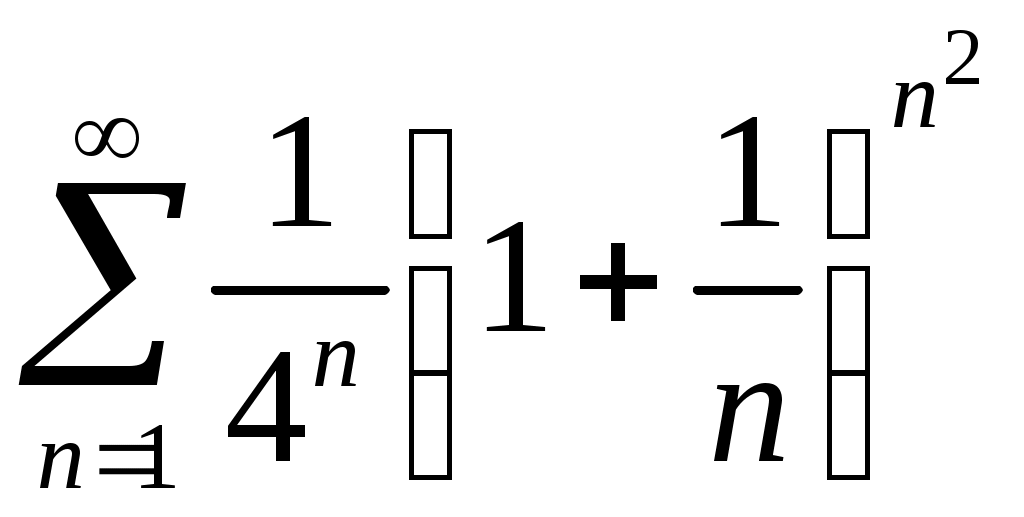 . .6.3. 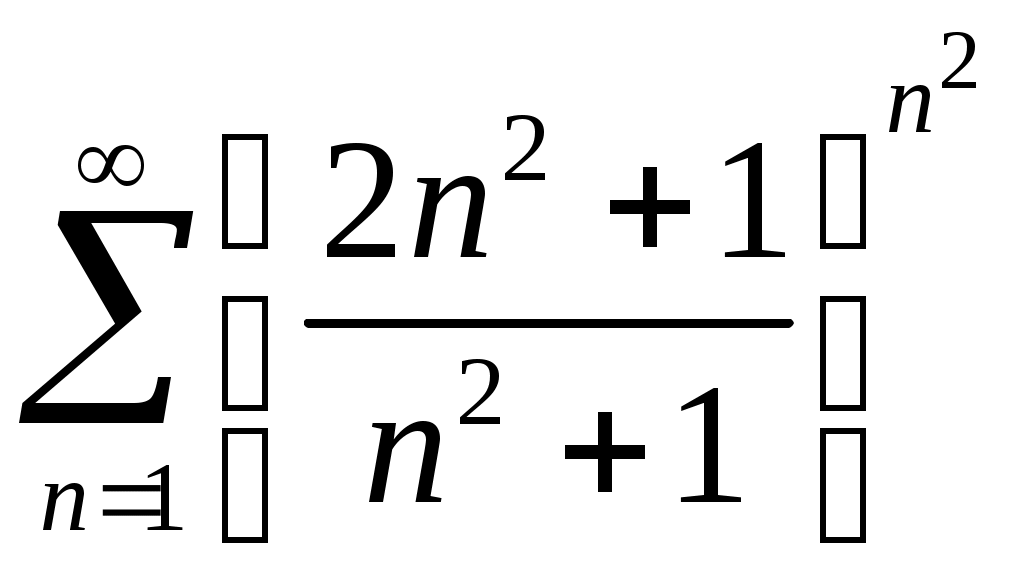 . 6.4. . 6.4. 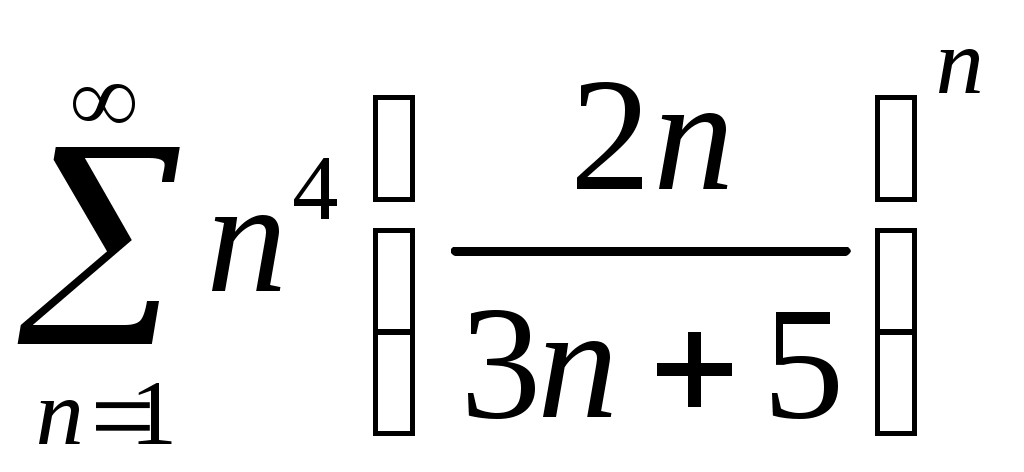 . .6.5. 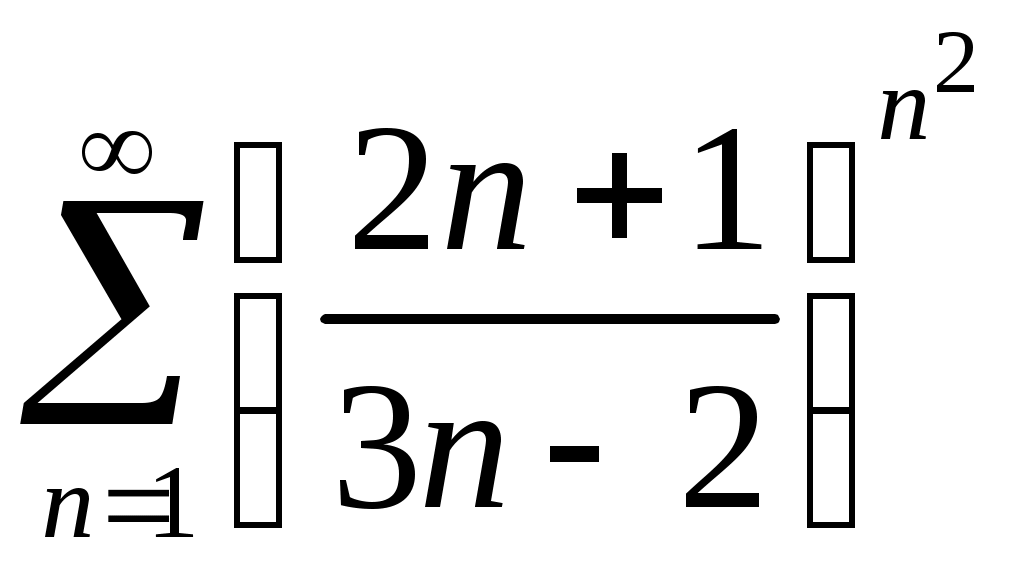 . 6.6. . 6.6. 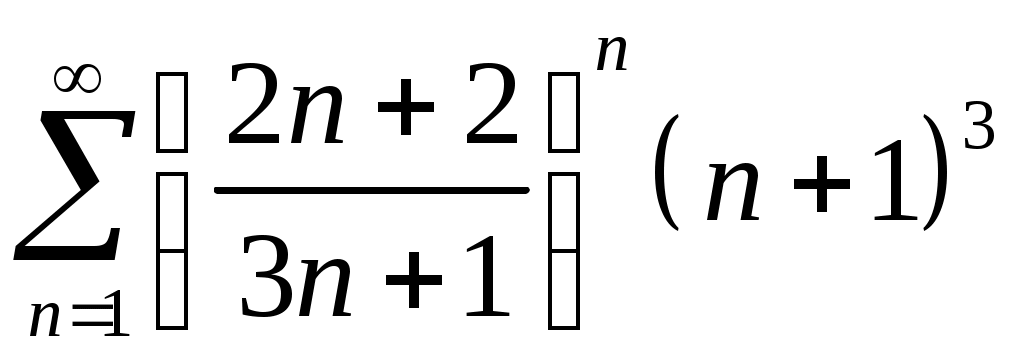 . .6.7. 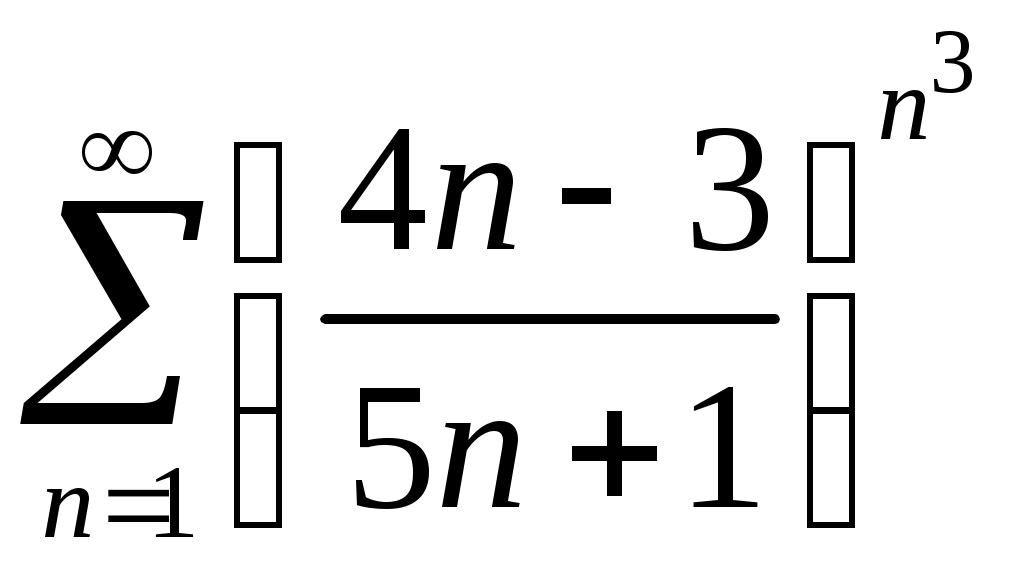 . 6.8. . 6.8. 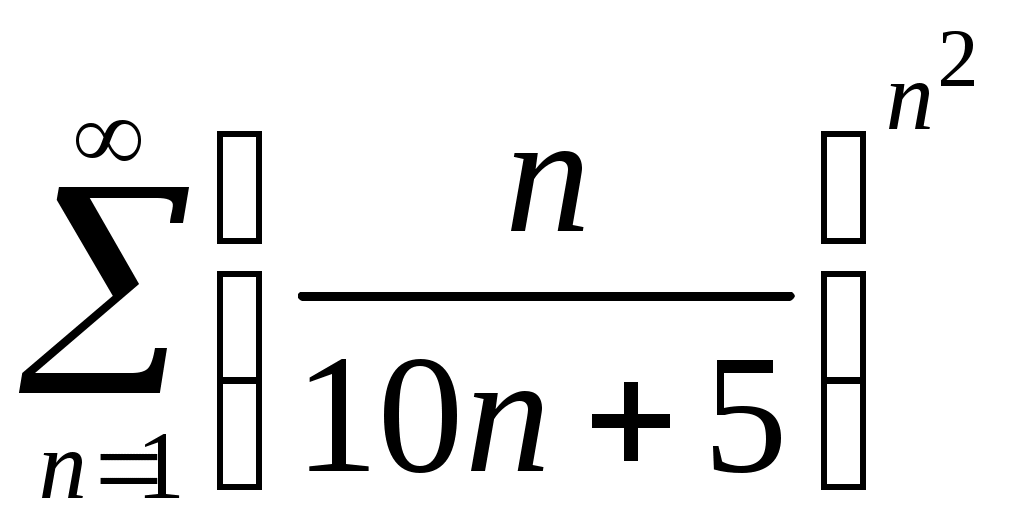 . .6.9.  . 6.10. . 6.10. 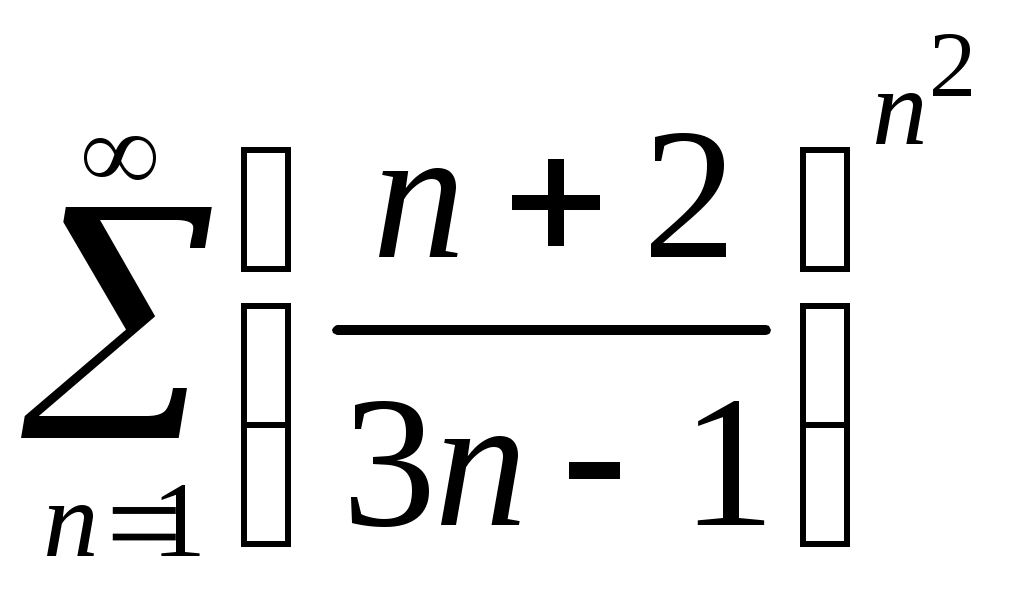 . .6.11. 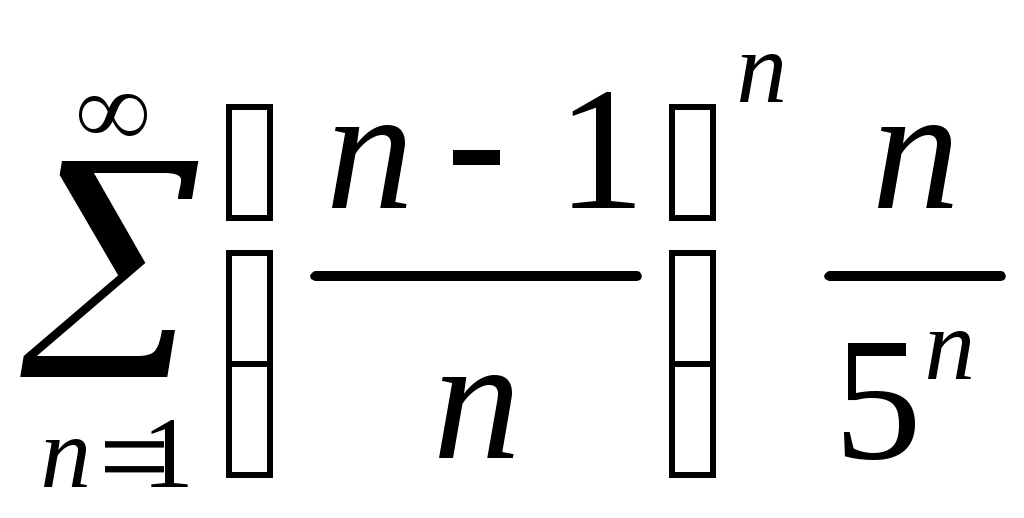 . 6.12. . 6.12. 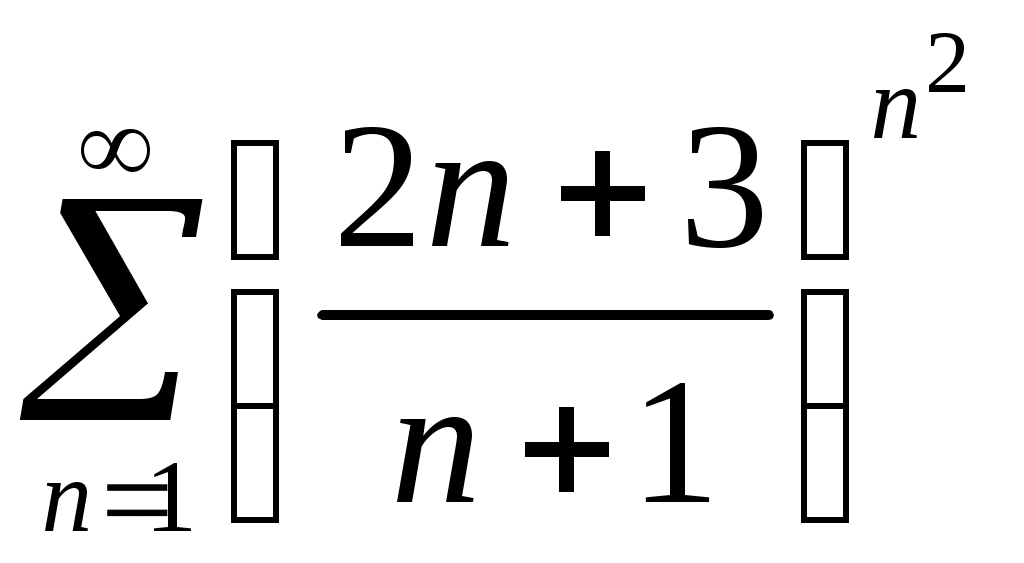 . .6.13. 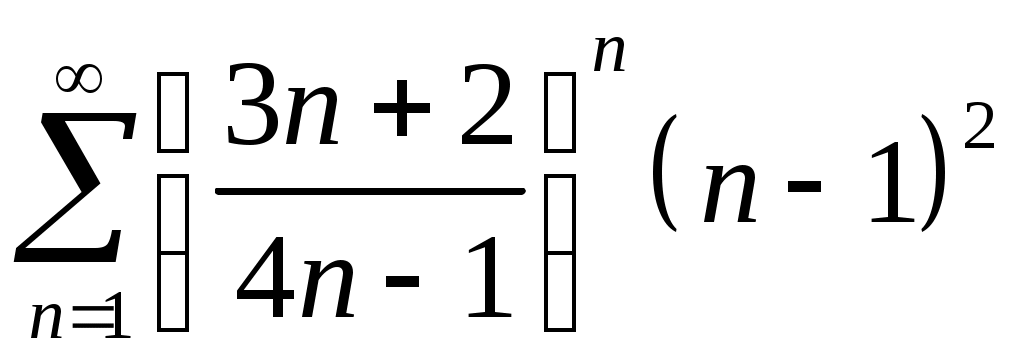 . 6.14. . 6.14. 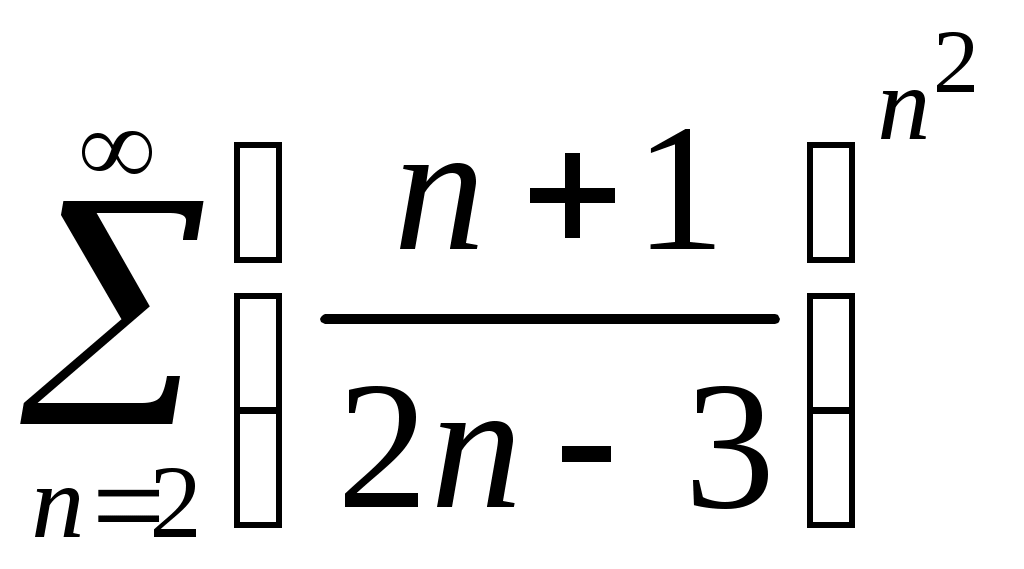 . .6.15. 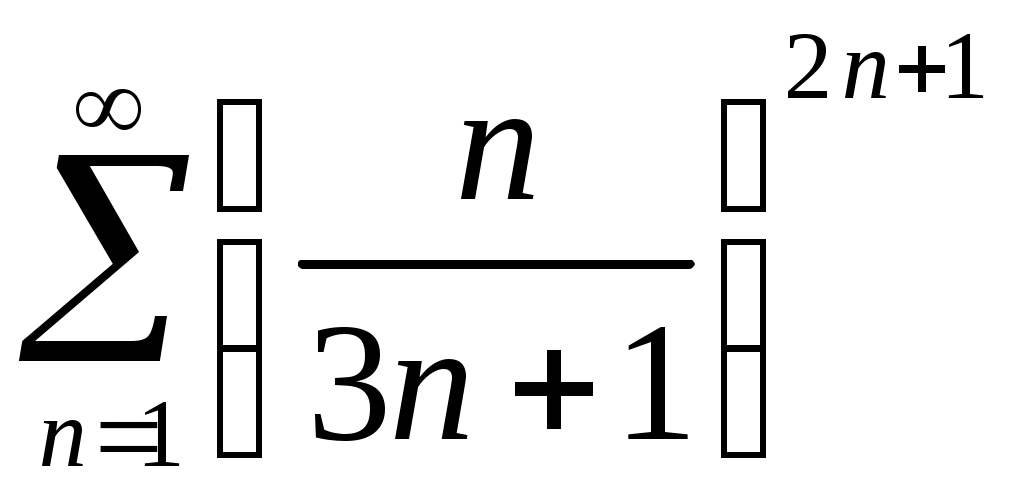 . 6.16. . 6.16. 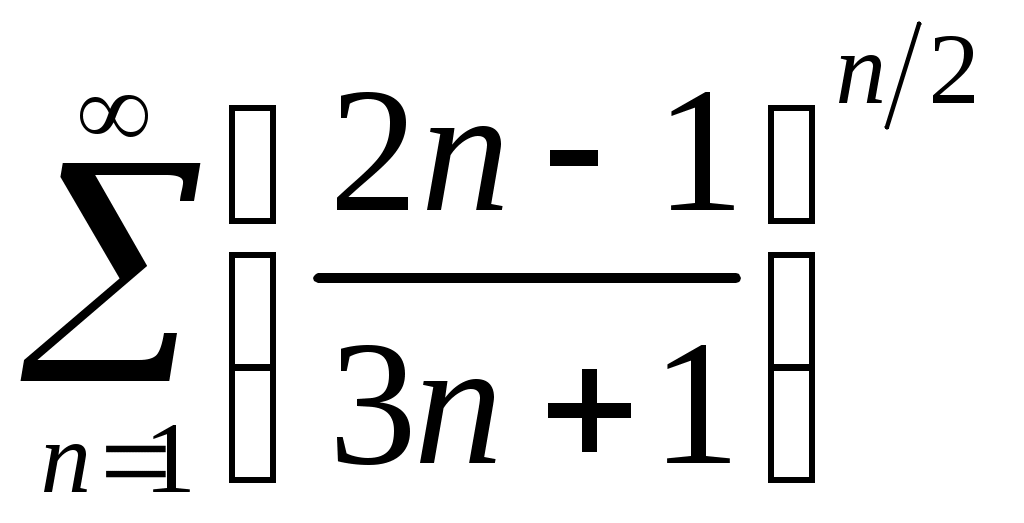 . .6.17. 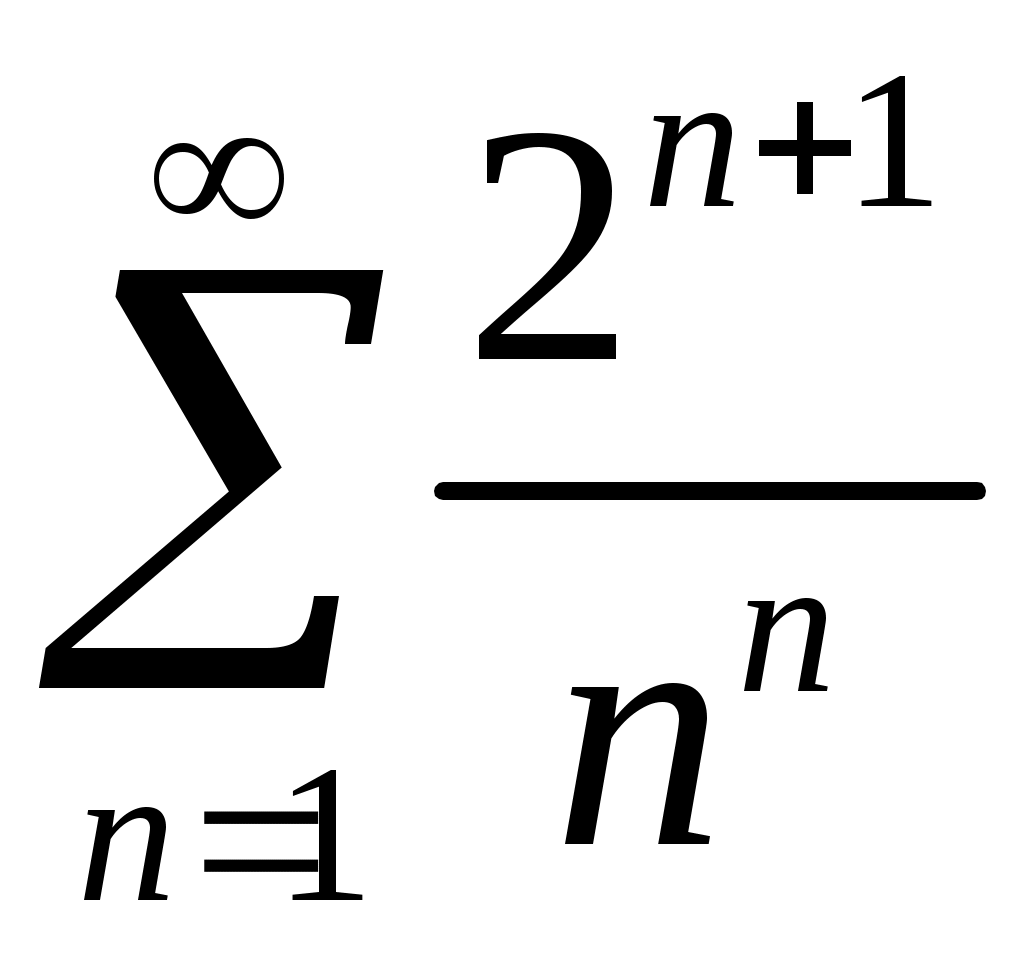 . 6.18. . 6.18. 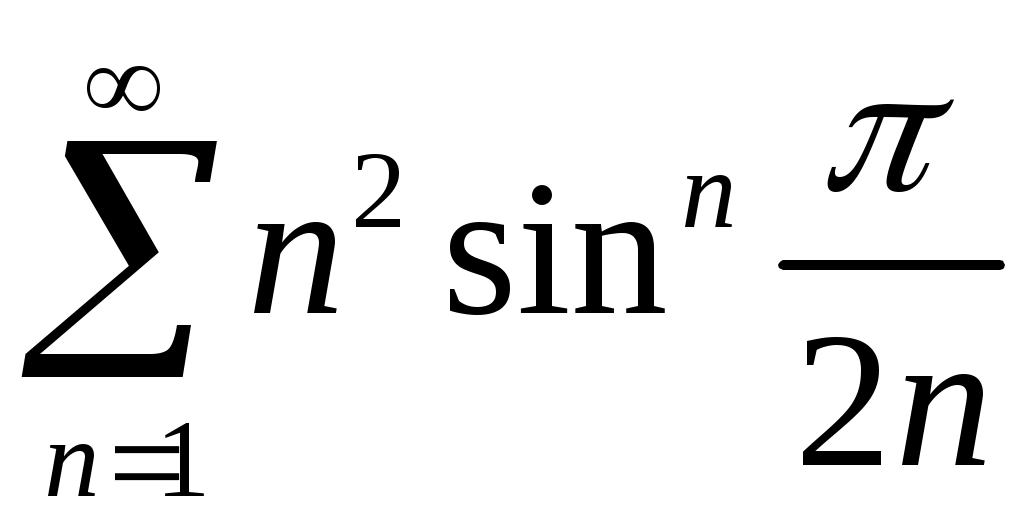 . .6.19. 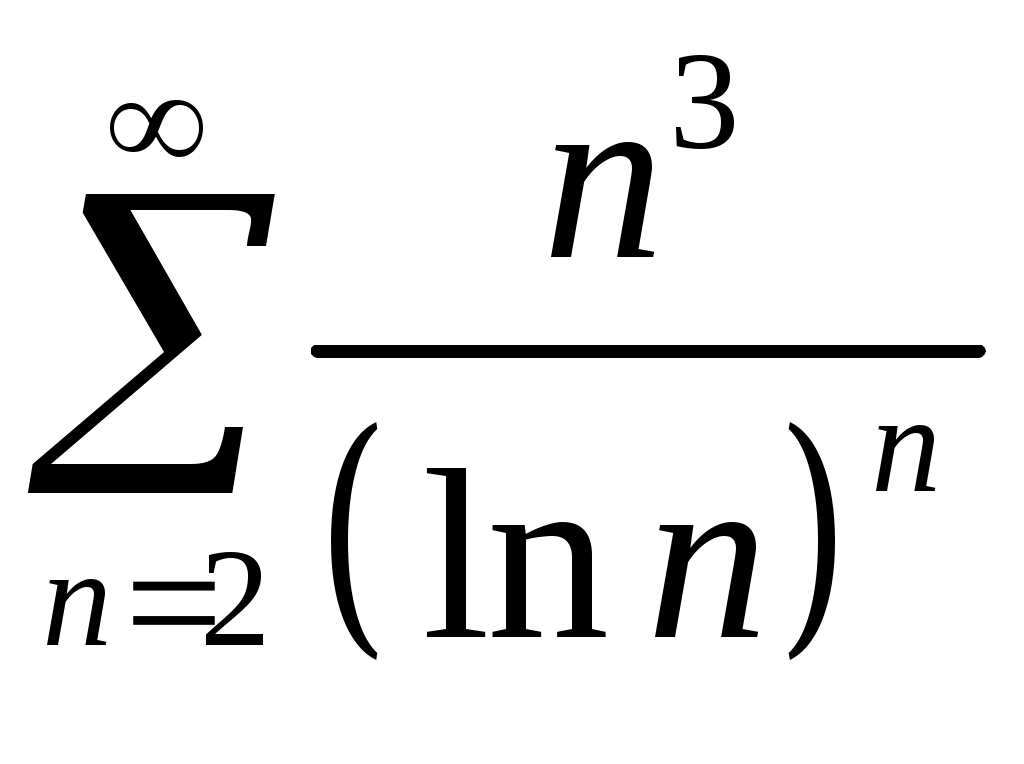 . 6.20. . 6.20. 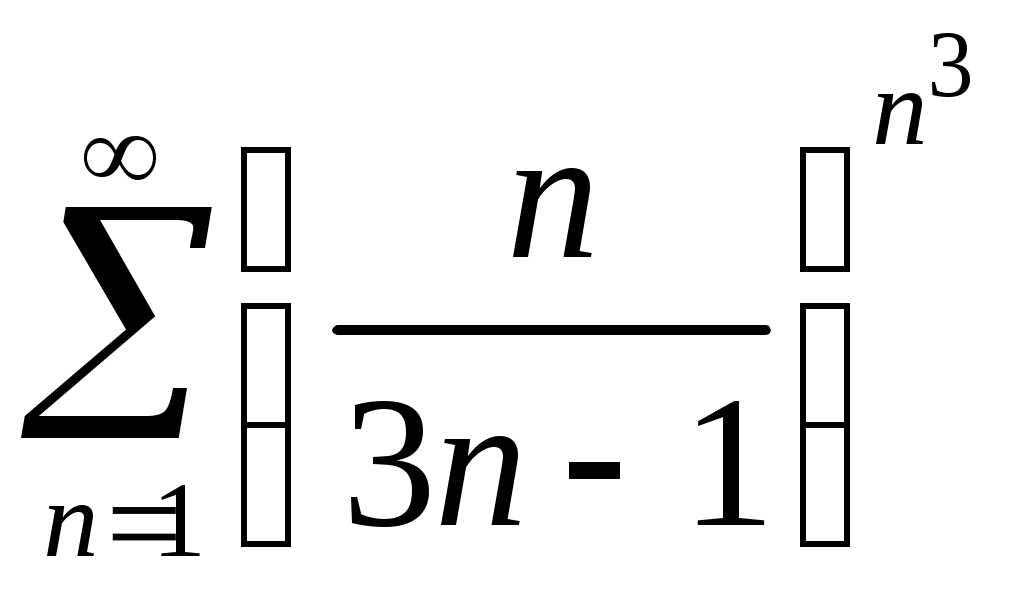 . .6.21. 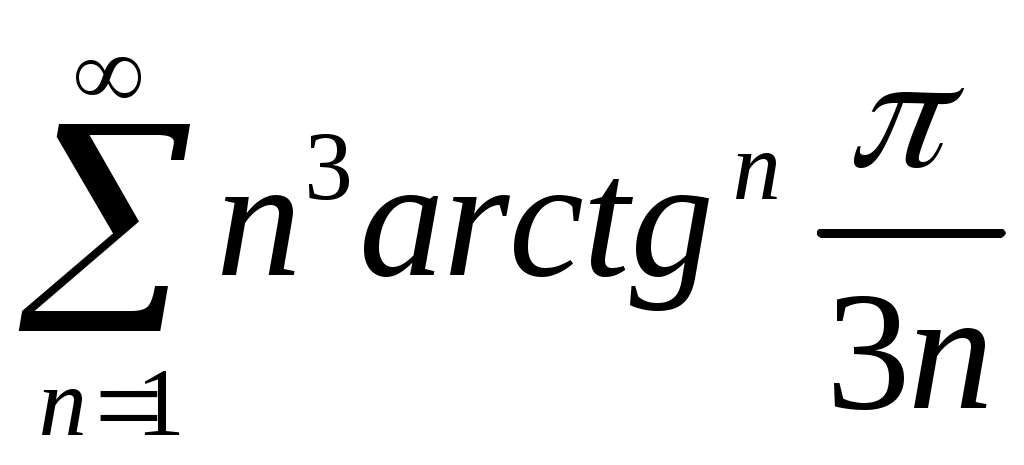 . 6.22. . 6.22. 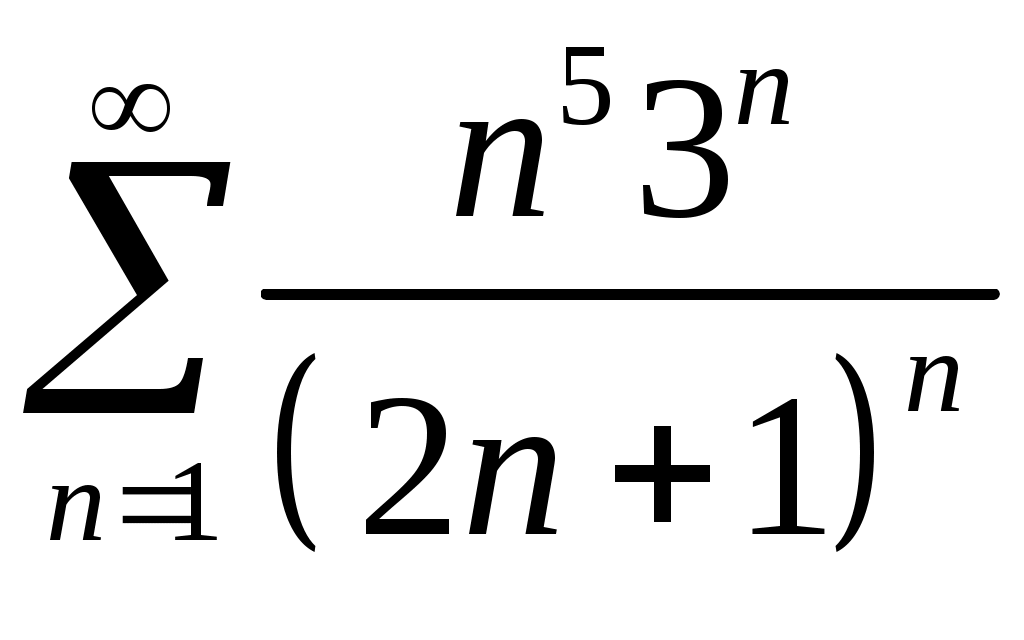 . .6.23. 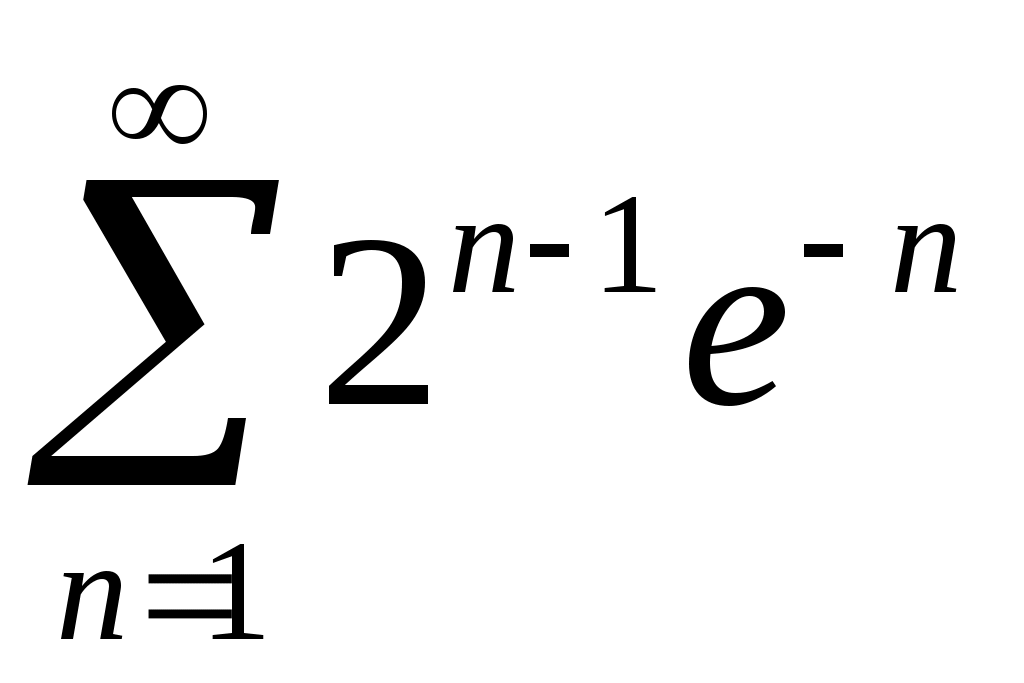 . 6.24. . 6.24. 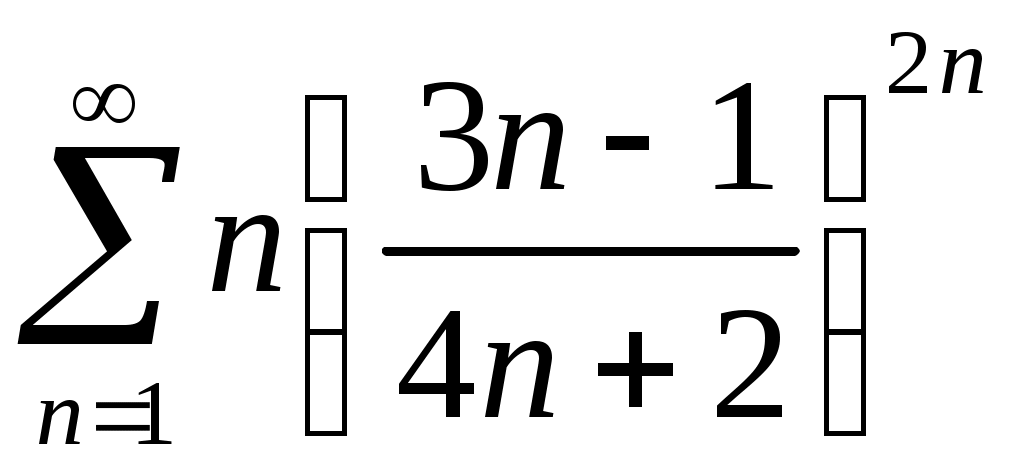 . . 6.25. 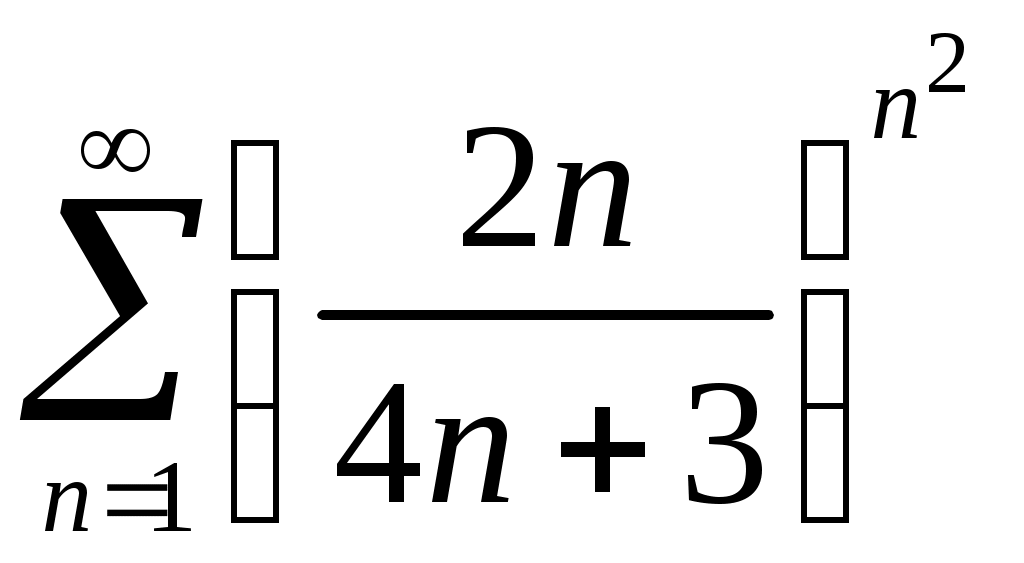 . 6.26. . 6.26. 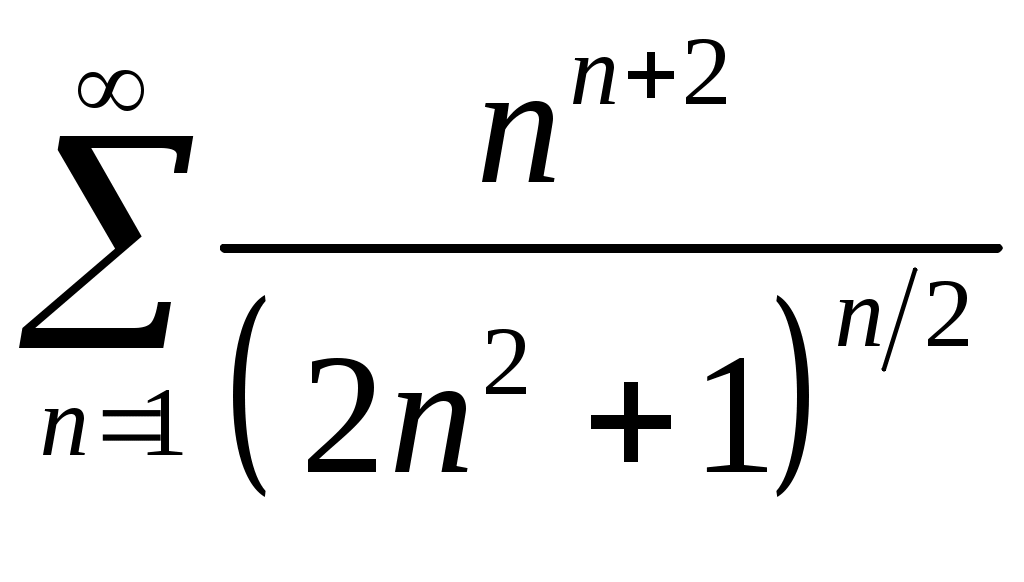 . .6.27. 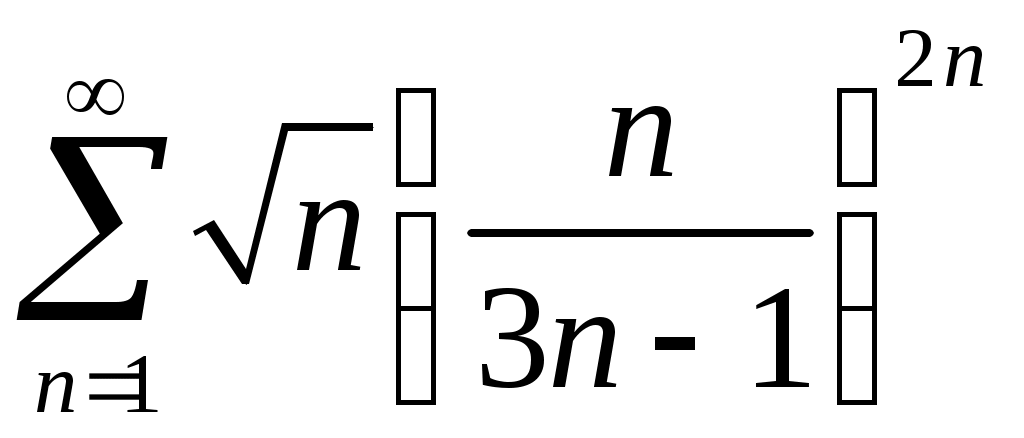 . 6.28. . 6.28. 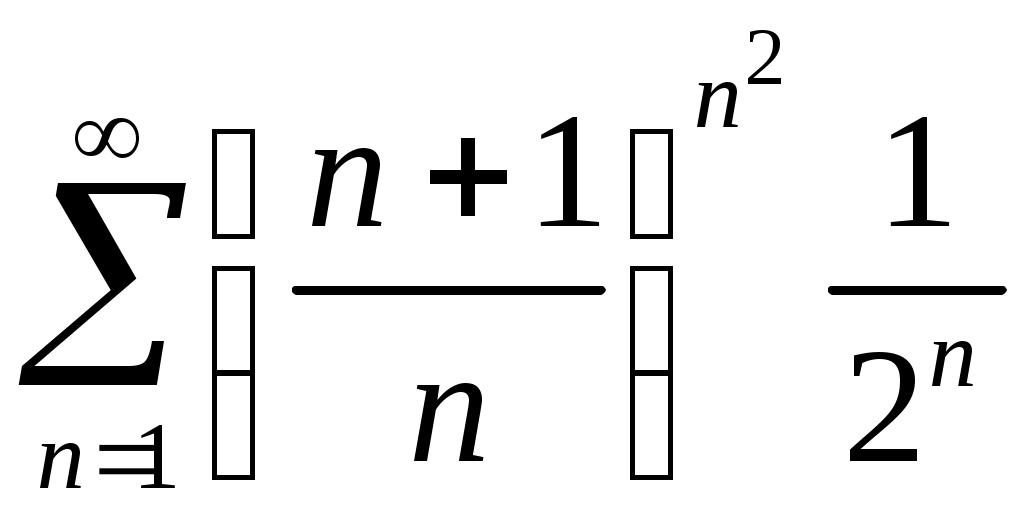 . .6.29. 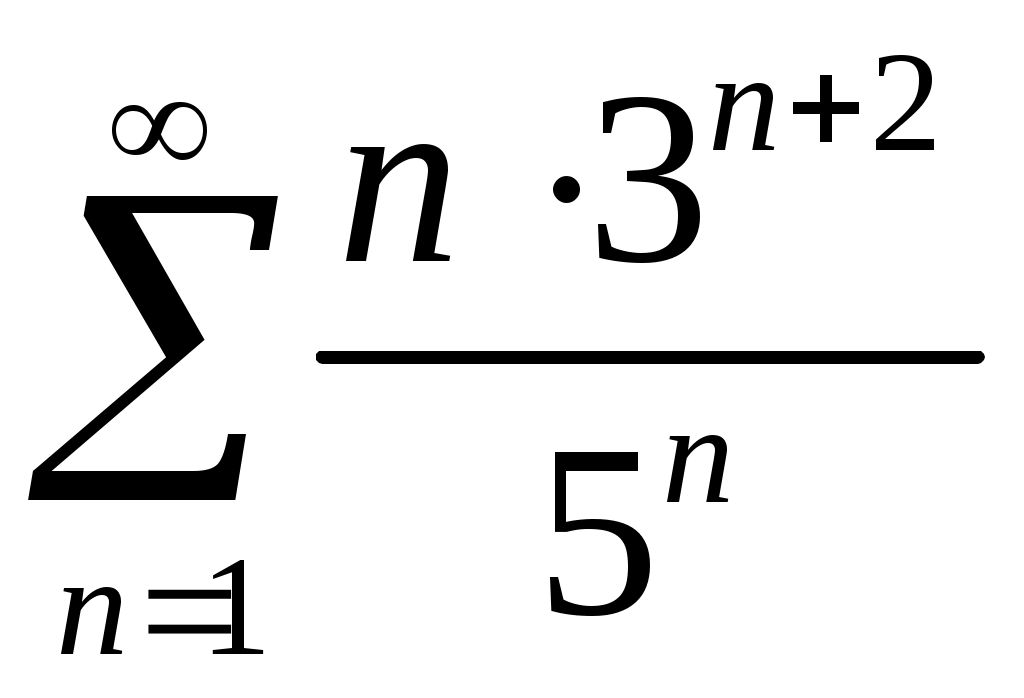 . 6.30. . 6.30. 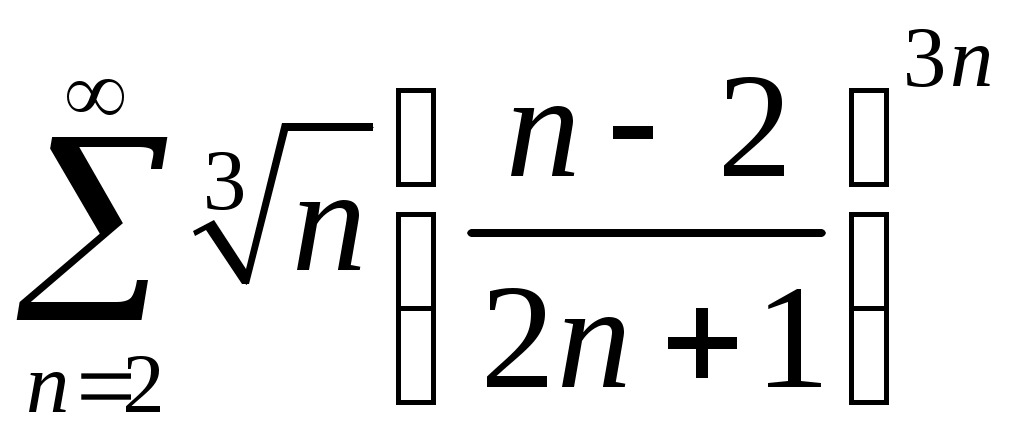 . .6.31. 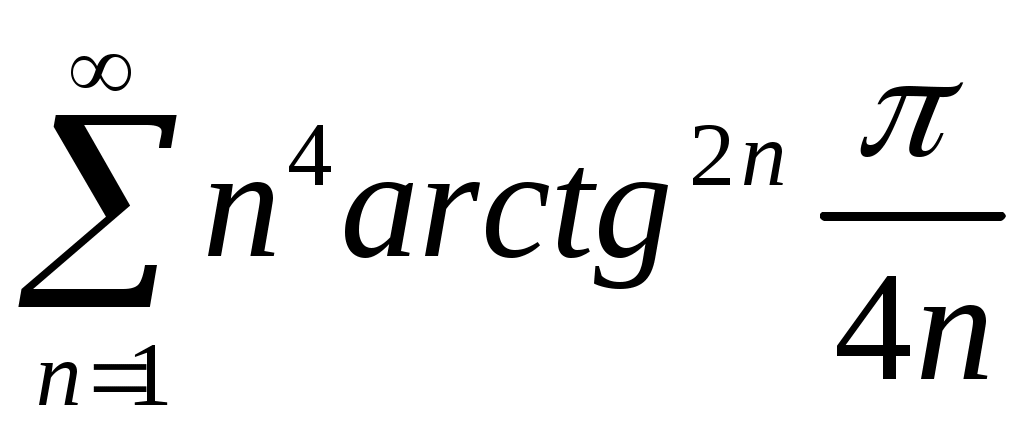 . .Задача 7. Исследовать на сходимость ряд. 7.1. 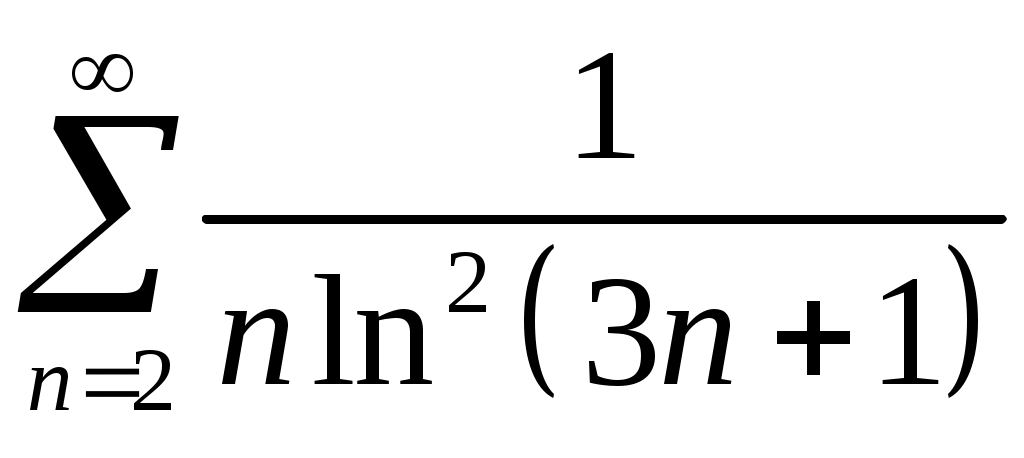 . 7.2. . 7.2. 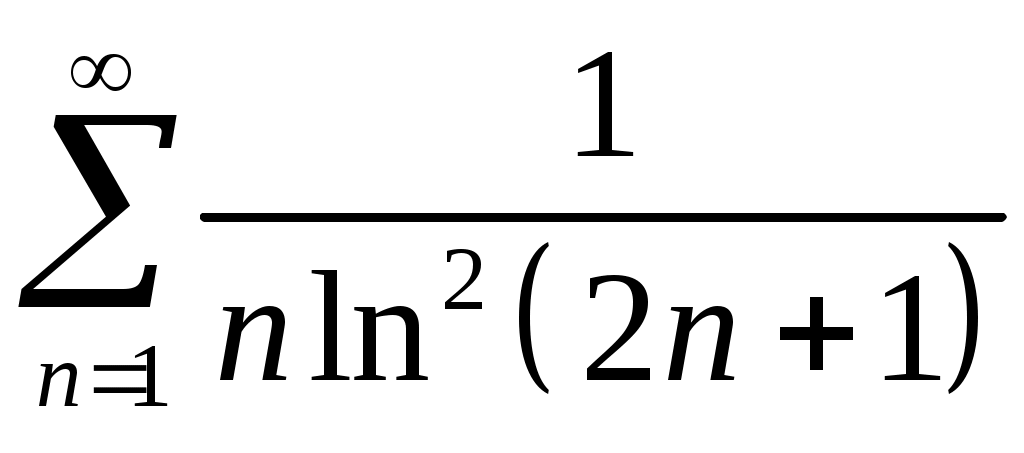 . .7.3. 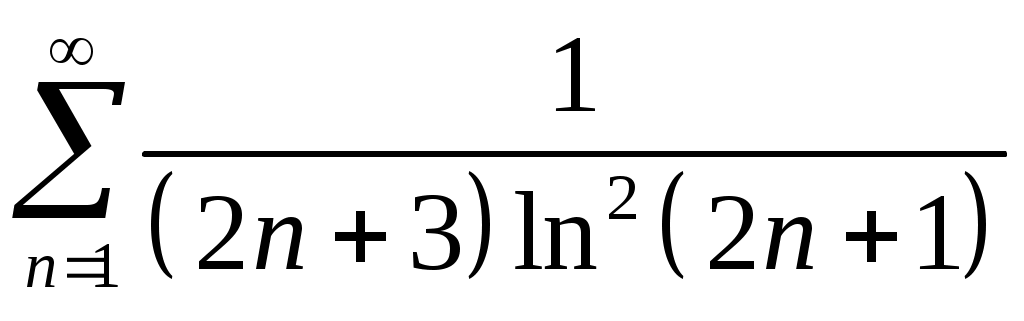 . 7.4. . 7.4. 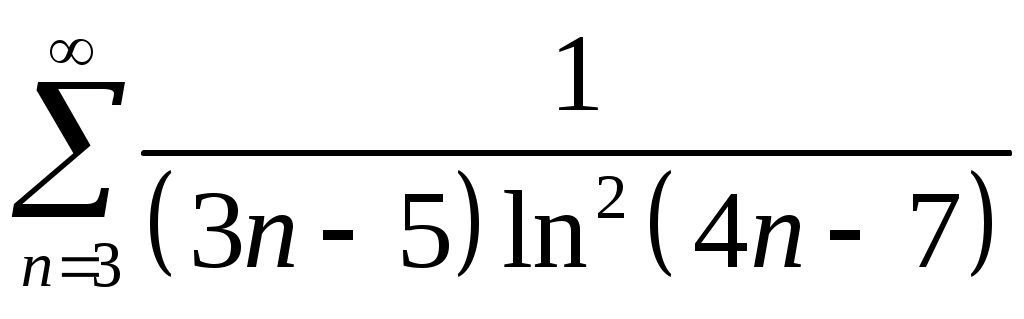 . .7.5. 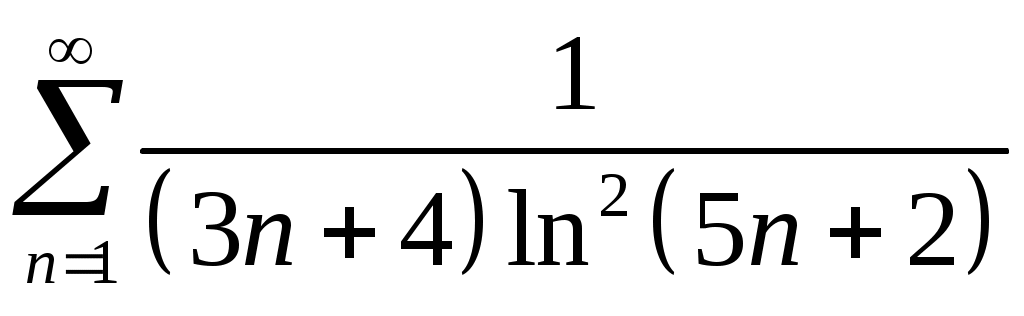 . 7.6. . 7.6. 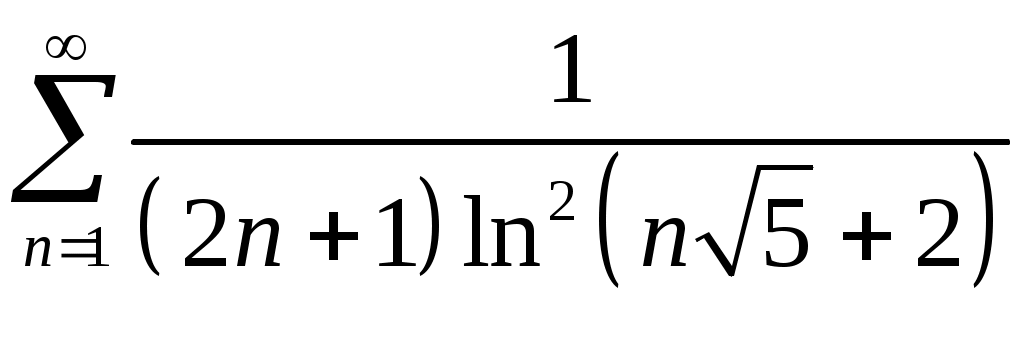 . .7.7. 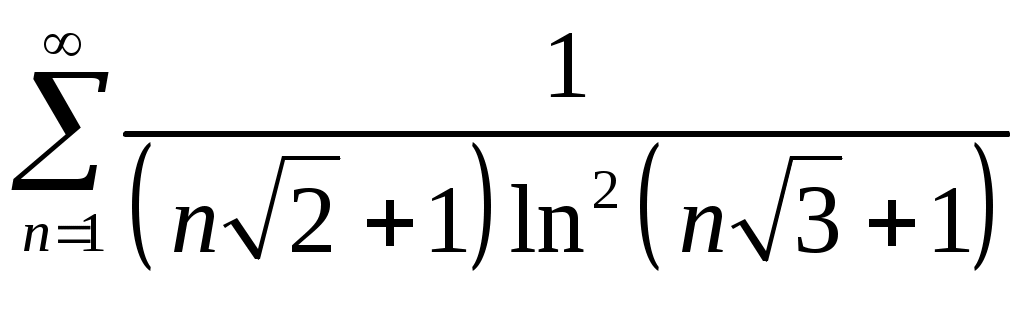 . 7.8. . 7.8. 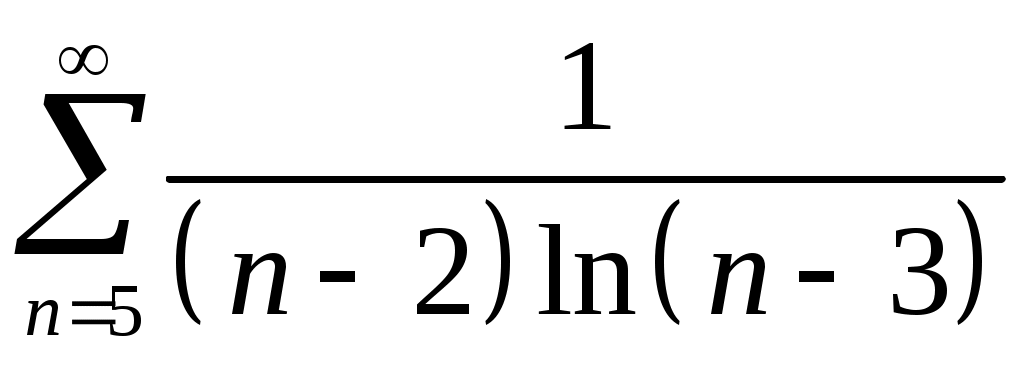 . .7.9. 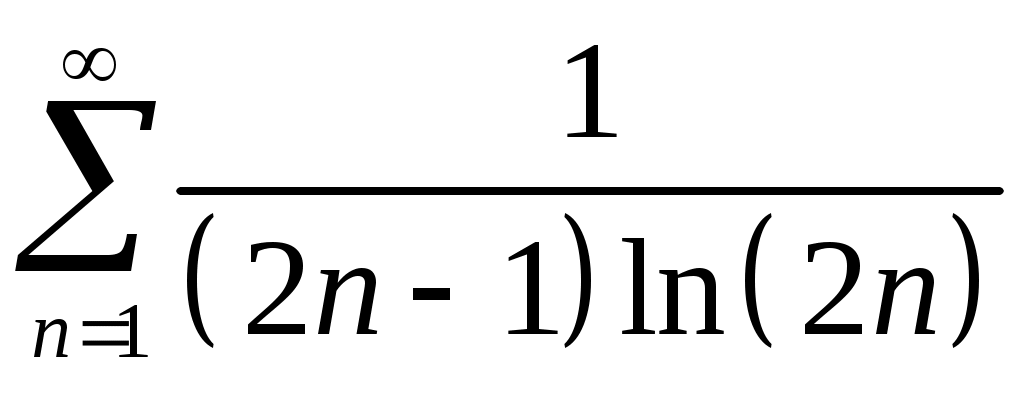 . 7.10. . 7.10. 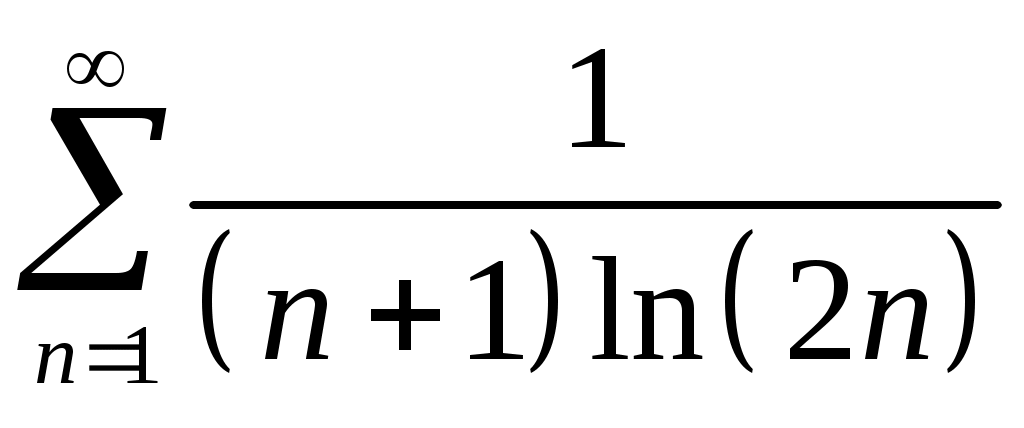 . .7.11. 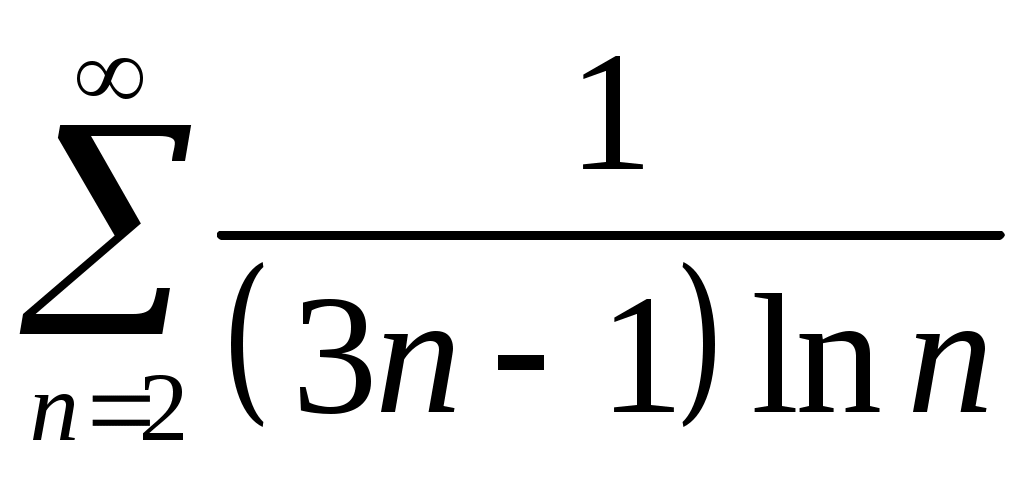 . 7.12. . 7.12. 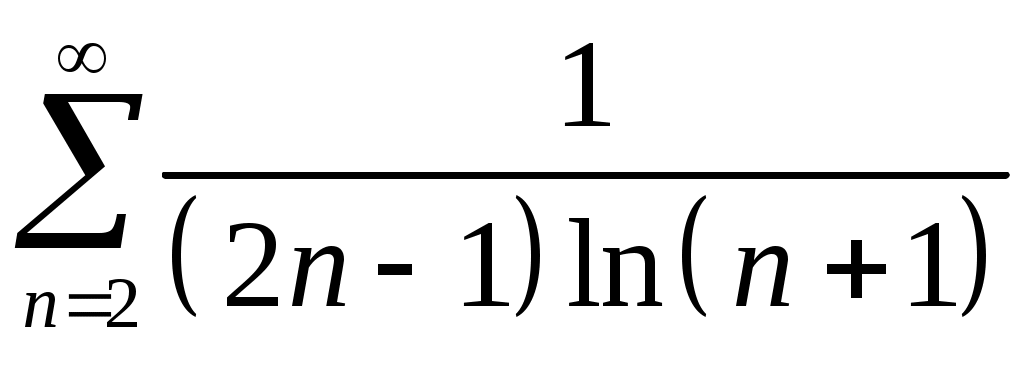 . .7.13. 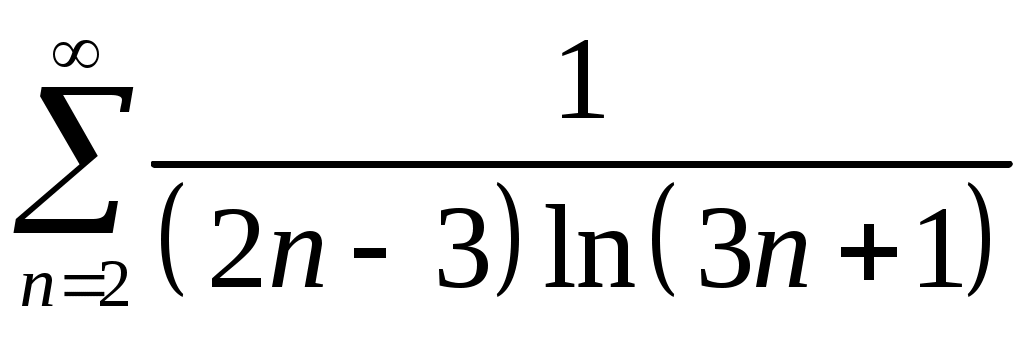 . 7.14. . 7.14. 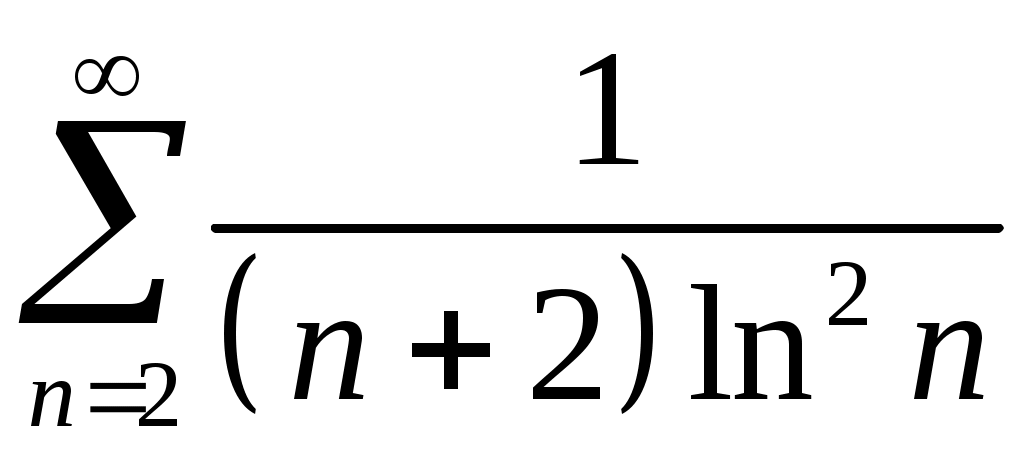 . .7.15. 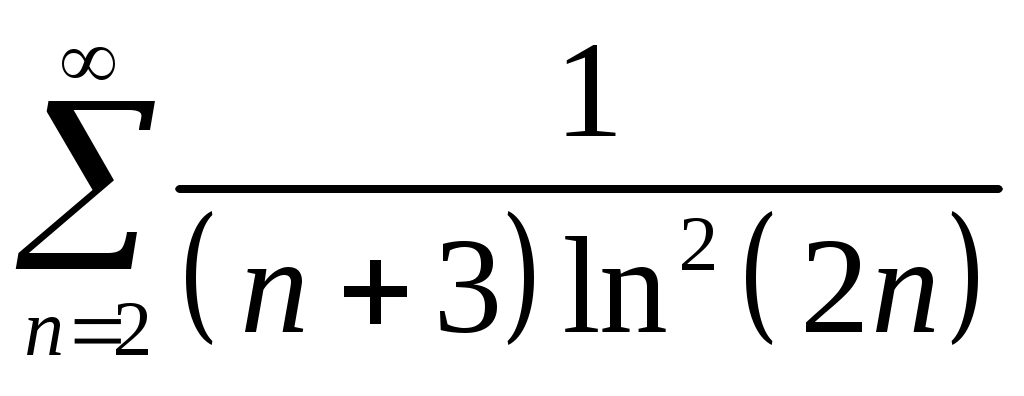 . 7.16. . 7.16. 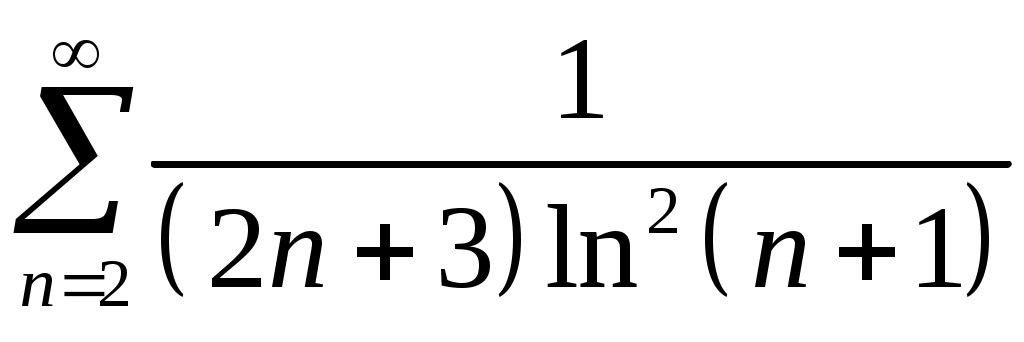 . .7.17. 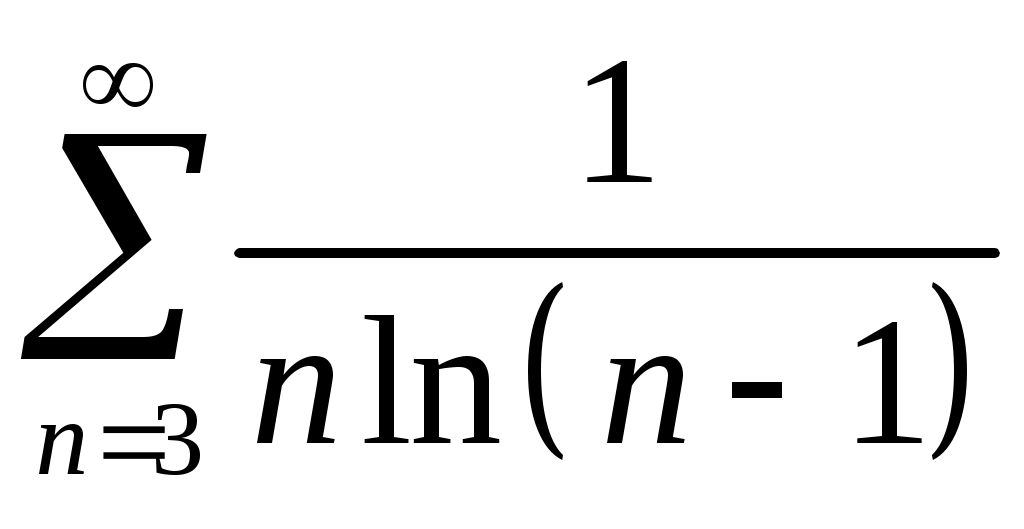 . 7.18. . 7.18. 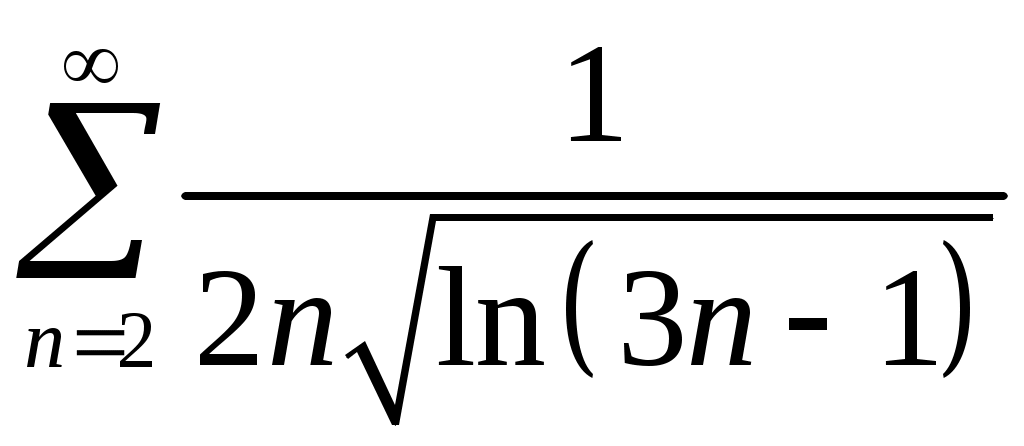 . .7.19. 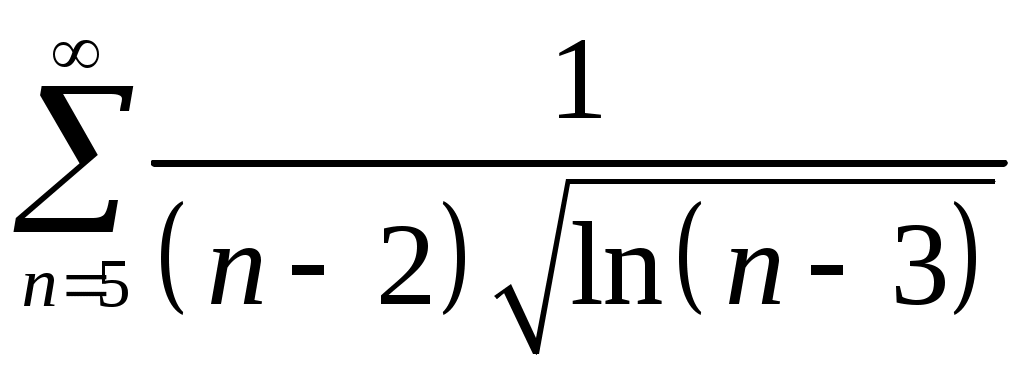 . 7.20. . 7.20. 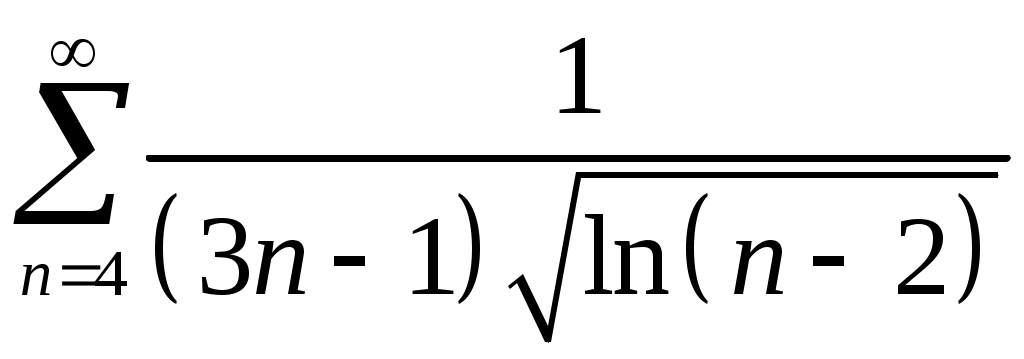 . .7.21. 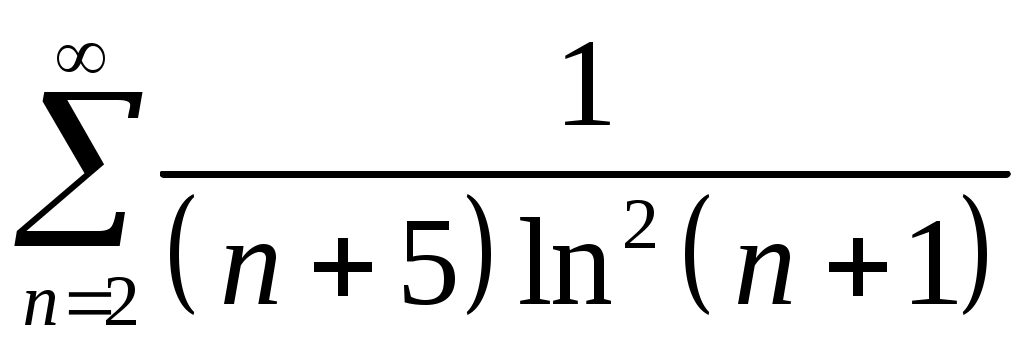 . 7.22. . 7.22. 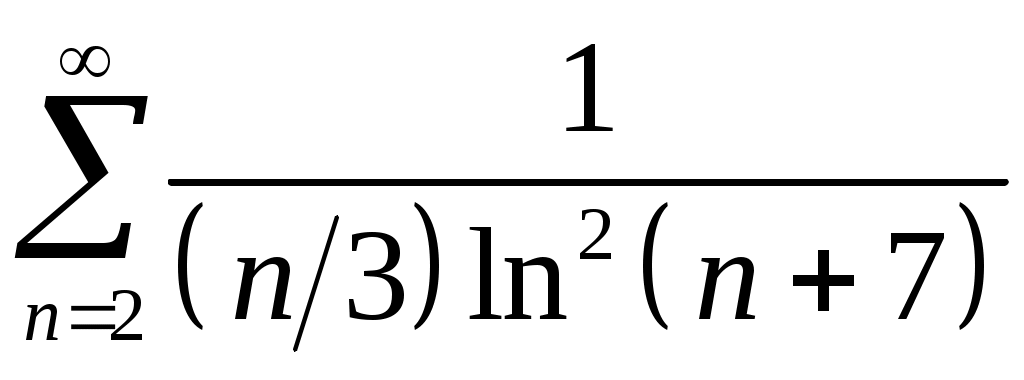 . .7.23. 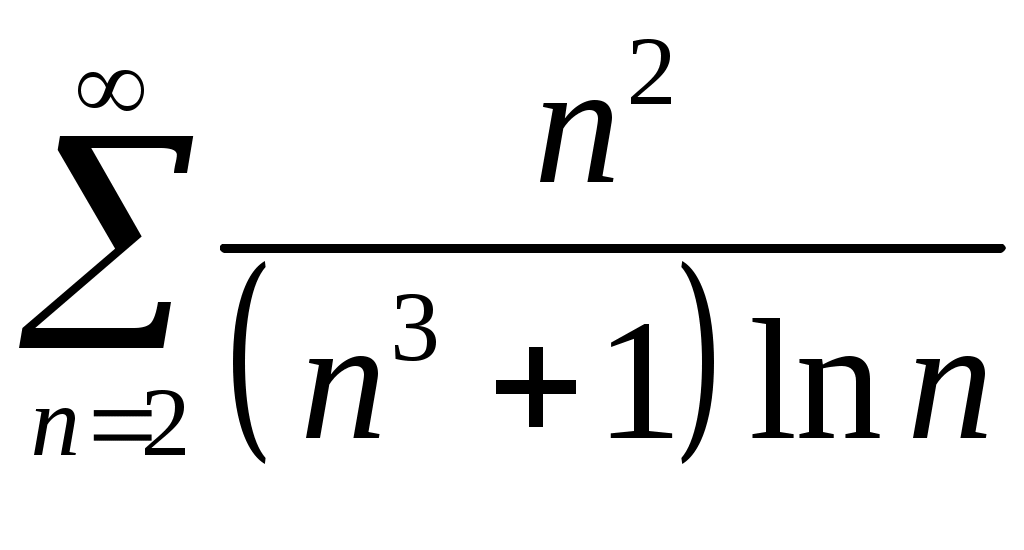 . 7.24. . 7.24. 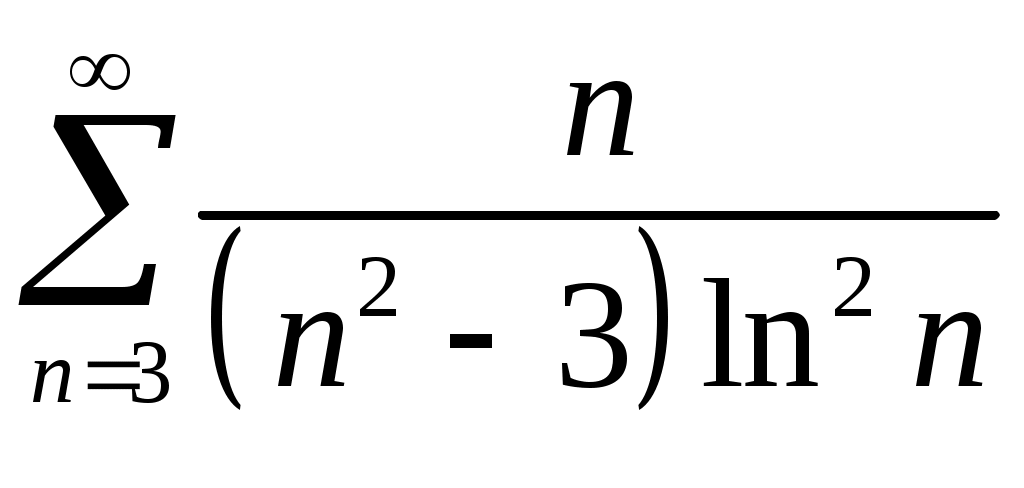 . .7.25. 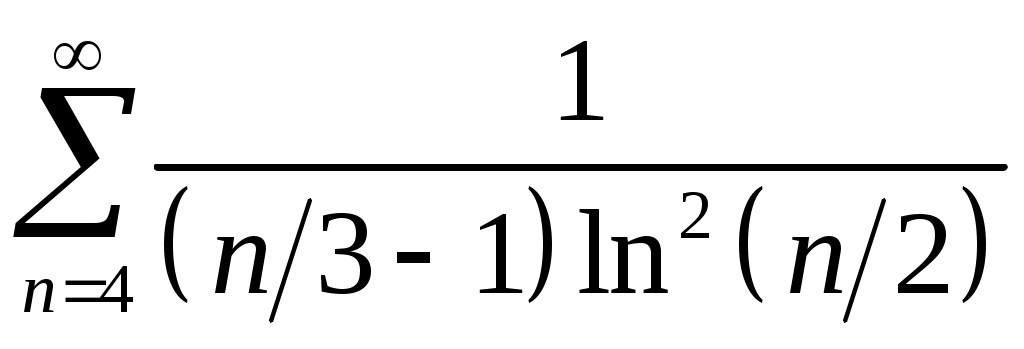 . 7.26. . 7.26. 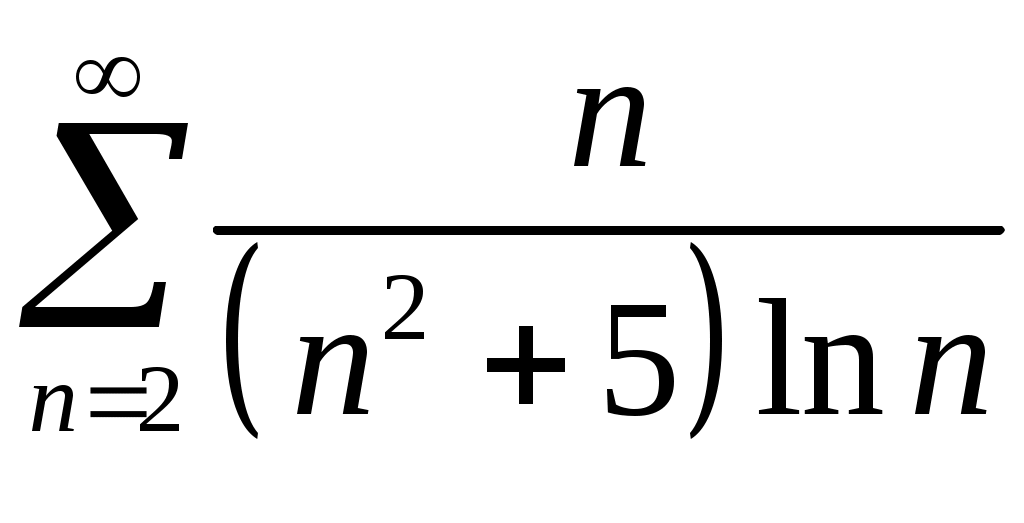 . .7.27. 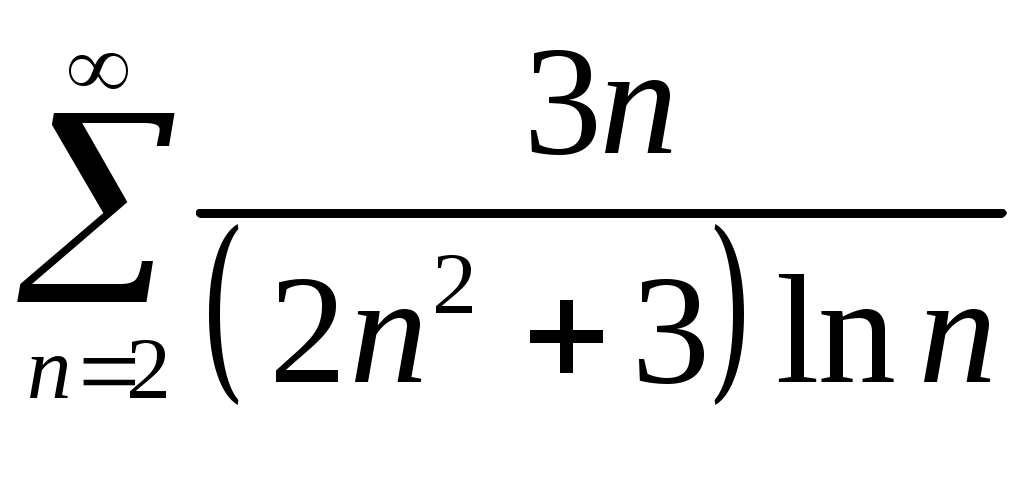 . 7.28. . 7.28. 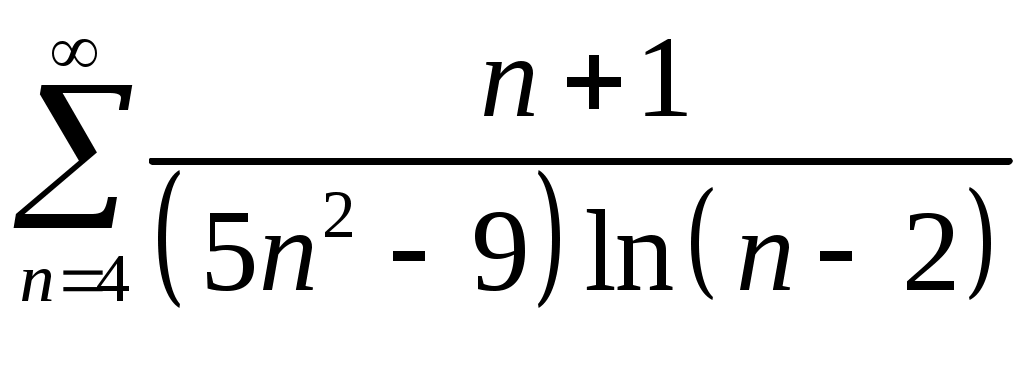 . .7.29. 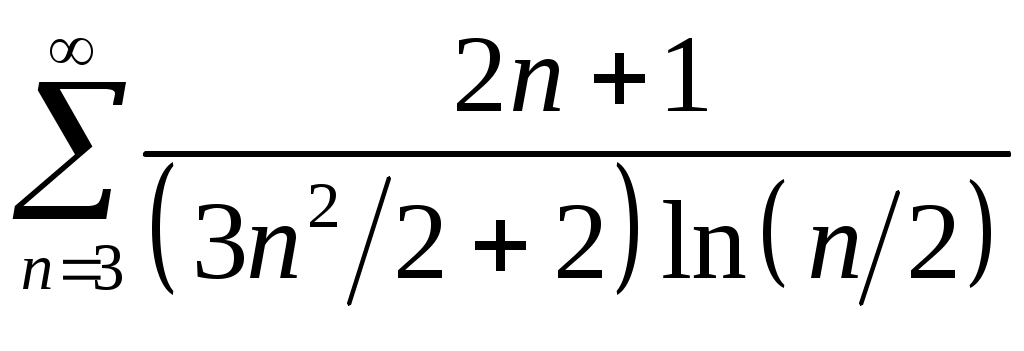 . 7.30. . 7.30. 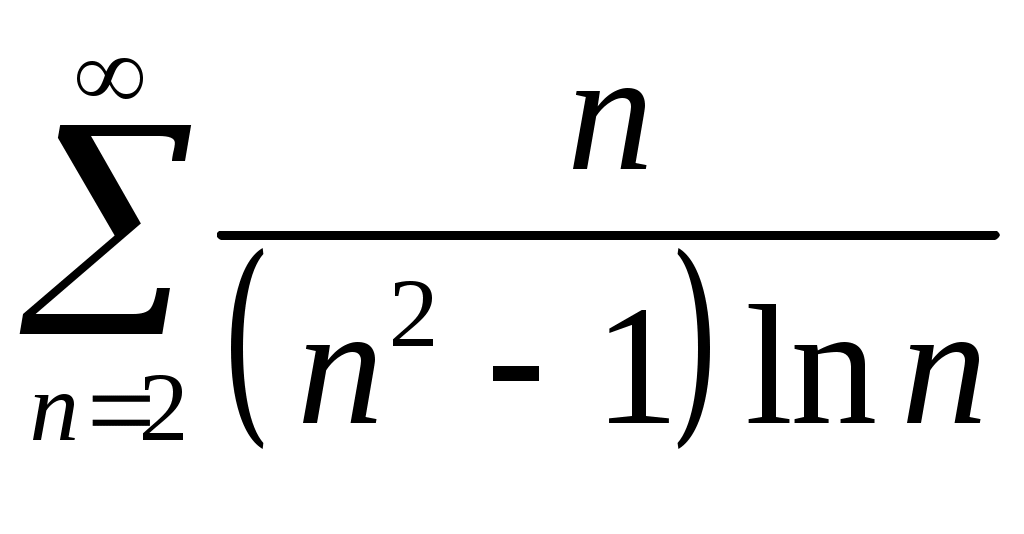 . .7.31. 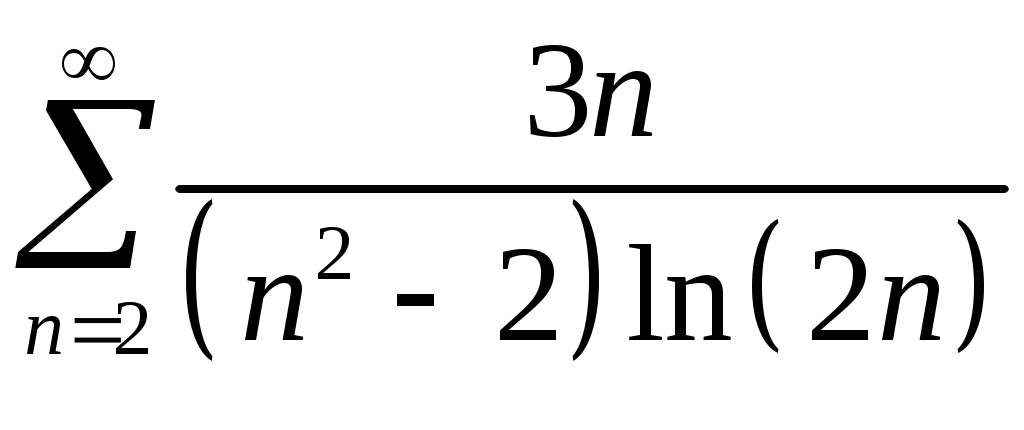 . .Задача 8. Исследовать на сходимость ряд. 8.1. 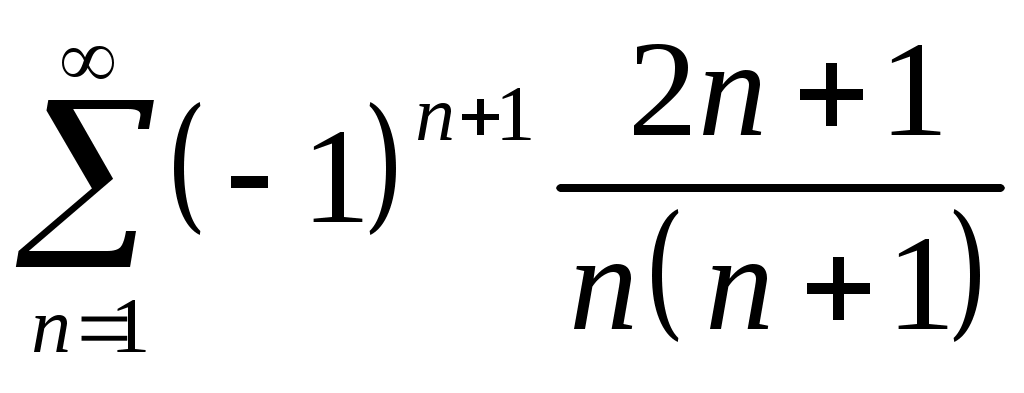 . 8.2. . 8.2. 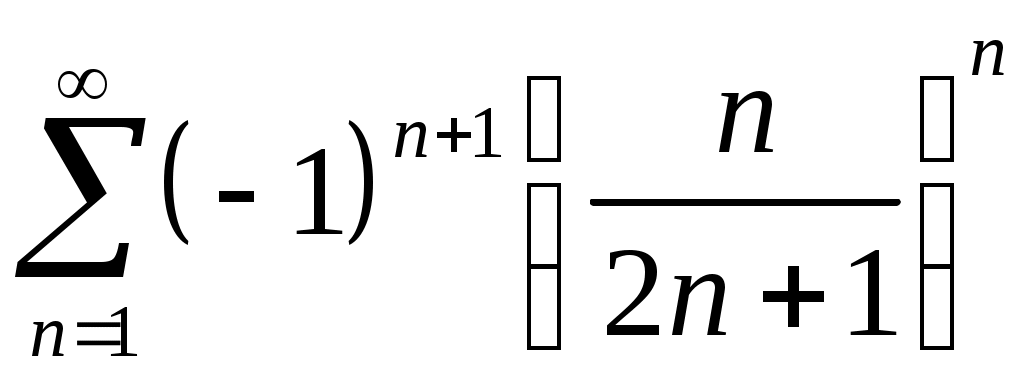 . .8.3. 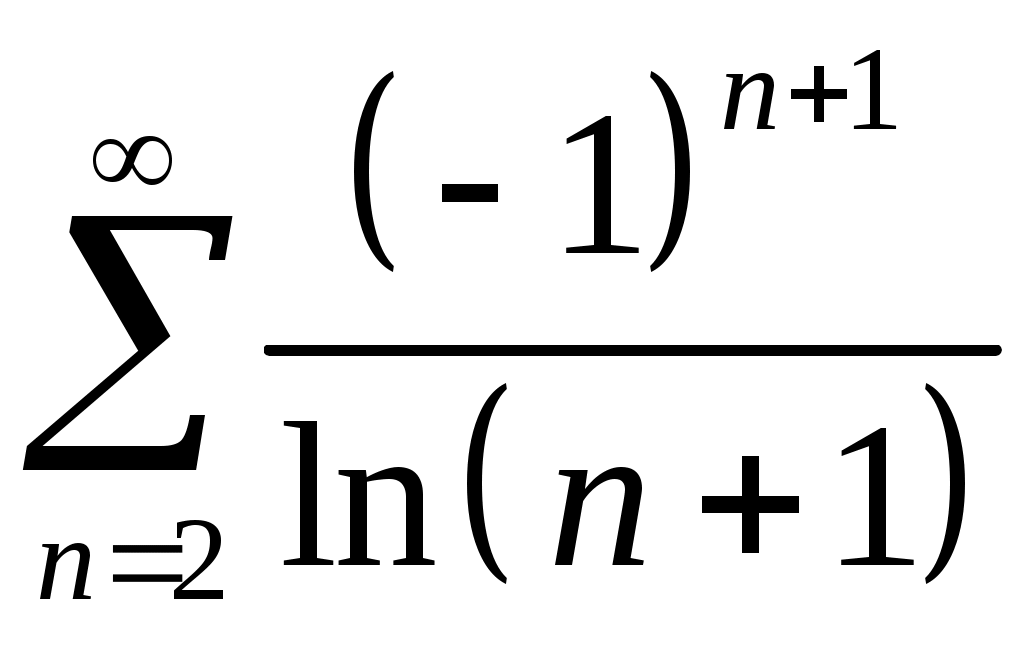 . 8.4. . 8.4. 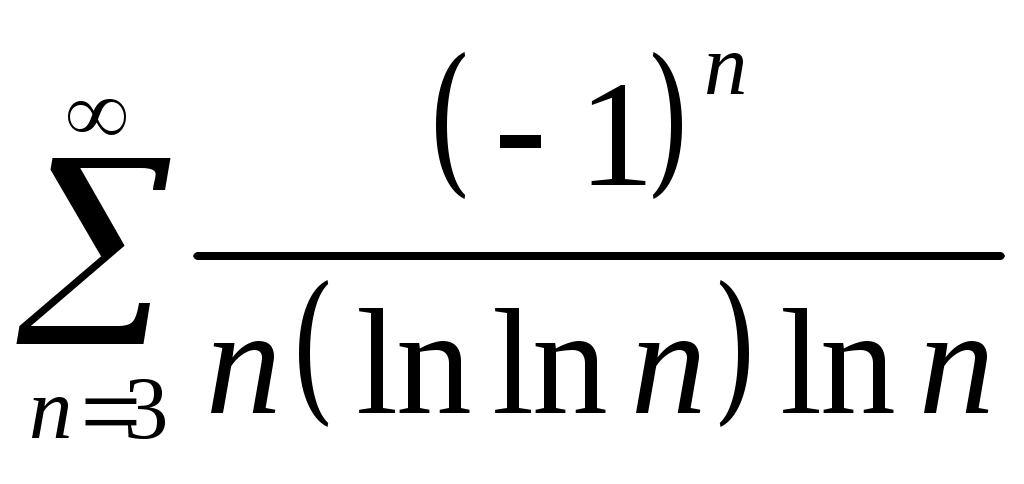 . .8.5. 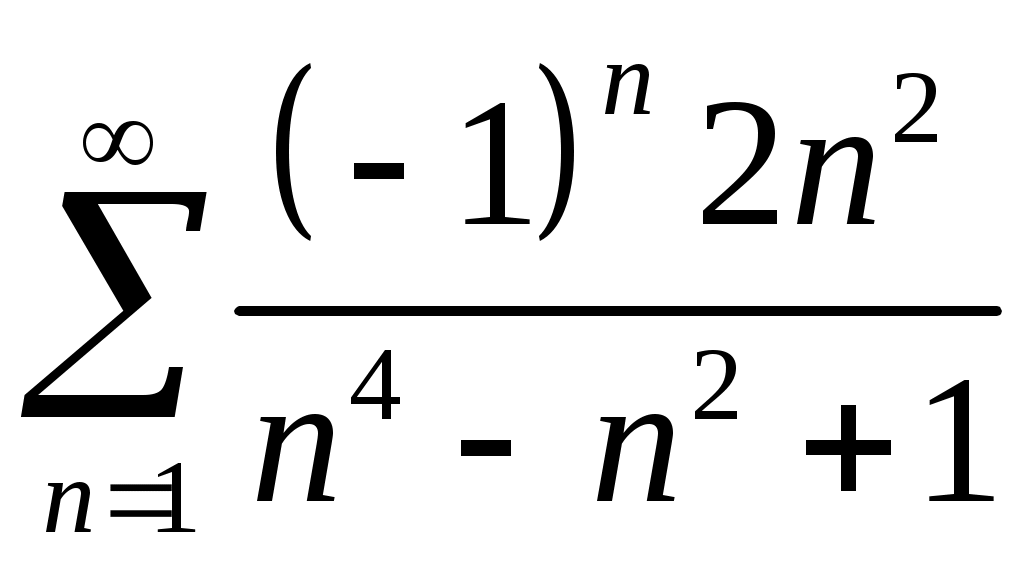 . 8.6. . 8.6. 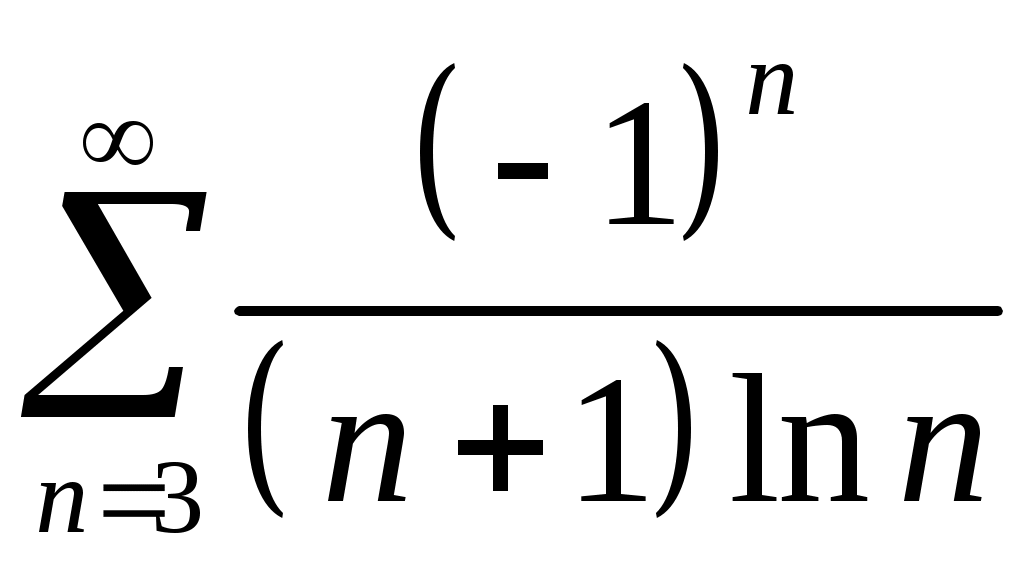 . .8.7. 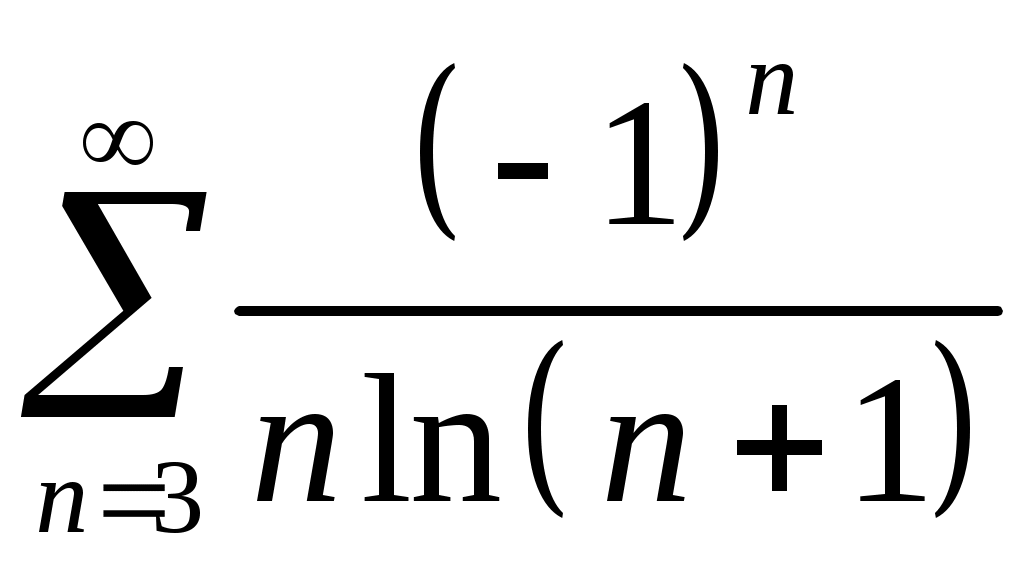 . 8.8. . 8.8. 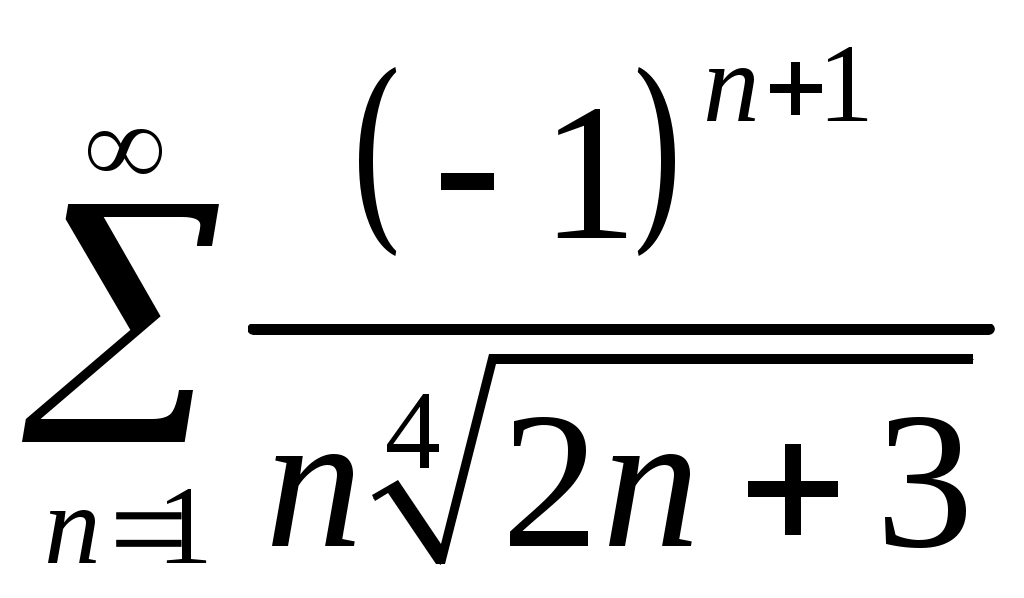 . .8.9. 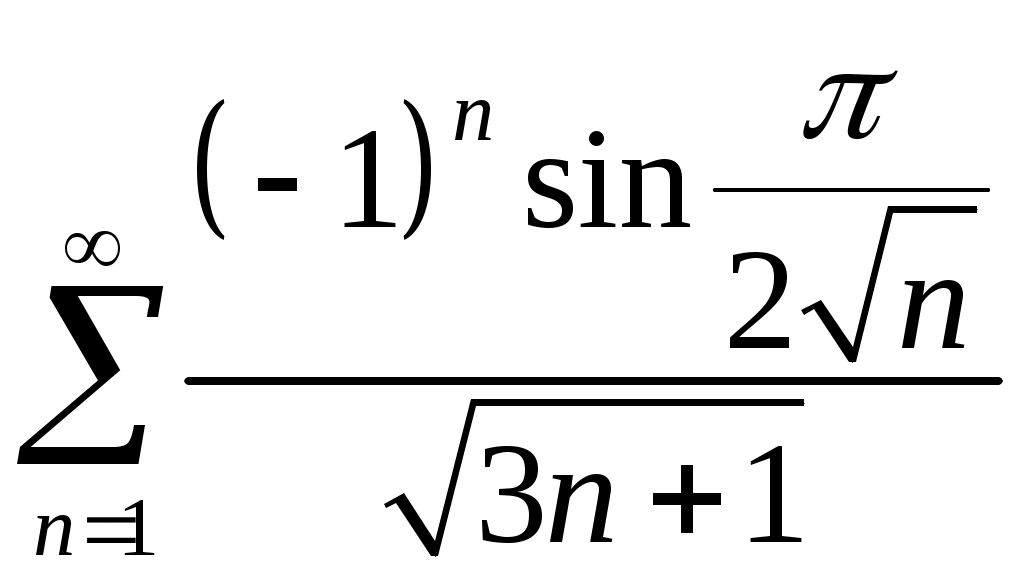 . 8.10. . 8.10. 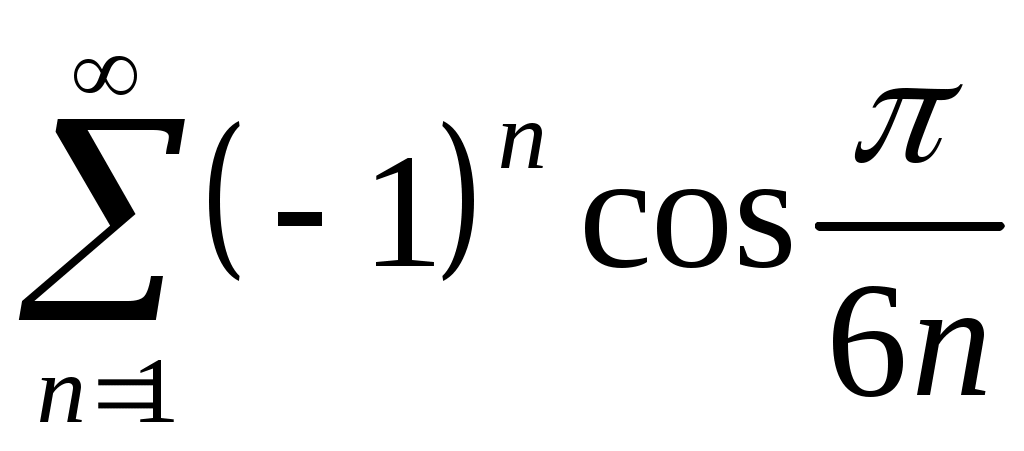 . .8.11. 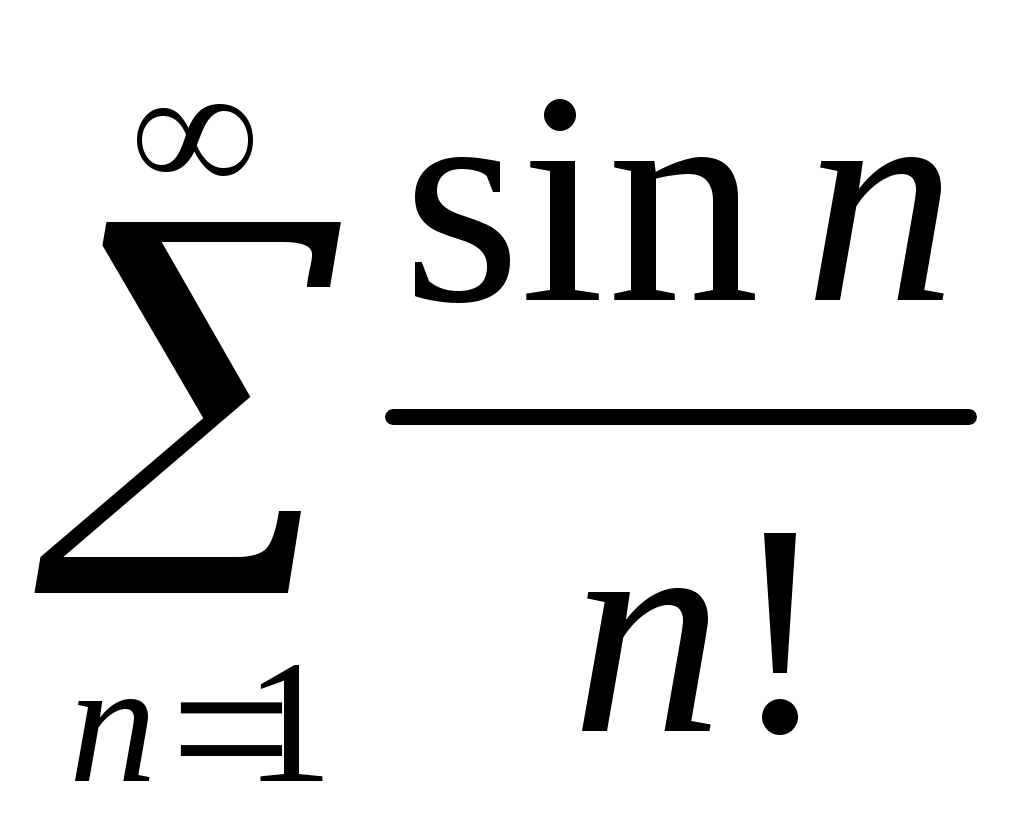 . 8.12. . 8.12. 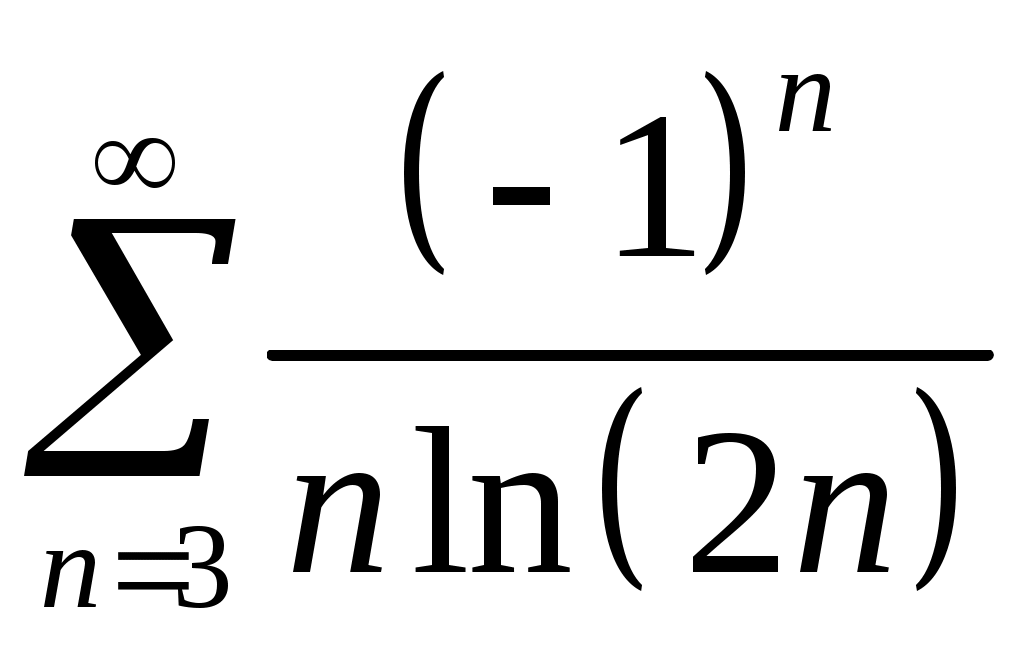 . .8.13. 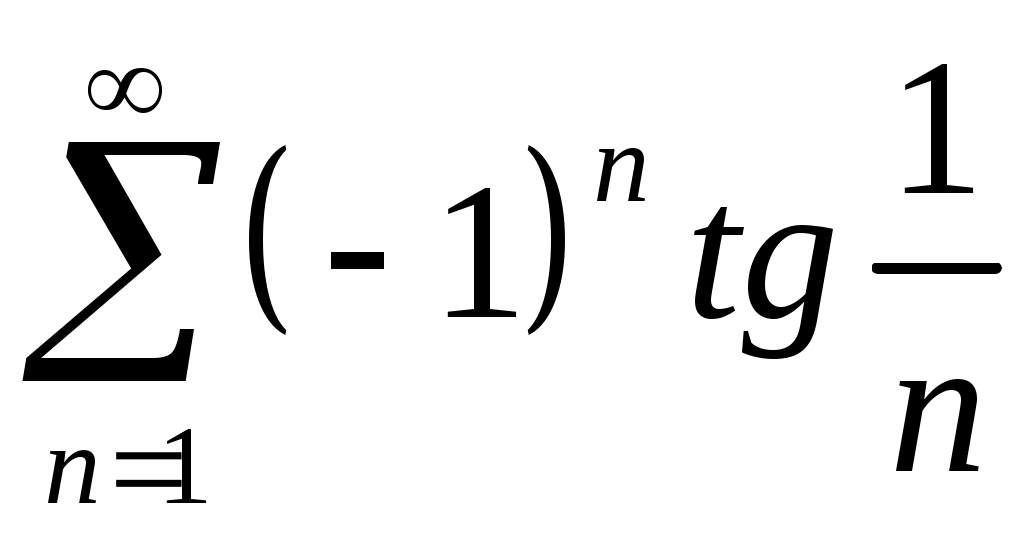 . 8.14. . 8.14. 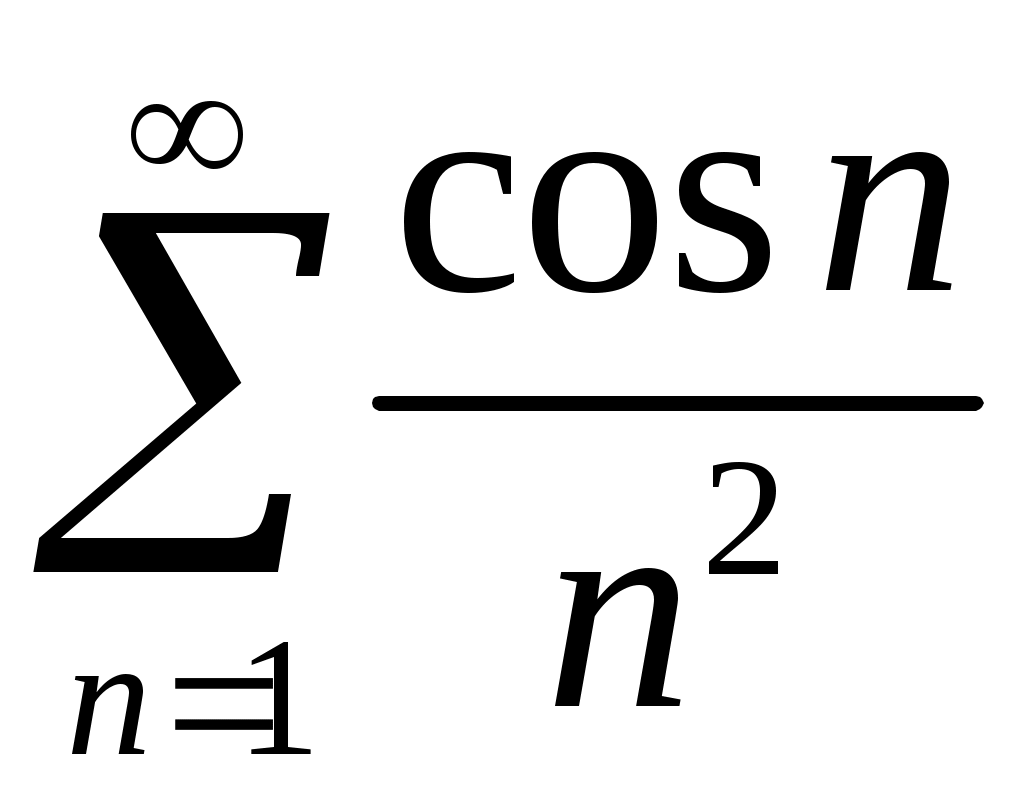 . .8.15. 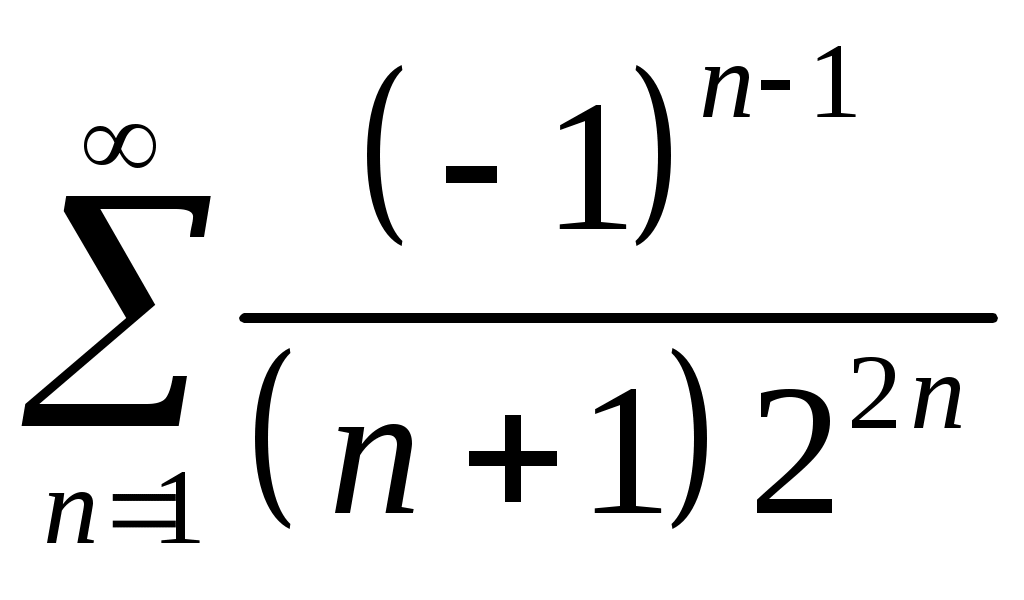 . 8.16. . 8.16. 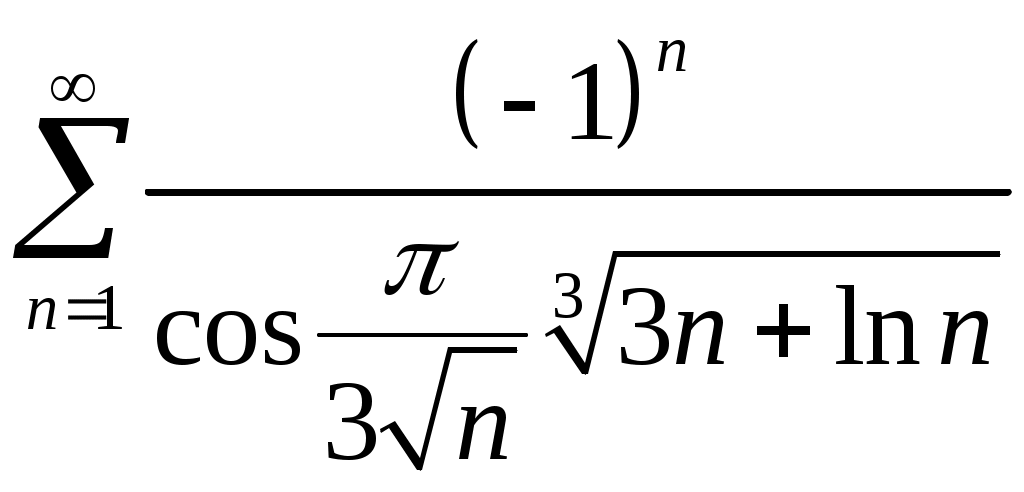 . .8.17. 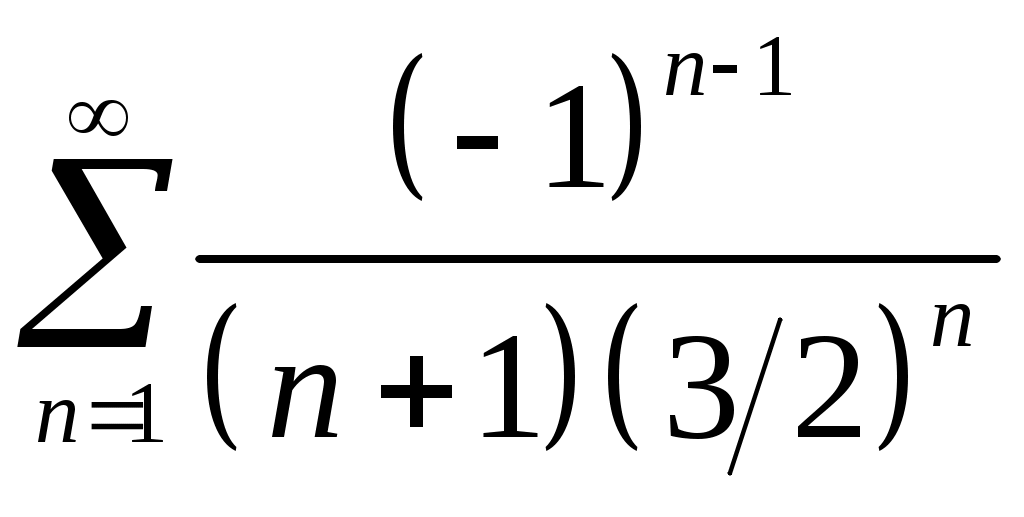 . 8.18. . 8.18. 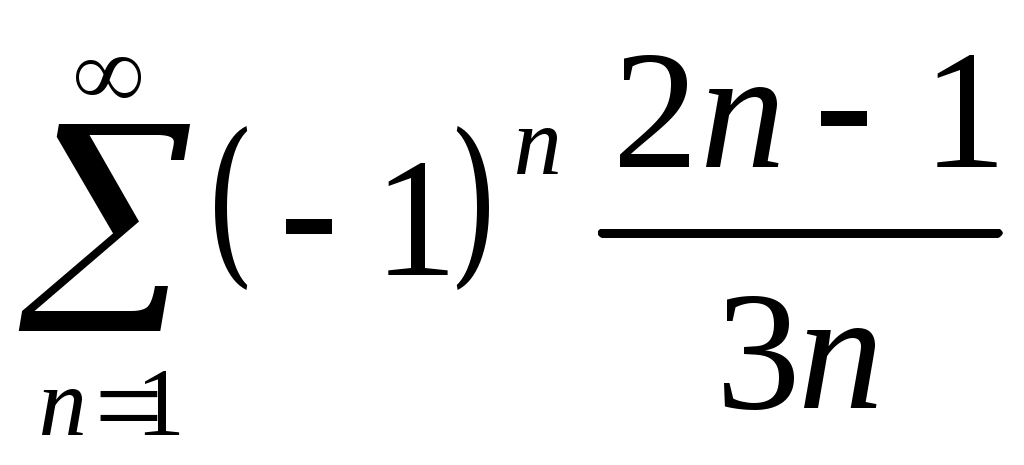 . .8.19. 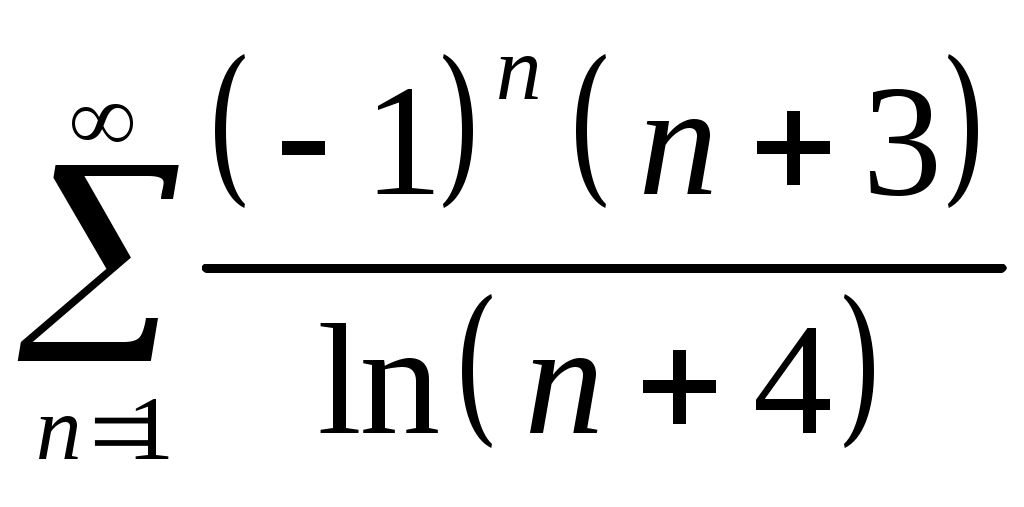 . 8.20. . 8.20. 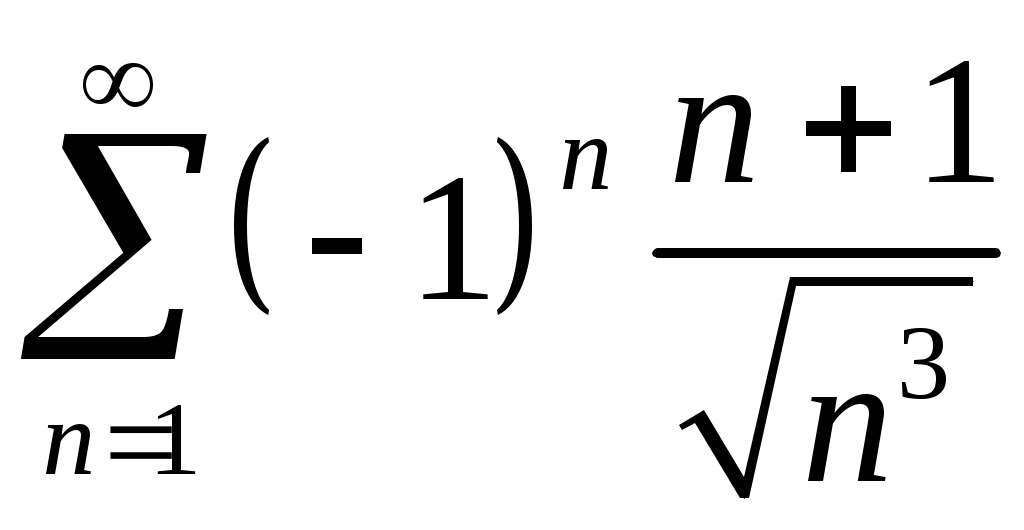 . .8.21. 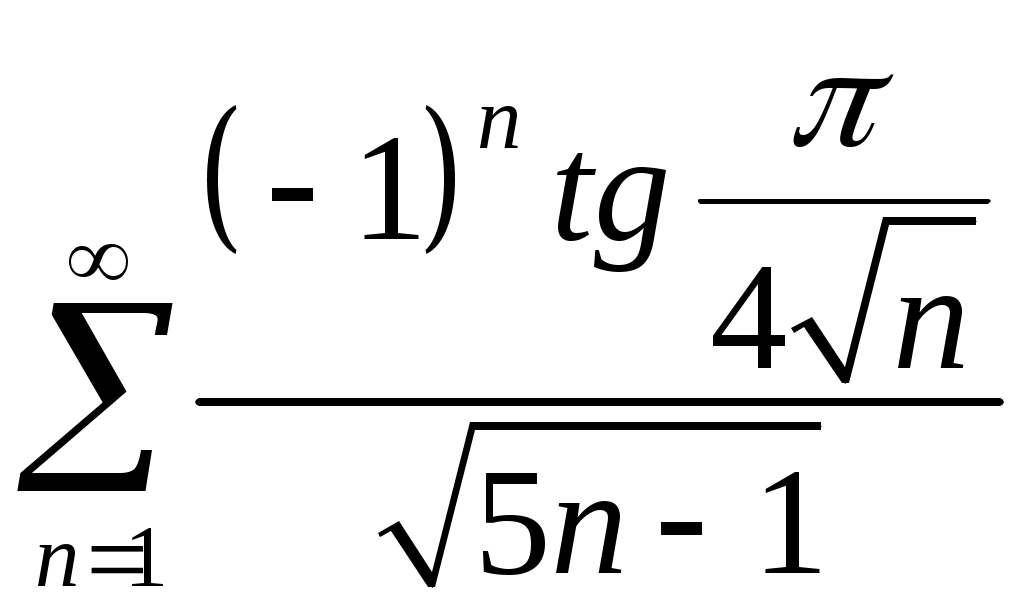 . 8.22. . 8.22. 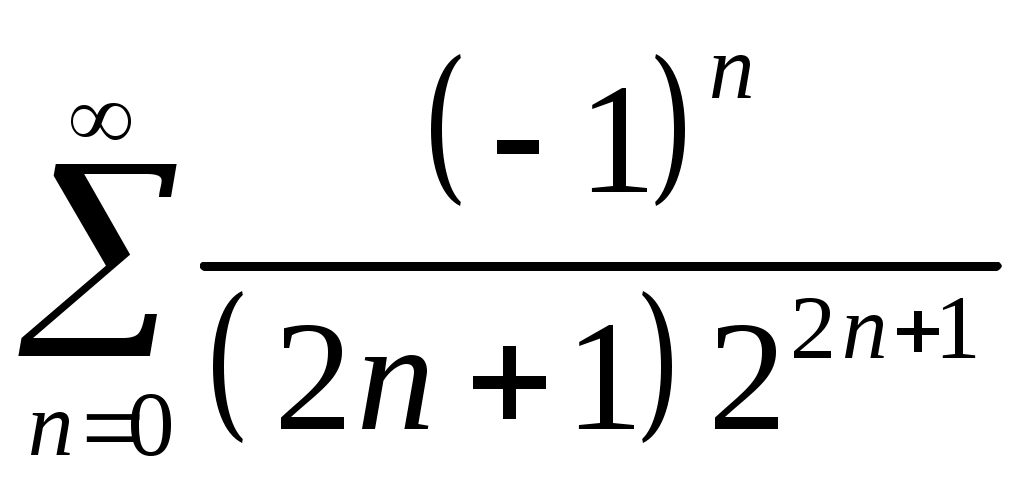 . .8.23. 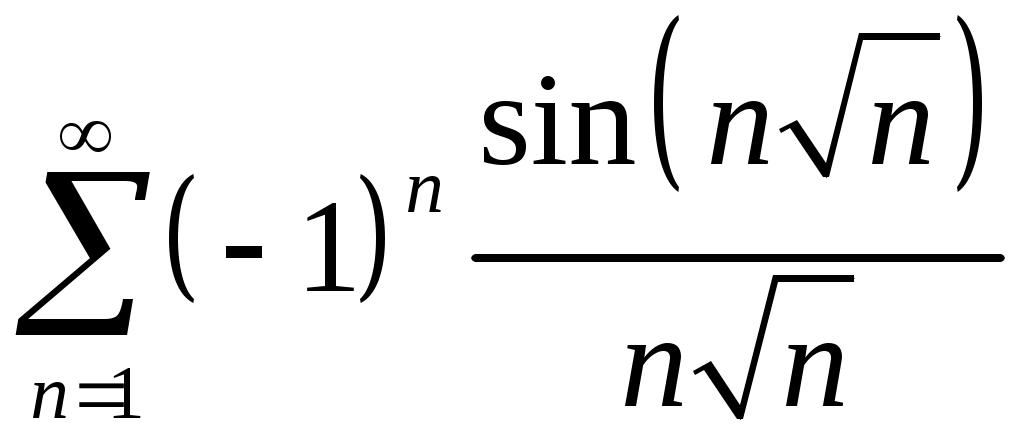 . 8.24. . 8.24. 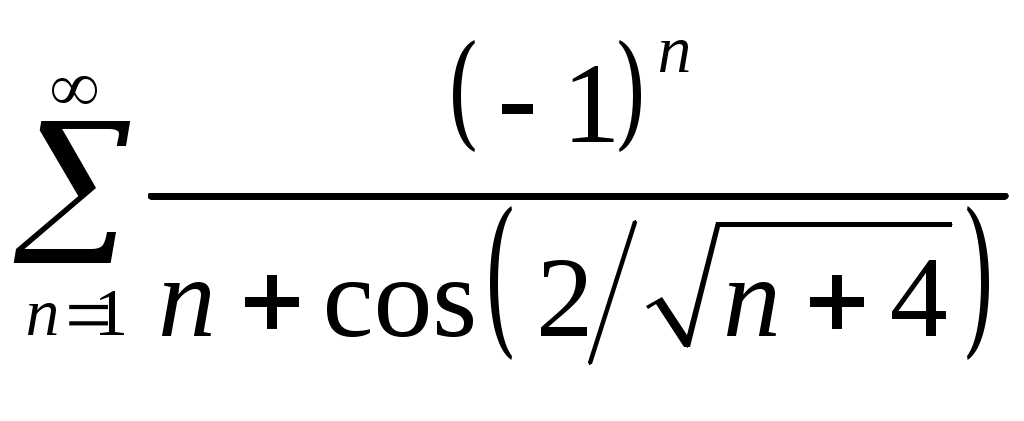 . .8.25. 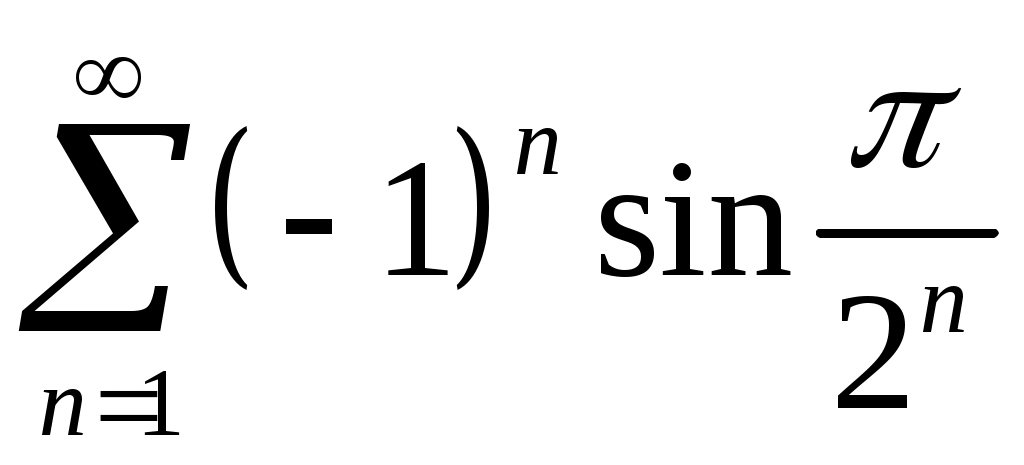 . 8.26. . 8.26. 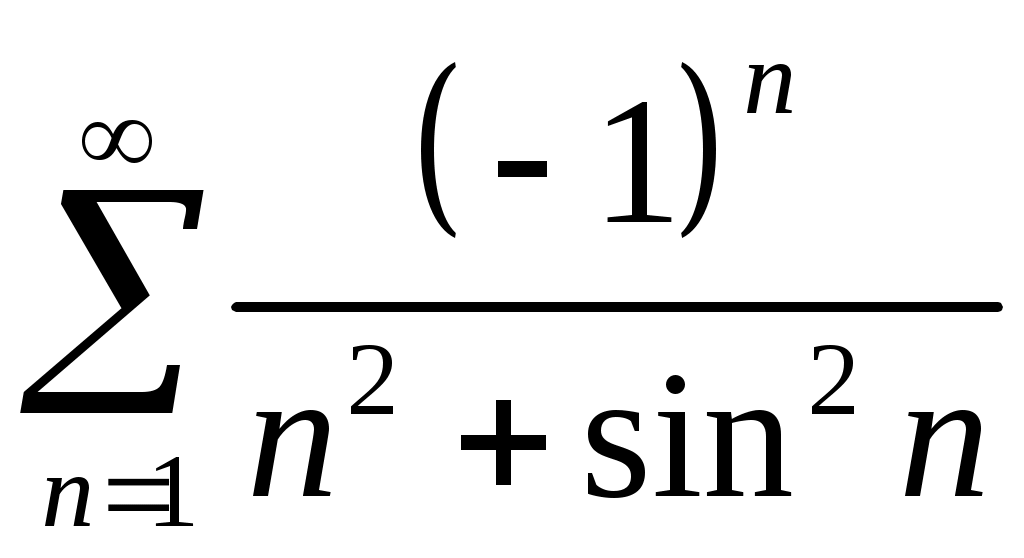 . .8.27. 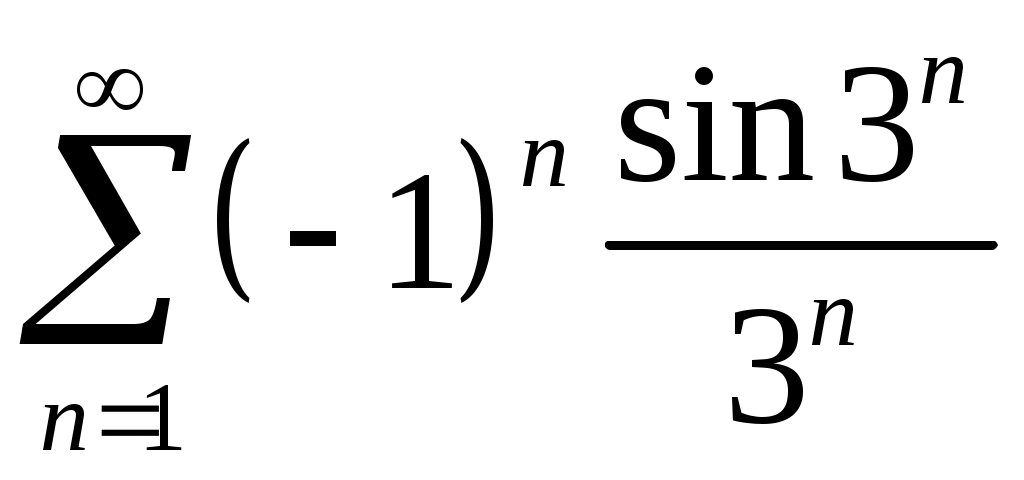 . 8.28. . 8.28. 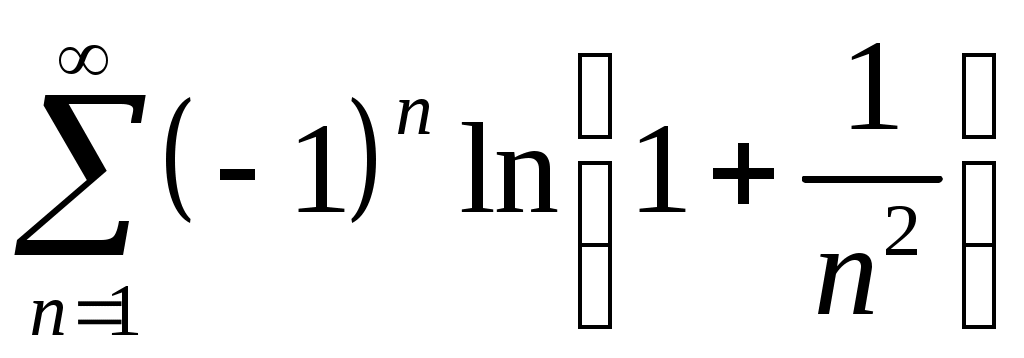 . .8.29. 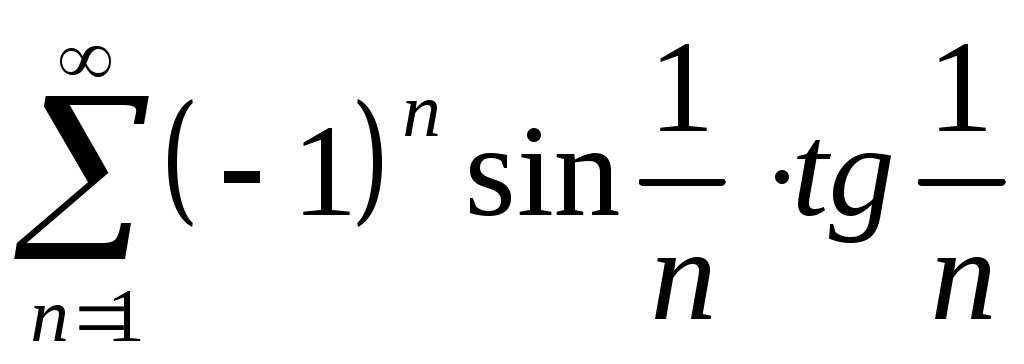 . 8.30. . 8.30. 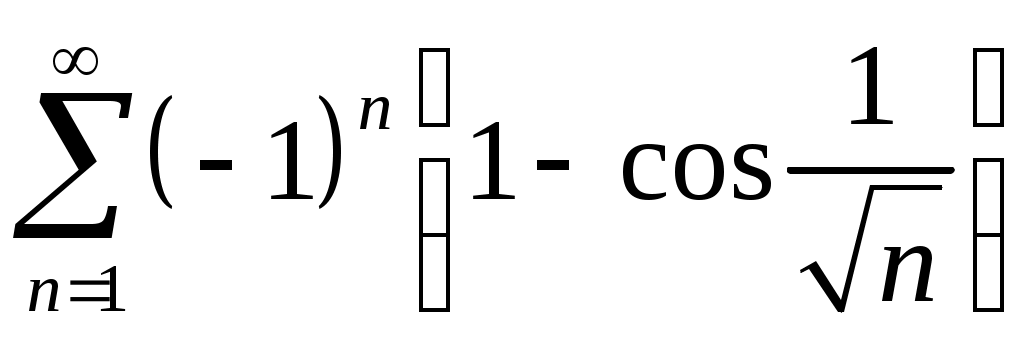 . .8.31. 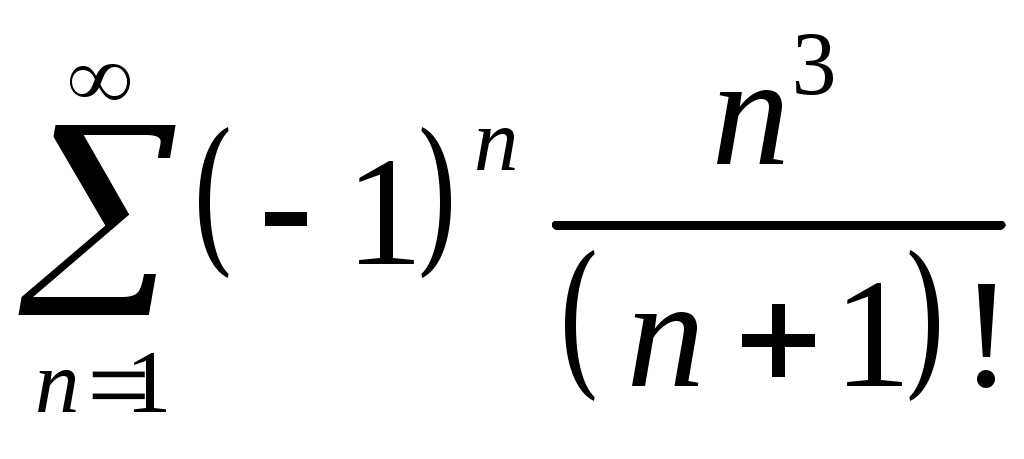 . .Задача 9. Вычислить сумму ряда с точностью 9.1. 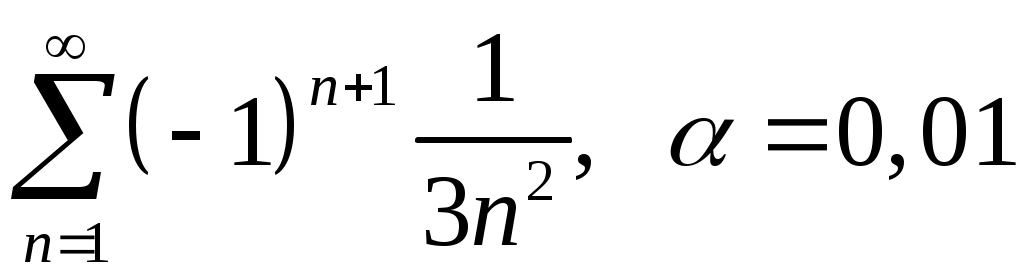 . 9.2. . 9.2. 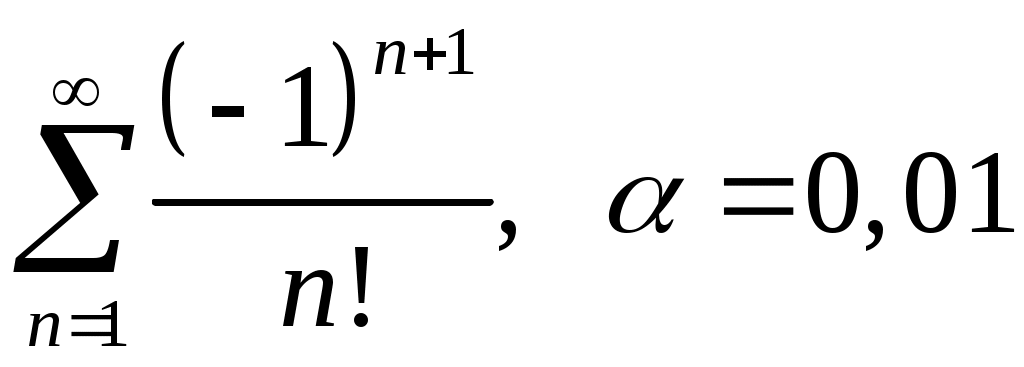 . .9.3. 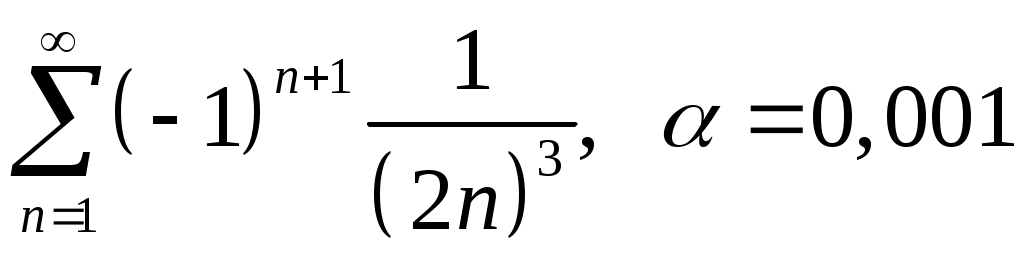 . 9.4. . 9.4. 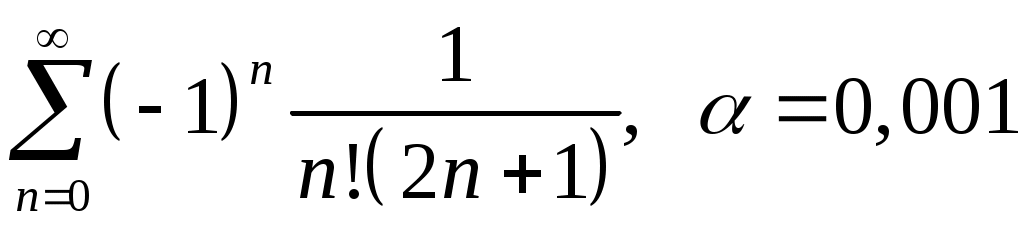 . .9.5. 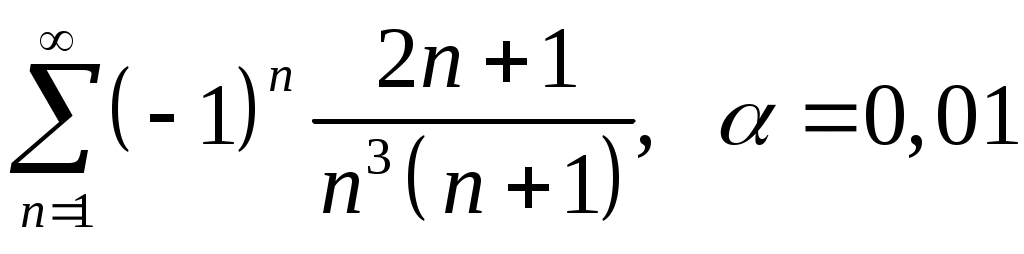 . 9.6. . 9.6. 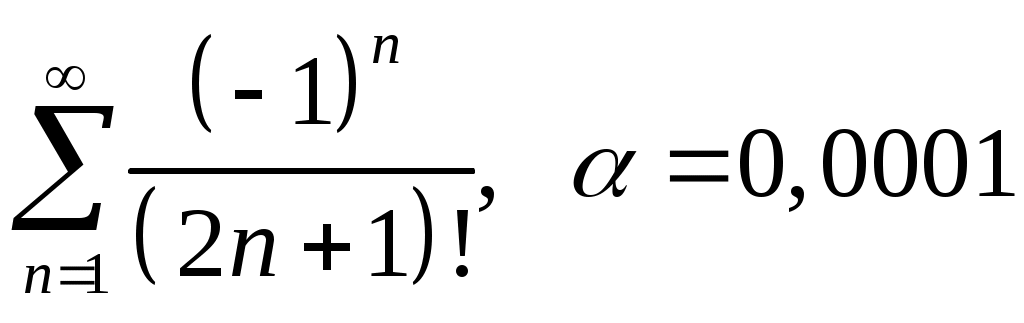 . .9.7. 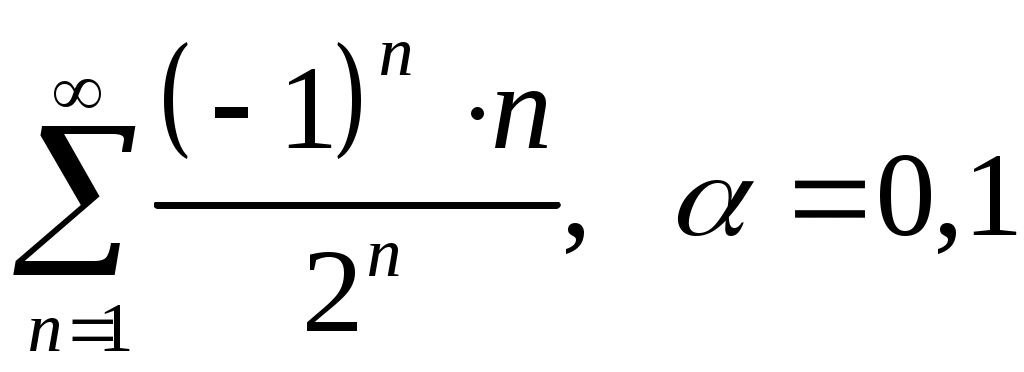 . 9.8. . 9.8. 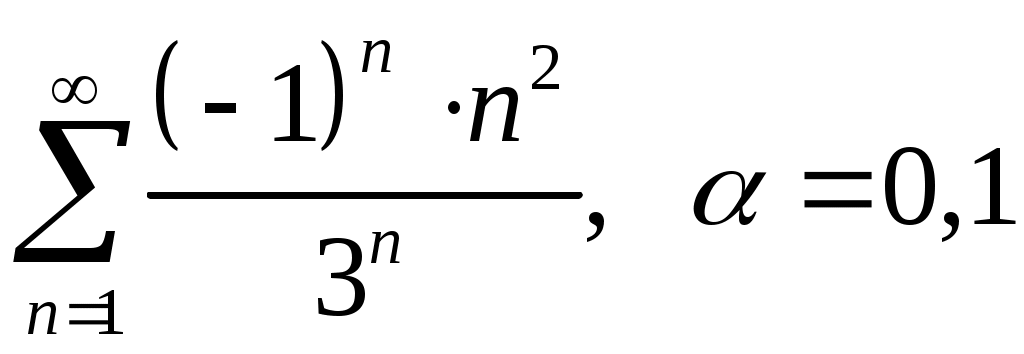 . .9.9. 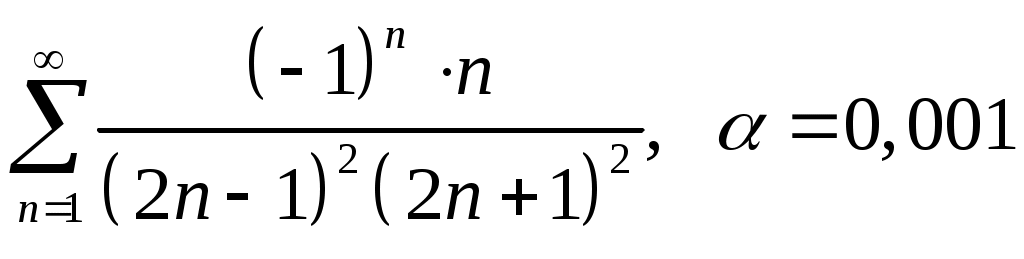 . 9.10. . 9.10. 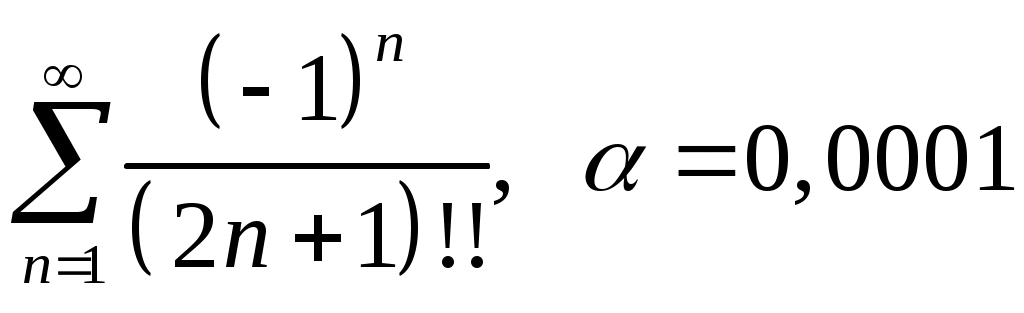 . .9.11. 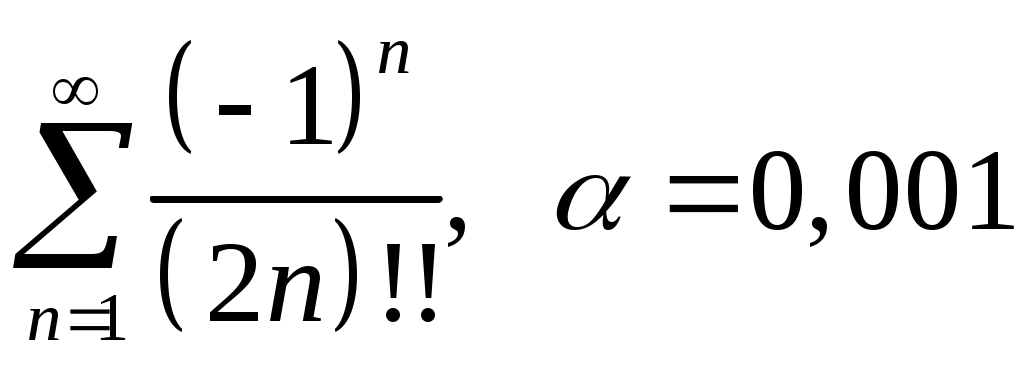 . 9.12. . 9.12. 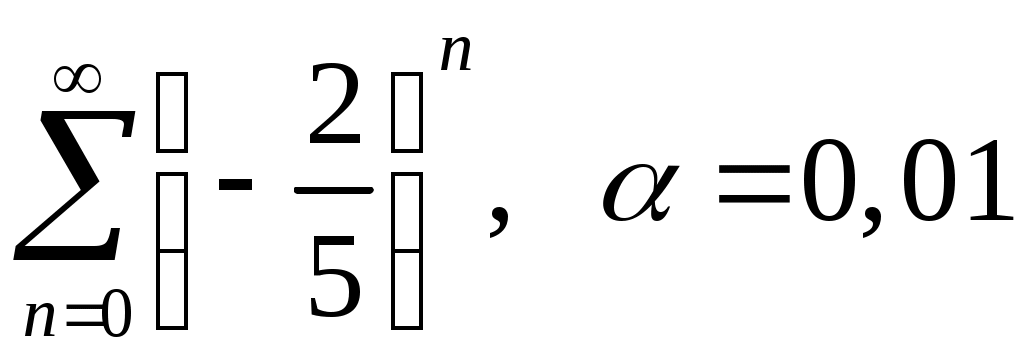 . .9.13. 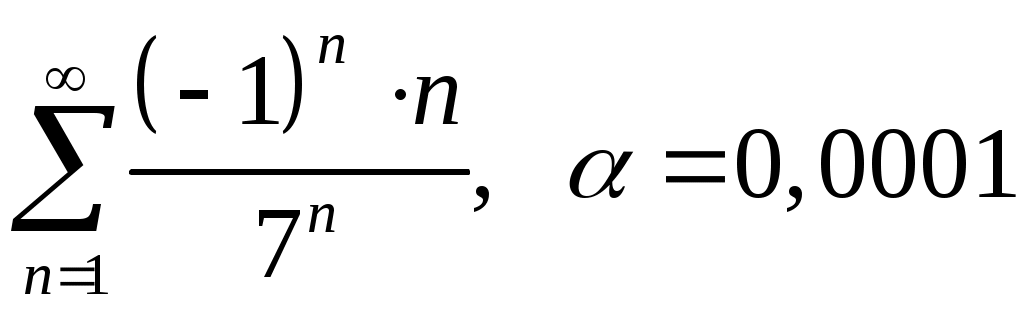 . 9.14. . 9.14. 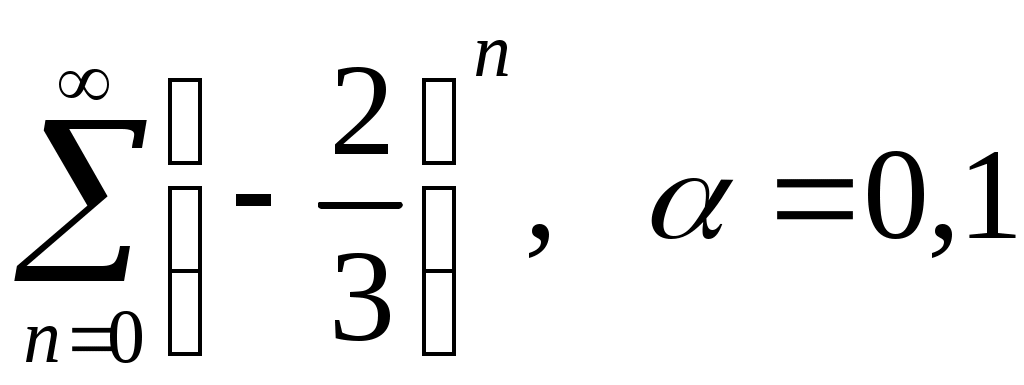 . .9.15. 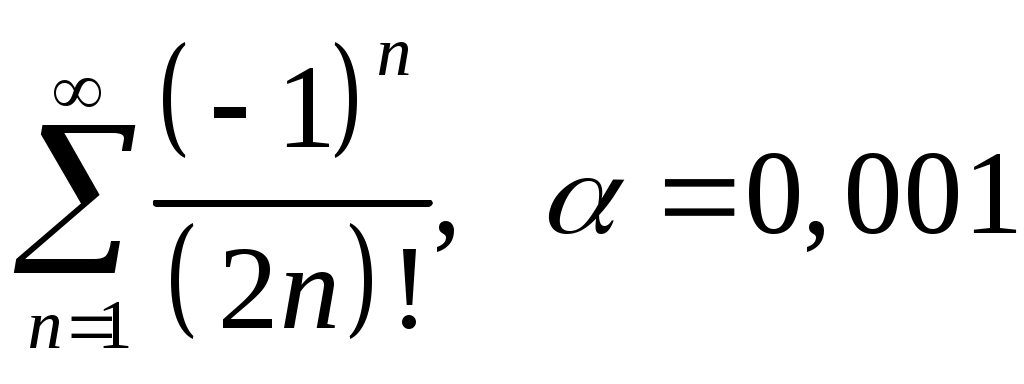 . 9.16. . 9.16. 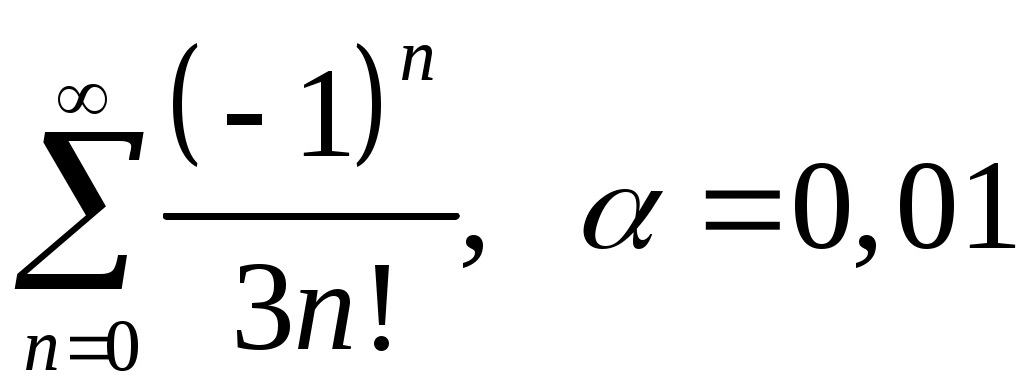 . .9.17. 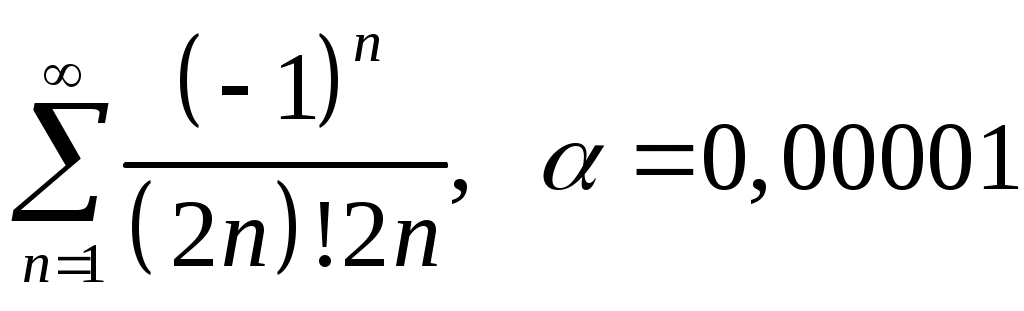 . 9.18. . 9.18. 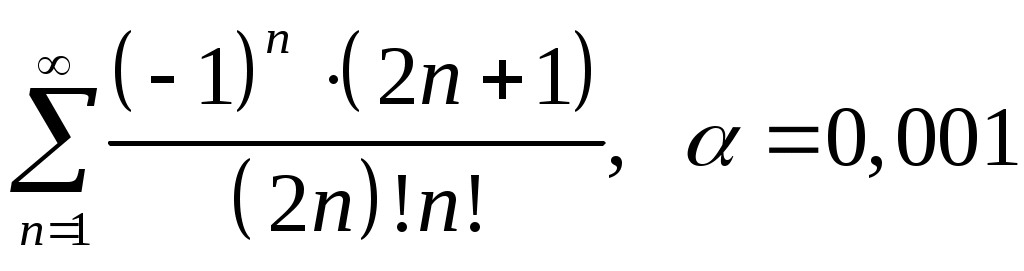 . .9.19. 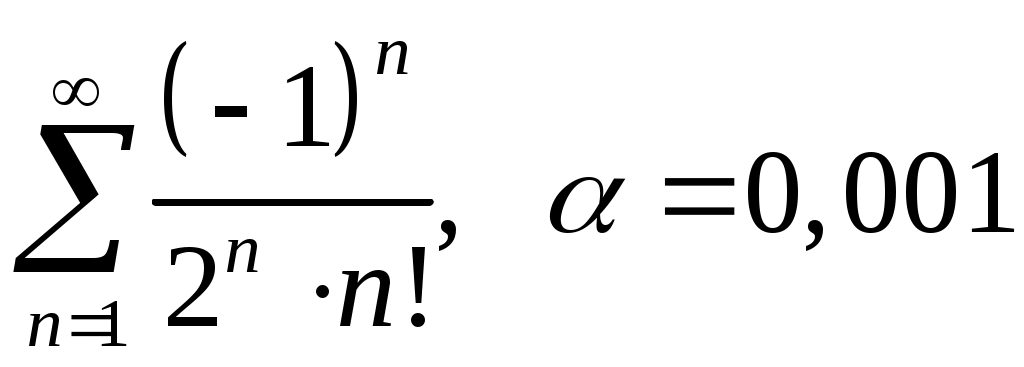 . 9.20. . 9.20. 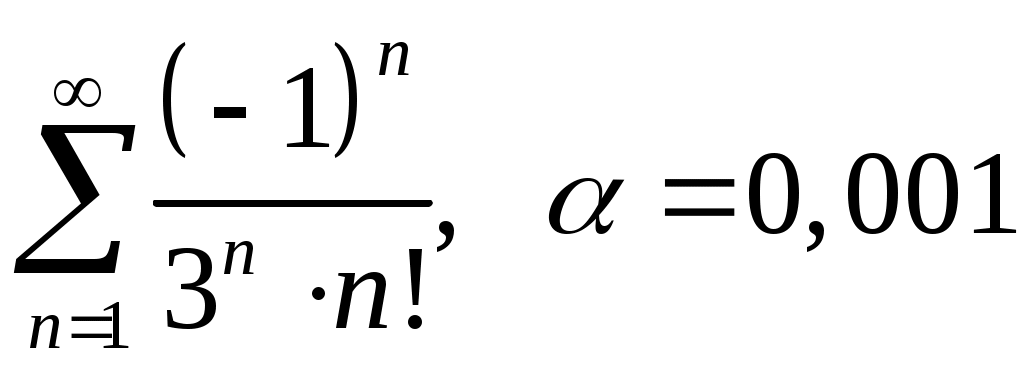 . .9.21. 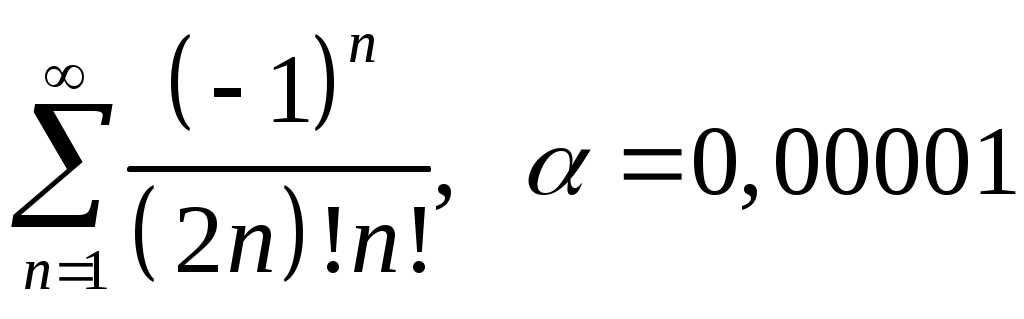 . 9.22. . 9.22. 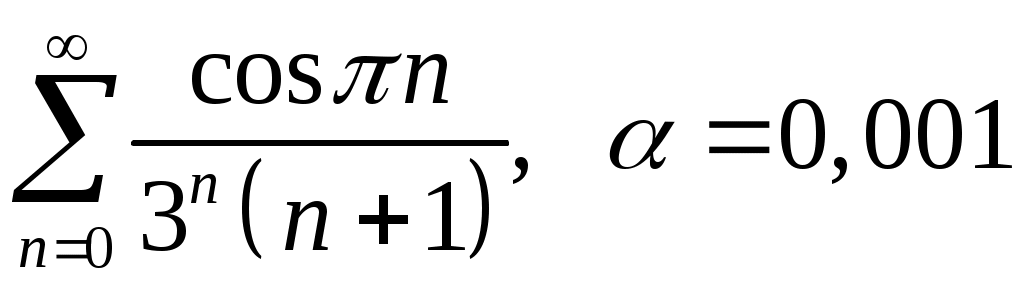 . .9.23. 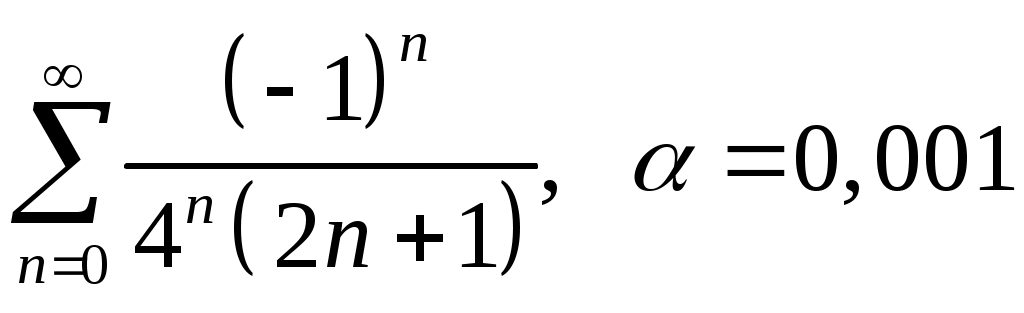 . 9.24. . 9.24. 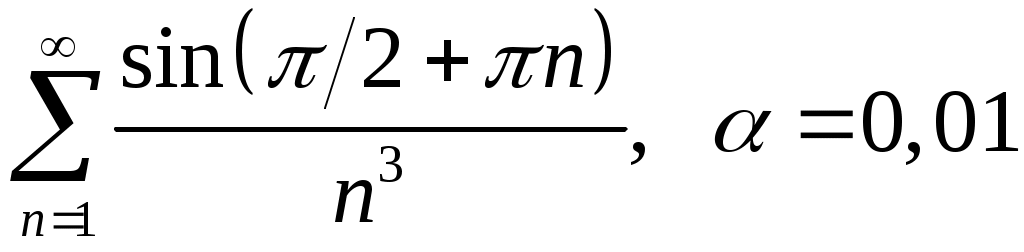 . .9.25. 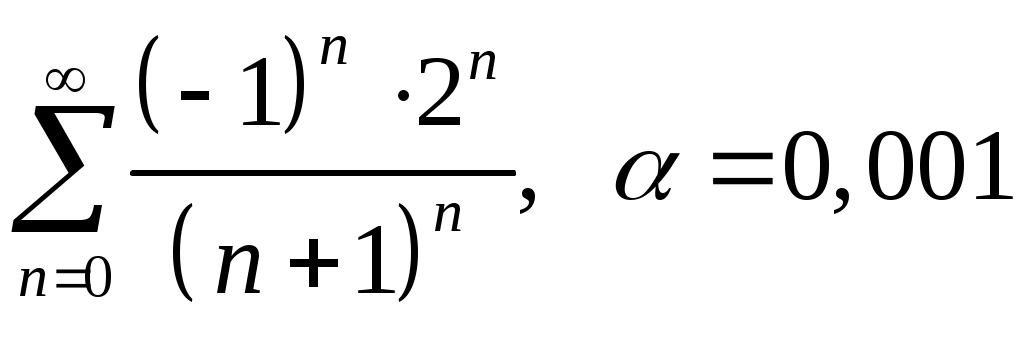 . 9.26. . 9.26. 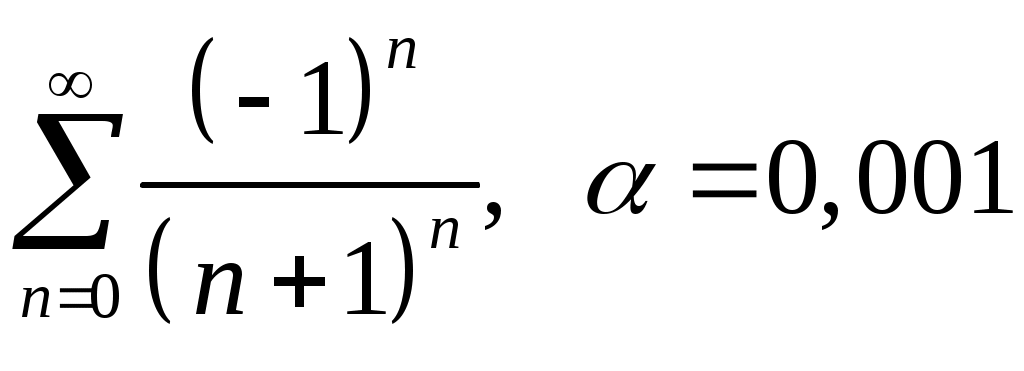 . .9.27. 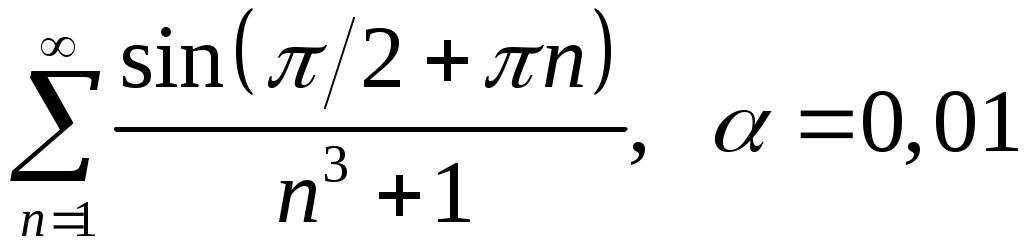 . 9.28. . 9.28. 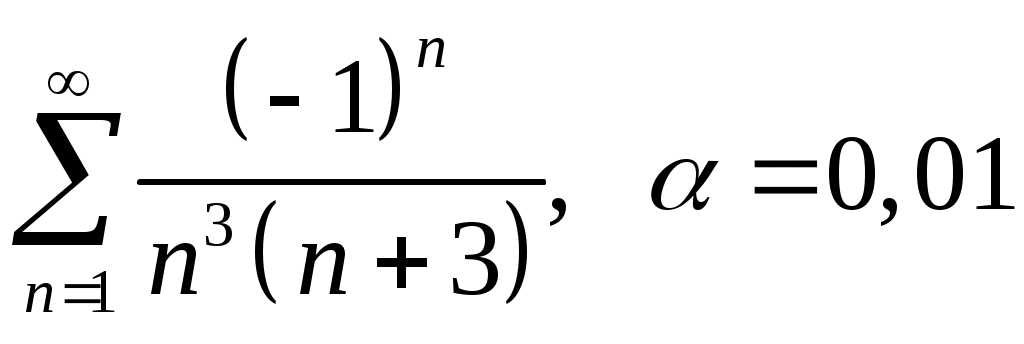 . .9.29. 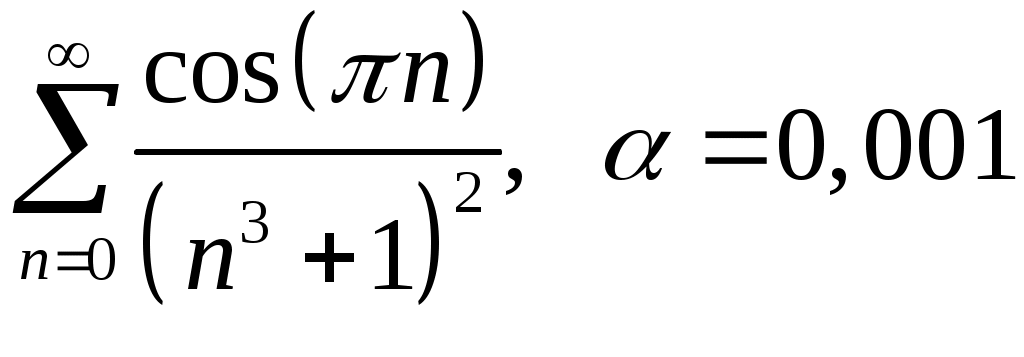 . 9.30. . 9.30. 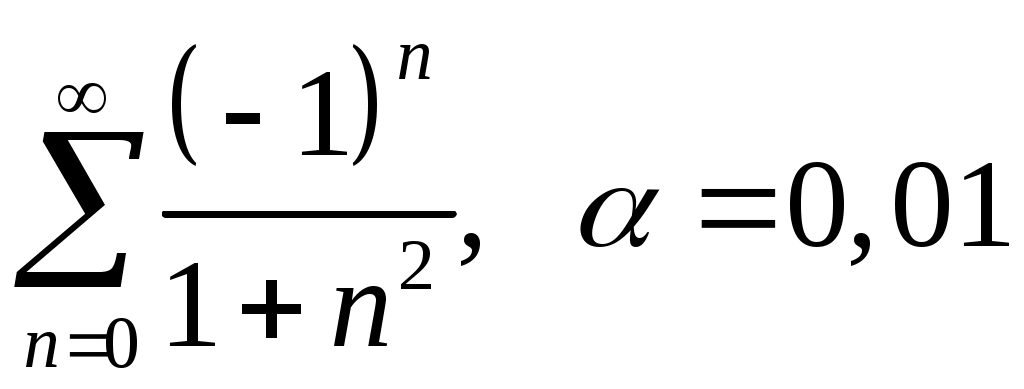 . .9.31. 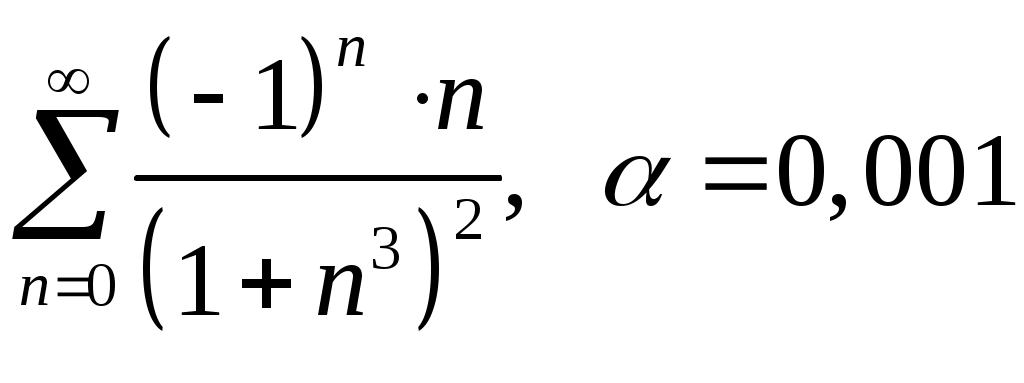 . .Задача 10. Доказать справедливость равенства. (Ответом служит число 10.1. 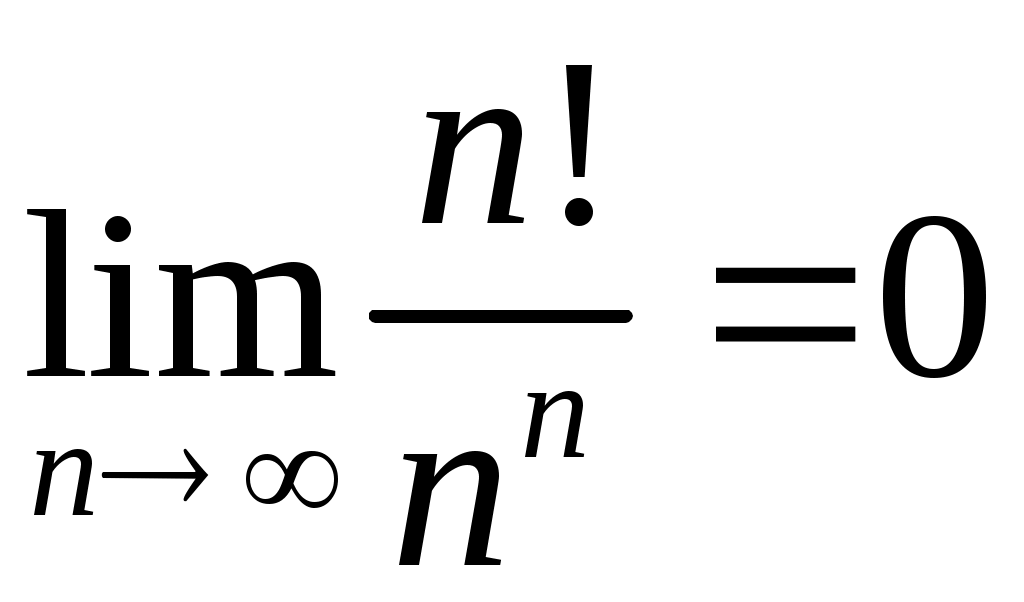 . 10.2. . 10.2. 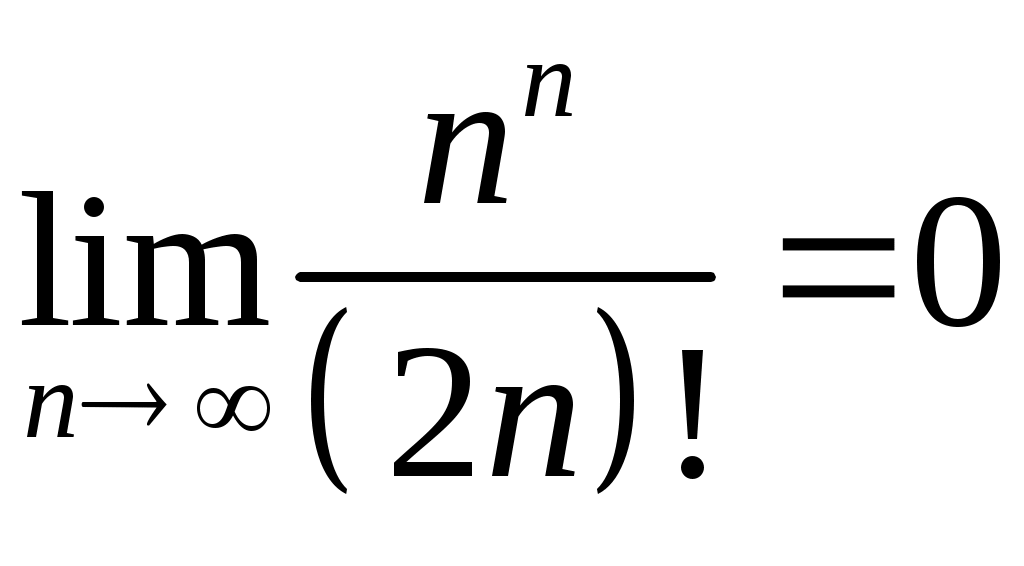 . .10.3. 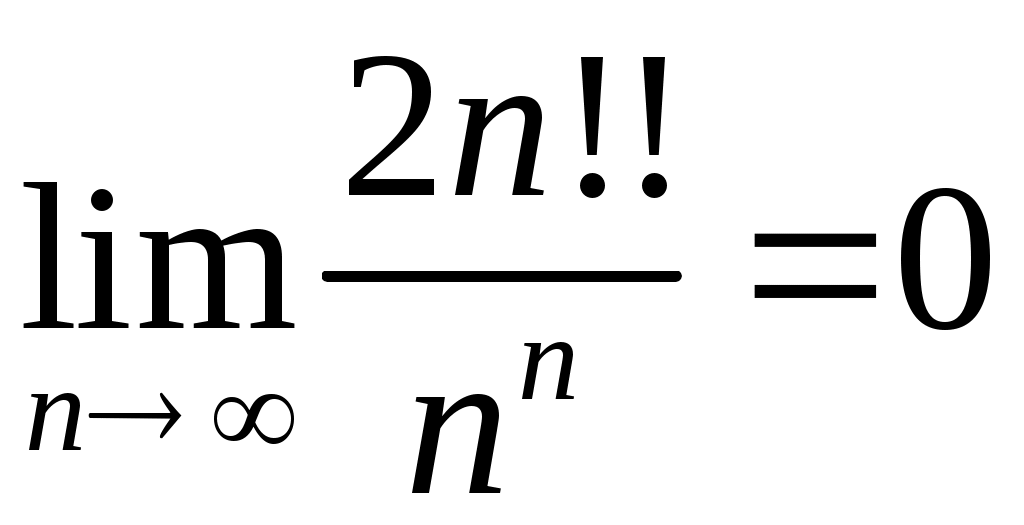 . 10.4. . 10.4. 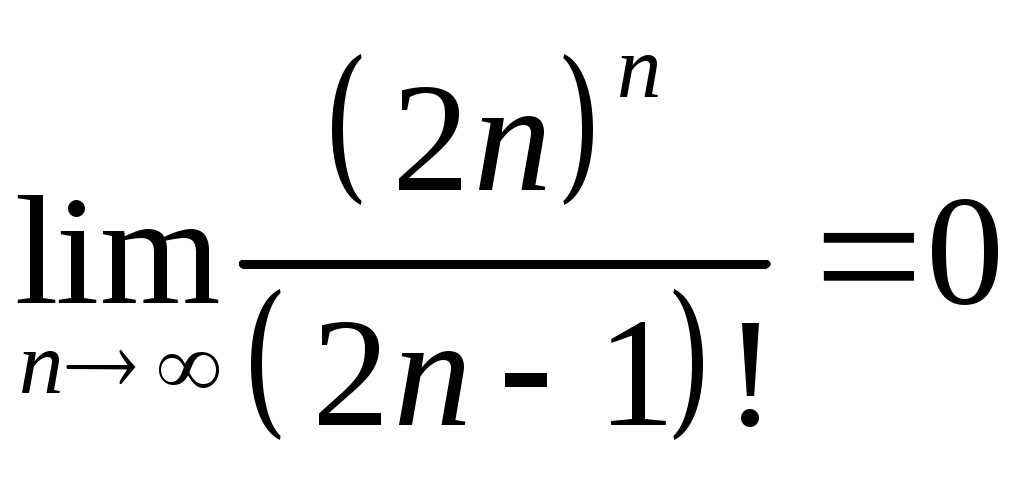 . .10.5. 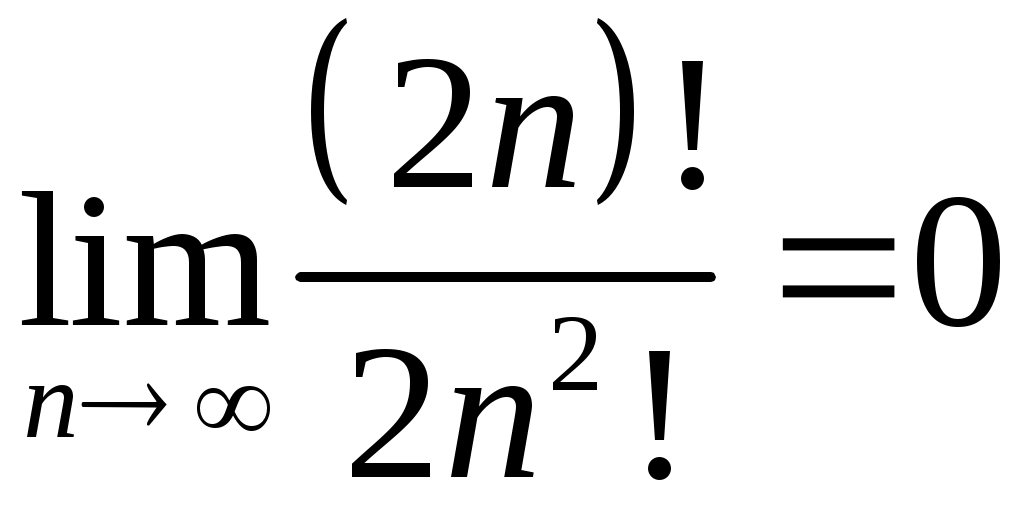 . 10.6. . 10.6. 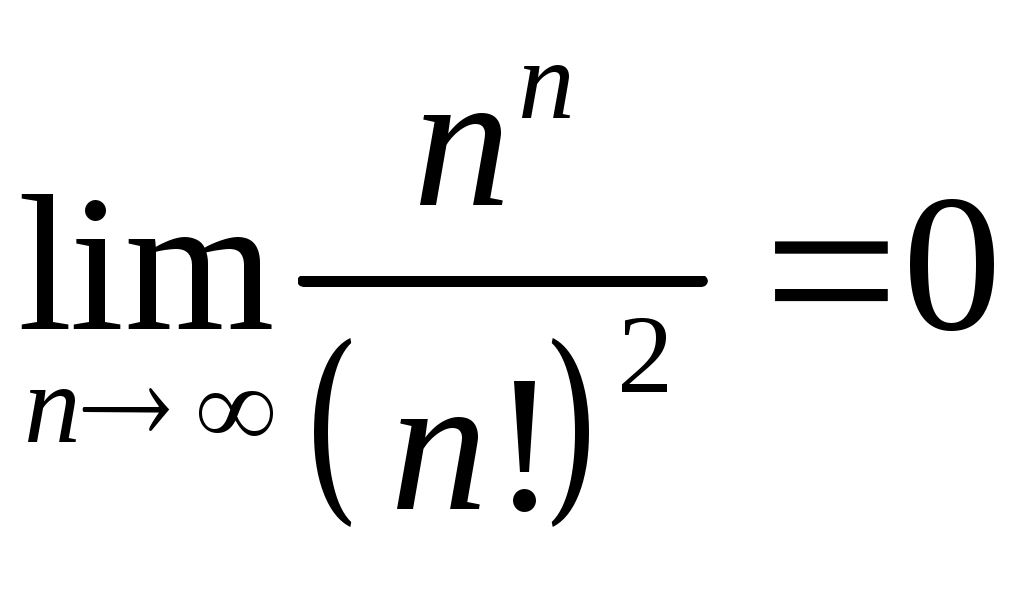 . .10.7. 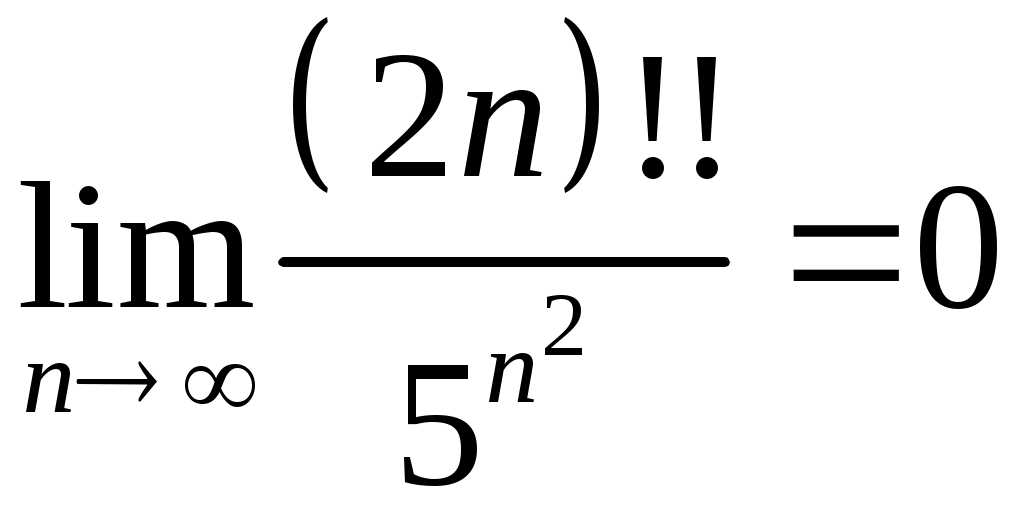 . 10.8. . 10.8. 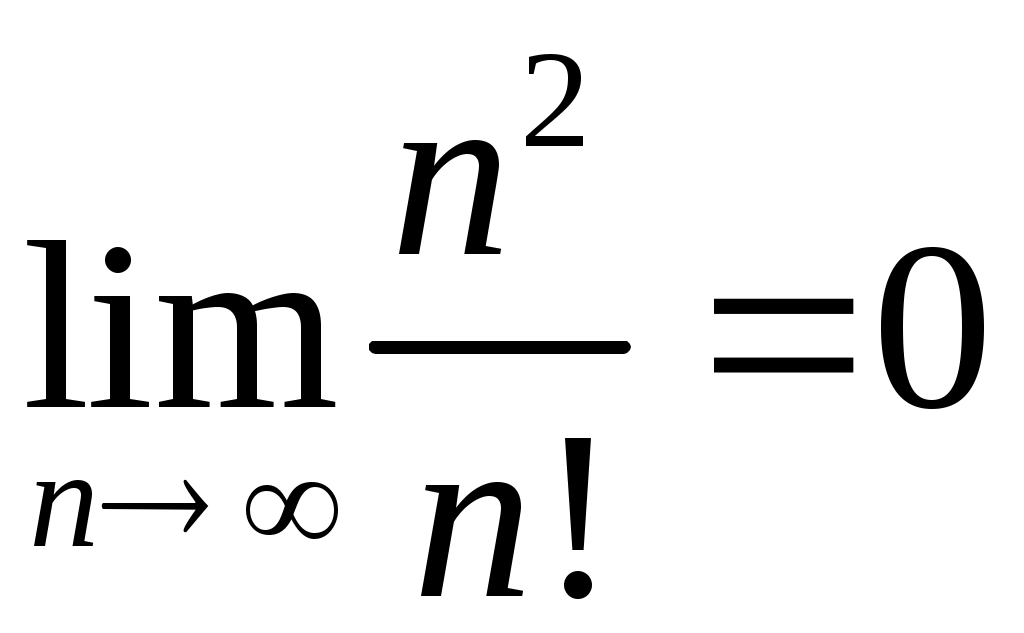 . .10.9. 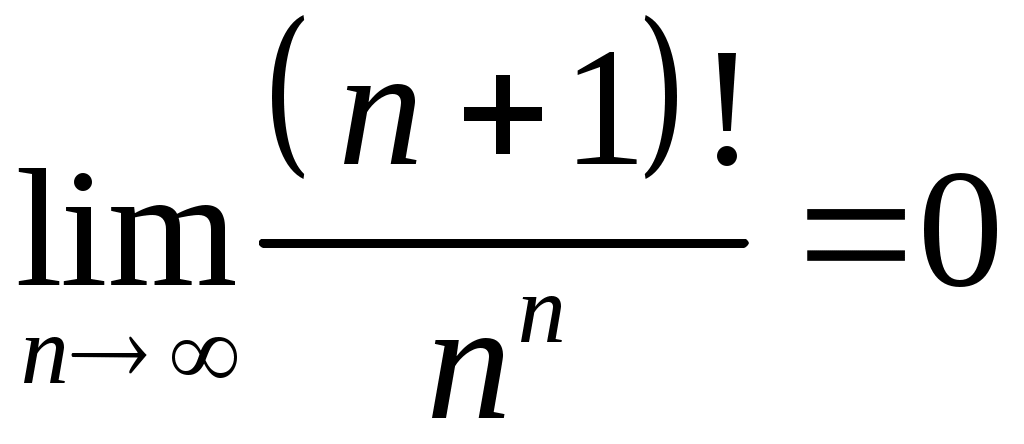 . 10.10. . 10.10. 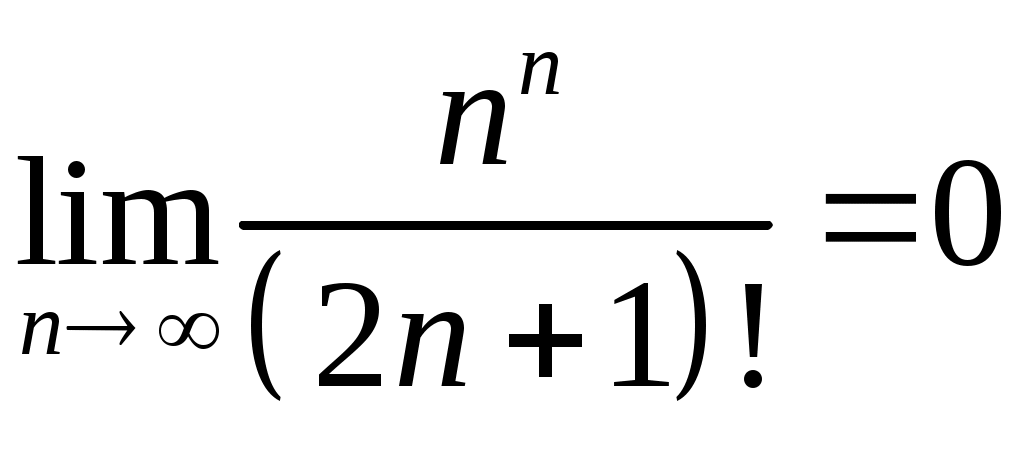 . .10.11. 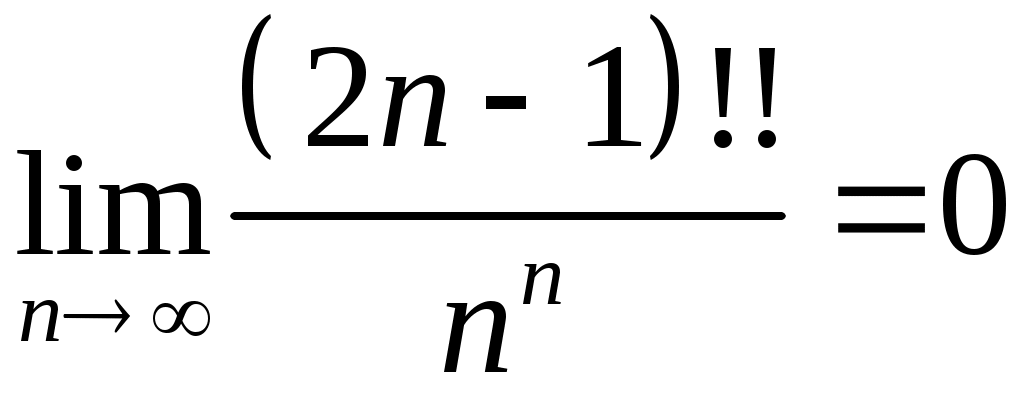 . 10.12. . 10.12. 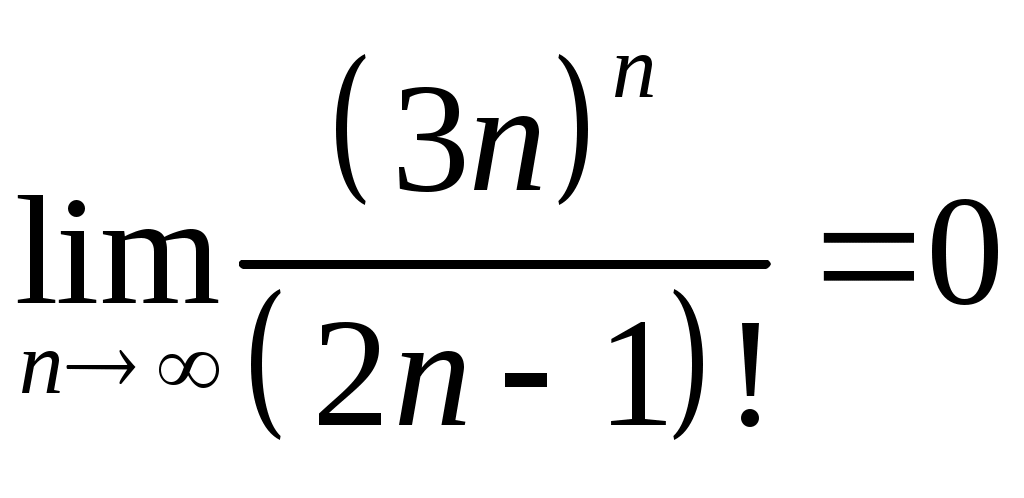 . .10.13. 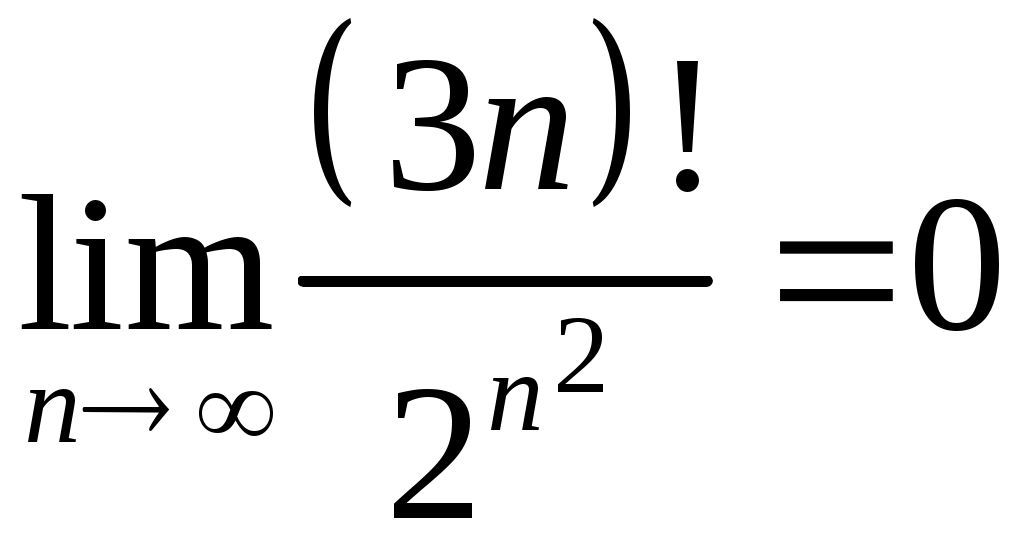 . 10.14. . 10.14. 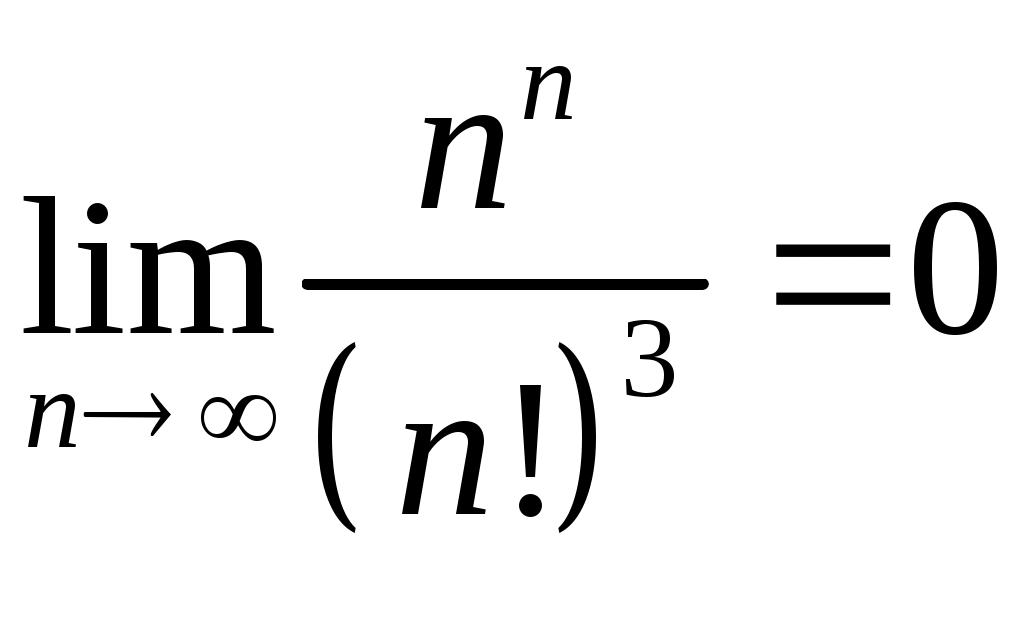 . .10.15. 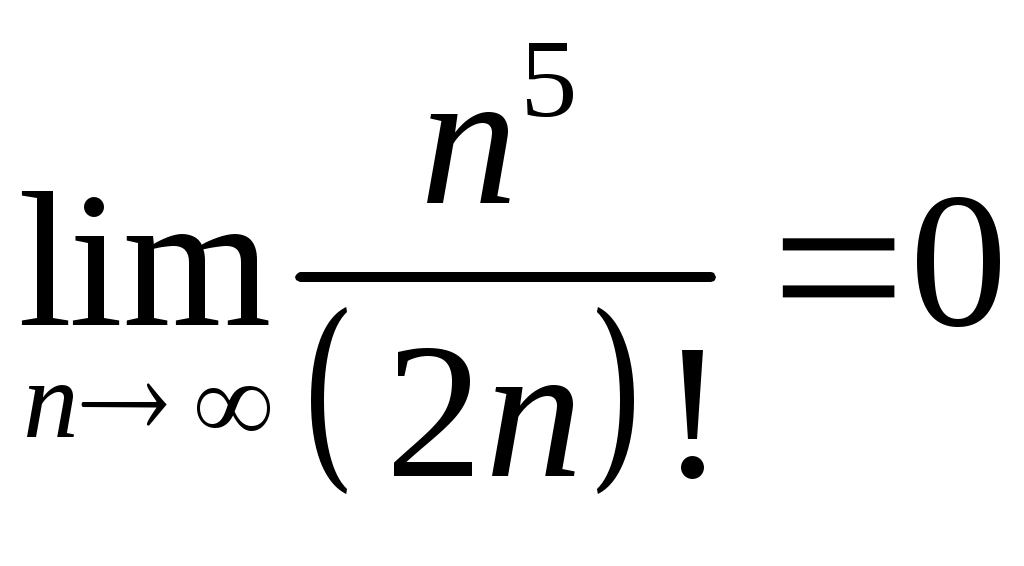 . 10.16. . 10.16. 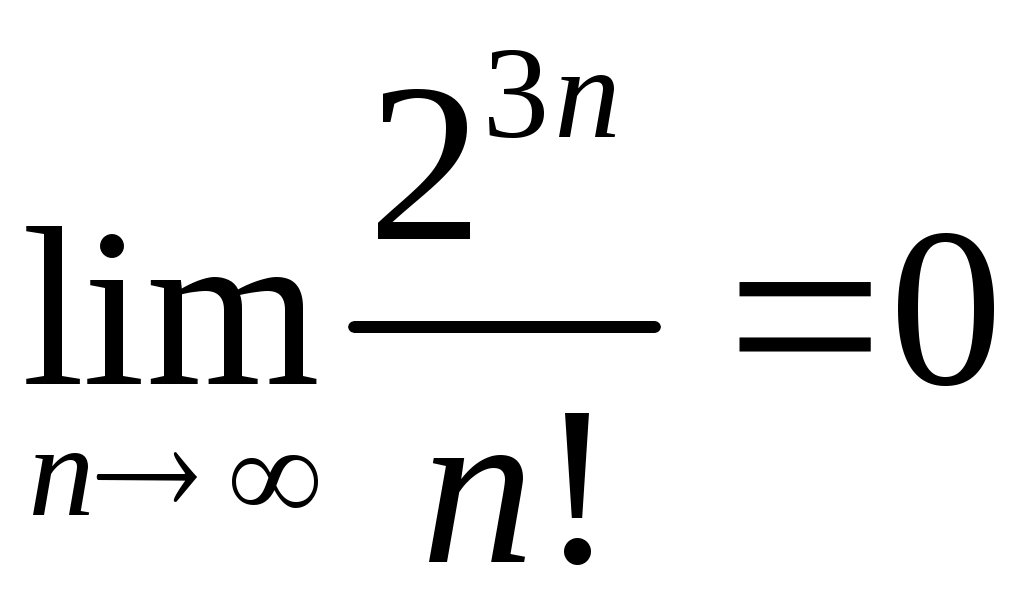 . .10.17. 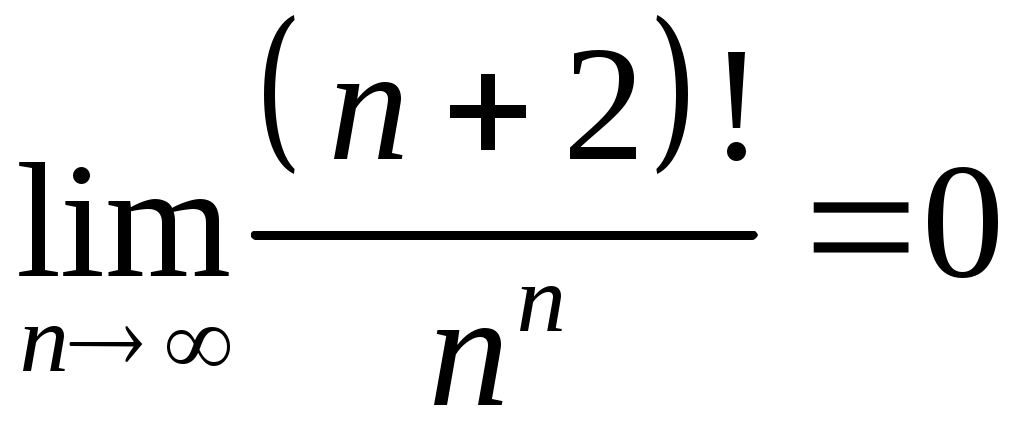 . 10.18. . 10.18. 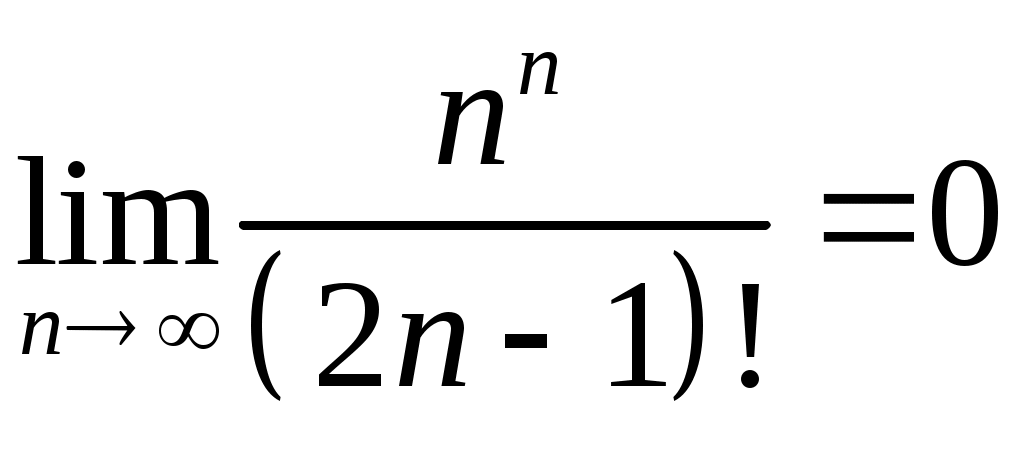 . .10.19. 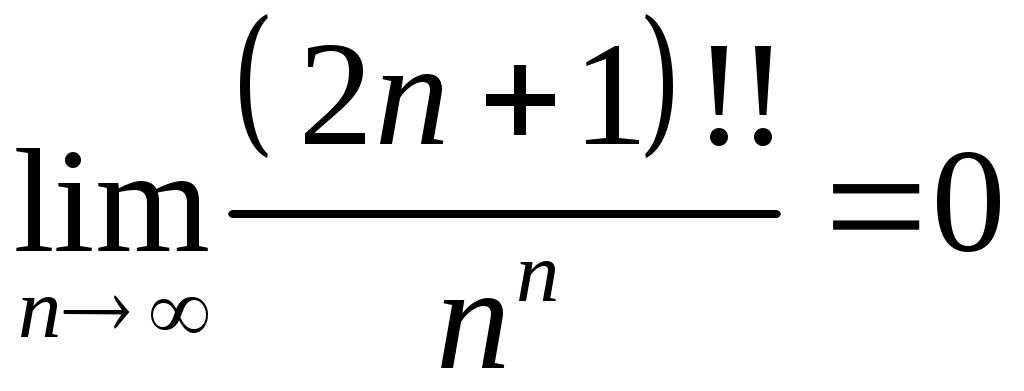 . 10.20. . 10.20. 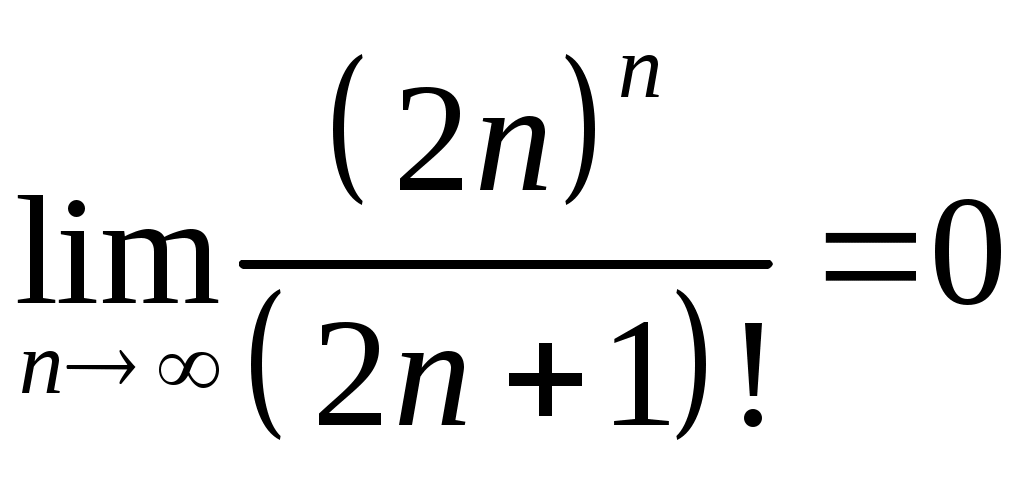 . .10.21. 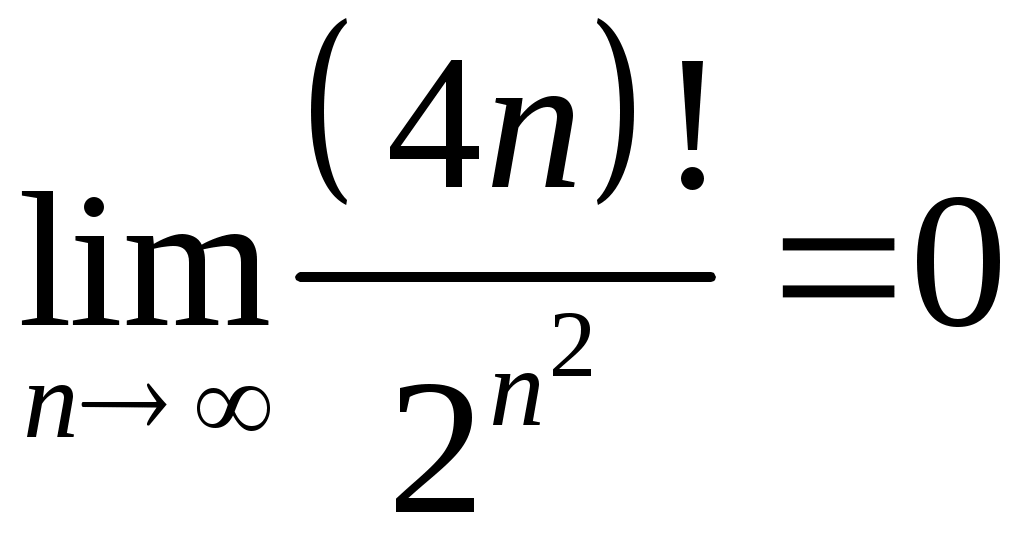 . 10.22. . 10.22. 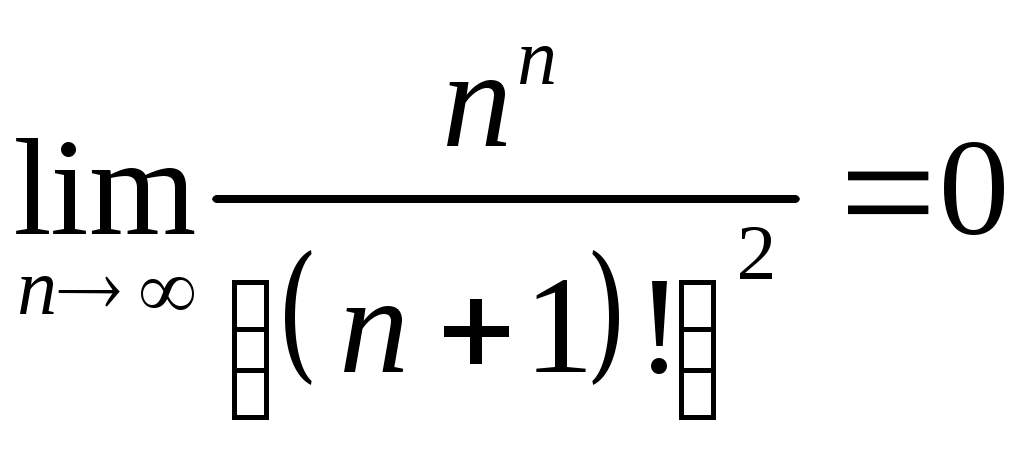 . .10.23. 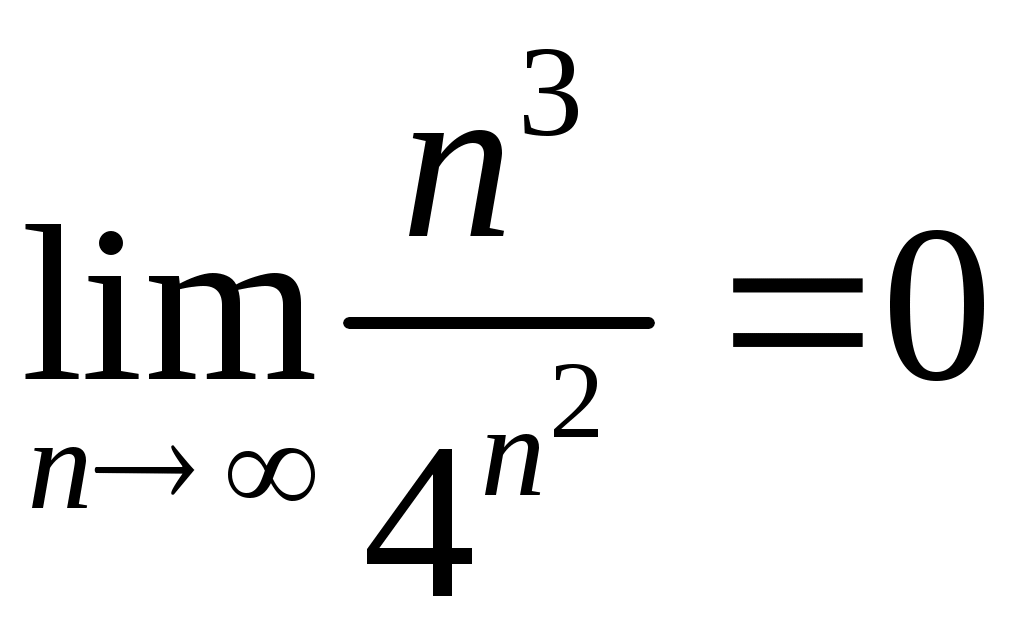 . 10.24. . 10.24. 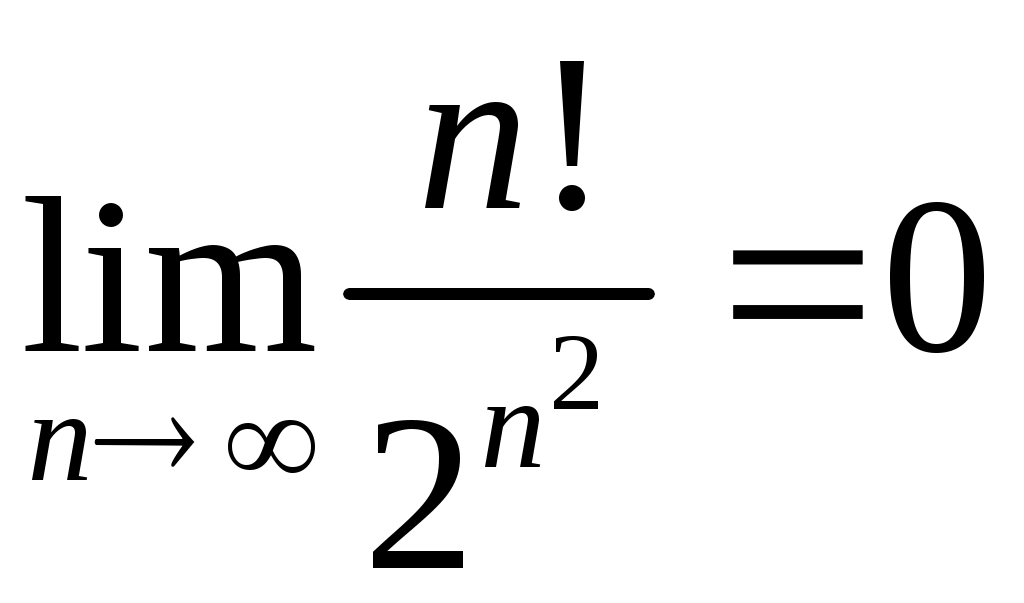 . .10.25. 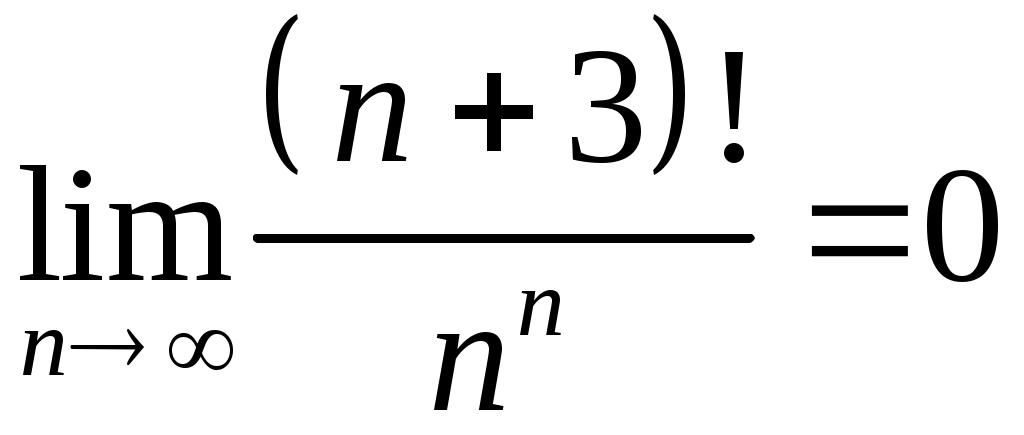 . 10.26. . 10.26. 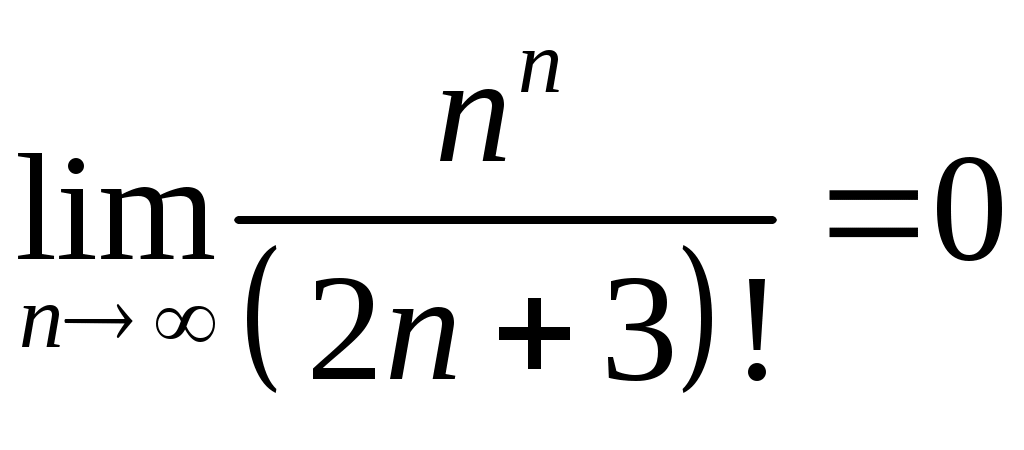 . .10.27. 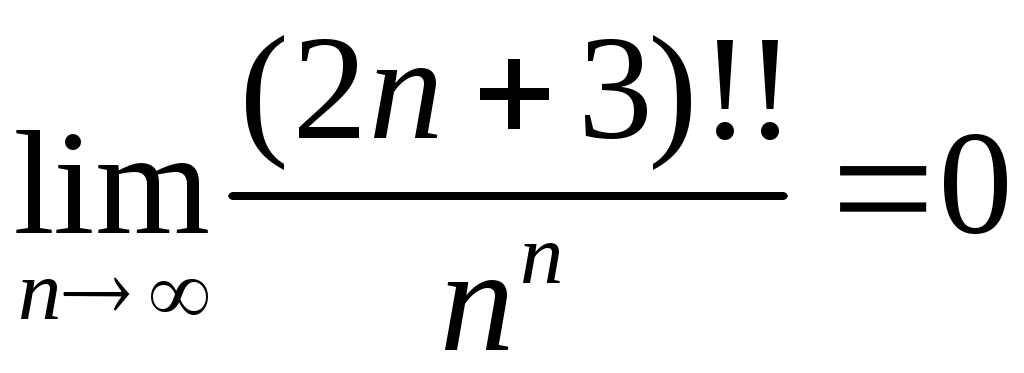 . 10.28. . 10.28. 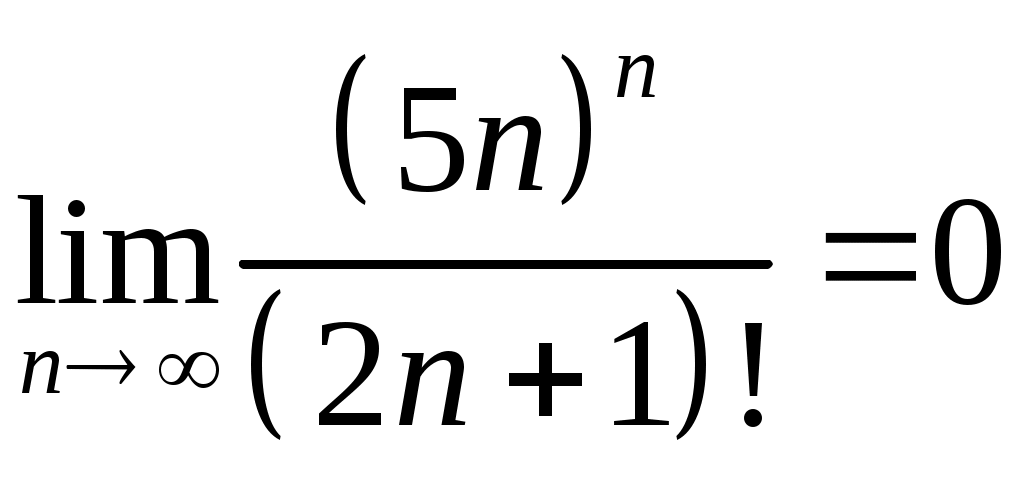 . .10.29. 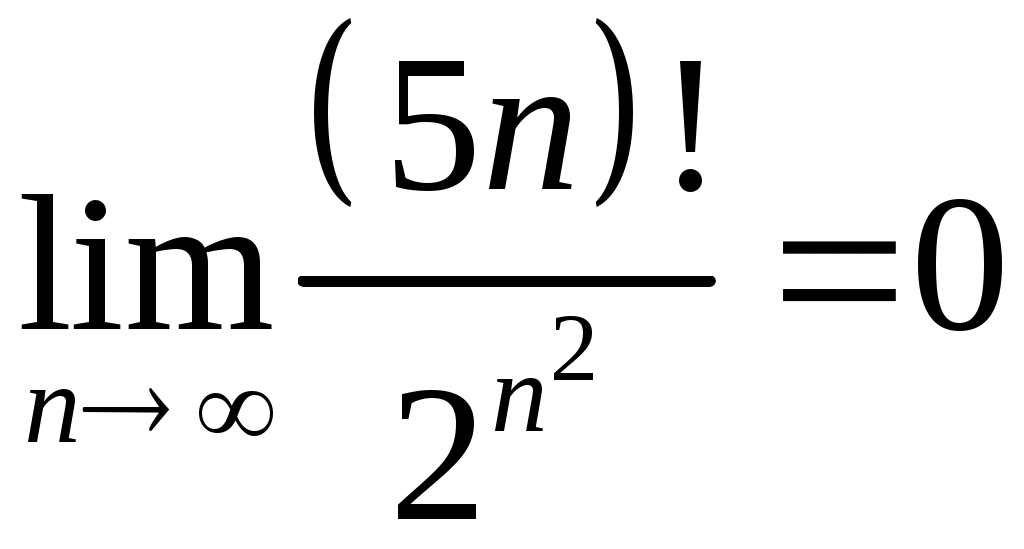 . 10.30. . 10.30. 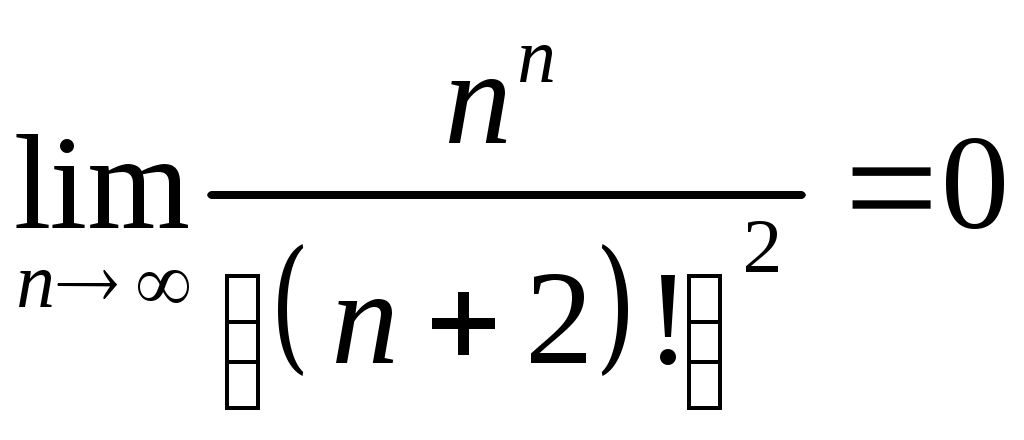 . .10.31. 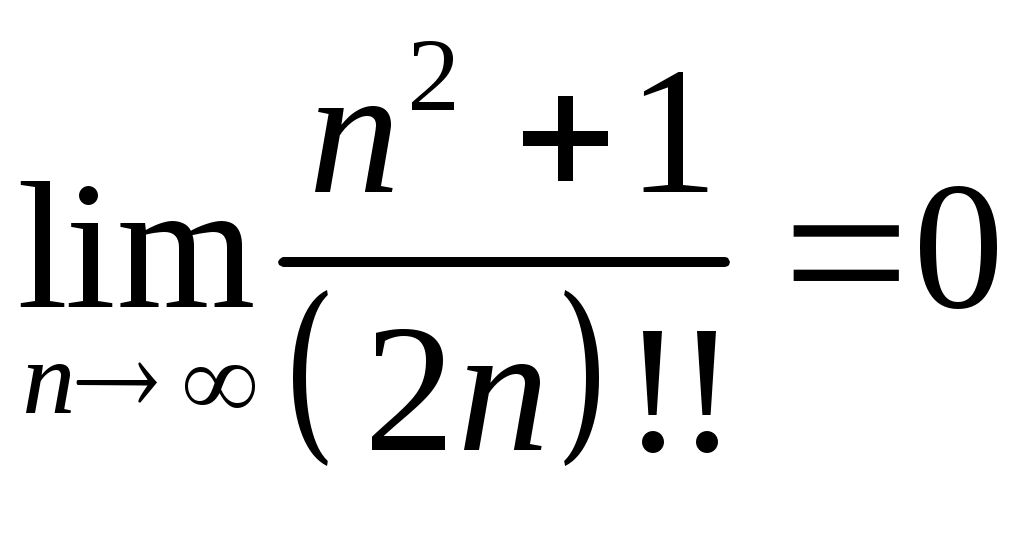 . .Задача 11. Найти область сходимости функционального ряда. 11.1. 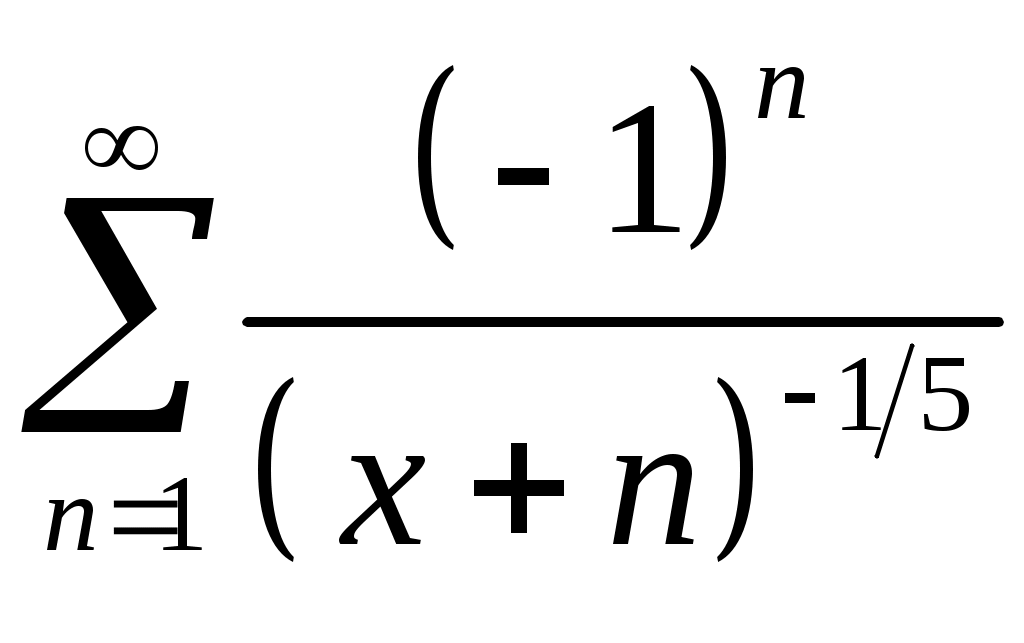 . 11.2. . 11.2. 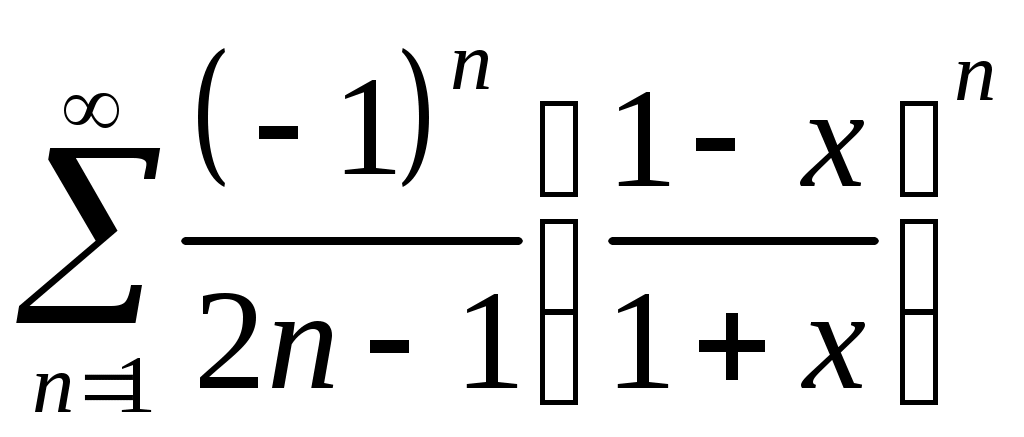 . . 11.3. 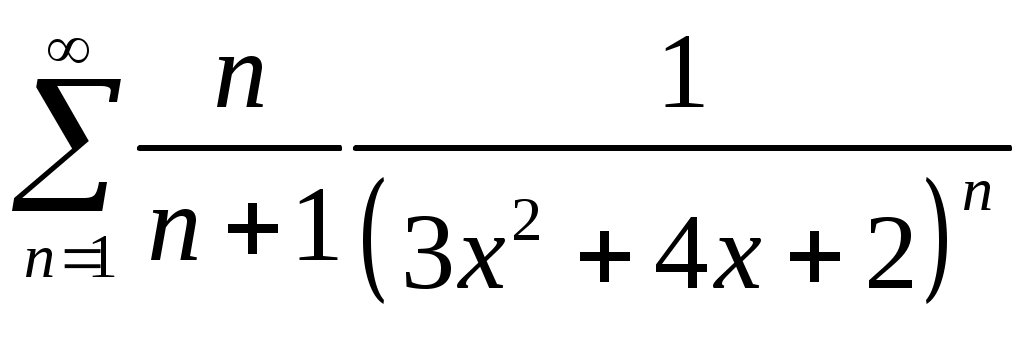 . 11.4. . 11.4. 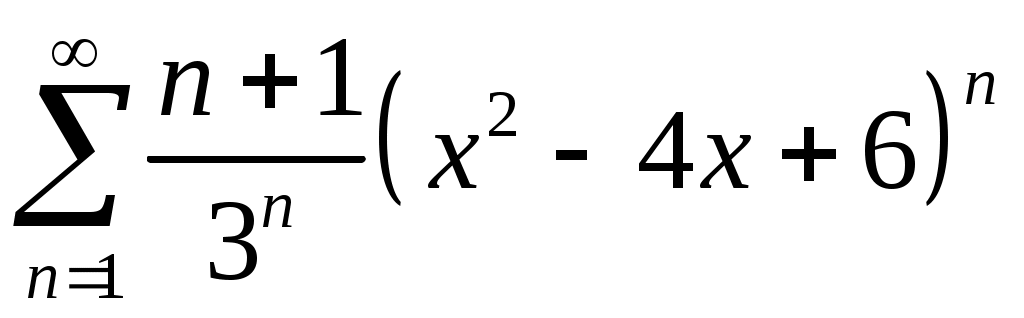 . .11.5. 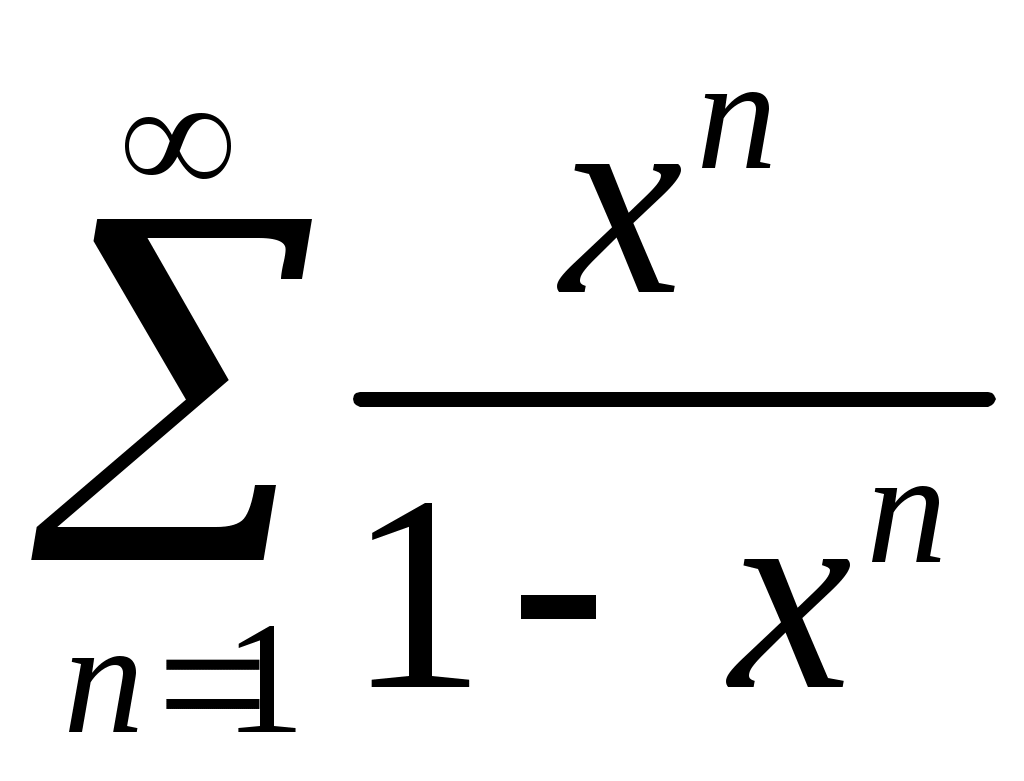 . 11.6. . 11.6. 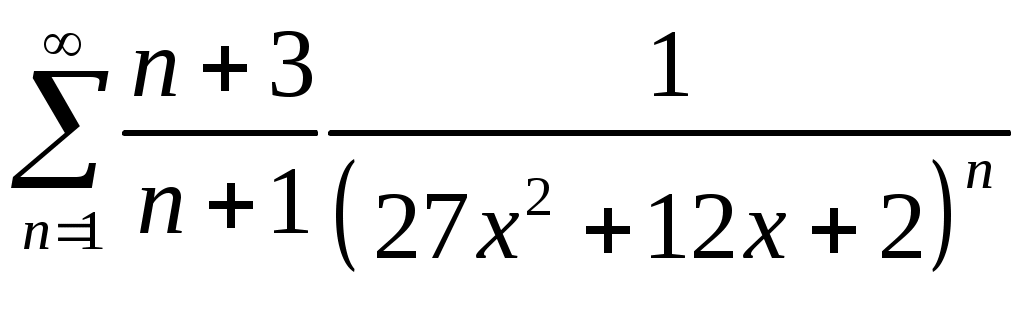 . .11.7. 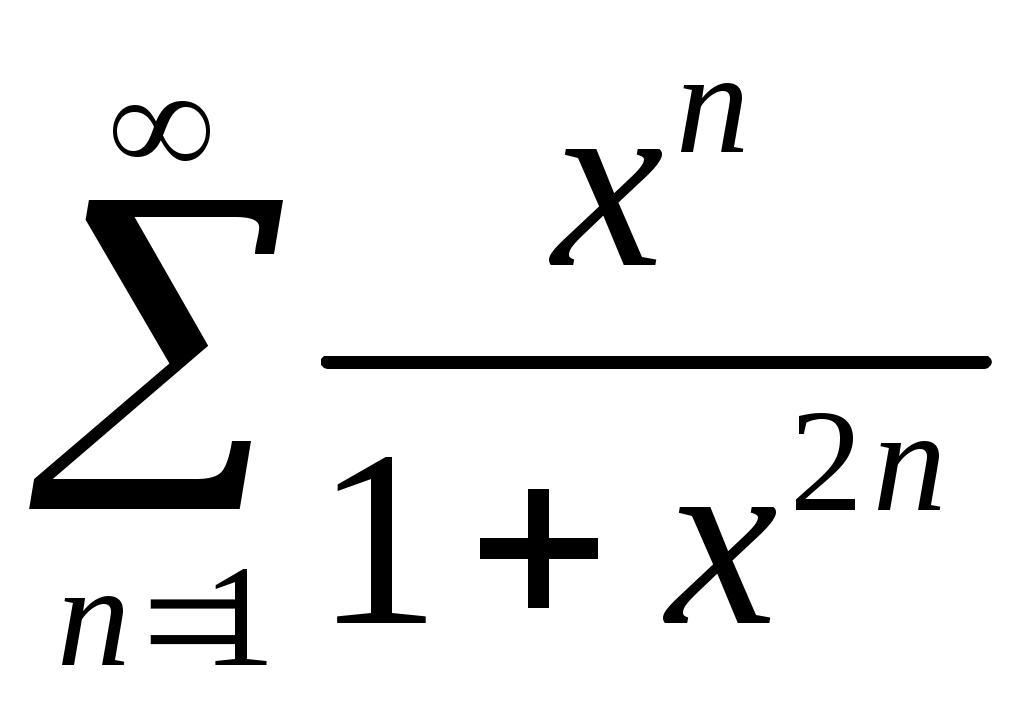 . 11.8. . 11.8. 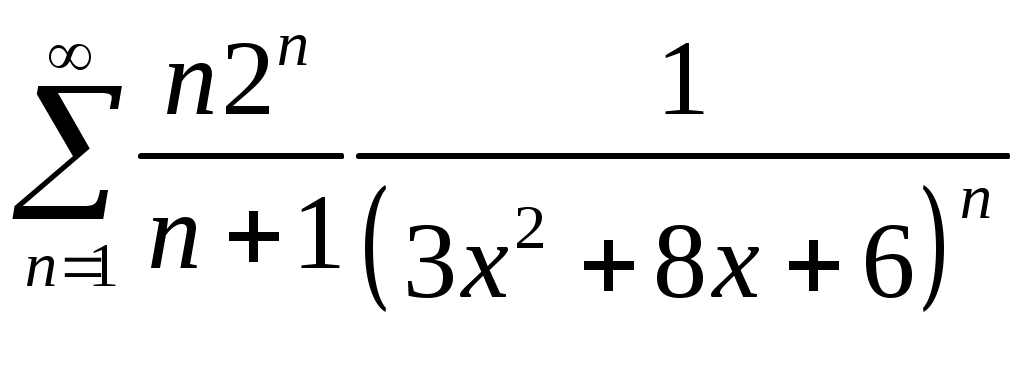 . .11.9. 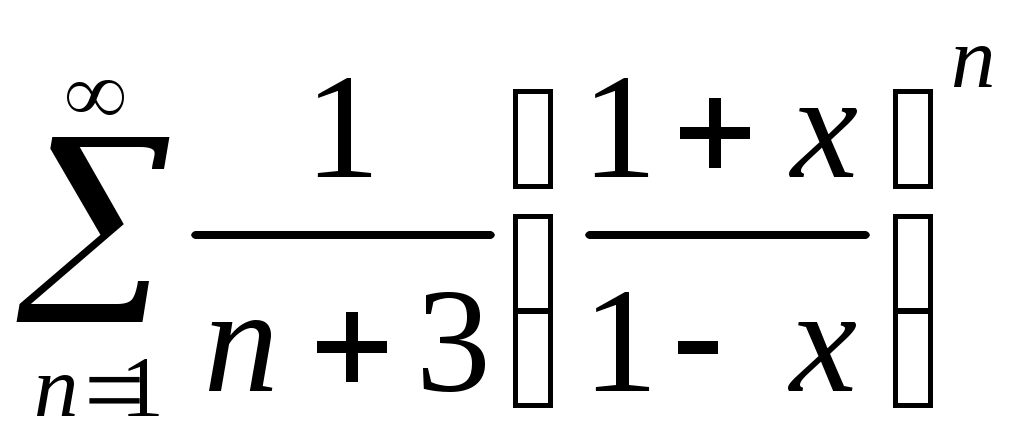 . 11.10. . 11.10. 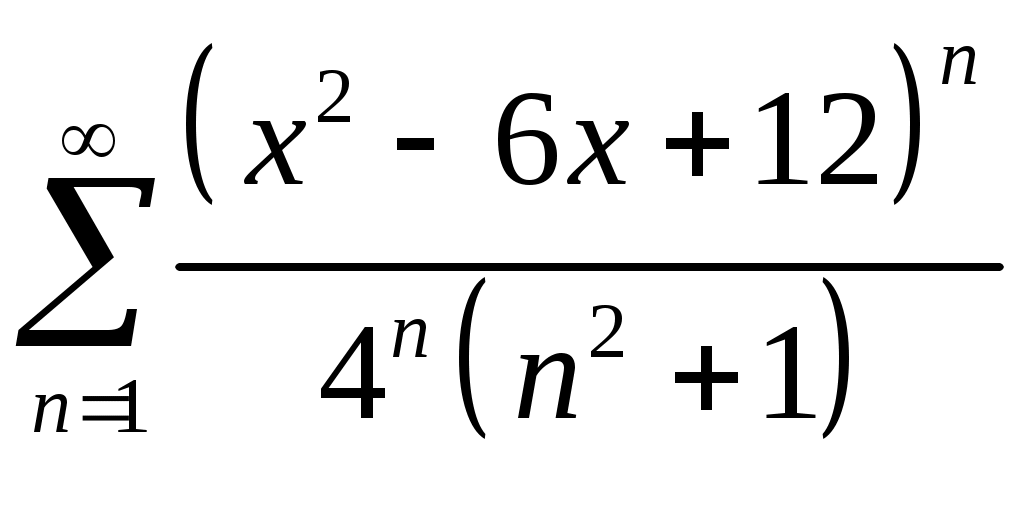 . .11.11. 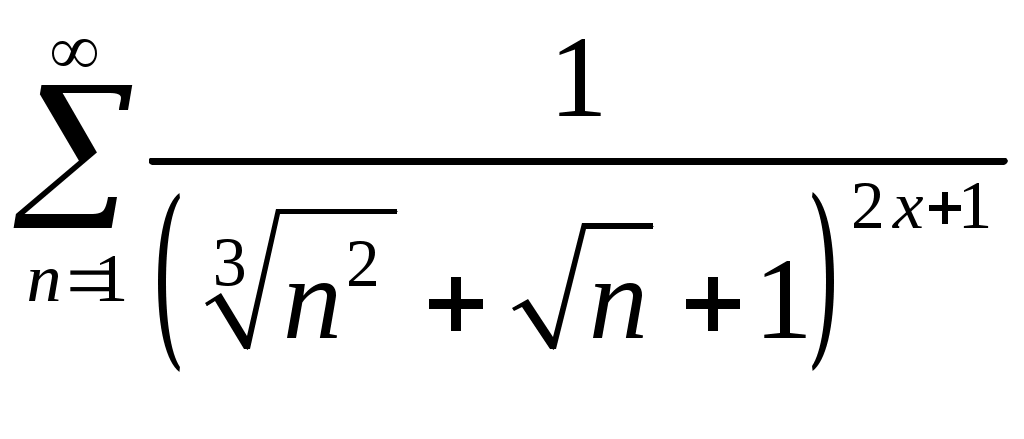 . 11.12. . 11.12. 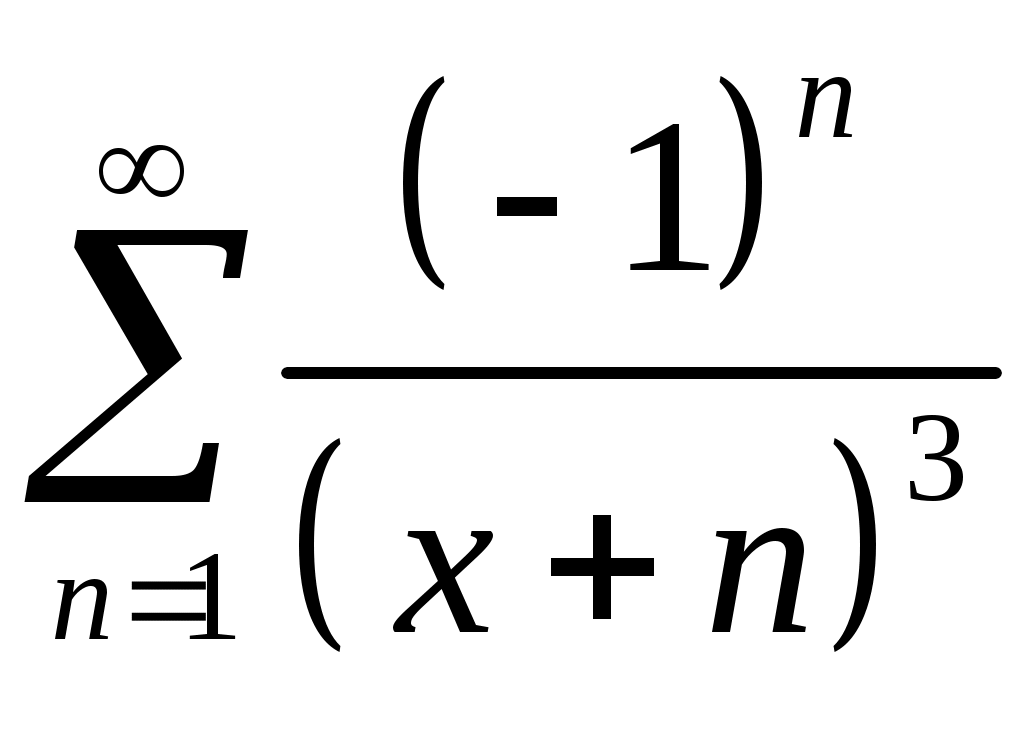 . .11.13. 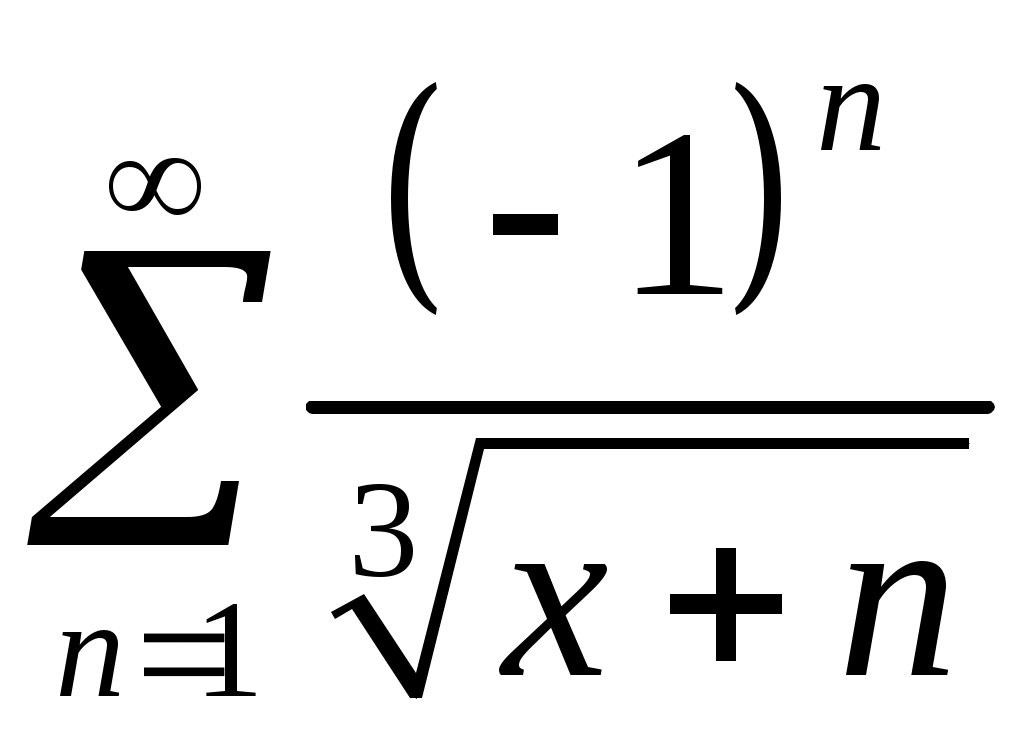 . 11.14. . 11.14. 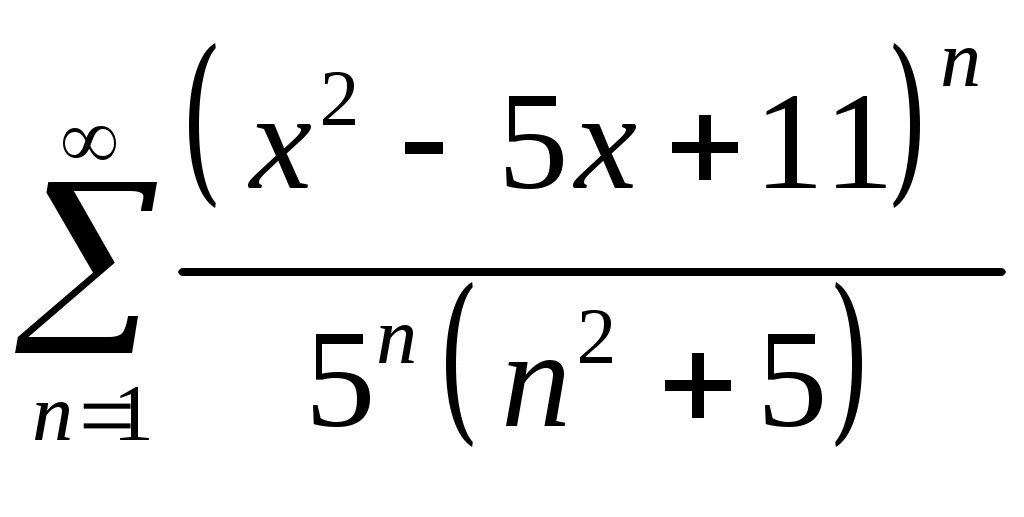 . .11.15. 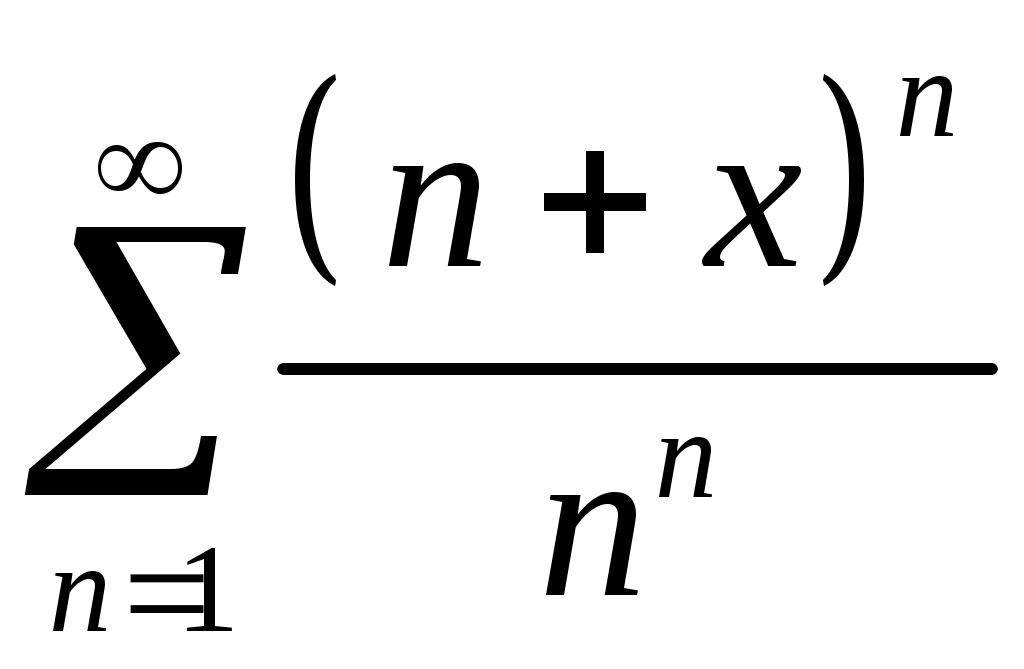 . 11.16. . 11.16. 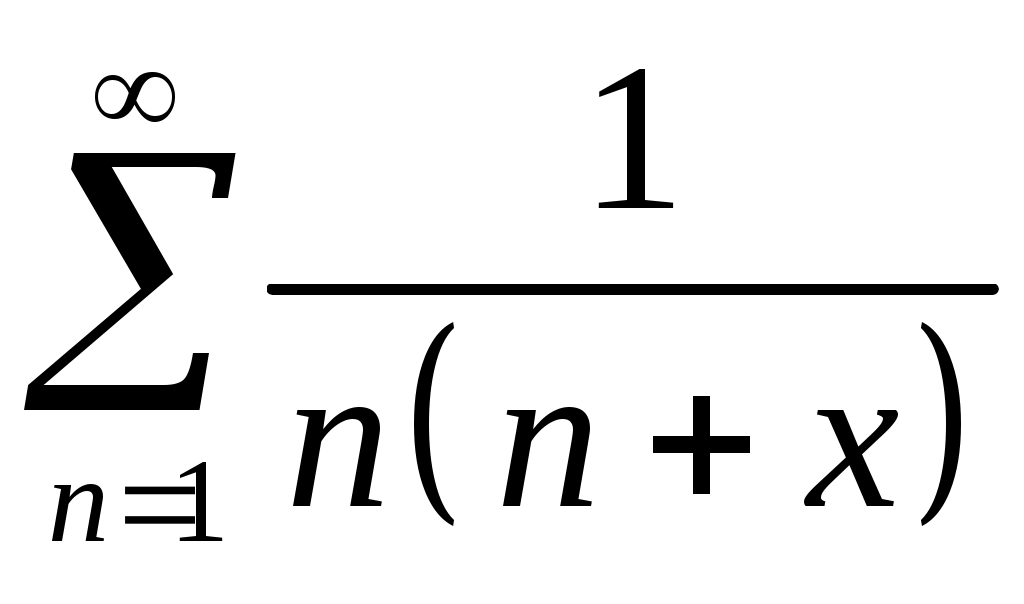 . .11.17. 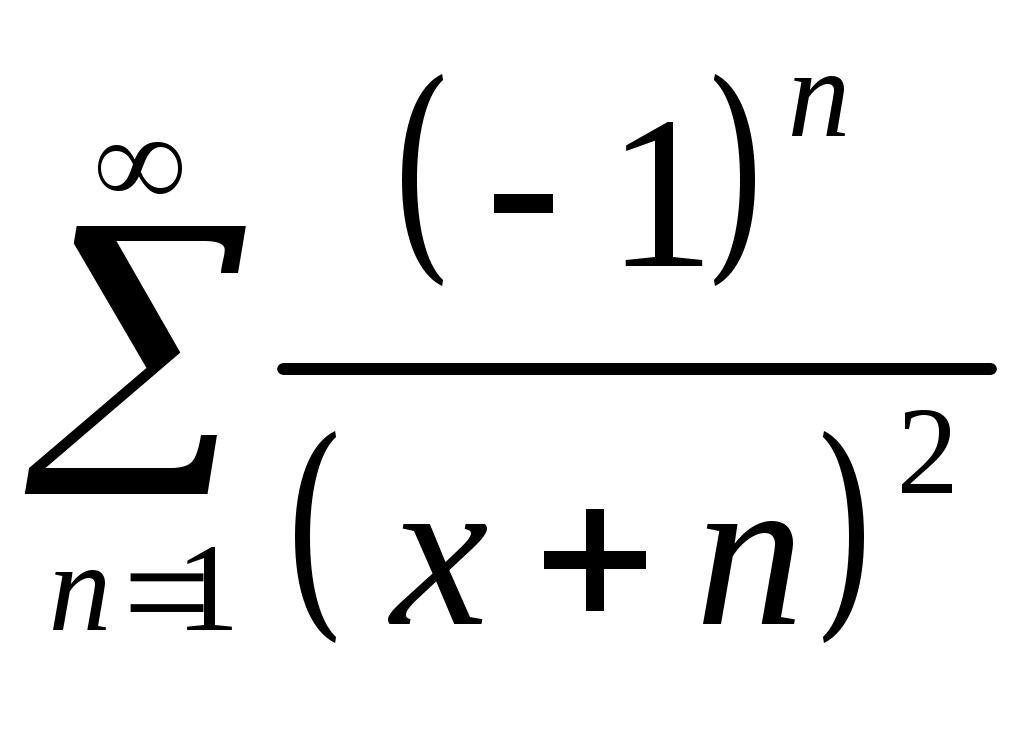 . 11.18. . 11.18. 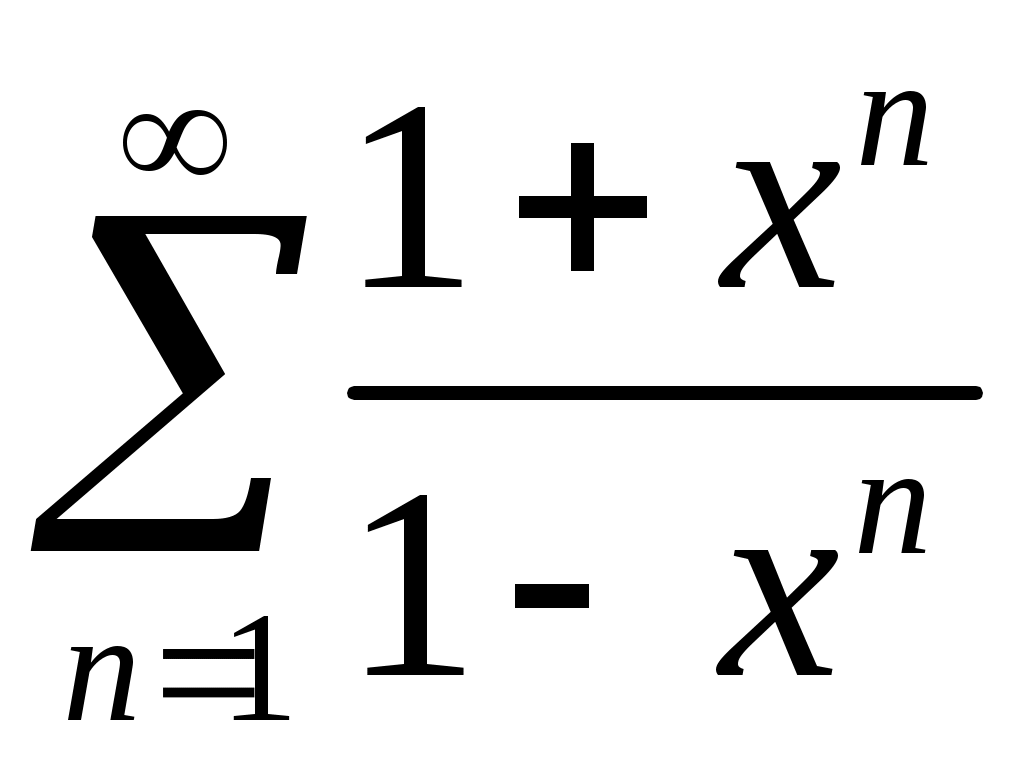 . .11.19. 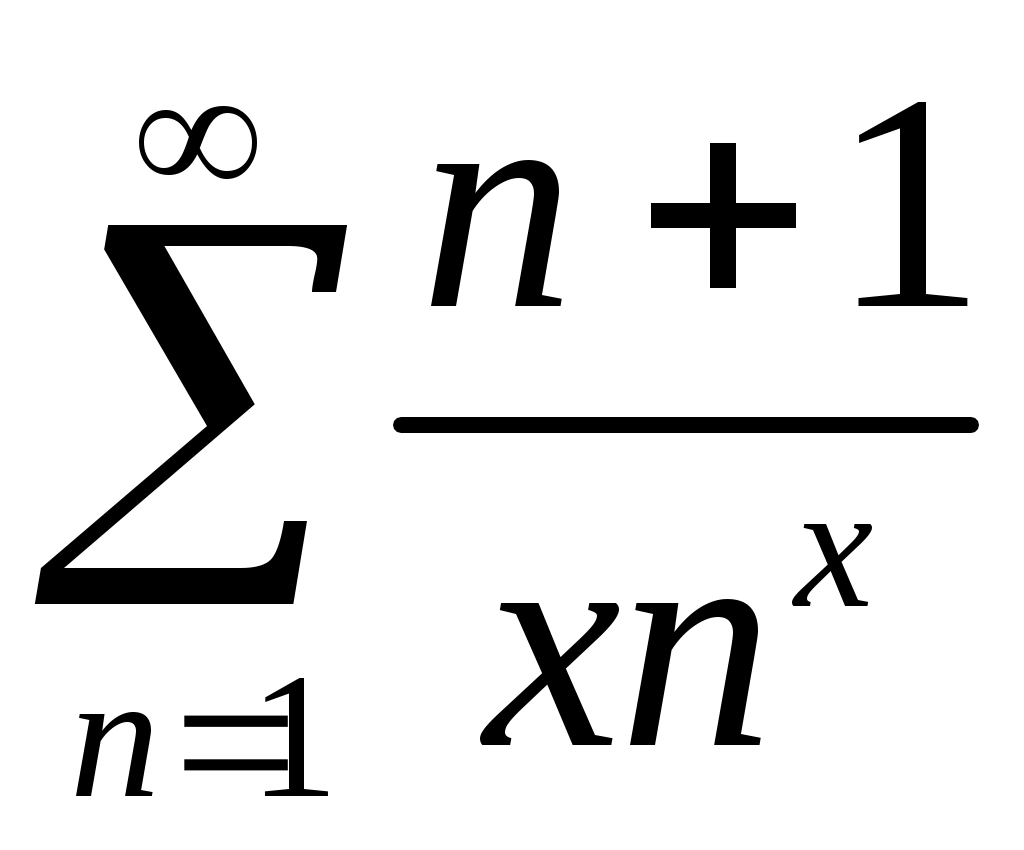 . 11.20. . 11.20. 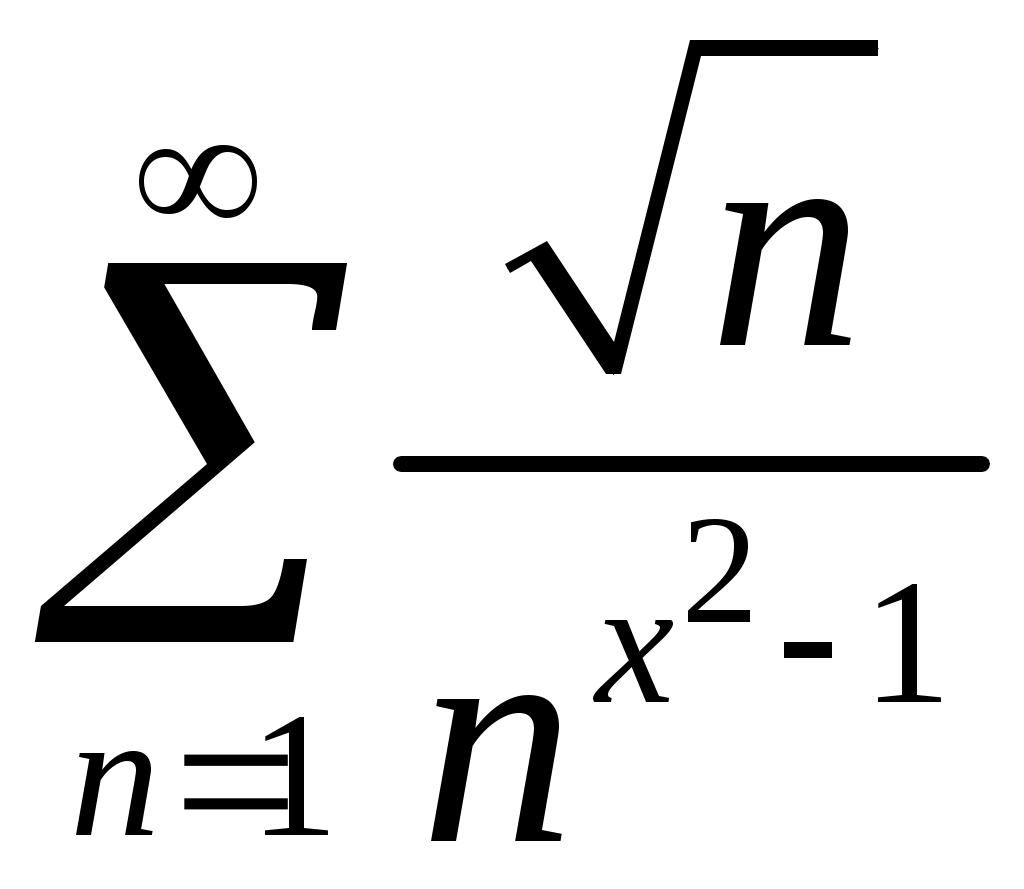 . .11.21. 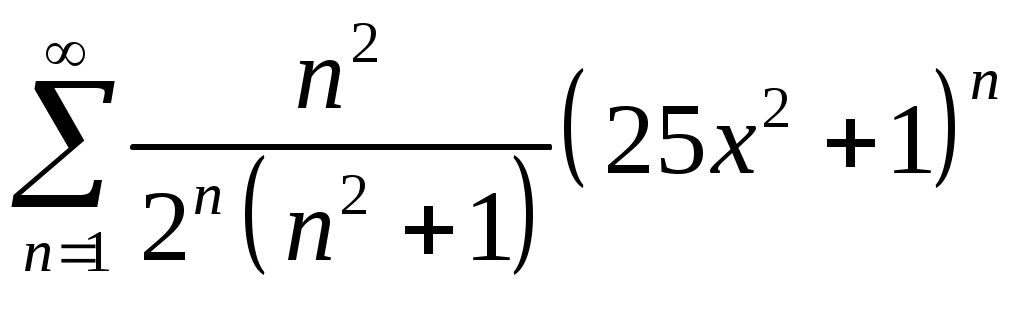 . 11.22. . 11.22. 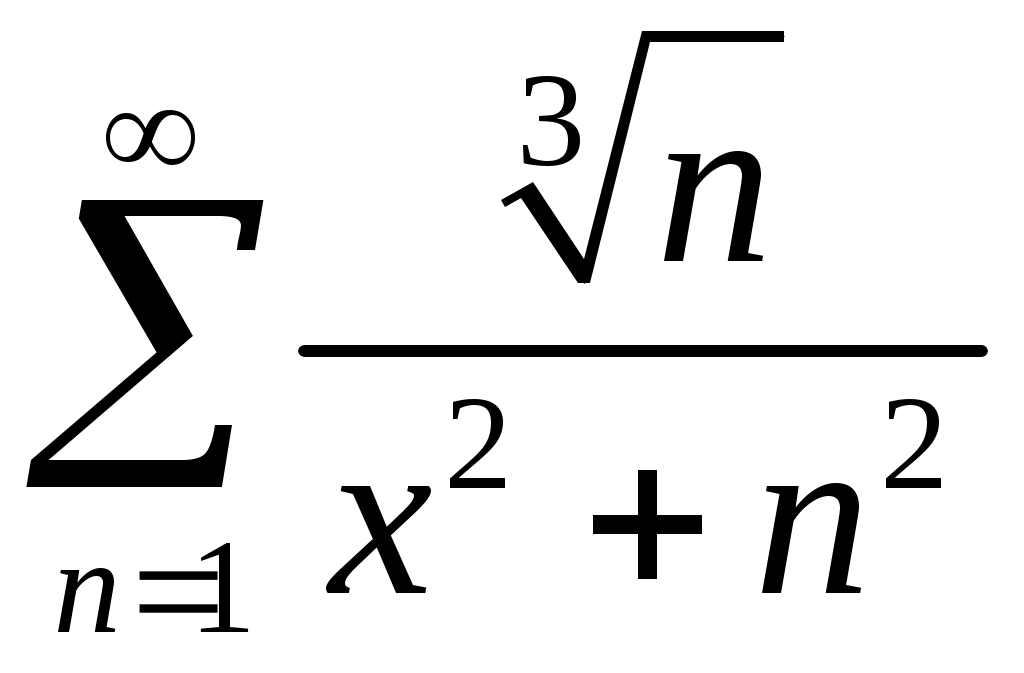 . .11.23. 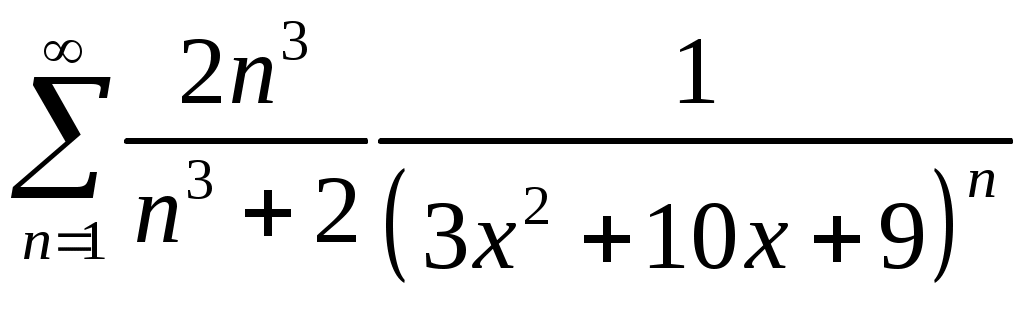 . 11.24. . 11.24. 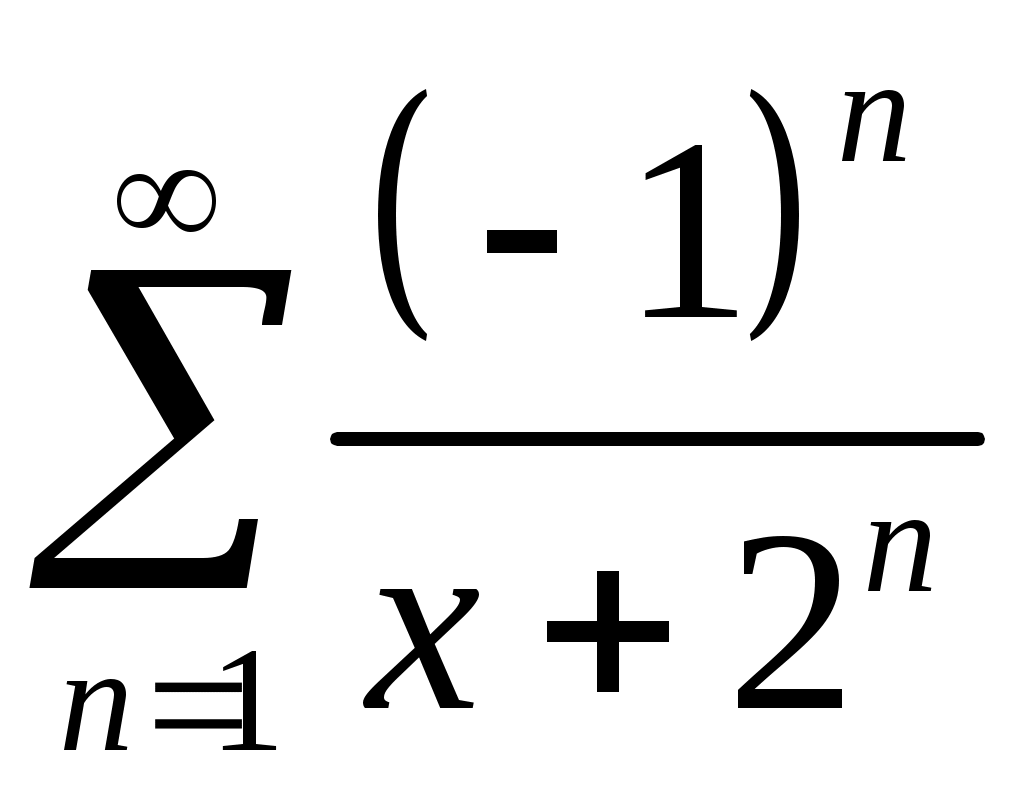 . .11.25. 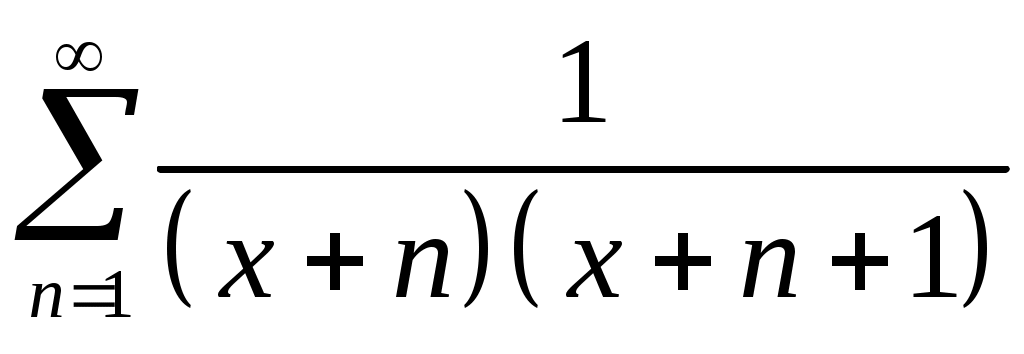 . 11.26. . 11.26. 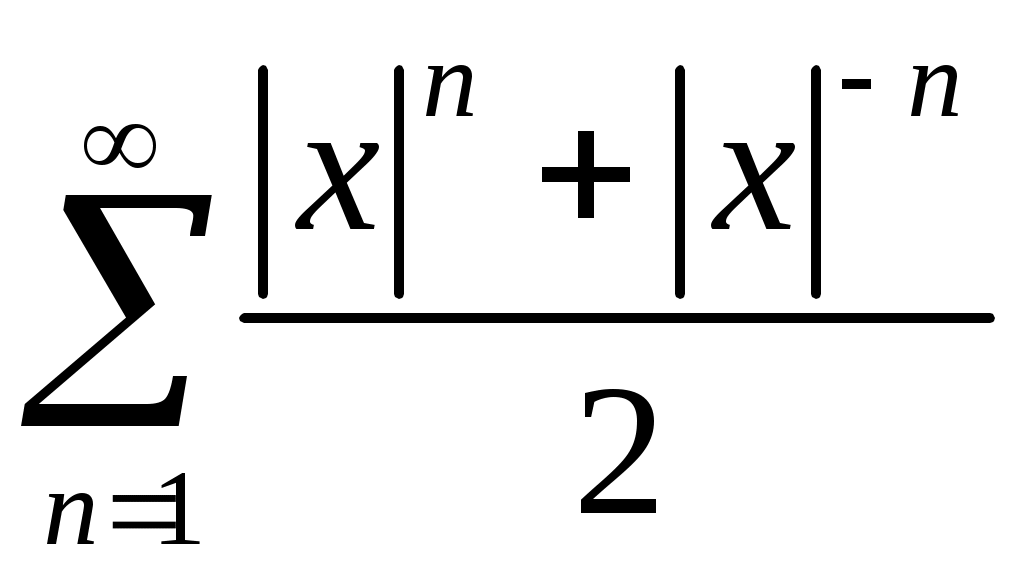 . .11.27. 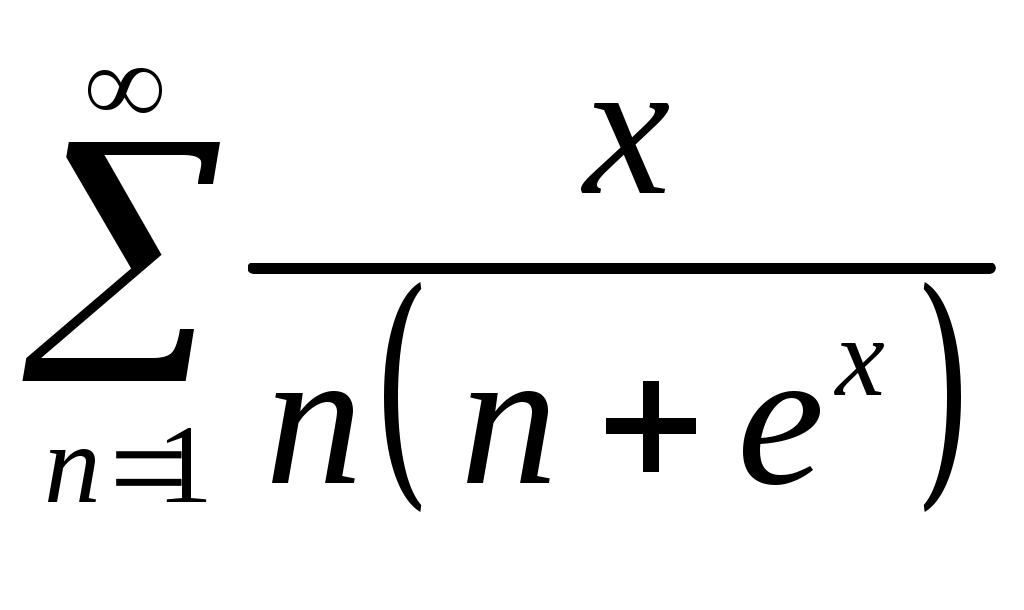 . 11.28. . 11.28. 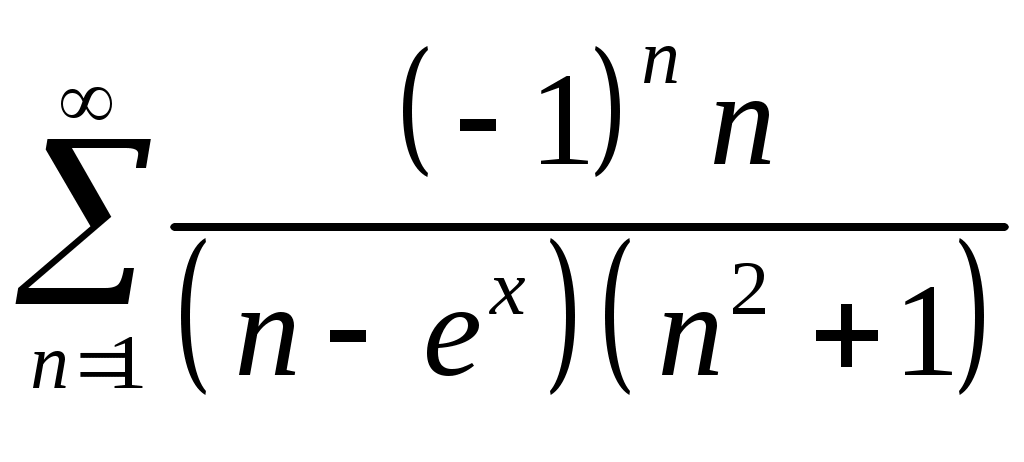 . .11.29. 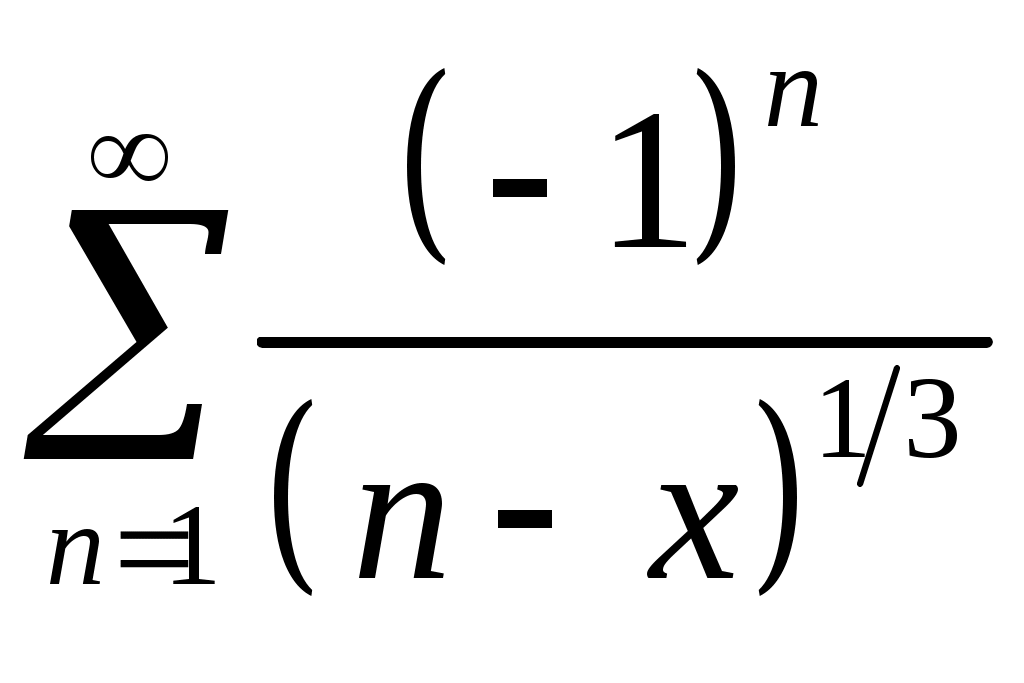 . 11.30. . 11.30. 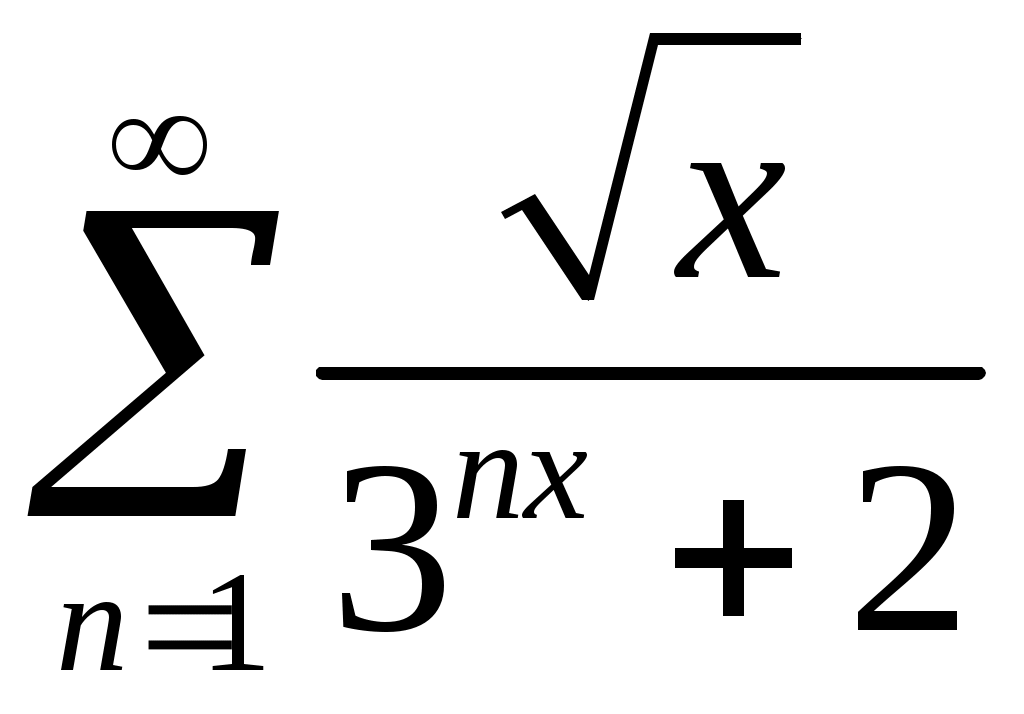 . .11.31. 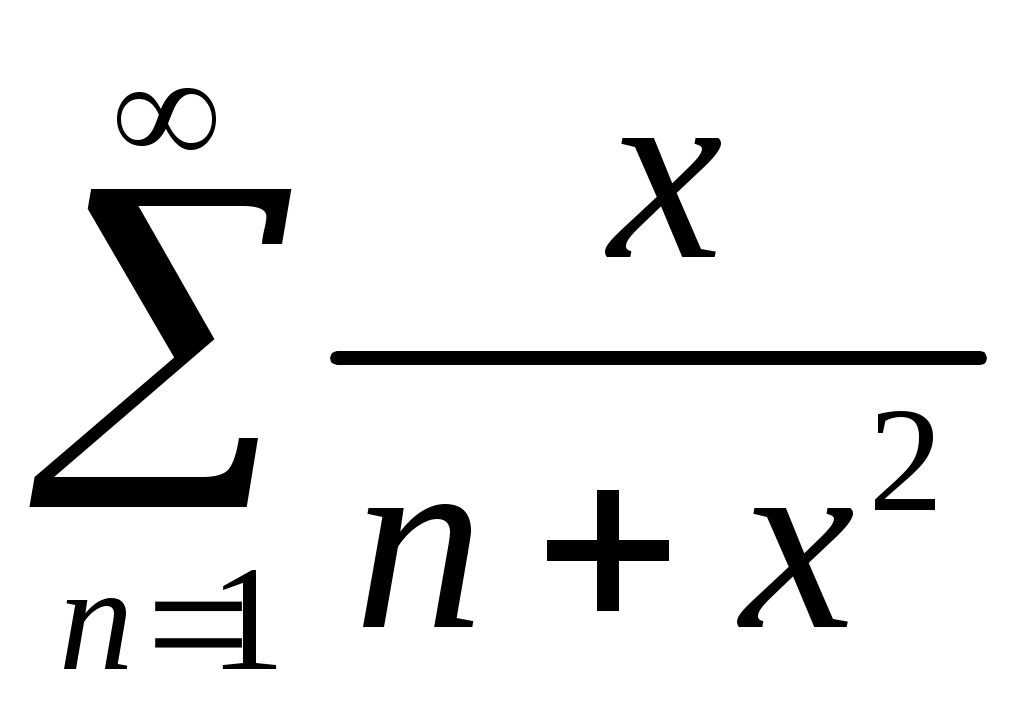 . .Задача 12. Найти область сходимости функционального ряда. 12.1. 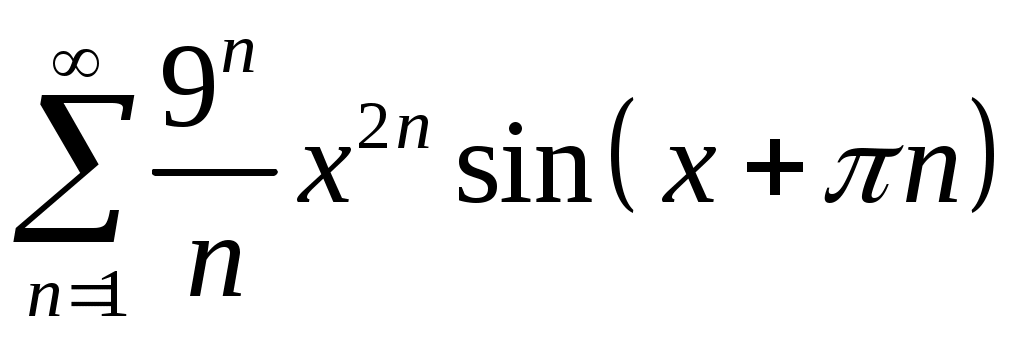 . 12.2. . 12.2. 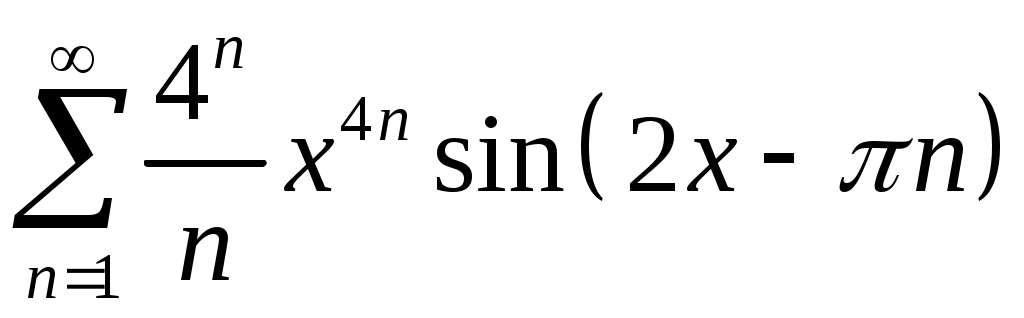 . .12.3. 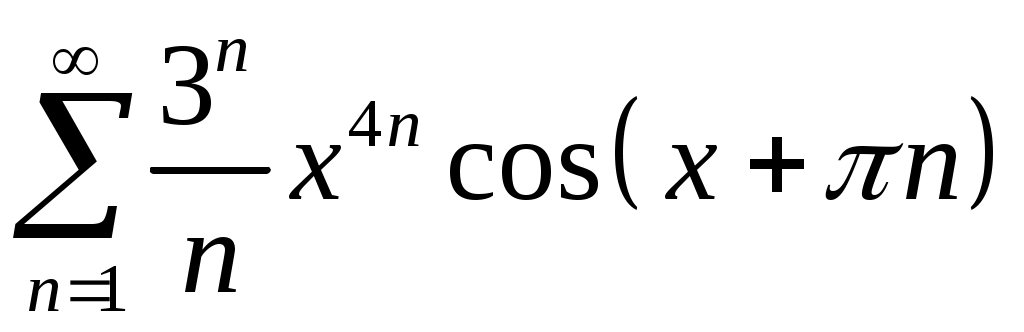 . 12.4. . 12.4. 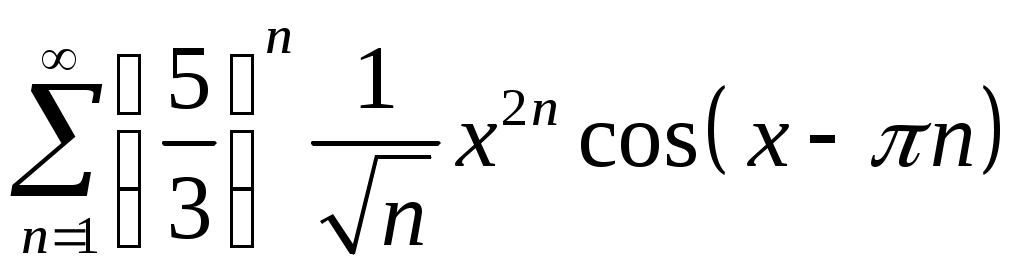 . .12.5. 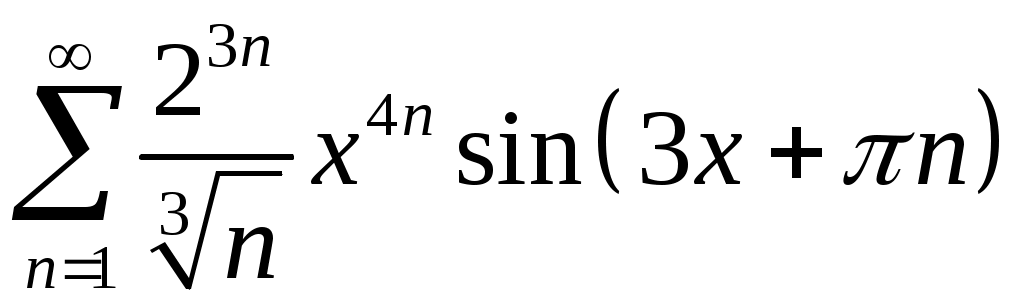 . 12.6. . 12.6. 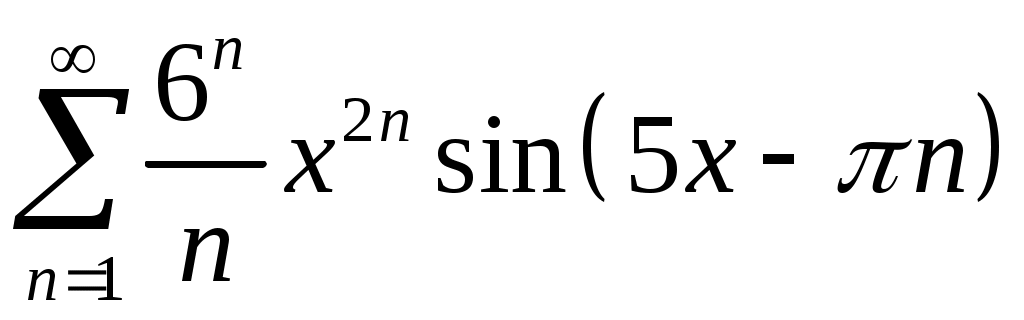 . .12.7. 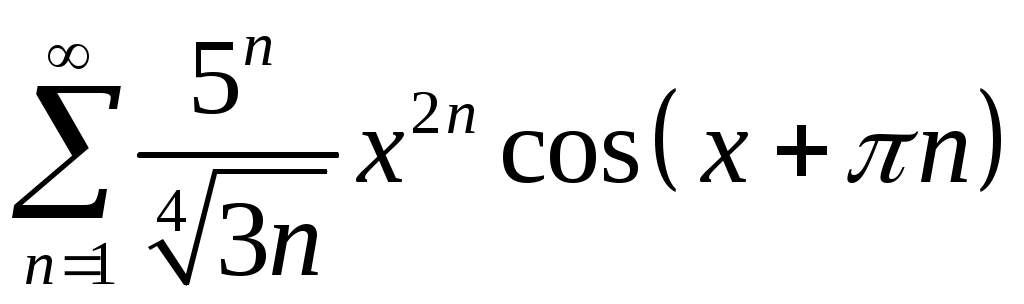 . 12.8. . 12.8. 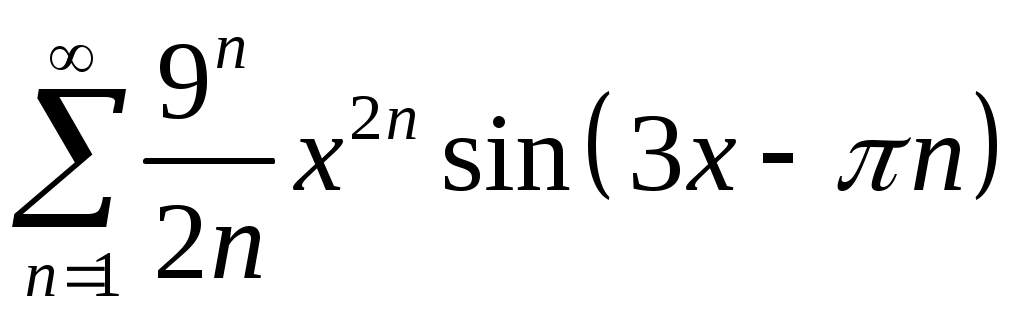 . .12.9. 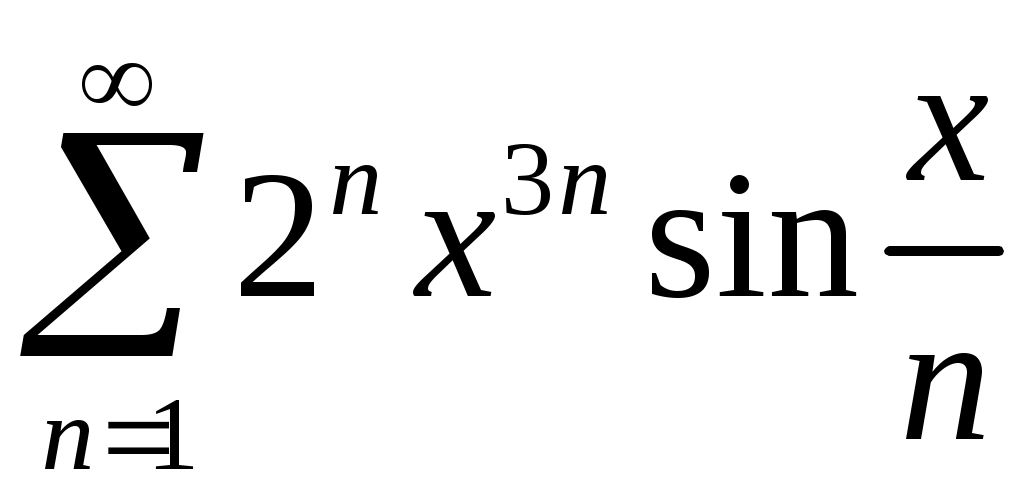 . 12.10. . 12.10. 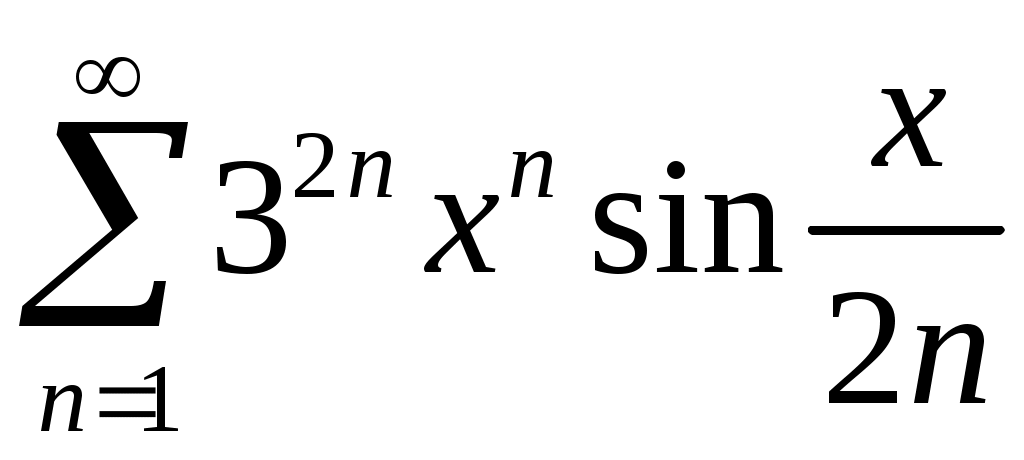 . .12.11. 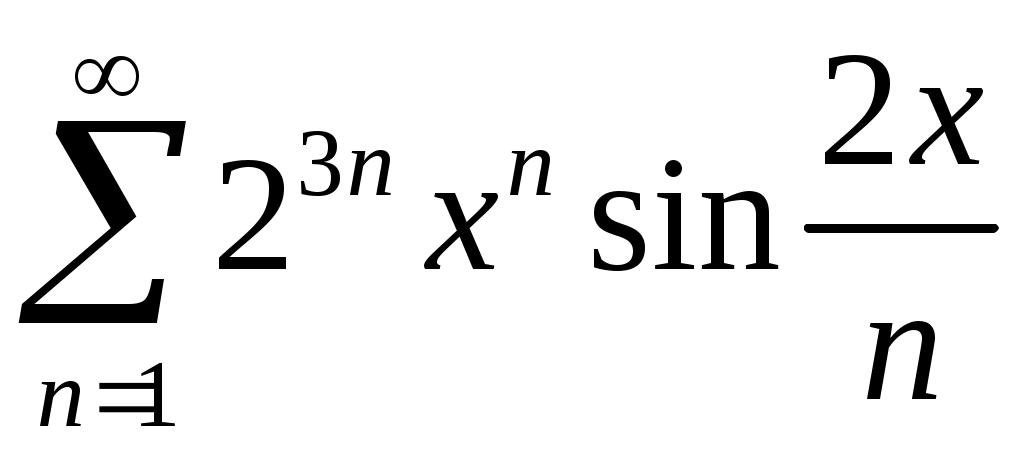 . 12.12. . 12.12. 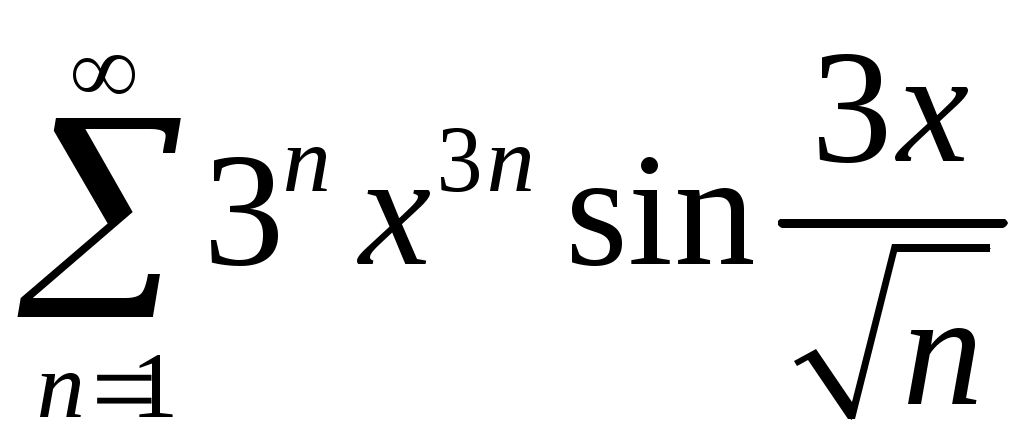 . .12.13. 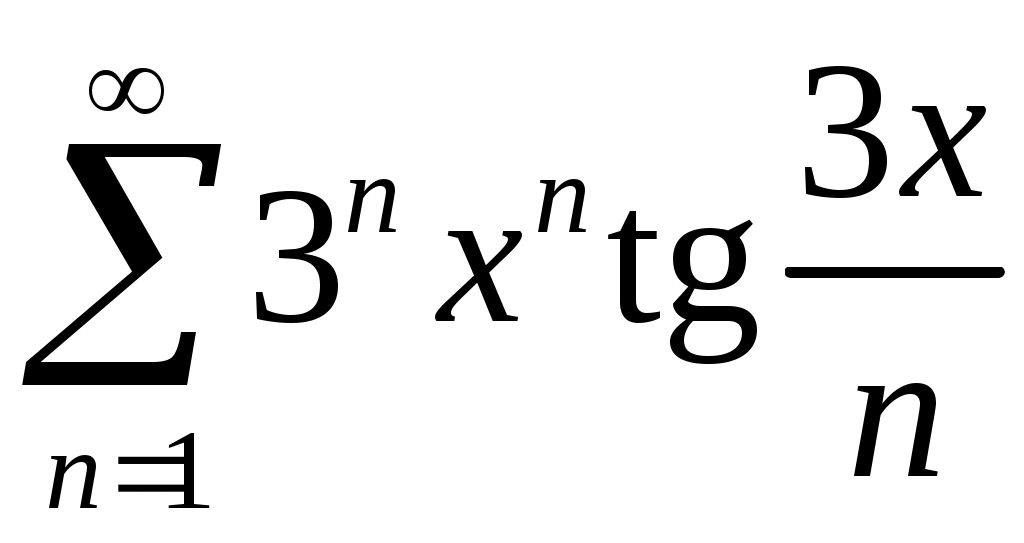 . 12.14. . 12.14. 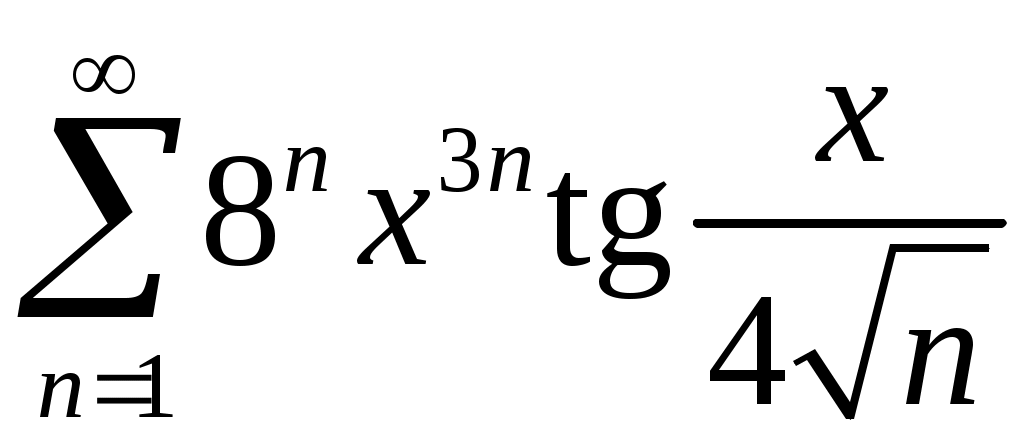 . .12.15. 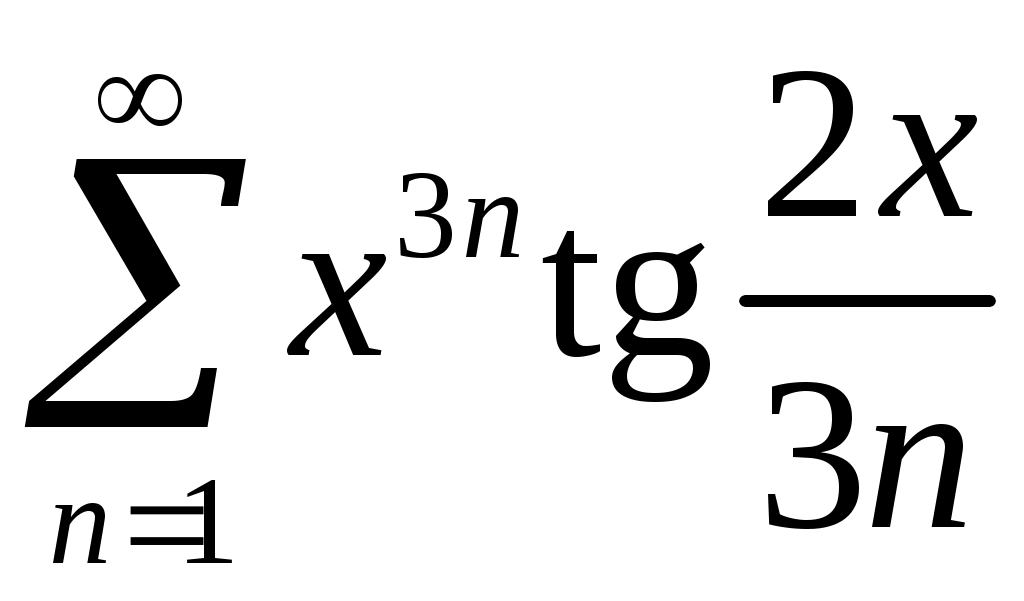 . 12.16. . 12.16. 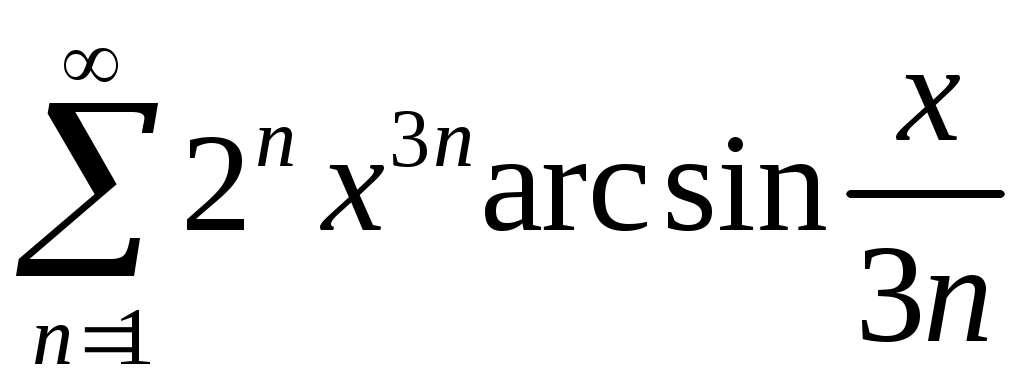 . .12.17. 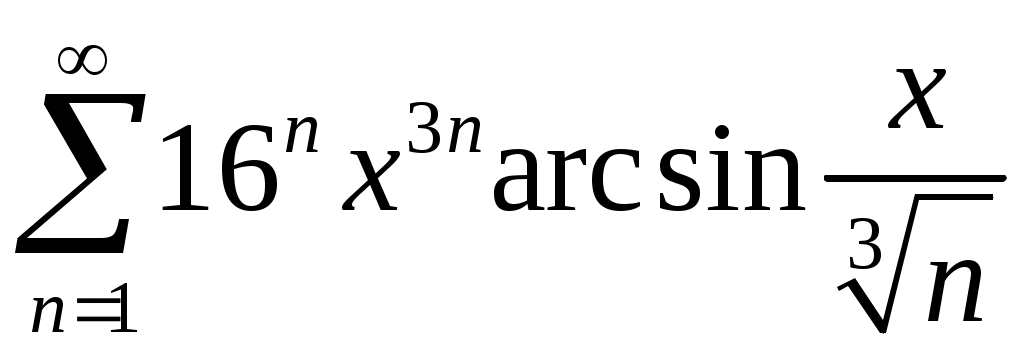 . 12.18. . 12.18. 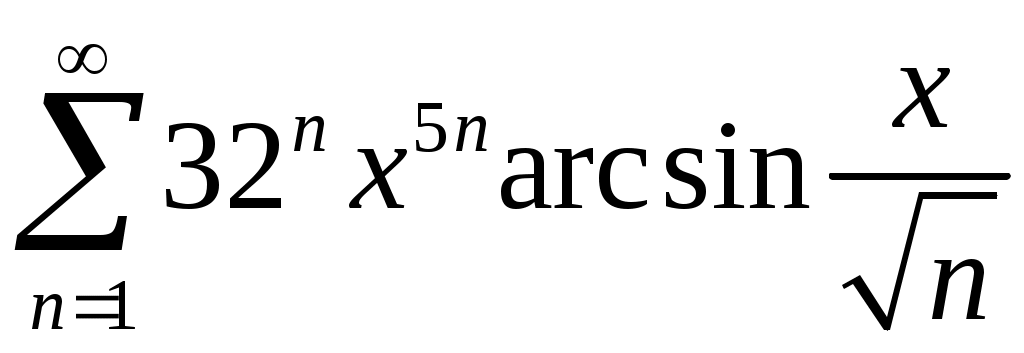 . .12.19. 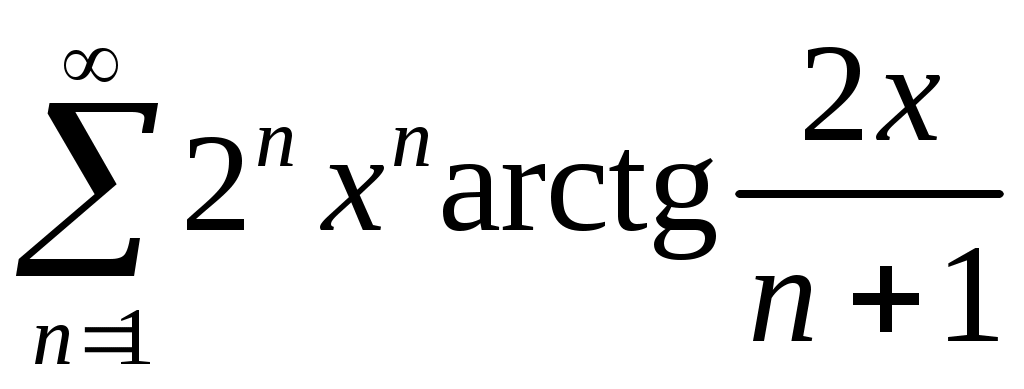 . 12.20. . 12.20. 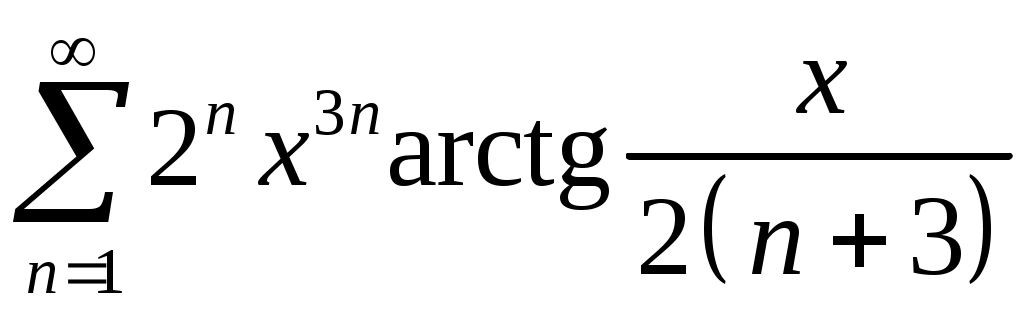 . .12.21. 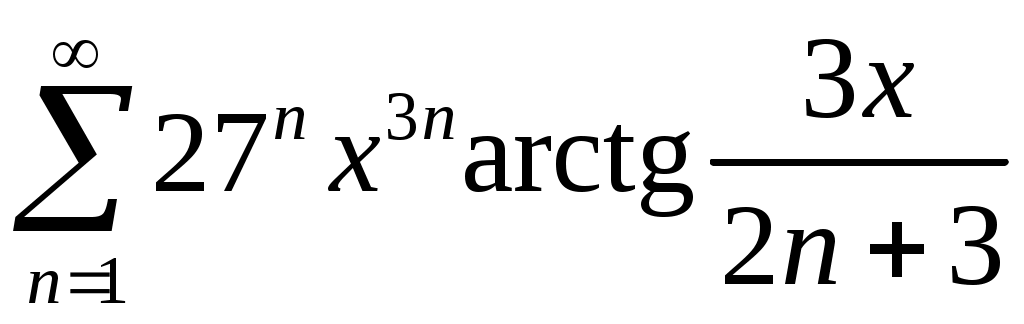 . 12.22. . 12.22. 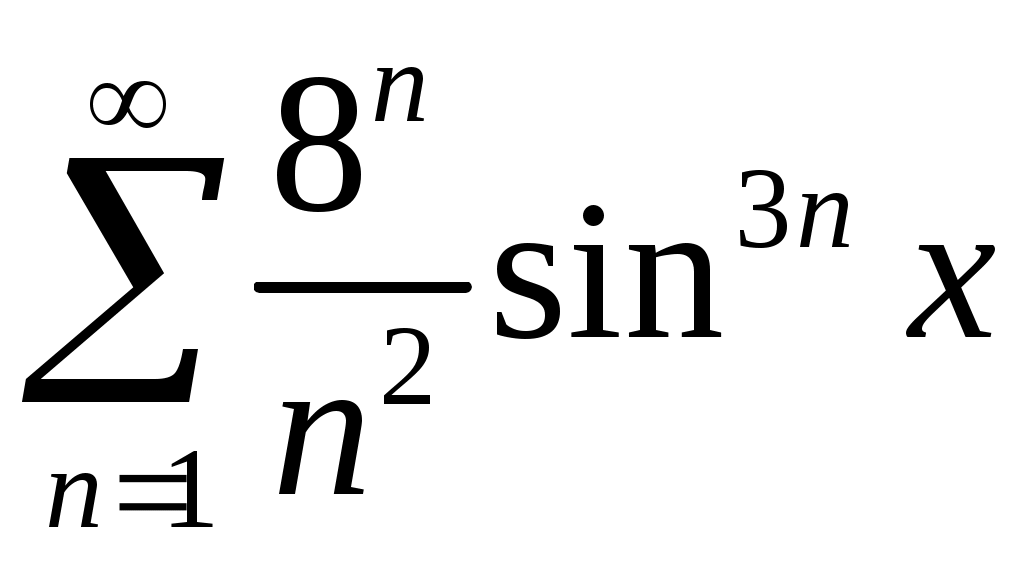 . .12.23. 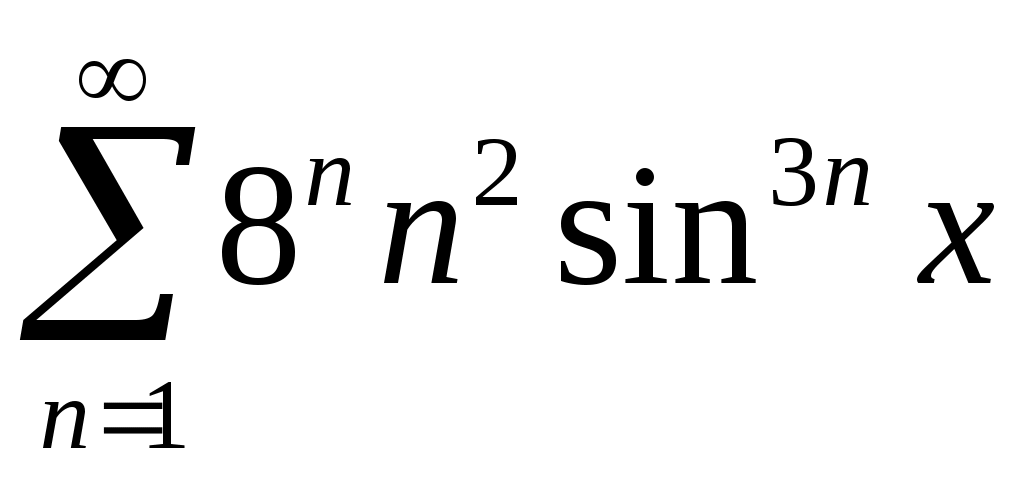 . 12.24. . 12.24. 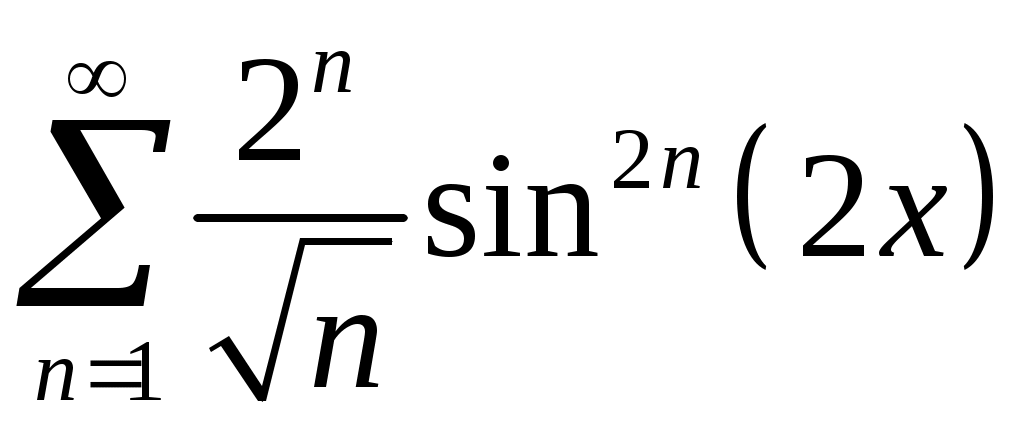 . .12.25. 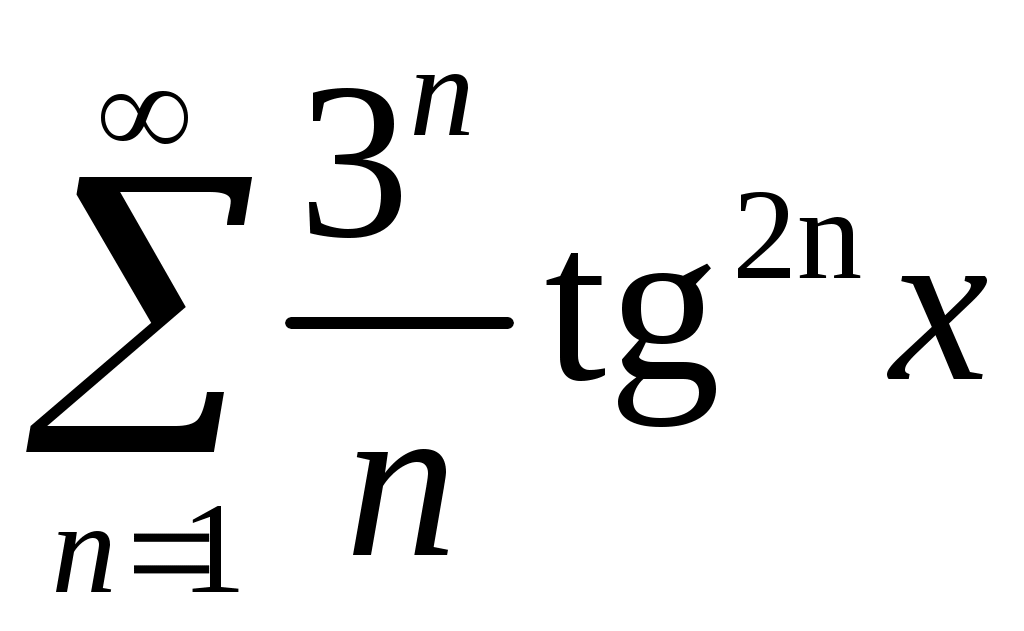 . 12.26. . 12.26. 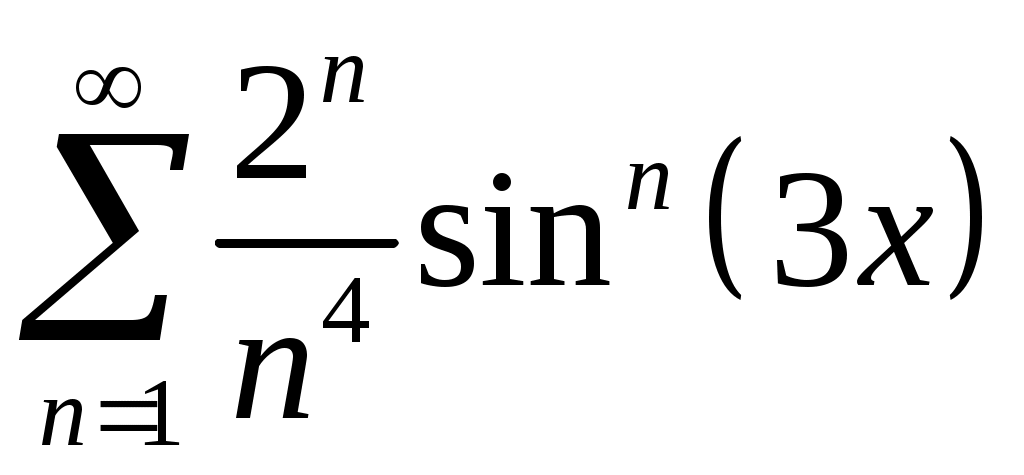 . .12.27. 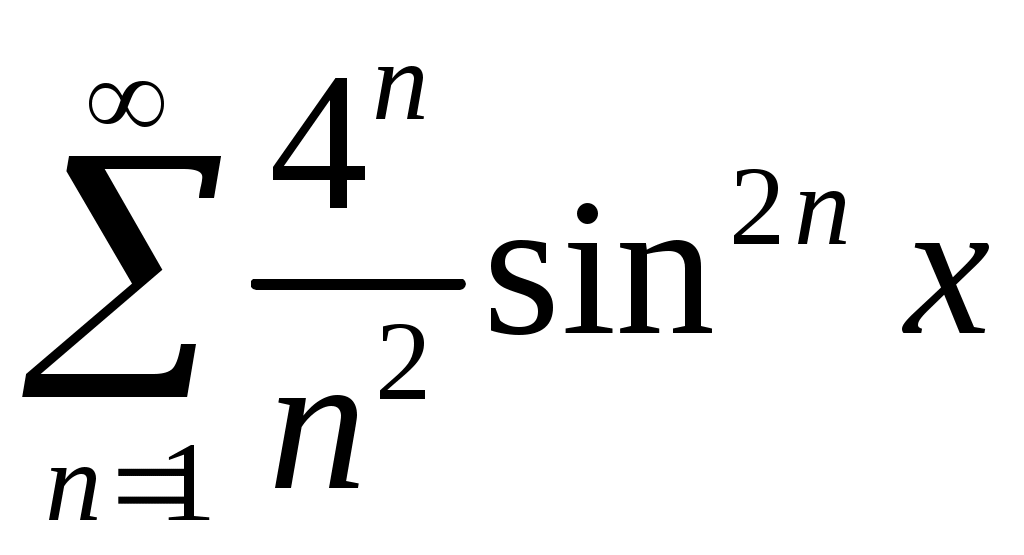 . 12.28. . 12.28. 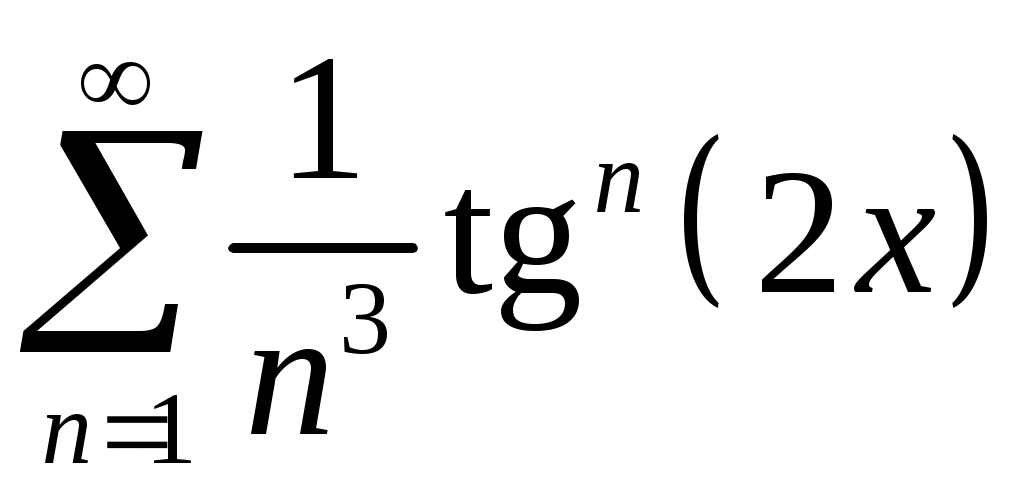 . .12.29. 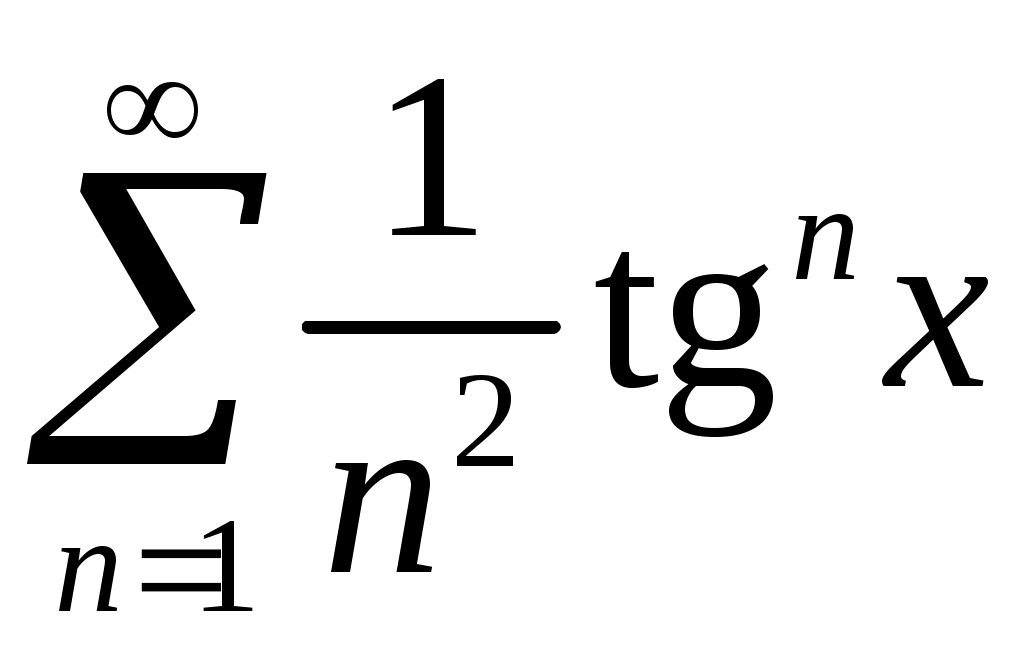 . 12.30. . 12.30. 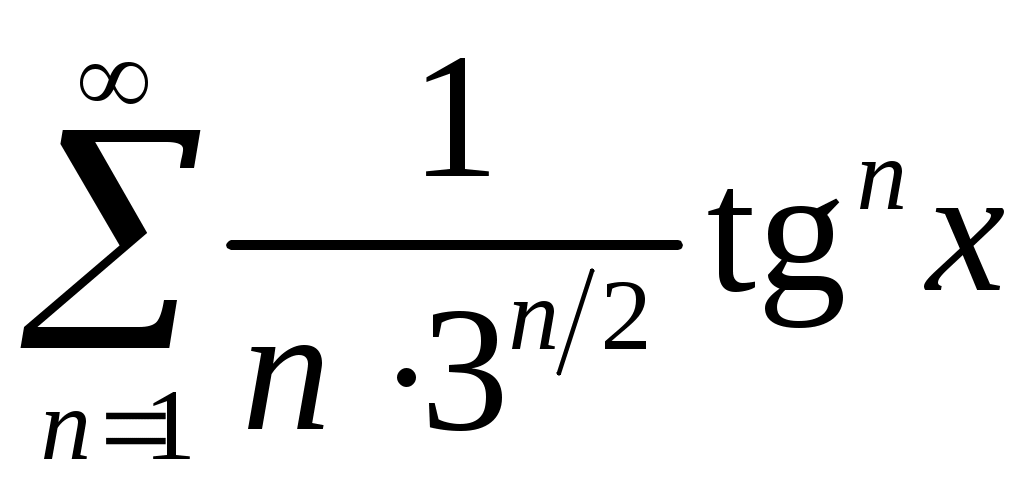 . .12.31. 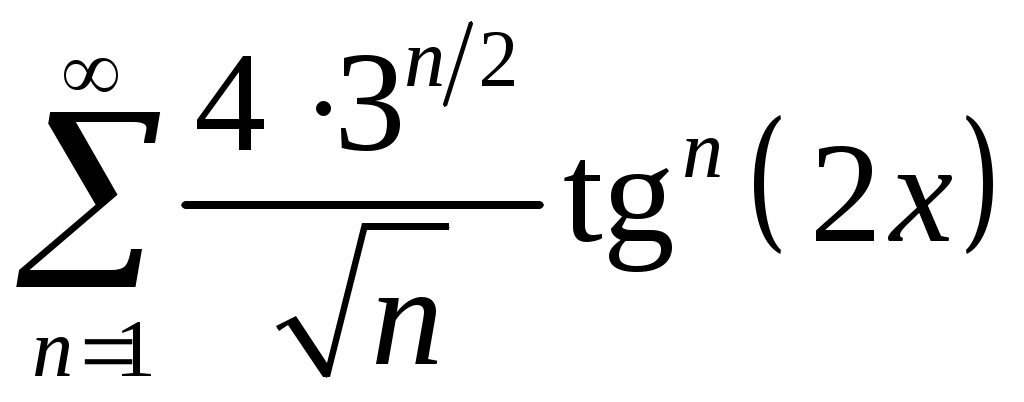 . .Задача 13. Найти область сходимости функционального ряда. 13.1. 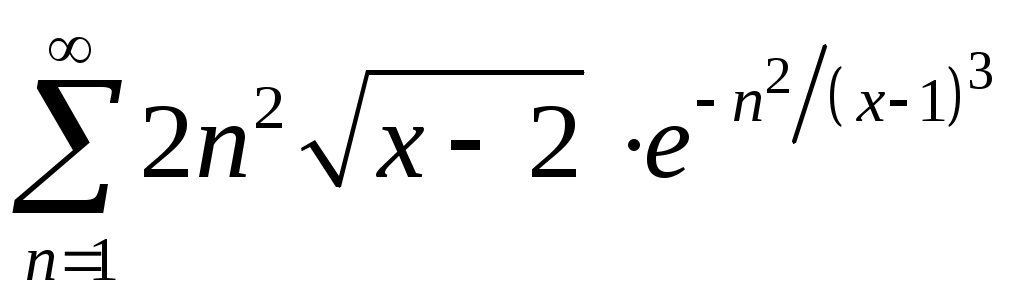 . 13.2. . 13.2. 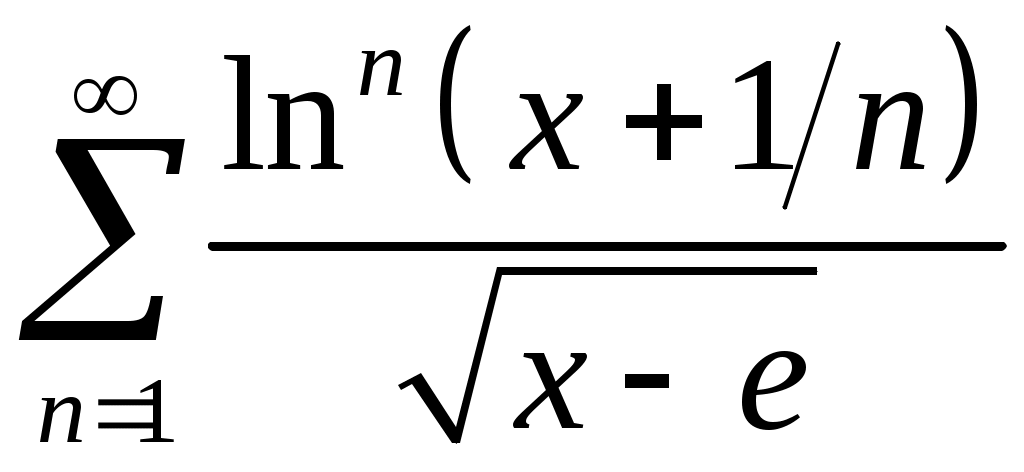 . .13.3. 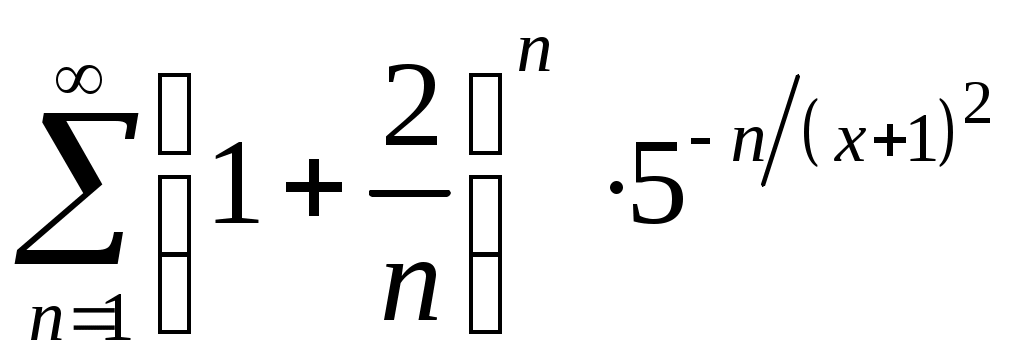 . 13.4. . 13.4. 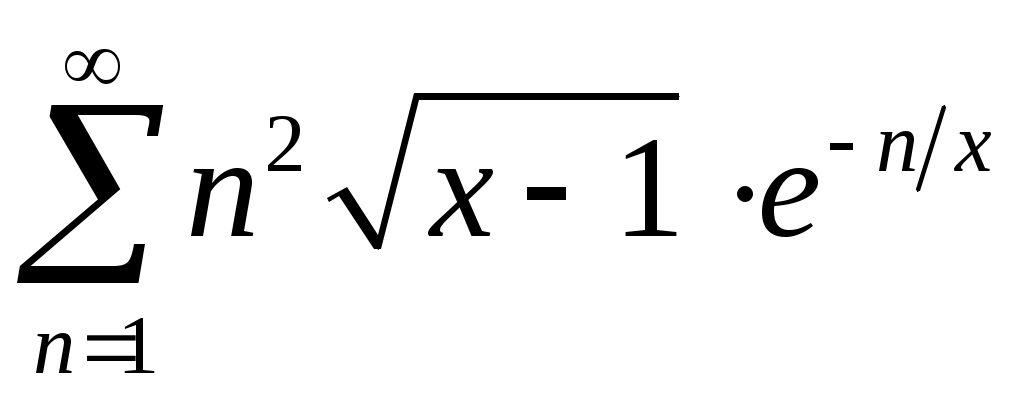 . .13.5. 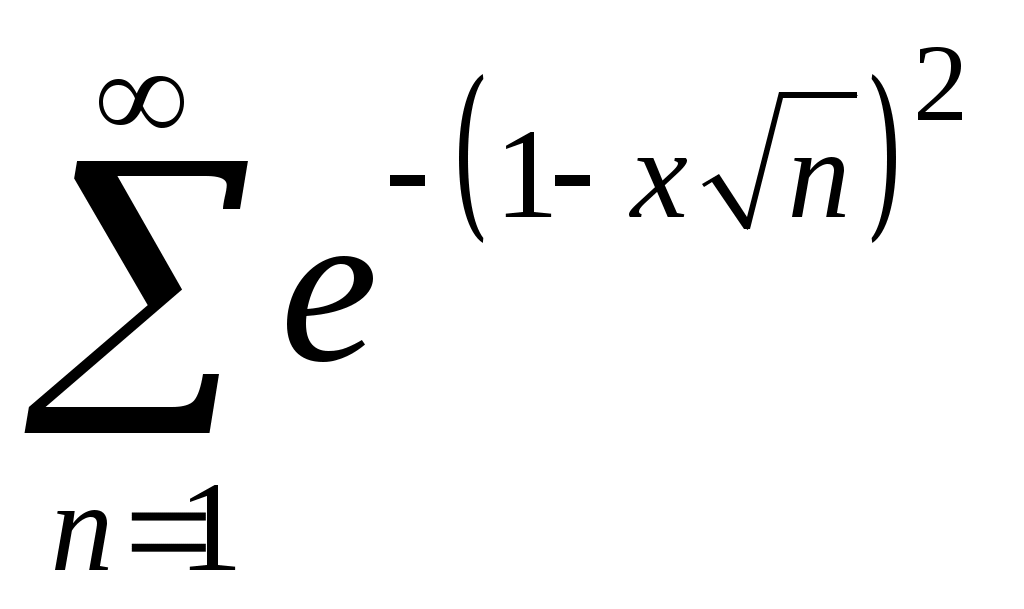 . 13.6. . 13.6. 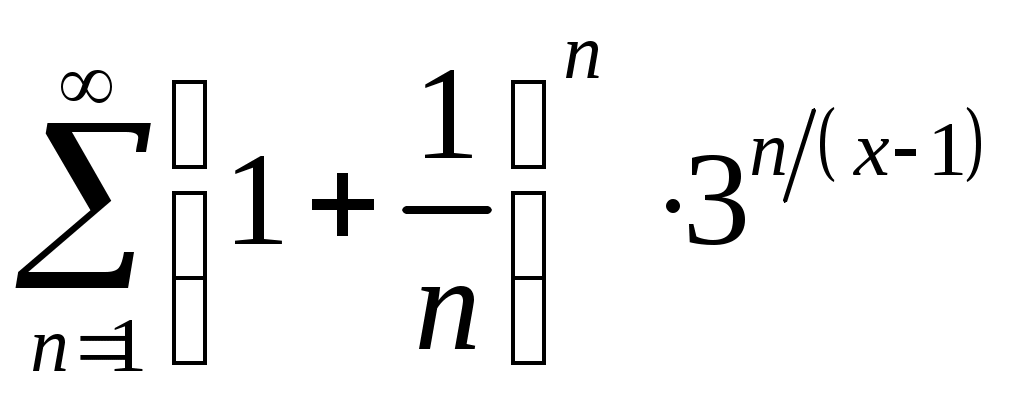 . .13.7. 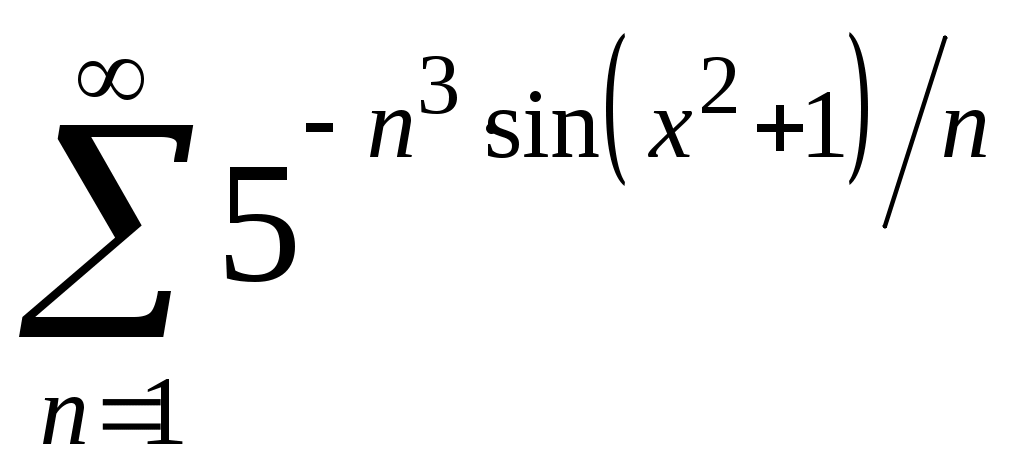 . 13.8. . 13.8. 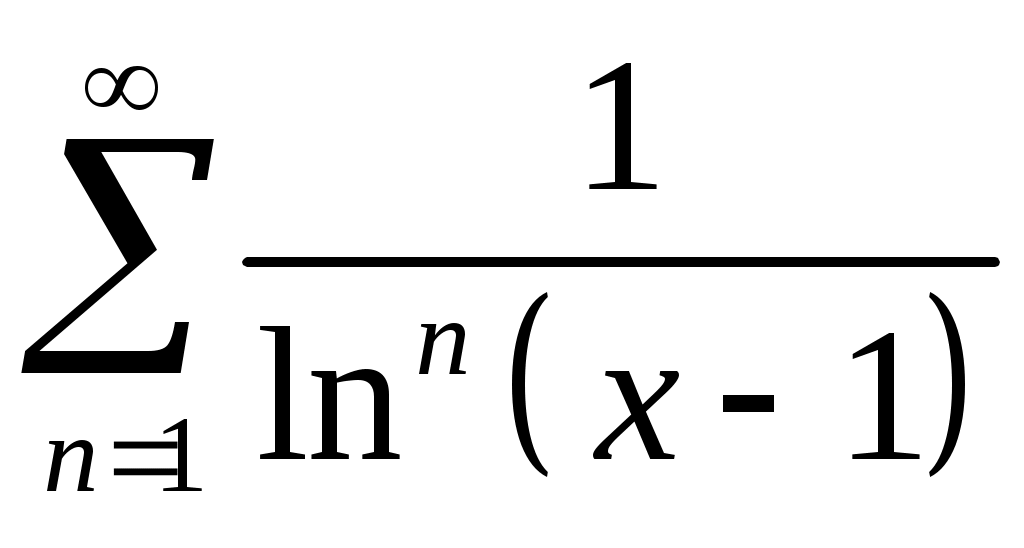 . .13.9. 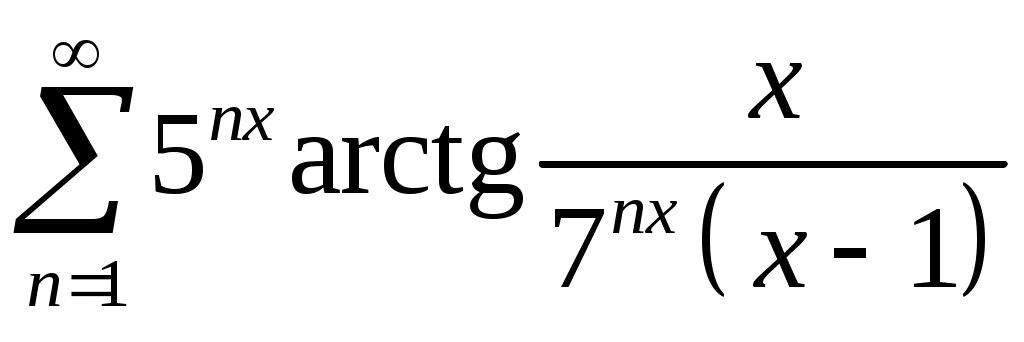 . 13.10. . 13.10. 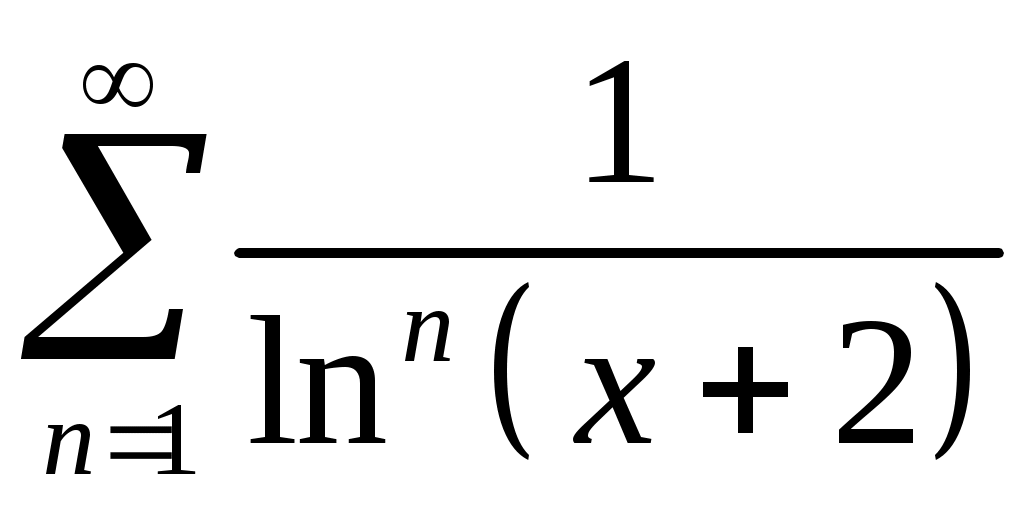 . .13.11. 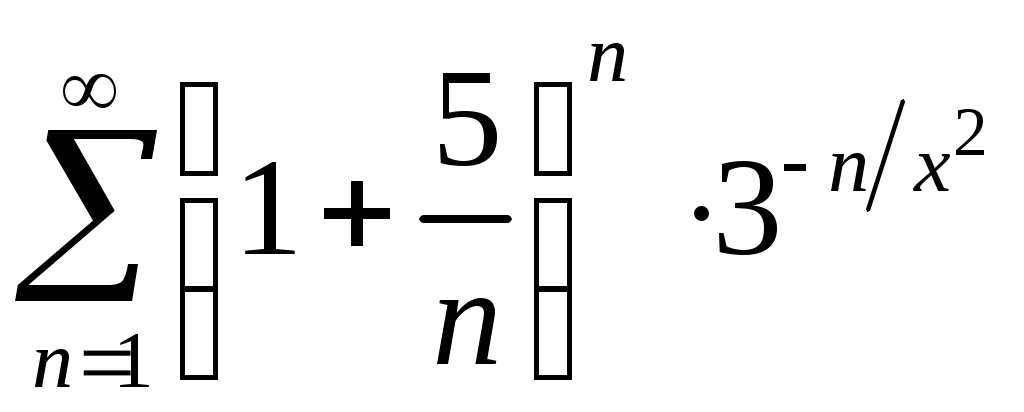 . 13.12. . 13.12. 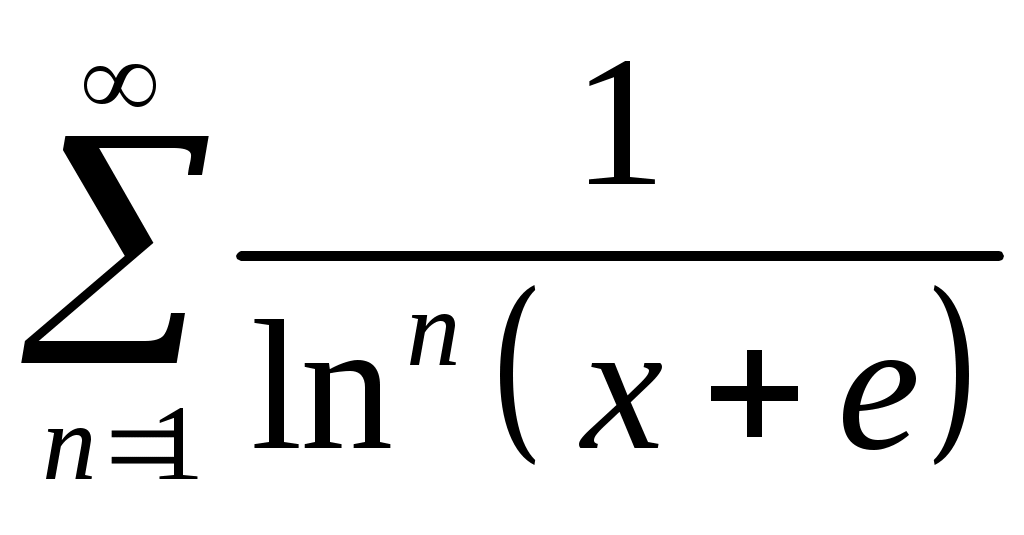 . .13.13. 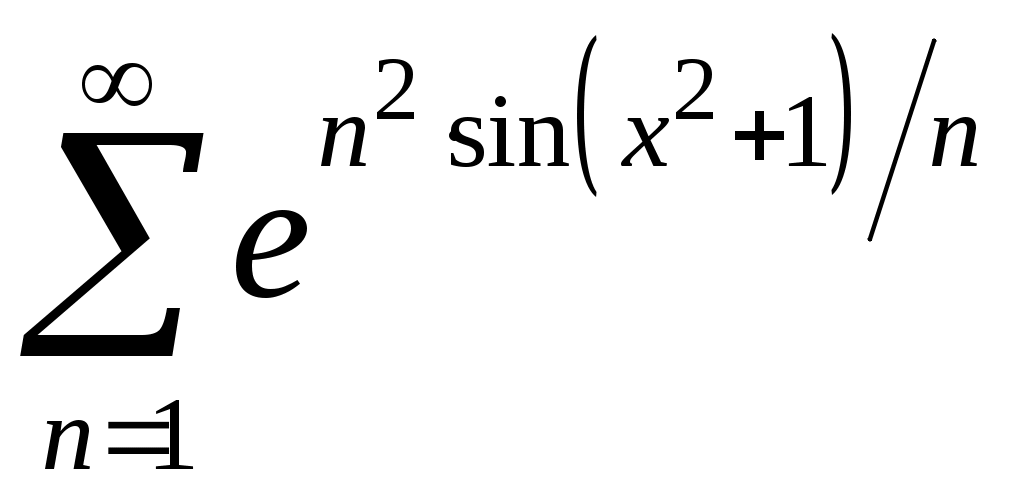 . 13.14. . 13.14.  . .13.15. 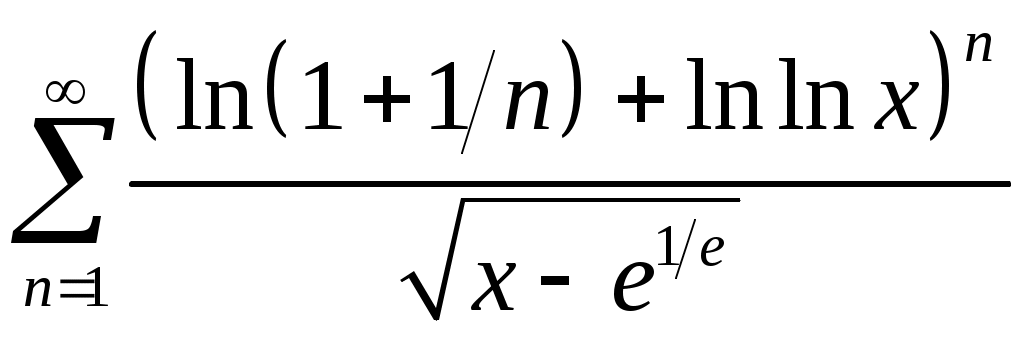 . 13.16. . 13.16. 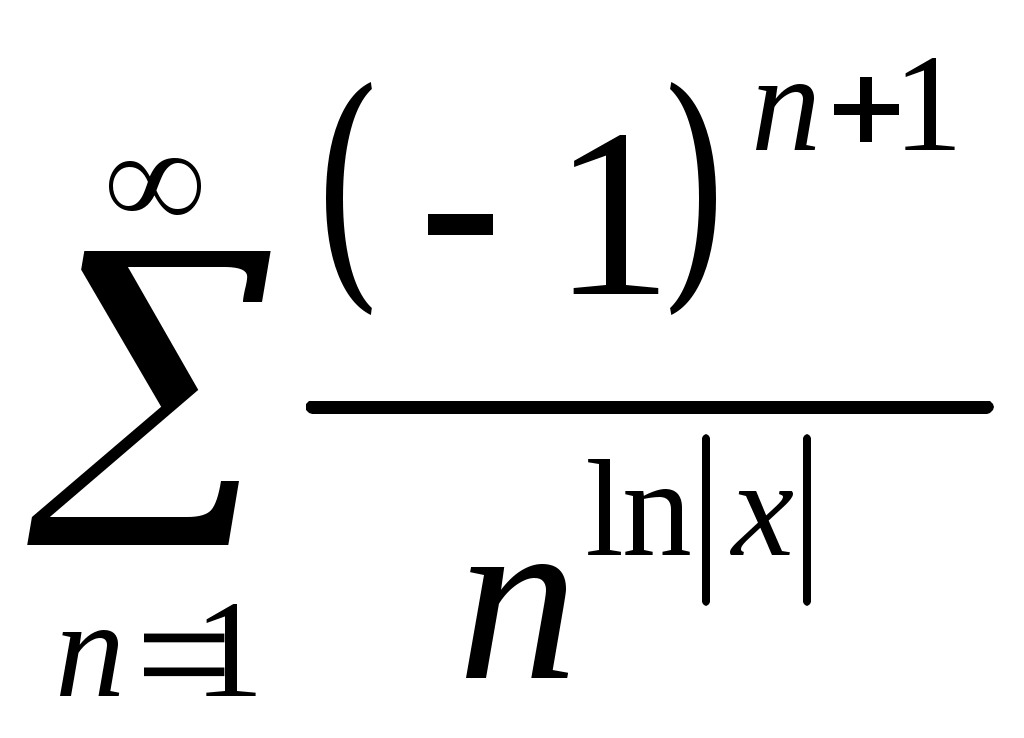 . .13.17. 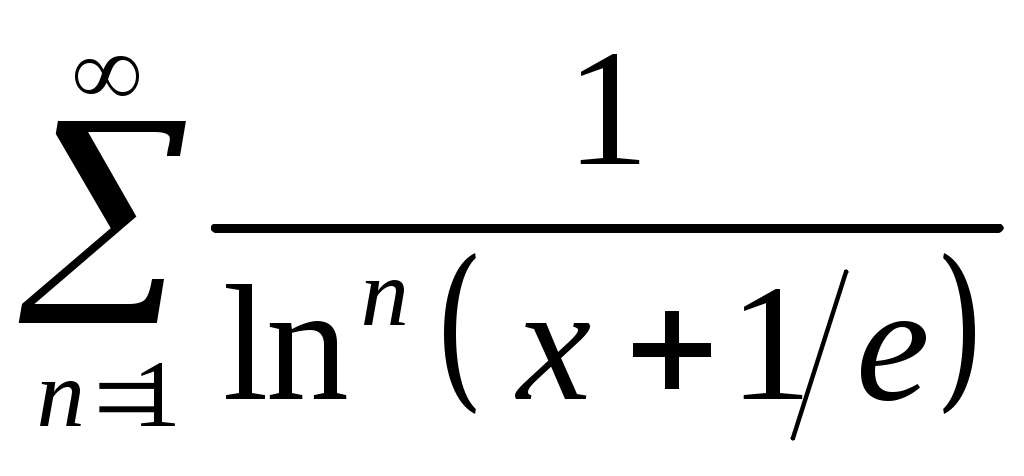 . 13.18. . 13.18. 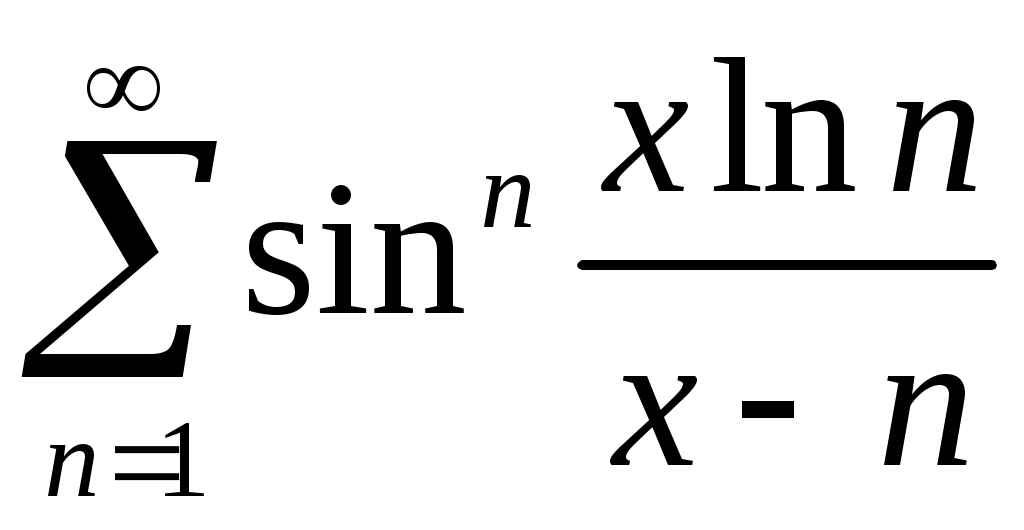 . .13.19. 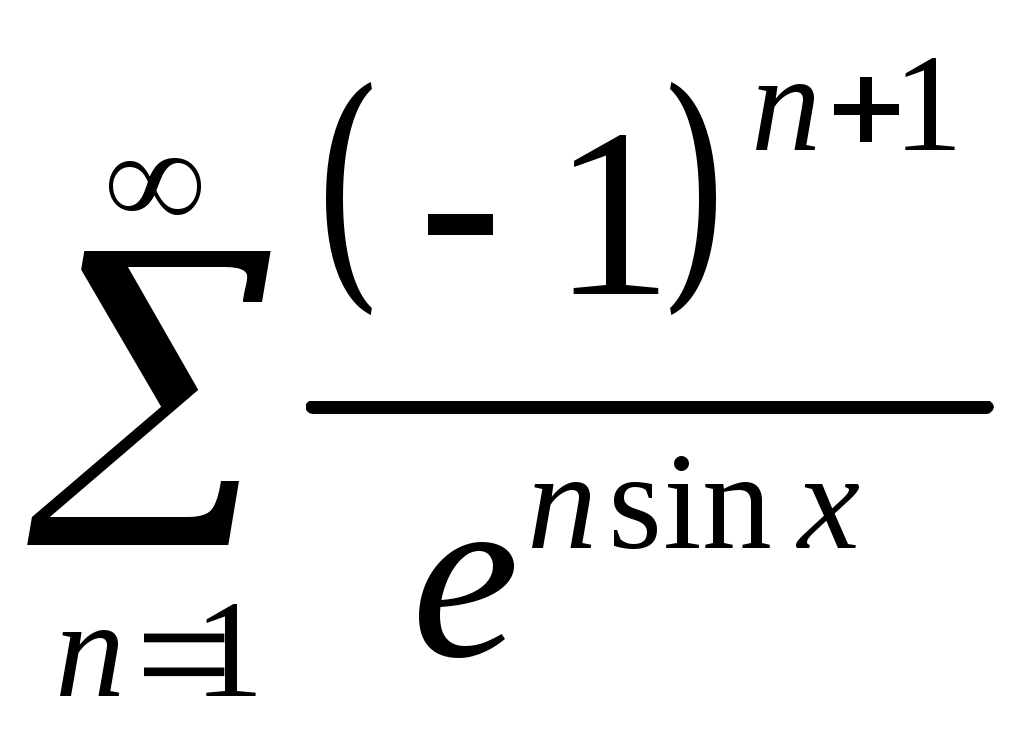 . 13.20. . 13.20. 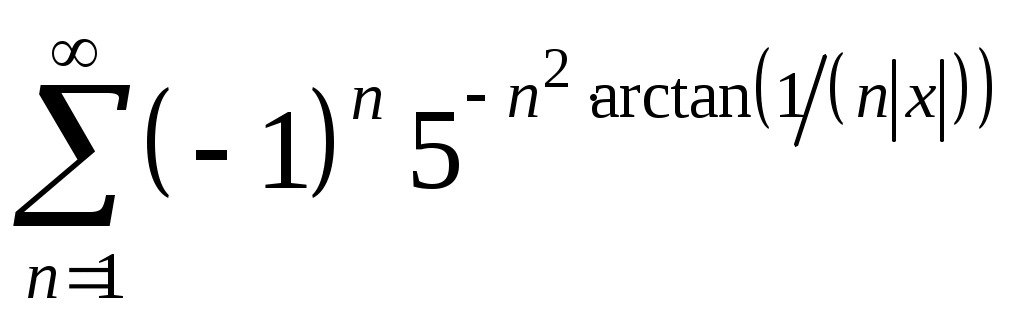 . .13.21. 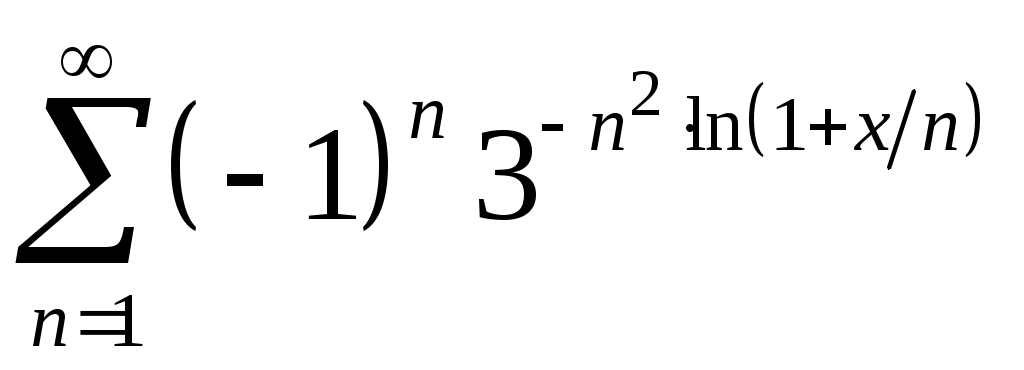 . 13.22. . 13.22. 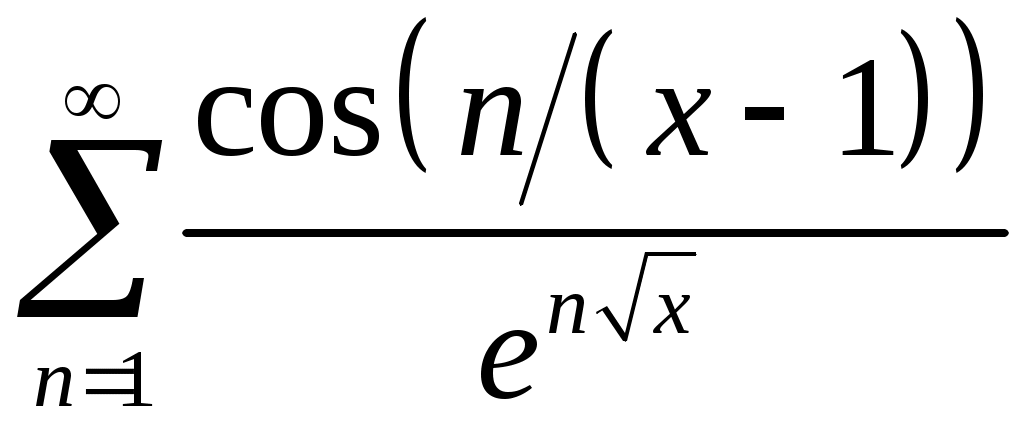 . .13.23. 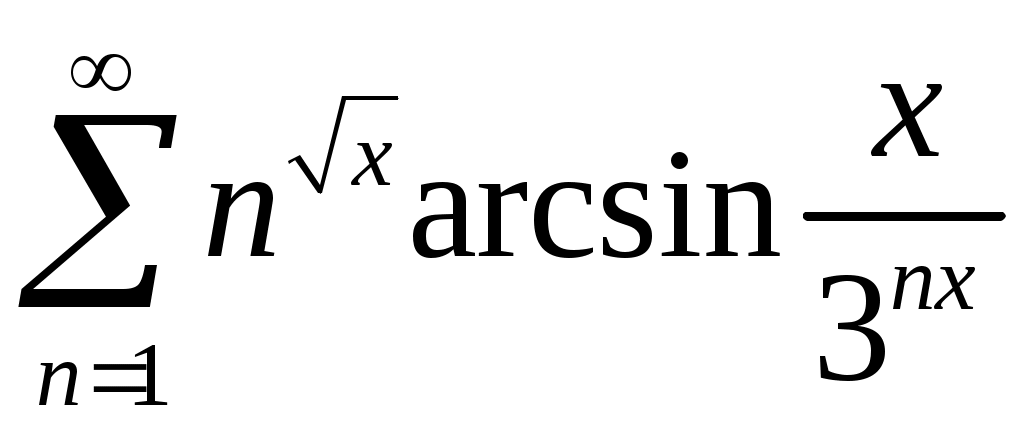 . 13.24. . 13.24. 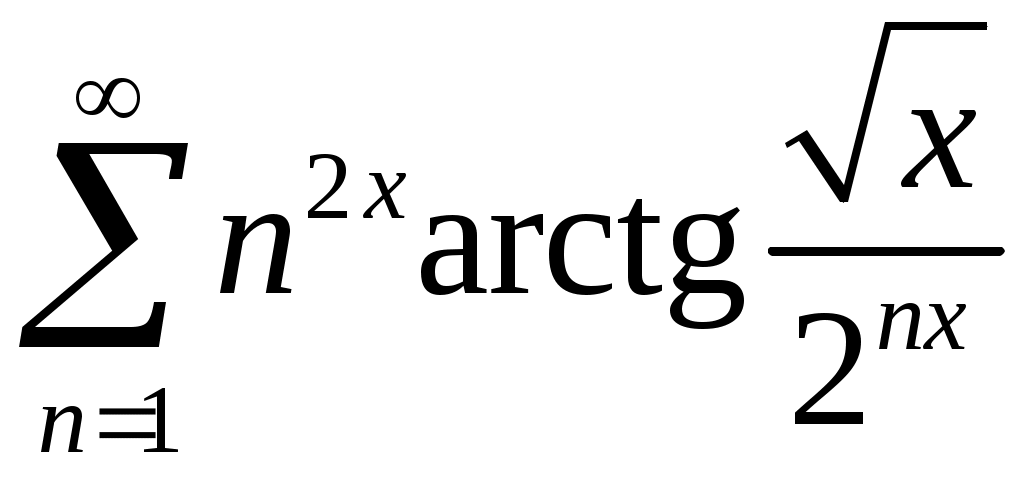 . .13.25. 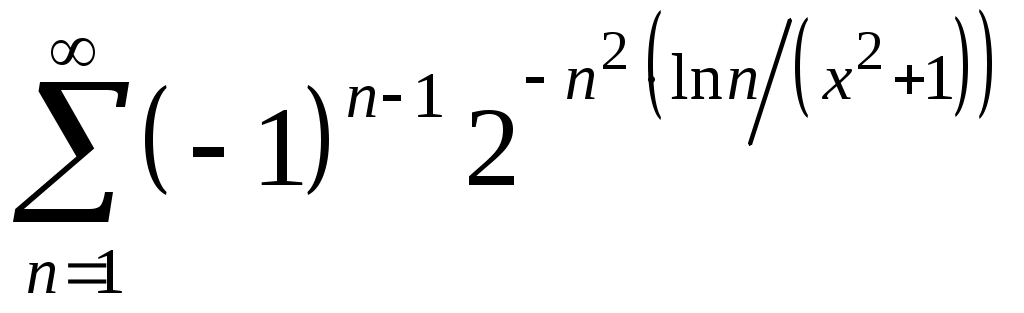 . 13.26. . 13.26. 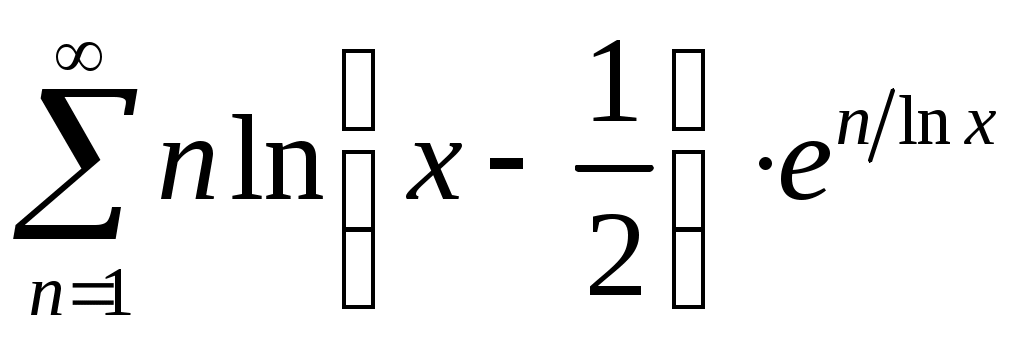 . .13.27. 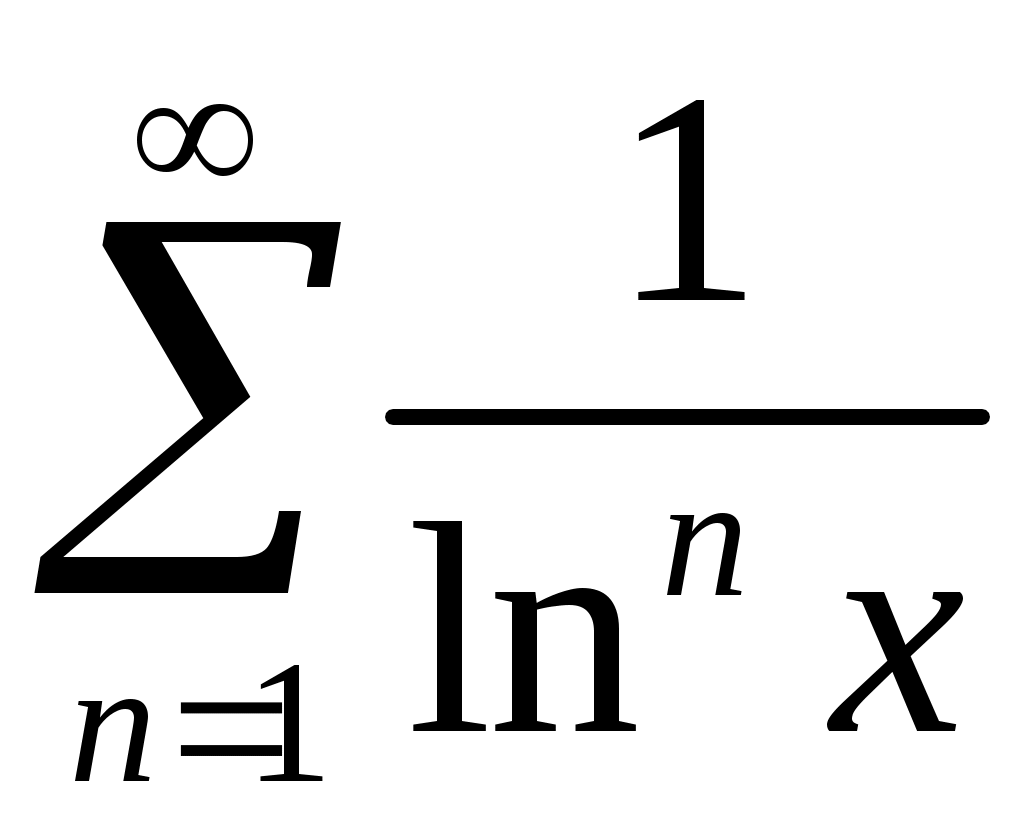 . 13.28. . 13.28. 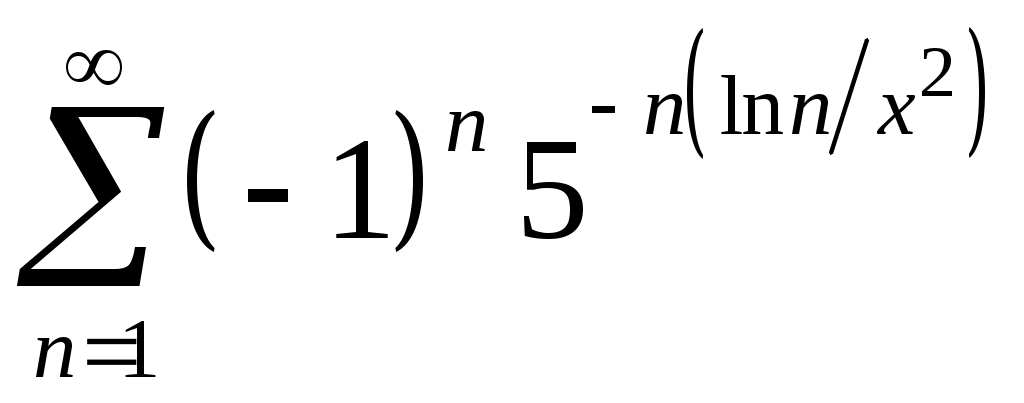 . .13.29. 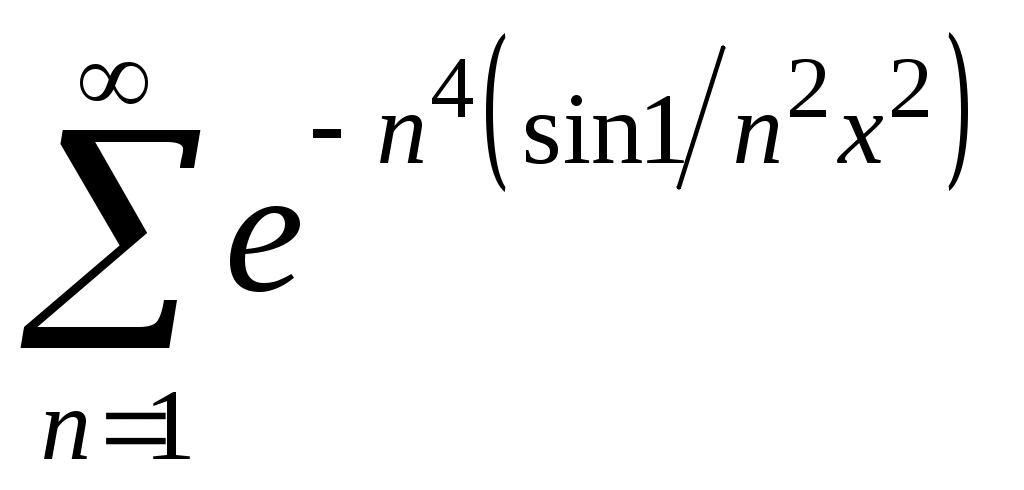 . 13.30. . 13.30. 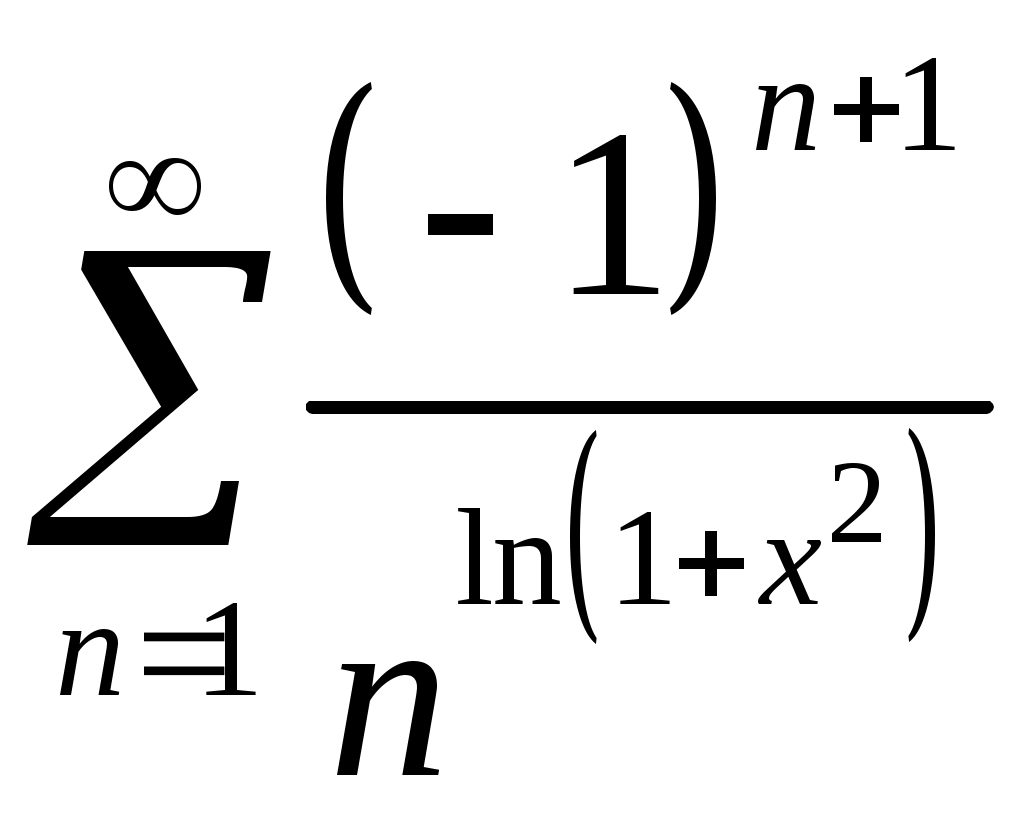 . .13.31. 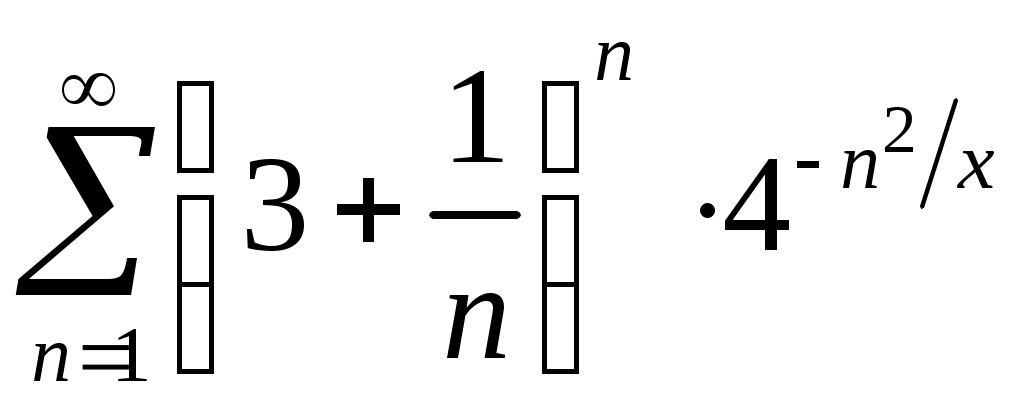 . .Задача 14. Найти область сходимости функционального ряда. 14.1. 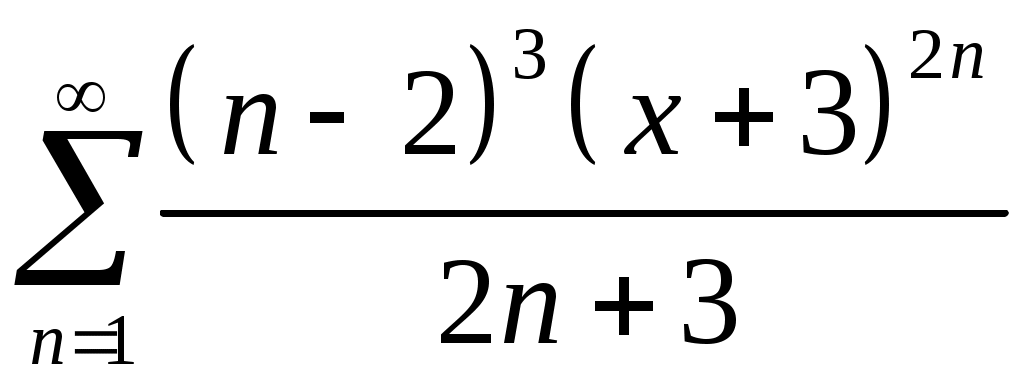 . 14.2. . 14.2. 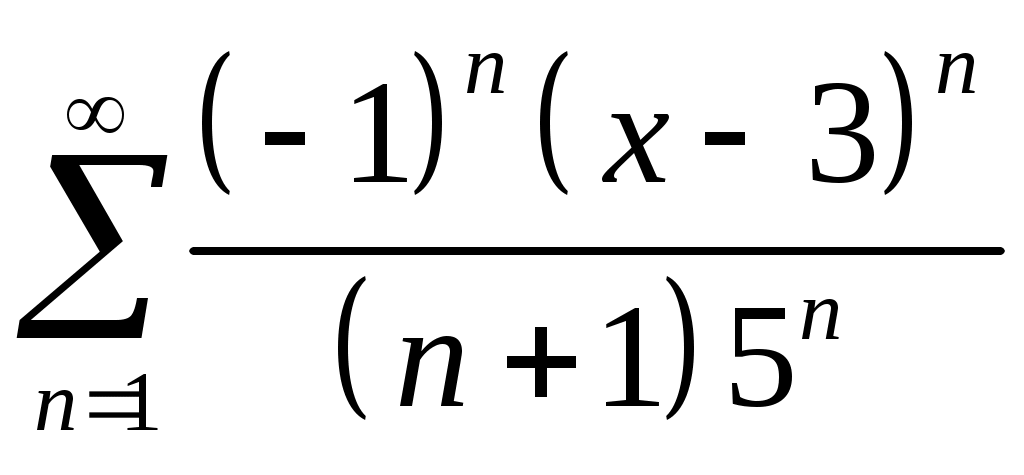 . .14.3. 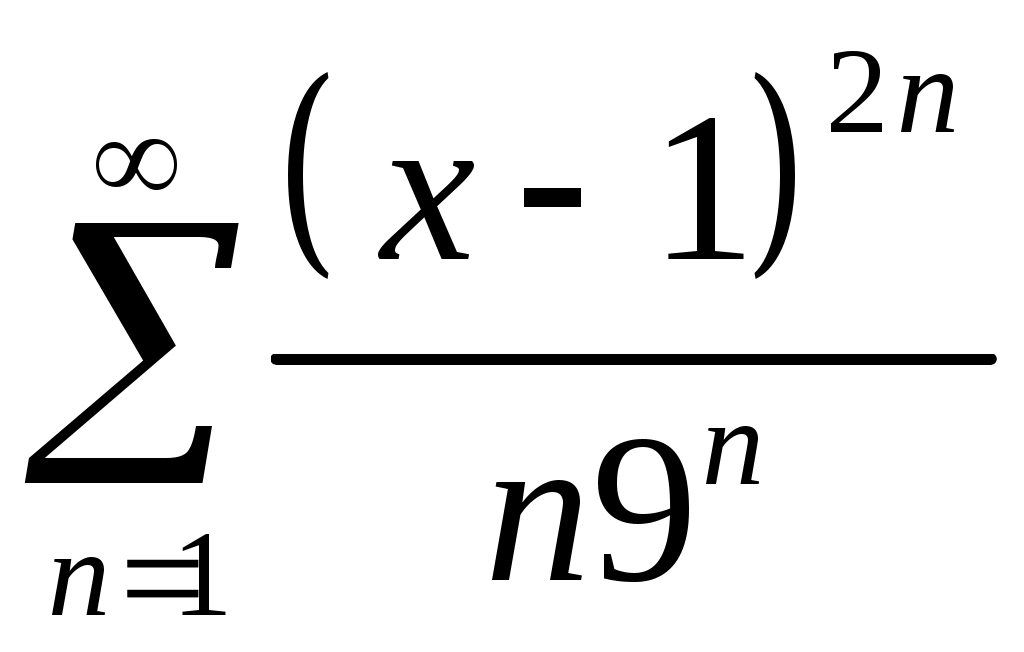 . 14.4. . 14.4. 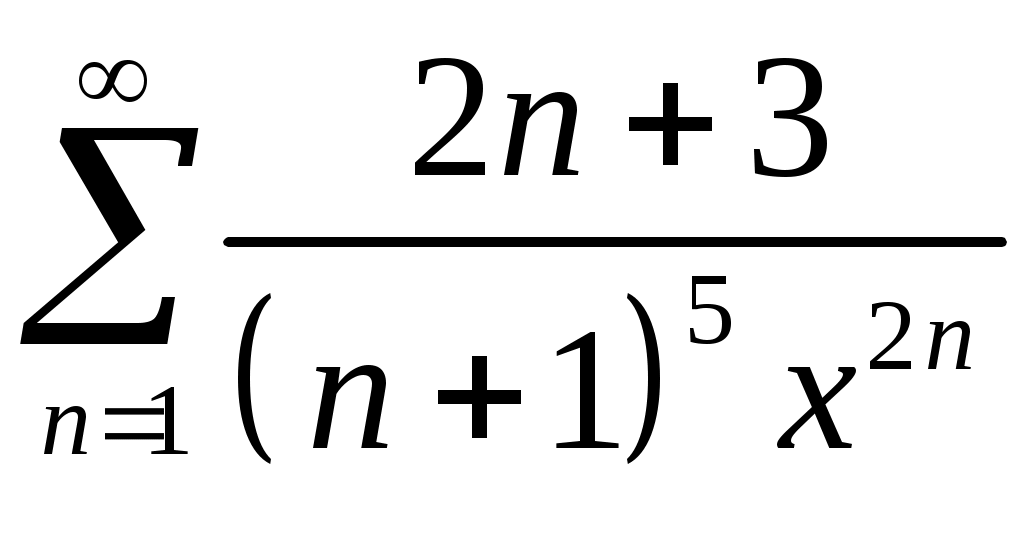 . .14.5. 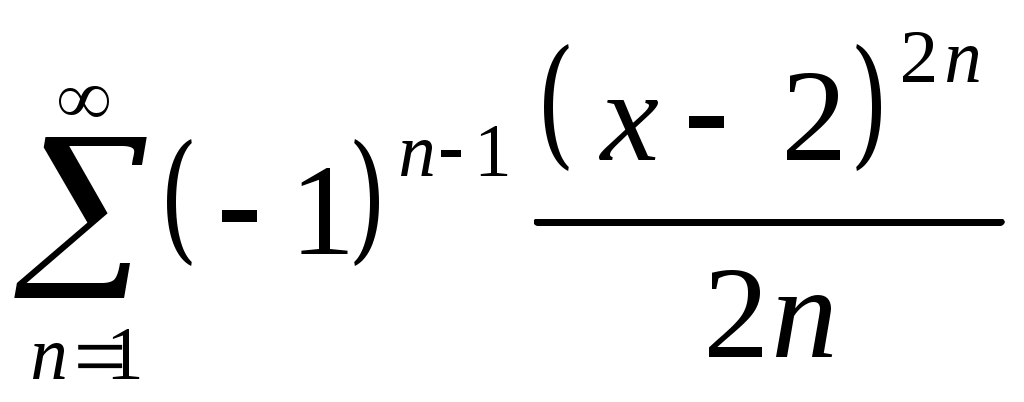 . 14.6. . 14.6. 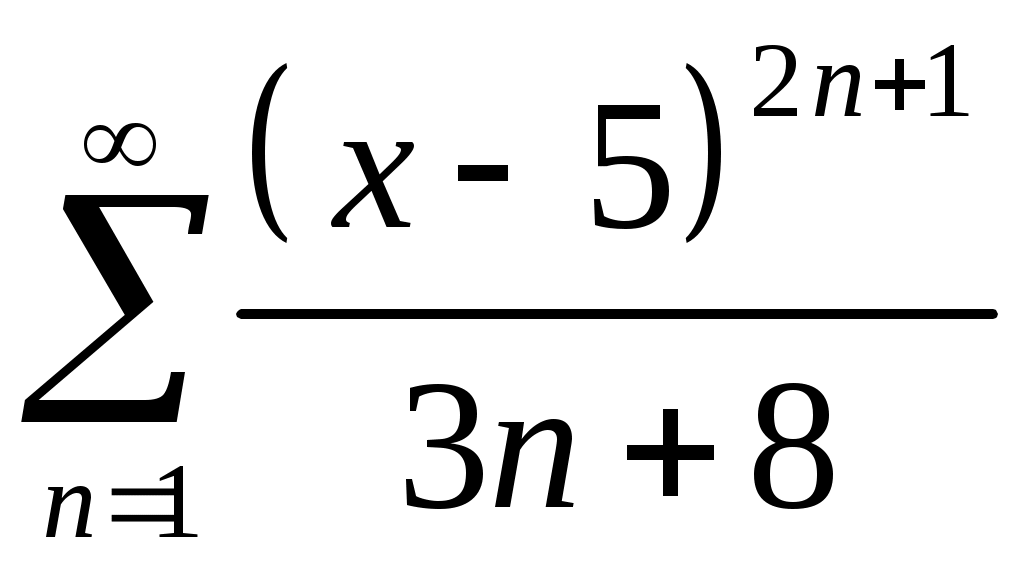 . .14.7. 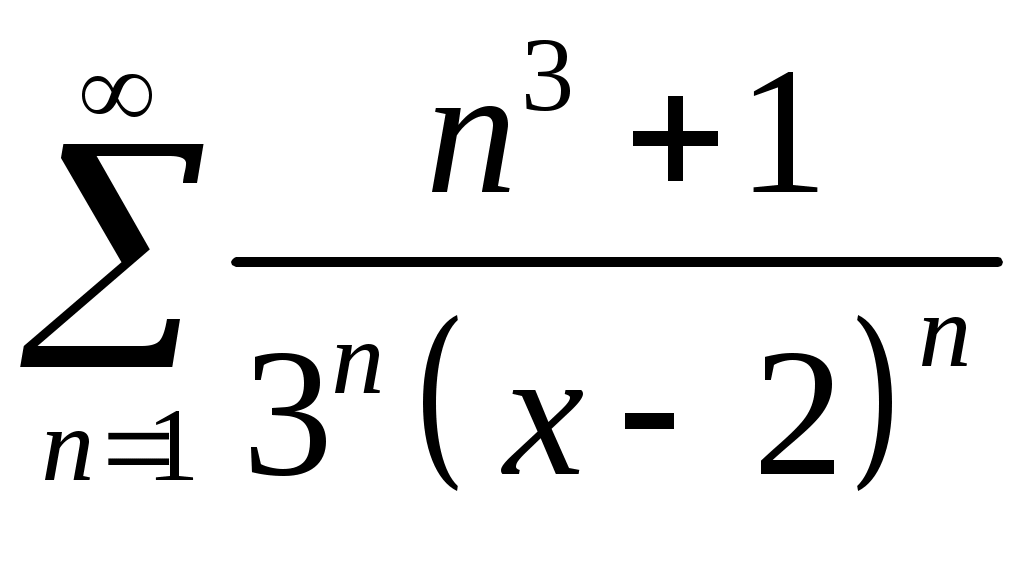 . 14.8. . 14.8. 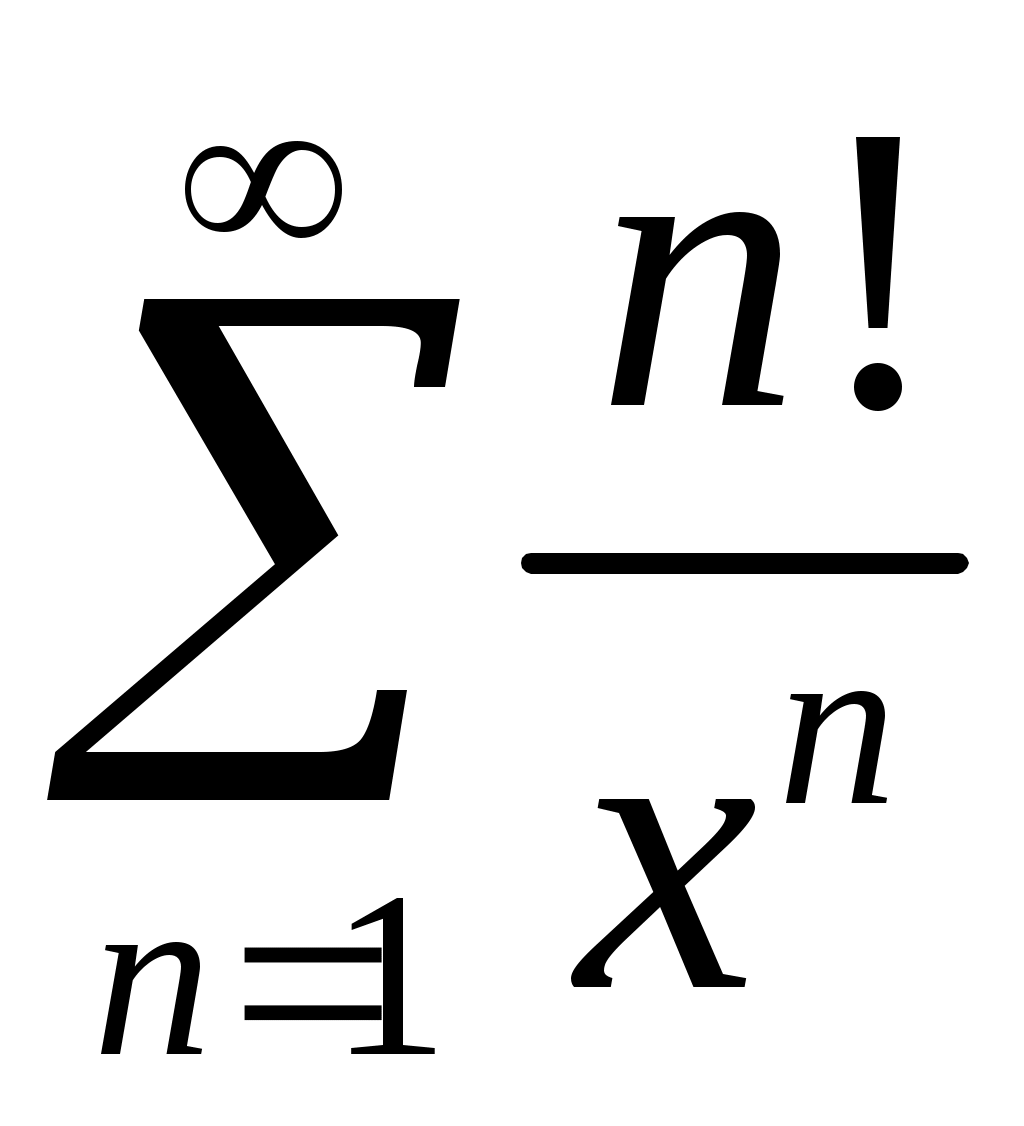 . .14.9. 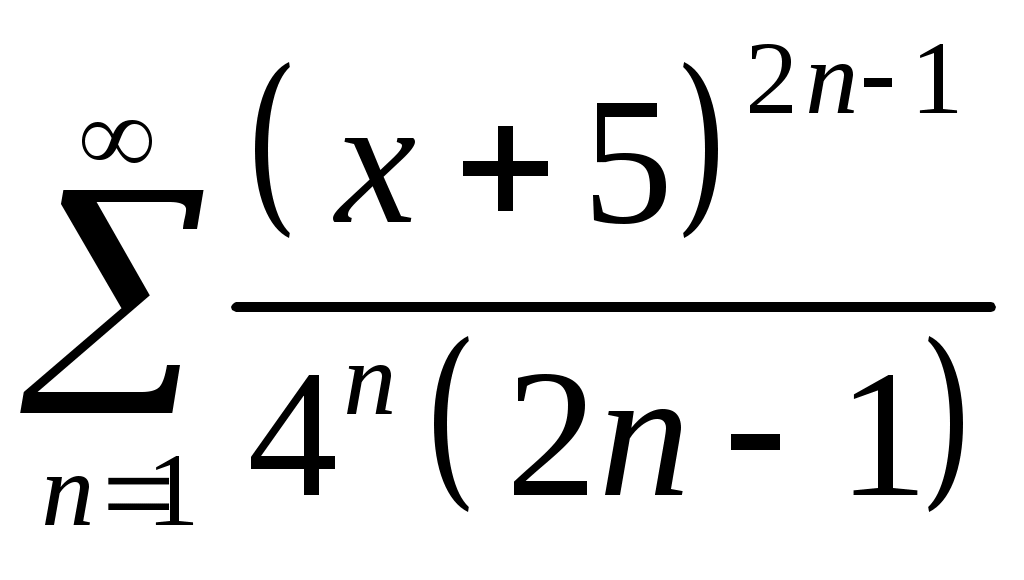 . 14.10. . 14.10. 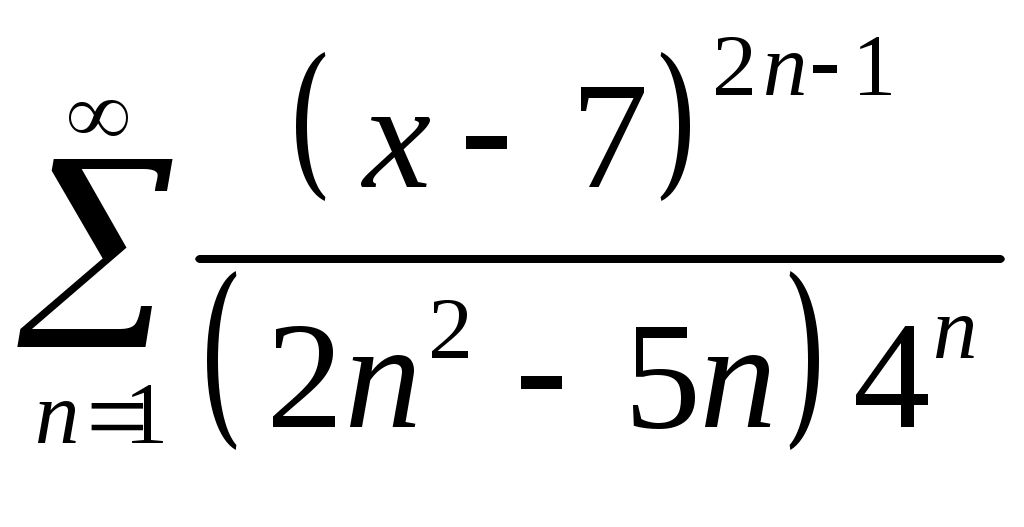 . .14.11. 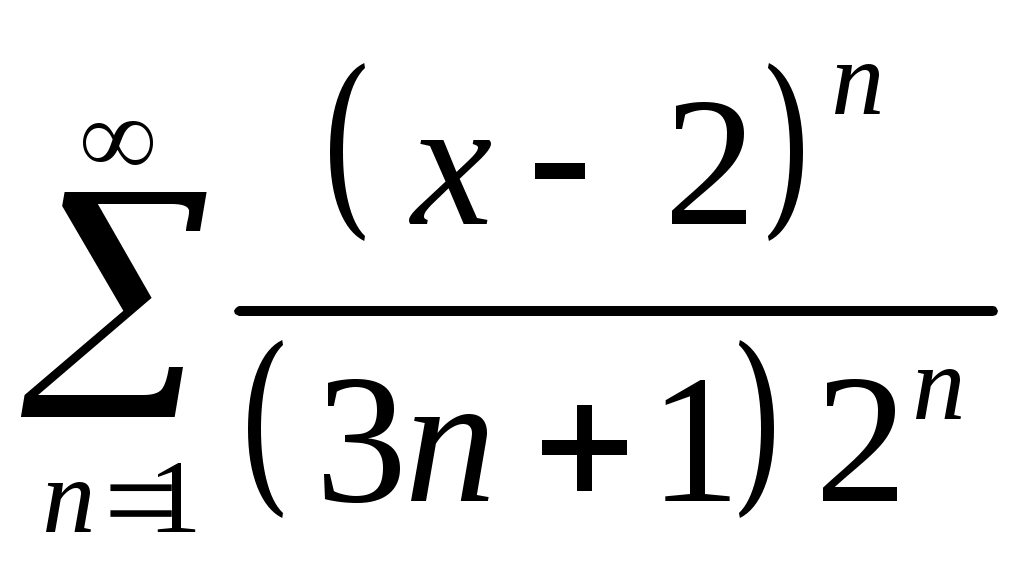 . 14.12. . 14.12. 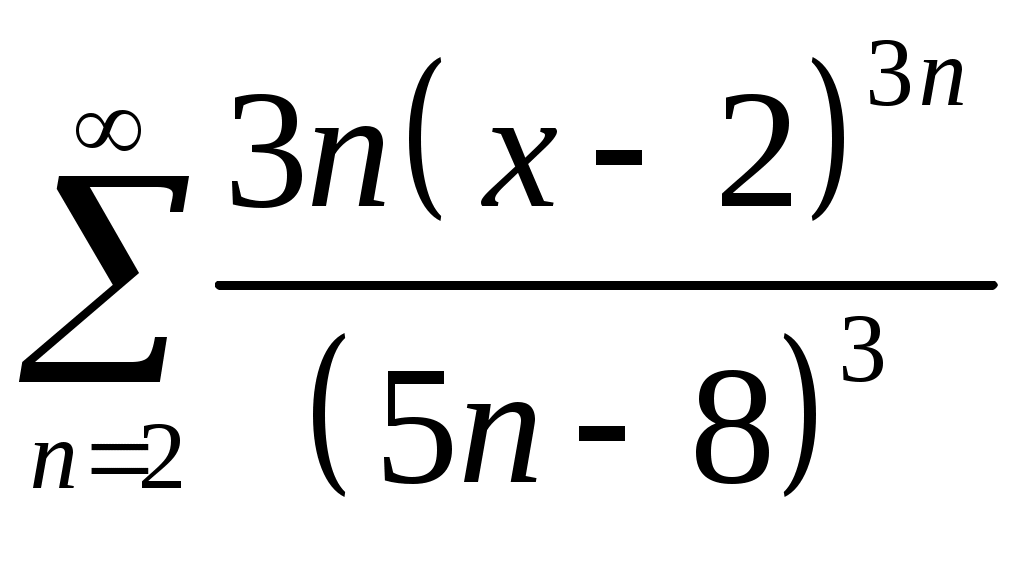 . .14.13. 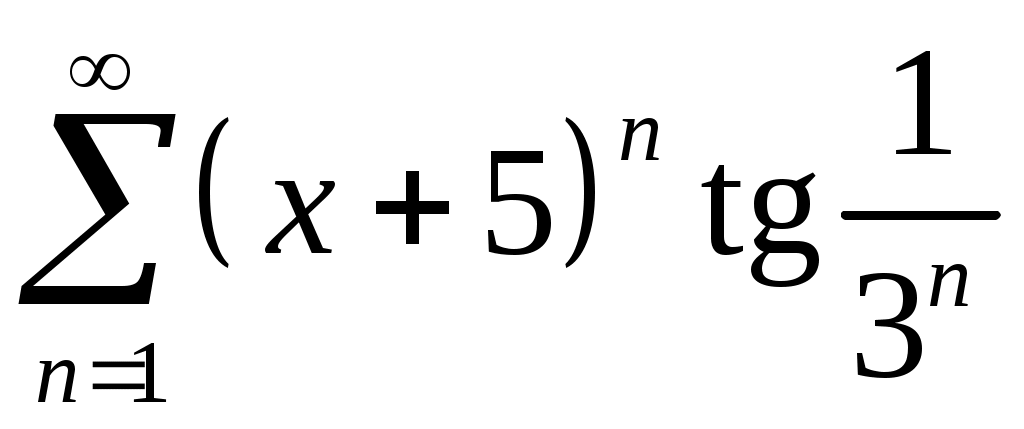 . 14.14. . 14.14. 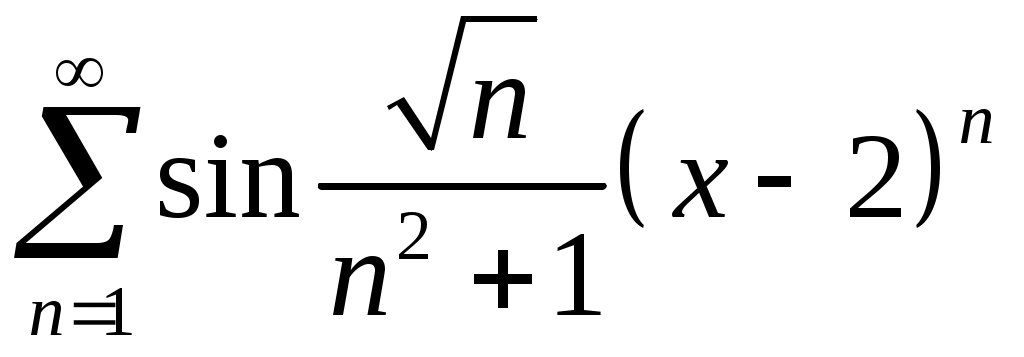 . .14.15. 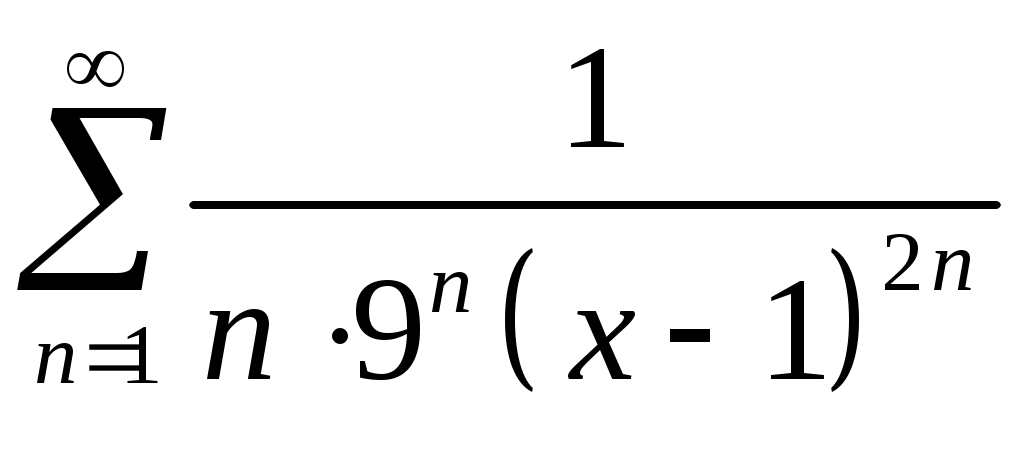 . 14.16. . 14.16. 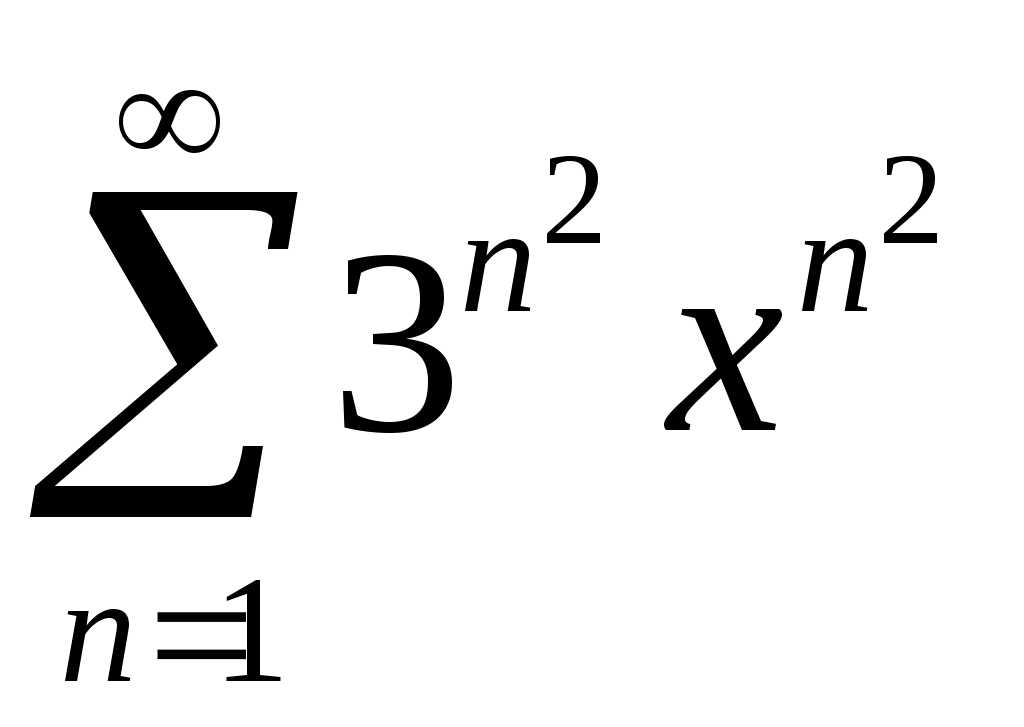 . .14.17. 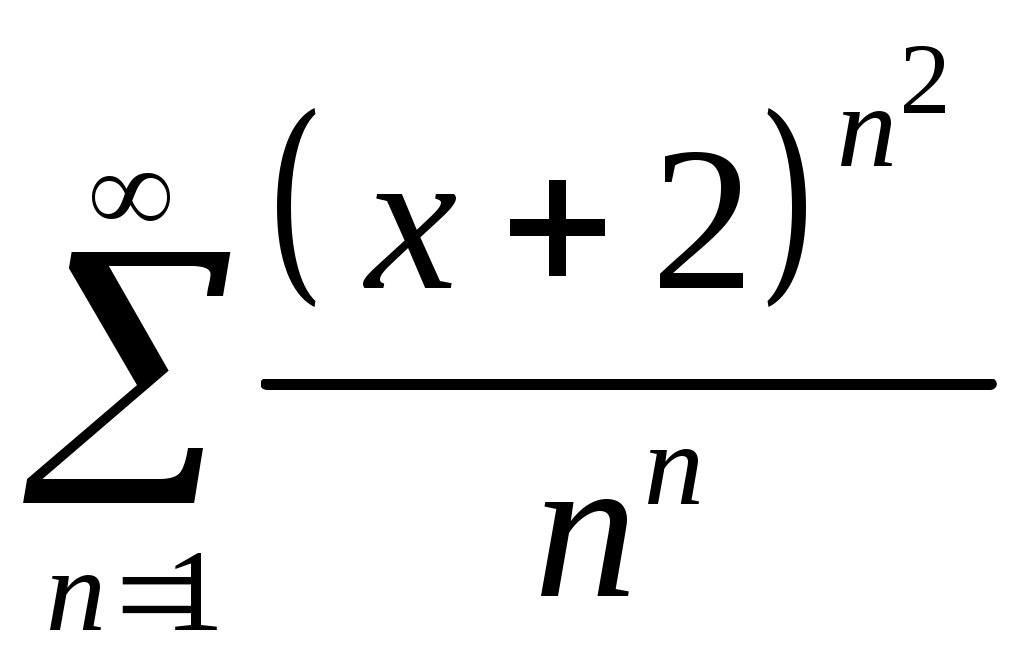 . 14.18. . 14.18. 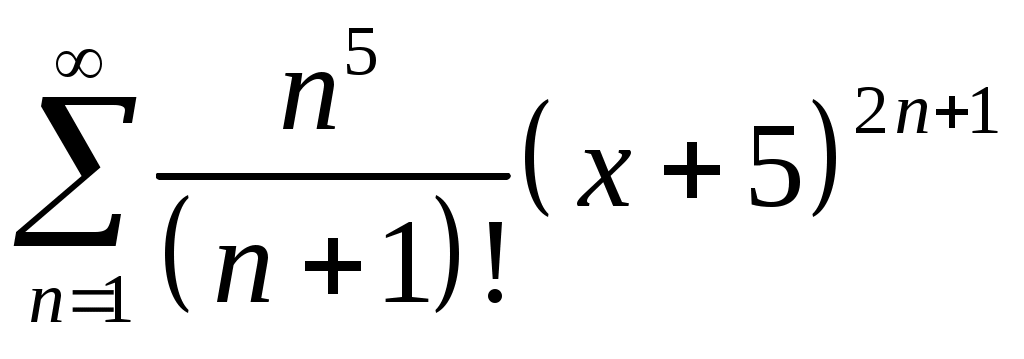 . .14.19. 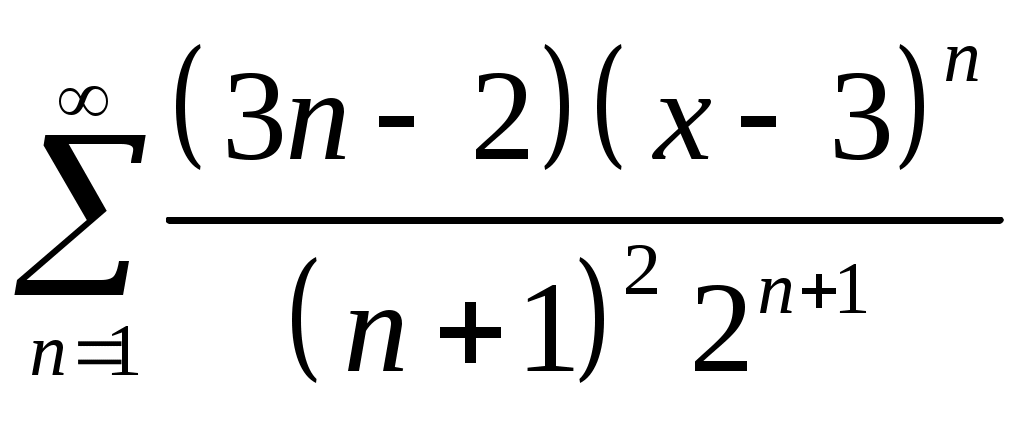 . 14.20. . 14.20. 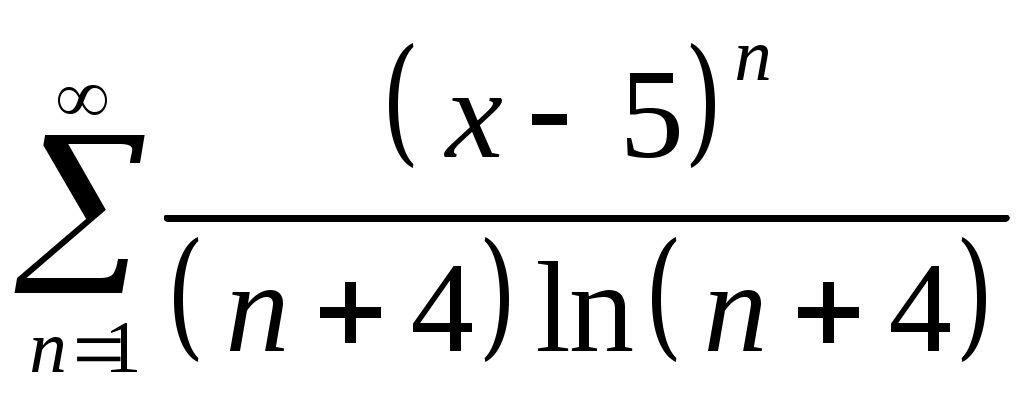 . .14.21. 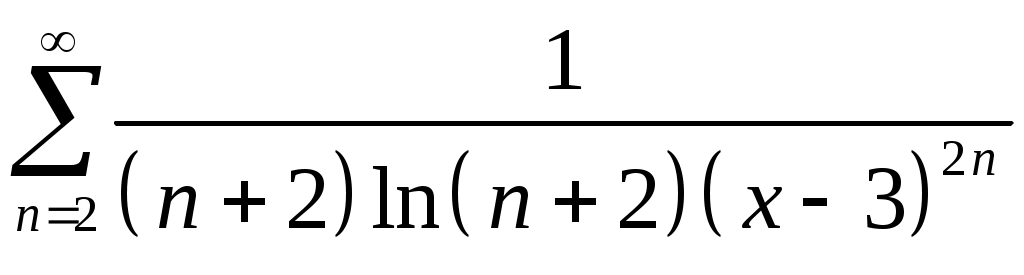 . 14.22. . 14.22. 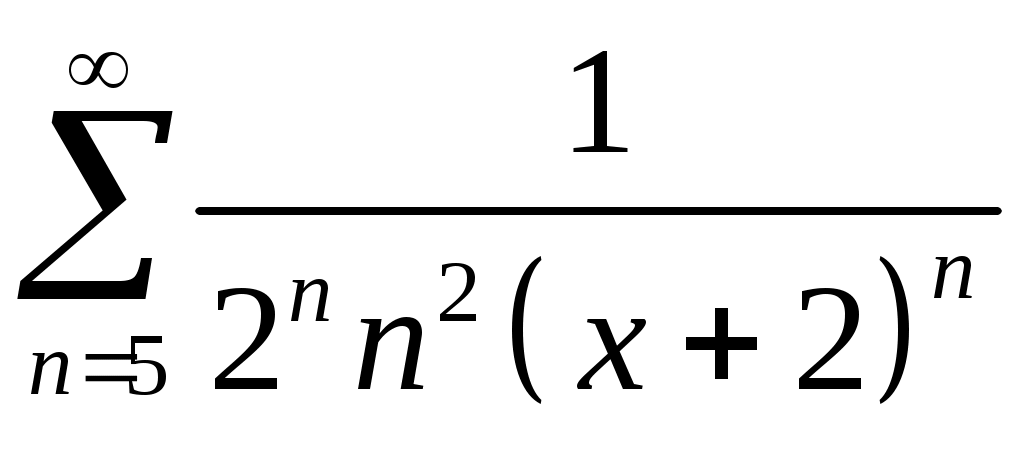 . .14.23. 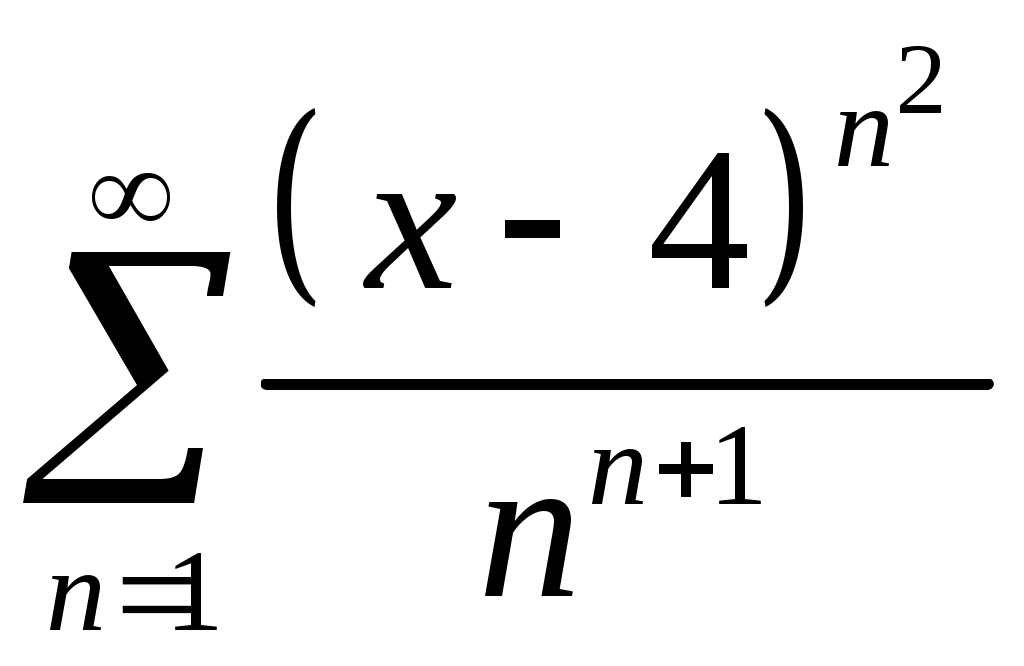 . 14.24. . 14.24. 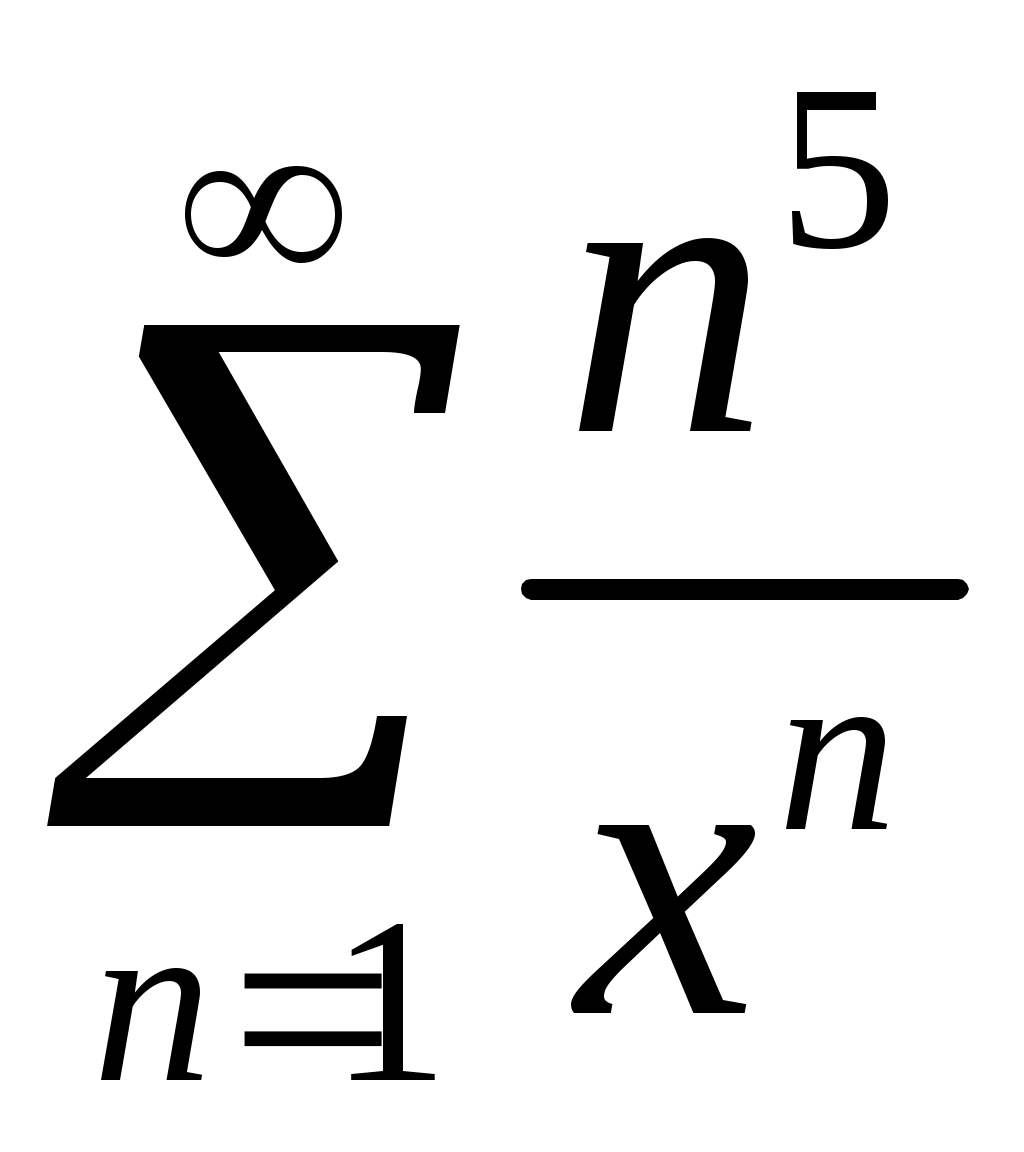 . .14.25. 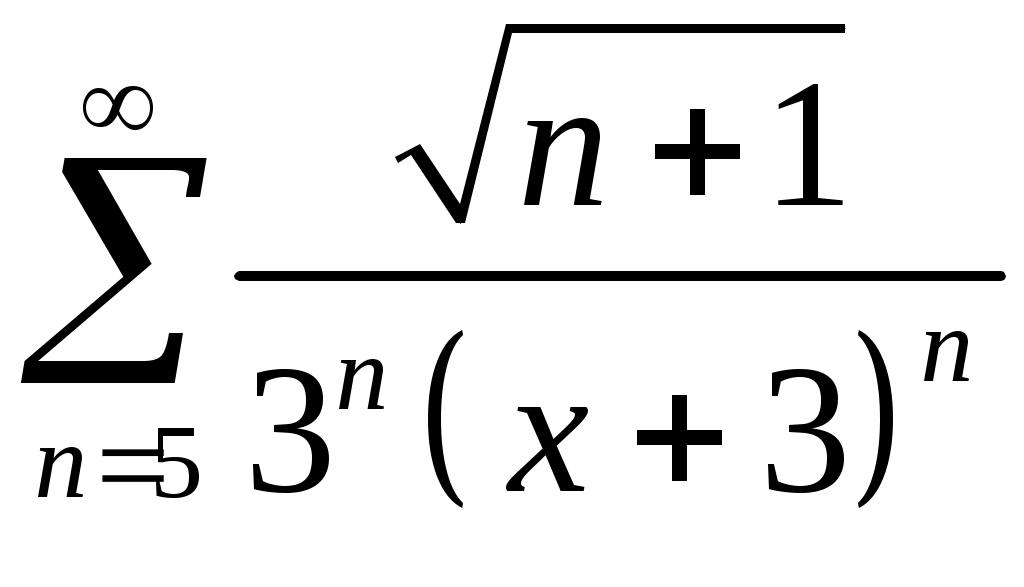 . 14.26. . 14.26. 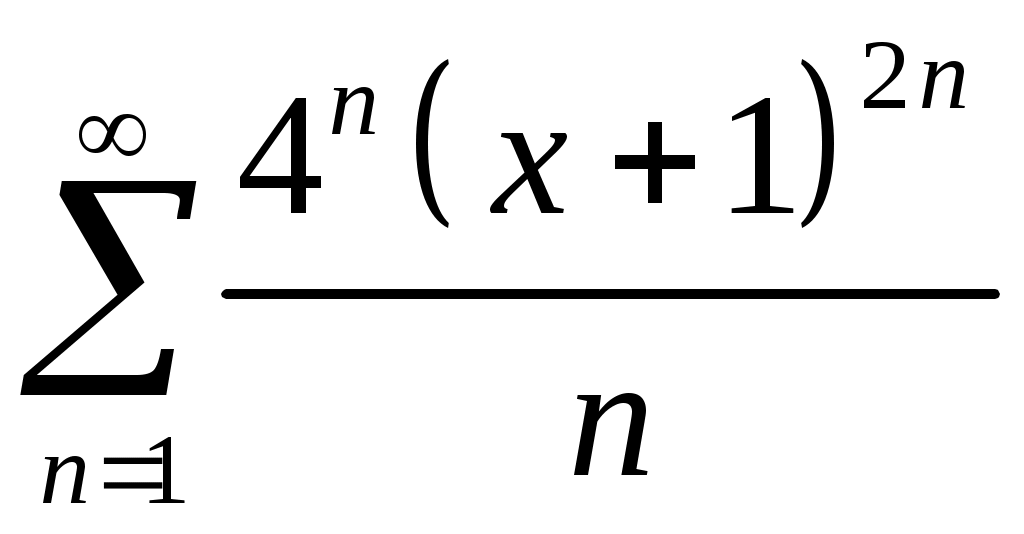 . .14.27. 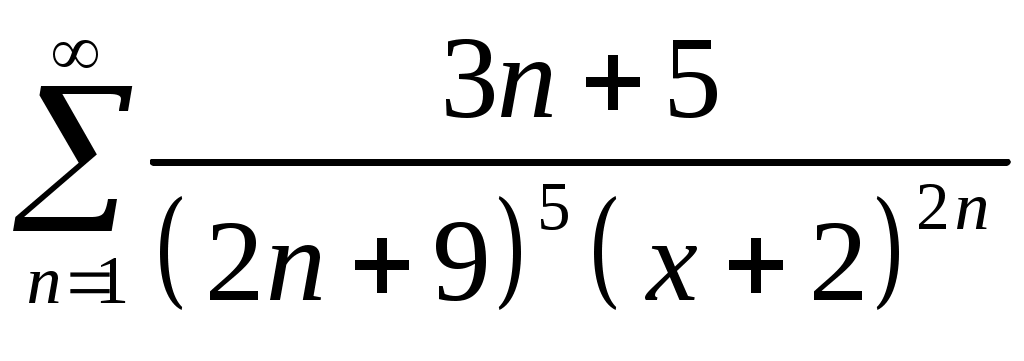 . 14.28. . 14.28. 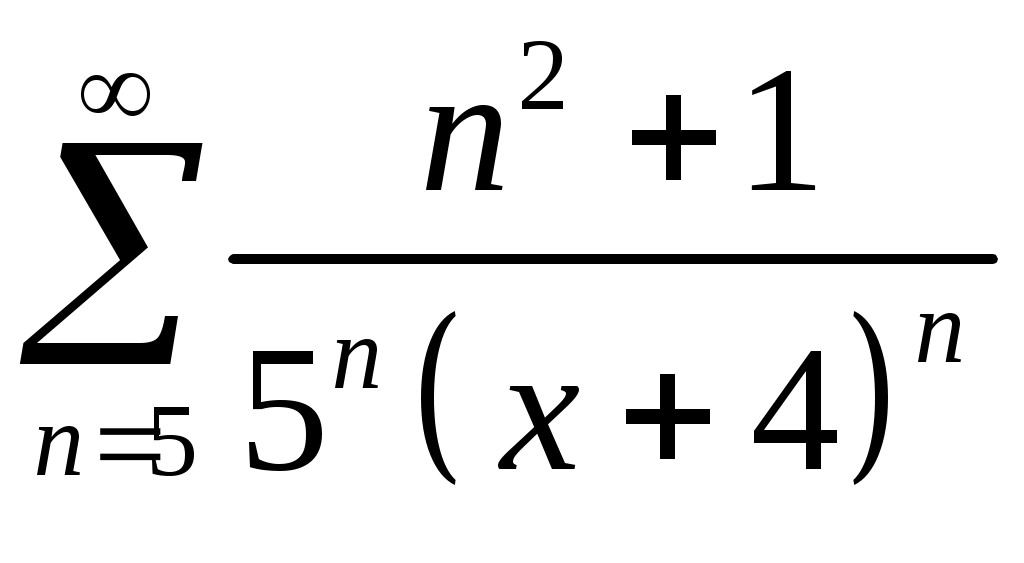 . .14.29. 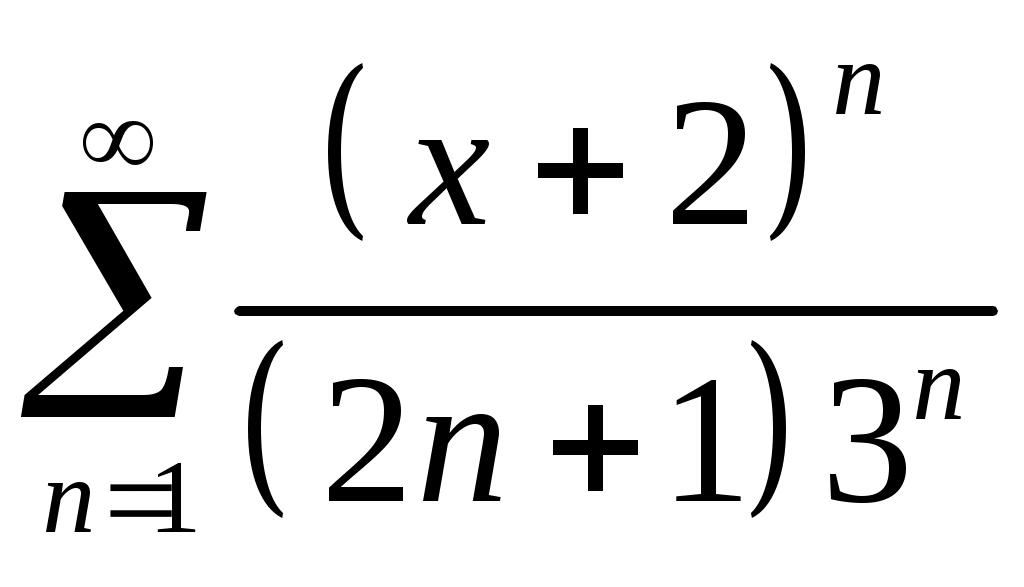 . 14.30. . 14.30. 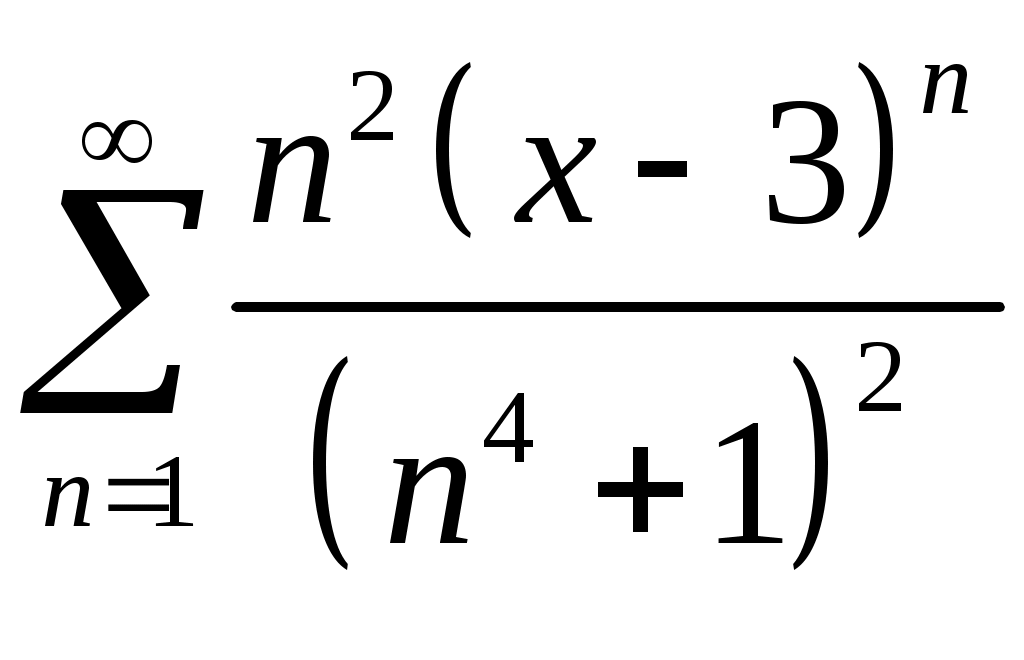 . .14.31. 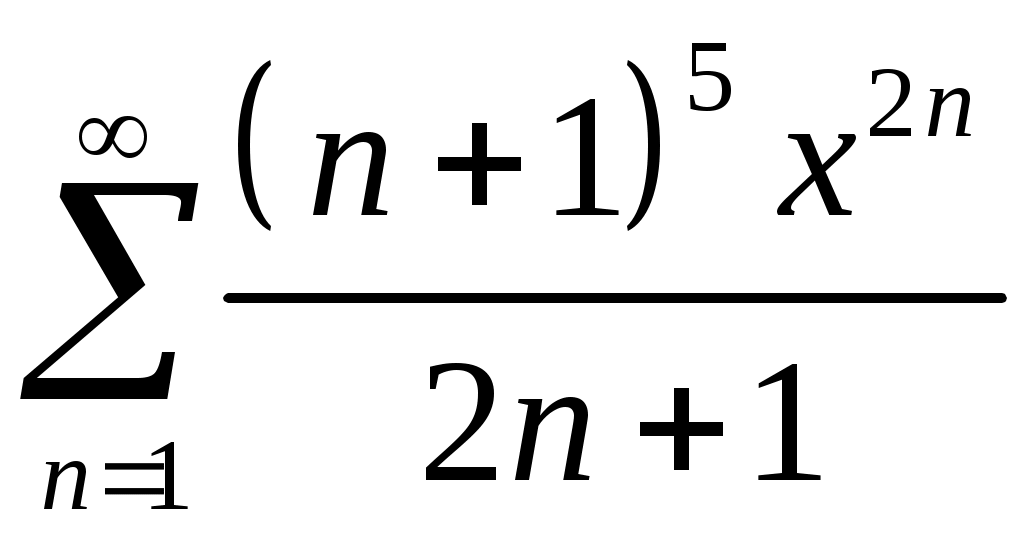 . .Задача 15. Доказать, исходя из определения, равномерную сходимость функционального ряда на отрезке 15.1.  . 15.2. . 15.2.  . .15.3.  . 15.4. . 15.4.  . .15.5.  . 15.6. . 15.6. 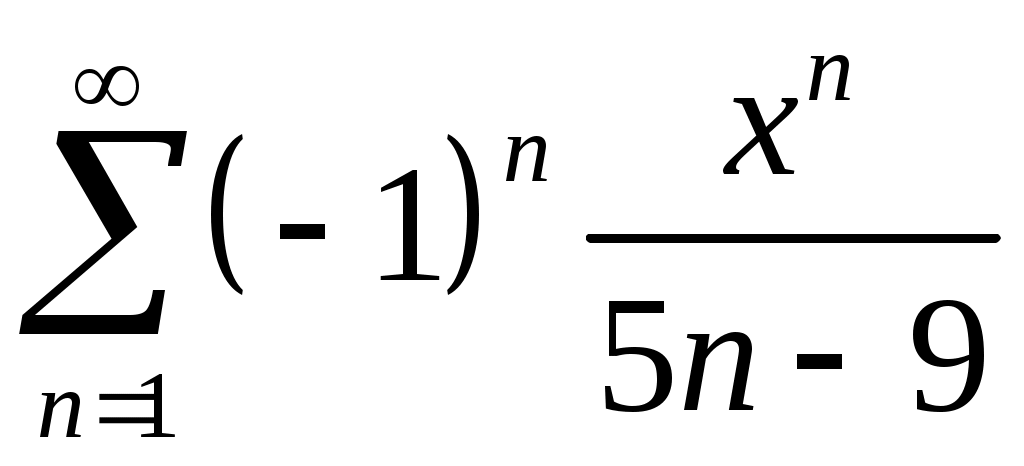 . .15.7. 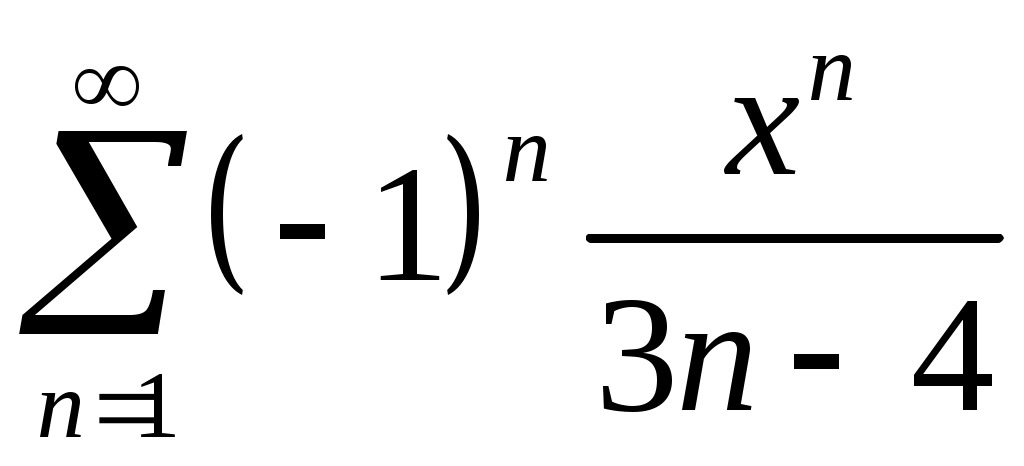 . 15.8. . 15.8. 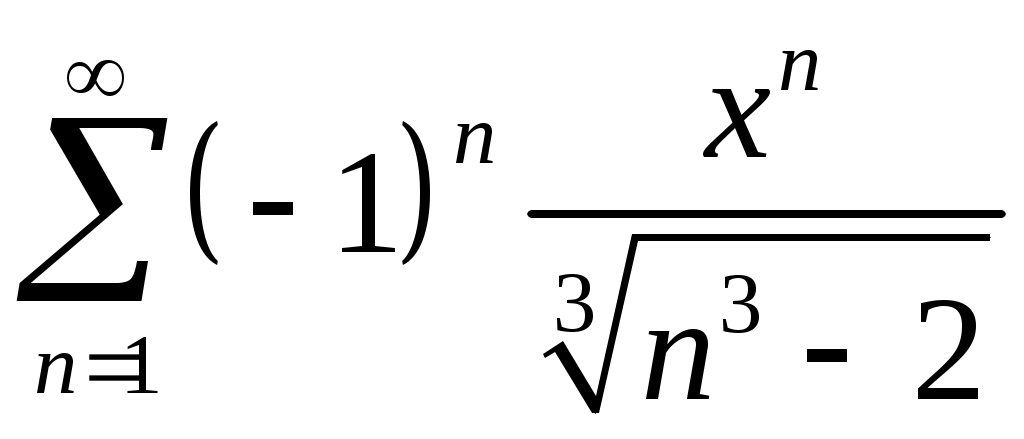 . .15.9. 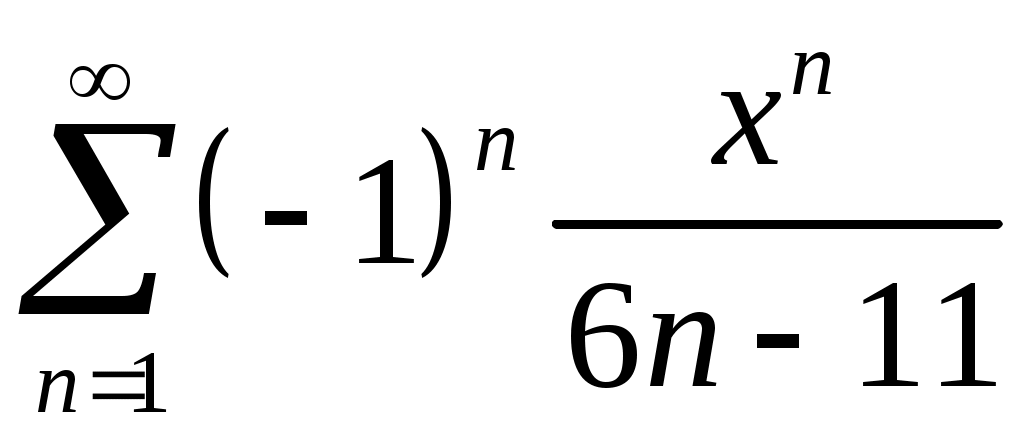 . 15.10. . 15.10. 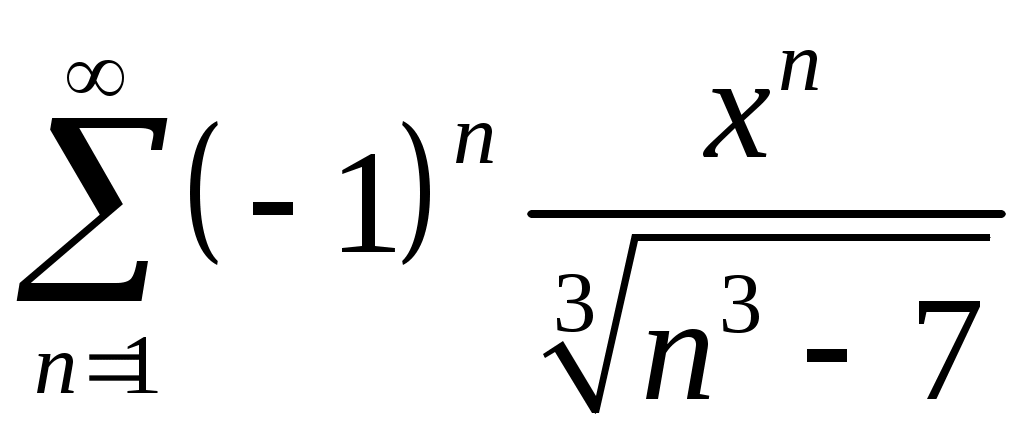 . .15.11. 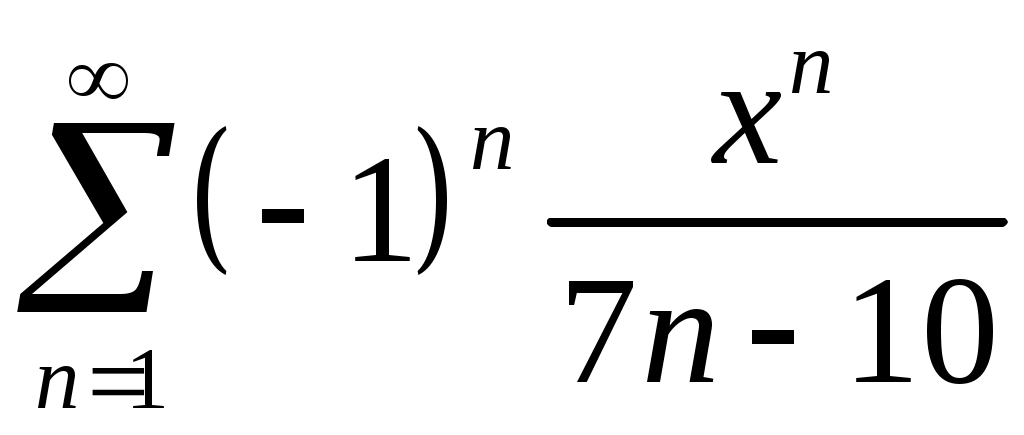 . 15.12. . 15.12. 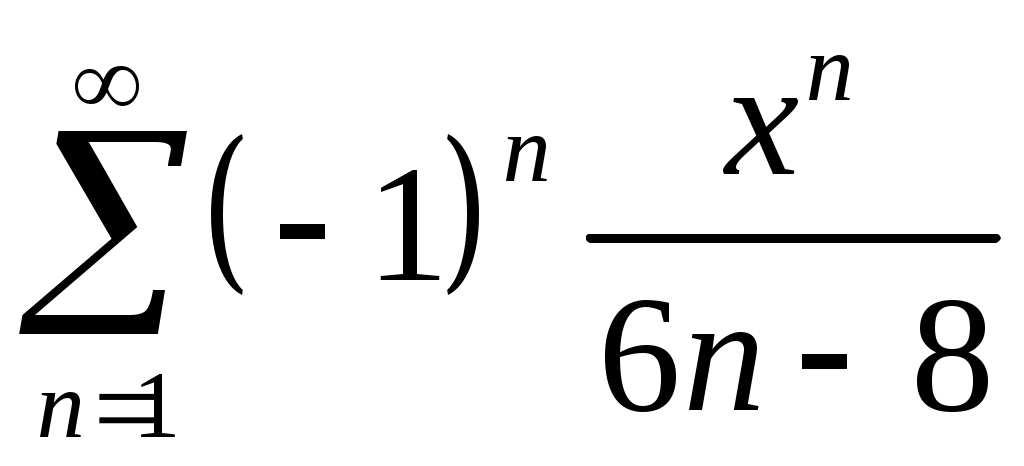 . .15.13. 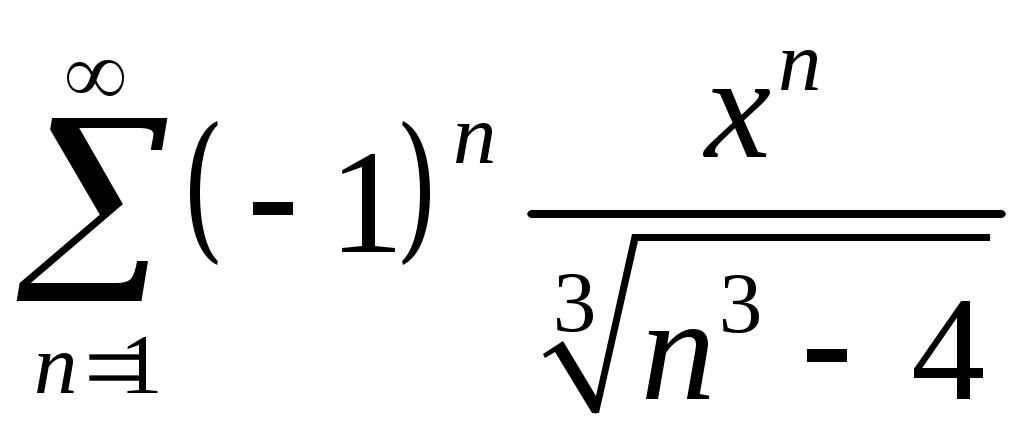 . 15.14. . 15.14. 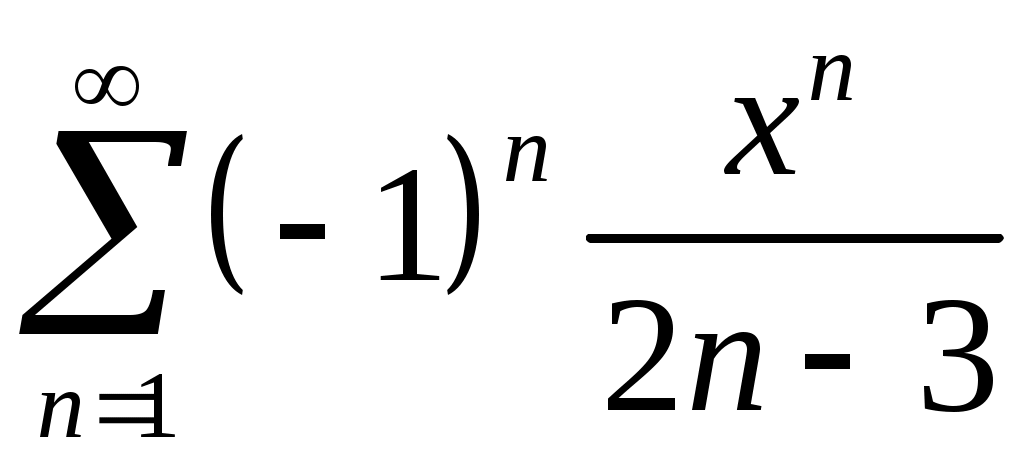 . .15.15. 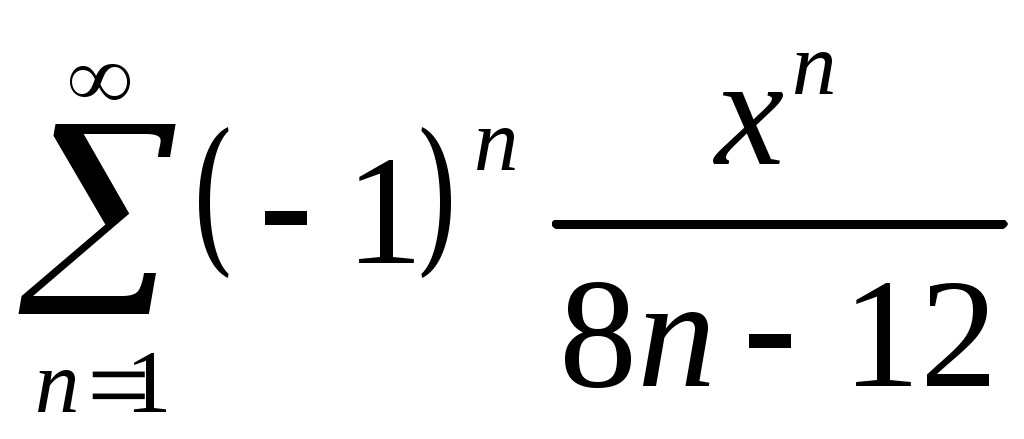 . 15.16. . 15.16. 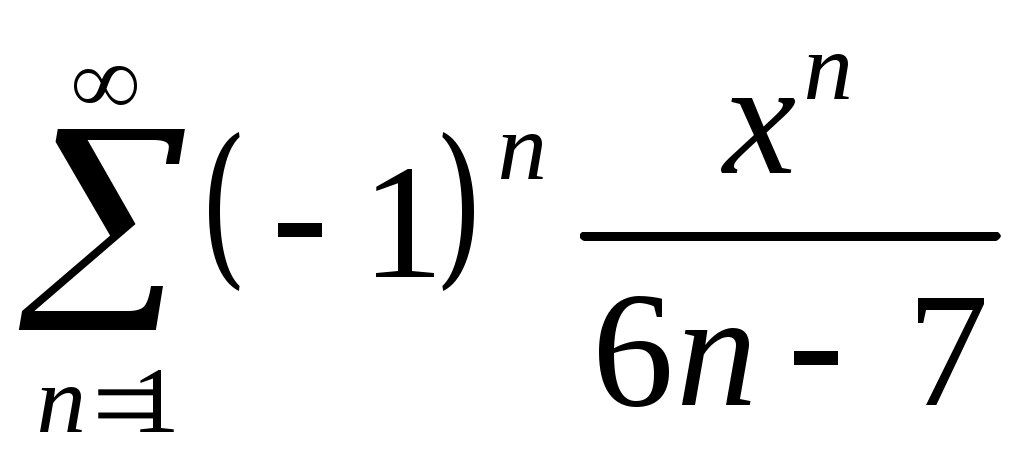 . .15.17. 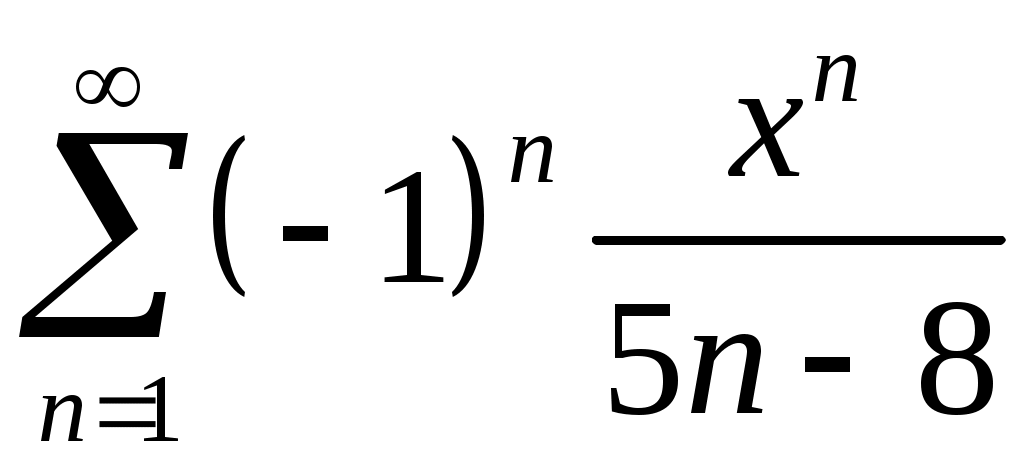 . 15.18. . 15.18. 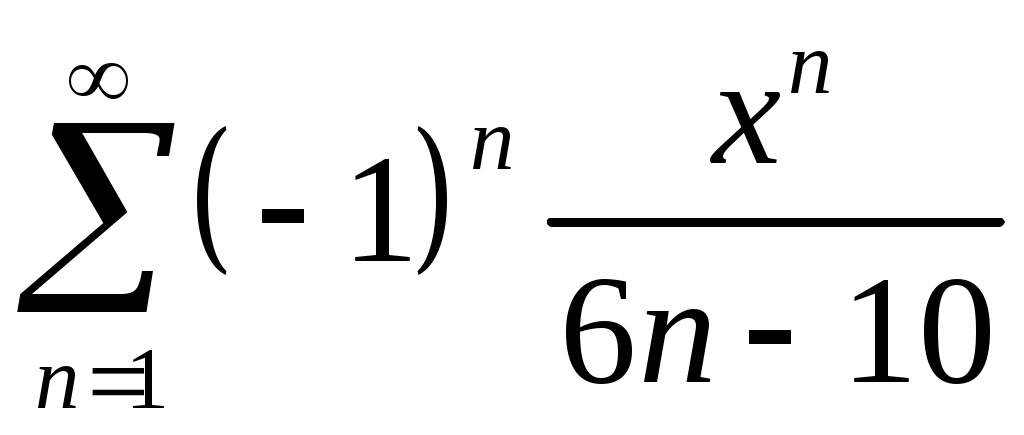 . .15.19. 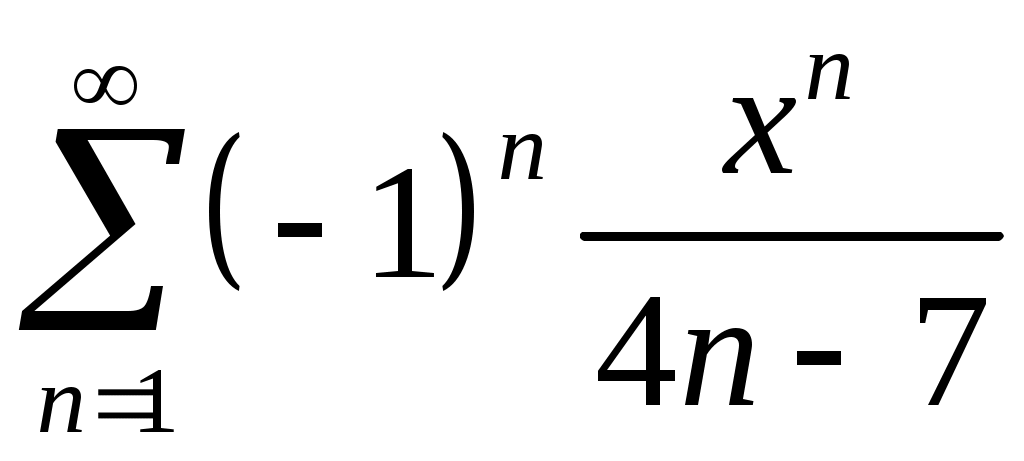 . 15.20. . 15.20. 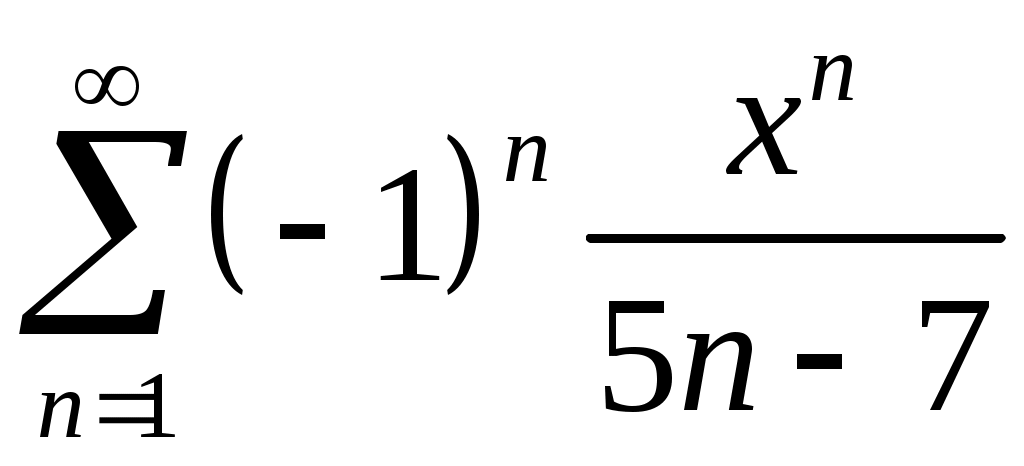 . .15.21. 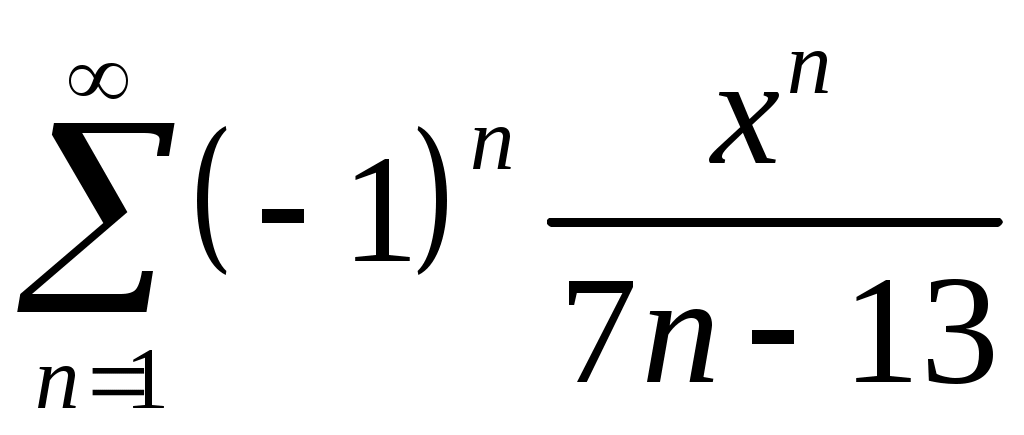 . 15.22. . 15.22. 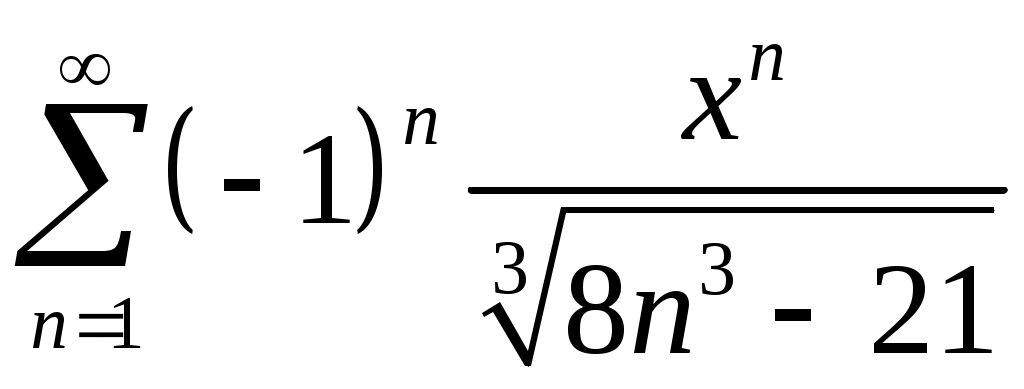 . .15.23. 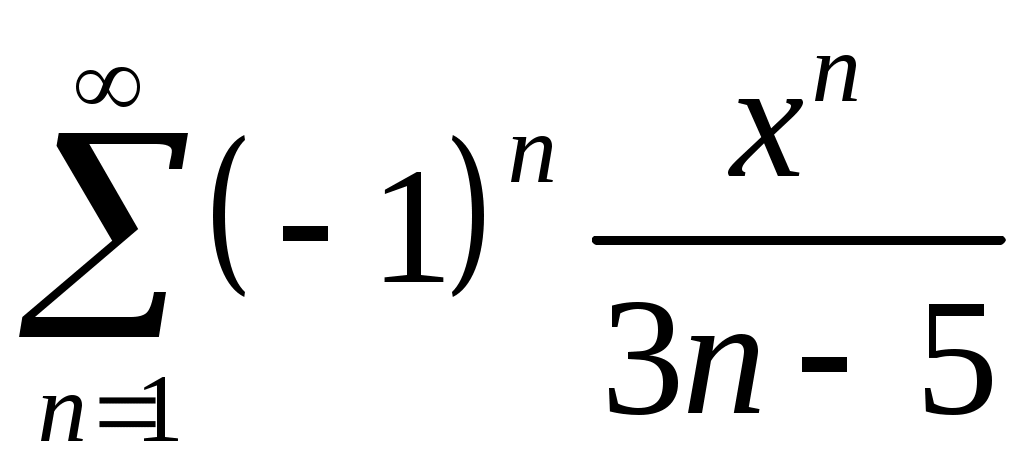 . 15.24. . 15.24. 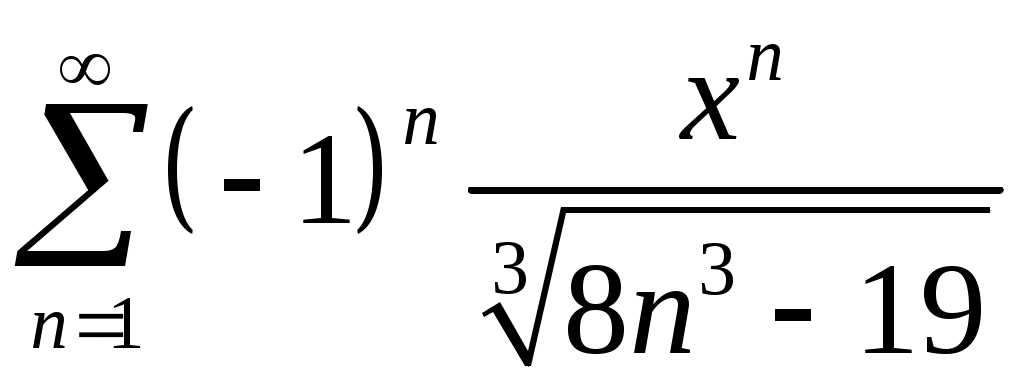 . .15.25. 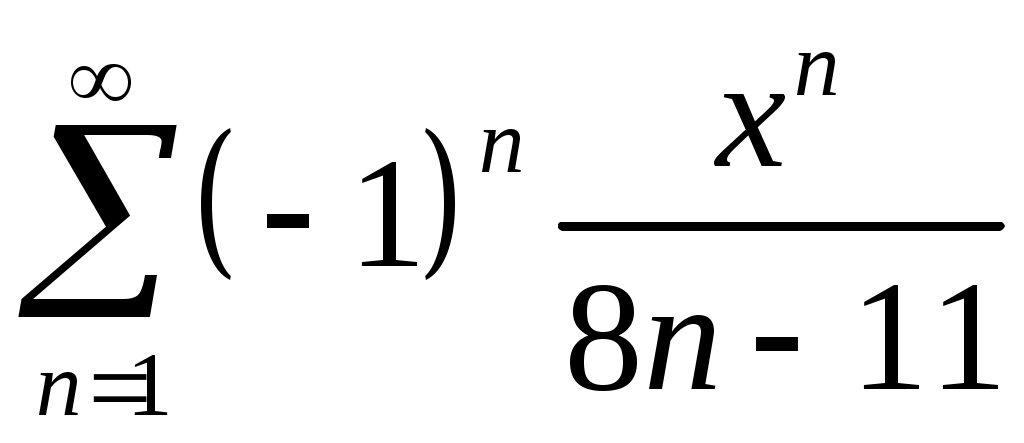 . 15.26. . 15.26. 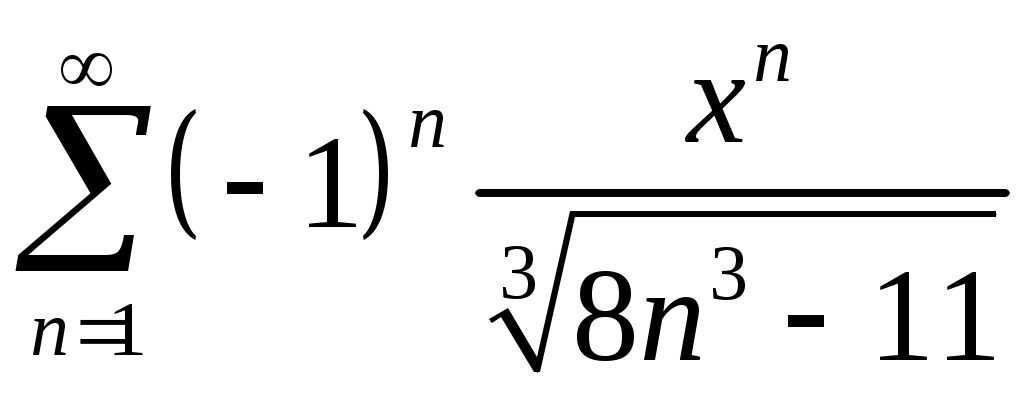 . .15.27. 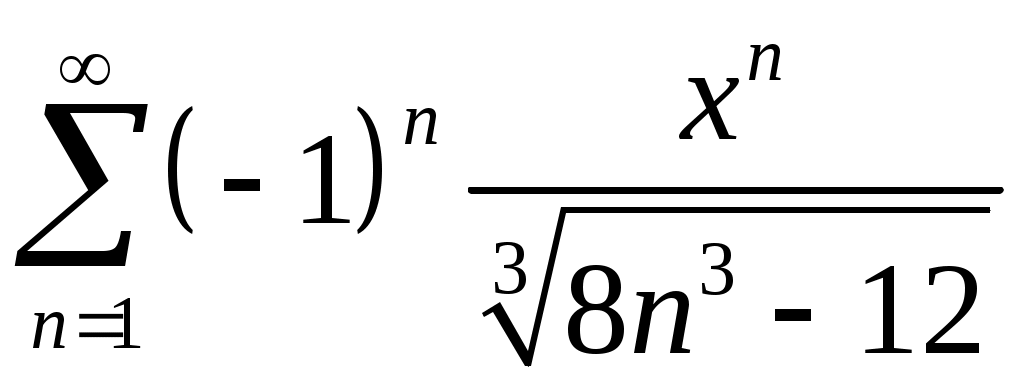 . 15.28. . 15.28. 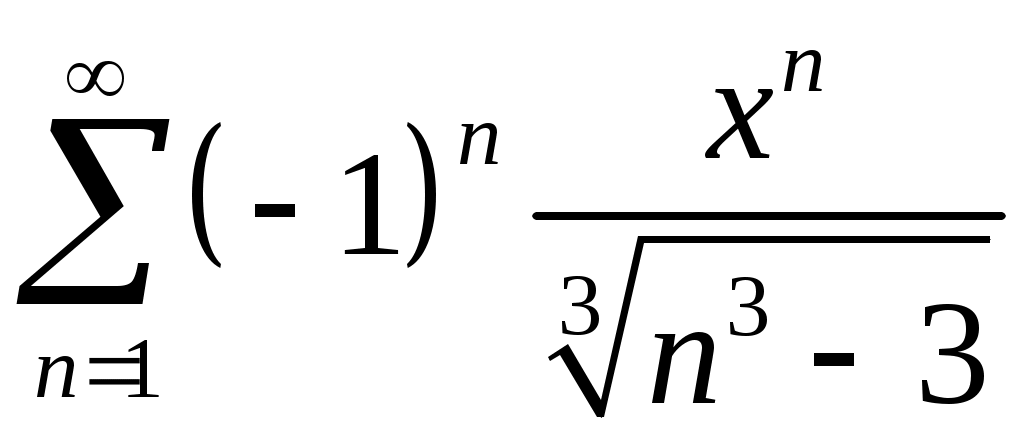 . .15.29. 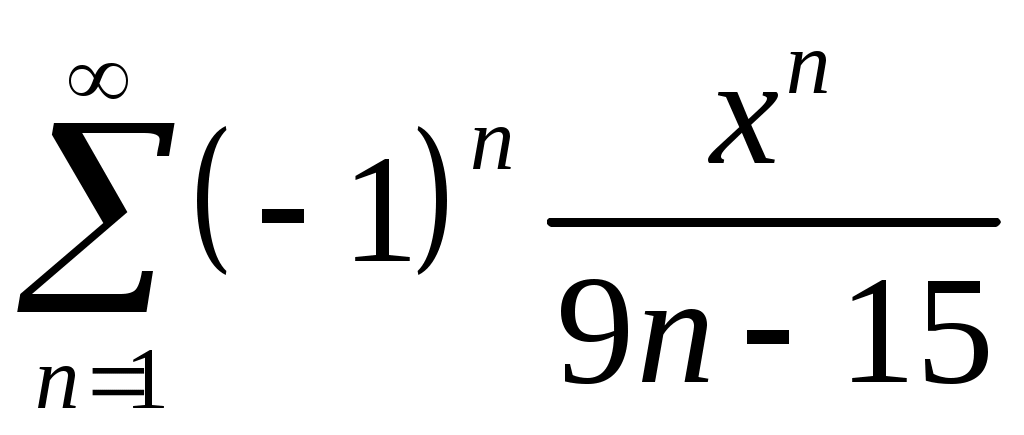 . 15.30. . 15.30. 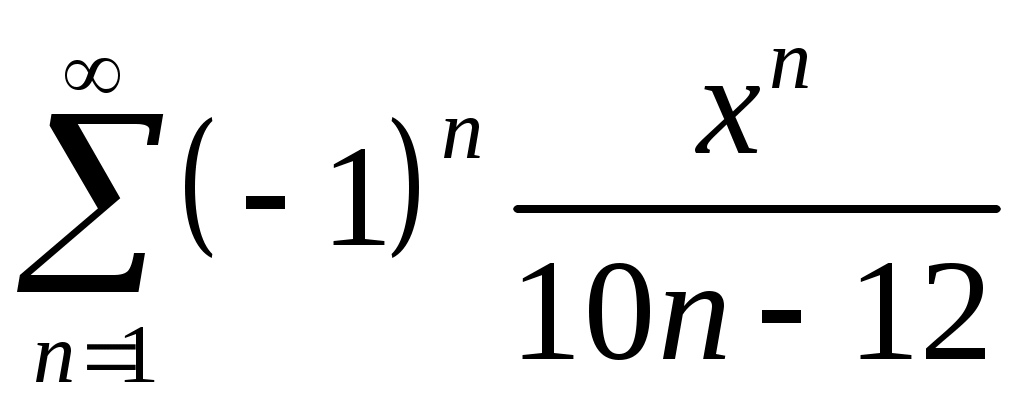 . .15.31. 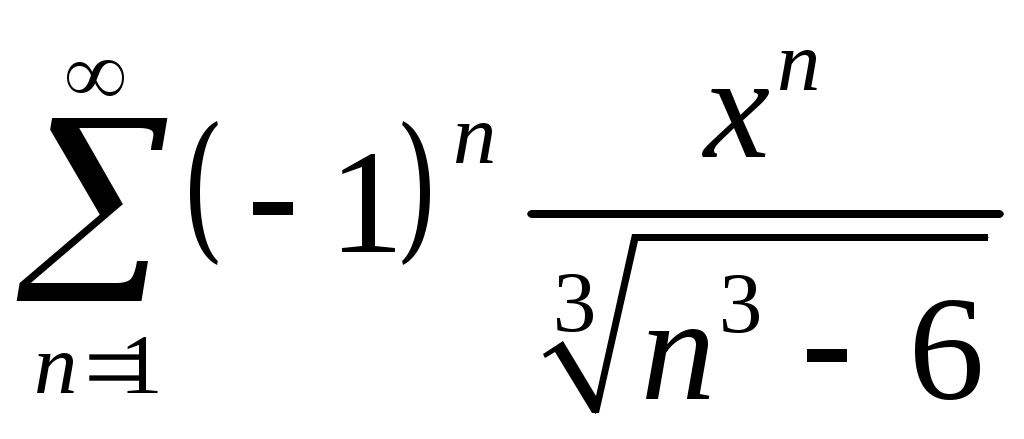 . .Задача 16. Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке. 16.1. 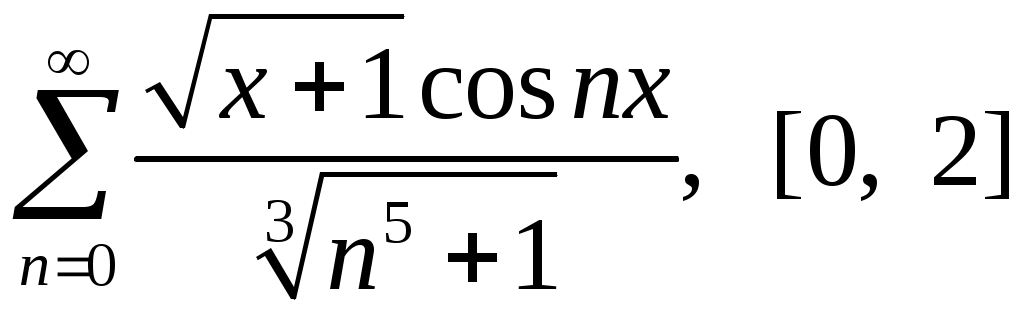 . 16.2. . 16.2. 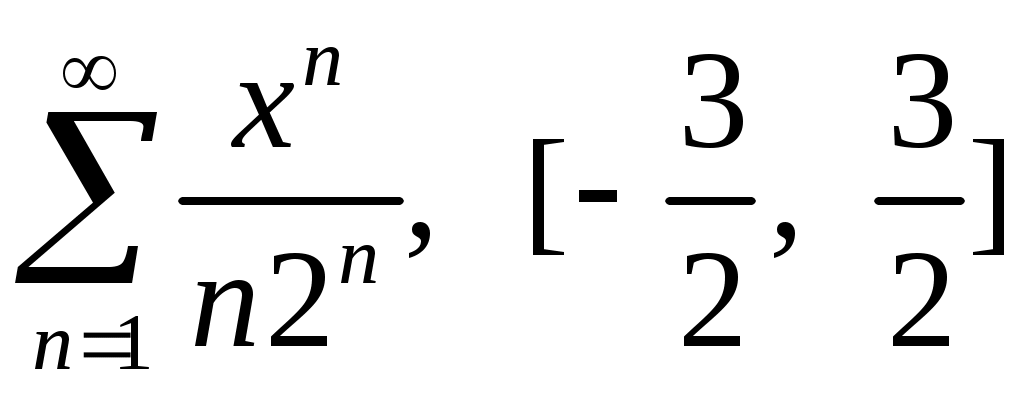 . .16.3. 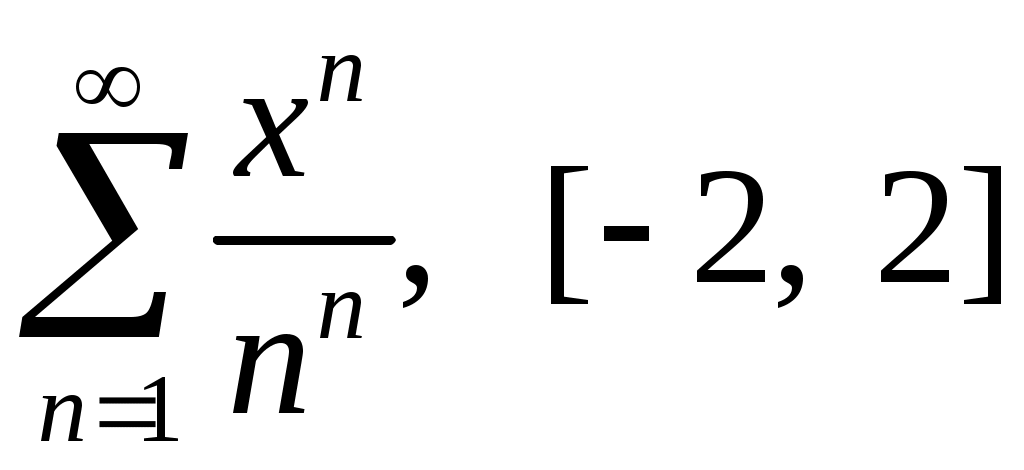 . 16.4. . 16.4. 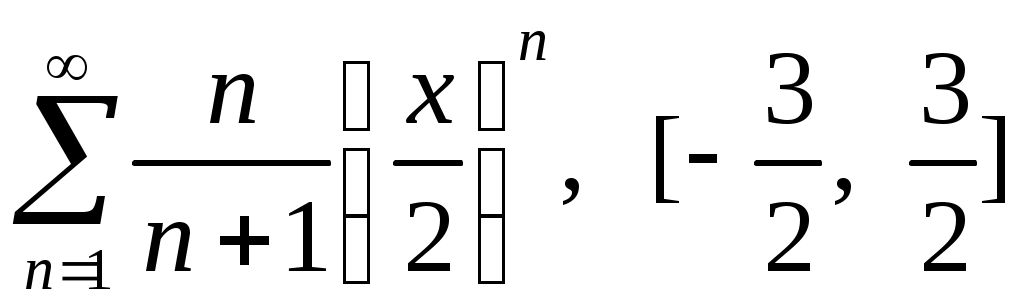 . .16.5. 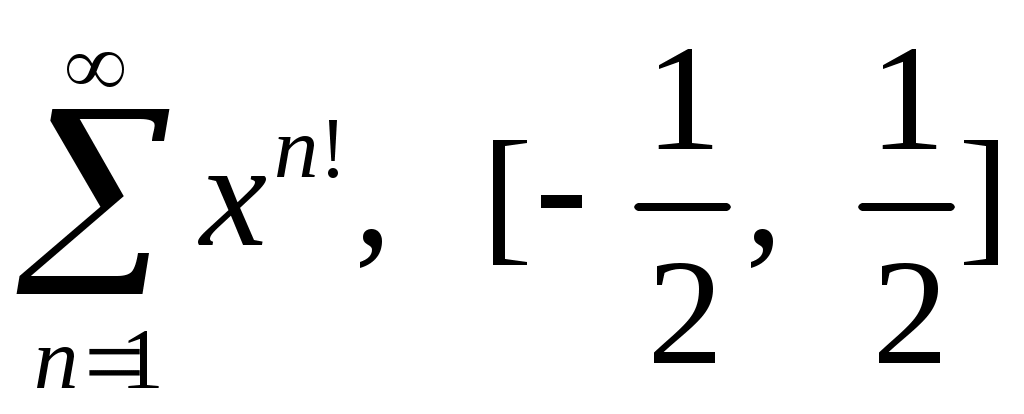 . 16.6. . 16.6. 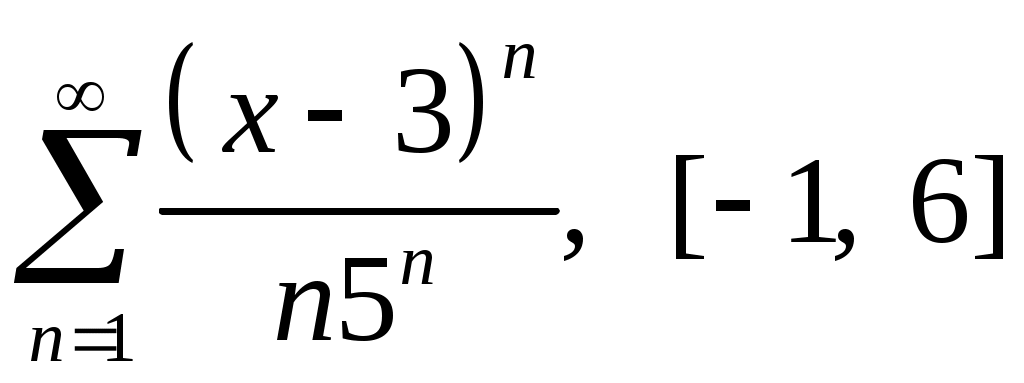 . .16.7. 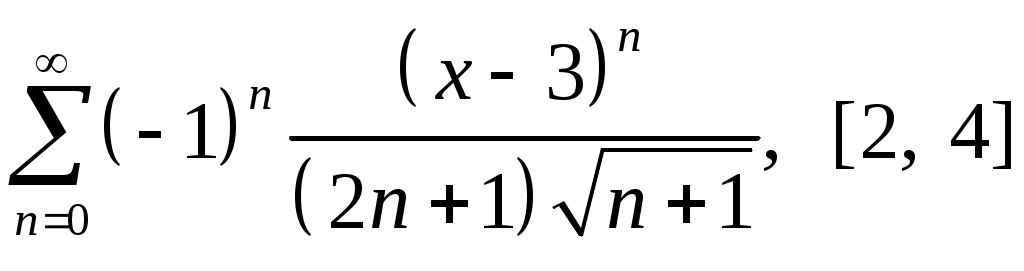 . 16.8. . 16.8. 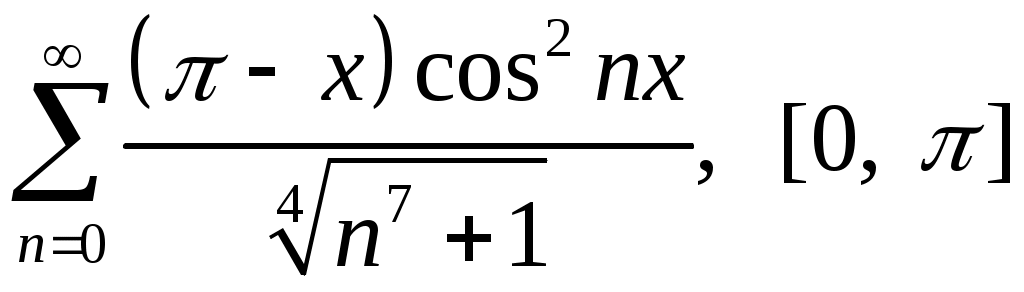 . .16.9. 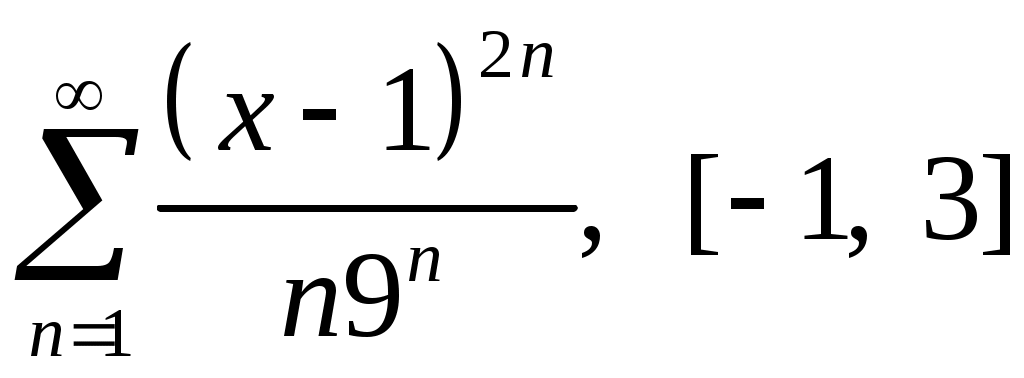 . 16.10. . 16.10. 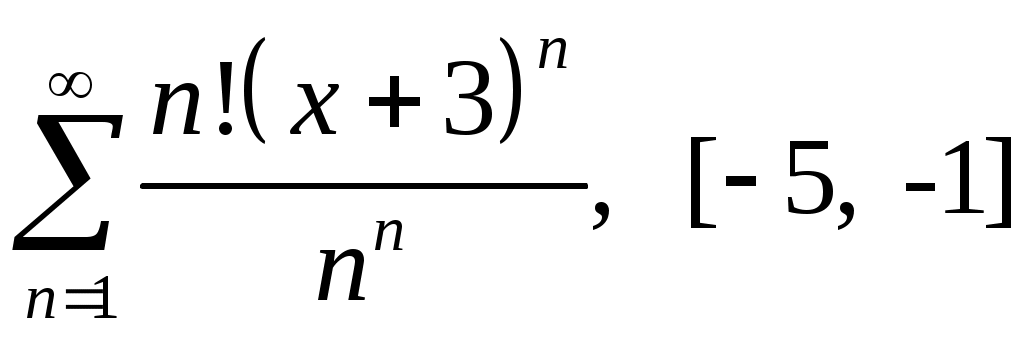 . .16.11. 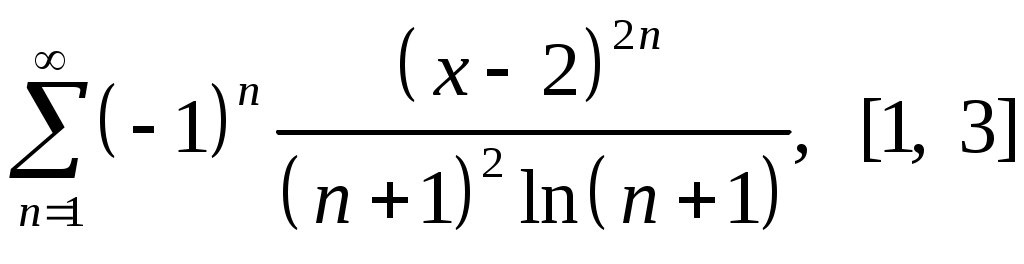 . 16.12. . 16.12. 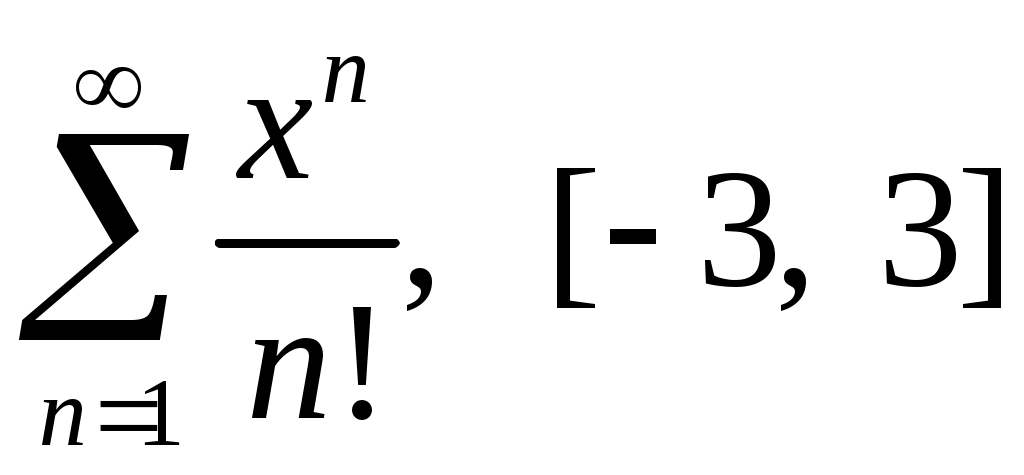 . .16.13. 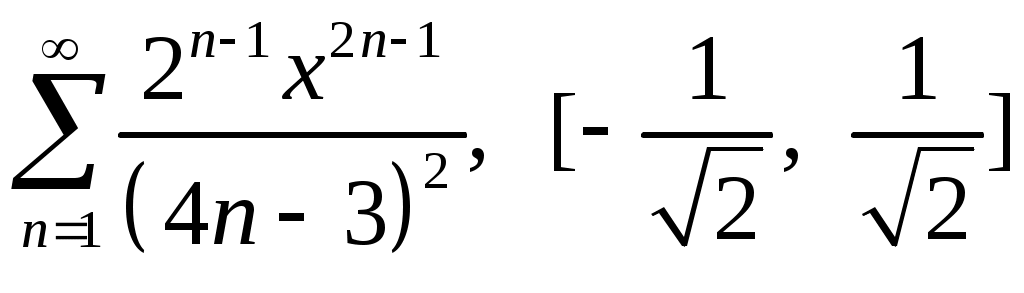 . 16.14. . 16.14. 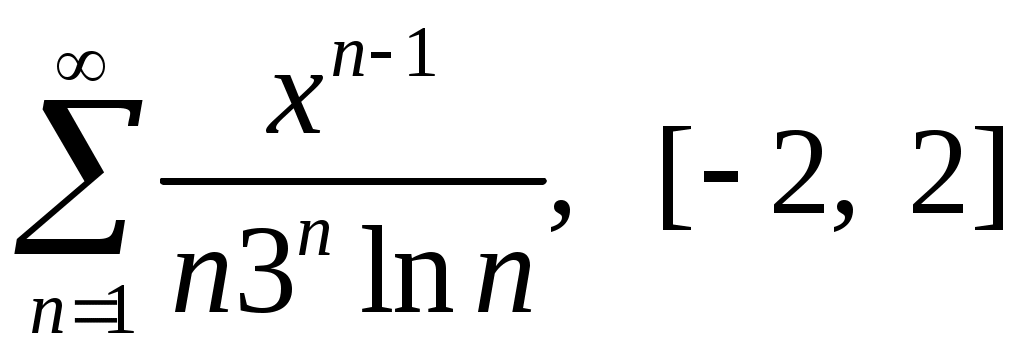 . .16.15. 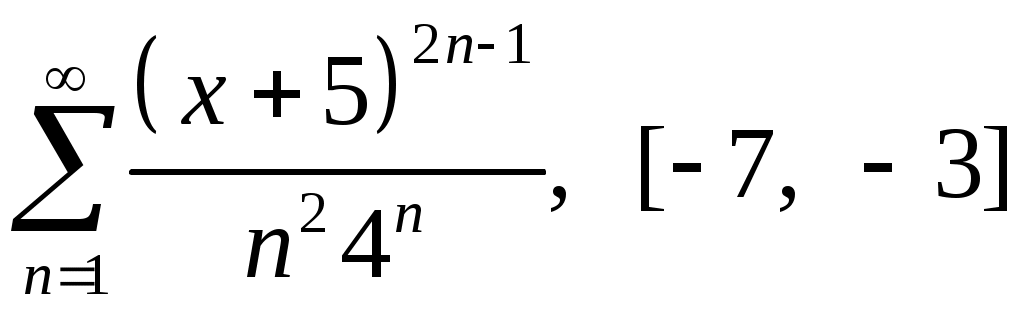 . 16.16. . 16.16. 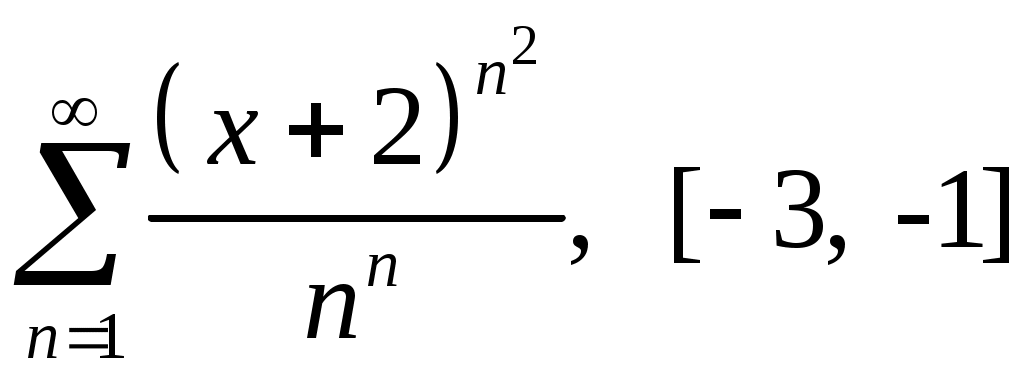 . .16.17. 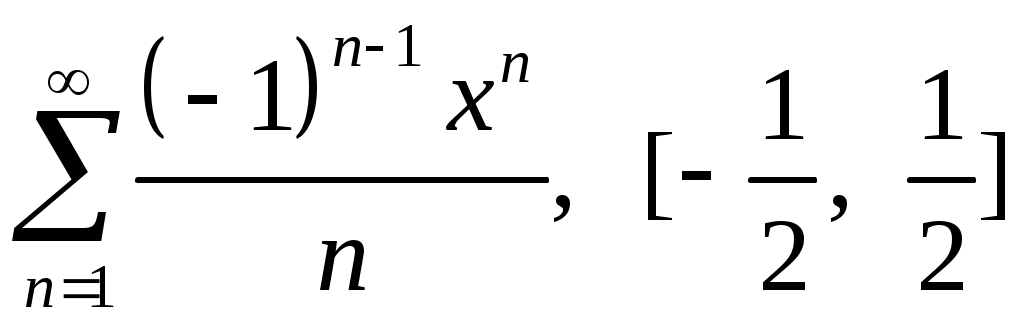 . 16.18. . 16.18. 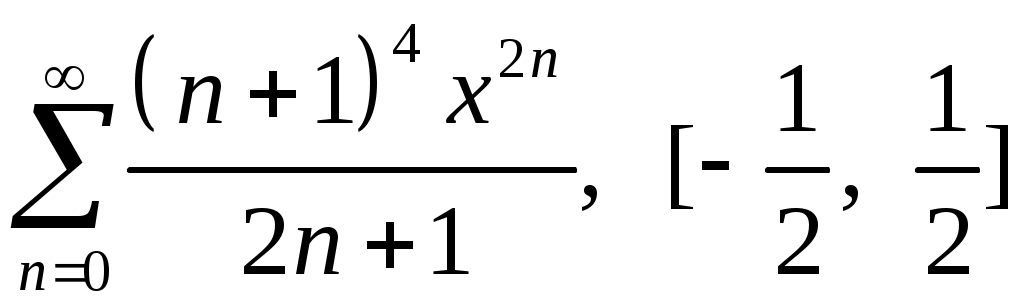 . .16.19. 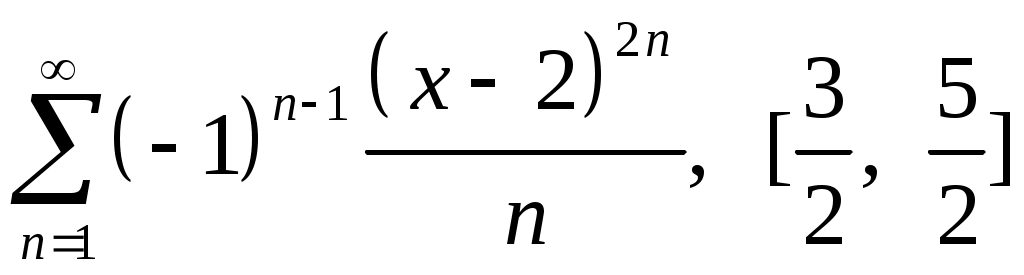 . 16.20. . 16.20. 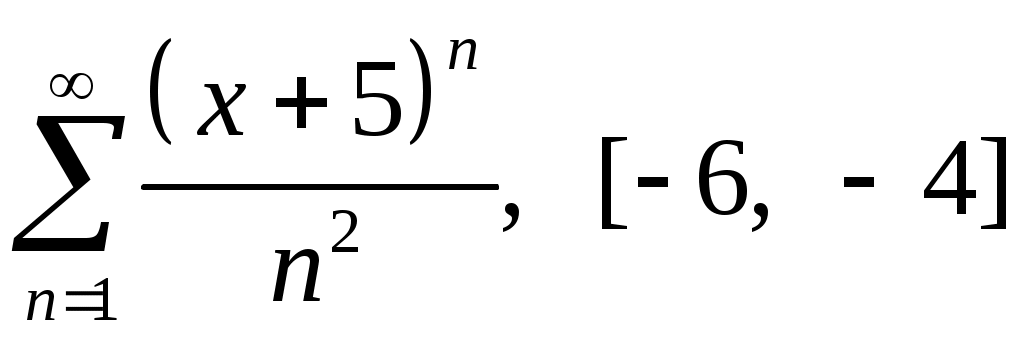 . .16.21. 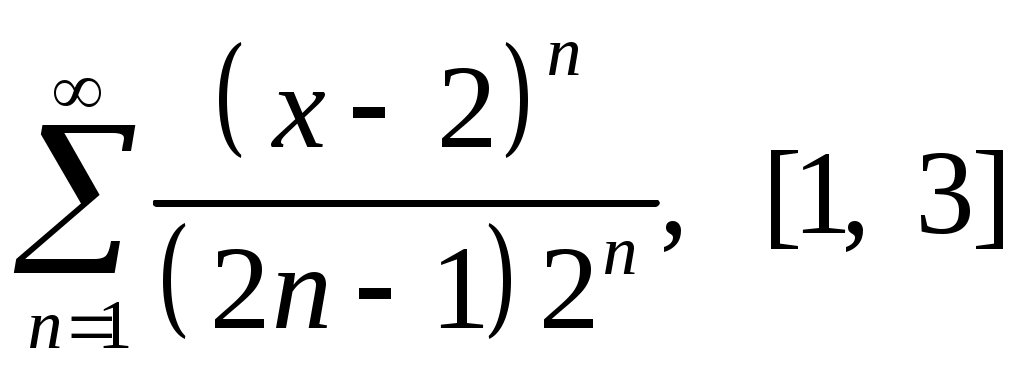 . 16.22. . 16.22. 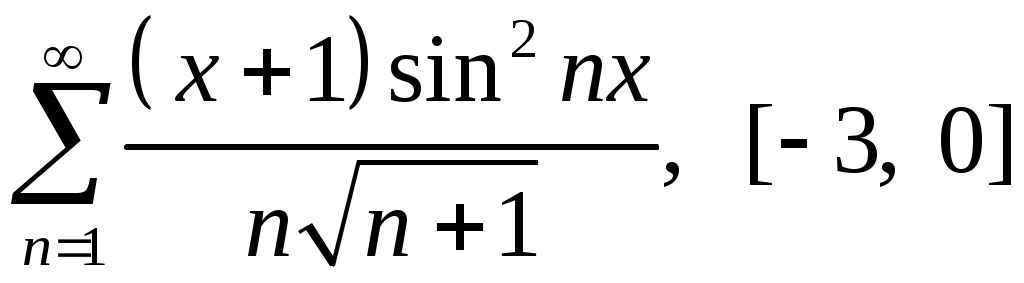 . .16.23. 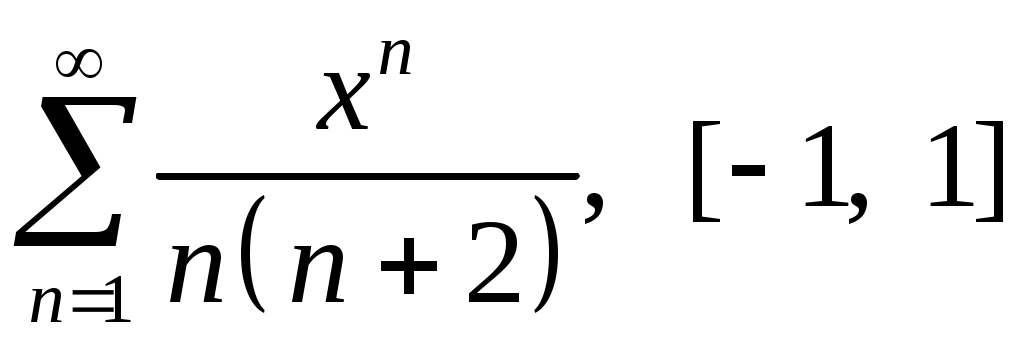 . 16.24. . 16.24. 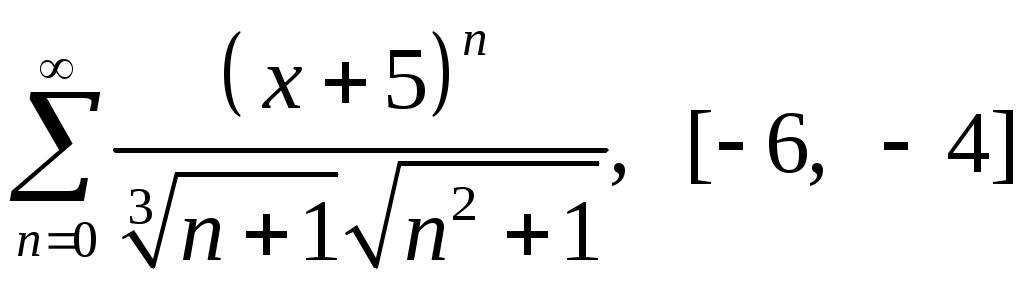 . .16.25. 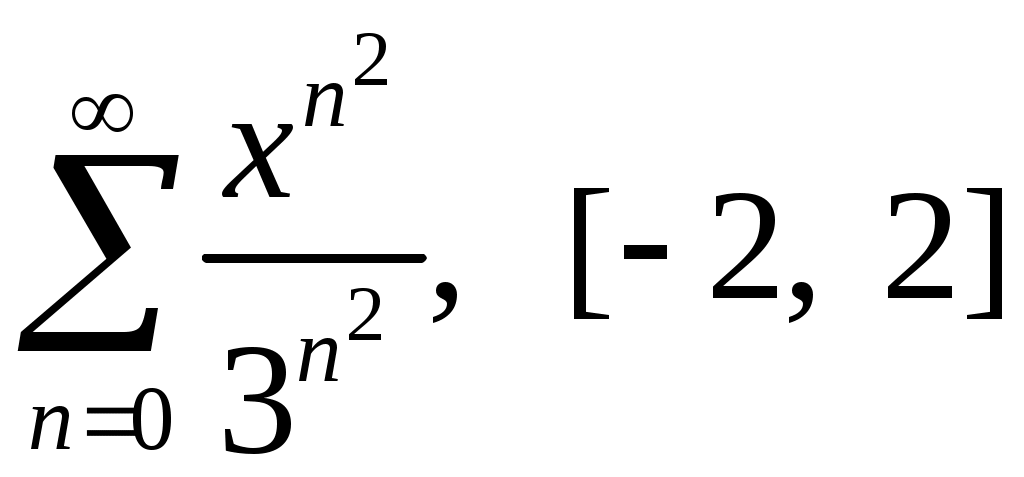 . 16.26. . 16.26. 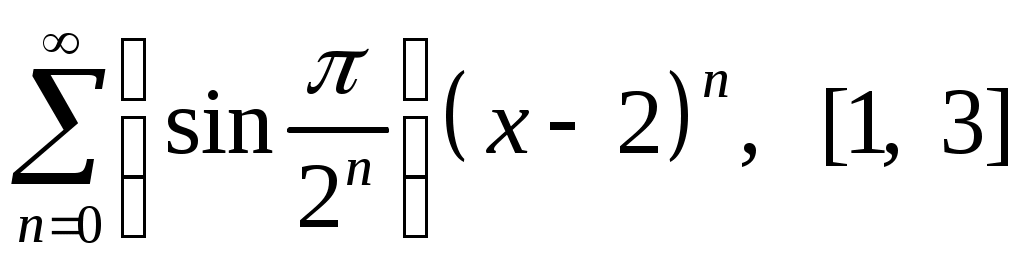 . .16.27. 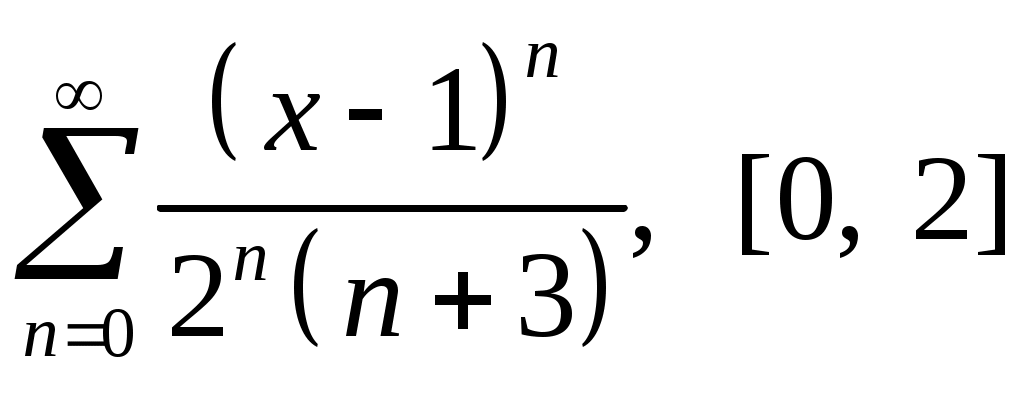 . 16.28. . 16.28. 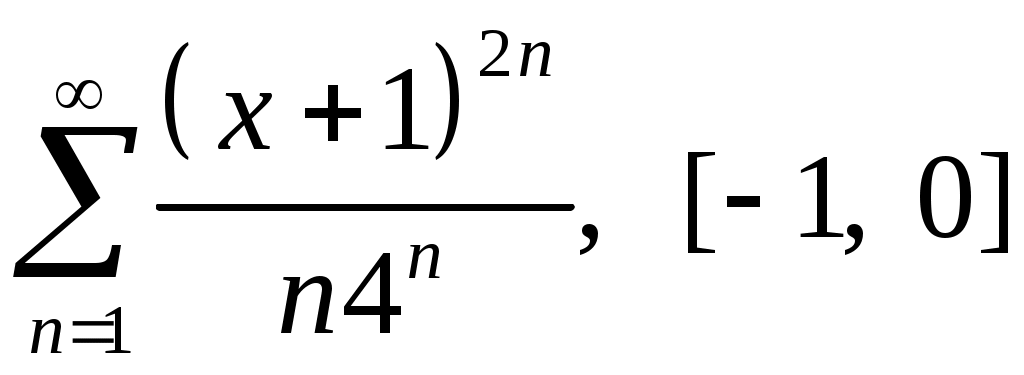 . .16.29. 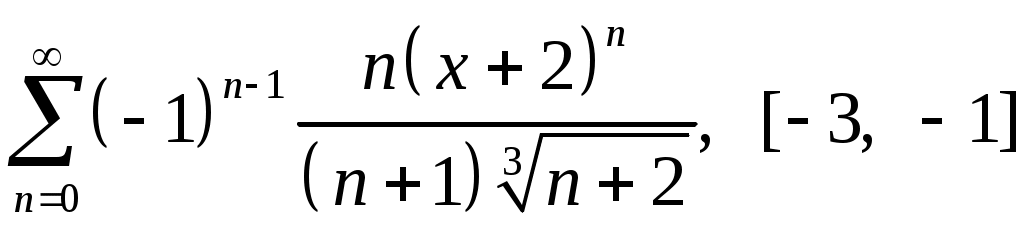 . 16.30. . 16.30. 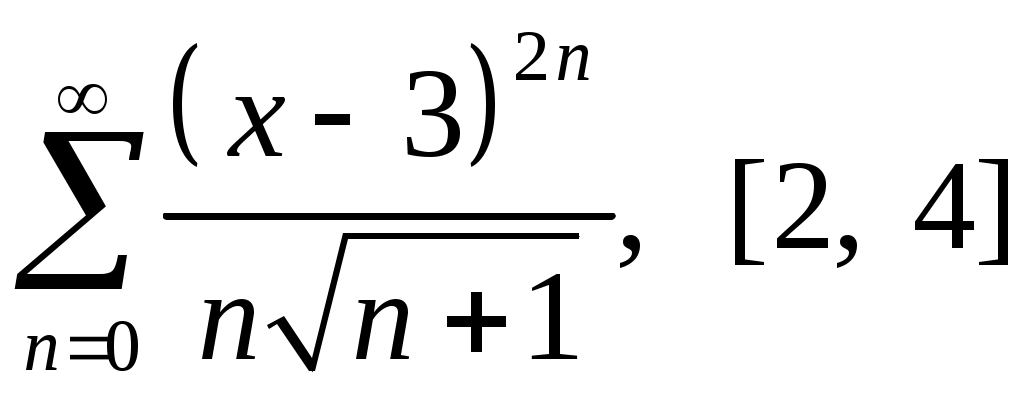 . .16.31. 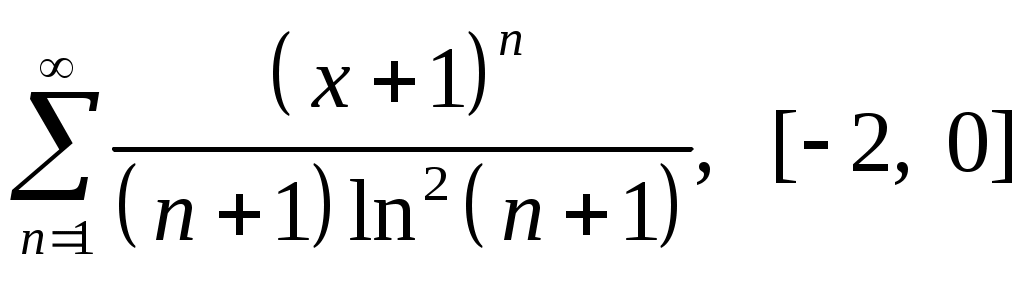 . . |
