доклад по специальному семенару. Реферат специальный семинар. "Вычисление дпф любой длины"
 Скачать 137.28 Kb. Скачать 137.28 Kb.
|
 ФЕДЕРАЛЬНОЕ АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования “Государственный университет морского и речного флота имени адмирала С.О. Макарова”  Институт водного транспорта Кафедра прикладной математики РЕФЕРАТ по дисциплине: Специальный семинар На тему “Вычисление ДПФ любой длины” Выполнил: Студент гр. ИП-31, Устюжанина Н.Н. ________________ (подпись) Проверил: Доцент кафедры ПМ, д.т.н., Васин А.В. _________________ (оценка, подпись) Санкт-Петербург 2022 г. Дискретное преобразование Фурье (ДПФ) – это отображение 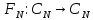 , сопоставляющее сигналу , сопоставляющее сигналу 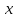 сигнал сигнал 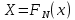 со значениями: со значениями: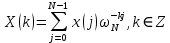 Определение 1. Сигнал 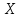 называется спектром Фурье сигнала называется спектром Фурье сигнала 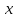 или просто спектром, а величины или просто спектром, а величины 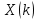 - компонентами спектра или спектральными составляющими. - компонентами спектра или спектральными составляющими.Определение 2. Быстрое преобразование Фурье (БПФ) представляет собой алгоритм, который вычисляет дискретное преобразование Фурье (ДПФ) последовательности, или его обратного. Одним из вариантов быстрого преобразования Фурье является алгоритм Кули-Тьюки с прореживанием по времени. Алгоритм чтобы быстро вычисляет ДПФ длины, равной степени двойки. Рассмотрим этот алгоритм. В пространстве 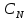 при при 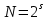 строим строим 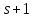 ортогональных базисов ортогональных базисов 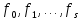 . Возьмём сигнал . Возьмём сигнал 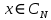 . Его можно разложить по любому из этих базисов. Далее разложим сигнал . Его можно разложить по любому из этих базисов. Далее разложим сигнал 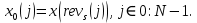 ( (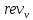 -перестановка. Она определена на множестве натуральных чисел {0,1,…,2v-1} и сопоставляет числу -перестановка. Она определена на множестве натуральных чисел {0,1,…,2v-1} и сопоставляет числу 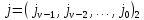 число число 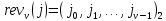 , двоичный код которого равен перевернутому двоичному коду числа , двоичный код которого равен перевернутому двоичному коду числа 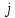 . Идентификатор . Идентификатор 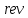 связан с английским словом связан с английским словом 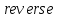 . Индекс . Индекс 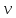 у у 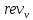 определяет количество ревертируемых разрядов.) определяет количество ревертируемых разрядов.)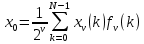 (1) (1)Для определения коэффициентов 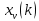 умножим обе части уравнения (1) скалярно на умножим обе части уравнения (1) скалярно на 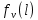 . . Теорема 1. (устанавливает, что система сигналов (2) образует ортогональный базис в пространстве 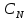 ). ).При каждом 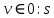 система сигналов система сигналов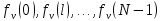 (2) (2)ортогональна и 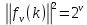 при всех при всех 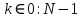 . .Согласно этой теореме получаем 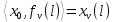 , так что: , так что: 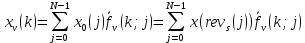 (3) (3)В частности: 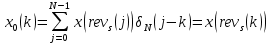 Домножая равенства скалярно на 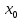 имеем: имеем: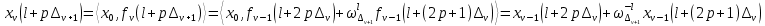 Аналогично 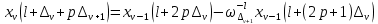 Таким образом переходим к рекуррентной схеме: 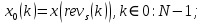 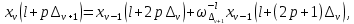 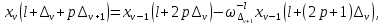 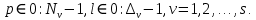 (4) (4)По этой схеме вычисляются коэффициенты разложения сигнала 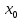 по всем базисам по всем базисам 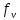 вплоть до вплоть до 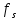 . Отметим, что . Отметим, что 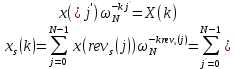 Таким образом, коэффициенты 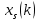 есть не что иное, как компоненты спектра сигнала есть не что иное, как компоненты спектра сигнала 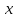 на основном периоде. на основном периоде.Вычисления по формулам (4) требуют: умножений: 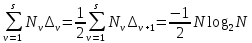 сложений: 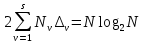 Схема (4) является одним из вариантов быстрого преобразования Фурье при 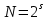 и называется алгоритмом Кули-Тьюки с прореживанием по времени. и называется алгоритмом Кули-Тьюки с прореживанием по времени. Формулы (4) допускают обращение: 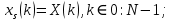 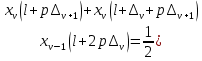 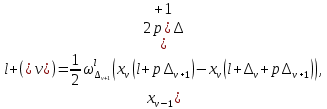 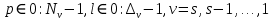 (5) (5)По формулам (5) спустимся до 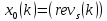 . Заменив . Заменив 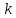 на на 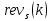 , получим , получим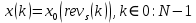 Тем самым указан быстрый алгоритм восстановления сигнала 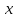 по его спектру по его спектру 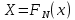 при при 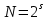 . .Однако, довольно часто на практике оказывается, что это достаточно неудобное ограничение. Ниже покажем, что вычисление ДПФ любой длины 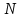 можно свести к вычислению ДПФ длины можно свести к вычислению ДПФ длины 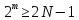 . .Замечание 1. Вычисление спектра 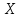 можно интерпретировать как вычисление значений полинома можно интерпретировать как вычисление значений полинома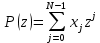 в 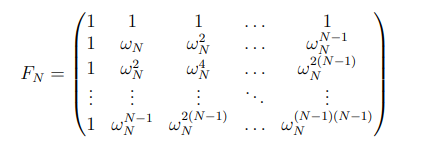 точках единичной окружности точках единичной окружности 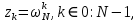 и как вычисление произведения матрицы и как вычисление произведения матрицына вектор 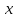 . .Как было показано в замечании 1, ДПФ сигнала, определяемое формулой 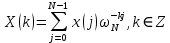 , можно записать в виде умножения матрицы , можно записать в виде умножения матрицы 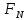 из замечания (1) на вектор сигнала из замечания (1) на вектор сигнала 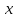 . .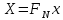 Определение 3. Матрица 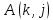 называется теплицевой или диагонально-постоянной матрицей, если на всех её диагоналях, параллельных главной, стоят равные элементы. Является обобщением понятия правоциркулянтной матрицы. называется теплицевой или диагонально-постоянной матрицей, если на всех её диагоналях, параллельных главной, стоят равные элементы. Является обобщением понятия правоциркулянтной матрицы.Определение 4. Правоциркулянтная матрица – это квадратная матрица, каждая строка которой, начиная со второй, получается сдвигом предыдущей вправо на один элемент; тот элемент, что при этом сдвиге “выходит” за пределы матрицы, переставляется в начало строки. В 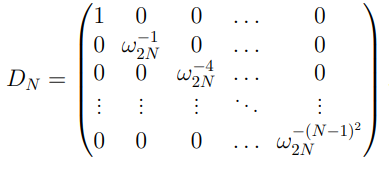 ведем в рассмотрение диагональную матрицу ведем в рассмотрение диагональную матрицу 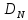 , ,и симметричную теплицеву матрицу 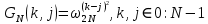 Справедливо следующее равенство Лемма 1. 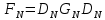 (6) (6)Доказательство. Запишем очевидное равенство 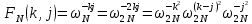 С другой стороны 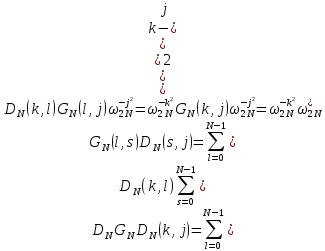 Введем обозначения 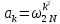 . Тогда матрицу . Тогда матрицу 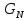 можно представить в следующем виде: можно представить в следующем виде: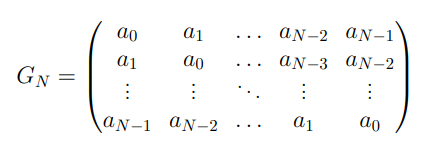 З 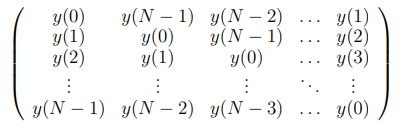 амечание 2. Вычисление циклической свёртки x*yможно интерпретировать как вычисление произведения правоциркулянтной матрицы амечание 2. Вычисление циклической свёртки x*yможно интерпретировать как вычисление произведения правоциркулянтной матрицына вектор х. Вложим 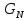 в правоциркулянтную матрицу в правоциркулянтную матрицу 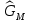 порядка порядка 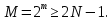 строку с индексом 0 матрицы строку с индексом 0 матрицы 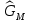 определим следующим образом определим следующим образом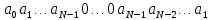 (7) (7)Нулей поставлено столько, чтобы длина строки равнялась M. из строки (7) с помощью циклических сдвигов вправо формируется квадратная матрица 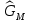 . Например, если . Например, если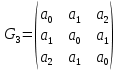 т 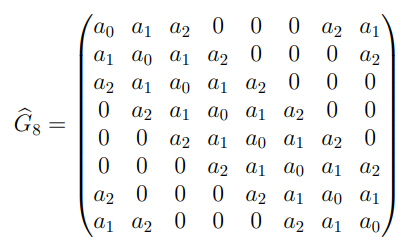 о оПо построению матрица 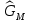 правоциркулянтная и симметричная, при этом подматрица правоциркулянтная и симметричная, при этом подматрица 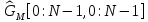 совпадает с совпадает с 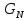 , т.е. , т.е.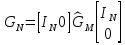 (8) (8)где 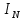 обозначает единичную матрицу размерности N. обозначает единичную матрицу размерности N.Из (6) и (8) получаем 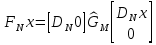 (9) (9)Введем следующие обозначения: 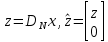 Через 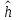 обозначим сигнал из обозначим сигнал из 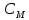 , который на основном периоде имеет вид (7). Так как , который на основном периоде имеет вид (7). Так как 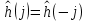 , то , то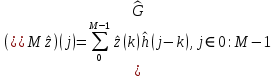 (10) (10)В правой части равенства (10) по определению стоит циклическая свёртка 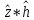 . . Теорема 2 (о свертке). Пусть 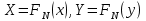 . Тогда . Тогда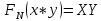 , ,где справа стоит покомпонентное произведение спектров. По теореме 2 (о свёртке) имеем 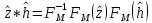 (11) (11)Заметим, что спектр 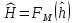 не зависит от х. Его компоненты можно вычислить заранее по формуле не зависит от х. Его компоненты можно вычислить заранее по формуле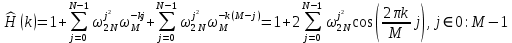 (12) (12)Таким образом, приходим к следующему алгоритму вычисления спектра 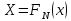 . .Шаг 1. Формируем вектор 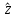 размерности М: размерности М: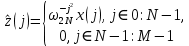 Шаг 2. Вычисляем 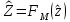 Шаг 3. Вычисляем вектор 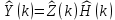 . Компоненты вектора . Компоненты вектора 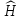 вычислены заранее согласно (12). вычислены заранее согласно (12).Шаг 4. Вычисляем 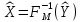 . .Шаг 5. Находим компоненты спектра 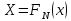 : :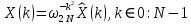 Замечание 3. Самыми «плохими» для вышеприведенного алгоритма являются N вида 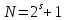 . Для них . Для них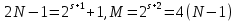 Список используемой литературыУчебное пособие «Математические методы цифровой обработки сигналов», авторы Поздняков С.Н., Рыбин С.В. |
