|
Выделим в бесконечном несчетном множестве M счетное подмножество 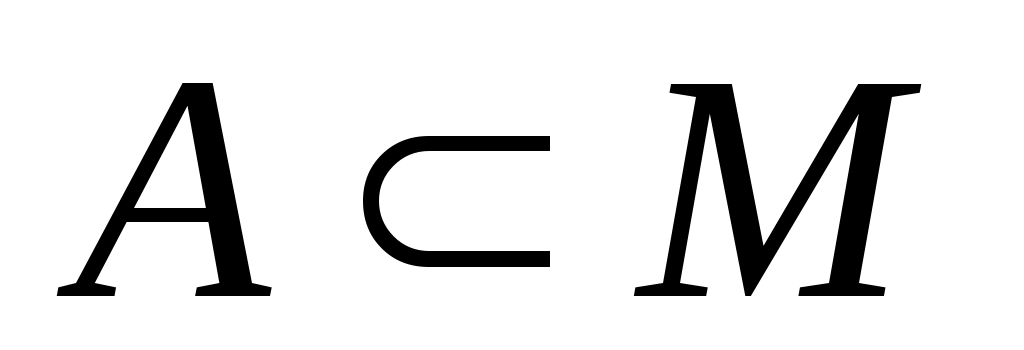 . В каком отношении находятся мощности множеств M\A и M? . В каком отношении находятся мощности множеств M\A и M?
|
мощность множества M равна мощности множества M\A;
мощность множества M меньше мощности множества M\A;
мощность множества M больше мощности множества M\A;
|
|
Выделим в бесконечном несчетном множестве М счетное подмножество 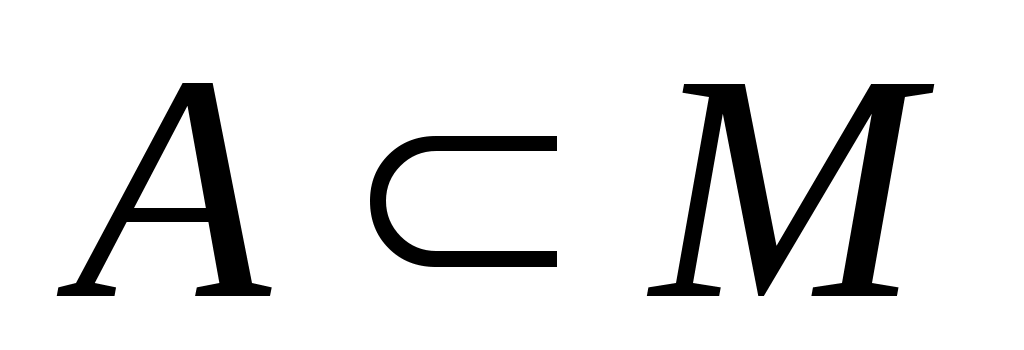 . В каком отношении находятся мощности множеств М\А и М? . В каком отношении находятся мощности множеств М\А и М?
|
мощность множества М равна мощности множества М\А;
мощность множества М больше мощности множества М\А;
мощность множества М меньше мощности множества М\А;
|
|
Выразите дизъюнкцию  через импликацию и отрицание: через импликацию и отрицание:
|
 . .
 ; ;
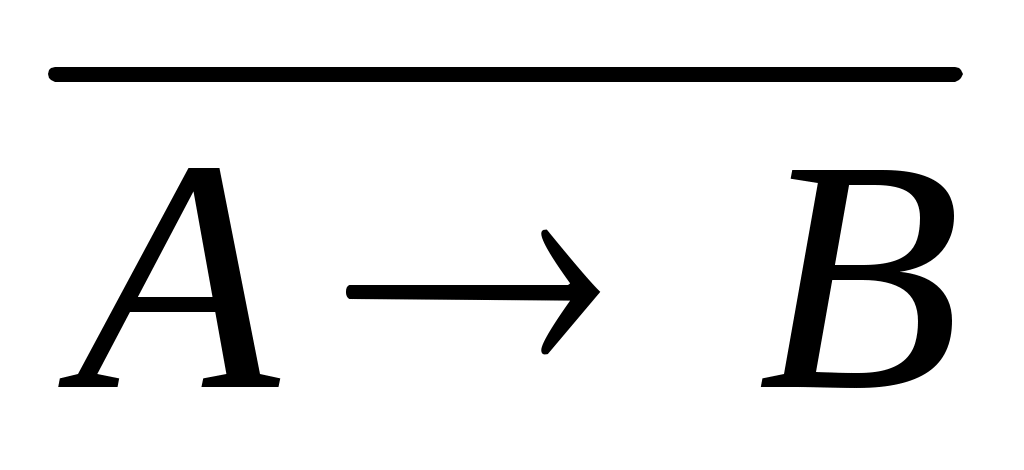 ; ;
|
|
Выразите конъюнкцию A^B через импликацию и отрицание:
|
 . .
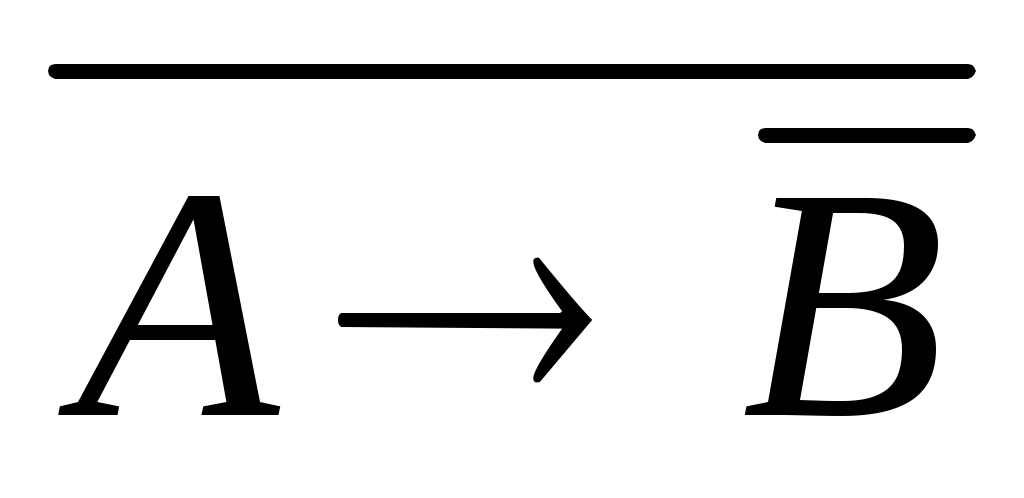 ; ;
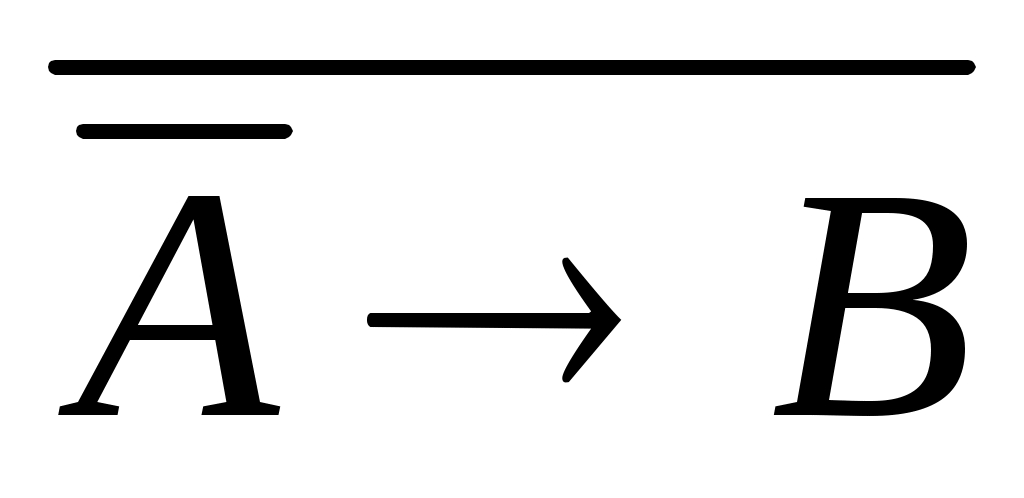 ; ;
|
|
Высказывание 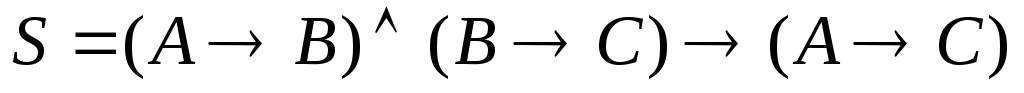 является: является:
|
переменным.
тождественно истинным;
тождественно ложным;
|
|
Высказывание  является: является:
|
тождественно истинным;
переменным.
тождественно ложным;
|
|
Высказывание 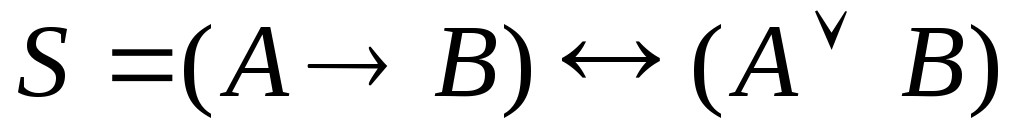 является: является:
|
тождественно ложным;
переменным.
тождественно истинным;
|
|
Высказывание 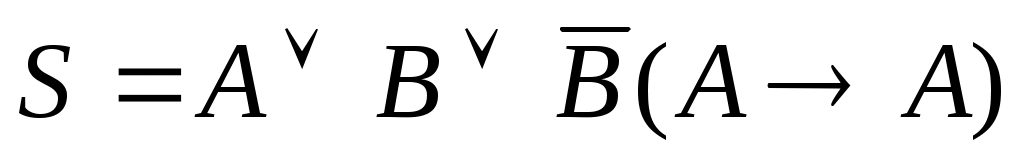 является: является:
|
переменным.
тождественно ложным;
тождественно истинным;
|
|
Высказывание: "Если а – нечетное число, b – четное число, то их произведение делится на 2" в символической форме имеет вид:
|
 . .
 ; ;
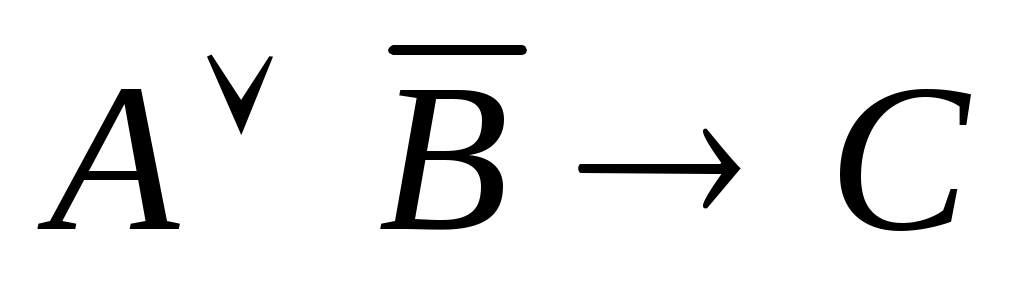 ; ;
|
|
Высказывание: "Если а – четное число, b – нечетное число, то их произведение делится на 2" в символической форме имеет вид
|
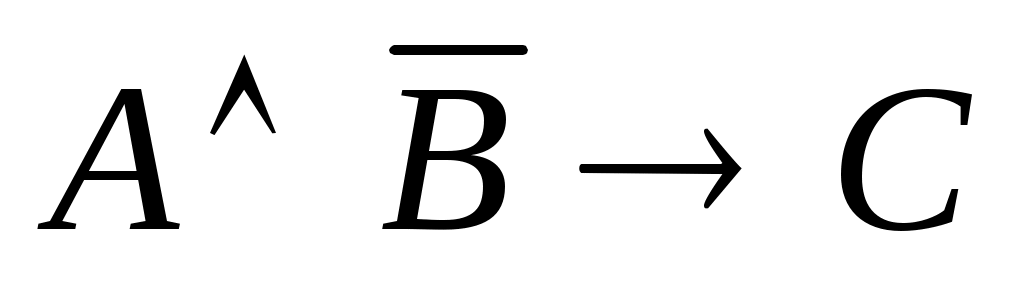 . .
 ; ;
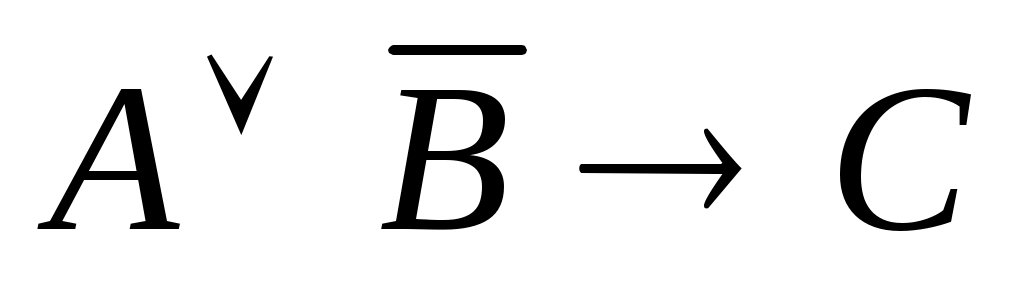 ; ;
|
|
Вытекает ли из равенства A\B=C, что 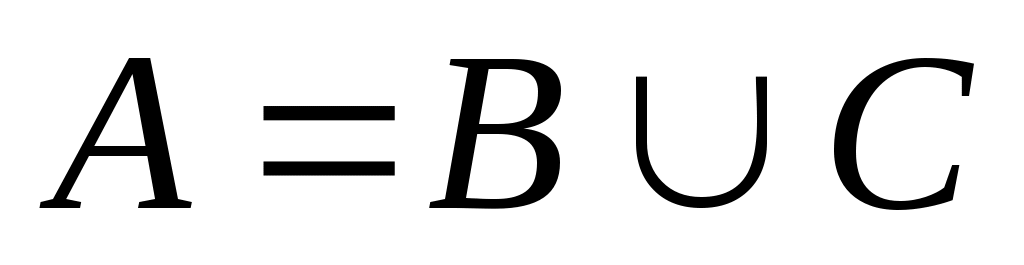 ? ?
|
в общем случае неверно, но в частном случае возможно.
да;
нет;
|
|
Граф G получен из графов G1 и G2 путем операции:
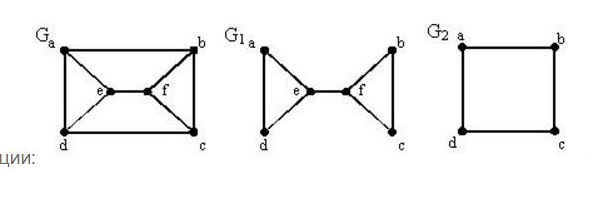 ? ?
|
пересечение;
объединение;
декартово произведение.
|
|
Графы G1 и G2 заданы матрицами смежности A1 и A2 соответственно. С помощью какой операции был получен граф G, заданный матрицей A
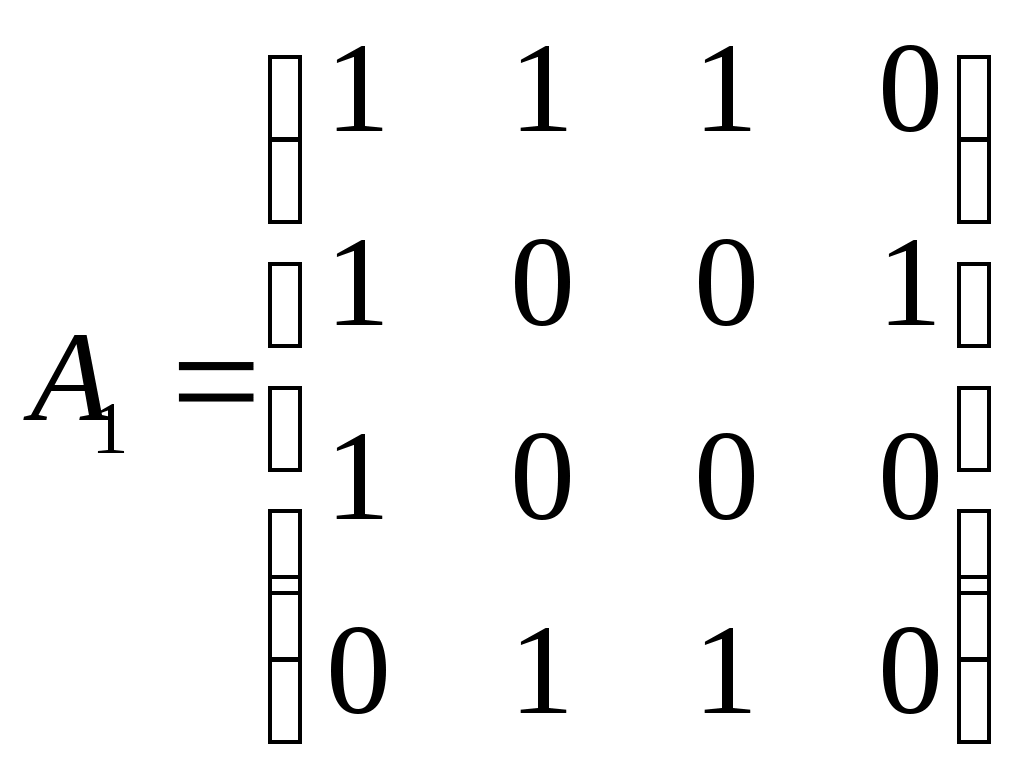  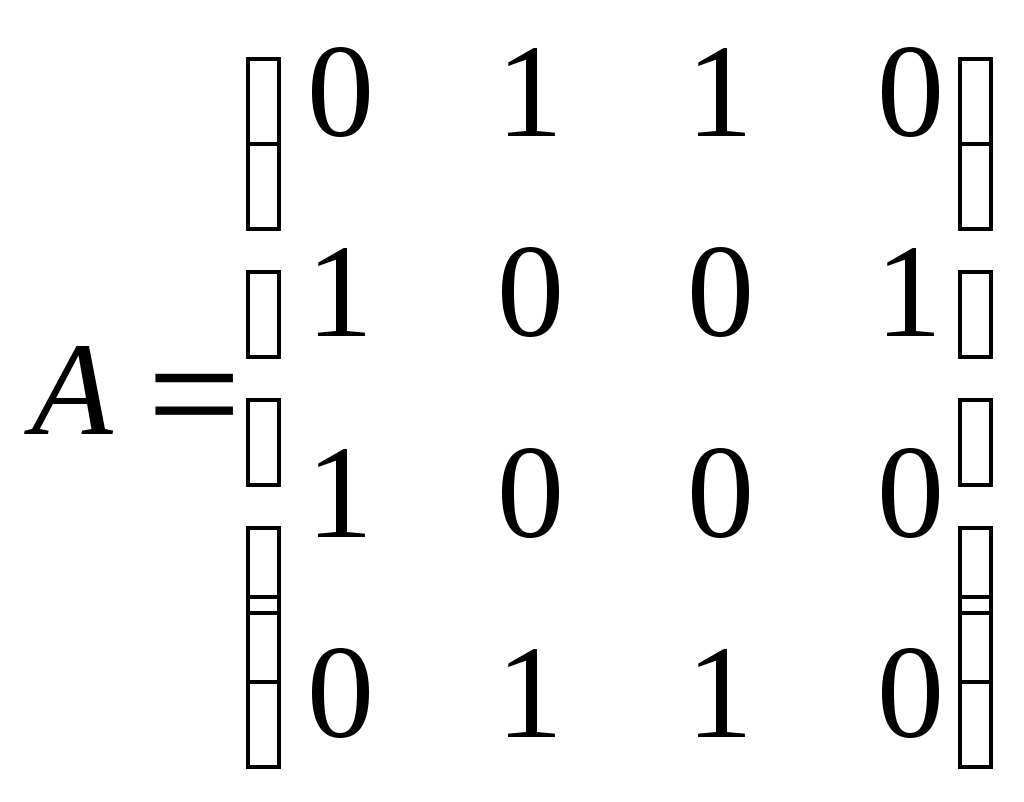 ? ?
|
декартово произведение.
пересечение;
объединение;
|
|
Графы G1 и G2 заданы матрицами смежности A1 и A2 соответственно. С помощью какой операции был получен граф G, заданный матрицей A
 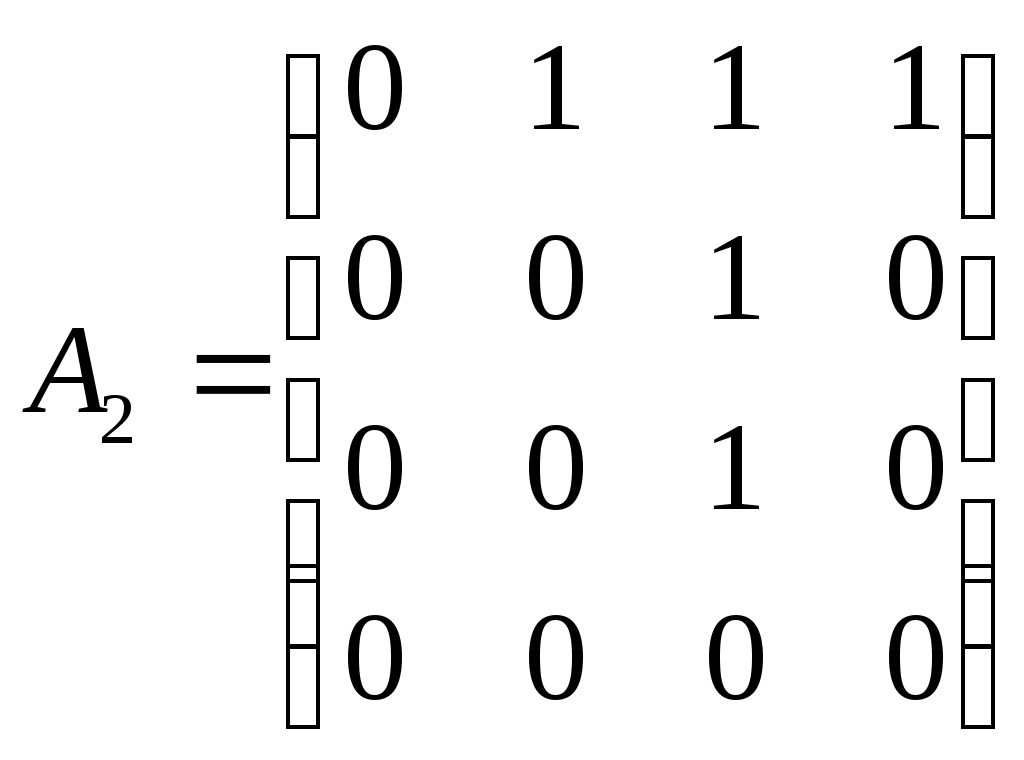 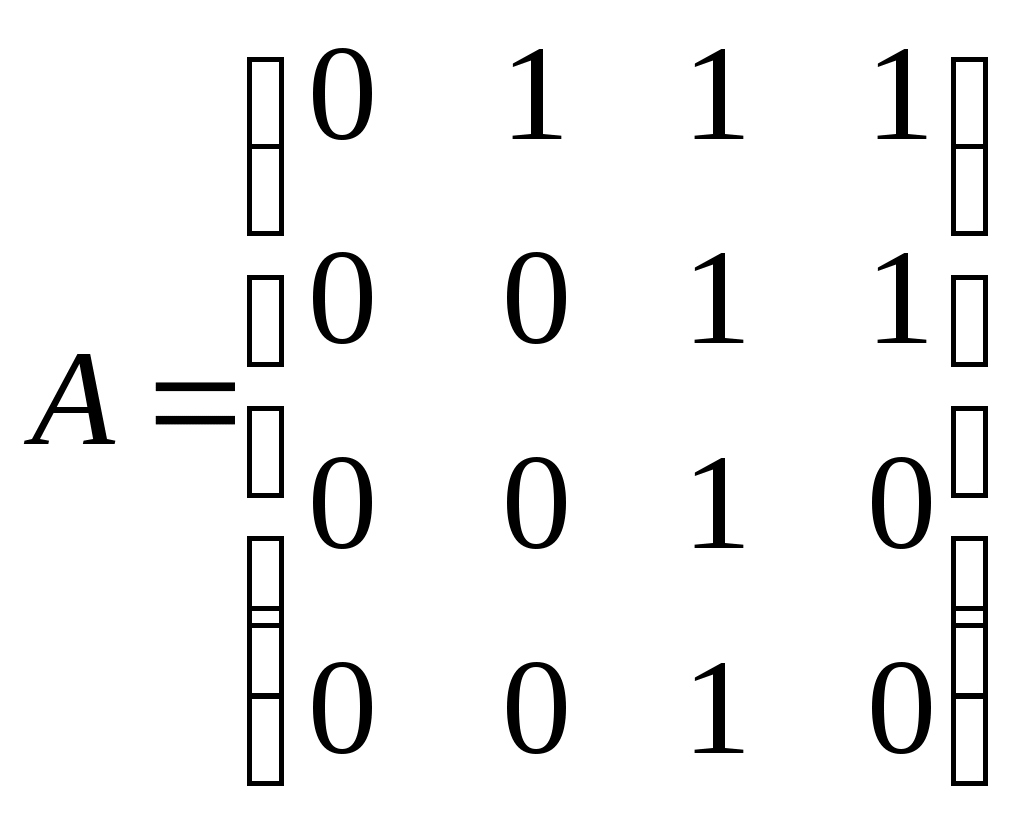 ? ?
|
объединение;
декартово произведение.
пересечение;
|
|
Даны два высказывания S1: "Если треугольники равны, то равны их стороны", S2: "Стороны треугольников равны тогда и только тогда, когда равны треугольники". Существует ли отношение следствия между S1 и S2?
|
ни одно из высказываний не следует из другого.
из S1 следует S2;
из S2 следует S1;
|
|
Для предиката  , заданного на множестве действительных чисел, укажите набор значений кванторов , заданного на множестве действительных чисел, укажите набор значений кванторов 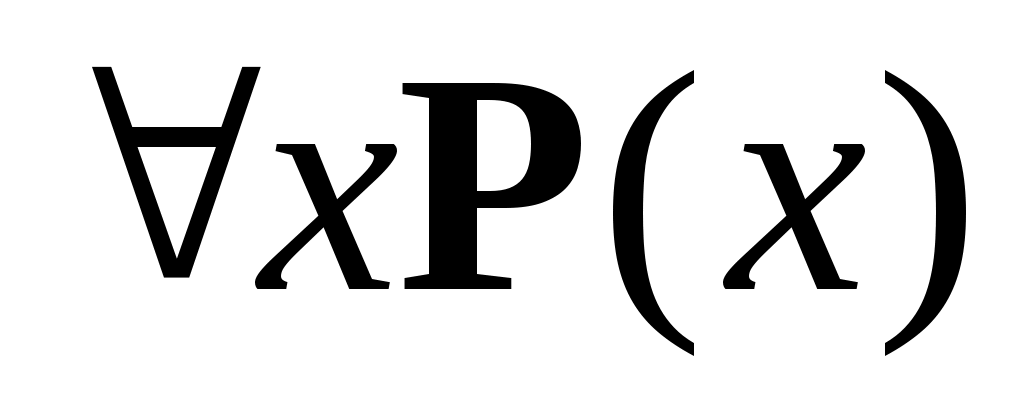 , , 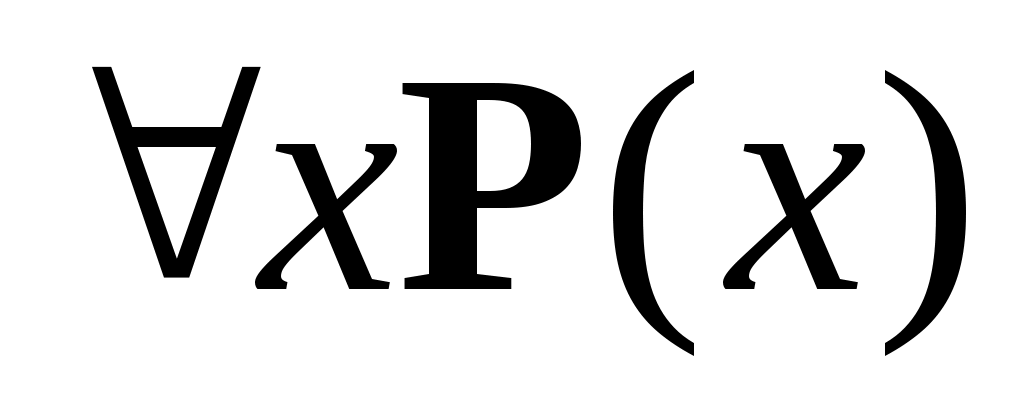 : :
|
0,1
0,0
1,1
1,0
|
|
Для предиката P(x,y)=(x+y)=0, заданного на множестве действительных чисел, укажите набор значений кванторов 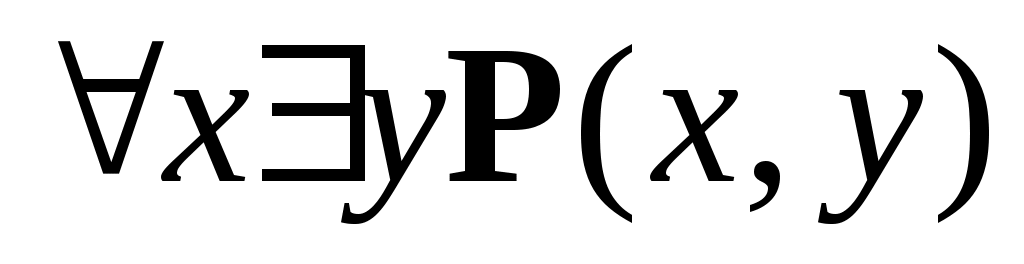 , , 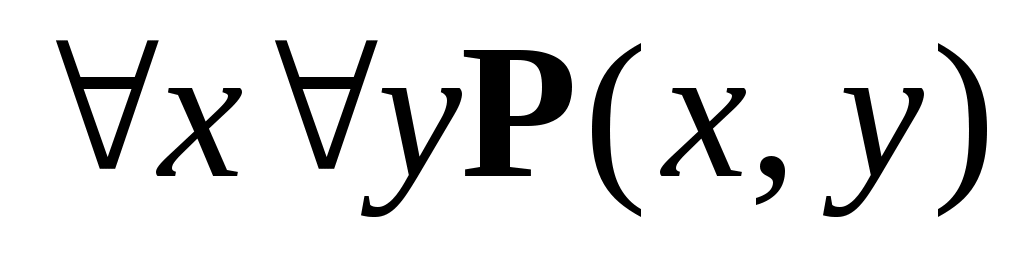 : :
|
1,0
0,0
1,1
0,1
|
|
Для сетевого графа, соответствующего некоторому проекту, критический путь представляет собой:
|
путь минимальной длины от входа к выходу;
путь произвольной длины от входа к выходу.
путь максимальной длины от входа к выходу;
|
|
Для сетевого графа, соответствующего некоторому проекту, скорейшее время завершение всего проекта совпадает с длиной:
|
максимального пути от входа к выходу;
произвольного пути от входа к выходу.
минимального пути от входа к выходу;
|
|
Если высказывания эквивалентны, существуют ли между ними отношения следствия?
|
существуют;
могут существовать, а могут и не существовать.
не существуют;
|
|
Если из высказывания S1 следует S2 и наоборот из S2 следует S1 , являются ли высказывания S1 и S2 эквивалентными?
|
не являются;
могут являться, а могут и нет.
являются;
|
|
Если к некоторому бесконечному множеству M прибавить счетное множество A, то в каком соотношении будут находиться мощности множеств 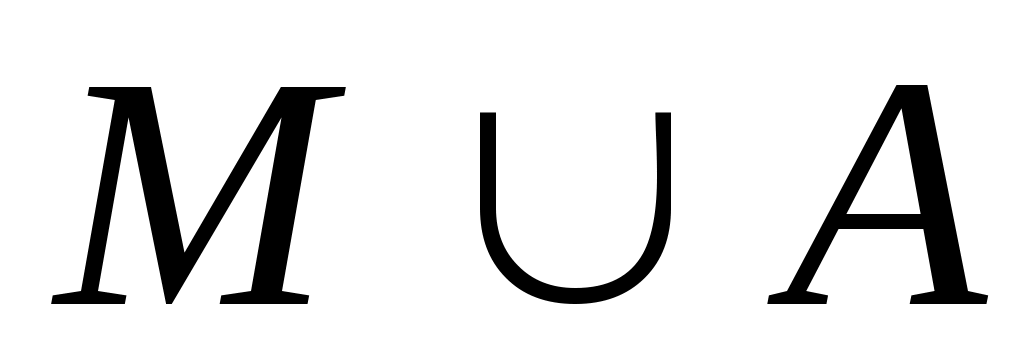 и M? и M?
|
мощность множества M меньше мощности множества 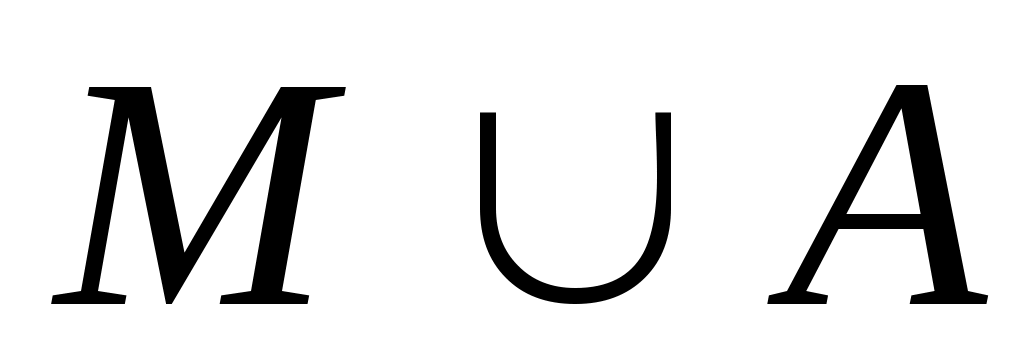 ; ;
мощность множества M равна мощности множества 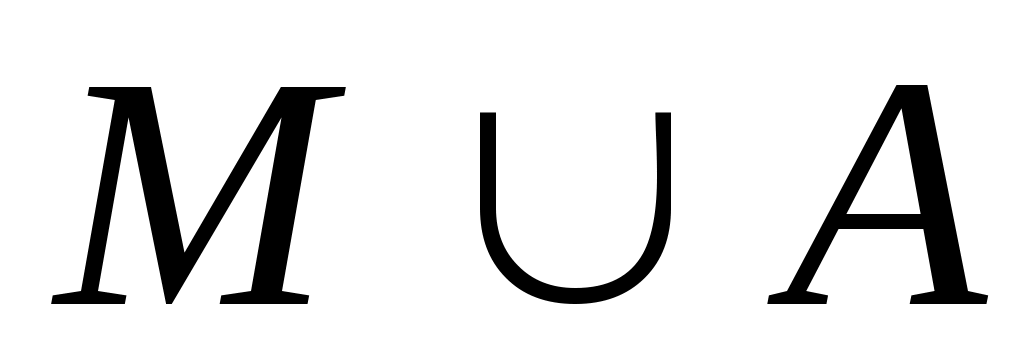 ; ;
мощность множества M больше мощности множества 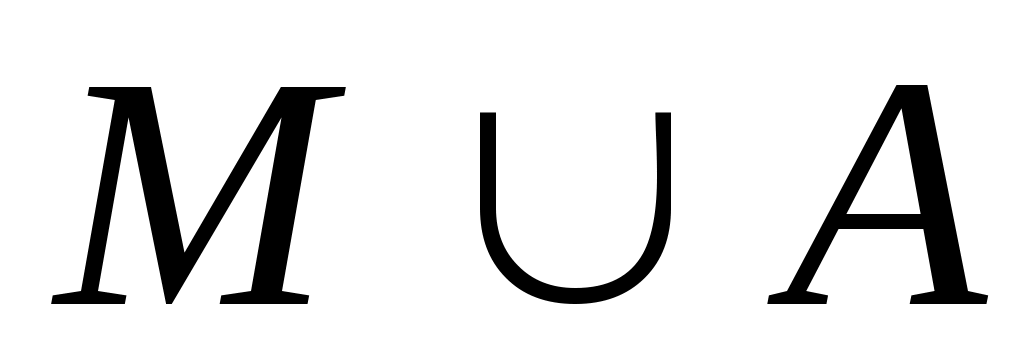 ; ;
|
|
Если матрица смежности симметрична, то граф является:
|
ориентированным с петлями.
неориентированным;
ориентированным с нечетным числом дуг;
|
|
Если на главной диагонали матрицы смежности стоит единица, то:
|
из данной вершины выходит дуга, заканчивающаяся в другой вершине;
в данной вершине находится петля.
в данную вершину входит дуга, начинающаяся в другой вершине;
|
|
Если отношение А на множестве М рефлексивно, симметрично и транзитивно, можно ли разбить множество М на непересекающиеся классы?
|
да;
можно, но не всегда.
нет;
|
|
Если при проверке правильности рассуждения получен результат 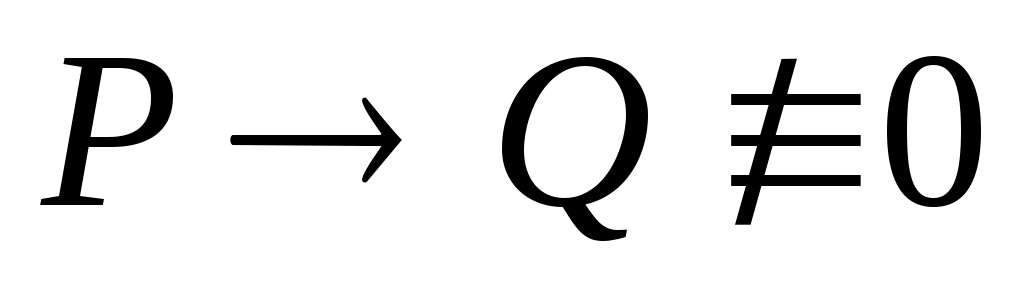 , где P – конъюнкция посылок, Q – заключение, то, в таком случае, данное рассуждение является: , где P – конъюнкция посылок, Q – заключение, то, в таком случае, данное рассуждение является:
|
может быть правильным, а может быть и неправильным.
неправильным;
правильным;
|
 Скачать 178 Kb.
Скачать 178 Kb.