Теория графов. Виды и способы задания графов

• Название: Виды и способы задания графов
• Анкор: Теория графов
• Дата: 09.06.2022
• Размер: 244 Kb.
• Имя файла: 3_Teoria_grafov.doc
• Тип: Документы; #582325

1. 
   Виды и способы задания графов.
   

Графом называется алгебраическая система G=<M,R>, где R – двухместный предикатный символ. Элементы носителя М называются вершинами графа G, а элементы бинарного отношения - дугами. Таким образом, дугами являются пары вершин . При этом дуга (a,b) называется исходящей из вершины a и заходящей в вершину b.

Мультиграфом G называется тройка <M,U,P>, в которой M – множество вершин, U – множество дуг, а - трехместный предикат, называемый инцидентором и представляемый следующим образом: тогда и только тогда, когда дуга u исходит из вершины a и заходит в вершину b.

Граф G=<M,R> называется ориентированным (орграфом), если найдется дуга такая, что .

Граф G называется неориентированным (неорграфом), если отношение R симметрично, т.е. из следует .

Если одновременно пары (a,b) и (b,a) принадлежат R, то информацию об этих дугах можно представить множество [a,b]={(a,b),(b,a)}, называемым ребром, соединяющим вершины a и b.

Понятия морфизмов алгебраических систем для графов представляются следующим образом. Пусть G=<M,R>, G’=<M’,R’> - графы. Тогда отображения φ=M→M’ является изоморфизмом графов, если .

Информация о структуре графа может быть задана матрицей бинарного отношения. Пусть G=<M,R> - граф, в котором множество вершин имеет n элементов M={a₁,…,a_n}. Матрицей смежности A_G=(A_ij) графа G называется матрица порядка n, определенная следующим образом: 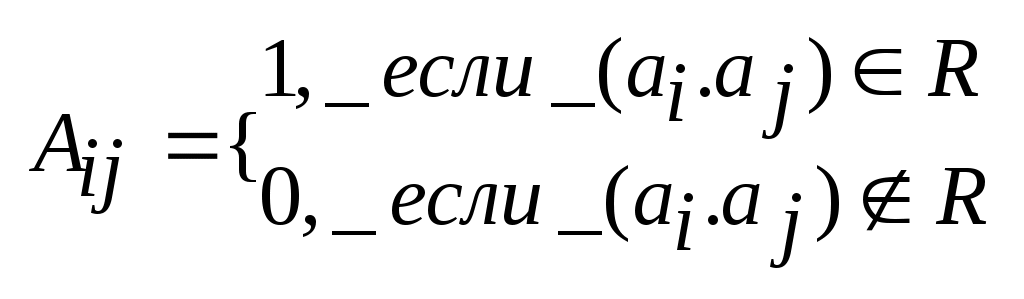. Если A_ij=1, то вершина a_jназывается последователем вершины a_i, а a_i – предшественником a_j. Вершины a_i и a_j называются смежными, если A_ij=1 или A_ji=1. Если G -мультиграф, то в матрице смежности элемент A_ij равен числу дуг, исходящих из вершины a_i и заходящих в вершину a_j.

Петлей в графе G называется дуга, соединяющая вершину саму с собой.

Теорема: Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов.

Матрицей инцидентности B_G=(B_ij) мультиграфа G называется матрица размера m на n (где m – количество дуг в графе), определяемая по правилу: .

Теорема: Мультиграфы G и G’ изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк и столбцов.
Пометкой или распределением меток графа G= называется пара функций f:M→S_M (распределение меток вершин), g:R→S_R (распределение меток дуг). Четверка называется взвешенным или помеченным графом.

Информацию о весах дуг во взвешенном графе можно представить в виде матрицы весов W=(w_ij), где w_ij – вес дуги (a_i,a_j), если эта дуга существует и ∞ в противном случае.

Если граф G=<M,R> является разреженным, т.е. |R|<<|M|, то можно задать граф в виде списка дуг: два набора , где (a_mi,a_ni) – i-ая дуга графа G.

При добавлении или удалении вершин графа, удобно представить его в в виде структуры смежности, получаемой составлением для каждой вершины a списка номеров ее последователей.

2. 
   Подграфы и части графа. Операции над графами. n-Мерные кубы.
   

Граф G’= называется подграфом графа G=, если и . Граф G’ называется частью графа g, если и .
Операции над графом G=<M,R>:

1. 
   Добавление вершины:
   
2. 
   Добавление дуги:
   
3. 
   Удаление вершины:
   
4. 
   Удаление дуги:
   
5. 
   Отождествление вершин:
   
6. 
   Дополнением графа без петель G= 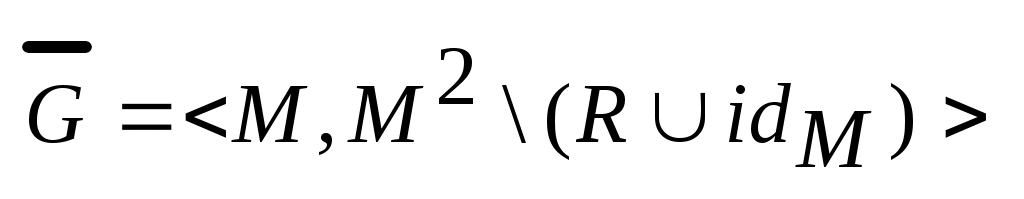называется граф .
   

Двухместные операции над графами G₁=1,R₁>, G₂=2,R₂>:

1. 
   Объединение: .
   
2. 
   Пересечение: , если .
   
3. 
   Кольцевая сумма: .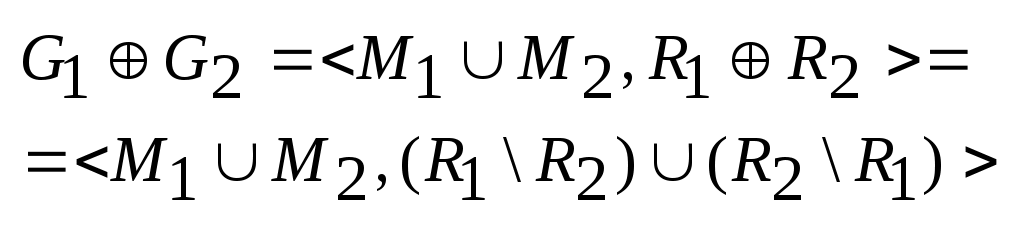
   
4. 
   Соединение: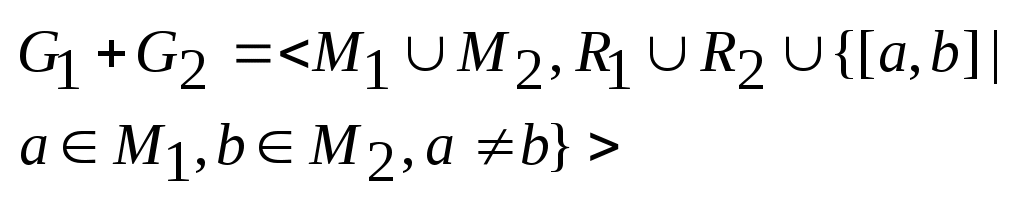
   
5. 
   Произведение: 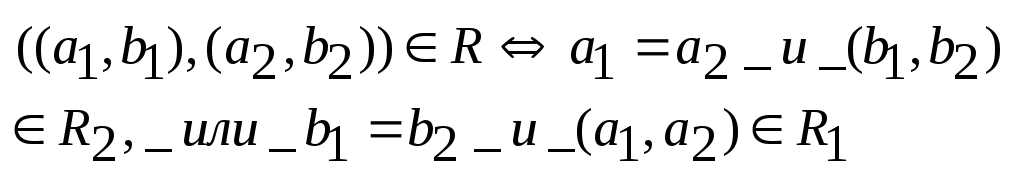, где
   
6. 
   Композиция: , где . Т.е. каждая вершина a графа G₁ заменяется на изоморфную копию G_a графа G₂, а затем, если , то между любыми вершинами b₁ из G_a1 и b₂ из G_a2 проводится дуга (b₁,b₂).
   

Неорграф без петель называется полным, если его любые две различные вершины смежны. Полный граф, имеющий n вершин обозначается K_n.

Определим по индукции важный класс графов, называемых n-мерными кубами. Рассмотрим граф K₂, вершины которого обозначим 0 и 1. n-куб Q_n определяется по следующим правилам: Q₁=K₂, , n>1. Вершинами n-куба являются всевозможные n-ки, состоящие из наборов нулей и единиц (всего таких наборов 2ⁿ), а ребра задаются по следующему правилу: вершины смежны тогда и только тогда, когда соответствующие кортежи различаются ровно одной координатой.

3. 
   Маршруты, циклы, цепи. Достижимость и связность (матрицы достижимости, контрдостижимости, связности).
   

Пусть G= - граф. Последовательность a₁,u₁,a₂,u₂,…,u_n,a_n+1, где , называется маршрутом, соединяющим вершины a₁ и a_n+1, если u_i=(a_i,a_i+1). Число n дуг в маршруте называется его длиной.

Пусть G – неорграф. Маршрут (a₁,a_n+1) называется цепью, если все ребра [a₁,a₂],…,[a_n,a_n+1] различны, и простой цепью, если все его вершины, кроме, возможно, первой и последней, различны. Маршрут называется циклическим, если a₁=a_n+1. Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом.

Пусть G – орграф. Маршрут называется путем, если все его дуги различны. Путь называется контуром, если a₁=a_n+1. Граф, не имеющий контура, называется бесконтурным. Вершина b называется достижимой из вершины a, если существует (a,b) – путь.

Неорграф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Граф G называется связным, если соответствующий ему неорграф F(G) тоже является связным. Граф G называется сильно связным, если для каждой пары различных вершин a и b существуют (a,b)-маршрут и (b,a)-маршрут. Аналогично определяются понятия связности и сильной связности для мультиграфов.

Всякий максимальный по включению (сильно) связный подграф данного графа называется его (сильной) связной компонентой или (сильной) компонентой связности.

Теорема: Любой граф представляется в виде объединения непересекающихся связных (сильных) компонент. Разложение графа на связные (сильные) компоненты определяется однозначно.

Теорема: Если A_G – матрица смежности графа G, то (i,j)-й элемент матрицы есть число (a_i,a_j)-маршрутов длины k.

Следствие: 1) В графе G мощности n тогда и только тогда существует (a_i,a_j)-маршрут (a_i≠a_j), когда (i,j)-й элемент матрицы не равен нулю.

2) В графе G мощности n тогда и только тогда существует цикл, содержащей вершину a_i, когда (i,i)-й элемент матрицы не равен нулю.
Образуем из матрицы (b_ij)=E+A_G+A_G²+…+A_G^n-1 матрицу C=(c_ij) порядка n по следующему правилу: 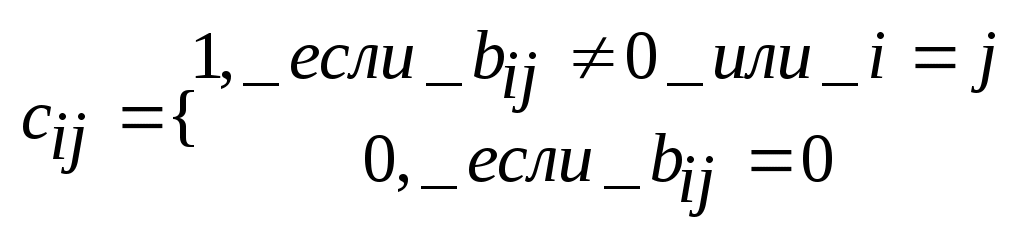. Матрица С называется матрицей связности, если G – неорграф, и матрицей достижимости, если G-орграф.

Определим матрицу контрдостижимости Q=(q_ij): . Причем Q=C^T.

Рассмотрим матрицу сильных компонент S=C*Q, где операция * означает поэлементное произведение матриц С и Q: s_ij=c_ij•q_ij. Таким образом, матрица S является матрицей отношения эквивалентности E: выполнимо a_iEa_j тогда и только тогда, когда a_i и a_j находятся в одной сильной компоненте.

4. 
   Расстояние в графах. Центральные и периферийные вершины.
   

Пусть G= - связный неорграф, a,b – две его несовпадающие вершины. Длина кратчайшего (a,b)-маршрута называется расстоянием между вершинами a и b и обозначается ρ(a,b). Положим ρ(a,a)=0.

Аксиомы метрики:

1. 
   ρ(a,b)≥0;
   
2. 
   ρ(a,b)=0  a=b
   
3. 
   ρ(a,b)= ρ(b,a)(симметричность)
   
4. 
   ρ(a,b)≤ ρ(a,с)+ ρ(с,b) (неравенство треугольника)
   

Если M={a₁,…,a_n}, то матрица P=(p_ij), в которой p_ij=ρ(a_i,a_j), называется матрицей расстояний. Заметим, что P^T=P.

Эксцентриситетом вершины a называется величина .

Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается через d(G): . Вершина a называется периферийной, если e(a)=d(G). Минимальный из эксцентриситетов графа G называется его радиусом r(G): . Вершина a называется центральной, если e(a)=r(G). Множество всех центральных вершин графа называется его центром.

5. 
   Взвешенное расстояние. Алгоритм Форда-Беллмана.
   

Пусть G=<M,R> - взвешенный граф, в котором вес каждой дуги (a,b) есть некоторое вещественное число μ(a,b). Весом маршрута a₁,…,a_n+1называется число . Взвешенным расстоянием (ω-расстоянием) ρ_ω(a,b) между вершинами a и b называется минимальный из весов (a,b)-маршрутов). Маршрут с минимальным весом называется кратчайшим. Взвешенным эксцентриситетом вершины a называется величина . Взвешенной центральной вершиной называется вершина a, для которой . Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом.

Пусть G=<M,R> - взвешенный граф, имеющий n вершин и матрицу весов W=(ω_ij). Предположим, что в G отсутствуют контуры с отрицательным весом, поскольку двигаясь по такому контуру достаточное число раз можно получить маршрут бесконечно малого веса.

Алгоритм Форда-Беллмана (для нахождения взвешенного расстояния от вершины a_i (источника) до всех вершин графа G):

Зададим строку , полагая . Определим строку , полагая . Нетрудно заметить, что - минимальный из весов (a_i,a_j)-маршрутов, состоящих не более чем из двух дуг.

Продолжая процесс, на шаге s определим строку , полагая . Искомая строка ω-расстояний получается при s=n-1: . Алгоритм можно завершить на шаге k, если D^(k)=D^(k+1).

6. 
   Степени вершин. Эйлеровы графы, циклы, цепи. Алгоритм построения эйлерова цикла.
   

Степенью или валентностью вершины a неорграфа G называется число ребер, инцидентных вершине a (петли считаются дважды). Вершина степени 0 называется изолированной, степени 1 – концевой или висячей.

Лемма о рукопожатиях: Сумма степеней всех вершин графа является четным числом и равна удвоенному числу ребер.
Критерий «эйлировости» графа: Связный неориентированный мультиграф тогда и только тогда является эйлеровым, когда степень каждой из его вершин – четное число.

Алгоритм построения эйлерова цикла:

1. 
   Выбрать произвольно некоторую вершину a.
   
2. 
   Выбрать произвольно некоторое ребро u, инцидентное a, и присвоить ему номер 1 (назовем это ребро пройденным).
   
3. 
   Каждое пройденное ребро вычеркнуть и присвоить ему номер, на единицу больший предыдущего вычеркнутого ребра.
   
4. 
   Находясь в вершине x, не выбирать ребро, соединяющее x с a, если есть возможность иного выбора.
   
5. 
   Находясь в вершине x, не выбирать ребро, которое является перешейком (т.е. ребром, при вычеркивании которого граф распадается на две компоненты связности).
   
6. 
   После того как в графе будут занумерованы все ребра, образуется эйлеров цикл.
   

Теорема: Если связный граф содержит k вершин нечетной степени, то минимальное число покрывающих его реберно непересекающихся цепей равно k/2.

Доказательство: Набор реберно непересекающихся цепей покрывает граф G, если каждое его ребро входит в одну из этих цепей.

Пусть связный граф G содержит k вершин нечетной степени. По лемме о рукопожатиях число k четно. Рассмотрим граф G’, полученной добавлением к G новой вершины a и ребер, соединяющих a со всеми вершинами нечетной степени графа G. Граф G’ будет содержать эйлеров цикл. Если удалить из этого цикла все ребра, инцидентные вершине a, то получится не более k/2 цепей, покрывающих G. С другой стороны, граф, являющийся объединением r реберно непересекающихся цепей имеет не более 2r верши нечетной степени. Поэтому граф G нельзя покрыть цепями, число которых меньше k/2.

7. 
   Гамильтоновы графы. Постановка задачи коммивояжера.
   

Граф называется гамильтоновым, если в нем имеется простой цикл (гамильтонов цикл), содержащий каждую вершину этого графа. Простая цепь, содержащая все вершины графа, также называется гамильтоновой.
Пусть G – связный неорграф без петель, имеющий n≥3 вершин.

Достаточные условия существования гамильтоновых циклов:

1. 
   Если для любых двух различных несмежных вершин a и b графа G выполняется условие dega+degb≥n, то существует гамильтонов цикл.
   
2. 
   Если для любой вершины a графа G выполнено условие dega≥n/2, то существует гамильтонов цикл.
   

Задача коммивояжера:

Район, который должен посетить бродячий торговец, содержит некоторое количество городов, расстояния между которыми известны. Требуется найти кратчайший маршрут, проходящий через все пункты по одному разу и возвращающийся в исходный город.

8. 
   Деревья, леса. Остовы графов. Цикломатическое число, коранг. Алгоритм построения остова минимального веса. Обходы графов по глубине и ширине.
   

Деревом называется связный неорграф, не содержащий циклов. Любой неорграф без циклов называется ациклическим графом или лесом.
Теорема: Для неорграфа G без петель содержащего n вершин следующие условия эквивалентны:

1. 
   G – дерево
   
2. 
   G – связный граф, содержащий n-1 ребро
   
3. 
   G – ациклический граф, содержащий n-1 ребро
   
4. 
   любые две несовпадающие вершины графа G соединяет единственная простая цепь
   
5. 
   G – ациклический граф, такой, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл
   

Пусть G= - неорграф. Часть G’= графа G называется остовом или каркасом графа G, если M=M’ и G’ – лес, который на любой связной компоненте графа G образует дерево.

Теорема: Число ребер произвольного неорграфа G, которое необходимо удалить для получения остова не зависит от последовательности их удаления и равно m-n+c, где m – число ребер, n – число вершин, c – число компонент связности.

Доказательство: Действительно, если i-я компонента связности C_i, графа G содержит n_i врешин, то по предыдущей теореме соответствующее дерево K_i остова содержит n_i-1 ребро. Следовательно для получения K_i из компоненты C_i нужно удалить m_i-(n_i-1) ребер. Суммируя удаляемые ребра по всем компонентам связности, получаем, что необходимо удалить m-n+c ребер.
Число υ(G)=m-n+c называется цикломатическим числом или цикломатическим рангом графа G. Число υ^*(G)=n-c называется коциклическим рангом или корангом.

Неоргарф G является лесом тогда и только тогда, когда υ(G)=0.

Неорграф G имеет единственный цикл тогда и только тогда, когда υ(G)=1.
Алгоритм построения остова минимального веса:

1. 
   Строим граф T₁=1>, где u₁ – ребро минимального веса.
   
2. 
   Если граф T_i уже построен и ii₊₁=T_i+u_i+1, где u_i+1 – ребро минимального веса среди ребер, не входящих в T_i и не составляющих циклов с T_i.
   

Обход графа по глубине и ширине:

Пусть G=<M,R> связный неорграф, T – некоторый остов графа, a – некоторая фиксированная вершина, корень дерева T. Разместим вершины из M по этажам таким образом, чтобы корень a находился в верхнем этаже, смежные с ним вершины занимали этаж на единицу ниже, смежные с отмеченными вершинами еще на единицу ниже и тд. Получаем e(a)+1 этаж, где e(a) – эксцентриситет вершины a.

При обходе графа по глубине после очередной рассмотренной вершины выбирается смежная с ней вершины следующего этажа. Если очередная рассмотренная вершина висячая и ее достижение не дает решения задачи, то возвращаемся до ближайшей вершины степени ≥3 и просматриваем вершины другого, еще не пройденного маршрута.

При обходе графа по ширине просмотр вершин дерева ведется по этажам, переход к вершинам следующего этажа происходит только после просмотра всех вершин данного этажа.

9. 
   Упорядоченные и бинарные деревья. Соответствия между ними.
   

Определим по индукции понятие упорядоченного дерева:

1. 
   пустое множество и список (a), где a – некоторый элемент, является упорядоченным деревом;
   
2. 
   если T₁, T₂,…, T_n– непустые упорядоченные деревья, a – некоторый новый элемент, то список T=(a, T₁,…,T_n) образует упорядоченное дерево. При этом элемент a называется корнем упорядоченного дерева T;
   
3. 
   любое упорядоченное дерево строится в соответствии с пп. 1 и 2.
   

Если T₁,…,T_n – упорядоченные деревья, то список (T₁,…,T_n) называется упорядоченным лесом.

Для заданного упорядоченного дерева T определим множество S(T) его упорядоченных поддеревьев:

- если , то

- если T=(a), то S(T)={(a)}

- если T=(a,T₁,…,T_n), то

Непустое упорядоченное дерево Т может интерпретироваться в виде системы пронумерованных непустых множеств, каждое из которых взаимно однозначно соответствует упорядоченному поддереву из S(T) так, что:

1. 
   если T’ – поддерево упорядоченного дерева T’’; , то для соответствующих множеств X’ и X’’ выполняется включение
   
2. 
   если T’ не является поддеревом упорядоченного дерева T’’; , соответствующие множества не пересекаются.
   

Упорядоченное дерево может также интерпретироваться в виде уступчатого списка, который обычно используется в оглавлениях. Любая иерархическая классификационная схема интерпретируется некоторым упорядоченным деревом. Частным случаем упорядоченного дерева является бинарное дерево. Определение понятия бинарного дерева повторяет определение для упорядоченного дерева с ограничением в п.2. Любой упорядоченный лес взаимно однозначно соответствует некоторому бинарному дереву.

Опишем алгоритм преобразования упорядоченного леса T=(T₁,…,T_n) в бинарное дерево B(T):

1. 
   Если n=0,
   
2. 
   Если n>0, то корнем бинарного дерева B(T) является корень упорядоченного дерева T₁, левое поддерево дерева B(T) – бинарное дерево B(T₁₁,…,T_1m), где T₁=((a₁),T₁₁,…,T_1m), правое поддерево дерева B(T) – бинарное дерево B(T₂,…,T_n).
   

10. 
    Фундаментальные циклы, разрезы. Матрицы фундаментальных циклов, разрезов.
    

Пусть G=<M,R> - неорграф, имеющий n вершин, m ребер и c компонент связности, Т – остов графа G, имеет υ^*(G)=n-c ветвей и υ(G)=m-n+c хорд. Если к лесу Tдобавить произвольную хорду υ_i, то в полученном графе найдется ровно один цикл C_i, который называется фундаментальным циклом графа Gотносительно хорды υ_iи остова T. Множество {C₁,..,C_m-n+c} называется фундаментальным множеством циклов. Мощность этого множества равна цикломатическому числу υ(G)=m-n+c.

Фундаментальное множество циклов можно задать с помощью матрицы фундаментальных циклов С=(a_ij), где 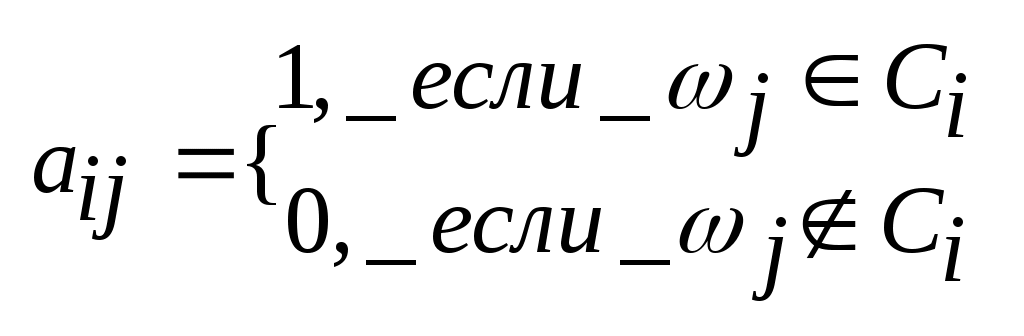. Т.к. каждый фундаментальный цикл содержит ровно одну хорду, то матрица С=(С₁|C₂), где С₁ – единичная матрица порядка υ(G).

Пусть G= - неорграф, m={M₁,M₂} – разбиение множества М. Разрезом графа G по разбиению m называется множество всех ребер, соединяющих вершины из M₁ c вершинными из M₂. В связном графе любой разрез непуст.

Непустой разрез К неорграфа G называется простым разрезом или коциклом, если любое непустое собственное подмножество не является разрезом ни по какому разбиению. Т.е. из К нельзя удалить ни одно ребро так, чтобы полученное множество было непустым разрезом.

Теорема: В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым из разрезов графа.

Теорема: В связном неорграфе любой цикл имеет любым разрезом четное число общих ребер.
Рассмотрим неорграф G с остовом Т. Пусть u₁,…,u_n-c – ветви остова Т. Удаляя из Т произвольную ветвь u_i получаем лес с (с+1) компонентой связности, т.е. каждое ребро u_i является разрезом остова Т по некоторому разбиению {М₁,М₂}. В графе G могут найтись еще ребра v_i1,…,v_ij (хорды Т), также являющиеся разрезами по {M₁,M₂}. Множество K_i={u_i,v_i1,…,v_ij} образует простой разрез, который называется фундаментальным разрезом графа G относительно ветви u_i остова Т. Множество {K₁,…,K_n-c} называется фундаментальным множество коциклов. Мощность этого множества равна корангу υ^*(G)=n-c. Фундаментальное множество коциклов можно задать матрицей K=(b_ij), где 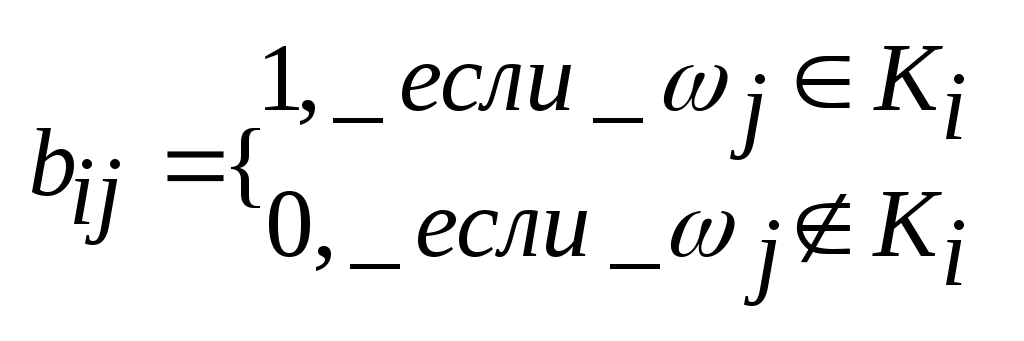. Поскольку каждый фундаментальный разрез содержит одну ветвь, то матрица К=(K₁|K₂), где К₂ – единичная матрица порядка υ^*(G).

11. 
    Раскраска графов. Планарные графы.
    

Пусть G=<M,R> - неорграф без петель. Раскраской (вершин) графа G называют такое задание цветов вершинам G, что если [a,b] – ребро, то вершины a и b имеют различные цвета. Хроматическим числом χ(G) графа G называется минимальное число цветов, требующееся для раскраски графа G.

Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин реберного мультиграфа L(G). Для произвольного неориентированного мультиграфа G=<M,U,P> реберным мультиграфом называется тройка L(G)=<U,M,P’>, где , и тогда и только тогда, когда в мультиграфе G вершина u является концом ребер u и v.

Неорграф G называется бихроматическим, если χ(G)=2. Неорграф G=<M,R> называется двудольным, если множество всех ребер графа G образует разрез графа G, т.е. для некоторого разбиения множества вершин {M₁,M₂} концы любого ребра принадлежат разным частям разбиения.

Теорема: Пусть G – неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны:

1. 
   G – бихроматический граф;
   
2. 
   G – двудольный граф;
   
3. 
   G не содержит циклов нечетной длины.
   

Следствие: Если G – лес, то χ(G)≤2.
Теорема: Для любого неорграфа без петель выполняется неравенство χ(G)≤deg(G)+1.
Алгоритм последовательной раскраски:

1. 
   Произвольная вершина a₁ графа G принимает цвет 1.
   
2. 
   Если вершиныa₁,…,a_i раскрашены l цветами 1,2,…,l, l≤2, то новой произвольно взятой вершине a_i+1 припишем миимальный цвет, не использованный при раскраске вершин из множества {a_j|ρ(a_j,a_i+1)=1,j<i}.
   

Неорграф G называется планарным, если его можно изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме, может быть, общего конца этих ребер. Такое изображение графа называется плоским.

Рассмотрим операцию подразбиения ребра в графе G=<M,R>. После подразбиения ребра [a,b] из R получается граф G’=<M’,R’>, где , , т.е. ребро [a,b] заменяется на (a,b)-цепь длины два. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью последовательности подразбиений ребер.
Критерий планарности (теорема Понтрягина-Куратовского): Граф G планарен тогда и только тогда, когда G не содержит подграфа, гомеоморфного K₅ или K_3,3 (или подграфов, стягиваемых к K₅ или K_3,3, т.е. получаемых последовательным отождествлением связанных друг с другом вершин).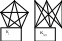
Теорема: Любой конечный граф может быть расположен в трехмерном пространстве без пересечения ребер.

Если G– планарный граф, то χ(G)≤4.

Толщина графа – минимальное количество плоскостей, в которых можно осуществить раскладку графа без пересечений.

Минимальное число ребер, которые нужно удалить из графа для его плоского отображения называют числом планарности графа.