Его. Выполнение алгоритмов для исполнителя
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
Ещё пример задания:Р-09. Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w) Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v) Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется. Дана программа для исполнителя Редактор: НАЧАЛО ПОКА нашлось (222) ИЛИ нашлось (888) ЕСЛИ нашлось (222) ТО заменить (222, 8) ИНАЧЕ заменить (888, 2) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку. Решение: из программы видим, что Редактор что-то делает только тогда, когда в строке есть цепочка 222 или цепочка 888; то есть, если ни одной из этих цепочек нет, программа останавливается если в строке есть 222, то, в первую очередь, именно эта цепочка меняется (на 8) если в строке нет цепочки 222, но есть 888, то цепочка 888 меняется на 2 попробуем формально выполнить первые шаги алгоритма для цепочки цифр 8 сначала первые 888 меняются на 2, получается 2 [65 цифр 8] дальше так же меняем следующие две тройки из цифр 8: 222 [59 цифр 8] теперь (внимание!) у нас появилась цепочка 222, поэтому в соответствии с алгоритмом она сразу будет заменена на 8, получаем [60 цифр 8] таким образом, за первые 4 шага работы цикла мы заменили 9 восьмерок на 1 или, что то же самое, удалили 8 восьмерок очевидно, что следующие 4 шага удалят ещё 8 восьмерок и т.д. сколько раз мы сможем это сделать? видимо, 8 раз, после этого останется 68 - 8·8 = 4 восьмерки итак, в цепочке 8888 на последнем шаге заменяем 888 на 2 и получаем 28 Ответ: 28.
Ещё пример задания:Р-08. Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1). Цикл ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа): НАЧАЛО сместиться на (–1, –2) ПОВТОРИ n РАЗ сместиться на (a, b) сместиться на (-1, -2) КОНЕЦ ПОВТОРИ сместиться на (–24, -12) КОНЕЦ Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку. Решение: запишем общее изменение координат Чертёжника в результате выполнения этого алгоритма: поскольку Чертёжник должен вернуться в исходную точку, эти величины должны быть равны нулю; следовательно, нужно найти набольшее натуральное n, при котором система уравнений 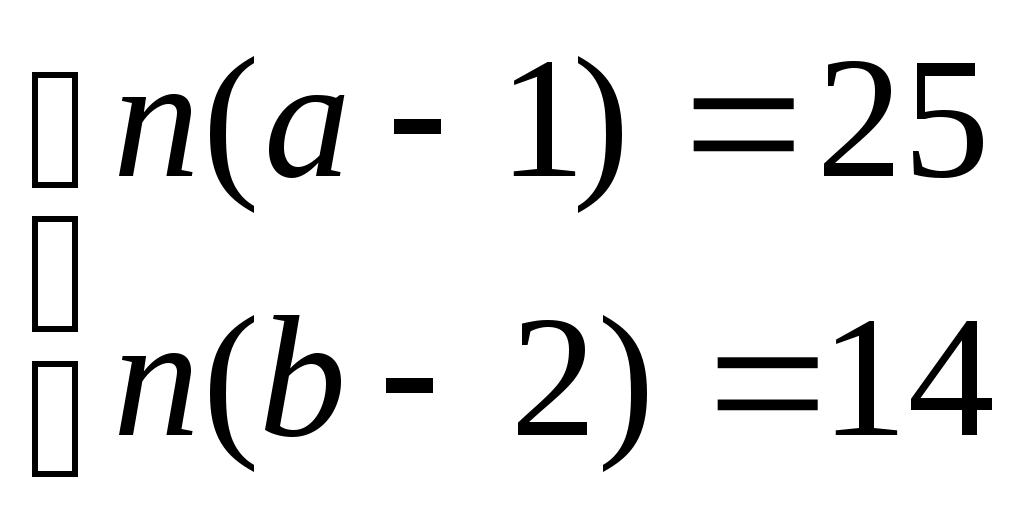 разрешима в целых числах относительно a и b несложно заметить, что для этого число n должно быть одновременно делителем чисел 14 и 25 наибольший общий делитель чисел 14 и 25 равен 1 ответ – 1. |
