Главная страница
Навигация по странице:

  • Мета роботи Експериментально визначити радіус кривизни плоскоопуклої лінзи, використовуючи інтерференційну картину у вигляді кілець НьютонаПрилади і матеріали

  • Теоретичні відомості та опис установки

  • Кінцевий результат R = (0.145 + 0.005) м з відносною похибкою δR = 3.44 % Висновок

    		•

    кільця ньютона. Визначення радіуса кривизни лінзи допомогою кілець Ньютона


    Скачать 138 Kb.
    НазваниеВизначення радіуса кривизни лінзи допомогою кілець Ньютона
    Анкоркільця ньютона
    Дата11.04.2021
    Размер138 Kb.
    Формат файлаdoc
    Имя файла71.doc
    ТипДокументы
    #193648

    http://antibotan.com/ - Всеукраїнський студентський архів

    МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

    НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»


    З В І Т

    до лабораторної роботи №27

    з курсу: «Фізика, частина 3»

    на тему: «Визначення радіуса кривизни лінзи допомогою кілець Ньютона»


    Мета роботи

    Експериментально визначити радіус кривизни плоскоопуклої лінзи, використовуючи інтерференційну картину у вигляді кілець Ньютона

    Прилади і матеріали

    Мікроскоп, плоскоопукла лінза великого радіуса кривизни, плоскопаралельна пластинка, освітлювач з блоком живлення, світлофільтри

    Теоретичні відомості та опис установки

    Оптична схема для спостереження кілець Ньютона у відбитому світлі в даній лабораторній роботі наведена на рис. 1.

    На предметному столику мікроскопа знаходиться плоскопаралельна прозора скляна пластинка, а поверх неї – плоскоопукла лінза L. Монохроматичний пучок світла від освітлювача S направляють на скляну світлоподільну пластинку С, яка розміщенапід кутом 45° до напрямку поширення світла. Після відбивання в точці А опуклої поверхні лінзи і дотичної до неї поверхні пластини в точці В світло поширюється у зворотному напрямку паралельним пучком та потрапляє в об’єктив мікроскопа L1. Відбиті хвилі є когерентними. Всі точки, що знаходяться на однаковій відстані 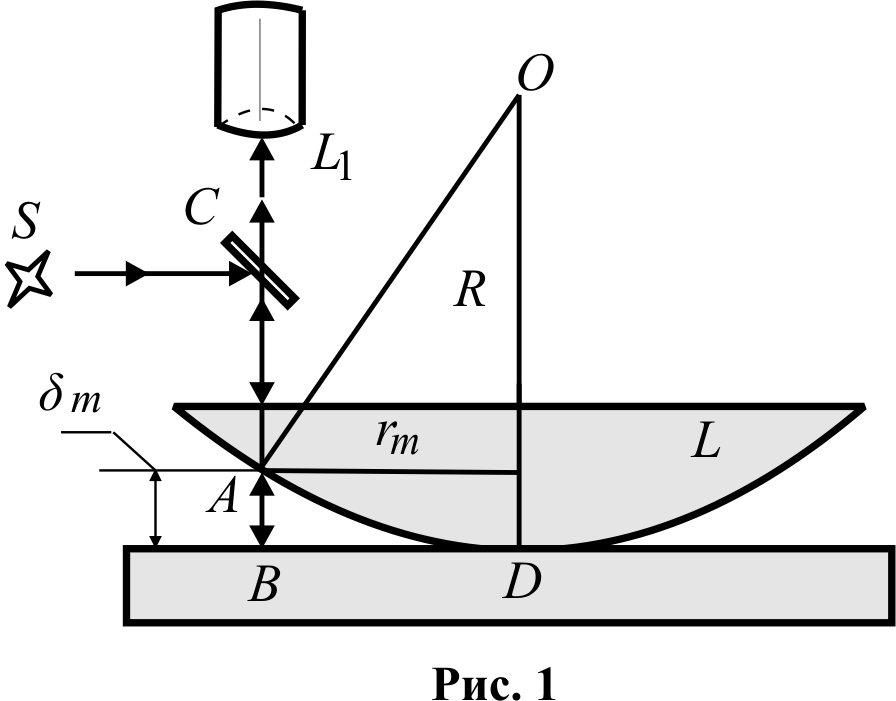від оптичного центра лінзи перебувають в однакових умовах для спостереження інтерференційної картини. Тому в окулярі мікроскопа будуть спостерігатися світлі і темні концентричні кільця – кільця Ньютона.



    Якщо визначити експериментально радіуси темних – го і – го кілець Ньютона, то із співвідношень (2.19) (див.§2.1.5)

    і

    можна отримати формулу для знаходження радіуса R кривизни сферичної поверхні плоскоопуклої лінзи:

    або ,

    .

    Результати

    Таблиця 1

    Номер кільця
    Відлік зліва

    k, мм
    Відлік справа

    l, мм
    Діаметр кільця

    d= l-k, мм
    Радіус кільця

    r=d/2, мм

    8
    0,60
    7,67
    7,07
    3,53

    7
    0,72
    7,53
    6,81
    3,40

    6
    0,94
    7,34
    6,40
    3,20

    5
    1,10
    7,15
    6,05
    3, 02

    4
    1,31
    6,96
    5,65
    2,82

    3
    1,53
    6,67
    5,14
    2,57

    2
    1,82
    6,41
    4,59
    2,29

    1
    2,13
    6,05
    3,92
    1,96
    Таблиця 2

    №

    m
    rm , мм
    n
    rn , мм
    rm - rn, мм
    rm + rn, мм
    R, м
    ΔR, м
    δR,%

    1
    8
    3,53
    5
    3,02
    0.51
    6.55
    0.137
    0.008
    3.44

    2
    7
    3,40
    4
    2,82
    0.58
    6.22
    0.148
    0.003

    3
    6
    3,20
    3
    2,57
    0.63
    5.77
    0.150
    0.005

    сер.
    __
    ____
    __
    ____
    ____
    ____
    0.145
    0.005











    δ %

    Кінцевий результат

    R = (0.145+0.005) м з відносною похибкою δR = 3.44%

    Висновок

    Під час цієї лабораторної роботи я експериментально визначив радіус кривизни плоскоопуклої лінзи, використовуючи інтерференційну картину у вигляді кілець Ньютона за допомогою мікроскопа, плоскоопуклої лінза великого радіуса кривизни, плоскопаралельної пластинки і освітлювача з блоком живлення.

    написать администратору сайта