Влияние качества напряжения сети на работу асинхронного двигателя
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Влияние качества напряжения сети на работу асинхронного двигателя Введение Самыми распространенными электрическими машинами, применяемыми в электроприводе, являются асинхронные электрические машины. Широкому распространению асинхронного двигателя (АД) способствует создание систем Самый распространенным в настоящее время способом регулирования скорости вращения асинхронного электропривода является частотное управление. Чаще всего его динамика исследуется с помощью упрощенных моделей с отклонениями в малом. Более точную структурную схему для дальнейшего компьютерного моделирования можем получить благодаря использованию векторной модели асинхронного двигателя. Теоретическое обоснование и исходные данные для математического моделирования АД. В стандартной библиотеке Simulink уже присутствует готовая блок-функция асинхронного двигателя. Данный блок включает в себя математическую модель асинхронного двигателя на основе упрощенной схемы замещения с постоянными параметрами. При самостоятельном построении математической дели можно учесть зависимость параметров схемы замещения в зависимости частоты протекающего тока. [1] Исходными данными для математического моделирования АД являются: Напряжение сети U1, В; Частота питающей сети f1, Гц; Активное сопротивление обмотки статора r1, Ом; Активное сопротивление обмотки ротора приведенное к обмотке статора r2`, Ом; Реактивное сопротивление обмотки статора Х1, Ом; Реактивное сопротивление обмотки ротора, приведённое к обмотке статора Х2`, Ом; Активное сопротивление эквивалентное потерям в стали сердечника статора r0, Ом; Индуктивное сопротивление эквивалентное действию основного магнитного потока на обмотку статора Х0, Ом; Момент инерции асинхронного двигателя J, кг • м2 коэффициент а = 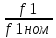 , то параметры схемы замещения изменятся следующим образом: , то параметры схемы замещения изменятся следующим образом:X1a= X1 • a ; X` 2a = X2 • a; X 0a = X0• a. А 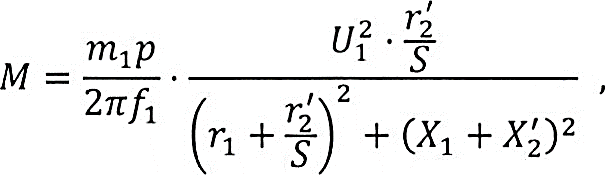 ктивное сопротивление обмотки статора r1 и ротора r`2 , момент инерции асинхронного двигателя J, остаются постоянными при изменении частоты. Механическая характеристика асинхронного двигателя определяется по следующей формуле [2]: ктивное сопротивление обмотки статора r1 и ротора r`2 , момент инерции асинхронного двигателя J, остаются постоянными при изменении частоты. Механическая характеристика асинхронного двигателя определяется по следующей формуле [2]:(1) где все параметры, кроме скольжения S постоянны. П M пуск (2) Максимальный момент машины находим через уравнение производной 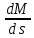 приравненной нулю. И из полученного равенства определим скольжение smax, при котором момент будет максимален: приравненной нулю. И из полученного равенства определим скольжение smax, при котором момент будет максимален: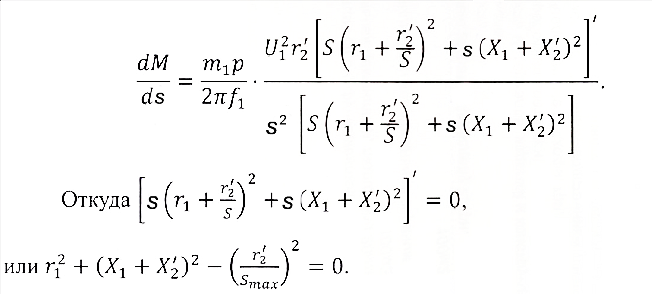 (3) Скольжение, соответствующее максимальному моменту: 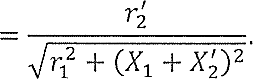  s max (4) Подставив значение smax в выражение вращающего момента, найдем максимальный момент [2]:  Mmax 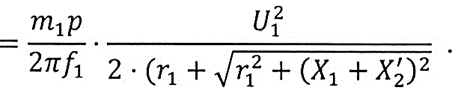 (5) Согласно закону Костенко, чтобы обеспечить оптимальный режим работы асинхронного двигателя при всех значениях частоты и нагрузки, относительное напряжение двигателя необходимо изменять пропорционально произведению относительной частоты на корень квадратный из относительного момента двигателя. Закон Костенко описывается уравнением [3]: 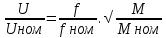 (6) При частотном регулировании удовлетворяющим закону (2) абсолютное скольжение асинхронного двигателя остается практически неизменным. Диапазон регулирования скорости вращения двигателя по рассматриваемому закону ограничен сверху и снизу. Закон был получен в пренебрежении падением напряжения в активных сопротивлениях статора и насыщением магнитной цепи. Составление алгоритма и программы вычисления механической модели На основе вышеприведенных формул составлен алгоритм и программа вычисления механической характеристики АД. Исходные данные для расчета приведены в таблице 1. Таблица 1. Параметры рассчитываемой трехфазной асинхронной машины.   На рисунке 1 приведена механическая характеристика асинхронного двигателя (АД) при разных частотах питающего напряжения. 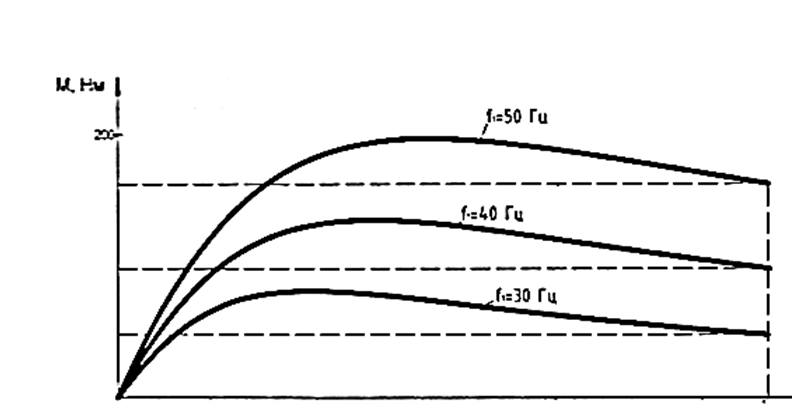 Рис. 1. Механическая характеристика АД при разных частотах Для более детального изучения из изменения параметров асинхронного двигателя вычислим его параметры из математической модели АД. Рассмотрим математическую модель в системе координат 0ху, вращающейся синхронно со скоростью вращения магнитного поля статора. Синусоидальный характер распределения параметров в трехфазном асинхронной машине дает возможность представить МДС или токи обобщенным пространственным вектором на комплексной плоскости. Учитывая симметричность трехфазной системы обмоток главный (обобщенный) вектор тока будет иметь следующий вид: 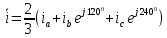 (7) Принимая допущение, что обмотки электродвигателя подключены к симметричным трехфазным источникам питания, то уравнения Кирхгофа для фазных напряжений статора АД [4]. 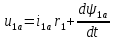 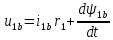 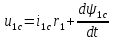 Где 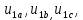 напряжение фаз А, В и С; напряжение фаз А, В и С; r 1 сопротивление обмотки статора; 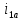 , ,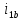 , ,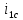 - токи фаз А,Б и С; - токи фаз А,Б и С;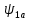 , , 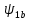 , ,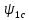 потокосцепления фаз статора. потокосцепления фаз статора.Модуль электромагнитного момента АД, выраженный через векторы потокосцепления статора ф1 и вектор тока ротора 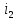 [4]: [4]: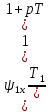 ( ( 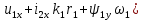 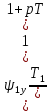 ( ( 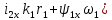 (12) (12)Основное уравнение привода: 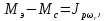 (13) (13)где 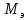 — электромагнитный момент асинхронного двигателя; — электромагнитный момент асинхронного двигателя;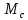 — противодействующий момент АД; — противодействующий момент АД;J— суммарный момент инерции, состоящий из момента инерции самой машины и приведенного к валу двигателя момента инерции нагрузки; 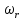 — угловая скорость вращения ротора АД; — угловая скорость вращения ротора АД; p— оператор Лапласса. Тогда, с учетом основного уравнения привода (13) получим полную систему уравнений для его реализации в системе пакетов Matlab/Simulink. Исходными данными для математического моделирования является частота сети, напряжение сети, момент нагрузки, а также параметры схемы замещения асинхронного двигателя. Параметры Т-образной схемы замещения приведены в литературе [5]. Индуктивности обмотки статора и приведенной обмотки ротора вычислены по следующим формулам: 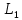 = =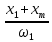 ; (14) ; (14)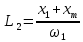 , ,Где 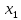 индуктивное сопротивление обмотки статора; индуктивное сопротивление обмотки статора; 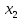 — приведенное индуктивное сопротивление обмотки ротора; — приведенное индуктивное сопротивление обмотки ротора;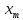 — индуктивное сопротивление намагничивания контура; — индуктивное сопротивление намагничивания контура; 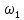 — угловая скорость вращения магнитного поля статора. — угловая скорость вращения магнитного поля статора.Индуктивность основного магнитного потока определяется как: 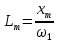 . (15) . (15) Коэффициенты 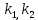 определяются следующим образом : определяются следующим образом :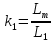 (16) (16)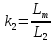 (17) (17)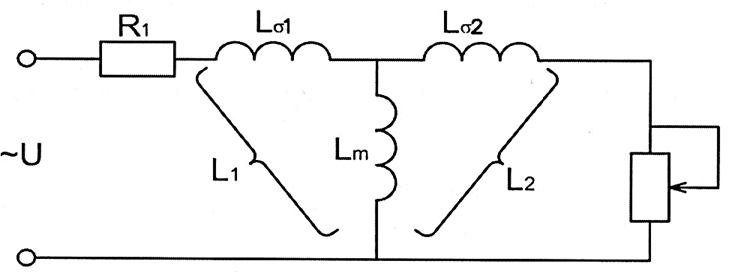 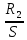 Рис. 2. Т-образная схема замещения АД Выражения вида 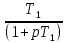 и и 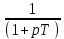 являются передаточными функциями соператором Лапласа -р = являются передаточными функциями соператором Лапласа -р = 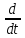 . Для их реализации пакет Simulink имеет вычислительный блок «transfer function». Аргументом данной функции являются только лишь входной сигнал. В нашей модели переменные . Для их реализации пакет Simulink имеет вычислительный блок «transfer function». Аргументом данной функции являются только лишь входной сигнал. В нашей модели переменные 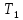 и T` зависят от угловой скорости вращения поля статора и T` зависят от угловой скорости вращения поля статора 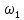 . Для исследования переходных процессов в АД необходимо будет изменять значения частоты питающего напряжения, что затрудняет использование блок-функций из стандартной библиотеки Simulink. Для решения этой проблемы необходимо реализовать пользовательский блок. Реализовать такой блок можно используя методику моделирования передаточных функций, изложенную в [1]. . Для исследования переходных процессов в АД необходимо будет изменять значения частоты питающего напряжения, что затрудняет использование блок-функций из стандартной библиотеки Simulink. Для решения этой проблемы необходимо реализовать пользовательский блок. Реализовать такой блок можно используя методику моделирования передаточных функций, изложенную в [1].На рисунке 3 приведена разработка математической модели частотного регулирования. Согласно приведенной блок-схема (рис.3.) вычисление параметров схемы замещения приведена на рис. 4 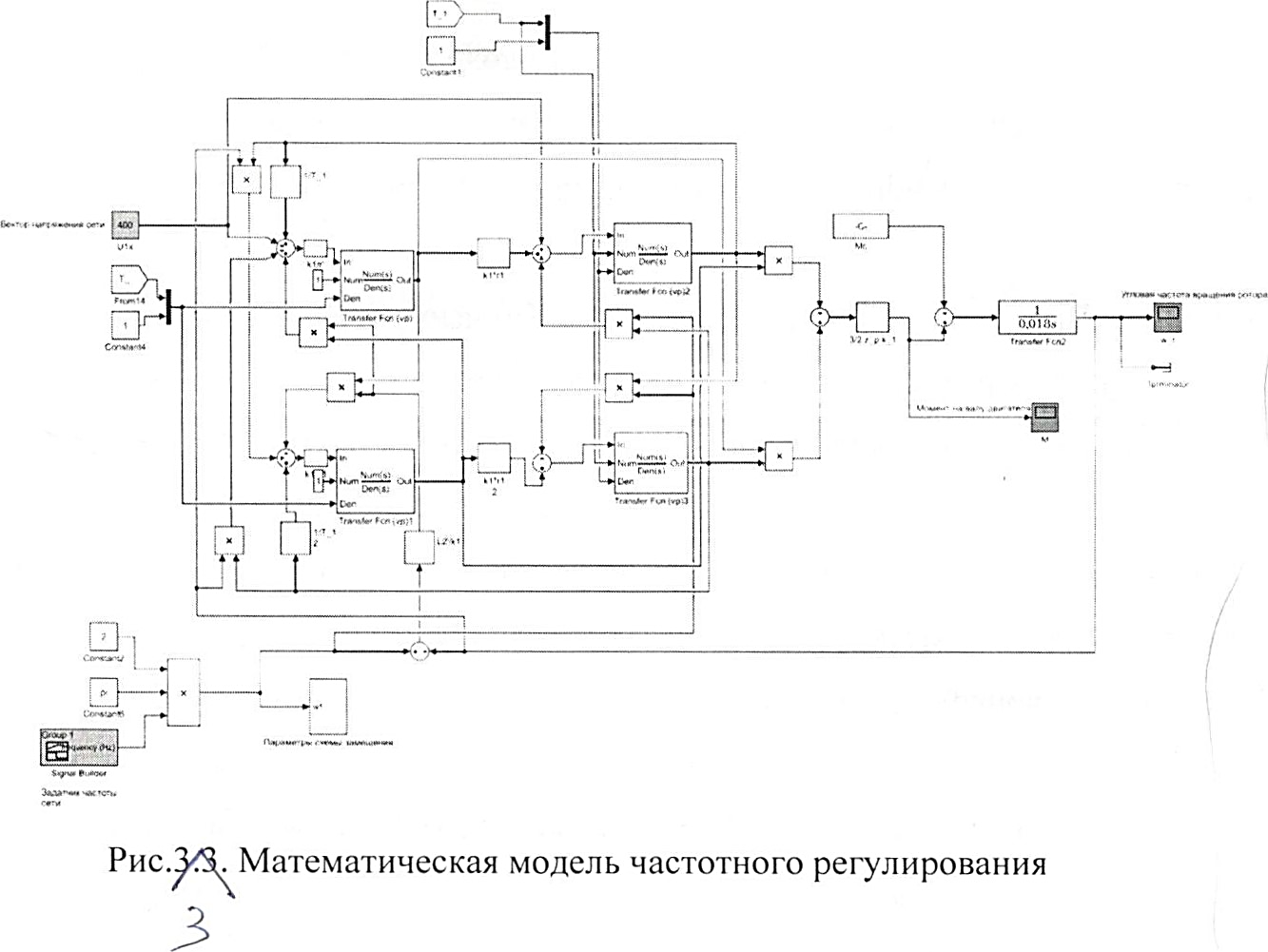 Рис.3. Математическая модель частотного регулирования 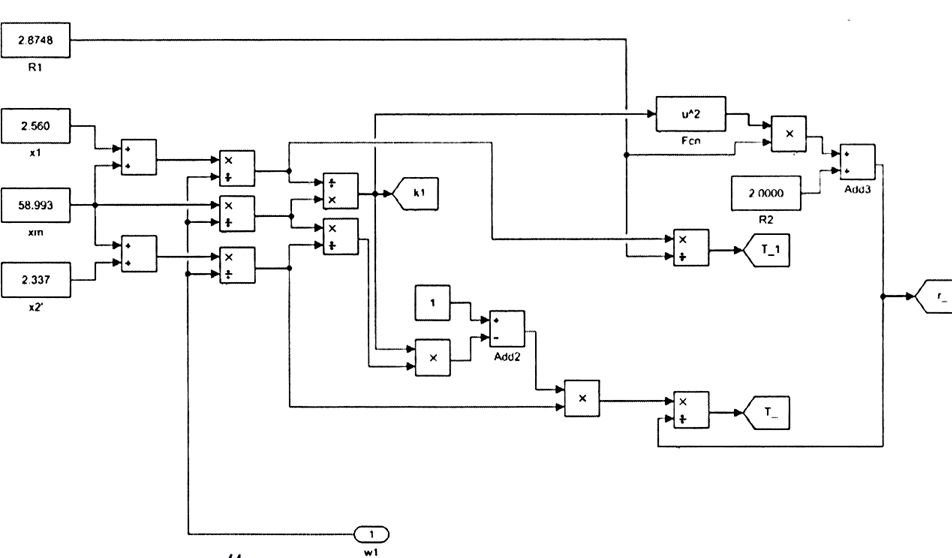 Рис. 4. Вычисление параметров схемы замещения. Выходными характеристиками математической модели являются угловая скорость вращения ротора 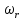 и электромагнитный момент и электромагнитный момент 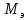 . .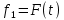 приведена на рис 5. приведена на рис 5.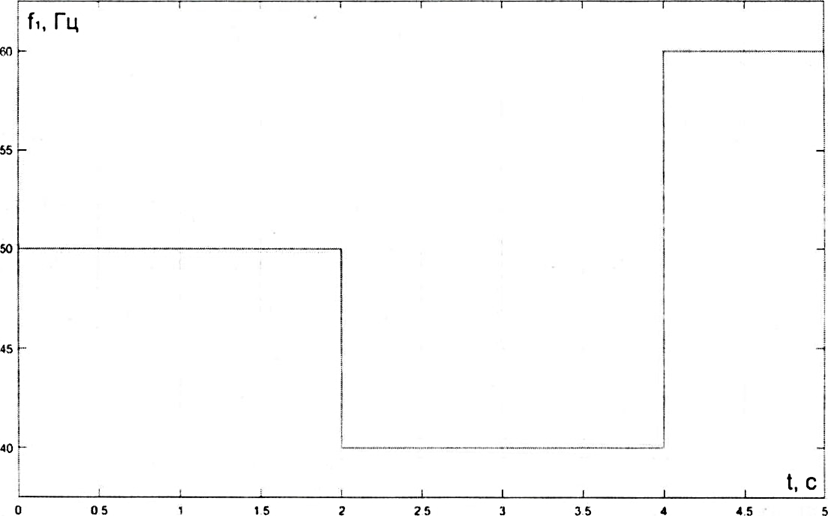 Рис. 5. График функции частоты тока сети от времени На рисунке 6 приведен график угловой скорости вращения ротора  = F(t). График изменения момента асинхронной машины от времени = F(t). График изменения момента асинхронной машины от времени  = F(t) приведен на рисунке 7. = F(t) приведен на рисунке 7.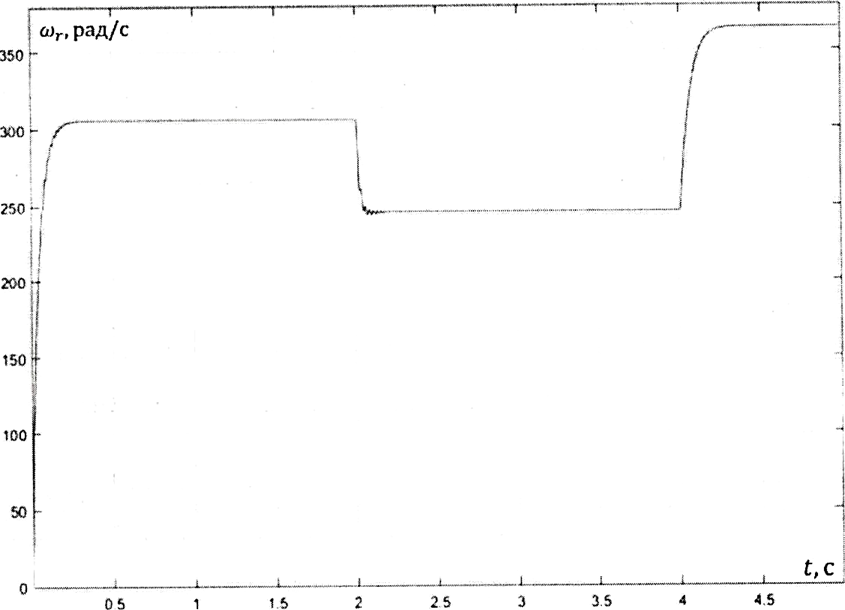 Рис.6. График угловой скорости вращения ротора. 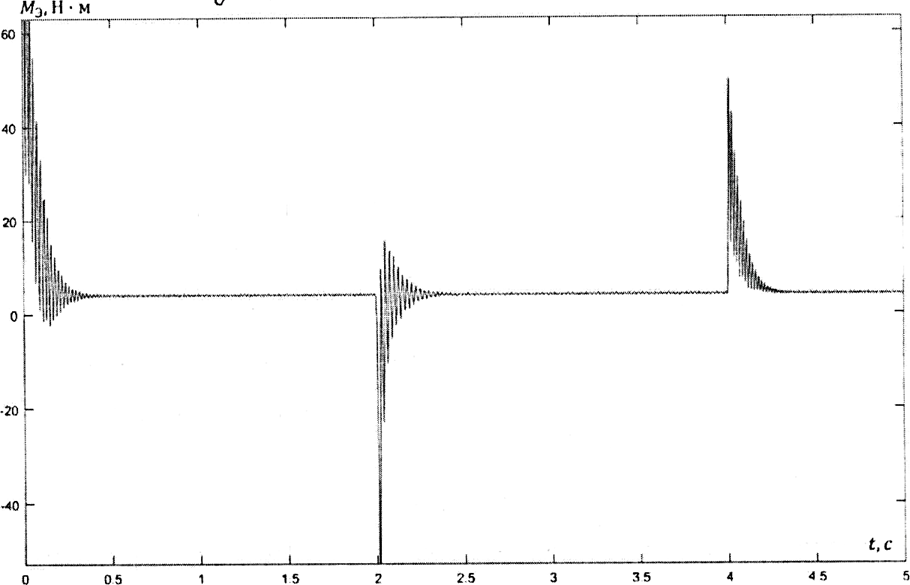 Рис.7. График изменения момента асинхронной машины Для исследования асинхронного двигателя также удобна система 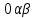 ортогональных координат, неподвижных относительно статора. Это удобство объясняется тем, что в такой системе все электромагнитные величины, связанные с осью ортогональных координат, неподвижных относительно статора. Это удобство объясняется тем, что в такой системе все электромагнитные величины, связанные с осью 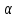 , равны соответствующим величинам фазы А естественной системы[6]. Система дифференциальных уравнений асинхронного двигателя в неподвижной системы координат , равны соответствующим величинам фазы А естественной системы[6]. Система дифференциальных уравнений асинхронного двигателя в неподвижной системы координат 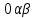 [6]: [6]: (18) (18)г 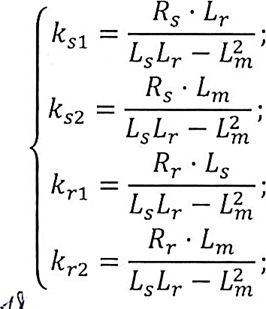 де 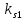 , , 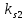 , , 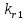 , , 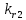 определяются из уравнений: определяются из уравнений:Система уравнений (18) дает полную математическую модель АД. На основе вышеперечисленных уравнений методом Рунге-Кутта вычислим значения электромагнитного момента Мэ и угловую скорость вращения ротора 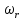 . .Результаты расчетов получены программой блок- схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значениях частоты питающей сети, приведена на рисунке 8. Подробный алгоритм работы программы приведен на рис 9. 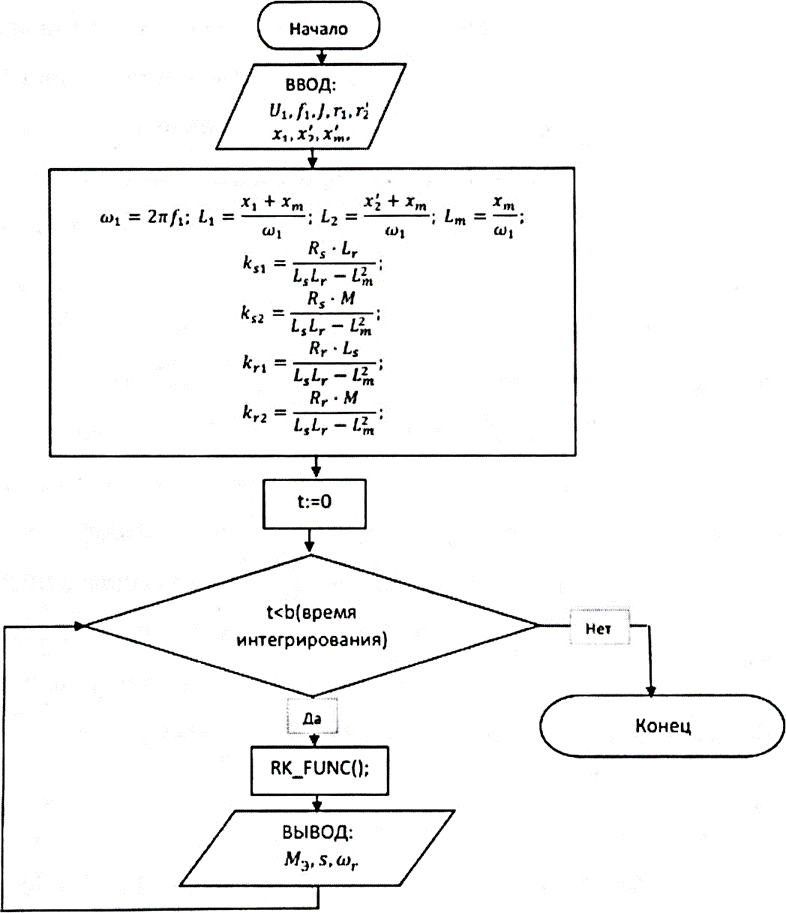 Рис. 8. Блок-схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значения частоты питающей сети.  Рис.9. Функция численного интегрирования 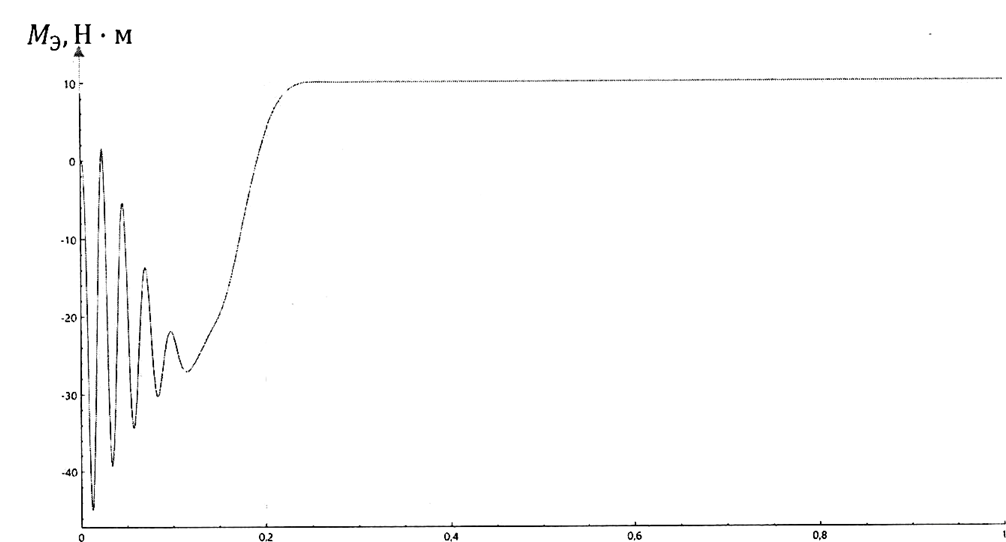 t,c Рис.10. График изменения момента асинхронной машины рад 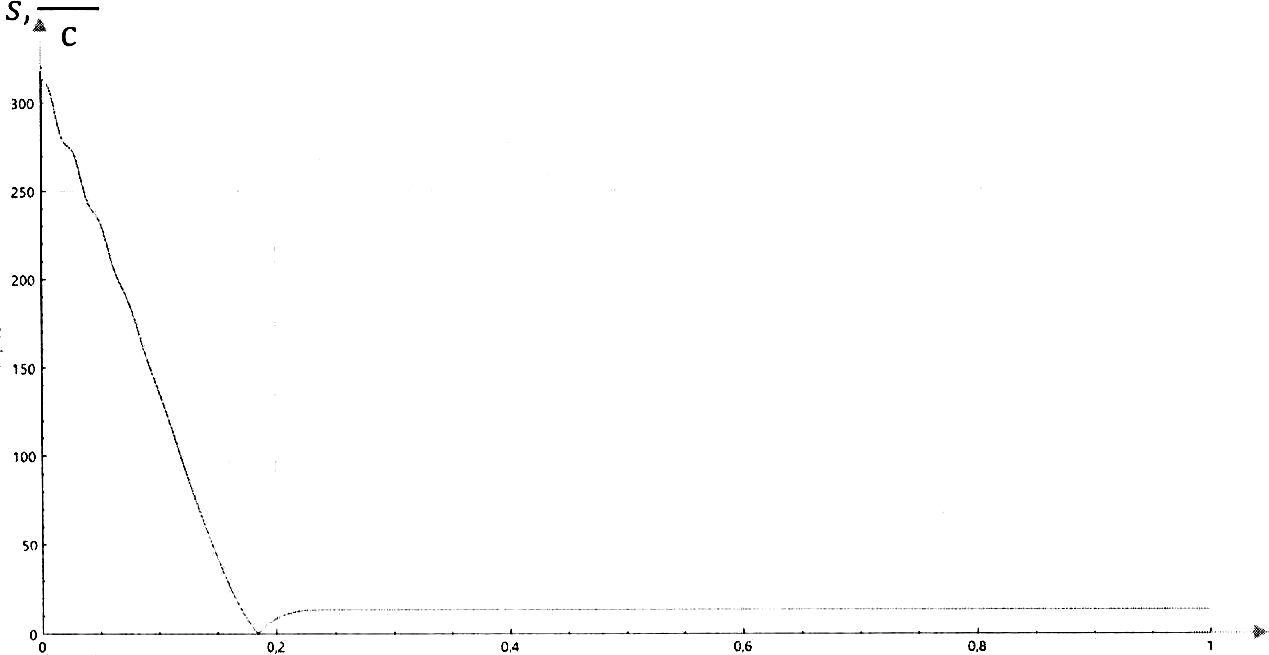 t, c t, cРис. 11. График изменения абсолютного скольжения асинхронной машины   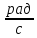 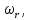  t t,c  Рис. 12 График изменения угловой скорости вращения ротора асинхронной машины Выводы На основе исследования режима работы асинхронного двигателя можно сделать следующие выводы: 1. Исследование работы асинхронного двигателя показывает, что основными факторами влияющим на устойчивость двигателя является его загрузка по активной мощности и значение внешнего сопротивления системы. Повышение этих показателей приводит к понижению запаса устойчивости. 2. Компенсация реактивной мощности оказывает благоприятное влияние на статическую устойчивость асинхронного двигателя. З. При полной компенсации реактивной мощности (tan 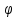 = 0) ухудшается динамическая устойчивость двигателя. Следовательно, в узлах где присутствуют асинхронные двигатели рекомендуется не полностью компенсировать реактивную мощность. = 0) ухудшается динамическая устойчивость двигателя. Следовательно, в узлах где присутствуют асинхронные двигатели рекомендуется не полностью компенсировать реактивную мощность.Построена векторная математическая модель частотного управления асинхронным электродвигателем. Данная модель позволяет моделировать переходные процессы механических характеристик асинхронный двигателей. В отличии от стандартной модели, реализованной в пакете Simulink, данная модель позволяет учитывать изменение параметров схемы замещения при изменении питающей сети. Простая реализация модели позволяет ее применять для исследования поведения асинхронных машин, перед их использованием в тех или иных режимах. На основе математической модели АД составлена программа для расчета механических характеристик при изменении частоты сети. Список литературы 1. Акимов Л.В. Динамические параметры асинхронных двигателей частотно-регулируемых электроприводов / Л.В. Акимов, В.О. Котляров, Д.Г. Литвиненко// Электрические машины и аппараты. -2011.-№3.-с72 2.Булгаков А.А. Частотное управление асинхронными двигателями: Учебное пособие. СПБ: СПБ ГУ ИТМО,2006,-94с 3. Е.И. Визгина Математическая модель асинхронного двигателя большой мощности// Вестник Чувашского университета.- 2011.№3. –с.85. 4.Китаев В.Е. Электрические машины Ч II. Машины переменного тока: Учебное пособие. М.;Высш. школа, 1978.- 184с. 5.Усольцев А.А. Частное управление асинхронными двигателями : Учебное пособие. СПб: СПбГУ ИТМО, 2006,-94с |
