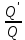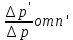Курсовая работа Влияние радиуса скважины на ее дебит. Влияние радиуса скважины на ее производительность по дисциплине
 Скачать 209.65 Kb. Скачать 209.65 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ университет» Филиал ТИУ в г. Сургуте Кафедра «Нефтегазовое дело» КУРСОВАЯ РАБОТА на тему: Влияние радиуса скважины на ее производительность по дисциплине: Подземная гидромеханика нефтяного и газового пласта
Сургут, 2021 г СОДЕРЖАНИЕВведение 3 1. Цель и задачи курсовой работы …………………………………………………..6 2. Теоретическая часть……………………………...…………………………..……8 3. Расчетная часть…………………………………………..……………………....17 Заключение. …………………………….…………………………………....……..23 Список использованных источников………………………………….….……….25 ВведениеОбщеизвестно, что нефтегазовый комплекс является значимым сектором промышленности России. Эффективное функционирование его предприятий способствует социально-экономическому развитию регионов страны, а также других отраслей промышленности. Более того, около 50 % федерального бюджета формируется за счет доходов нефтегазовых компаний. В настоящее время Россия обладает 6% разведанных мировых запасов нефти и почти 24% мировых разведанных запасов газа, которых ориентировочно хватит на 20 и 70 лет соответственно. Из этого факта следует, что перед нефтегазодобывающими предприятиями актуальна задача введения в разработку ранее консервированных, ввиду их нерентабельности, и своих малых запасов, месторождений и освоение новых. При любом способе добычи нефти и газа возбуждается их движение в пласте; поэтому без знания подземной гидромеханики нельзя обоснованно решить важнейшие задачи технологии нефтедобычи и добычи газа - нельзя выбрать систему разработки месторождения и режим эксплуатации скважин, которые были бы наиболее рациональны для данных пластовых условий и в то же время наиболее удовлетворяли планово-экономическим требованиям. Указывая на необходимость знания законов подземной гидромеханики для решения проблем технологии нефтедобычи, нужно подчеркнуть, что знания только этих законов недостаточно для изучения сложных процессов фильтрации жидкостей и газов в пластовых условиях. Действительно, громадная удельная поверхность пористой среды (величина поверхности стенок поровых каналов, приходящаяся на единицу объема образца пористой горной породы) и малые диаметры зерен и поровых каналов указывают на то, что роль молекулярных сил может быть относительно велика. Поэтому необходимо считаться с прямым и косвенным влиянием поверхностных явлений на процессы движения жидкости в гористой среде. Кроме того, для очень многих месторождений характерны высокие и снижающиеся в процессе разработки пластовые давления, высокие пластовые температуры; часто в одних и тех же порах пласта одновременно находятся не нефть, газ и вода, причем иногда физико-химические свойства законтурной (краевой) воды сильно отличаются от свойств связанной (сингенетичной, реликтовой, погребенной) воды, пленка которой обволакивает зерна нефтесодержащей породы. По мере падения пластового давления, выделения газа из раствора и продвижения краевой воды внутрь контура нефтеносности в пласте могут развиваться сложные физико-химические процессы, оказывающие существенное влияние на особенности движения жидкостей и газов в пластах. Не менее сложные физико-химические явления возникают при закачке в нефтеносный пласт воды, воздуха или газа, например для поддержания или восстановления пластового давления. Следовательно, физика и физикохимия пласта столь же важны для изучения поведения нефтегазоносного месторождения в процессе его разработки и эксплуатации, как и подземная гидромеханика. Подземная гидромеханика — наука о движении жидкости, газов и их смесей в пористых и трещиноватых горных породах. Подземная гидромеханика рассматривает особый вид движения жидкости — фильтрацию. В нефтегазовой отрасли она позволяет определить характер изменения скоростей фильтрации и движения жидкости, распределения давления по длине пласта от контура питания до скважины; определение дебита, коэффициента продуктивности, время прохождения фильтрующейся жидкости от контура до скважины. Полученные данные позволяют решать задачи прогнозирования и контроля разработки нефтяных, газовых, нефтегазовых и газоконденсатных пластов. Кроме того, в решении учитываются характер неоднородности пласта, характер несовершенства скважины. Математические модели фильтрации основываются на законах сохранения движения сплошной среды и следствиях этих законов. Также стремительно увеличивается необходимость в использовании математических методов исследования. Перед специалистами, изучающими фильтрационные процессы с помощью математических вычеслений, стоит непростая задача, заключающаяся в более глубоком изучении данных, полученных в результате разработки месторождений и построения на их основе математических моделей, отражающих основные свойства и характеристики фильтрационных процессов. Данные задачи так же невозможны без знания законов нефтегазовой гидромеханики. Актуальность исследования в курсовой работе В условиях высокого темпа развития промышленности, соответственно, потребления всех видов энергии, в Российской Федерации все более актуальным становится вопрос увеличения количества добываемых углеводородов. Падение производительности скважин за счёт истощения традиционных крупных месторождений ставит перед нефтегазодобывающими предприятиями задачу разработки новых и введения в разработку ранее консервированных, ввиду их нерентабельности и своих малых запасов, месторождений. Для того, чтобы максимально эффективно эксплуатировать продуктивные пласты, необходимо точно знать, какие параметры повлияют на дебит скважины и понимать рентабельность их изменения. Одним из таких параметров, который относительно легко поддается изменению, является радиус скважины. 1 Цель и задачи курсовой работы Целью курсовой работы является изучение влияния радиуса скважины на ее производительность. Скважина это горная выработка круглого сечения диаметром 75—400 мм, сооружаемая без доступа в неё человека, предназначенная для добычи либо разведки нефти и попутного газа. Как правило, скважины бурят вертикально, но могут бурить под заданным наклонным углом. В вертикальном строении скважины различают начало (устье), ствол и конец (забой). Скважины сооружаются путём последовательного бурения горных пород, удаления разбуренного материала и укрепления стенок скважины от разрушения (при необходимости, зависит от характера пород). Для бурения применяются буровые станки, буровые долота и другие механизмы. Средняя глубина добывающих скважин на данный момент в различных нефтегазовых провинциях Российской Федерации составляет 1500—3000 м, в перспективе из-за выработанности существующей ресурсной базы углеводородов России она растет и может достигнуть значения 4000—6000 м. На конец 2017 года средняя глубина новых скважин приближалась к 3 км. С ростом глубины увеличиваются расходы на их бурение и себестоимость добычи нефти и газа. Некоторые виды скважин: Газовые Нефтяные Добывающие Нагнетательные Добыча углеводородов через нефтяную скважину может осуществляться путём фонтанирования (при наличии избыточного давления в нефтяных пластах) или при помощи нагнетательных скважин для поддержания пластового давления.Различают вертикальные, горизонтальные, наклонные скважины. Начало скважины называется её устьем, дно — забоем, внутренняя боковая поверхность — стенками. Диаметры скважин колеблются от 25 мм до 3 метров. Скважины могут иметь боковые стволы, в том числе горизонтальные. Дебит скважины — объём продукции, добываемой из скважины за единицу времени (секунду, сутки, час и др.). Может характеризовать добычу нефти, газа, газоконденсата, воды. Дебит нефтяных скважин измеряется в кубических метрах либо тоннах в единицу времени (м³/час, м³/сутки). В ходе выполнения курсовой работы необходимо решить следующие задачи: 1)Привести математические уравнения для определения зависимости дебита скважины от её радиуса 2)Описать гидродинамические модели данных задач 3)Привести примеры численных расчетов. 4)На основе проделанной работы сделать заключение и вывод. 2 Теоретическая часть 2.1 Условия притока флюида и производительность скважины. При разных условиях притока флюида к забою скважины, ее радиус будет оказывать разное влияние на ее производительность. Для целей данной работы, формулы дебита и соответствующие им условия притока жидкостей и газов к скважинам имеет смысл разделить на четыре типа: 1) Плоский радиальный приток к скважинам по линейному закону фильтрации. 2) Плоский радиальный приток к скважинам по нелинейному закону фильтрации. 3) Сферический радиальный приток к скважинам по линейному закону фильтрации. 4) Сферический радиальный приток к скважинам по нелинейному закону фильтрации. 2.2 Влияние радиуса скважины на ее производительность в условиях плоского радиального притока жидкостей по линейному закону фильтрации. Рассмотрим влияние радиуса скважины на ее производительность в условиях плоского радиального притока жидкостей по линейному закону фильтрации. Плоско-радиальный фильтрационный поток: Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; поверхности равных скоростей (изотахи) и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными, поэтому для исследования рассматриваем движение жидкости в одной горизонтальной плоскости. При установившемся движении жидкости давление Р и скорость фильтрации в любой точке зависят только от расстояния r данной точки до оси скважины; поэтому этот поток является всего лишь другим видом одномерного фильтрационного потока. 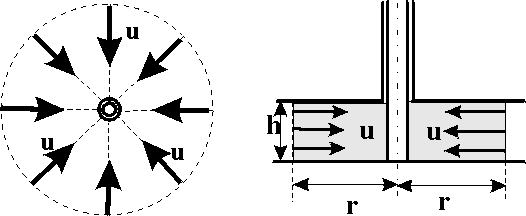 Рис.1 - Плоско-радиальный фильтрационный поток Для фильтрационных потоков первого типа зависимость дебита скважины Q от ее радиуса Rc и от радиуса RK контура области питания имеет вид: 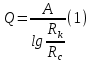 Где А - величина, равная произведению группы множителей, отражающих влияние проницаемости и мощности пласта, вязкости жидкости или газа, статического и динамического пластовых давлений и т. д. Чтобы выяснить влияние радиуса скважины на ее дебит, допустим, что при прочих неизменных условиях радиус скважины изменен в n' раз. Сохраним обозначение Q для дебита скважины с радиусом Rc и обозначим буквой Q дебит скважины с измененным радиусом R'c = n'Rc. Из формулы (1) получим: 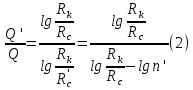 Формулы (1) - (2) справедливы для несжимаемой и сжимаемой жидкости, для газа и газированной жидкости при любом режиме пласта, лишь бы установившийся приток любой из перечисленных жидкостей (или газа) к скважине был плоско-радиальным и подчинялся линейному закону фильтрации. Природа жидкости и режим пласта оказывают влияние лишь на характер зависимости величины А от статического и динамического пластовых давлений в скважине.  Рис. 2. - График зависимости дебита скважины от ее радиуса Rc и от радиуса Rk контура области питания для случая плоскорадиального притока к скважине по линейному закону фильтрации. Рис. 2 подтверждает, что изменение радиуса скважины сравнительно мало отражается на изменении ее дебита. 2.3 Влияние радиуса скважины на ее производительность в условиях плоского радиального притока жидкостей по нелинейному закону фильтрации. Рассмотрим влияния радиуса скважины на ее производительность в условиях плоского радиального притока жидкостей по нелинейному закону фильтрации. Графики, характеризующие изменение забойного давления и дебита скважины при изменении ее радиуса в п раз; случаи плоско-радиального притока к скважине по закону Краснопольского - Рис. 3. 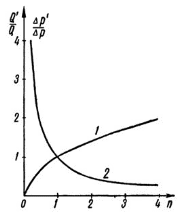 При плоско-радиальном притоке газа или жидкости к скважине по нелинейному закону фильтрации влияние радиуса скважины следует учитывать по формуле: 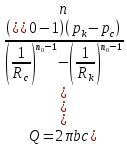 при n0 = 2 получим: 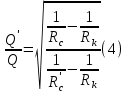 где Q΄ и Q - дебиты скважины, отвечающие соответственно, радиусам Rc и RK, где R΄c = n'Rc понижение забойного давления в скважине остается постоянным. Учитывая, что RK > Rc, последнюю формулу можно упростить 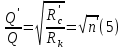 Для плоско-радиального притока несжимаемой жидкости к скважине по закону фильтрации Краснопольского влияние радиуса на перепад давления можно оценить следующим образом: 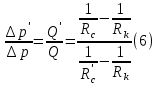 где Δр и Δр' - перепады давления, отвечающие соответственно радиусам R'c и Rc при сохранении постоянного дебита скважины. Учитывая, что Rk > Rc формулу можно упростить: 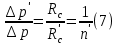 Таблица 1 – Зависимость величин и 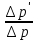 от n' от n'
Из сравнения правой и средней колонок табл. 1, видно, что изменение радиуса скважины меньше сказывается на изменении ее дебита, чем на изменении перепада давления. Кроме того, можно сделать следующий вывод: в условиях движения жидкостей по линейному закону фильтрации влияние изменения радиуса скважины оказывается значительно менее интенсивным, чем в условиях движения жидкостей по закону Краснопольского. Так, например, двукратное увеличение радиуса скважины в первом случае вызывает увеличение дебита на 5 - 8% (в зависимости от отношения величин RK и Rc) при сохранении перепада давления, тогда как во втором случае дебит увеличивается на 40%. Ранее было установлено, что в практически интересных случаях плоско-радиального движения нельзя ожидать нарушения линейного закона фильтрации во всем фильтрационном потоке; размеры области кризиса этого закона тем больше, чем больше дебит скважины. Отсюда следует, что в реальных условиях, когда этот закон фильтрации нарушается в призабойной зоне, влияние изменения радиуса скважины на ее дебит должно быть более интенсивным, чем на то указывает формула (2) и менее интенсивным, чем указывает формула (5). Эти формулы дают как бы крайние пределы интенсивности влияния радиуса скважины в условиях плоско-радиального движения. Далее, поскольку с увеличением размеров области кризиса линейного закона фильтрации растет влияние нарушения этого закона на дебит скважины, постольку справедлив следующий вывод: с увеличением дебита скважины интенсивность влияния ее радиуса на дебит и на перепад давления должна возрастать. 2.4 Влияние радиуса скважины на ее производительность в условиях сферического радиального притока жидкостей по линейному закону фильтрации. Радиально-сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. 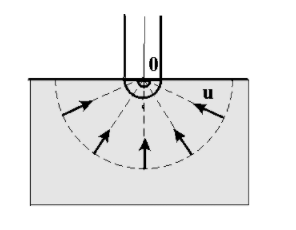 рис.4 – Схема радиально сферического фильтрационного потока Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным. 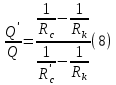 В этой формуле, иллюстрирующей влияние изменения радиуса скважины на ее дебит при сохранении перепада давления, приняты те же обозначения, которые были использованы в предыдущих формулах Учитывая, что RK > Rc, упрощенная формула: 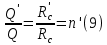 Из формулы 9 ясно видно, что в рассматриваемых условиях потока третьего типа влияние изменения радиуса скважины на ее дебит значительно интенсивнее, чем в условиях потоков первых двух типов. Данный вывод позволяет сформулировать следующее заключение, представляющее несомненный интерес для практики: чем сильнее скважина отклоняется от гидродинамически совершенной по степени вскрытия пласта, тем сильнее радиус скважины влияет на ее дебит. 2.5 Влияние радиуса скважины на ее производительность в условиях сферического радиального притока жидкостей по нелинейному закону фильтрации. Рассмотрим влияние радиуса скважины на ее производительность в условиях сферического радиального притока жидкостей по нелинейному закону фильтрации – закону Краснопольского. Окончательная формула, иллюстрирующая влияние радиуса скважины на ее дебит при сохранении постоянного перепада давления: 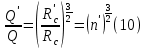 Эта формула справедлива для притока не только жидкости, но и газа к скважине в условиях фильтрационных потоков четвертого типа. Влияние радиуса скважины на ее дебит сказывается в данном случае еще сильнее, чем во всех ранее разобранных случаях, хотя и здесь следует напомнить, что допущение справедливости закона фильтрации Краснопольского во всем пласте преувеличивает возможности нарушения линейного закона фильтрации. При плоско-радиальном движении жидкостей и газов в пласте по линейному закону фильтрации влияние радиуса скважины на её дебит и на перепад давления оказывается наиболее слабым. Однако в реальных условиях скважины чаще всего бывают гидродинамически несовершенными и по степени и по характеру вскрытия пласта. Это нарушает в призабойной зоне плоско-параллельность потока, делает его трехмерным и, кроме того, облегчает возможности нарушения линейного закона фильтрации. Поведение скважины особенно сильно зависит от условий движения жидкостей и газов именно в призабойной зоне. Нарушения линейного закона фильтрации и двухмерности потока вызывают значительно более сильное влияние радиуса скважины на ее дебит и перепад давления, чем то обнаруживается из исследований потоков первого типа (см. начало данного параграфа). Отсюда следует, что нельзя, как это часто делают, обосновывать на формуле типа (1) якобы универсальный вывод о слабом влиянии радиуса скважины на ее производительность. Влияние изменения радиуса скважины на ее дебит не остается постоянным, а может возрастать с увеличением дебита Влияние изменения радиуса скважины на перепад давления при сохранении постоянного дебита либо столь же интенсивно (в условиях водонапорного режима при движении жидкости по линейному закону фильтрации, когда дебит пропорционален перепаду давления и, следовательно, индикаторные линии прямолинейны), как и влияние радиуса на дебит при сохранении постоянного перепада давления, либо еще более интенсивно (при притоке к скважине газа и газированной жидкости, при притоке несжимаемой жидкости со свободной поверхностью в условиях гравитационного режима, а также в условиях водонапорного режима при нарушении линейного закона фильтрации). 3 Расчетная часть 3.1 Расчет изменения дебита при плоскорадиальной фильтрация жидкости по закону Дарси. Определить объемные Q 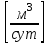 дебиты совершенной нефтяной скважины радиусами дебиты совершенной нефтяной скважины радиусами 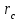 =0,1 м и =0,1 м и 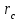 =0,2 м. и их отношение. =0,2 м. и их отношение.В пласте радиусом 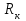 = 6700 м. , происходит установившаяся плоскорадиальная фильтрация жидкости по закону Дарси. Плотность нефти ρ = 6700 м. , происходит установившаяся плоскорадиальная фильтрация жидкости по закону Дарси. Плотность нефти ρ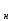 =835 кг/м3, коэффициент динамической вязкости μ =835 кг/м3, коэффициент динамической вязкости μ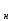 =5,9∙10-3 Па. Давление на контуре питания P =5,9∙10-3 Па. Давление на контуре питания P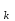 =11,2∙106 Па, давление на забое скважины p =11,2∙106 Па, давление на забое скважины p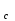 =9∙106 Па, коэффициент проницаемости пласта k=8,2∙10-16 м2, мощность пласта h=6м. =9∙106 Па, коэффициент проницаемости пласта k=8,2∙10-16 м2, мощность пласта h=6м.Дебит при первом радиусе скважины находим из формулы: 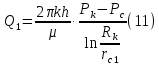 Где Q1 – дебит скважины радиусом 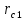 k - коэффициент проницаемости пласта h - мощность пласта Pk - давление на контуре питания Pс - давление на забое скважины Rk – радиус пласта rc1 – первый радиус скважины Для нахождения дебита скважины с радиусом rc1, подставим исхлдные данные в формулу (11). Тогда: 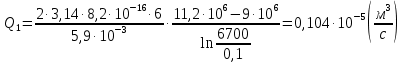 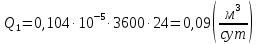 Дебит скважины с радиусом rc2 находим по аналогичной формуле, заменив rc1 на rc2 : 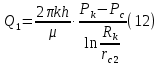 где rc2 – второй радиус скважины. Подставив исходные данные в формулу (12) получим: 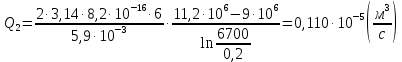 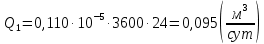 Для того, чтобы найти велечину изменения дебита, разделим второй дебит на первый: 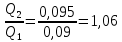 Следует отметить, что используя формулу (2) приведенную в теоретической части работы, можно сразу вычислить во сколько раз изменится дебит скважины. Для этого: 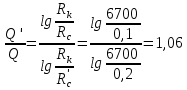 Таким образом, при изменении радиуса скважины в два раза дебит изменится в 1,06 раз. 3.2 Расчет изменения дебита при плоскорадиальной фильтрация жидкости по закону Краснопольского. Определить объемные Q 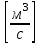 дебиты совершенной нефтяной скважины радиусами дебиты совершенной нефтяной скважины радиусами 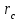 =0,1 м и =0,1 м и 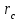 =0,2 м. и их отношение. =0,2 м. и их отношение.В пласте радиусом 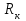 = 6700 м. , происходит установившаяся плоскорадиальная фильтрация жидкости по закону Краснопольского. Плотность нефти ρ = 6700 м. , происходит установившаяся плоскорадиальная фильтрация жидкости по закону Краснопольского. Плотность нефти ρ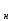 =835 кг/м3, коэффициент динамической вязкости μ =835 кг/м3, коэффициент динамической вязкости μ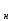 =5,9∙10-3 Па. Давление на контуре питания P =5,9∙10-3 Па. Давление на контуре питания P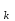 =11,2∙106 Па, давление на забое скважины p =11,2∙106 Па, давление на забое скважины p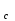 =9∙106 Па, коэффициент проницаемости пласта k=8,2∙10-16 м2, мощность пласта h=6м. =9∙106 Па, коэффициент проницаемости пласта k=8,2∙10-16 м2, мощность пласта h=6м.Дебит при первом радиусе скважины находим из формулы: 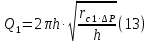 где Q1 – дебит скважины радиусом 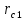 h - мощность пласта ΔP – разность Pk и Pс rc1 – первый радиус скважины Для нахождения дебита скважины с радиусом rc1, подставим исхлдные данные в формулу (13). Тогда: 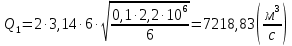 Аналогично находим Q2 при rc2: 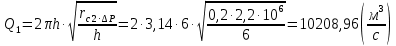 Для того, чтобы узнать во сколько раз изменился второй дебит разделим Q2 на Q1 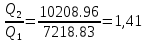 При использовании формулы (4) из теоретической части, можно сразу найти величину изменения второго дебита относительно первого. Для этого 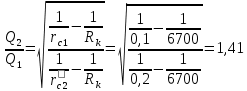 Таким образом, при изменении радиуса скважины в два раза дебит изменится в 1,41 раз. 3.3 Расчет изменения дебита при радиально-сферической фильтрация жидкости по закону Дарси. Необходимо определить во сколько изменится начальный дебит скважины равный 25 м3/сут если изменить радиус данной скважины = 0,1 м. в 4 раза. В пласте радиально-сферическая фильтрация жидкости по закону Дарси. Сначала найдем новый радиус скважины. Для этого: 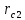 = =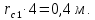 Чтобы определить во сколько раз изменится дебит при изъменении радиуса скважины, воспользуемся формулой (9): 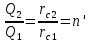 где: Q1 – дебит скважины с радиусом 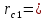 0,1 м. 0,1 м.Q2 – дебит скважины с радиусом 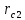 = 0,4 м. = 0,4 м.Подставив исходные данные в формулу (9) получим: 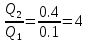 Таким образом дебит скважины с радиусом 0,4 будет отличаться от дебита скважины с радиусом 0,1 в 4 раза в большую сторону. Дебит второй скважины численно будет равен: 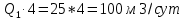 3.4 Расчет изменения дебита при радиально-сферической фильтрация жидкости по закону Краснопольского. Необходимо определить во сколько изменится начальный дебит скважины равный 25 м3/сут если изменить радиус данной скважины = 0,1 м. в 4 раза. В пласте радиально-сферическая фильтрация жидкости по закону Краснопольского. Сначала найдем новый радиус скважины. Для этого: 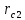 = =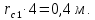 Чтобы определить во сколько раз изменится дебит при изъменении радиуса скважины, воспользуемся формулой (10): 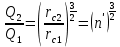 где: Q1 – дебит скважины с радиусом 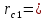 0,1 м. 0,1 м.Q2 – дебит скважины с радиусом 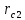 = 0,4 м. = 0,4 м.Подставив исходные данные в формулу (10) получим: 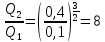 Таким образом дебит скважины с радиусом 0,4 будет отличаться от дебита скважины с радиусом 0,1 в 8 раз в большую сторону. Дебит второй скважины численно будет равен: 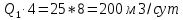 ЗаключениеВ курсовой работе была подробно рассмотренна зависимость производитеьности скважины от ее радиуса. Определено, что ключивыми факторами оказывающим силу влияния радиуса скважины на ее дебит являются условия притока жидкости к забою скважины. При плоско-радиальном движении жидкостей и газов в пласте по линейному закону фильтрации влияние радиуса скважины на её дебит и на перепад давления оказывается наиболее слабым. Однако в реальных условиях скважины чаще всего бывают гидродинамически несовершенными и по степени и по характеру вскрытия пласта. Это нарушает в призабойной зоне плоско-параллельность потока, делает его трехмерным и, кроме того, облегчает возможности нарушения линейного закона фильтрации. Поведение скважины особенно сильно зависит от условий движения жидкостей и газов именно в призабойной зоне. Нарушения линейного закона фильтрации и двухмерности потока вызывают значительно более сильное влияние радиуса скважины на ее дебит и перепад давления, чем то обнаруживается из исследований потоков первого типа. Отсюда следует, что нельзя, как это часто делают, обосновывать якобы универсальный вывод о слабом влиянии радиуса скважины на ее производительность. Влияние изменения радиуса скважины на ее дебит не остается постоянным, а может возрастать с увеличением дебита Влияние изменения радиуса скважины на перепад давления при сохранении постоянного дебита либо столь же интенсивно (в условиях водонапорного режима при движении жидкости по линейному закону фильтрации, когда дебит пропорционален перепаду давления и, следовательно, индикаторные линии прямолинейны), как и влияние радиуса на дебит при сохранении постоянного перепада давления, либо еще более интенсивно (при притоке к скважине газа и газированной жидкости, при притоке несжимаемой жидкости со свободной поверхностью в условиях гравитационного режима, а также в условиях водонапорного режима при нарушении линейного закона фильтрации). До сих пор слишком мало внимания уделяли возможному влиянию радиуса скважины на перепад давления. Обычно, ссылаясь на промысловые наблюдения, утверждали, что дебиты скважин разного диаметра в однородном пласте оказывались приблизительно одинаковыми. Однако не учитывали, ценой создания какого перепада давления достигали равенства дебитов. Следует всемерно поощрять новые практические решения вопроса об увеличении диаметра забоя скважины, ибо это во многих случаях способствует увеличению ее дебита и снижению перепада давления. В пластах, сложенных известняками, увеличение диаметра скважины может значительно способствовать увеличению ее производительности не только по причинам, рассмотренным выше, но и потому, что это часто бывает связано со включением новых трещин в систему микроканалов пласта, питающих скважину. Список использованной литературы 1. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика: Учебник для вузов. – М.: Недра, 1993. – 416 с. 2. Гиматудинов Ш. К., Ширковский А. И. Физика нефтяного и газового пласта. Изд. третье. Издательство Недра, Москва, 1989 г., 311 с. 3. Муравьёв К.А. Подземная гидромеханика нефтяного и газового пласта: Учебно-методическое пособие для студентов направления 21.03.01 «Нефтегазовое дело» всех форм обучения / К.А. Муравьёв - 2016, 59 с 4. Пыхачев Г. Б., Исаев Р. Г. Подземная гидравлика. Издательство Недра, Москва, 1973 г., 359 с. 5. Чарный И. А. Подземная гидрогазодинамика. Гостоптехиздат, Москва, 1962 г., 396 с. 6. Щелкачев В.Н., Лапук Б.Б. Подземная гидравлика. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.– 736 с. | ||||||||||||||||||||||||||||||||||||||||||