ответы. ЭиЭА. Вопросы к экзамену по предмету Эиэа нагревание проводников постоянным и переменным током, поверхностный эффект, эффект близости
 Скачать 467.74 Kb.
|
|
Ответы на вопросы к экзамену по предмету ЭиЭА Нагревание проводников постоянным и переменным током, поверхностный эффект, эффект близости. Одним из свойств электрического тока является нагрев проводников, по которым он протекает. Этот эффект был замечен многими исследователями, но его понимание пришло только выяснения механизма взаимодействия заряженных частиц с атомами и молекулами проводников. Нагрев приводит к выделению тепла и повышению температуры, а количество выделяемого тепла можно рассчитать с помощью формулы закона Джоуля-Ленца. Электрический ток — это упорядоченное движение заряженных частиц. В проводниках этими частицами выступают отрицательно заряженные электроны. Воздействие электрического поля сообщает электронам дополнительную кинетическую энергию. В процессе движения они сталкиваются с атомами (или молекулами) проводника, отдавая часть приобретенной энергии. По этой причине начинает увеличиваться внутренняя энергия вещества, что приводит к повышению температуры и выделению тепла. При нагревании проводников переменным током необходимо считаться с двумя явлениями: с поверхностным эффектом и эффектом близости. Напомним, что поверхностным эффектом называется явление неравномерного распределения тока по сечению проводника, причем плотность тока имеет наибольшую величину на его периферии и уменьшается по мере удаления от нее. Вследствие этого сопротивление проводника возрастает. Основные условия нагрева и охлаждения электрооборудования рассмотрим на примере однородного проводника, охлаждающегося равномерно со всех сторон. Если через проводник, имеющий температуру окружающей среды, проходит ток, то температура проводника постепенно повышается, так как вся энергия потерь при прохождении тока переходит в тепло. Скорость нарастания температуры проводника при нагреве током зависит от соотношения между количеством выделяющегося тепла и интенсивностью его отвода, а также теплопоглощающей способности проводника. Рассмотрим явления, оказывающие влияние на параметры электрической цепи. 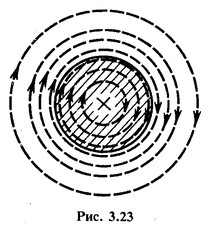 На рис. 3.23 схематически показаны магнитные линии в плоскости поперечного сечения уединенного провода с током. Представим себе этот провод в виде совокупности нитей, параллельных его оси. Чем ближе нить расположена к оси провода, тем с большим числом магнитных линий она сцеплена. При периодическом изменении тока изменяется магнитное поле и в нитях наводятся ЭДС, противодействующие изменениям тока. Это противодействие тем значительнее, чем больше ЭДС (чем больше магнитных линий сцеплено с нитью), т. е. чем ближе нить провода расположена к оси провода. В результате плотность тока в различных точках поперечного сечения получается неодинаковой: наибольшая на периферии провода и наименьшая на его оси. Рассмотренное явление концентрации переменного тока в поверхностном слое проводника называют поверхностным эффектом. Резкость проявления его возрастает с увеличением частоты f, диаметра провода d, относительной магнитной проницаемости 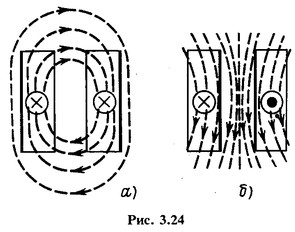 и удельной проводимости  материала провода. Это объясняется тем, что увеличение приводит к возрастанию магнитного поля внутри провода, увеличение d создает большую разницу в сцеплениях с магнитными линиями осевых и периферийных нитей провода, а повышение  увеличивает роль наводимых в нитях ЭДС, противодействующих изменению тока в них. Так, в предельном случае  весь ток должен концентрироваться на поверхности провода в бесконечно тонком слое. На распределение переменного тока в проводе оказывают влияние токи соседних проводов. Это явление называют эффектом близости. Как показано на схематических картинах магнитных полей двух проводов с токами (рис. 3.24), различные части сечений проводов сцеплены с неодинаковым числом магнитных линий. На основании рассуждений, аналогичных приведенным для одиночного провода, можно прийти к заключению, что наибольшая плотность тока будет в тех частях сечения проводов, которые сцеплены с наименьшим числом магнитных линий. Если токи в проводах направлены одинаково (рис. 3.24, а), наибольшая плотность тока наблюдается в наиболее удаленных друг от друга частях сечений; при различных направлениях токов (рис. 3.24, б) наибольшая плотность тока получается в наиболее близких друг к другу частях сечений проводов. Области наибольших плотностей тока отмечены на рис. 3.24 толстыми линиями. Вызываемая эффектом близости неравномерность распределения тока по сечению проводов приводит к увеличению потерь энергии, к увеличению разницы в сопротивлениях проводов переменному и постоянному токам. Электродинамические силы в параллельных проводниках при однофазном переменном токе Рассмотрим силы, действующие между параллельными проводниками, сначала при однофазном токе, а затем при трехфазном. Согласно (2-15) электродинамические силы  При переменном токе i = Im sin ωt сила 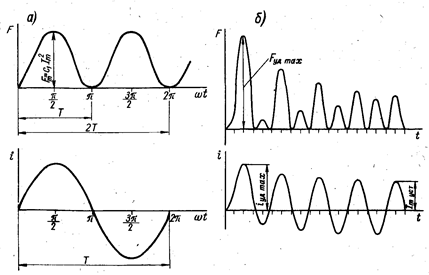 (2-52) Рис. 2-9. Электрические силы при однофазном переменном токе т.е. сила меняется с частотой, в два раза большей частоты тока (рис. 2-9, а). Силу f можно представить как сумму двух составляющих: постоянной c1I2m/2 и переменной c1I2mcos2ωt/2, меняющейся с двойной частотой по закону косинуса. Так как косинус угла принимает значения от +1 до – 1, то сила будет изменяться от f = с1I2m до f =0, не меняя своего знака. В расчетах учитывается максимальное значение силы  (2-53)Из (2-53) видно, что при переменном однофазном токе максимальное значение электродинамической силы при одном и том же токе (действующем) оказывается в два раза большим, чем при постоянном. При переменном токе следует иметь в виду еще одно весьма важное обстоятельство. В отличие от постоянного тока, при котором максимальное значение тока короткого замыкания равно его установившемуся значению Iуст (если пренебречь изменением сопротивления за счет нагрева), при переменном токе в зависимости от момента короткого замыкания первая амплитуда ударного тока iуд max может существенно превосходить амплитудное значение установившегося тока короткого замыкания (рис. 2-9, б):  (2-54)Максимальное усилие, на которое следует в таком случае рассчитывать устройство, будет  (2-55)т. е. при равном значении установившегося тока короткого замыкания при переменном токе электродинамическая сила может быть почти в 6,5 раза большей, чем при постоянном токе. При трехфазной сети токи в фазах будут сдвинуты на 120 электрических градусов: 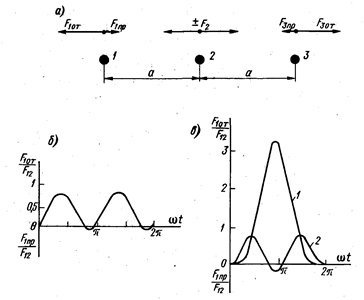   . Рис. 2-10. Электродинамические силы при трехфазном переменно токе (проводники расположены в одной плоскости) Рассмотрим случай, когда проводники расположены в одной плоскости (рис. 2-10, а). Проводник 1 будет взаимодействовать с проводниками 2 и 3. Пусть сила взаимодействия между проводниками 1 и 2 при единице тока равна f12, а между проводниками 1 и 3 – F13. Токи в фазах равны. Тогда полная сила, действующая на проводник 1, определится выражением  . (2-56)В отличие от однофазного тока при трехфазном токе сила меняется не только во времени, но и по знаку. При положительных значениях sin 2ωt и cos2ωt получим силу, притягивающую проводник 1 к двум другим. При отрицательных значениях sin 2ωt и cos 2ωt получим силу, отталкивающую проводник 1 от двух других. Проводники обычно располагаются на равном расстоянии друг от друга. В таком случае F13 =0,5F12, и тогда в установившемся режиме (рис. 2-10,б) максимальная притягивающая сила  (2-57)а максимальная отталкивающая сила   (2-58)где F1 2 = 10-7 c (1)2 = c1 (1)2. Силы, действующие на проводник 3, будут такими же, как и силы, действующие на проводник 1, но обратными по направлению. Усилия, действующие на средний проводник, F2 определятся уравнениями, аналогичными предыдущим. Если принять силу взаимодействия при единице тока между проводниками 2 и 3 равной F2 3, а между проводниками 2 и 1 – равной F2 1=F1 2, то при равных токах и равных расстояниях между проводниками F2 3 = F2 1= F1 2 и максимальная сила, действующая на средний проводник, определится из уравнения  (2-60)Таким образом, при расположении проводников в одной плоскости сила, действующая на средний проводник, оказывается большей, чем сила, действующая на крайний проводник. С учетом переходной составляющей, возникающей в момент короткого замыкания, максимальные силы будут большими, чем приведенные выше. Максимальное отталкивающее усилие будет иметь место при коротком замыкании в момент φ = –15° и составит  . (2-60)Притягивающая сила при φ = –15° будет близка к нулю. Максимум притягивающей силы имеет место при коротком замыкании в момент φ = 75°:  (2.61)Значение отталкивающей силы при φ = 75° составит 0,75F12. Изменение сил во времени при φ = –15° (кривая 1) и φ = 75° (кривая 2) в переходном режиме короткого замыкания приведено на рис. 2-10, в. Электродинамические силы при трехфазном переменном токе при расположении проводников в одной плоскости и треугольником Рассмотрим случай, когда провода трехфазной цепи расположены правильным треугольником (рис. 2-11). Определим силы, действующие на проводник 1. Сила взаимодействия между проводниками 1и 2 (F1 2) будет направлена по прямой I, а сила взаимодействия между проводниками 1 и 3 (F1 3) – по прямой II. Каждая из сил будет переменной во времени, а общая сила (F1), полученная путем геометрического сложения переменных по значению сил F1 2 и F1 3, будет переменной не только во времени, но и по направлению. Изменение полученной силы F1 по направлению и по значению может быть охарактеризовано вектором ОА, конец которого будет скользить по окружности, как это показано на рис. 2-11, а:  (2-62)Проекция силы на ось х всегда направлена в одну сторону. 3нак ± в уравнении (2-62) означает, что для 2ωt >180° следует брать знак минус. Изменение силы во времени не связано с изменением знака. Каждый из двух других проводников испытывает такие же силы, но с соответствующим сдвигом во времени и пространстве. С учетом ударного тока максимум силы получается при условии φ = 0, и сила меняете» по закону  (2-63)Знак минус следует брать для всех отрицательных значений sin  .Направление и значение силы для любого момента времени определятся вектором ОА, скользящим по кривой рис. 2-11, б и отложенным под углом ωt/2 к оси ординат. 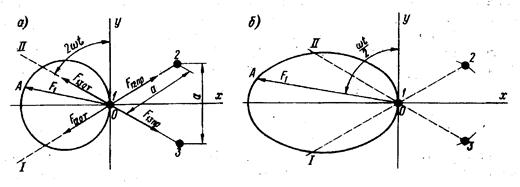 Рис. 2-11. Электродинамические силы при трехфазном переменном токе (проводники расположены треугольником) В трехфазной сети могут иметь место однофазные, двухфазные и трехфазные короткие замыкания, но так как токоведущие части должны противостоять электродинамическим силам при любом виде короткого замыкания, то, следовательно, расчет надо вести на тот вид короткого замыкания, при котором силы получаются большими. При двухфазном коротком замыкании электродинамические силы получаются большими, чем при трехфазном, если предположить, что ударный ток в обоих случаях одинаков. Практически ударный ток при двухфазном коротком замыкании меньше, чем при трехфазном. Поэтому расчет токов короткого замыкания рекомендуется вести всегда на случай трехфазного короткого замыкания. Расчет ведется на максимальное усилие, получаемое при ударном токе. Однако, учитывая, что сила переменна и ее максимум существует очень короткое время, для допустимых напряжений в материале берут большие значения, чем при постоянно действующей силе. Вывод переходного процесса при коротком замыкании в сети переменного тока Рассмотрим процесс короткого замыкания. Для понимания этого процесса необходимо знать закон коммутации: в цепях, имеющих индуктивности и емкости, мгновенные значения тока i напряжения и ЭДС е, магнитного потока Ф и электрического заряда Q не могут в момент коммутации мгновенно изменить свои значения. И для того, чтобы в цепи был обеспечен непрерывный переход из одного состояния в другое (в нашем случае из нормального режима в режим короткого замыкания), в момент коммутации в цепи появляются свободные ток, напряжение, ЭДС, магнитный поток, заряд, которые обеспечиваются за счет изменения магнитных потоков в индуктивностях и заряда в емкостях. На рисунке 5.8 приведены расчетная схема короткого замыкания и кривая изменения тока в цепи, полученная при помощи осциллографа (сплошная линия). Пунктиром показано, как можно разложить ту кривую на две более простые, поддающиеся детальному анализу. Это, во-первых, кривая iпр принудительного (периодического) тока, который устанавливается через 2...4 с (с учетом нагрева элементов цепи) после момента воз никновения короткого замыкания, и, во-вторых, кривая iсв свободного (апериодического) тока, обусловленная наличием в цепи магнитных полей и их перераспределением в первые 2...4 с после момента короткого замыкания. 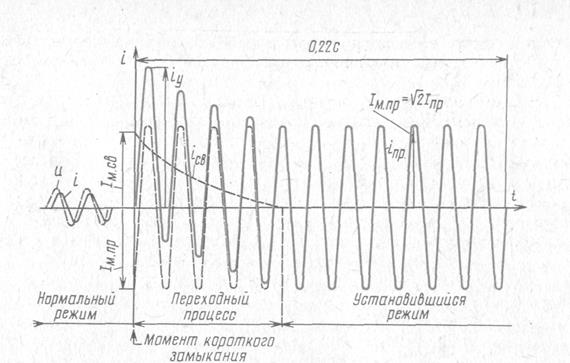 Рисунок - Изменение тока короткого замыкания. Действующее значение принудительного тока 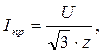 где U - напряжение на зажимах источника; Z - полное сопротивление цепи. Амплитуда тока  Мгновенное значение свободного тока для любого момента времени t  где Iтсв - начальное значение свободного тока, равное в наиболее тяжелом случае амплитуде Iтпр -тока короткого замыкания; Т= L / r = Х / (ωr) - постоянная времени экспоненциальной кривой, описывающей характер изменения свободного тока; L - индуктивность цепи; r - активное сопротивление цепи. Наибольшее мгновенное значение тока короткого замыкания возникает через полпериода (через 0,01 с) после момента замыкания, то есть в самом тяжелом случае, когда момент замыкания совпал с максимальной амплитудой периодического принудительного тока. Этот мгновенный максимальный ток называется ударным, и он составляет  где ky —коэффициент ударного тока, показывающий, во сколько раз ударный ток больше максимального значения периодической — принудительной составляющей тока короткого замыкания. Теоретически постоянная времени Т может меняться от 0 при L = 0 до бесконечности при r = 0. В этих случаях краевые значения ударного коэффициента составят соответственно 1 и 2. На практике максимальное значение ky = 1,8. При коротких замыканиях в сетях 10 кВ и 0,38 кВ ky = 1. Электродинамическая устойчивость аппаратов, механический резонанс. Проверка электродинамической стойкости аппаратов и проводников при КЗ. Электродинамические силы, возникающие в токоведущих частях аппаратов, стремятся деформировать как сами проводники, так и изоляторы, с помощью которых эти проводники укреплены к заземленным частям аппарата. Электродинамической устойчивостью аппарата называется его способность противостоять силам, возникающим при протекании токов короткого замыкания. Эта устойчивость может выражаться либо непосредственно амплитудным значением тока £дин, при котором механические напряжения в деталях аппарата не выходят за пределы допустимых величин, либо кратностью этого тока относительно амплитуды номинального тока. Как показывают наблюдения, чем выше температура, воздействию которой подвергаются изоляционные материалы, входящие в конструкции аппаратов, тем быстрее ухудшаются их механические и электрические качества. Ухудшение электрических и механических свойств изоляционных материалов приводит к нарушению нормальной работы аппарата. Естественно, что изоляционные материалы обладают разной стойкостью в отношении воздействия температур. Кроме того, в различных условиях степень воздействия температуры на изоляционные материалы меняется. Так, например, воздействие температуры на изоляцию проводников катушек, пропитанных лаком, значительно слабее, чем непропитанных, и старение изоляции в них соответственно будет протекать медленнее. В настоящее время в соответствии с ГОСТ 8865—58 и нормами МЭК (Международная электротехническая комиссия) изоляционные материалы разбиты по нагревостойкости на семь классов Y, А, Е, В, F, Н, С. В ГОСТах обычно наряду с допустимой температурой часто указывается допустимое превышение температуры аппарата над температурой окружающего воздуха, определяемое как разность допустимой температуры и температуры окружающего воздуха. При этом температура окружающего воздуха чаще всего принимается 35 или 40° С. В настоящее время во многих ГОСТах на электрические аппараты приведенная классификация изоляционных материалов пока не нашла отражения. Так, например, в ГОСТ 8024—56 «Аппараты переменного тока высокого напряжения» в зависимости от нагрева при длительной работе все изоляционные материалы разделяются на классы О, А, В, С снаибольшей температурой нагрева только 110° С. Для трансформаторного масла согласно ГОСТ 8024—56 допускается превышение температуры 40° С, если масло используется в качестве дугогасящей среды, и 55° С — для случаев, когда масло используется только как изолирующая среда. Применительно к аппаратам низкого напряжения (до 1000 В)разработан ГОСТ 12434—66, в котором электрические аппараты разделяются на аппараты распределения энергии и аппараты управления приемниками энергии. К аппаратам распределения энергии относятся автоматические выключатели, переключатели, плавкие предохранители, контактные разъемы. К аппаратам управления — приемникам энергии относятся контакторы, реле управления и промышленной автоматики, командоконтроллеры, кнопки управления, конечные и путевые выключатели, резисторы, реостаты, электромагниты, контроллеры, ручные и электромагнитные пускатели. Нагрев и охлаждение, однородного проводника при продолжительном режиме работы. При изучении данного вопроса необходимо знать следующие параметры: - P dt – количество теплоты, выделяемого в проводнике; - G – масса проводника; - F – площадь поверхности излучения проводника; - с – удельная теплоемкость проводника; - kт – коэффициент теплоотдачи; - τ – превышение температуры проводника по отношению к окружающей среде. Для любогопроводника при нагреве (t = 0) справедливоуравнение теплового баланса P dt = G c dt + F kтτ dt Количество теплоты выделяемое в проводнике равно количеству теплоты, поглащаемому проводником, плюс количество теплоты излучаемому с поверхности проводника. Для установившегося режима работы проводника (t = ) справедливо уравнение теплового равновесия: P dt = F kт τ dt Количество теплоты, выделяемое в проводнике равно количеству теплоты излучаемому с поверхности проводника. При отключении работающего проводника наступает его охлаждение. Уравнение теплового баланса при охлаждении имеет вид: 0 = G c dt + F kт τ dt Продолжительным (S1) называется режим работы, при котором нагрев продолжается столько времени, что температура проводника успевает достичь установившихся значений. Уравнение нагрева проводника при продолжительном режиме работы с холодного состояния имеет вид: τ = τ уст (1-е -t / Т) Уравнение нагрева проводника при продолжительном режиме работы с некоторой температуры имеет вид: τ = τ уст (1 – е -t / Т) + τ 0 е -t / Т |