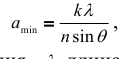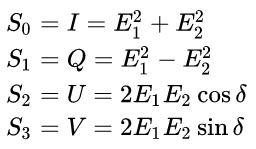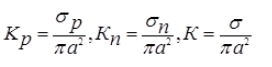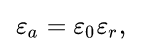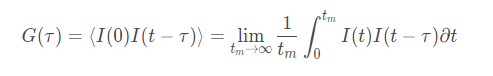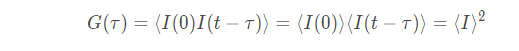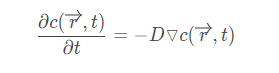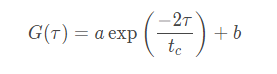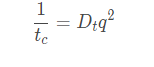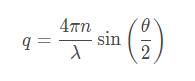Вопросы к экзамену по спецкурсу «Синтез и оптические свойства плазмонных наночастиц»
Характерные размеры наночастиц, проявляющих плазмонные свойства. Характерная область на шкале размеров: от атомов к объемным образцам.
Общий обзор основных типов наночастиц: золотые наносферы, наностержни, нанозвезды, нанооболочки на двуокиси кремния, наноматрешки, золотосеребряные наноклетки, золотосеребряные наностержни, наночастицы, покрытые двуокисью кремния.
Основные принципы методов синтеза top-down and down-top.
Характерное число атомов (оценки по порядку величины) для металлических частиц
Нанолитография – метод получения наноструктур с контролируемыми размерными параметрами с помощью латексных субмикронных частиц.
Принципы и задачи стабилизации наночастиц различными молекулярными лигандами.
Основные понятия теории рассеяния света: амплитудная матрица рассеяния, параметры Стокса, матрица Мюллера.
Основные интегральные характеристики: сечения и коэффициенты (факторы эффективности) рассеяния, поглощения и ослабления.
Дипольный момент шара. Поляризуемость маленького шара. Отличие оптических диэлектрических констант от электростатических.
Электромагнитное рассеяние диполя. Полное решение, ближнее поле, дальнее поле.
Зависимость диаграммы рассеяния от направления и поляризации падающей волны по отношению к диполю (вертикальный диполь, горизонтальный диполь, неполяризованный свет).
Интегральные сечение рассеяния и поглощения маленького шара в дипольном приближении.
Ослабление света ансамблем частиц. Закон Бугера. Пропускание и поглощение (экстинкция), связь между ними.
Однолучевой спектрофотометр. Двухлучевой спектрофотометр. Недостатки и преимущества каждой схемы.
Зависимость оптических констант от частоты (дисперсия) в терминах простейшей теории Лоренца. Теория Друде для металлов. Поправки оптических констант на наноразмер частиц.
Оценка длины волны резонанса на основе простейших формул (комбинация дипольного приближения и формулы Друде). Золото в воде и серебро в воде.
Реальные зависимости оптических констант (реальной и мнимой части показателя преломления от длины волны света, табличные данные).
Зависимость максимальных факторов эффективности золотого или серебряного шарика от размера.
Металлические наностержни. Характерные размеры, характерные спектры экстинкции. Продольный и поперечный резонанс. Зависимость длины волны резонанса от осевого отношения.
Метод динамического рассеяния света.
Ответы на вопросы по спец. курсу
Синтез и оптические свойства плазмонных наночастиц»
1. Наноплазмоника изучает явления, связанные с колебаниями электронов проводимости в металлических наноструктурах и наночастицах и взаимодействием этих колебаний со светом, атомами и молекулами c целью создания сложных оптических устройств. Плазмонные колебания в наночастицах (рис. 2) существенно отличаются от электромагнитных волн, распространяющихся по поверхности металла («поверхностных плазмонов»). Именно эти колебания, которые называют локализованными плазмонами, являются основой всех приложений наноплазмоники.
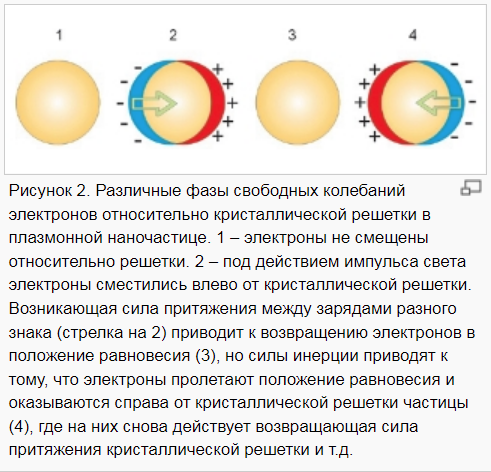
Считается, что наноплазмоника позволит создать новую элементную базу для компьютеров и устройств обработки данных за счет использования малых размеров металлических наноструктур и оптического быстродействия происходящих в них процессов. Устройства на основе наноплазменных частиц позволяют устранить недостатки фотонных устройств (оптоволоконная техника), которые связаны с больщим физическим размером таких устройств. И в то же время работать с высокой частотой, которая ограничивается в электрических проводниках, связанная с неустранимым выделением в проводниках тепла. Характерные размеры плазмонных наночастиц составляют от 10-100 нм.
2. Золотые и серебряные наночастицы с плазмонным резонансом (ПР) нашли разнообразные применения в нанобиотехнологии и наномедицине благодаря возможности настройки спектрального положения и амплитуды ПР за счет изменения природы металла, размера, формы, структуры частиц иих диэлектрического окружения. Последнее означает как локальное окружение, сформированное адсорбированными биомолекулами, так и глобальные диэлектрические свойства, обусловленные буферной средой или металл/диэлектрической подложкой, на которой могут адсорбироваться молекулы. Хотя изменения ПР, индуцированные адсорбцией биомолекул, обычно достаточно малы, они с успехом используются для детекции биоспецифического связывания макромолекул и клинической экспресс диагностики.
Золотые наносферы
Согласно классической модели Сведберга, восстановление золотохлористоводородной кислоты (ЗХВК) и образование коллоидных частиц происходит в три этапа. В начальный период происходит быстрое восстановление около 30% ЗХВК с образованием высоко пересыщенного раствора восстановленного золота. На втором этапе, согласно закону действующих масс, восстановление резко замедляется, и в пересыщенном растворе происходит конденсация новой фазы с образованием очень мелких“зародышевых” частиц диаметром менее 2 нм. В этот момент раствор приобретает синюю окраску, что, по-видимому, объясняется флоккуляцией некоторой доли образовавшихся частиц. Процесс восстановления золота ими
роста этих частиц протекает сравнительно медленно до достижения некоторого критического размера (порядка 2 нм), после чего первоначально сформированные частицы становятся ядрами конденсации для дальнейшего восстановления ионов золота. На третьем этапе процесс восстановления ускоряется, и по его завершении суспензия приобретает ярко красную окраску.
Наиболее широко распространенным методом получения золотых частиц с размерами в пределах 8-70 нм для медико-биологических приложений остается метод цитратного восстановления ЗХВК. Биологи при этом ссылаются на Френса [6], а материаловеды чаще упоминают работу Туркевича [23] по изучению процессов нуклеации и роста при синтезе КЗ (коллоидное золото).
Суммарную реакцию цитратного восстановления коллоидного золота можно выразить:
2AuCl3+3Na3C6H5O7→2Au+3Na2C5H4O5+3CO2+3NaCl+3HCl
Исходя из стехиометрических соотношений уравнения реакции, 2 моля Au(III) реагируют с 3 молями Na3Cit. Действительно, при таком соотношении образуются золи с размерами частиц 35-40 нм в диаметре
Золотые наностержни
Процедура получения золотых НСт по всей видимости не может быть одношаговой и протекает по механизму роста, опосредованного зародышами В качестве зародышей используют ультрадисперсные золи золота (средний размер около 3 нм), полученные восстановлением ЗХВК борогидридом натрия в присутствии цитрата натрия либо ЦТАБ. Следующий этап заключается в объединении ростового раствора (ЗХВК, аскорбиновая кислота, ЦТАБ) и суспензии зародышей При этом раствор сначала обесцвечивается, что, по мнению авторов [49], свидетельствует о восстановлении Au3+ или AuCl– до Au– ионов (не Au) аскорбиновой кислотой. После внесения зародышей раствор постепенно приобретает синюю, фиолетовую или красно-бурую окраску в зависимости от осевого отношения образующихся наночастиц.
В дальнейшем для увеличения осевого соотношения в однокомпонентной системе ПАВ было предложено вводить в ростовой раствор варьируемое количество ионов серебра. В результате приобретения сфероидальной и цилиндрической формы золотые частицы начинают проявлять химическую анизотропную реактивность.
3. Основные принципы методов синтеза top-down and down-top.
Подход «сверху-вниз» основан на уменьшении размеров физических тел механической или ионной обработкой, вплоть до получения объектов с ультрамикроскопическими, нанометровыми параметрами.
В качестве простого примера можно указать некоторые полупроводниковые устройства, структура которых создается фотолитографической обработкой. При фотолитографии полупроводниковая заготовка подвергается обработке лазерным лучом, что позволяет получить в ней заранее спланированную конфигурацию схемы. Разрешающая способность (то есть минимальный размер элементов изготавливаемой схемы) определяется при этом длиной волны лазерного излучения.
Другим примером может служить применение тонкого перемола материала (или его измельчения). При этом под измельчением понимают уменьшение начального размера частиц материала путем разрушения их под действием внешних усилий, преодолевающих внутренние силы сцепления.
Идея технологии «снизу-вверх» заключается в том, что сборка создаваемой «конструкции» осуществляется непосредственно из элементов «низшего порядка» (атомов, молекул, структурных фрагментов биологических клеток и т.п.), располагаемых в требуемом порядке (рис. 7). Этот подход можно считать «обратным» по отношению к привычному методу миниатюризации «сверху-вниз», когда мы просто уменьшаем размеры деталей.
Типичным примером подхода «снизу-вверх» может служить поштучная укладка атомов на кристаллической поверхности при помощи сканирующего туннельного микроскопа или других устройств этого типа. Метод позволяет наносить друг на друга не только отдельные атомы, но и слои атомов. Конечно, в настоящее время описываемый подход характеризуется очень низкой эффективностью и производительностью, однако ему принадлежит будущее.
Необходимо отметить следующее важное обстоятельство. При использовании технологии «сверху-вниз» в конечных наночастицах сохраняется структура исходного материала с большими размерами. Однако при формировании объектов сборкой «снизу-вверх» свойства этих объектов могут определяться как природой и количеством исходных элементов (атомов, молекул), так и их взаимным расположением. Таким образом, нанотехнология позволяет варьировать свойства нанообъектов в зависимости от числа и взаимного расположения атомов. Изготовление нанообъектов с нанометровой точностью дает возможность получать уникальные функциональные характеристики.
4. Характерное число атомов (оценки по порядку величины) для металлических частиц
Кластер - это группа из небольшого (счетного) и, вообще говоря, переменного числа взаимодействующих частиц (атомов, молекул, ионов).
Минимальное число членов образующих группу равно двум. Верхняя граница размыта и неотчетлива. Но ясно, что она должна находиться в той же области, где добавление еще одного члена уже не изменит свойств кластера: в этой области заканчивается переход из количества в качество. Ниже мы увидим, что эта граница не вполне однозначна, но практически большая часть изменений, существенных для химика, заканчивается при103 частицах в группе. Следует различать свободные кластеры и стабилизированные теми или иными факторами в последнем случае кластер имеет более сложный состав и приобретает структуру, в которой целесообразно выделять «тело» кластера (т. е. группу взаимодействующих частиц рассматриваемого типа) и стабилизирующие элементы, например «оболочку» из лигандов, или центральную частицу (часто это ион), или совокупность того и другого.
Разнообразие типов кластеров определяется возможностью сочетания различных сред и способов стабилизации с множеством вариантов построения тела кластера из частиц той или иной природы.
Отвлекаясь от «частностей», можно усмотреть лишь два общих пути образования кластеров — агрегация в кластер одиночных («мономерных») частиц или кластеров меньшего размера и дезагрегация до кластеров больших коллективов взаимодействующих частиц.
В качестве примера приведем малоизвестный случай металлических кластеров — продуктов взаимодействия твердых поверхностей с растворами металлов (наиболее известный пример подобных растворов— серебряная вода). В объеме раствора металлические кластеры не обнаруживаются; они возникают и стабилизируются только благодаря адсорбции на поверхности.
Ультрадисперсное состояние вещества и металлов в частности, имеющих размер частиц менее 300 Å (<30 нм), занимает особое положение между индивидуально молекулой или атомом, с одной стороны, и веществом в компактном («обычном») состоянии, с другой. Его отличительными особенностями являются: 1-доля поверхностных атомов соизмерима с числом атомов внутренних; 2- соизмеримы и их энергии; 3-структура частицы отличается от структуры массивного вещества, например металла, часто отсутствует плотная упаковка, изменены расстояния и т.п.; 4- форма и структура носят ярко выраженный неравновесный характер, которые отвечают энергонасыщенным состояниям. Последнее обстоятельство может проявляться в значительном снижении т. пл., в выделении энергии в процессе хранения, причем в количествах достаточных для самопроизвольного спекания частиц или для их взаимодействия с матрицей, в которой они диспергированы, и т.д.
1. Металлические частицы с числом атомов от 3 до 12 (так называемые малые кластеры или малые металлические частицы)
Характерная особенность строения таких частиц состоит в том, что при формировании путем последовательного присоединения одиночных атомов наиболее плотными конфигурациями с минимальной энергией, отвечающими различному числу атомов, являются правильный треугольник, тетраэдр, тригональная бипирамида, тетрагональная бипирамида и т. п.
2. Частицы с числом атомов металлов от 13 до 150 (с размерами от 0,8 до 2 нм)
При числе атомов металла в частице меньше 13 реализуется только такая плотная упаковка, когда каждый атом является поверхностным. Начиная с N, равного 13, появляется возможность образования таких плотноупакованных структур, в которых внутрь полиэдра (например, икосаэдра) можно поместить атом металла так, что возникают два сорта атомов - внутренние и поверхностные; следовательно, максимальное отношение числа поверхностных атомов к внутренним равно 12. При N>150 и геометрии частицы, близкой к сферической, это отношение приближается к единице, Следовательно, рассматриваемая группа частиц характеризуется появлением внутренних атомов и первых слоев, но все еще значительным превышением числа поверхностных атомов.
3. Частицы с размерами от 2 до 10 нм
Здесь количество поверхностных и внутренних атомов сравнимо. Это наиболее интересная и наименее изученная область объектов. Именно в этой области наблюдаются основные аномалии физических свойств. Частицы таких размеров получают методом газофазной нуклеации паров металлов или стабилизацией в полимерных матрицах
4. Частицы с размерами от 10 до 30 нм
Это переходная область, где в Центре кластера появляется все большее число внутренних слоев, упаковка которых начинает соответствовать структуре данного компактного металла. По мере роста размеров частиц энергия упругой деформации растет пропорционально объему и в какой-то момент может превысить поверхностную энергию, ответственную за устойчивость икосаэдрических структур. В частицах возникает два типа упаковки атомов — внутренняя кристаллическая и внешняя икосаэдрическая, что неизбежно связано с возникновением внутренних пустот и упругих деформаций.
Увеличение размера кластера сопровождается определенной структурной перестройкой (своеобразным фазовым переходом), в результате которой постепенно стираются различия физических свойств кластера и компактного металла. Эти различия были вызваны высоким значением отношения поверхностной энергии в кластере к объемной; они прежде всего касаются изменения теплофизических свойств кластеров, Температура плавления и температура Дебая у малых частиц ниже, чем у массивного металла. Колебания поверхностных атомов в кластере происходят с большей амплитудой и меньшей частотой, чем вибрация атомов в объеме компактного образца; это обусловливает изменение колебательного спектра и увеличение теплоемкости кластера по сравнению с массивным образцом.
5. Нанолитография – метод получения наноструктур с контролируемыми размерными параметрами с помощью латексных субмикронных частиц.
Нанолитографией (литография на нанометровом масштабе) называется нанесение на подложку рисунка, один из размеров которого лежит в нанодиапазоне до 100 нм. Литографией в микроэлектронике называют различные методы микрогравировки диэлектрических, металлических и полупроводниковых слоев, используемых при изготовлении интегральных микросхем (ИМС). Основным методом в технологии ИМС в настоящее время является фотолитография - фотохимический метод микрогравировки. Кроме оптической литографии, в зависимости от источника излучения, используются рентгенолитография, электронолитография и ионолитография. Это лучевые и пучковые методы литографии.
Разрешающей способностью на практике в методе фотолитография подразумевается характеристика ширины amin линий в количестве N. Для проекционной системы разрешающая способность определяется дифракционным критерием Рэлея ( изображение двух близко расположенных точек видны раздельно)
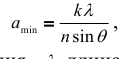
где k = 0,3 - 0,6 для УФ излучения, λ - длина волны излучения; n - показатель преломления, θ - половина апертурного угла выхода, n sin θ - числовая апертура.
При данной длине волны можно отобразить детали на поверхности фоторезиста размером до половины длины волны.
Нанолитография в дальнем экстремальном вакуумном ультрафиолете (ЭУФ).
Излучение (ЭУФ) лежит в диапазоне 10-50 нм, и граничит с мягким рентгеном 0,5-10 нм. Эта нанолитография предназначена для изготовления микропроцессорных интегральных микросхем сверхвысокого уровня интеграции до 108-1010 элементов на кристалле.
Принцип действия ЭУФ – нанолитографа основан на пошаговом экспонировании чипов при помощи проекционной отражательной оптической системы с последующим сканированием
Устройство состоит из 4 главных блоков:
1) Источник УФ излучения, который является ксеноновый лазер. При взаимодействии импульсного лазерного пучка с поверхностью мишени образуется облачко плазмы в 50-100 мкм.
2) Узел маски. Поверхность шаблона - плоское зеркало с брэгговским покрытием. На его поверхности наносится поглощающий слой вольфрама, таллия, хрома W,Ta,Cr , в котором гравируется увеличенный рисунок ИМС.
3) Оптическая система состоит из конденсора и объектива. Конденсор направляет излучение на шаблон. Объектив переносит уменьшенное изображение рисунка маски шаблона на поверхность пластины, покрытой резистом. Зеркала конденсора и объектива имеют расчетную кривизну и брэгговские покрытия, состоящие из нескольких десятков чередующихся слоев молибдена и кремния толщиной λ/4. Покрытия обеспечивают высокий коэффициент отражения, максимум которого достигается при длине волны 13,4 нм. 8-зеркальный промышленный ЭУФ-литограф сможет обеспечить апертуру 0,4 и разрешение 20 нм.
Образец с нанесенным резистом. Необходимы специальные резисты с высоким контрастом и чувствительностью.
Рентгенолитография позволяет достигать разрешения до 15 нм при использовании источника излучения с длиной волны 1 нм. Электронно-лучевая литография для построения рисунка использует пучок электронов. Это медленный последовательный процесс в отличии фотолитографии, в которой рисунок наносится сразу на всю поверхность.
6. Принципы и задачи стабилизации наночастиц различными молекулярными лигандами.
1) Обеспечить стабильность частиц и их существование в виде отдельных частиц при существовании низкомолекулярных ионов, например ионы Na+ и Cl-. Покрывая поверхность наночастиц лигандом (полимером), он должен соответствовать некоторым функциям таким как:
а) Нетоксичен
б) Биосовместим
в) Легко адсорбироваться на поверхности наночастицы
Если частица не защищена лигандом, то она может слипаться с другими наночастицами, образуя димер из двух наночастиц.
Если наночастица защищена лигандом, то работает стерический фактор стабилизацию Это означает, что один молекулярный слой одной частицы не может проникнуть в молекулярный слой другой частицы.
Т.к. низкомолекулярные ионы могут адсорбироваться на защищенную лигандом частицу, то наночастицы оказываются стабилизированными сразу по двум критериям - по стерическому и по электрическому, т.к. адсорбированные ионы на поверхности наночастицы эти ионы не могут снизить заряд наночастицы до нуля.
Функционализация - это способ придания частице определенной функции с помощью химической модификации поверхности.
Процесс функционализации включает несколько принципов:
а) Физический. Это адсорбция, силы Ван-Дер-Ваальса, электростатика
б) Химический. Он заключается в том, что проводится хим. реакция между стабилизирующим поверхность наночастицы лигандом и молекулой, которую хотим функционализировать. S-H группа хорошо связывается хим. связью с поверхностью золотой наночастицы. Сама SH присоединенная группа называется тиольной, а молекула с группой SH назывется тионильной.
В качестве примера можно рассмотреть стабилизацию наночастиц оксида цинка ( ZnO) полимерными молекулами этиленгликолями (ПЭГ), которые связываются с присутствующими на поверхности оксида цинка ионами ОН- через водородные связи.
Хотя оксид цинка считается достаточно безопасным материалом, проведенные различными группами ученый исследования показали, что наночастицы оксида цинка обладают токсическим действием по отношению к клеткам млекопитающих, бактерий, рыб и других классов животных и растений.
Результаты изучения биологической токсичности показало, что оксид цинка, полученный методом лазерной абляции в дистиллированной воде, обладает острым токсическим действием (2 класс опасности). Стабилизация наночастиц оксида цинка полиэтиленгликолем значительно уменьшает уровень токсичности до 4 класса. Данное явление можно объяснить процессами микрокапсулирования и закрытия активной поверхности наночастиц полимерными макромолекулами.
Таким образом, полученные в работе результаты свидетельствуют о том, что стабилизация наночастиц макромолекулами полимеров может служить эффективным методом пассивации активной поверхности наночастиц и уменьшения тем самым их биологической токсичности. Из результатов исследования сорбционной емкости можно заключить, что благодаря лиофильности поверхности наночастиц оксида цинка происходит связывание ОН- групп имеющегося на поверхности ZnO гидроксида цинка с функциональными группами полиэтиленгликоля через водородные связи.
7. Основные понятия теории рассеяния света: амплитудная матрица рассеяния, параметры Стокса, матрица Мюллера.
Изменение какой-либо характеристики потока оптического излучения при его взаимодействии с веществом называют рассеянием света.
Процесс рассеяния света (электромагнитных волн) состоит в заимствовании молекулой или частицей энергии у распространяющейся в среде электромагнитной волны и излучении этой энергии в телесный угол, вершиной которого является рассматриваемая частица. Молекула или частица физически одинаково рассеивает свет, однако механизм этого рассеяния зависит от размеров частицы.
В прозрачной однородной среде плоская волна распространяется только в одном направлении, не испытывая рассеяния в стороны. Такой результат сложения всех вторичных волн обусловлен их когерентностью. Когерентность - это согласованность нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.
С макроскопической точки зрения рассеяние света может быть обусловлено только неоднородностями среды. При слабых нарушениях однородности рассеянный в стороны свет составляет лишь малую долю первичного пучка.
Рассеяние света происходит и тогда, когда сами частицы имеют размеры, меньшие длины волны видимого света. Такие среды называют мутными. Основные закономерности рассеяния света в мутных средах были впервые экспериментально исследованы Дж. Тиндалем в 1869 г. Электромагнитная волна в среде определяется суперпозицией падающей и рассеянной волн электрического и магнитного полей. Для сплошной среды рассеяние по своему физическому содержанию сводится к дифракции волн на неоднородностях среды.
Физическая причина оптической неоднородности в идеально чистых средах была указана польским физиком М. Смолуховским в 1908 г. Из-за хаотического характера теплового движения молекул в среде возникают флуктуации плотности и, следовательно, флуктуации показателя преломления. Такой тип рассеяния света называют молекулярным. Флуктуации плотности - это отклонение ее от среднего значения. Такой тип рассеяния света называют молекулярным.
Упругое рассеяние, т.е. такое, при котором рассеянный свет характеризуется той же частотой, что и падающее излучение. Различают несколько типов рассеяния, при этом характер рассеяния зависит соотношения между длиной волны света λ и линейным размером частиц a .
1) Рэлеевское рассеяние – размеры частиц малы по сравнению с длиной волны: a ≤ λ/15. Это обычно рассеяние в мутных средах.
2) Если a > 1/15 λ – рассеяние Ми.
3) Рассеяние на оптических неоднородностях – здесь много различных случаев. Среди них, например, важный случай рассеяния на оптических неоднородностях, создаваемых звуковой волной. Т.е. под ее воздействием возникает гармоническое распределение оптической неоднородности. В результате наблюдается дифракция света на волне, при этом наблюдается изменение частоты дифрагированного света. Это – явление Мандельштама - Бриллюэна– напоминает (и является следствием) доплеровского изменения частоты при отражении от акустической волны.
4) Специфическое рассеяние – комбинационное рассеяние или Рамановское рассеяние, характеризуется изменением частоты рассеянного света по сравнению с частотой падающего. Это рассеяние носит квантовый характер.
5) Можно выделить многократное рассеяние – рассеяние в каждом из последовательных осуществляется по законам однократного рассеяния. Результат рассматривается как сумма результатов однократных рассеяний с учетом статистических характеристик их следования друг за другом.
Амплитудная матрица рассеяния

Параметры Стокса
Параметры Стокса — это набор величин, описывающих вектор поляризации электромагнитных волн, введенный в физику Дж. Стоксом в 1852 году[1]. Параметры Стокса являют собой альтернативу описанию некогерентного или частично поляризованного излучения в терминах полной интенсивности, степени поляризации и формы эллипса поляризации.
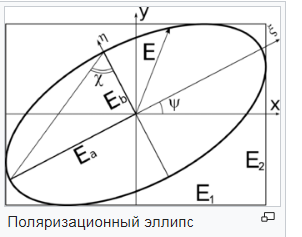
В случае плоской монохроматической волны параметры Стокса связаны с параметрами поляризационного эллипса следующим образом:
S0 = I = Ea2 + Eb2
S1 = Q = I cos 2Ψ cos 2χ
S2 = U = I sin 2Ψ cos 2χ
S3 = V = I sin 2χ
Здесь Ea и Eb – большая и малая полуоси поляризационного эллипса, Ψ – угол поворота поляризационного эллипса относительно произвольной лабораторной системы координат – носит название азимута эллиптически поляризованного излучения, а угол χ, определяемый из условия отношения малой полуоси к большой tg χ = Eb / Ea – угол эллиптичности эллипса поляризации. Нетрудно заметить, что S1, S2, S3 являются проекциями S0 на некие координатные оси. В итоге независимыми являются всего три параметра Стокса, поскольку:
I2 = Q2 + U2 + V2

Физический смысл параметров Стокса, представляющих собой четыре действительных величины, следует из (1.10). Параметр S1 представляет собой интенсивность электромагнитной волны, которая определяется как сумма квадратов амплитуд волны двух взаимно ортогональных направлений:
Параметр S2 равен разности интенсивности двух компонент волны и может иметь любой знак в зависимости от соотношения между компонентами, характеризующими линейную поляризацию по направлениям хну.
Параметр S3 указывает на соотношение в волне между линейно-поляризованными компонентами по направлениям ±П/4.
Для S4 можно построить соотношение, аналогичное предыдущему, из компонент волны типа (Ех±iЕу), характеризуюших циркулярно поляризованные компоненты.
Параметры Стокса обладают рядом преимуществ. Это прежде всего то, что эти парметры являются измеряемыми величинами. Они могут быть выражены через соответствующие значения измеренных интенсивностей. Также преимущество практического применения вектора Стокса состоит в том, что есть возможность применения матричного формализма, который в выражении взаимодействия электромагнитной волны с веществом записывается через матрицу взаимодействия.
Параметры Стокса можно связать с величинами, непосредственно измеряемыми. Пусть E1 и E2 – амплитуды изменения вектора E в двух произвольных ортогональных направлениях, а δ – разность фаз колебаний в этих направлениях. Тогда:
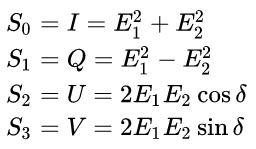
Матрица Мюллера
Матрица Мюллера (матрица рассеяния, поляризационная матрица или фазовая матрица) — математический оператор в теории рассеяния света, разработанный американским физиком Гансом Мюллером. Введен для описания взаимодействия произвольно поляризованного электромагнитного излучения, заданного вектором Стокса с рассеивающим объектом, поверхностью или элементом среды. Представляет собой матрицу с размерностью 4×4, которая преобразует вектор Стокса падающего света в вектор-параметр Стокса рассеянного излучения.
8. Основные интегральные характеристики: сечения и коэффициенты (факторы эффективности) рассеяния, поглощения и ослабления.
После решения математической задачи теории Ми необходимо применить эти решения для для получения формул для физически измеряемых величин. Это интенсивность рассеянного излучения и парметры Стокса.
Под интенсивностью света принято принимать средний по времени вектор потока энергии электромагнитных волн оптического диапазона на единичную площадку, нормальную к направлению распространения, называемый в фотометрии облученностью и определяемый вектором Умова— Пойнтинга.
Интенсивность рассеянного излучения сложным образом зависит от угла рассеяния. Но при любой угловой зависимости появление рассеянного излучения происходит за счет убывания вектора падающей энергии в направлении распространения волн, т. е. за счет энергетического ослабления падающего излучения. Для количественной характеристики энергетического ослабления излучения вводятся понятия коэффициентов рассеяния и ослабления, а также поглощения (для поглощающих частиц).
стиц).
Коэффициентом рассеяния частиц σр называют отношение суммарного потока электромагнитной энергии, рассеянной во всех направлениях, к интенсивности падающего потока. Аналогично, коэффициент поглощения частицы σп — отношение со знаком минус полного потока энергии (падающей и рассеянной) через большую сферу вокруг частицы к интенсивности падающего потока. Учитывая единицы потока энергии (Вт) и интенсивности потока (Вт/м2), единицей коэффициента рассеяния (поглощения) частицей будет м2, т. е. площадь. Поэтому эти коэффициенты нередко называют эффективными сечениями рассеяния и поглощения.
Часто удобными являются безразмерные величины, представляющие собой отношение коэффициентов (сечений) рассеяния, поглощения или ослабления к геометрическому сечению частицы, которые называются соответственно факторами эффективности рассеяния или поглощения.
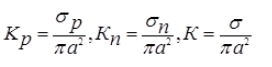
9. Дипольный момент шара. Поляризуемость маленького шара. Отличие оптических диэлектрических констант от электростатических.
Вводятся абсолютная εа и относительная εr диэлектрические проницаемости.
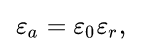
ε0 – электрическая постоянная. Величина εr– безразмерна, а εа – совпадает с ε0 фарад на метр Ф/ м.
Проницаемость εr показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме, для которого εr = 1.
Электри́ческий дипо́льный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ими поля и действия на неё внешних полей.
Простейшая система зарядов, имеющая определённый (не зависящий от выбора начала координат) ненулевой дипольный момент — диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда на расстояние между зарядами и направлен от отрицательного заряда к положительному, или:



10. Электромагнитное рассеяние диполя. Полное решение, ближнее поле, дальнее поле.
Электромагнитное излучение возникает во всех случаях, когда в пространстве создается переменное электромагнитное поле. В свою очередь электромагнитное поле будет изменяться во времени, если меняется распределение электрического заряда или является переменной плотность электрического тока.
Электрическим диполем является система, состоящая из неподвижного положительного заряда и совершающего около него колебание отрицательного заряда.
Если диполь излучает, отдавая при этом свою внутреннюю энергию, или, как это имеет место в антенне, превращая в энергию излучения энергию сторонних источников, то такой диполь можно назвать первичным излучателем. Однако, кроме подобных случаев, значительный интерес представляет и вторичное излучение, т.е. такое явление, при котором диполь приходит в колебание благодаря действию электромагнитной волны и становится излучателем лишь по этой причине.
Под действием электрической силы электронное облако смещается по отношению к атомным ядрам и молекула приобретает дипольный момент, меняющийся во времени с частотой падающей волны.
В ряде случаев явление вторичного излучения приводит к разнообразным явлениям рассеяния электромагнитных волн. Эффекты рассеяния электромагнитной волны одной молекулой становятся заметны при не слишком длинных падающих волнах.
Длина световой волны в сотни и тысячи раз превышает размеры обычных молекул. Поэтому все электроны молекулы приводятся внешним полем в колебание с одной той же фазой. Для световых волн, для ультрафиолетовых волн и даже для длинноволнового рентгеновского излучения молекула ведет себя, как элементарный электрический диполь.
Но картина существенно меняется, если речь идет о рентгеновском излучении с длиной волны порядка 1 А. Теперь уже размеры молекулы больше длины волны и различные участки электронного облака молекулы колеблются в разных фазах. Чтобы вычислить интенсивность рассеянной волны, нужно учесть явления интерференции, которые возникнут между волнами, рассеянными разными частями молекулы.
Если частичка мала по сравнению с длиной волны, то она будет рассеивать как один элементарный диполь. В противном случае возникнут интерференционные эффекты, а также будет превалировать рассеяние вперед.
Ближнее и Дальнее поле
Характеристики электромагнитного поля определяются:
- источником;
- окружающей его средой;
расстоянием от источника до точки наблюдения.
Вблизи источника свойства поля определяются в основном характеристиками источника. Вдали от источника свойства поля зависят, главным образом, от среды, в которой распространяется поле. Поэтому пространство, окружающее источник, можно разделить на две области: рядом с источником расположено ближнее, или индуктивное, поле. На расстоянии, превышающем
λ/2p, располагается дальнее поле, или поле излучения. Область на расстоянии λ /2p является переходной между ближним и дальним полями.
Отношение напряженности электрического поля Е к напряженности магнитного поля Н представляет собой полное волновое сопротивление Zw. В дальнем поле это отношение равно полному характеристическому сопротивлению среды Z0. Например, для воздушного или свободного пространства (вакуума) Z0=Zw =377 Ом. В ближнем поле величина этого отношения определяется параметрами источника и расстоянием от него до рассматриваемой точки. Если в источнике генерируются большой ток и низкое напряжение, Е/Н<377Ом, и ближнее поле является в основном магнитным. И наоборот, если в источнике малый ток и высокое напряжение, Е/Н>377Ом, ив ближнем поле преобладает электрическая составляющая.
Для антенны в виде штыря или натянутого провода волновое сопротивление вблизи антенны велико, и преобладающим является электрическое поле. По мере увеличения расстояния интенсивность электрического поля падает, так как оно создает дополняющее его магнитное поле. В ближнем поле его электрическая составляющая затухает пропорционально (1/r)3, в то время как магнитная составляющая затухает пропорционально (1/r)2. Таким образом, полное волновое сопротивление с увеличением расстояния от штыревой антенны падает и асимптотически приближается к полному сопротивлению, которым обладает свободное пространство в дальнем поле.
Для поля, в котором преобладает магнитная составляющая (такое поле создает, например, антенна в виде кругового витка провода – петлевая антенна), полное волновое сопротивление вблизи антенны мало. С увеличением расстояния от антенны магнитное поле затухает пропорционально (1/r)3, а электрическое – пропорционально (1/r)2. Поэтому полное волновое сопротивление с расстоянием увеличивается и приближается на расстоянии от антенны λ/2p к значению характеристического сопротивления вакуума.
В дальнем поле как электрическая, так и магнитная составляющие поля затухают пропорционально 1/r.
В ближнем поле электрическое и магнитное поля необходимо рассматривать раздельно, поскольку отношение их напряженностей не является постоянным. Однако в дальнем поле эти составляющие взаимодействуют, образуя плоскую волну с полным сопротивлением 377 Ом, т. е. при рассмотрении плоских волн предполагается, что они соответствуют дальнему полю. При раздельном рассмотрении электрического и магнитного полей считается, что они соответствуют ближнему полю.
Интегральные сечение рассеяния и поглощения маленького шара в дипольном приближении.

Сечение рассеяние имеет размерность площади. Его смысл состоит в том, что из падающего потока рассеивается та часть, которая падает на площадь, равную сечению рассеяния.
Ослабление света ансамблем частиц. Закон Бугера. Пропускание и поглощение (экстинкция), связь между ними.




Однолучевой спектрофотометр. Двухлучевой спектрофотометр. Недостатки и преимущества каждой схемы.
В ключевое отличие между однолучевым и двухлучевым спектрофотометром заключается в том, что в однолучевом спектрофотометре все световые волны проходят через образец, тогда как в двухлучевом спектрофотометре луч света разделяется на две части, и только одна часть проходит через образец. Спектрофотометры - это аналитические инструменты, используемые для количественного определения аналитов в данном образце с помощью светового луча. Следовательно, этот метод измеряет поглощение света образцом.
Однолучевой спектрофотометр - это аналитический прибор, в котором все световые волны, исходящие от источника света, проходят через образец. Следовательно, измерения проводятся по интенсивности света до и после прохождения света через образец. Эти однолучевые спектрофотометры компактнее и оптически проще, чем двухлучевые спектрофотометры. К тому же эти инструменты дешевле.
Чувствительность обнаружения светового луча после того, как он проходит через образец, высока, поскольку он использует неразделенный световой луч (следовательно, повсюду присутствует высокая энергия). Однолучевые спектрофотометры доступны для анализа в видимом и ультрафиолетовом диапазонах длин волн.
Однолучевой спектрофотометр измеряет концентрацию аналита в образце путем измерения количества света, поглощенного этим аналитом. Здесь вступает в силу закон Бэра-Ламберта. Этот закон гласит, что концентрация аналита прямо пропорциональна оптической плотности.
Двухлучевой спектрофотометр - это аналитический прибор, в котором луч света, исходящий от источника света, разделяется на две части. Одна фракция действует как эталон (эталонный луч), в то время как другая часть проходит через образец (эталонный луч). В результате эталонный луч не проходит через образец.
Луч образца может измерять оптическую плотность образца. Эталонный луч может измерять поглощение (эталонный луч можно сравнить с эталонным лучом). Следовательно, поглощение - это отношение между пучком образца (после прохождения через образец) и опорным пучком. Спектрофотометр имеет монохроматор, который изолирует желаемые длины волн от светового луча. Перед переходом к монохроматору эталонный пучок и пучок образца рекомбинируют. Следовательно, это в равной степени позволяет избежать или компенсировать электронные и механические воздействия как на образец, так и на эталонный луч.

20. Метод динамического рассеяния света
Динамическое рассеяние света
(другие названия данного метода: фотонная корреляционная спектроскопия; квазиупругое рассеяние света)
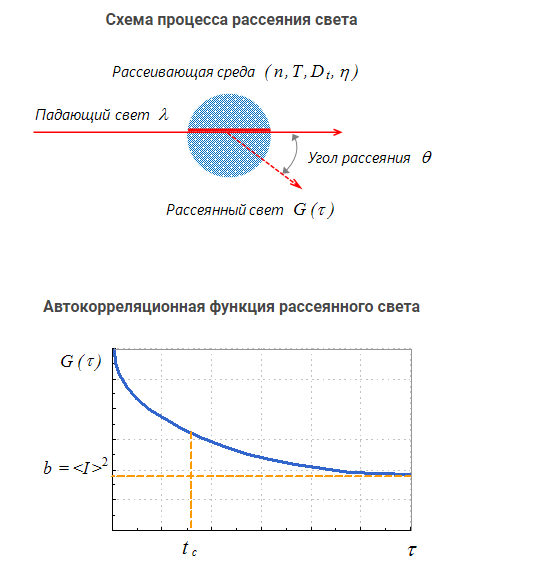
Для измерения размеров наночастиц используется метод динамического рассеяния света (ДРС). Данный метод позволяет определить коэффициент диффузии дисперсных частиц в жидкости путем анализа корреляционной функции флуктуаций интенсивности рассеянного света. Далее, из коэффициента диффузии рассчитывается радиус наночастиц.
Основные идеи метода динамического рассеяния света
Броуновское движение дисперсных частиц или макромолекул в жидкости приводит к флуктуациям локальной концентрации частиц. Результатом этого являются локальные неоднородности показателя преломления и соответственно - флуктуации интенсивности рассеянного света при прохождении лазерного луча через такую среду.
Коэффициент диффузии частиц обратно пропорционален характерному времени релаксации флуктуаций интенсивности рассеянного света. Это характерное время, в свою очередь, есть время затухания экспоненциальной временной корреляционной функции рассеянного света, которая измеряется с помощью цифрового коррелятора.
Размер частиц (гидродинамический радиус) рассчитывается по формуле Стокса-Эйнштейна, которая связывает размер частиц с их коэффициентом диффузии и вязкостью жидкости.
Метод динамического рассеяния света используется также для измерения скоростей потоков жидкостей и газов. Традиционно, этот вариант метода носит название лазерной доплеровской анемометрии (ЛДА). В частности, данная конфигурация метода ДРС используется для измерения электрофоретической подвижности наночастиц, откуда рассчитывается их дзета-потенциал.
В качестве примера рассмотрим диффузию монодисперсных наночастиц, диспергированных в жидкости. Хаотическое броуновское движение дисперсных частиц приводит к микроскопическим флуктуациям их локальной концентрации и соответствующим локальным неоднородностям показателя преломления среды. При прохождении лазерного луча через такую среду часть света будет рассеяна на этих неоднородностях. Флуктуации интенсивности рассеянного света будут соответствовать флуктуациям локальной концентрации дисперсных частиц. Информация о коэффициенте диффузии частиц содержится в зависящей от времени корреляционной функции флуктуаций интенсивности. Временная автокорреляционная функция согласно определению имеет следующий вид:
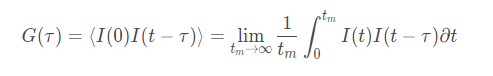
где интенсивность I имеет различные значения во время t и (t-τ). tm - это время интегрирования (время накопления корреляционной функции). Очевидно, что при τ = 0, автокорреляционная функция равна среднеквадратичной интенсивности рассеяния 2>. Для бесконечного времени корреляция отсутствует, и автокорреляционная функция равна квадрату средней интенсивности рассеяния:
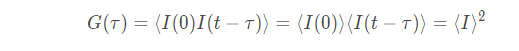
В соответствии с гипотезой Онзагера, релаксация микроскопических флуктуаций концентрации к равновесному состоянию может быть описана первым законом Фика (уравнением диффузии):
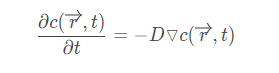
где c(r, t) - концентрация и D - коэффициент диффузии частиц. Можно показать, что в такой системе автокорреляционная функция интенсивности рассеяния света экспоненциально затухает во времени, и характерное время релаксации однозначно связано с D. Корреляционная функция интенсивности рассеянного света (для случая квадратичного детектирования) имеет вид:
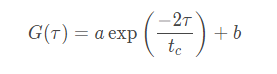
где в соответствии с решением уравнения диффузии обратное время корреляции равно
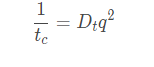
Волновой вектор флуктуаций концентрации описывается выражением:
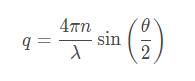
В выражениях 4-6: a и b - экспериментальные константы, n- показатель преломления жидкости, в которой взвешены дисперсные частицы,λ - длина волны лазерного света и θ - угол рассеяния.

 |
 Скачать 1.64 Mb.
Скачать 1.64 Mb.