Проверочная. Подготовка к проверочной работе. Все 4буквенные слова, составленные из букв М, А, Р, Т, записаны в алфавитном порядке

• Название: Все 4буквенные слова, составленные из букв М, А, Р, Т, записаны в алфавитном порядке
• Анкор: Проверочная
• Дата: 28.03.2022
• Размер: 0.74 Mb.
• Имя файла: Подготовка к проверочной работе.docx
• Тип: Документы; #423579

1. 
   Все 4-буквенные слова, составленные из букв М, А, Р, Т, записаны в алфавитном порядке.
   

 

Вот начало списка:

1. АААА

2. АААМ

3. АААР

4. АААТ

5. ААМА

……

Запишите слово, которое стоит на 250-м месте от начала списка.

Ответ: ТТРМ

2. 
   Все 4-буквенные слова, составленные из букв М, У, Х, А записаны в алфавитном порядке и пронумерованы.
   

 

Вот начало списка:

1. АААА

2. АААМ

3. АААУ

4. АААХ

5. ААМА

……

Запишите слово, которое стоит под номером 254.

Ответ: ХХХМ

3. 
   Все 5-буквенные слова, составленные из 5 букв А, К, Л, О, Ш, записаны в алфавитном порядке.
   

Вот начало списка:

1. ААААА

2. ААААК

3. ААААЛ

4. ААААО

5. ААААШ

6. АААКА

……


На каком месте от начала списка стоит слово ШКОЛА?

Ответ: 2711

4. 
   В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
   

Ответ: 6.

5. 
   Решите уравнение: 121_x + 1₁₀ = 101₇
   

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Ответ: 20.

6. 
   Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
   

1. Итак, нужно найти все целые числа   (цифра 4 присутствует в системах счисления только с таким основанием), такие что остаток от деления 31 на N равен 4, или (что то же самое)  , где k  — целое неотрицательное число (0, 1, 2, …);

 2. Из формулы   получаем  , так что задача сводится к тому, чтобы найти все делители числа 27, которые больше 4;

3. В этой задаче есть только два таких делителя:   и  .

 

Примечание.

Некоторые читатели могут подумать, что основанием системы счисления может быть также число 17, поскольку при записи числа 31 в этой системе количество единиц равно 14, то есть оканчивается на 4. Но число 14 в системе счисления с основанием 17 будет записано в виде буквы Е, следовательно, число 31 будет иметь вид 1Е.

7. 
   Сколько единиц содержится в двоичной записи значения выражения:
   

4²⁰²⁰ + 2²⁰¹⁷ – 15?

Преобразуем выражение:

 

Число 2⁴⁰⁴⁰ в двоичной записи записывается как единица и 4040 нулей. Добавив число 2²⁰¹⁷, получаем 100...00100...000 (единица, 2022 нулей, единица, 2017 нулей, всего 4041 разрядных цифр). Если вычесть из этого числа 2⁴ = 10000₂ и прибавить 2⁰, то число примет вид 100...001...10001. В полученном числе единица, 2023 нуля, 2013 единиц, три нуля и одна единица. Значит, всего в числе 2015 единиц.

 

Ответ: 2015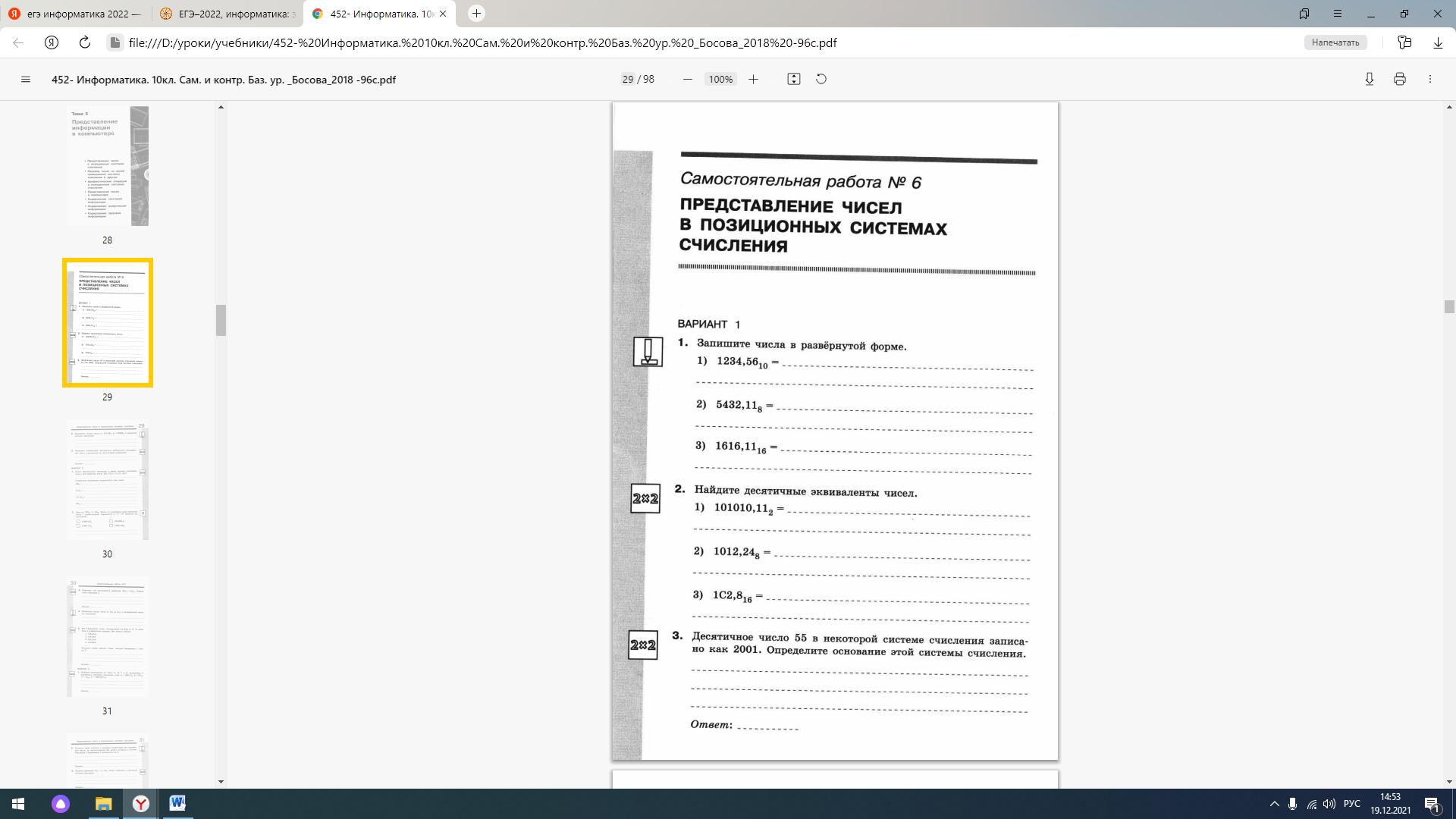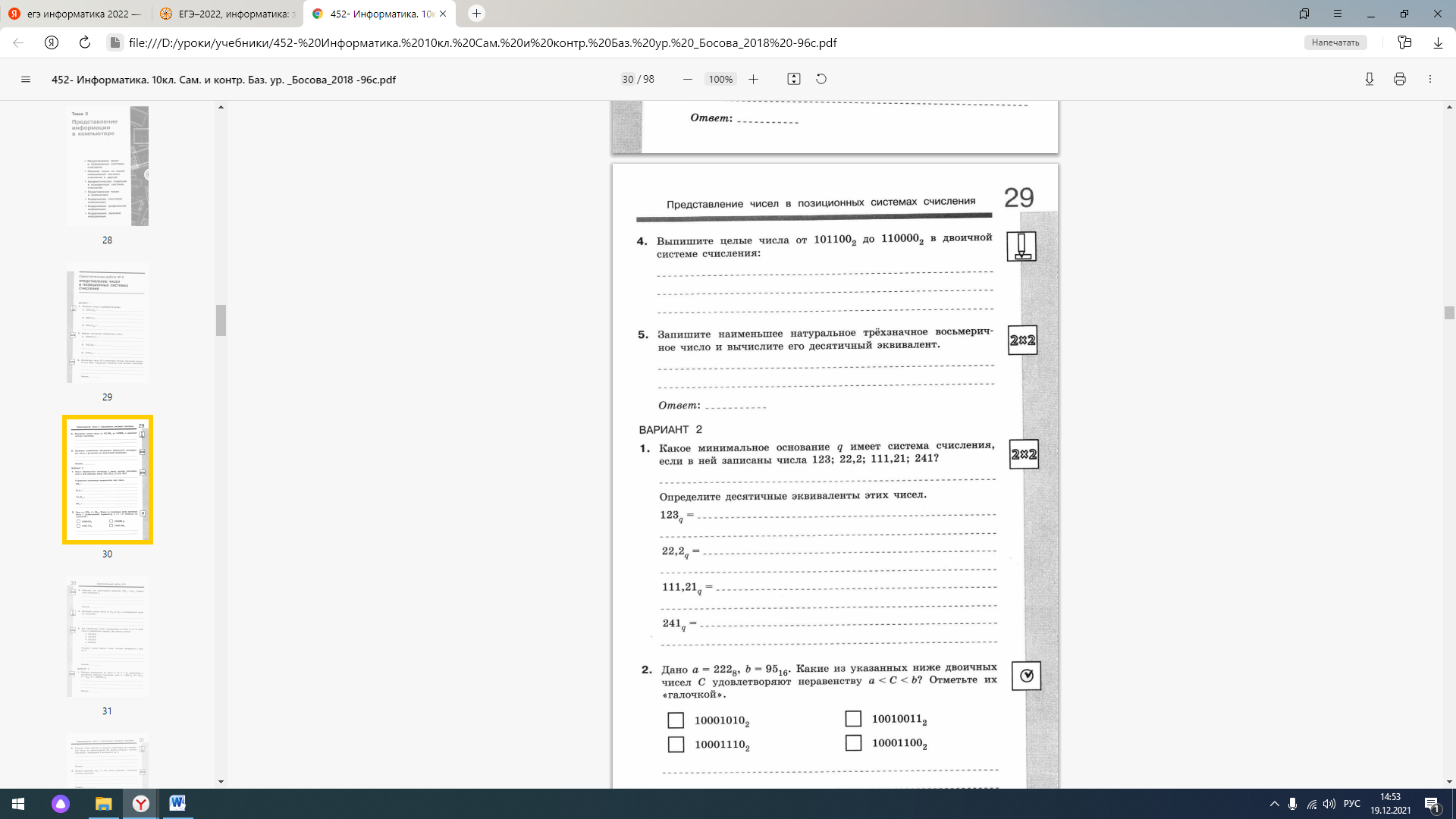