Производная сложной функции. Все табличные шаблоны применимы и в том случае, если икс заменить любой дифференцируемой функцией
 Скачать 44.15 Kb.
|
|
Пример 1.  Сначала находим производную внешней функции  (синуса), смотрим на таблицу производных элементарных функций и замечаем, что  . Все табличные шаблоны применимы и в том случае, если «икс» заменить любой дифференцируемой функцией  . В данном примере ВМЕСТО «икс» у нас  : Обратите внимание, что внутренняя функция  не изменилась, её мы не трогаем.Ну и совершенно очевидно, что  Результат применения формулы  в чистовом оформлении выглядит так: Далее мы берем производную внутренней функции, она очень простая:  Постоянный множитель обычно выносят в начало выражения:  Готово Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения. Пример 2 Найти производную функции  Это пример для самостоятельного решения . Пример 3 Найти производную функции  Как всегда записываем:  Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения  при  . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:  , значит, многочлен  – и есть внутренняя функция: И, только потом выполняется возведение в степень 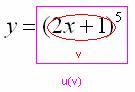 , следовательно, степенная функция – это внешняя функция: Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:  . Повторяем еще раз: любой табличный шаблон справедлив не только для «икс», но и для любой дифференцируемой функции . Таким образом, результат применения правила дифференцирования сложной функции следующий: Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется: Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:  Готово. Пример 4 Найти производную функции  Это пример для самостоятельного решения (ответ в конце урока). Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так? Пример 5 Найти производную функции  Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени  . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид: Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции : Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:  Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять). Пример 6 Найти производную функции  Это пример для самостоятельного решения . Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного  , но такое решение будет выглядеть Пример 7 Найти производную функции  Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции: Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель: 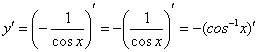 Косинус – внутренняя функция, возведение в степень – внешняя функция. Используем наше правило : Находим производную внутренней функции, косинус сбрасываем обратно вниз:  Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть. |