Ее. Введение в данной расчётнографической работе рассматриваются характеристики рекурсивных и нерекурсивных цепей. Также в этой работе рассматривается zпреобразование.

• Название: Введение в данной расчётнографической работе рассматриваются характеристики рекурсивных и нерекурсивных цепей. Также в этой работе рассматривается zпреобразование.
• Дата: 10.10.2022
• Размер: 0.78 Mb.
• Имя файла: kr_Raschet_kharakteristik_TsF_v.docx
• Тип: Документы; #725183

Введение
В данной расчётно-графической работе рассматриваются характеристики рекурсивных и нерекурсивных цепей. Также в этой работе рассматривается z-преобразование.

Изучение данных характеристик очень важно, так как это позволяет понять процесс оцифровки информации.

С помощью данной расчётно-графической работы мы также познакомимся с рекурсивными и нерекурсивными фильтрами.
Задание 1
1. Вычислить Z-преобразование дискретной последовательности отсчетов сигнала {x(n)}, согласно своему варианту.

2. Определить дискретную свертку {y(n)}, если импульсная характеристика системы имеет вид. Определить системную функцию H(Z).

3. Построить схему нерекурсивного фильтра, которому соответствует системная (передаточная) функция H(Z) и позволяющего получить рассчитанные выходные отсчеты {y(n)}.

4. По заданному согласно своему варианту Z-преобразованию X(Z) определить отсчеты дискретного сигнала {x(n)}.

Исходные данные:

Var 1

x = {0, 1, 0, 0, 1, 1, 0, 0}

h = {2, 1, 2, 1, 1, 1}
Var 2

x = {1, 1, 0, 1, 1, 1, 0}

h = {3, 2, 1, 1, 1, 1, 1, 1, 1}
Var 3

x = {0, 1, 1, 1, 1, 0, 0, 1}

h = {3, 2, 2, 1, 1, 1, 1}
Var 4

x = {0, 1, 0, 0, 1, 1, 1, 0}

h = {2, 2, 2, 1, 1, 1, 1}
Var 5

x = {0, 1, 0, 0, 0, 1, 0}

h = {2, 1, 1, 1, 1, 1, 1}
Var 6

x = {1, 0, 0, 0, 1, 1, 0, 1}

h = {1, 2, 1, 1, 1, 1}
Var 7

x = {0, 0, 1, 0, 1, 0, 1, 1, 0, 1}

h = {1, 2, 2, 1, 1, 1, 1}
Var 8

x = {1, 0, 0, 1, 1, 1, 0}

h = {2, 2, 1, 1, 1, 1}

Var 9

x = {1, 0, 1, 1, 1, 0, 1}

h = {3, 1, 1, 1, 1, 1, 1}
Var 10

x = {1, 1, 0, 0, 1, 1, 0}

h = {1, 2, 2, 1, 1, 1}
Var 11

x = {0, 0, 0, 1, 1, 0, 1, 1}

h = {1, 2, 1, 1, 1, 1, 1, 1}
Var 12

x = {0, 0, 1, 1, 1, 0, 0, 0, 1, 0}

h = {1, 1, 1, 1, 1, 1, 1, 1, 1}
Var 13

x = {1, 0, 0, 0, 0, 0, 1, 0}

h = {2, 1, 1, 1, 1}
Var 14

x = {1, 0, 0, 0, 0, 1, 1, 1, 1, 0}

h = {3, 2, 1, 2, 1, 1, 1, 1, 1}
Var 15

x = {1, 0, 1, 1, 1, 0, 1, 1, 0, 0}

h = {2, 1, 2, 1, 1, 1, 1}
Var 16

x = {0, 1, 1, 1, 0, 0, 1}

h = {3, 2, 1, 2, 1, 1, 1, 1}

Var 17

x = {1, 1, 0, 1, 0, 0, 1, 1}

h = {1, 2, 2, 1, 1, 1, 1, 1, 1}
Var 18

x = {0, 0, 0, 1, 0, 0, 0}

h = {1, 2, 1, 1, 1}
Var 19

x = {1, 1, 0, 0, 0, 0, 1, 0}

h = {3, 1, 1, 2, 1, 1, 1, 1, 1}
Var 20

x = {1, 1, 0, 0, 0, 1, 1, 1, 1}

h = {2, 2, 1, 1, 1}
Var 21

x = {1, 0, 1, 0, 0, 0, 0, 0, 0, 0}

h = {3, 2, 2, 2, 1, 1, 1, 1, 1}
Var 22

x = {0, 1, 0, 1, 1, 1, 1, 1, 0, 0}

h = {2, 1, 2, 1, 1, 1, 1}
Var 23

x = {0, 0, 0, 0, 0, 0, 0}

h = {2, 1, 1, 1, 1, 1, 1}
Var 24

x = {0, 0, 0, 1, 0, 1, 0, 1}

h = {1, 1, 1, 1, 1}


Var 25

x = {0, 0, 0, 1, 0, 0, 1, 1, 1, 0}

h = {1, 1, 1, 2, 1, 1, 1, 1}
Var 26

x = {0, 1, 1, 1, 1, 0, 1, 1}

h = {2, 1, 2, 1, 1, 1, 1, 1}
Var 27

x = {1, 1, 1, 1, 1, 1, 0, 0, 0, 0}

h = {1, 1, 1, 1, 1, 1, 1, 1}
Var 28

x = {1, 1, 1, 1, 0, 0, 1, 1, 1}

h = {2, 1, 1, 1, 1}
Var 29

x = {1, 0, 1, 0, 0, 0, 1, 1, 0}

h = {1, 1, 1, 1, 1, 1, 1, 1, 1}
Var 30

x = {1, 0, 0, 0, 0, 1, 1}

h = {3, 1, 2, 1, 1, 1, 1, 1}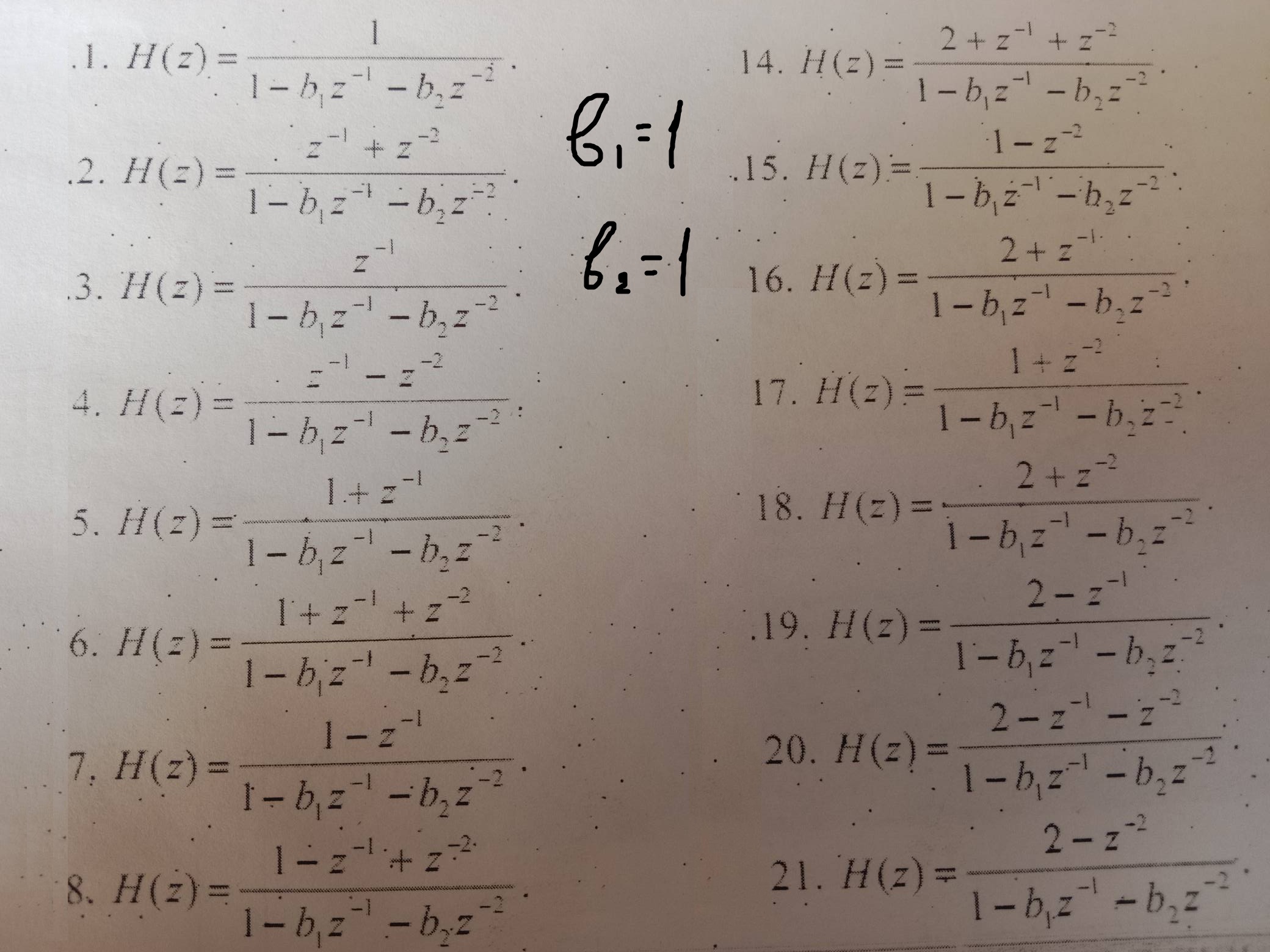

Выполнение задания

1) Вычислим Z-преобразование дискретной последовательности {x(n)}. Для этого воспользуемся следующей формулой: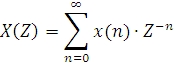



В результате получим:



) Теперь найдём дискретную свёртку {y(n)} с помощью импульсной характеристики {h(m)}. Она находится по формуле: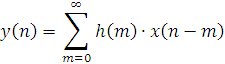

Получаем:

n
0	y(0)=h(0)*x(0)+h(1)*x(-1)+…=1*1=1
1	y(1)=h(0)*x(1)+h(1)*x(0)+…=1*1+2*1=1+2=3
2	y(2)=h(0)*x(2)+h(1)*x(1)+h(2)*x(0)+…=1*0+2*1+2*1=4
3	y(3)=h(0)*x(3)+h(1)*x(2)+h(2)*x(1)+h(3)*x(0)=1*0+2*0+2*1+3*1=5
4	y(4)=h(0)*x(4)+h(1)*x(3)+h(2)*x(2)+h(3)*x(1)+h(4)*x(0)+…=1*1+2*0+2*0+3*1+1*1=1+3+1=5
5	y(5)=h(0)*x(5)+h(1)*x(4)+h(2)*x(3)+h(3)*x(2)+h(4)*x(1)+h(5)*x(0)=1*0+2*1+2*0+3*0+1*1+0=2+1=3
6	y(6)=h(0)*x(6)+h(1)*x(5)+h(2)*x(4)+h(3)*x(3)+h(4)*x(2)+h(5)*x(1)+h(6)*x(0)=0+2*0+2*1+3*0+1*0+0+0=2
7	y(7)=h(0)*x(7)+h(1)*x(6)+h(2)*x(5)+h(3)*x(4)+h(4)*x(3)+h(5)*x(2)+h(6)*x(1)+h(7)*x(0)=0+0+0+3*1+0+0+0+0=3
8	y(8)=h(0)*x(8)+h(1)*x(7)+h(2)*x(6)+h(3)*x(5)+h(4)*x(4)+h(5)*x(3)+h(6)*x(2)+h(7)*x(1)+h(8)*x(0)=0+0+0+0+1*1+0+0+0=1
9	y(9)=h(0)*x(9)+h(1)*x(8)+h(2)*x(7)+h(3)*x(6)+h(4)*x(5)+h(5)*x(4)+h(6)*x(3)+h(7)*x(2)+h(8)*x(1)+h(9)*x(0)=0

{y(n)}={1,3,4,5,5,3,2,3,1,0}


Рисунок 1 - Дискретная свёртка {y(n)}



Рисунок 2 - Дискретная последовательность отсчётов сигнала {x(n)}


Рисунок 3 - Импульсная характеристика {h(m)}

Теперь определим системную функцию H(Z). Её можно определить двумя способами:

или

Найдём системную функцию по первой формуле, так как импульсная характеристика нам уже известна: {h(m)}={1,2,2,3,1}

Получим: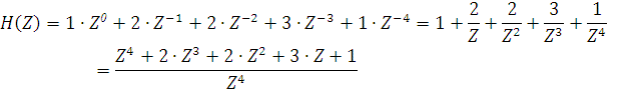



3) Построим схему нерекурсивного фильтра, которая соответствует системной функции H(Z).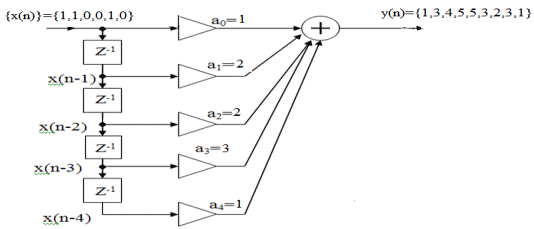



Рисунок 4 - Структурная схема нерекурсивного цифрового фильтра.

Данный фильтр является КИХ-фильтром и реализуется на основе алгоритма:



где - а₀, а₁, …а_m действительные постоянные («весовые») коэффициенты; m - порядок нерекурсивного фильтра, т.е. максимальное число запоминаемых чисел.

По заданному преобразованию X(Z) определим отсчёты дискретного сигнала {x(n)}. Для этого сначала разобьём наше z-преобразование на простейшие дроби:







Получаем: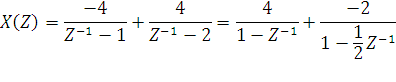



Имея следующие формулы: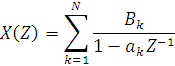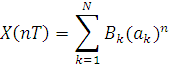







Найденные отсчеты:

{x(n)}={2; 3; 3,5; 3,75; 3,875…}

10Задание 2
1. Определить передаточную характеристику передаточную (системную) функцию рекурсивного ЦФ.

Коэффициенты числителя « » и знаменателя « » определяются согласно своему варианту.
2. Разработать структурную схему рекурсивного фильтра, реализующую полученную передаточную функцию (прямую, каноническую и транспонированную реализации).

3. Рассчитать первые три отсчета импульсной характеристики фильтра {h(n)}, полученные при прохождении через разработанный фильтр сигнала {x(k)}={1,0,0}.
Исходныеданные

Var 1

a0=3, a1=1, a2=2, a3=2, a4=1, a5=1, a6=1

b1=2, b2=2, b3=2, b4=1, b5=1, b6=1
Var 2

a0=2, a1=2, a2=1, a3=1, a4=1

b1=2, b2=2, b3=1, b4=1, b5=1
Var 3

a0=3, a1=1, a2=2, a3=1, a4=1

b1=1, b2=1, b3=1, b4=1, b5=1
Var 4

a0=2, a1=3, a2=2, a3=1, a4=1, a5=1, a6=1

b1=2, b2=2, b3=1, b4=1, b5=1
Var 5

a0=2, a1=2, a2=2, a3=2, a4=1, a5=1

b1=2, b2=2, b3=2, b4=1, b5=1, b6=1
Var 6

a0=2, a1=1, a2=1, a3=2, a4=1, a5=1

b1=1, b2=2, b3=2, b4=1, b5=1, b6=1, b7=1
Var 7

a0=2, a1=2, a2=1, a3=1, a4=1, a5=1

b1=2, b2=1, b3=1, b4=1, b5=1, b6=1
Var 8

a0=3, a1=1, a2=2, a3=1, a4=1, a5=1

b1=3, b2=2, b3=2, b4=1, b5=1, b6=1, b7=1

Var 9

a0=1, a1=2, a2=1, a3=2, a4=1, a5=1

b1=2, b2=2, b3=2, b4=1, b5=1, b6=1, b7=1
Var 10

a0=2, a1=1, a2=1, a3=1, a4=1

b1=1, b2=1, b3=1, b4=1, b5=1, b6=1, b7=1
Var 11

a0=1, a1=1, a2=1, a3=2, a4=1, a5=1

b1=2, b2=1, b3=1, b4=1, b5=1, b6=1
Var 12

a0=1, a1=1, a2=2, a3=2, a4=1, a5=1

b1=2, b2=1, b3=1, b4=1, b5=1
Var 13

a0=1, a1=2, a2=2, a3=2, a4=1, a5=1

b1=1, b2=2, b3=2, b4=1, b5=1, b6=1
Var 14

a0=3, a1=1, a2=2, a3=1, a4=1

b1=2, b2=2, b3=1, b4=1, b5=1, b6=1, b7=1
Var 15

a0=2, a1=2, a2=2, a3=1, a4=1

b1=3, b2=2, b3=1, b4=1, b5=1, b6=1, b7=1
Var 16

a0=3, a1=1, a2=2, a3=2, a4=1, a5=1

b1=1, b2=2, b3=1, b4=1, b5=1, b6=1

Var 17

a0=3, a1=3, a2=1, a3=1, a4=1, a5=1, a6=1

b1=1, b2=1, b3=1, b4=1, b5=1
Var 18

a0=1, a1=1, a2=2, a3=1, a4=1, a5=1

b1=2, b2=2, b3=1, b4=1, b5=1, b6=1, b7=1
Var 19

a0=2, a1=1, a2=2, a3=2, a4=1, a5=1, a6=1

b1=2, b2=2, b3=1, b4=1, b5=1, b6=1
Var 20

a0=3, a1=2, a2=2, a3=1, a4=1, a5=1

b1=2, b2=2, b3=1, b4=1, b5=1
Var 21

a0=3, a1=2, a2=2, a3=1, a4=1

b1=1, b2=1, b3=2, b4=1, b5=1, b6=1
Var 22

a0=1, a1=2, a2=2, a3=1, a4=1, a5=1

b1=1, b2=1, b3=1, b4=1, b5=1
Var 23

a0=2, a1=1, a2=1, a3=1, a4=1

b1=2, b2=1, b3=1, b4=1, b5=1
Var 24

a0=2, a1=1, a2=2, a3=1, a4=1, a5=1, a6=1

b1=1, b2=1, b3=2, b4=1, b5=1, b6=1
Var 25

a0=1, a1=1, a2=2, a3=1, a4=1, a5=1

b1=2, b2=1, b3=2, b4=1, b5=1, b6=1
Var 26

a0=3, a1=2, a2=1, a3=1, a4=1, a5=1

b1=2, b2=1, b3=2, b4=1, b5=1, b6=1
Var 27

a0=3, a1=3, a2=1, a3=2, a4=1, a5=1, a6=1

b1=1, b2=1, b3=1, b4=1, b5=1
Var 28

a0=1, a1=2, a2=1, a3=1, a4=1

b1=2, b2=1, b3=1, b4=1, b5=1, b6=1
Var 29

a0=3, a1=1, a2=1, a3=1, a4=1, a5=1

b1=1, b2=1, b3=1, b4=1, b5=1, b6=1
Var 30

a0=1, a1=1, a2=1, a3=1, a4=1, a5=1

b1=1, b2=1, b3=1, b4=1, b5=1

Выполнение задания

1) Найдём передаточную функцию по следующей формуле:

в результате получим:
_H (Z) =
) Разработаем структурную схему рекурсивного фильтра, реализующего данную передаточную функцию.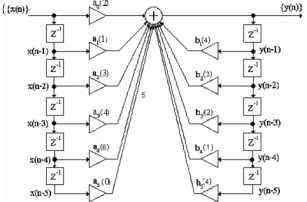


Рисунок 5 - Прямая структура рекурсивного фильтра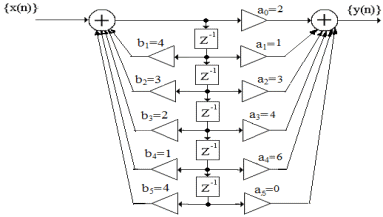


Рисунок 6 - Прямая каноническая структура рекурсивного фильтра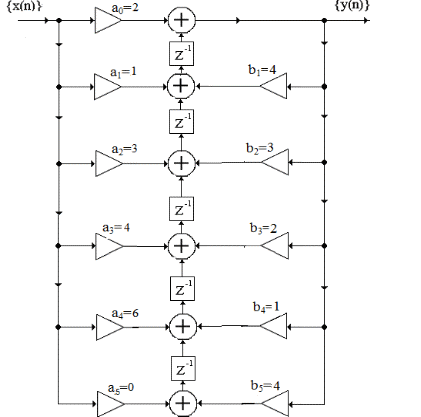


Рисунок 7 - Транспонированная структура рекурсивного фильтра
) Рассчитаем первые три отсчета импульсной характеристики фильтра.

Импульсная характеристика рекурсивного фильтра рассчитывается значительно сложнее, чем нерекурсивного. Рассмотрим формирование нескольких первых ее отсчетов.

На вход поступает единичный импульс, умножается на a₀ и проходит на выход. Получим

Далее входной единичный импульс попадает на входную линию задержки, а выходной отсчет а₀ - в выходную линию задержки. В результате второй отсчет импульсной характеристики будет формироваться как

Если продолжить рассмотрение перемещения входного единичного импульса вдоль входной линии задержки и заполнения выходными отсчетами выходной линии задержки, можно получить

В итоге получаем:

{h(n)}={2,9,45,…}
Заключение
В данной расчётно-графической работе мы рассмотрели рекурсивные и нерекурсивные цепи, а также рассмотрели их характеристики.

Также мы научились переходить от обычной дискретной записи в z-преобразование.

При изучении аналоговых сигналов и линейных аналоговых цепей введение преобразования Лапласа оказалось очень полезной. На его основе определяются такие фундаментальные понятия, как передаточная функция, частотных характеристики, устойчивость цепей и т.д. В цифровой обработке сигналов подобным преобразование является Z - преобразование. Оно позволяет упростить многие формулы, определить основные фундаментальные понятия и оказывается очень наглядной и удобной формой представления процессов, протекающие при цифровой обработке.
Список использованной литературы

дискретный свертка нерекурсивный фильтр

1) Солонина А.И., Улахович Д.А. и другие. Основы цифровой обработки сигналов. - С-П. «БХВ-Петербург», 2003. - 608 с.

) Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 2003. - 462 с.

) Карамов З.С., Колесниченко Г.И. Цифровая обработка сигналов: Учебное пособие/ МИС. - М.: 1990. - 41 с.

) Нефедов В.И. Основы радиоэлектроники и связи. - М.: Высшая школа, 2002. - 510 с.

) Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. - СПб., 1999. - 592 с.