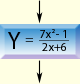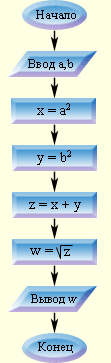Языки программирования низкого и высокого уровня. Классификация алгоритмических языков. Языки программирования низкого и высокого уровня. Классификация. Введение язык программирования
 Скачать 348 Kb. Скачать 348 Kb.
|
|
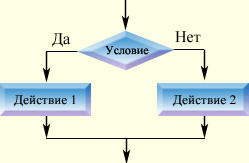
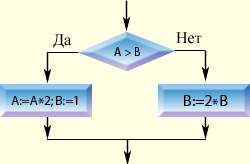
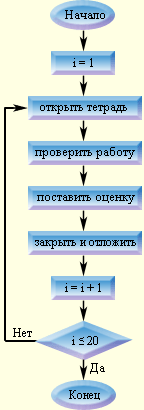
Понятие об алгоритме Алгоритм - это одно из самых широких понятий математики и информатики. Более 1000 лет назад в Багдаде, крупном научном центре Востока, жил абд Джафар Мужамед ибн Муса Аль-Хорезми. Ему принадлежит книга по математике, которая в течение нескольких столетий пользовалась широкой популярностью. В ней Аль-Хорезми сформулировал правила выполнения четырёх арифметических действий над многозначными числами. При переводе на латынь имя автора переделали в Algorithmi (Алгоритми). В книге Аль-Хорезми приводились методы решения разных задач. Ссылаясь на них, европейцы упоминали: "Так говорил Алгоритми..." Со временем методы решения задач стали называться алгоритмами. В дальнейшем алгоритмом стали называть описание любой последовательности действий, которую следует выполнить для решения задачи. Алгоритм – строго упорядоченная последовательность действий, направленная на выполнение поставленной задачи. В широком смысле алгоритмизация включает в себя выбор метода решения задачи. Результатом выполнения этапа алгоритмизации является алгоритм решения задачи. В повседневной жизни нам приходится часто пользоваться всевозможными алгоритмами. Например, алгоритм действий, необходимый для того, чтобы поговорить с кем-либо по телефону: узнать необходимый телефонный номер; поднять трубку; набрать номер; дождаться ответа абонента. Мы пользуемся подобными алгоритмами достаточно часто, поэтому выполняет их автоматически (не задумываясь). Алгоритмы, предназначены для выполнения компьютерами, обычно называются компьютерными программами, или просто программами. Программа содержит команды на языке, понятном компьютеру. Она сообщает компьютеру, как надо обрабатывать данные для получения желаемого результата. Все функции компьютера, любое его действие задается программой. Программа - это алгоритм, представленный на языке, понятном компьютеру. Разветвляющийся алгоритм Алгоритмы исполняют в естественном порядке: команда за командой (смотрите повторение). Однако жизнь весьма разнообразна. А цели все же хочется достичь. Вот и ученик, собираясь в школу, продумывает следующие действия: Если чувствует себя хорошо, то собирается в школу Иначе - остается дома. Заметим, что алгоритм требует либо одного действия, либо двух. А именно: вначале измерить температуру, а уж затем, в зависимости от результатов выполнять или не выполнять следующее действие. Такой алгоритм называется разветвляющимся, а именно: алгоритм, который выполняется в зависимости от условия, т.е. от вопроса на который можно ответить "да" или "нет", т.е. условие может быть истинным (да), или ложным (нет). Алгоритм ветвления, как и другие алгоритмы, должны обладать следующими свойствами: Дикретность, т.е. все решение разбивается на простейшие шаги. Понятность, алгоритм должен быть понятен исполнителю. Точность, не должно быть неясностей и двусмысленностей. Массовость, с помощью одного и того же алгоритма можно решить множество задач. Результативность (или конечность) состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов. Полная форма. Полная форма - это форма записи развлетвляющегося алгоритма, в которой предусмотрены команды в ветви "да" и в ветви "нет".
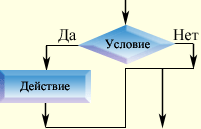
Происходит проверка условия. Если а>b, то происходит присваивание к переменной "а" значение "а*2", а к переменной "b", значение "1". Иначе, т.е. если а<=b, происходит присваивание переменной "b" значение "2*b". Неполная форма Неполная форма - это форма записи разветвляющегося алгоритма, в которой предусмотрены команды только в одной ветви.
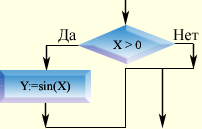
Происходит проверка условия. Если x>0, то переменной "y" присваивается значение "sin(x)" Иначе, т.е. если x<=0, то действия ветви "да" пропускаются. Разветвляющийся алгоритм можно записать несколькими способами: Словесный. В виде блок-схем (графический). На языке программирования. 1. Словесный способ Словесный способ записи разветвляющихся алгоритмов представляет собой описание последовательных этапов обработки данных. А алгоритм задается в произвольном изложении на естественном языке. Например: Задать два числа. Если числа равны, то взять любое из них в качестве ответа и остановиться, иначе продолжить выполнение алгоритма. Определить большее из чисел. Заменить большее из чисел разностью большего и меньшего из чисел. Повторить алгоритм с числа два. Словесный способ не имеет широкого распространения, т.к. такие описания: строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний. Машина поймет инструкцию, записанную на языке программирования, а человек наиболее ясно увидит ход решения задачи, если последовательность действий представлена на схеме. 2. Графический способ Графический способ представления разветвляющихся алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом представлении разветвляющийся алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. Блок-схемы и структурограммы Насси Шнейдермана-наиболее распространенные способы графического изображения алгоритмов.
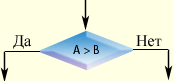
Блок "решение" используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет. Линейный алгоритм Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно. Например, алгоритм решения математической задачи: найдите гипотенузу, если известны катеты.
Циклический алгоритм Циклический алгоритм - это такой алгоритм, действия которого повторяются. Существует два типа циклических алгоритмов:
1. Циклический алгоритм типа "Для" Циклический алгоритм типа "Для" - это такой циклический алгоритм, в котором число повторений известно. Для организации циклов с известным числом повторений (типа "Для") используют оператор FOR - NEXT.
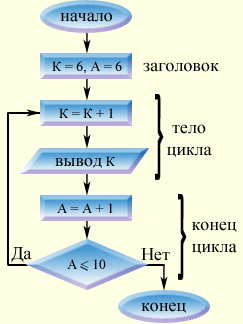
Любые арифметические выражения, не содержащие управляющей переменной (счетчика цикла), называют параметрами цикла. Например, запись: FOR A = 0 TO 12 STEP 2 означает, что управляющая переменная A (счетчик цикла) примет сначала значение 0 и при каждом повторении цикла будет увеличиваться на 2. Последним значением K будет 12. Если шаг равен 1, то часть STEP 1 в операторе можно опустить. Оператор FOR используется только в паре с оператором NEXT, который имеет вид: NEXT A, где A - имя управляющей переменной (счетчика) цикла. Операторы, которые требуется повторить многократно, записываются между FOR и NEXT и называются телом цикла. Чтобы организовать цикл с помощью оператора FOR, нужно: выделить тело цикла; выбрать управляющую переменную; определить границы ее изменения и шаг (параметры цикла); предусмотреть начальные присваивания (если это требуется). Рассмотрим применение оператора FOR - NEXT на следующем примере, где L (начальное значение счетчика цикла) = 1, R (конечное значение счетчика цикла) = 10:
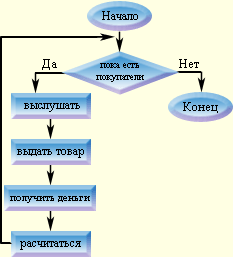
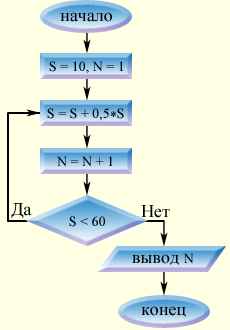
Работа оператора FOR - NEXT Счетчику присваивается первоначальное значение Выполняется тело цикла - операторы, которые повторяются Оператор NEXT выполняет 3 действия: Присваивает счетчику цикла новое значение Сравнивает полученное значение с конечным Если полученное значение меньше или равно конечному, то происходит возврат на начало тела цикла (на первый оператор после заголовка); если полученное значение больше конечного, то происходит выход из цикла 2. Циклический алгоритм типа "Пока" Циклический алгоритм типа "Пока" - это такой циклический алгоритм, действия которого будут выполнятся до тех пор пока выполняется заданное условие. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 50% от нормы предыдущего дня. Через сколько дней спортсмен пробежит суммарный путь 60 км?
Заключение Изобретение языка программирования высшего уровня позволило нам общаться с машиной, понимать её (если конечно Вам знаком используемый язык), как понимает американец немного знакомый с русским языком древнюю азбуку Кириллицы. Проще говоря, мы в нашем развитии науки программирования пока что с ЭВМ на ВЫ. Поверьте мне это не сарказм вы только посмотрите как развилась наука программирования с того времени, как появились языки программирования, а ведь язык программирования высшего уровня, судя по всему ещё младенец. Но если мы обратим внимание на темпы роста и развития новейших технологий в области программирования, то можно предположить, что в ближайшем будущем, человеческие познания в этой сфере, помогут произвести на свет языки, умеющие принимать, обрабатывать и передавать информации в виде мысли, слова, звука или жеста. Так и хочется назвать это детище компьютеризированного будущего: «языки программирования"высочайшего" уровня». Возможно, концепция решения этого вопроса проста, а ближайшее будущее этого проекта уже не за горами, и в этот момент, где-нибудь в Запорожье, Амстердаме, Токио или Иерусалиме, перед стареньким 133MHz горбится молодой, никем не признанный специалист и разрабатывает новейшую систему искусственного интеллекта, которая наконец-то позволит человеку, с помощью своих машинных языков, вести диалог с машиной на ТЫ. Размышляя над этим, хочется верить в прогресс науки и техники, в высоко - компьютеризированное будущее человечества, как единственного существа на планете, пусть и не использующего один, определенный разговорный язык, но способного так быстро прогрессировать и развивать свой интеллект, что и перехода от многоязыковой системы к всеобщему пониманию долго ждать не придется. Завершить свой труд хорошо бы на такой оптимистичной ноте, но нет, напоследок хочется процитировать человека, фрагменты работы которого, в виде информации о языке Си, вам уже попадались на страницах этого текста: Единственный способ изучать новый язык программирования – писать на нём программы. Список литературы Роберт У. Себеста. Основные концепции языков программирования Concepts of Programming Languages / Пер. с англ. — 5-е изд. — М.: 2001. Вольфенгаген В. Э. Конструкции языков программирования. Приёмы описания. — М.: Центр ЮрИнфоР, 2001. Паронджанов В. Д. Как улучшить работу ума. Алгоритмы без программистов — это очень просто!. — М.: Дело, 2001. Давидов М. И., Антонов В. Г. LEX - генератор программ лексического анализа / М. – 1985; Justin J. Crom / "BASIC Face-off", PC Tech Journal, September 1987. Перевод: Лопухов В.Н. Керниган Б. В., Д. Ритчи, А. Фьюэр. / Язык программирования Си. Русский перевод: Финансы и Статистика. М., 1985. Золотарев В. В. / Основы автоматизации, ч. 1, 1978. Ваулин А.С. / Языки программирования, кн. 5, 1993. Терренс П. / Языки программирования: разработка и реализация. 1979. Хротко Г. / Языки программирования высокого уровня. 1982. Малютин Э.А., Малютина Л.В. / Языки программирования. 1982. Ушкова В. / Новые языки программирования и тенденции их развития. 1982. Хьювенен Э., Сеппенен Й. / Мир Лиспа, т. 1, 1990. Янг С. / Алгоритмические языки реального времени 1985. |