Ямлеева. Ямлеева Э. У., доцент (Улгту ульяновск)

• Название: Ямлеева Э. У., доцент (Улгту ульяновск)
• Дата: 25.10.2022
• Размер: 199.45 Kb.
• Имя файла: Ямлеева.docx
• Тип: Документы; #754522

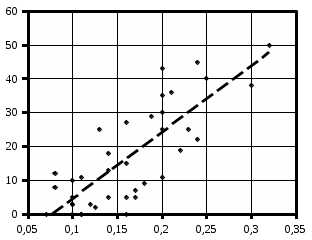
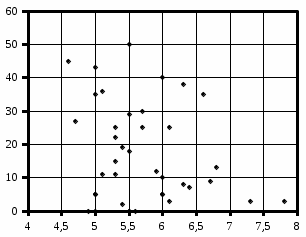
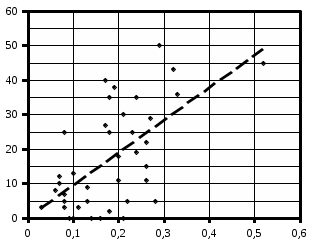
УДК 621.311.22

Теоретические и экспериментальные исследования процесса насыщения подпиточной воды кислородом

в баках-аккумуляторах ТЭЦ

Ямлеева Э.У., доцент (УлГТУ Ульяновск)

Основной причиной внутренней коррозии оборудования и трубопроводов водяных систем теплоснабжения является присутствие в сетевой воде растворенных коррозионно-активных газов (кислорода и диоксида углерода). На ТЭЦ и котельных традиционно уделяется большое внимание удалению коррозионно-агрессив­ных газов из воды, предназначенной для подпитки теплосети. Главным средством противокоррозионной обработки подпиточ­ной воды служит термическая деаэрация.

Однако практика эксплуатации систем централизованного теплоснабжения показывает, что во многих системах наблюдается большое количество по­вреждений, обусловленных внутренней коррозией, несмотря на качественную деаэрацию воды в соответствии с действующими нормативами.

При­чиной высокого уровня внутренней коррозии является повторное насыщение подпиточной и сетевой воды систем теплоснабжения кислородом О₂ и диоксидом углерода СО₂.

Основным источником попадания кислорода в подпиточную воду на ТЭЦ являются баки-аккумуляторы. Насыщение деаэрированной воды в баках-аккумуляторах кислородом происходит по открытой поверхности за счет диффузии [1].

Насыщение воды газами по закону молекулярной диффузии происходит очень медленно и толщина диффузионного слоя равняется нескольким миллиметрам. Однако если этот процесс сопровождается даже незначительным движением воды, тогда его интенсивность увеличивается многократно, а характер проникновения молекул газа в глубь воды определяется закономерностью ее движения, то есть имеет место конвективная диффузия.

При исследовании процесса насыщения подпиточной воды кислородом в период ее хранения в баке-аккумуляторе, когда в баке не происходит вынужденного движения воды, характерного для режима заполнения - опорожнения бака, предполагается, что вода движется в баке по закону естественной конвекции из-за разности плотностей, обусловленной разностью температур воды в объеме бака. Для подтверждения и выявления закономерностей движения воды в баке произведен расчет плоского температурного поля вертикального разреза бака-аккумулятора.

Результаты расчета температурного поля бака приведены рис.1.




Рис. 1. Результаты расчета температурного поля бака-аккумулятора
Расчет температурного поля бака-аккумулятора произведен при наружной температуре наиболее холодной пятидневки t_н= -31 ^оС и температуре воды t_воды= 80 ^оС. Бак-аккумулятор смонтирован по типовому проекту из листовой ста­ли толщиной δ = 4 ÷ 7 мм; коэффициент теплопроводности λ=58 Вт/м·К. Снаружи бак покрыт тепловой изоляцией толщиной δ=100 мм, состоящей из минеральной ваты (λ=0,06 Вт/м·К), связанной в маты, об­тянутой плетеной сеткой. Для защиты от атмосферных осадков бак-аккумулятор обшит алюминиевым листом (λ=221 Вт/м·К). Основание бака - слой песка, пропитанного мазутом, (λ=0,58 Вт/м·К) толщиной δ=20 мм, уложенный на грунт (λ=1,75 Вт/м·К).

По результатам расчетов установлено, что образование более нагретого основания под центральной частью днища бака и охлаждение поверхности жидкости паро-воздушной смесью создает устойчивое циркуляционное течение. Схема и эпюра конвективного движения воды в баке-аккумуляторе приведена на рис. 2.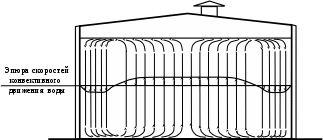

Рис. 2. Схема и эпюра конвективного движения воды в баке

Решение гидродинамической задачи конвективной диффузии в общем виде представляет большие трудности. Задача упрощается, если при хранении температура воды изменяется незначительно.

Для емкостей с жидкостью, хранящейся в условиях наружного воздуха, изменение температуры окружающей среды принимается с такой закономерностью [2]: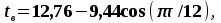

(1)

где τ – время, ч.

На основе баланса тепловых потерь получено дифференциальное уравнение:

(2)

где ; ; 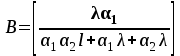V - объем воды, м³, ρ - плотность воды, кг/м³;c - теплоемкость воды, Дж/кг· ^оС ; α₁ - коэффициент теплоотдачи для жидкостной пленки, Вт/м²· ^оС; α₂ - коэффициент теплоотдачи от поверхности бака к воздуху, Вт/м²· ^оС; S - поверхность бака, м²; λ - теплопроводность изоляции, Вт/м· ^оС ; l- толщина изоляции, м; T- температура воды, ^оС.

В результате решения уравнения (2) получена формула для определения температуры воды после ее хранения в баке-аккумуляторе в течение τ часов: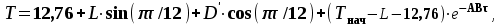

(3)

где 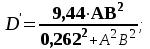T_нач- начальная температура воды.

В результате расчета доказано, что проектная тепловая изоляция бака в пределах нормируемого 10-ти часового режима хранения воды обеспечивает квазистационарные условия температурного поля. Для бака объемом 3000 м³ при начальной температуре T_нач=80 ^оС после 10 ч хранения температура воды составляет T=79,17 ^оС,

В целом перенос любой субстанции в жидкости описывается дифференциальным уравнением Фурье-Кирхгоффа: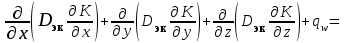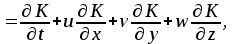



(4)

где D_эк – суммарный (эквивалентный) коэффициент диффузии, м²/с; К – концентрация вещества в единице объема, г/м³; q_w – выделение (или поглощение) данного вещества в единице объема воды, г/м³·с;u, v,w– проекции скоростей на оси х, у, z; τ – время.

На основе исследований переноса вещества в открытых водоемах, проведенных профессором Распопиным Г.А., исследовался процесс диффузии кислорода применительно к условиям эксплуатации баков-аккумуляторов [3, 4].

Дифференциальное уравнение конвективной диффузии кислорода в воде при одномерной задаче для квазистационарных условий 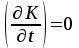записывается в виде

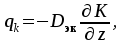(5)

где q_к – интенсивность конвективного переноса кислорода, г/м²·с; К – содержание кислорода, г/м³.

Знак минус показывает, что диффузионный поток частиц направлен от мест с большей концентрацией к местам с меньшей концентрацией.

Распределение D_экпо толще воды описывается зависимостью:

(6)

где D– коэффициент молекулярной диффузии, м²/с; η=z/H– относительное расстояние от дна.

Решение уравнения конвективной диффузии кислорода в воде бака-аккумулятора имеет вид:

(7)

где q_кп – поток кислорода через свободную поверхность, г/м²·с; а, к – коэффициенты; - динамическая скорость; τ_mах - касательное напряжение; 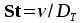- число Шмидта; К, К_д – содержание кислорода у поверхности воды и у дна соответственно, г/м³; D– коэффициент молекулярной диффузии, м²/с; Н – глубина, м.

Приведенные теоретические исследования относятся к режиму хранения воды в баках при неизменном уровне воды. Однако, в определенные периоды режим работы баков сопровождается интенсивным изменением уровня – это касается моментов заполнения-опорожнения баков. Массообмен в данных условиях зависит от очень большого числа факторов и математически описать его не возможно. По этому выполнено экспериментальное исследование процесса насыщения.

П олучена обширная выборка данных по изменению со­держания кислорода в подпиточной воде до и после баков-аккумуляторов на Ульяновской ТЭЦ-1 за три зимних месяца 2003-2004 гг. Содержание растворенного кислорода в подпи­точной воде достигало 150 и более мкг/дм³, несмотря на эф­фективную деаэрацию воды. В среднем содержание кислорода после деаэраторов составляло 10-30 мкг/дм³. На рис. 3 приведены данные за январь 2004 г.


Содержание кислорода, мкг/дм³


Рис. 7. Содержание кислорода в подпиточной воде в январе 2004 г.:

– содержание кислорода в подпиточной воде до баков-аккумуляторов;

– содержание кислорода в подпиточной воде после баков-аккумуляторов
Замеры производились три раза в сутки с помощью мало­габаритного анализатора растворенного кислорода МАРК-301Т.

Установлено, что насыщение кислородом деаэрированной подпиточной воды в баках-аккумуляторах наиболее интенсивно происходит в период их заполнени-опорожнения.

Для выявления факторов, оказывающих наибольшее влияние на величину насыщения воды кислородом, применен статистический метод корреляционного анализа [2, 5]. Показателем взаимосвязанности переменных величин служит коэффициент корреляции r, который варьируется от r=±1 при жест­кой линейной зависимости до r=0 при отсутствии взаимосвязи между переменными.

С помощью корреляционного анализа выявлена наибольшая связь между величиной насыщения и скоростью падения уровня в баке (коэффициент корреляции r=0,8). Зависимости насыщения от величины падения уровня (r=0,64) и падения уровня, отнесенного к уровню воды на момент замера (r=0,61), существуют, но менее выражены. Насыщение воды кислородом не зависит от уровня воды в баке на момент замера (r=0,3) (рис. 4).

ΔО_2,

мкг/дм³

ΔО_2,

мкг/дм³

r = 0,8


r = 0,64

Δh, м

Δh/τ, м/ч



ΔО_2,

мкг/дм³

ΔО_2,

мкг/дм³

б

а






r = 0,61





r = 0,3




∆h/h

h , м




в

г



Рис. 7. Насыщение подпиточной воды кислородом в баках-аккумуляторах в зависимости от: а – скорости падения уровня; б – величины падения уровня; в – величины падения уровня, отнесенной к уровню воды на момент замера; г – уровня воды в баках

Уровень воды в баке-аккумуляторе варьируется от 4,5 до 8 метров. При максимальном водоразборе уровень воды в баке не опускается ниже 4 метров, однако, несмотря на наличие слоя воды значительной толщины, насыщение имеет место. Полученные результаты исследований не подтверждают выводы [6, 7] о том, что коррозионно-агрессивными газами насыщает­ся лишь верхний слой воды в несколько сантиметров, а общая толща воды не подвергается заражению кислородом.

Приведенные теоретические и экспериментальные исследования описывающие процессы насыщения подпиточной воды кислородом в баках-аккумуляторах при режимах хранения и заполнения-опорожнения баков подтверждают необходимость при­менения средств защиты воды в них от повторного насыщения коррозионно-агрессивными газами.

Выводы

1. 
   Построением плоского температурного поля вертикального разреза бака-аккумулятора доказано наличие естественного конвекционного движения воды в нем, обусловленного изменением ее плотности по высоте бака в квазистационарном тепловом режиме его работы.
   
2. 
   Установлено, что образование более нагретого основания под центральной частью днища бака и охлаждение поверхности жидкости паро-воздушной смесью создает устойчивое циркуляционное течение.
   
3. 
   В результате теоретического расчетного исследования доказано, что проектная тепловая изоляция бака в пределах нормируемого 10-и часового режима хранения воды обеспечивает квазистационарные условия температурного поля.
   
4. 
   Получена математическая модель насыщения подпиточной воды кислородом в период хранения в баках-аккумуляторах ТЭЦ, происходящего по закону конвективной диффузии в квазистационарных температурных условиях.
   
5. 
   С помощью корреляционного анализа выявлена наибольшая связь между величиной насыщения и скоростью падения уровня в баке (коэффициент корреляции r=0,8). Зависимости насыщения от величины падения уровня (r=0,64) и падения уровня, отнесенного к уровню воды на момент замера (r=0,61), существуют, но менее выражены. Насыщение воды кислородом не зависит от уровня воды в баке на момент замера (r=0,3).
   

Список литературы

1. 
   Шарапов В.И., Ямлеева Э.У. Технологии защиты сетевой и подпиточной воды от аэрации. – М: Издательство «Новости теплоснабжения», 2012. – 176 с.
   
2. 
   Батунер Л.М., Позин М.Е. Математические методы в химической технике. Л.: Химия. 1971. 824 с.
   
3. 
   Распопин Г.А. Процессы переноса и диффузия кислорода в водной среде// Известия вузов. Строительство. 2003. № 3. С.132-137.
   
4. 
   Распопин Г.А., Ковалев Е.А. Расчет динамики речных потоков в нестационарных условиях// Метеорология и гидрология. 1981. № 10. С. 79-87.
   
5. 
   Езекиел М., Фокс К.А. Методы анализа корреляций и регрессий. М.: Статистика. 1966.
   
6. 
   Ефимов В.А., Туева А.А. Работа баков-аккумуляторов и качество воды// Электрические станции. 1967. № 5. С. 42-45.
   
7. 
   Курнык Л.Н. Исследование работы бака-аккумулятора под­питки теплосети// Энергетик. 1971. № 8. С. 21-23.