|
|
_Нақты сандар_ (8 сынып). за мерзімді жоспарды тарауы 4 Кні
Ұзақ мерзімді жоспардың тарауы: №4
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні: Манарбек Гүлсая
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Нақты сандар
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.1.1.1
иррационал және нақты сандар ұғымдарын меңгеру;
|
Сабақтың мақсаты
|
Барлық оқушылар:
Тақырыпты игере отырып, сендер екі өрнектің кубтарының қосындысы мен айырымының формулаларымен, екі өрнектің қосындысы мен айырымының толық емес квадратымен танысады; аталған формулаларды өрнектерді түрлендіру кезінде қолдануды үйренеді
|
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
. Натурал сандар деп санау үшін қолданылатын сандарды айтады .Натурал сандар жиынын латынның N әрпімен белгілеу келісілген. N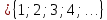 . .
Бүтін сандар деп барлық натурал сандар мен оларға қарама-қарсы сандар және 0 санынан тұратын жиынды айтады.Бүтін сандар жиынын Z әрпімен белгілеу келісілген. Z=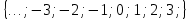 . .
Рационал сандар деп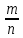 түріндегі жай бөлшекпен жазуға болатын сандарды айтамыз.Мұндағы m-бүтін сан, n- натурал сан. Рационал сандар жиынын Q әрпімен белгілеуге келісілген. Онда рационал сандар жиынын былай да көрсетуге Q= түріндегі жай бөлшекпен жазуға болатын сандарды айтамыз.Мұндағы m-бүтін сан, n- натурал сан. Рационал сандар жиынын Q әрпімен белгілеуге келісілген. Онда рационал сандар жиынын былай да көрсетуге Q=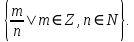
Мысалы:Q=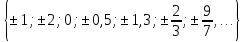
Шектеусіз периодсыз ондық бөлшектер иррационал сандар деп аталады, «ир» деген латынша кері ұғымды, яғни «иррационал» сөзі «рационал емес» деген мағынаны білдіреді.Иррационал сандарға түбірден шықпайтын,мысалы 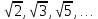 сандарымен қатар мектеп курсында бізге таныс сандарымен қатар мектеп курсында бізге таныс 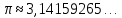 , e , e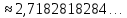 сандары да жатады. сандары да жатады.
Олай болса осы рационал сандар мен иррационал сандар жиыны мектеп курсындағы ең үлкен сандар жиыны болып табылатын нақты сандар жиынын құрайды. Нақты сандар жиынын латынның R әрпімен белгілеу қабылданған. Жиындардың арасындағы тиістілікті білдіретін сөйлемді былай жазып көрсетуге деN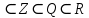 немесе Эйлер-Венн дөңгелектерімен де көрсетуге болады: немесе Эйлер-Венн дөңгелектерімен де көрсетуге болады:
|
көрсетуге болады:

R
RR
RRR

Q
 
N
Q
Z
Іс жүзінде квадрат түбірдің мәндері калькулятор көмегімен есептеледі.Ол үшін санды теріп,содан кейін « 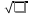 » белгісі бар батырманы басу жеткілікті.Сандардың квадрат түбірлері бүтін сан немесе шектеулі және шектеусіз ондық бөлшектер болуы мүмкін. Мысалы: » белгісі бар батырманы басу жеткілікті.Сандардың квадрат түбірлері бүтін сан немесе шектеулі және шектеусіз ондық бөлшектер болуы мүмкін. Мысалы: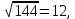
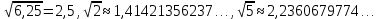 , , 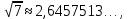
Мыса1. Калькулятордың көмегімен сандардың жуықтауларын табу:
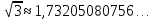
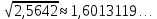
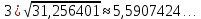
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Мысал2. Біздің заманымыздан 3000 жылдай бұрын Ежелгі Вавилон қолжазбаларында санның квадрат түбірін анықтауға арналған формула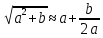 сақталынған. Осы формуланың көмегімен санның квадрат түбірін жуықтап анықтайық: сақталынған. Осы формуланың көмегімен санның квадрат түбірін жуықтап анықтайық:
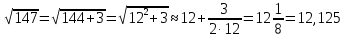
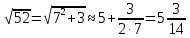 =5,21.. =5,21..
Сабақта орындалатын тапсырмалар:
.
|
№1. 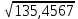 ; ;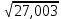 ; ; 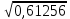 сандарының жуық мәндерін калькулятордың көмегімен анықтаңдар. сандарының жуық мәндерін калькулятордың көмегімен анықтаңдар.
№3.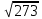 ; ; 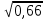 сандарының жуық мәндерін калькулятордың және квадрат түбірді табу формуласы көмегімен анықтаңдар. сандарының жуық мәндерін калькулятордың және квадрат түбірді табу формуласы көмегімен анықтаңдар.
№4. 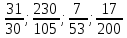 сандарын ондық бөлшек түрінде жазып ,қайсылары шектеулі.қайсылары шектеусіз ондық бөлшек екенін анықтаңдар. сандарын ондық бөлшек түрінде жазып ,қайсылары шектеулі.қайсылары шектеусіз ондық бөлшек екенін анықтаңдар.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақ соңы
|
Рефлексия
Бүгінгі сабақ қандай пәнмен байланысты болды?
Қандай қосымша жаңа сөздермен таныстыңыз?
Сабақтан қандай әсер алдыңыз?
Сабаққа бір ұсыныс.
|
Үй тапсырмасы:
№1. 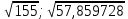 ; ; 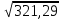 сандарының жуық мәндерін калькулятордың көмегімен анықтаңдар. сандарының жуық мәндерін калькулятордың көмегімен анықтаңдар.
№3.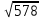 ; ; 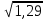 сандарының жуық мәндерін калькулятордың және квадрат түбірді табу формуласы көмегімен анықтаңдар. сандарының жуық мәндерін калькулятордың және квадрат түбірді табу формуласы көмегімен анықтаңдар.
№4. 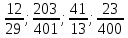 сандарын ондық бөлшек түрінде жазып ,қайсылары шектеулі.қайсылары шектеусіз ондық бөлшек екенін анықтаңдар. сандарын ондық бөлшек түрінде жазып ,қайсылары шектеулі.қайсылары шектеусіз ондық бөлшек екенін анықтаңдар.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақтың барысы
Ұзақ мерзімді жоспардың тарауы: №5
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні:
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Нақты сандар
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.1.1.1
иррационал және нақты сандар ұғымдарын меңгеру;
|
Сабақтың мақсаты
|
Барлық оқушылар:
Тақырыпты игере отырып, сендер екі өрнектің кубтарының қосындысы мен айырымының формулаларымен, екі өрнектің қосындысы мен айырымының толық емес квадратымен танысады; аталған формулаларды өрнектерді түрлендіру кезінде қолдануды үйренеді
|
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Санның бүтін бөлігідеп осы саннан артық емес ең үлкен бүтін санды айтады.
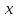 санының бүтін бөлігі санының бүтін бөлігі 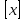 деп белгіленеді. Мысалы1: деп белгіленеді. Мысалы1:
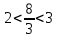 , демек , демек 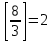 ; ;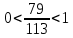 , демек , демек 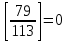 ; ;
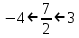 , демек , демек 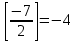 ; ;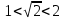 ,демек ,демек 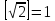 ; ;
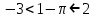 , демек , демек 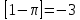 ; ;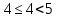 , демек , демек 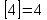 ; ;
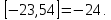
Санның бөлшек бөлігі деп берілген сан мен оның бүтін бөлігінің айырмасын айтады.
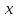 санының бөлшек бөлігі санының бөлшек бөлігі 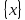 деп белгіленеді. деп белгіленеді.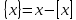 формуласымен есептейді. формуласымен есептейді.
|
Мысалы2: 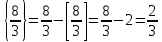 ; ;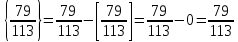 ; ;
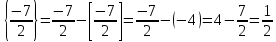 ; ;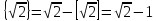 ; ;
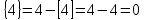 ; ; 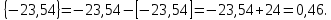
Мыса3. 1) 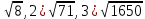 санынан кем ең үлкен натурал санды табу. санынан кем ең үлкен натурал санды табу.
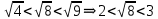 , демек , демек 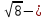 ден кіші ең үлкен натурал сан 2 ; ден кіші ең үлкен натурал сан 2 ;
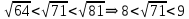 , демек , демек 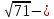 ден кіші ең үлкен натурал сан 8 ; ден кіші ең үлкен натурал сан 8 ;
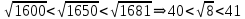 , демек , демек 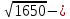 ден кіші ең үлкен натурал сан 40. ден кіші ең үлкен натурал сан 40.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Сан аралықтары және оларды теңсіздіктер арқылы өрнектеу
Теңсіздіктер
|
Аралықпен белгіленуі, атауы
|
Аралықтардың сан өсіндегі бейнесі
|
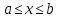
|
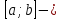 кесінді кесінді
|
   
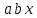
|
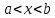
|
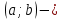 интервал интервал
|
   
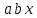
|
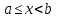
|
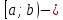 жартылай интервал жартылай интервал
|
   
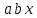
|
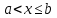
|
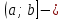 жартылай интервал жартылай интервал
|
   
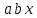
|
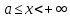
|
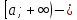 сәуле сәуле
|

  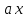
|
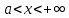
|
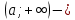 ашық сәуле ашық сәуле
|
  
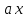
|
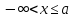
|
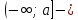 сәуле сәуле
|
  
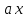
|
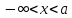
|
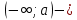 ашық сәуле ашық сәуле
|
  
|
.
|
Сан өсіндегі екі нүктенің арақашықтығы деп олардың координаталарының айырмасының модулін айтады. A(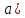 және B( және B(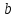 ) нүктелері берілсе, олардың арақашықтығы AB= ) нүктелері берілсе, олардың арақашықтығы AB=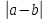 формуласымен есептеледі. Немесе сан өсіндегі орналасқан нүктелердің оң жақтағысының координатасынан сол жақтағының координатасын азайтуға да болады. формуласымен есептеледі. Немесе сан өсіндегі орналасқан нүктелердің оң жақтағысының координатасынан сол жақтағының координатасын азайтуға да болады.
Мысалы: A(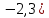 ; B( ; B(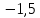 ) , AB= ) , AB=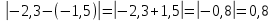
немесе AB=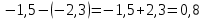
Сабақта орындалатын тапсырмалар:
№1. 1) 3,54; 2) 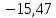 ; 3) ; 3) 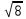 ; 4) ; 4) 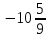 сандарының бүтін және бөлшек бөліктерін табыңдар. сандарының бүтін және бөлшек бөліктерін табыңдар.
№2. 1) 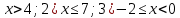 теңсіздіктерін аралықтар арқылы жазыңыздар. теңсіздіктерін аралықтар арқылы жазыңыздар.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақ соңы
|
Рефлексия
Бүгінгі сабақ қандай пәнмен байланысты болды?
Қандай қосымша жаңа сөздермен таныстыңыз?
Сабақтан қандай әсер алдыңыз?
Сабаққа бір ұсыныс.
|
Үй тапсырмасы:
№1. 1) 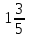 ; 2) ; 2) 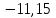 ; 3) ; 3) 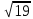 ; 4) ; 4) 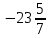 сандарының бүтін және бөлшек бөліктерін табыңдар. сандарының бүтін және бөлшек бөліктерін табыңдар.
№2. 1) 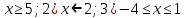 теңсіздіктерін аралықтар арқылы жазыңыздар теңсіздіктерін аралықтар арқылы жазыңыздар
|
Оқушылардың белсенділіген байланысты бағаланады.
|
| |
|
|
 Скачать 63.28 Kb.
Скачать 63.28 Kb.