сопромат для СибАДИ. сибади ДВСб18Z1 сопромат. Задача Растяжение сжатие Исходные данные Номер строки a, м
 Скачать 215.75 Kb. Скачать 215.75 Kb.
|
|
Задание по дисциплине «Сопротивление материалов» Расчетно-графическая работа №1 Эпюры внутренних усилий Задача № 1. Растяжение – сжатие 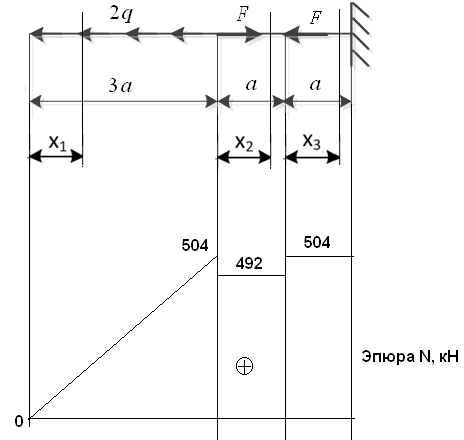 Исходные данные:
Первый участок. Произвольное сечение в границах 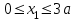 . . Согласно метода сечений, внутреннее усилие (продольная сила) в сечении 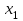 равно, по третьему закону Ньютона равно, по третьему закону Ньютона 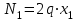 При 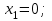 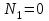 кН. кН. При 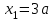 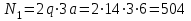 кН. кН.Второй участок. Произвольное сечение в границах 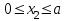 . Отсеченная часть второго сечения . Отсеченная часть второго сечения 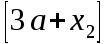 . .Усилие равно 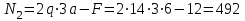 кН. кН.Третий участок. Произвольное сечение в границах 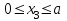 . Отсеченная часть третьего сечения . Отсеченная часть третьего сечения 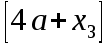 Усилие равно  кН. кН.Проверка эпюры 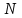 : Разрыв на эпюре : Разрыв на эпюре 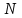 численно равен сосредоточенной силе в данном сечении. численно равен сосредоточенной силе в данном сечении.Задача № 2. Кручение Исходные данные: 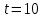 кНм/м; кНм/м; 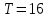 кНм; ; кНм; ; 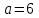 м. м.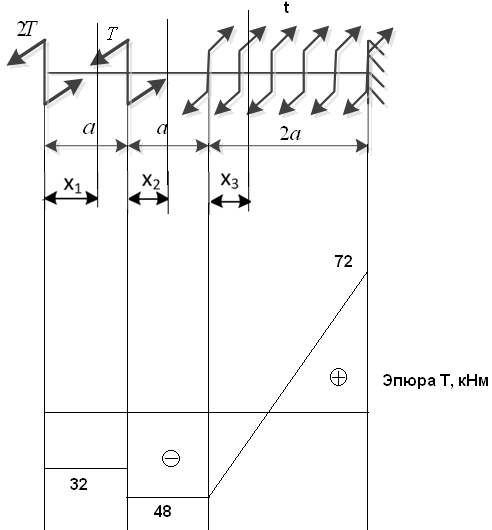 Первый участок. Произвольное сечение в границах 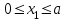 . . Внутреннее усилие (крутящий момент) в сечении 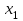 равно равно 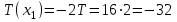 кНм. кНм. Знак крутящего момента определяется правилом винта (завинчивание – вращение отсеченной части по часовой стрелке  ). ).Второй участок. Произвольное сечение в границах 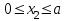 . Отсеченная часть второго сечения . Отсеченная часть второго сечения 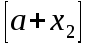 . .Момент во втором сечении 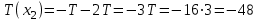 кНм. кНм.Третий участок. Произвольное сечение в границах 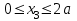 . Отсеченная часть третьего сечения . Отсеченная часть третьего сечения 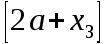 . . Момент в сечении 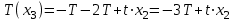 при 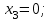 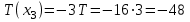 кНм; кНм;при 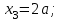 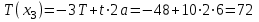 кНм. кНм.Проверка эпюры 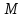 : Разрыв на эпюре : Разрыв на эпюре 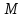 численно равен сосредоточенному моменту в данном сечении. численно равен сосредоточенному моменту в данном сечении.Поперечный изгиб Балка с защемлением Задача: Построить эпюры поперечных сил 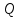 и изгибающих моментов и изгибающих моментов 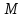 с проверкой. с проверкой.Исходные данные: 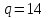 кН/м; кН/м; 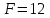 кН; кН; 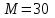 кНм; кНм; 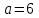 м. м.В задаче использован метод сечений. Назначение отсеченных частей. За начальную точку отсчета принята консоль. На каждом участке выбирается произвольное сечение с координатой привязки к началу каждого участка 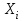 . Определяются границы изменения произвольных сечений . Определяются границы изменения произвольных сечений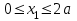 , ,Записываются уравнения равновесия сил и моментов отсеченных частей 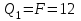 кН кН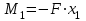 . .Определим значения моментов. При  ; ; 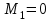 . кНм. . кНм. При 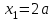 ; ; 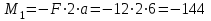 кНм. кНм. Участок 2. 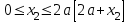 . Границы второго сечения и вторая отсеченная часть. . Границы второго сечения и вторая отсеченная часть. 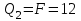 кН кН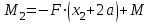 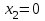 ; ; 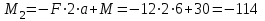 кНм; кНм;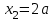 ; ; 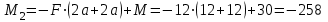 кНм. кНм.Участок 3. 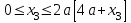 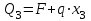 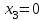 ; ; 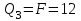 кН; кН;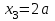 ; ; 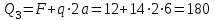 кН кН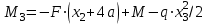 – квадратная парабола – квадратная парабола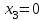 ; ; 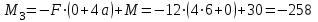 кНм; кНм;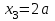 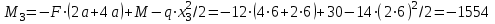 кНм. кНм.Эпюры поперечных сил и изгибающих моментов представлены на рис.2. 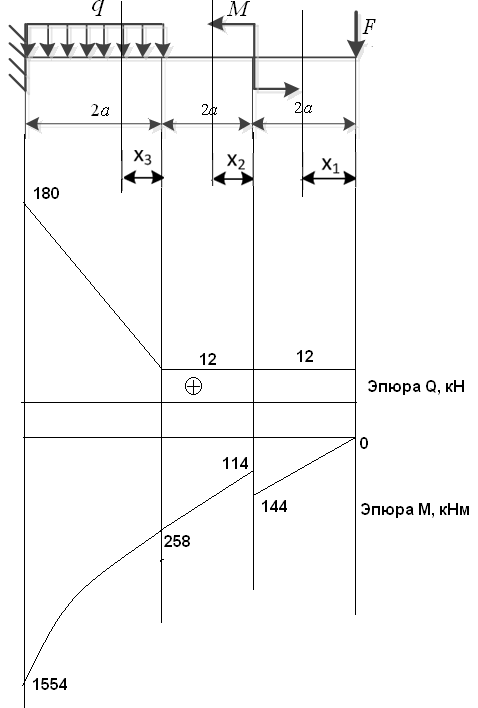 Рис.2. Балка с защемлением, эпюры поперечных сил и изгибающих моментов Шарнирно опертая балка 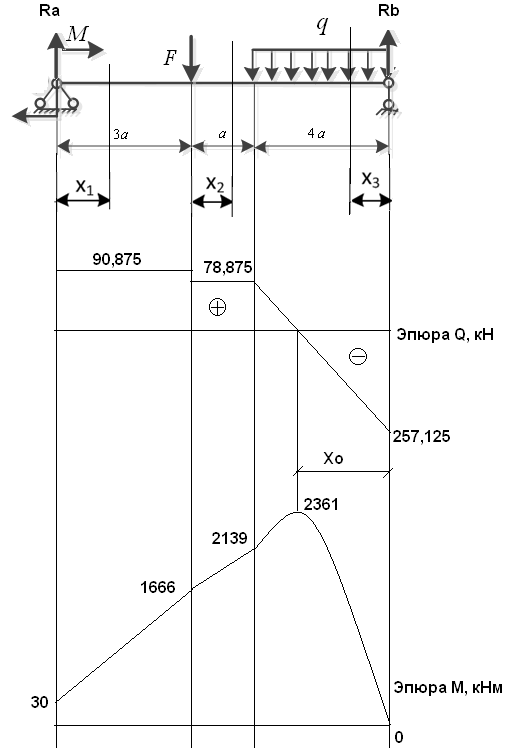 Рис.1. Шарнирно опертая балка, эпюры поперечных сил и изгибающих моментов Алгоритм расчета: Определение реакций в опорах. Левая опора – шарнирно неподвижная, правая – шарнирно подвижная, Необходимо определение трех реакций. При отсутствии продольных сил реакция 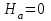 . Для оставшихся двух реакций составим уравнения статики . Для оставшихся двух реакций составим уравнения статики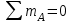 и и 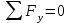 , см. рис.1. , см. рис.1.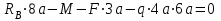 ; ;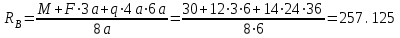 кН. кН.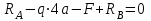 ; ;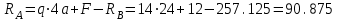 кН. кН.Назначают произвольные сечения на каждом участке с указанием отсеченных частей. Записывают уравнения равновесия отсеченных частей. Участок 1. 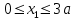 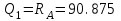 кН кН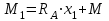 . .При  ; ; 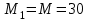 кНм. кНм.При 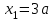 ; ; 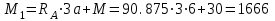 кНм. кНм.Участок 2. 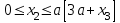 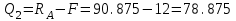 кН. кН.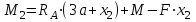 При 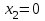 ; ; 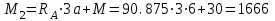 кНм. кНм.При 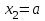 ; ;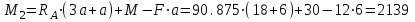 кНм. кНм.Участок 3. 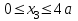 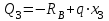 При 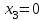 ; ; 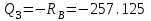 кН. кН.При 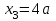 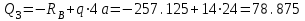 кН. кН.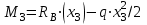 При 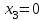 ; ; 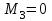 кНм. кНм.При 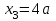 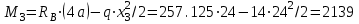 кНм. кНм.Координата экстремума для момента x0 = Rb/q=257.125/14=18.37 м 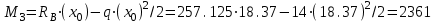 кНм. кНм. |
