319361 фин.м-ка. Задача 1 2 Задача 2 3 Задача 3 4 Задача 4 5 Задача 5 6 Задача 6 6 Список использованных источников 8
 Скачать 40.05 Kb. Скачать 40.05 Kb.
|
|
Содержание Задача 1 2 Задача 2 3 Задача 3 4 Задача 4 5 Задача 5 6 Задача 6 6 Список использованных источников 8 Задача 1Условие: Банк учитывает вексель за 2 года до срока его оплаты по простой учетной ставке d=6%. Какую сложную учетную ставку должен установить банк, чтобы его доход остался прежним? Решение: n=2 года, d=0,06 Доход банка: D=S-P При применении простой учетной ставки d 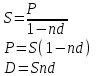 При применении сложной учетной ставки dc 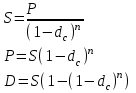 По условию доход должен быть одинаковым, поэтому должно выполняться соотношение 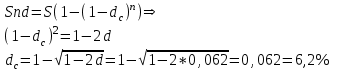 Ответ: dc=6,2% Задача 2Условие: На какой срок необходимо поместить денежную сумму под простую процентную ставку 10 % годовых, чтобы она увеличилась в 2 раза? Решение: i=10% Искомый срок определяем из равенства множителя наращения величине 2: 1+ni=2 1+n*0,1=2 0,1n=1 n=10 лет Ответ: n=10 лет Задача 3Условие: Предприниматель планирует после выхода на пенсию обеспечить себе ежегодный годовой доход в размере 60 тыс. руб. в течение 8 лет. Какую сумму ему необходимо для этого поместить на депозит в момент выхода на пенсию если банковская ставка по депозитам будет 10 % годовых? Предприниматель планирует снимать денежные средства с депозита в начале каждого года и за 8 лет исчерпать депозит полностью. Решение: R=60 тыс. руб, n=8 лет, i=10 %. Современную стоимость найдем по формуле: 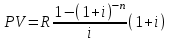 Подставим числовые значения: 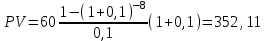 тыс. руб. тыс. руб.Ответ: PV=352,11 тыс. руб. Задача 4Условие: Номинал облигации равен 5000 руб, годовой купон – 8%, срок погашения – три года. При условии, что банковская процентная ставка составляет 7%, определить текущую стоимость этой облигации. Решение: N=5000 руб, k=8%, r=7%, n=3 года Определим текущую стоимость акции по формуле: 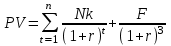 , ,где F – сумма погашения (как правило – номинал, т.е. F = N); k – годовая ставка купона; r – рыночная ставка (норма дисконта); n – срок облигации; N – номинал. 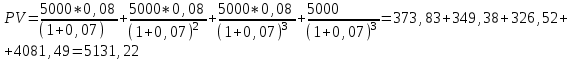 Ответ: PV=5131,22 руб. Задача 5Условие: Портфель состоит из двух ценных бумаг А и В, ценовая доля бумаги А в 2 раза меньше ценовой доли бумаги В, а их ожидаемые доходности соответственно равны 20 и 30%. Коэффициент корреляции равен 1. Найдите портфель, его доходность. Решение: х1 – доля бумаги А, х2 – доля бумаги В Ценовые доли бумаг относятся как 1:2, то получаем: х+2х=1 3х=1 х=1/3 Тогда х1=1/3=0,33, х2=2/3=0,67 Найдем доходность портфеля по формуле: 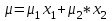 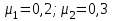 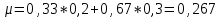 Ответ: Портфель имеет вид (0,33;0,67), доходность портфеля 0,267 Задача 6Условие: Компания А приобрела трехмесячный опцион покупателя у компании Б на 100 акций с ценой исполнения 1600 руб. Цена контракта – 20000 руб Цена спот ко времени исполнения контракта составит 2500 руб Определите финансовый результат компании А, выраженный в рублях. Решение: Для определения возможности получения дохода можно определить соотношение рыночной цены и величины (П + Ц / К) (П + Ц / К) = 1600 + 20000 : 100 = 1800 < 2500, что означает , что заключение контракта является выгодным Далее определим доход от покупки call –опциона. Он составит Дс = (2500 – 1600) · 100 – 20000 = 70000 руб. Покупая put – опцион, покупатель рассчитывает на понижение рыночной цены акции. Его доход будет равен Др = (П – Р) · К – Ц, где Др - доход покупателя put – опциона. Покупать put – опцион имеет смысл, если заранее купленный инструмент ( акции) есть в наличии и его цена меньше разности П - Ц : К, иначе покупатель опциона получит убытки. Продавец put – опциона имеет доход только в том случае, если рыночная цена фондового инструмента не уменьшается ниже величины ( П - Ц / К) Ответ: Дс=70000 руб. Список использованных источников1. Брусов, П.Н. Финансовая математика: Учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова. - М.: КноРус, 2017. - 224 c. 2. Касимов, Ю.Ф. Финансовая математика: Учебник и практикум для бакалавриата и магистратуры / Ю.Ф. Касимов. - Люберцы: Юрайт, 2018. - 459 c. 3. Копнова, Е.Д. Финансовая математика: Учебник и практикум для бакалавриата и магистратуры / Е.Д. Копнова. - Люберцы: Юрайт, 2019. - 413 c. |
