физика 23.10.21. Задача 1 2 Задача 2 5 Задача 3 7 Задача 1 9 Задача 2 13 Задача 3 16 Задача 1 Условие
 Скачать 243.45 Kb. Скачать 243.45 Kb.
|
|
Содержание Задача 1 2 Задача 2 5 Задача 3 7 Задача 1 9 Задача 2 13 Задача 3 16 Задача 1Условие: Частица движется равноускоренно в координатной плоскости ху с начальной скоростью 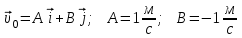 и ускорением и ускорением 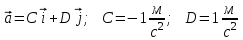 . Найти модули векторов скорости . Найти модули векторов скорости 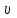 , тангенциального , тангенциального 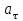 и нормального и нормального 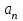 ускорений, а также радиус кривизны R траектории в момент времени ускорений, а также радиус кривизны R траектории в момент времени 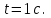 Дано: 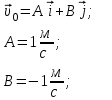 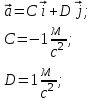 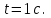 Найти: 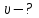 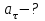 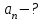 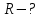 Решение: Запишем координаты вектора начальной скорости: 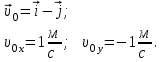 Запишем координаты вектора ускорения: 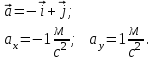 Запишем уравнение траектории частицы в параметрическом виде. 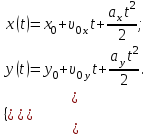 За начало координат принимаем точку с координатами 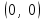 . После подстановки соответственных значений, получаем: . После подстановки соответственных значений, получаем: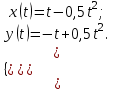 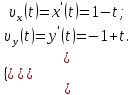 Для момента времени 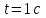 , получаем: , получаем: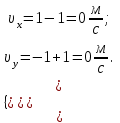 Тогда модуль вектора скорости будет: 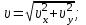 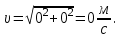 Вычисляем полное ускорение по формуле: 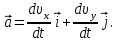 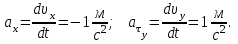 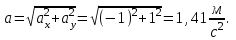 Тангенс угла, который образует касательная к траектории в момент времени 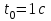 , вычисляется по формуле: , вычисляется по формуле: Тогда 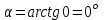 . .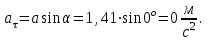 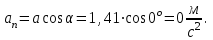 Нормальное ускорение вычисляется по формуле: 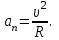 Откуда 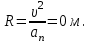 Ответ: 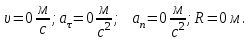 Задача 2Условие: На однородный цилиндрический блок массой m2 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой m1. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой m3 на расстоянии х от оси вращения. Грузы m3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения а груза m1 от расстояния х. Построить график этой зависимости в интервале изменения х от R до 3R. Ускорение свободного падения g=9,81 м/с2. 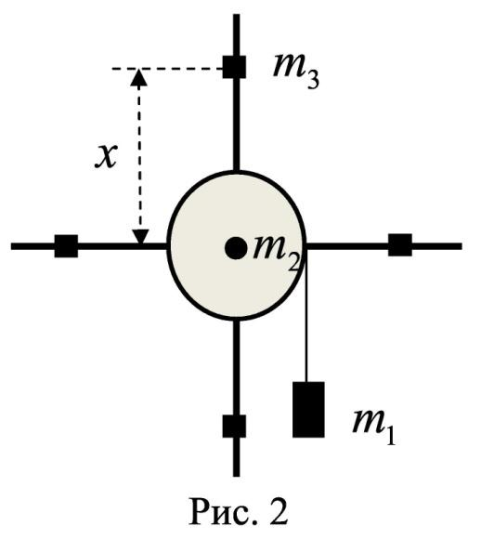 Ддано: R=0,1 м m1 =10 кг m2=2 кг m3=3 кг Найти: а-? Решение: Зададим систему отсчёта. За начало отсчёта принимаем поверхность земли, ось х направим вертикально вниз. По закону сохранения полной механической энергии, уменьшение потенциальной энергии груза 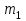 идёт на увеличения кинетической энергии груза идёт на увеличения кинетической энергии груза 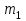 , вращательной кинетической энергии блока и грузов закреплённых на стержнях, поэтому можно записать: , вращательной кинетической энергии блока и грузов закреплённых на стержнях, поэтому можно записать: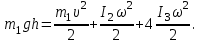 Где 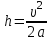 - расстояние, которое проходит груз - расстояние, которое проходит груз 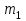 , , 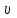 - его скорость, - его скорость, 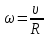 - угловая скорость блока, - угловая скорость блока, 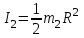 - момент инерции блока относительно оси вращения, - момент инерции блока относительно оси вращения, 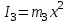 - момент инерции груза закреплённого на стержне относительно оси вращения. - момент инерции груза закреплённого на стержне относительно оси вращения.После подстановки, получаем: 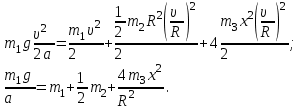 Подставим численные значения физических величин и найдём зависимость ускорения а груза 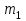 от расстояния х от расстояния х 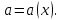 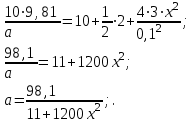 Строим график зависимости 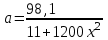 в интервале изменения х от R до 3R рисунок 4. в интервале изменения х от R до 3R рисунок 4.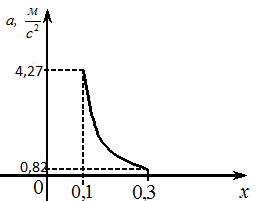 Ответ: 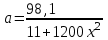 Задача 3Условие: Шар массой m1, летящий со скоростью v1, сталкивается с неподвижным шаром массой m2. После удара шары разлетаются под углом α друг у другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров u1, u2 после удара. Дано: СИ: m1=130 г 0,13 кг v1= 10 м/с m2=110 г 0,11 кг α=300 Найти: u1-? u2-? Решение: Запишем импульсы шаров: p0=m1v1 - величина импульса первого шара до удара; p1=m1u1 –величи1на импульса первого шара после удара p2=m2u2 – величина импульса второго шара после удара. Тогда из треугольника импульсов в соответствии с законом сохранения импульса и законом сохранения механической энергии получим: Разделим почленно уравнение 1 на 2 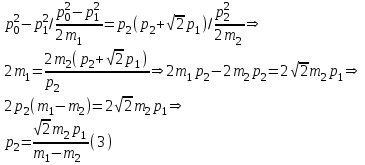 Подставим в уравнение 2 уравнение 3. 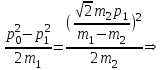 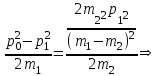 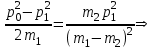 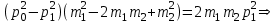 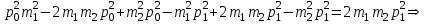 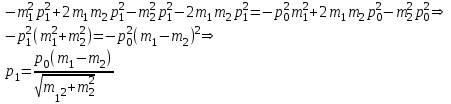 Тогда скорость шара первого после соударения: 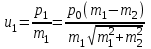 Подставим числовые значения: 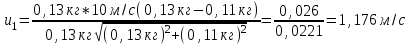 Скорость второго шара после удара: 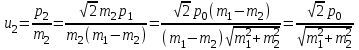 Подставим числовые значения 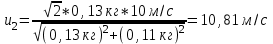 Ответ: u1=1,176 м/с, u2=10,81 м/с Задача 1Условие: Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1,V1 и P3,V3. Найти давление, объем и температуру газа P2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах P-V, P-T, V-T. Дано: СИ: Изохорный 1-2 Р1=105 Па V1=30 л 0,03 м3 Изотермический 2-3 Р3=2*105 Па V3=25 л. 0,025 м3 Найти: 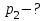 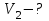 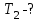 Изобразить: P – V P - T V – T Решение: Поскольку процесс 1-2 изохорный, то 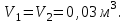 Поскольку процесс 2-3 изотермический, то Т2=Т3 Запишем уравнение Менделеева –Клапейрона для второго состояния газа: 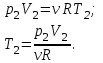 При изотермическом процессе: 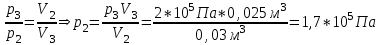 Где 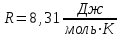 - универсальная газовая постоянная. - универсальная газовая постоянная.Подставим численные значения и произведём вычисления: 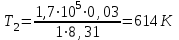 Для состояния 1 запишем уравнение Менделеева – Клапейрона: 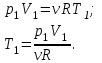 Подставим численные значения и произведём вычисления: 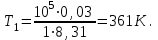 Для состояния 3 запишем уравнение Менделеева – Клапейрона: Т3=614 К Для построения графиков процессов запишем параметры газа в каждой точке. В 1-й точке - 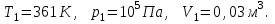 Во 2-й точке - 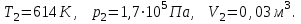 В 3- й точке - 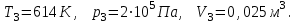 Изобразим процесс в координатах P – V. 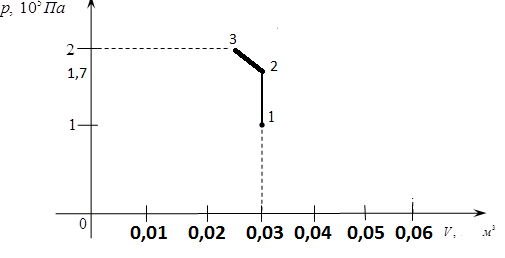 Изобразим процесс в координатах P – Т. 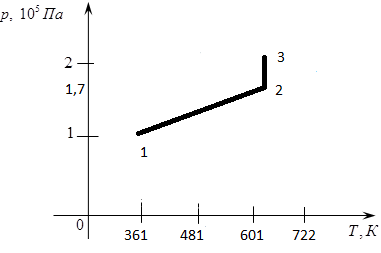 Изобразим процесс в координатах V – Т. 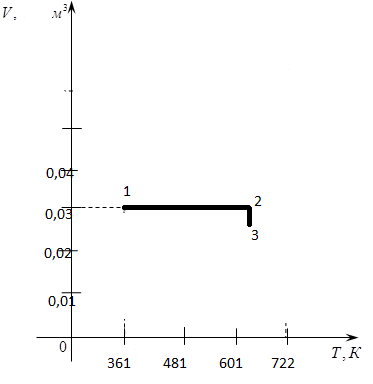 О  твет: твет: 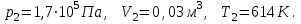 Задача 2Условие: Идеальный газ совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно P1, V1, P2, V2, P3, V3. Найти термический кпд цикла. Дано: СИ: Изохорный 1-2 P1=105 Па V1=3 л 3*10-3м3 Изотермический 2-3 P2=4*105 Па Изобарный 3-1 газ – N2 Найти: 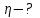 Решение: КПД цикла вычисляется по формуле: 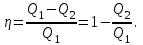 Где 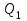 - количество теплоты, переданное газу за цикл от нагревателя; - количество теплоты, переданное газу за цикл от нагревателя; 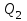 - количество теплоты, отданое газом за цикл холодильнику. - количество теплоты, отданое газом за цикл холодильнику.Работа газа при изохорном процессе равна 0. Изменение внутренней энергии в процессе 1 – 2 вычисляется по формуле: 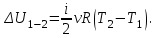 На основании первого закона термодинамики Q1-2=∆U1-2 Запишем уравнение Менделеева-Клапейрона для процесса 1-2 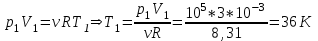 Где 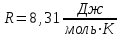 - универсальная газовая постоянная, - универсальная газовая постоянная,При изохорном процессе давление прямо пропорционально его абсолютной температуре. 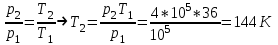 Тогда 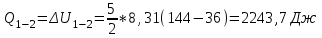 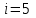 - степень свободы молекул двухатомного газа. - степень свободы молекул двухатомного газа.Учитывая, что для изотермического процесса 2 – 3 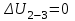 , по первому закону термодинамики, получаем: , по первому закону термодинамики, получаем: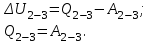 Работа газа при изотермическом процессе вычисляется по формуле: 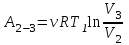 . .Согласно уравнению Менделеева – Клапейрона для третьего состояния газа, получаем: 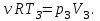 После подстановки, получаем: 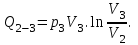 Найдём объём азота 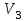 для третьего состояния. для третьего состояния.Для изобарного процесса 3-1 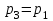 . .Для изотермического процесса 2 – 3, имеем: 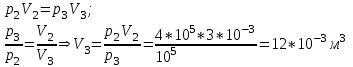 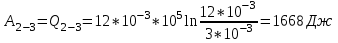 Работа газа при изобарном процессе 3-1 вычисляется по формуле: 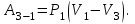 Подставим численные значения и произведём вычисления: 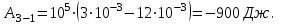 Изменение внутренней энергии в процессе 3-1 вычисляется по формуле: 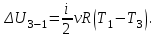 Применим уравнение Менделеева - Клапейрона для первого и третьего состояний газа: 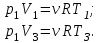 Находим разность второго и первого уравнений: 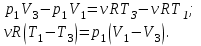 После подстановки в формулу изменения внутренней энергии, получаем: 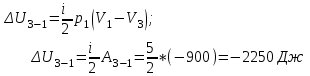 Вычисляем количество теплоты 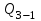 , полученное газом в процессе 3-1, применяя первый закон термодинамики: , полученное газом в процессе 3-1, применяя первый закон термодинамики: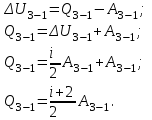 Подставим численные значения и произведём вычисления: 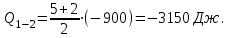 Количество теплоты, полученное газом за цикл от нагревателя: 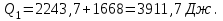 Количество теплоты, отданое газом за цикл холодильнику: 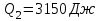 Теперь вычисляем КПД цикла: 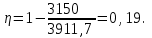 Ответ: 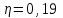 Задача 3Условие: Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М=29*10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h)=T0(1+ah). Найти давление газа Р на высоте h. На высоте h=0 давление газа P0=105 Па. Дано: 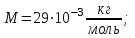 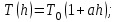 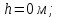 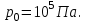 Т0=250 К, а=5*10-5м-1 h=100 м. Найти: Р-? Решение: Применим барометрическую формулу: 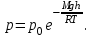 Где 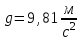 - ускорение свободного падения, - ускорение свободного падения, 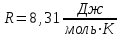 - универсальная газовая постоянная. - универсальная газовая постоянная.Учитывая условие задачи, получаем: 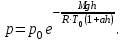 Подставим численные значения и вычислим: 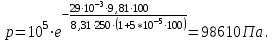 Ответ: 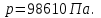 |
