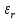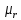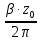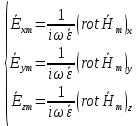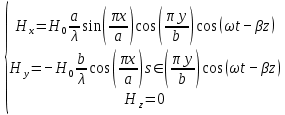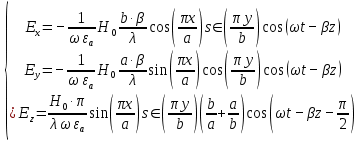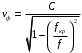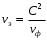контрольная. Задача 13 р ис. 1
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Задача №1-3
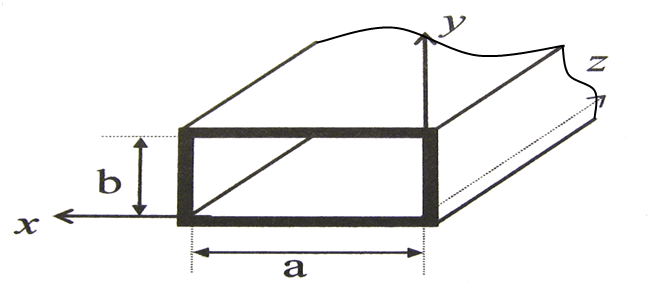
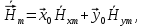 где где 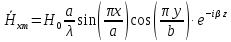 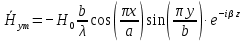  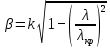 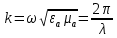 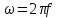 ; f- частота электромагнитных колебаний ; f- частота электромагнитных колебаний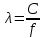 -длина волны, свободно распространяющейся в однородной изотропной среде с параметрами -длина волны, свободно распространяющейся в однородной изотропной среде с параметрами 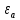 и и 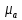 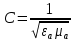 – скорость света в этой среде – скорость света в этой среде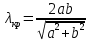 Таблица исходных данных
Решение 1. Используя уравнения Максвелла, определить комплексные амплитуды составляющих вектора 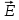 Проекции комплексной амплитуды вектора 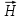 на оси координат: на оси координат: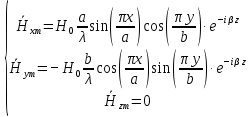 Для того чтобы найти выражение для вектора E (вектора электрического поля), воспользуемся уравнением Максвелла в комплексной форме: 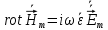 где 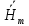 и и 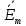 – комплексные амплитуды напряженностей магнитного и электрического полей соответственно, – комплексные амплитуды напряженностей магнитного и электрического полей соответственно,Выразим комплексную амплитуду вектора 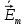 из уравнения Максвелла: из уравнения Максвелла: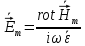 Спроектируем полученное равенство на оси координат:
Разложим 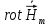 по декартовым координатам: по декартовым координатам: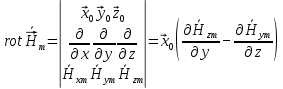 - -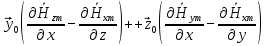 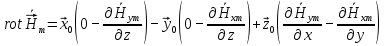 Найдём частные производные: 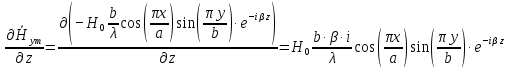 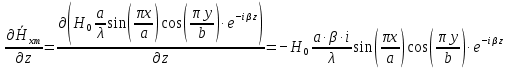 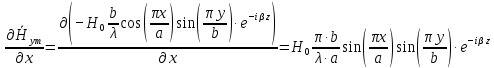 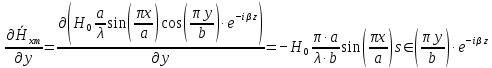 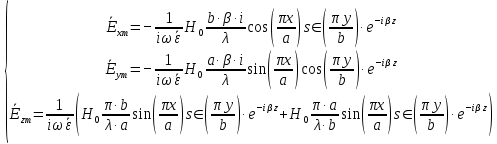 Преобразуем полученные выражения и получим выражения для проекций составляющих напряженности электрического поля для комплексных амплитуд напряженности электрического поля: 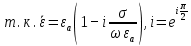 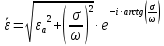 Комплексные амплитуды проекций векторов поля: 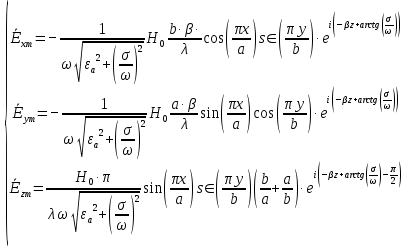 Стенки трубы идеально проводящие, соответственно 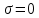 Комплексные амплитуды составляющих вектора 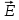 : : 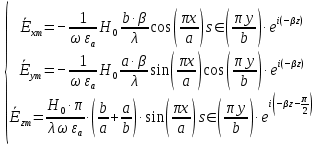 Комплексные амплитуды составляющих вектора 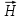 : : 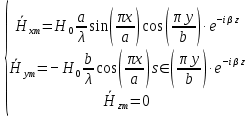 2.Определить диапазон частот, в котором 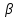 -действительное число, т. е. рассматриваемое поле – бегущая волна. -действительное число, т. е. рассматриваемое поле – бегущая волна.Электромагнитная волна распространяется по волноводу, если выполняется условие: 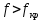 Из технического задания следует: 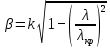 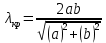 где a, b – внутренние поперечные размеры волновода Подставляя числовые данные, получаем: 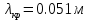 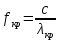 Где 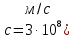 ) – скорость света ) – скорость света Рассчитаем 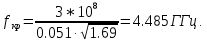 Получаем, что при f > 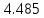 ГГц ГГц 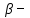 действительное число, действительное число, а при f < 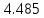 ГГц ГГц 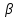 – мнимое число – мнимое число 3.Записать выражения для мгновенных значений всех составляющих векторов 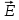 и и 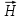 для двух случаев: когда f принадлежит найденному в п.2 диапазону частот и когда f не принадлежит этому диапазону. для двух случаев: когда f принадлежит найденному в п.2 диапазону частот и когда f не принадлежит этому диапазону.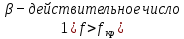 ) )Получим выражения для комплексных значений проекции составляющих напряженности магнитного и электрического полей (для этого каждое из выражений умножим на 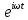 ) и получим следующие выражения: ) и получим следующие выражения: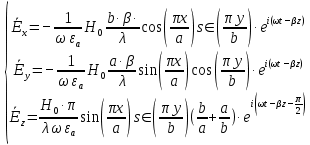 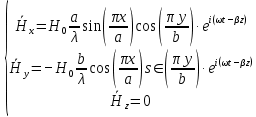 Выражения для проекций составляющих напряженности магнитного поля для мгновенных значений напряженности магнитного поля получим по общим формулам: 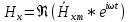 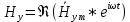
Выражение для проекции составляющей напряженности электрического поля для мгновенного значения напряженности электрического поля получим по общей формуле: 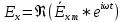
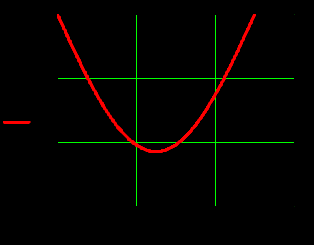
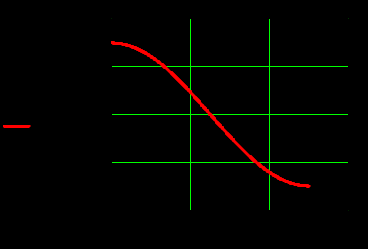
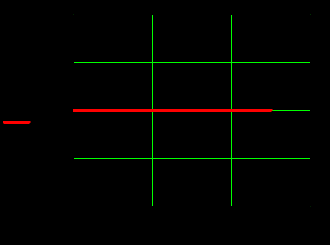
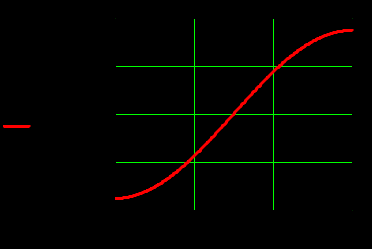
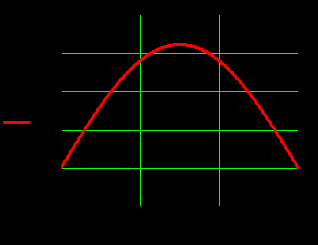
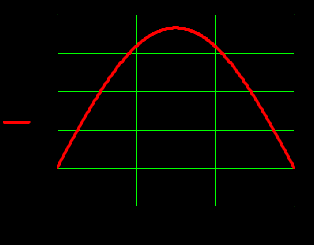
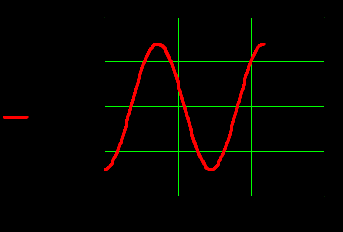
 ) )Запишем комплексные амплитуды составляющих векторов 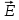 и и 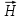 с учетом того, что с учетом того, что 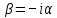 . .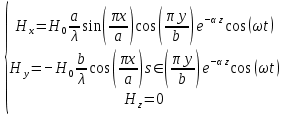 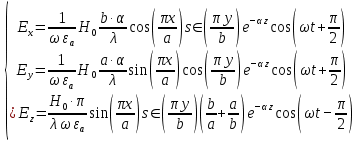 4.Рассчитать и построить графики зависимостей амплитуд составляющих векторов поля в сечении 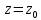 от координаты x при y=0.5b в интервале от координаты x при y=0.5b в интервале 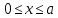 и от координаты y при x=0.5a в интервале и от координаты y при x=0.5a в интервале 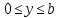 , а также зависимости тех же составляющих от координаты z вдоль линии x=0.5a; y=0.25b в интервале , а также зависимости тех же составляющих от координаты z вдоль линии x=0.5a; y=0.25b в интервале 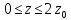 на частотах на частотах 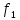 и и 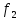 Примечание: расчёты и построение графиков произведём в математическом пакете MathCad 15.0 Графики зависимостей амплитуд составляющих векторов поля в сечении 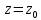 от координаты x при y=0.5b в интервале от координаты x при y=0.5b в интервале 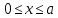
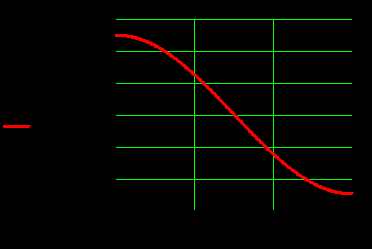
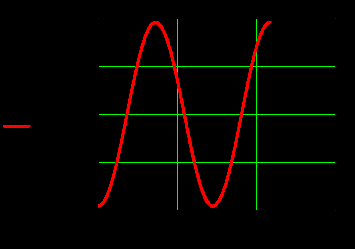
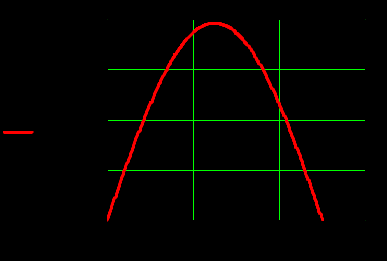 Графики зависимостей амплитуд составляющих векторов поля в сечении 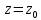 от координаты y при x=0.5a в интервале от координаты y при x=0.5a в интервале 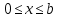
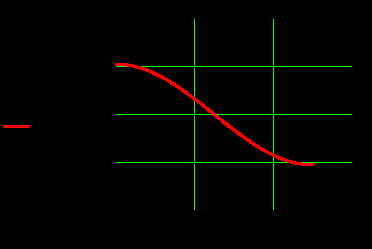
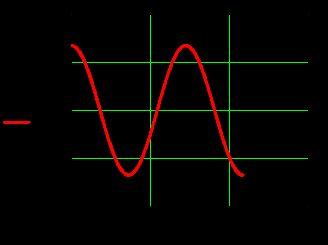
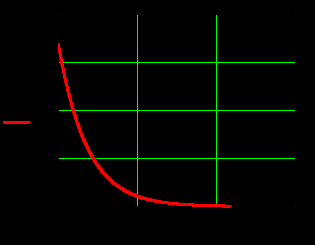
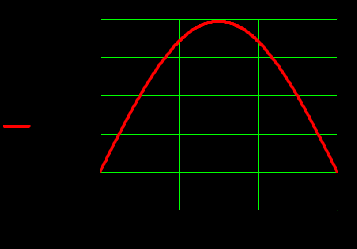 3. Графики зависимостей амплитуд составляющих векторов поля от координаты z вдоль линии x=0.5a; y=0.25b в интервале 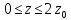 на частоте на частоте 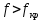
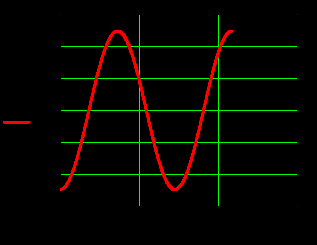
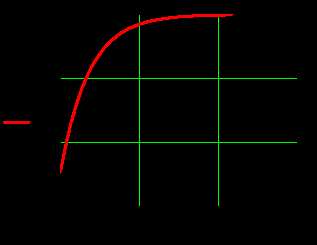
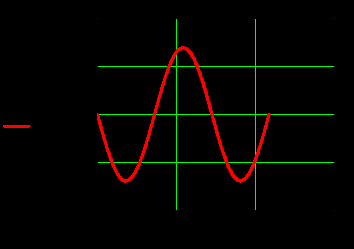 4.Графики зависимостей амплитуд составляющих векторов поля от координаты z вдоль линии x=0.5a; y=0.25b в интервале 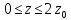 на частоте на частоте 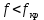
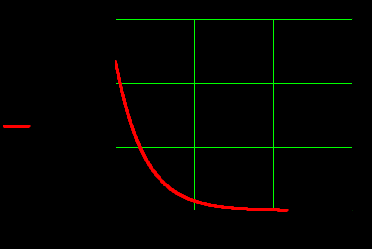 5. Проверить выполнение граничных условий для касательных составляющих вектора 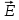 и нормальной составляющей вектора и нормальной составляющей вектора 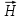 на верхней (y=b) стенке трубы. на верхней (y=b) стенке трубы.Проверка граничных условий заключается в проверке истинности утверждений 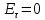 и и 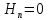 , т.е. равенста нулю касательной вектора , т.е. равенста нулю касательной вектора 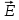 и нормальной вектора и нормальной вектора 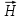 проекций (составляющих).Для верхней стенки волновода (y=b), касательными составляющими вектора электрического поля являются составляющие проекций (составляющих).Для верхней стенки волновода (y=b), касательными составляющими вектора электрического поля являются составляющие 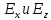 , а нормальной составляющей вектора магнитного поля является составляющая , а нормальной составляющей вектора магнитного поля является составляющая 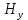 . .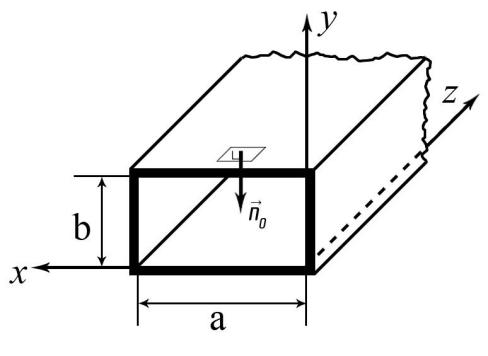 Возьмем необходимые ненулевые составляющие и подставим y=b. 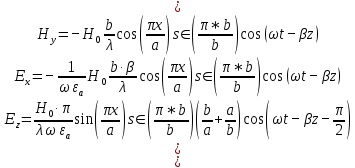 Получаем, что: 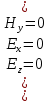 Таким образом, граничные условия на верхней стенке трубы волновода выполняются. 6.Найти комплексные амплитуды плотностей поверхностных токов и зарядов на боковой (x=a) стенке трубы. Комплексную амплитуду поверхностного тока можно найти по формуле: 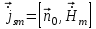 Комплексную амплитуду плотности зарядов можно найти по формуле: 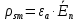  Для левой стенки волновода Для левой стенки волновода 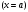 нормаль противоположна вектору нормаль противоположна вектору 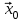 : : 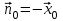 . .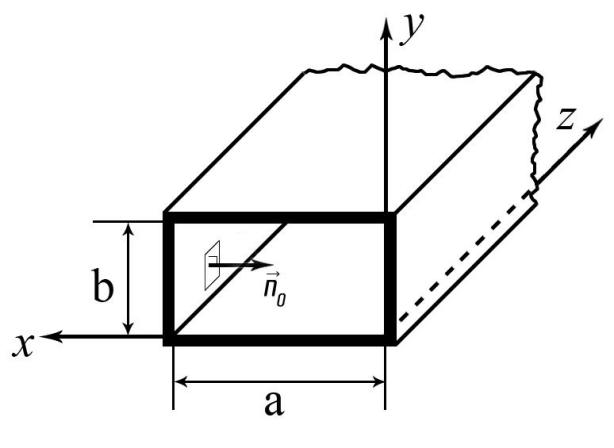 Касательными к этой стенке составляющими вектора 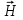 являются составляющие вдоль осей y и z, то есть: являются составляющие вдоль осей y и z, то есть: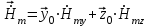 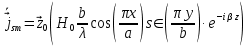 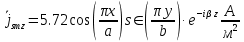 Нормальной к этой стенке составляющей вектора 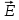 будет составляющая будет составляющая 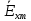 . Тогда комплексная амплитуда плотности поверхностных зарядов будет равна: . Тогда комплексная амплитуда плотности поверхностных зарядов будет равна: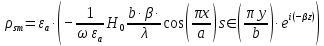 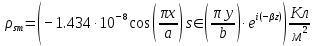 7.Вычислить средние за период значения объемных плотностей энергий электрического и магнитного полей. 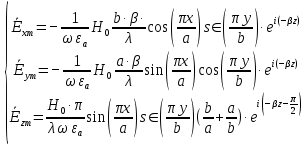 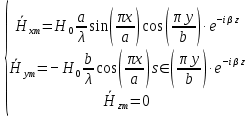 Объемная плотность энергии может быть найдена по формулам: 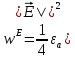 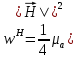 В данном случае, преобразуем эти выражения следующим образом: 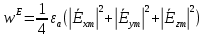 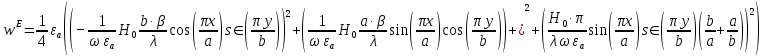 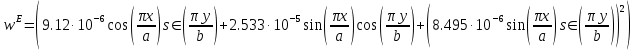 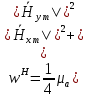 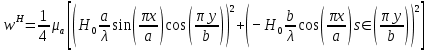 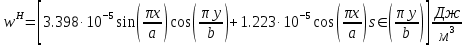 8.Записать выражение для комплексного вектора Пойтинга для двух случаев: когда частота принадлежит найденному в п. 2 диапазону и когда она не принадлежит этому диапазону. Определить среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии. Комплексное значение вектора Пойнтинга запишем по формуле: 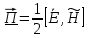 Где 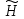 -комплексно-сопряженное выражение -комплексно-сопряженное выражение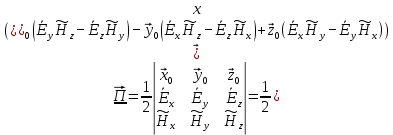 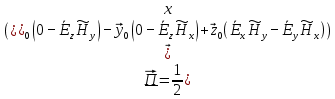 а) Рассмотрим режим бегущей волны: 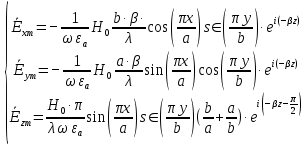 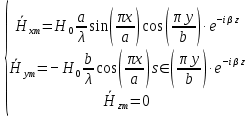 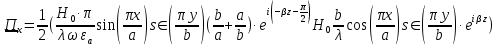 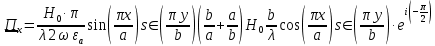 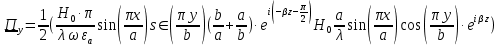 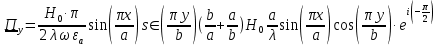 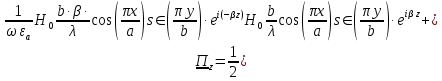 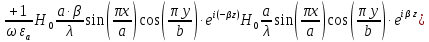 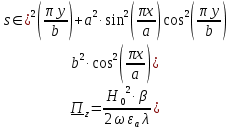 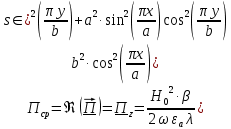 Cоставляющие по оси x, y чисто мнимые, следовательно: 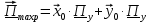 б) Во втором случае (f 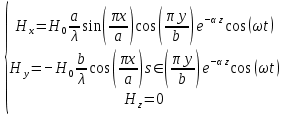 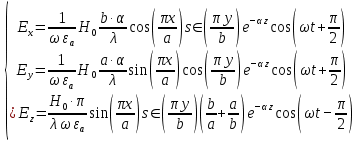 В этом случае вектор Пойтинга чисто мнимый и переноса энергии не происходит. 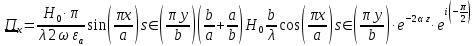 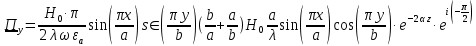 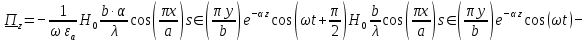 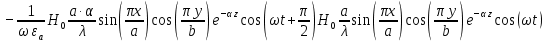 9.Записать выражения для мгновенных значений плотностей активного и реактивного потоков энергии для двух случаев, указанных п.8 Запись выражений для мгновенного значения вектора Пойнтинга: 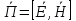 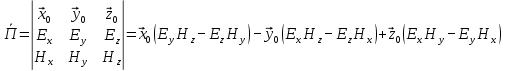 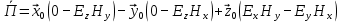 а) Рассмотрим режим бегущей волны:
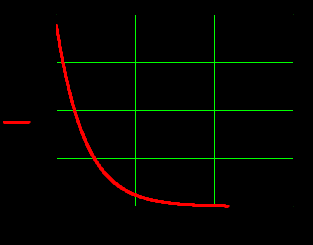
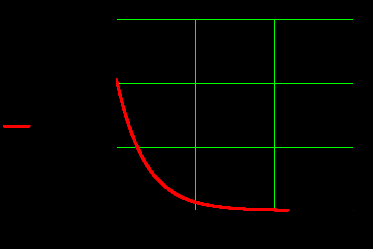
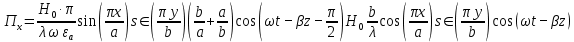 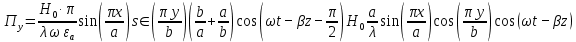 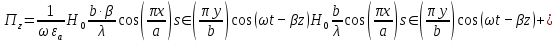 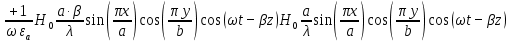 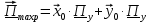 б) Во втором случае (f 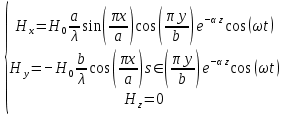 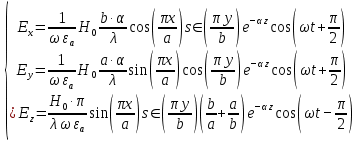 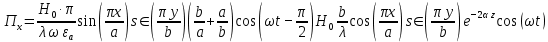 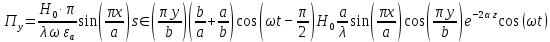 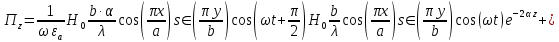 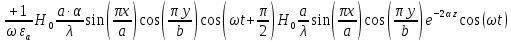 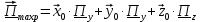 10.Вычислить средний за период поток энергии через поперечное сечение трубы. Мощность за период потока энергии через поперечное сечение волновда определяется по формуле: 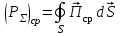 Вычисления производим на частоте f ( 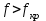 ) )Выражения для среднего значения вектора Пойнтинга найдем по формуле: 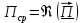 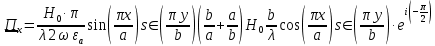 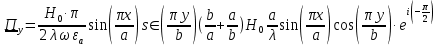 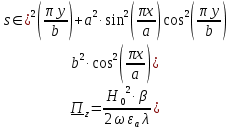 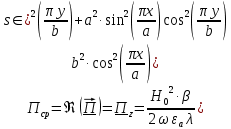 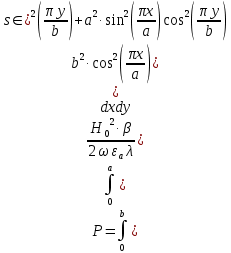 Расчет произведём в MathCad: 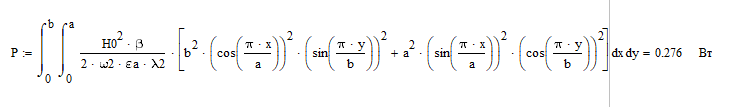 11. Определить фазовую скорость 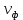 и скорость распространения энергии и скорость распространения энергии 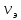 рассматриваемой волны. Рассчитать и построить графики зависимостей рассматриваемой волны. Рассчитать и построить графики зависимостей 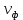 и и 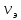 от частоты. от частоты. Фазовую скорость вычисляем по формуле:
Подставив в формулу значения констант и частоту, получим: 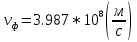 Фазовая скорость и скорость распространения энергии связаны следующим соотношением: 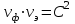 Отсюда скорость распространения энергии равна:
Подставив в формулу значение константы и найденное ранее значение фазовой скорости, получим: 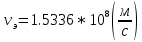 Графики зависимостей этих скоростей от частоты: 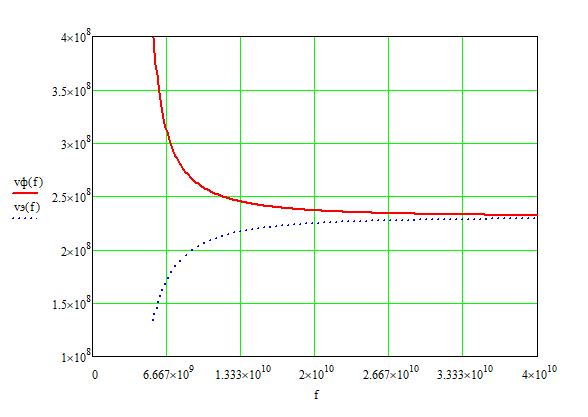 12. Считая, что стенки трубы выполнены из реального металла имеющего 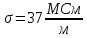 , на основе граничных условий Леонтовича-Щукина определить коэффициент затухания для заданной волны. , на основе граничных условий Леонтовича-Щукина определить коэффициент затухания для заданной волны.Формула для расчета коэффициента затухания на основе граничных условий Леонтовича-Щукина имеет вид: 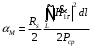 , , где 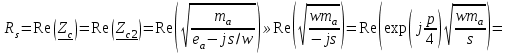 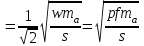 - это активная часть поверхностного сопротивления волновода - это активная часть поверхностного сопротивления волновода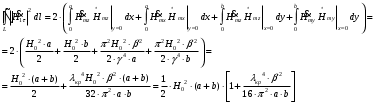 Раскроем частотную зависимость коэффициента затухания: 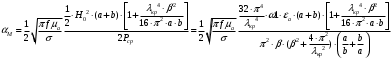 Сделав замену 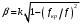 и подставив и подставив 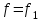 в полученное выражение для коэффициента затухания, получим: в полученное выражение для коэффициента затухания, получим: 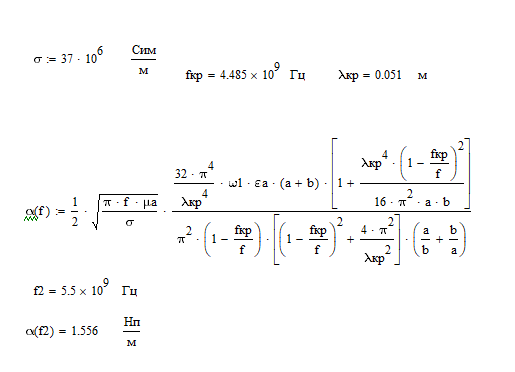 13. Рассчитать и построить частотную зависимость коэффициента затухания в волноводе. Оконечный результат и построение графика зависимости 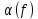 представим и выполним в математическом пакете MathCad 15.0 представим и выполним в математическом пакете MathCad 15.0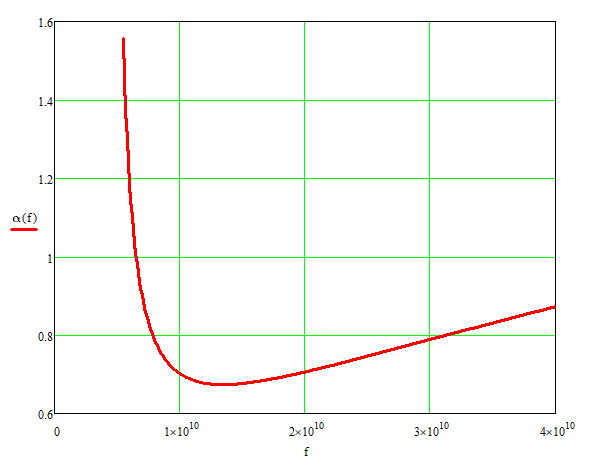 14.Определить тип волны, распространяющейся в волноводе. Нарисовать структуру силовых линий электрического и магнитного полей этой волны. Изобразить структуру силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода. В прямоугольном волноводе могут распространяться волны электрических ( 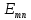 ) и магнитных ( ) и магнитных (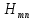 ) типов. ) типов. У волны электрического типа вектор напряженности электрического поля имеет продольную составляющую 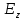 (совпадающую с направлением распространения) и поперечные составляющие, а вектор напряженности магнитного поля (совпадающую с направлением распространения) и поперечные составляющие, а вектор напряженности магнитного поля 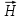 – только поперечные составляющие. – только поперечные составляющие. У волны типа 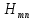 вектор напряженности магнитного поля вектор напряженности магнитного поля 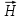 имеет продольную и поперечные составляющие, вектор напряженности электрического поля имеет продольную и поперечные составляющие, вектор напряженности электрического поля 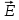 – только поперечные. – только поперечные. Индексы m и n связаны с функциями распределения амплитуд вдоль поперечных координат x и y. Для периодических функций распределения амплитуд индекс m определяет число полупериодов поля, укладывающихся вдоль широкой стенки волновода. Аналогично индекс n определяет число полупериодов поля, укладывающихся вдоль узкой стенки волновода. Таким образом, тип волны, распространяющейся в волноводе - 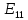 Под структурой поля волны в волноводе понимают показанное в виде векторных линий распределение составляющих поля 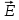 и и 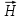 в фиксированный момент времени в фиксированный момент времени 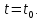 Структура силовых линий электрического и магнитного полей заданной волны 3Д-проекция: 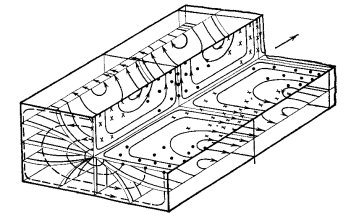 Проекции в различных плоскостях: 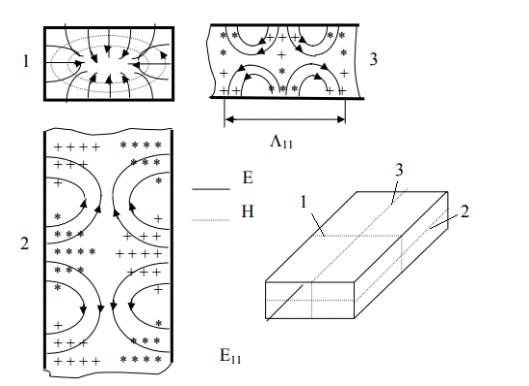 Структура силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода. 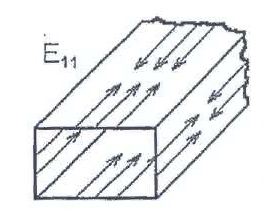 Использованная литература: [1]-Техническая электродинамика / Пименов Ю.В., Вольман В.И., Муравцов А.Д. Под ред. Ю.В. Пименова: Учебное пособие для вузов. – М.: Радио и связь, 2002. [2]-Конспект лекций за 2022 год. |

 ис.1
ис.1 ,А/м
,А/м