Задача 1 Дано Форма сечения неравнополочный уголок
 Скачать 18.43 Kb. Скачать 18.43 Kb.
|
Задача 1 Дано: Форма сечения «неравнополочный уголок». Расчетное усилие 315 кН. Сталь класса С245. Расчетная длина lef = 4100 мм. Требуется: подобрать сечение и проверить устойчивость сжатых элементов относительно оси х-х. РЕЗУЛЬТАТЫ РАСЧЕТА (МПа, мм): № профиля___16/10___ К___0.57___ Ry ___24___ ___79.61___ u___2.69___ __0.617____ с ___1___ ВЫВОД условие выполняется___________________________________________________________ Задача 1 Дано: Форма сечения – неравнополочный уголок; N = 315 кН; С 245 => Yc = 1; Ry = 24 кН/мм2; lef =4100 мм. Решение: 1) Определяем требуемую площадь поперечного сечения неравнополочного уголка, предварительно приняв φ=0,8. 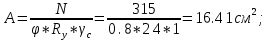 2) По сортаменту принимаем равнополочный уголок № 14/9 с площадью поперечного сечения А = 18.00 см2 и момент инерции imin = 4.49 см. 3) Определяем гибкость и условную гибкость сжатого элемента: 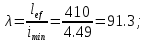 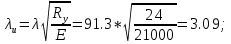 4) Определяем значение коэффициента φ с помощью линейной интерполяции: φ = 0.545 5) Проверяем устойчивость сжатого элемента в виде неравнополочного уголка № 14/9: 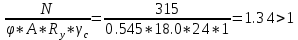 Условие не выполняется, следовательно, требуется увеличить номер прокатного профиля. 6) По сортаменту принимаем равнополочный уголок № 16/10 с площадью поперечного сечения А = 22.87 см2 и момент инерции imin = 5.15 см. 7) Определяем гибкость и условную гибкость сжатого элемента:  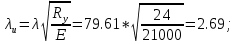 8) Определяем значение коэффициента φ с помощью линейной интерполяции: φ = 0.617 9) Проверяем устойчивость сжатого элемента в виде равнополочного уголка № 16: 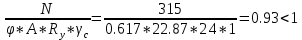 Условие выполняется. 10) К = 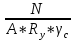 = =  = 0.57 = 0.57 |
