Контрольная.Термодинамика. Задача 1 Газ при давлении р11,4 мпа и температуре t119
 Скачать 29.36 Kb. Скачать 29.36 Kb.
|
|
Задача 6.1 Газ при давлении р1=1,4 МПа и температуре t1=19 ̊C нагревается при постоянном объеме до t2=300 ̊C. Найти конечное давление газа р2. Решение: По условию V=Const, процесс изохорный. Зависимость между начальными и конечными параметрами процесса определяется по формуле: 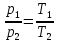 Отсюда: 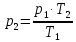 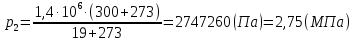 Ответ: конечное давление равно 2,75 МПа. Задача 6.2 В закрытом сосуде заключен газ при разряжении р1=6000 Па и температуре t1=19 ̊C. Показание барометра – 101325 Па. До какой температуры нужно охладить газ, чтобы разряжении стало р2=13000 Па. Решение: По условию V=Const, процесс изохорный. Зависимость между начальными и конечными параметрами процесса определяется по формуле: 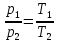 Отсюда: 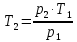 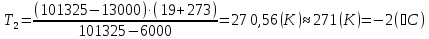 Ответ: газ надо охладить до -2 ̊C. Задача 6.3 Сосуд емкостью V=90 л. содержит воздух при давлении р1=0,8 МПа и температуре t1=30 ̊C. Определить количество теплоты, которое необходимо сообщить воздуху, чтобы повысить его давление при v = const до р2=1,6 МПа. Зависимость теплоемкости от температуры нелинейная. Решение: Найдем Т2 по формуле: 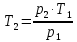 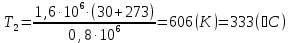 Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t1до t2затрачиваемой в процессе при постоянном объеме: 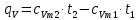 Найдем изохорные теплоемкости при температуре t1и t2 ͦC, воспользуемся таблицей теплоёмкостей воздуха: 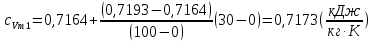 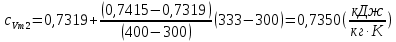 Таким образом: 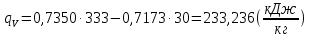 Массу воздуха в резервуаре определим из характеристического уравнения: 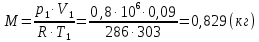 а сообщенное ему количество теплоты: 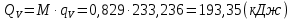 Ответ: количество теплоты, которое необходимо сообщить воздуху 193,35 кДж. Задача 6.4 В резервуаре, имеющем объем V=0,5 м3, находится углекислый газ при давлении р1=0,6 МПа и температуре t1=500 ̊C. Как изменится температура газа, если отнять от него при постоянном объеме 436 кДж? Зависимость теплоемкости от температуры считать линейной. Решение: Так как конечное давление газа неизвестно, то для определения конечной температуры нельзя воспользоваться соотношением параметров в изохорном процессе. Обратимся поэтому к выражению, определяющему количество отведенной теплоты в изохорном процессе: 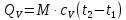 В этом уравнении теплота Qv=-436 кДж. Массу углекислого газа в резервуаре определим из характеристического уравнения: 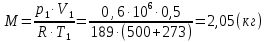 В пределах от 527 ℃ до t2 согласно справочной таблице средняя теплоемкость углекислого газа: 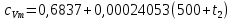 Подставляем данные и получаем: 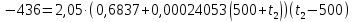 Решая получим: 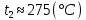 Ответ: 275 ͦС Задача 6.5 Какое количество теплоты необходимо затратить, чтобы нагреть V=2 м3 воздуха при постоянном избыточном давлении p=0,2 МПа от температуры t1=100℃ до температуры t2=500℃ ? Какую работу при этом совершит воздух? Решение: Затраченное удельное количество теплоты: 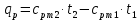 Пользуясь справочной таблицей, находим 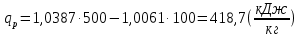 Массу воздуха определяем из характеристического уравнения 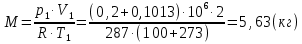 Таким образом, 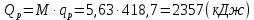 Работа газа при изобарном процессе равна: 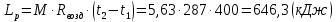 Ответ: количество теплоты необходимо затратить 2357 кДж, работа газа 646,3 кДж. Задача 6.6 В цилиндре находится воздух при давлении р=0,5 МПа и температуре t1=400℃. От воздуха отнимается теплота при постоянном давлении таким образом, что в конце процесса устанавливается температура t2=8℃. Объем цилиндра, в котором находится воздух, равен V=400 л. Определить количество отнятой теплоты, конечный объем, изменение внутренней энергии и совершенную работу сжатия. Зависимость теплоемкости от температуры считать нелинейной. Решение: Количество отнятой теплоты по формуле: 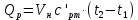 Объем воздуха при нормальных условиях равен: 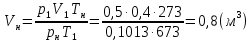 По справочной таблице находим 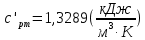 Следовательно, 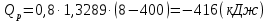 Конечный объем воздуха для изохорного процесса 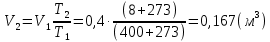 Изменение внутренней энергии 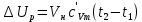 Пользуясь справочной таблицей, находим 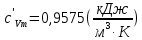 Следовательно, 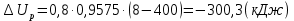 Работа, затраченная на сжатие 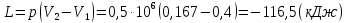 Ответ: Qp=-416 кДж, V2=0,167 м3, ∆Up=-300,3 кДж, L=-116,5 кДж. Задача 6.7 Воздух в количестве 1 кг при температуре t=24℃. и начальном давлении р1=0,1 МПа сжимается изотермически до конечного давления р2=1 МПа. Определить конечный объем, затрачиваемую работу и количество теплоты, отводимой от газа. Решение: Найдем начальный объем воздуха из уравнения состояния: 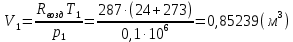 Так как в изотермическом процессе 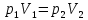 то конечный объем 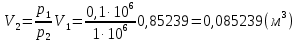 Работа, затрачиваемая на сжатие 1 кг воздуха: 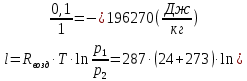 Количество теплоты, отводимой от воздуха, равно работе, затраченной на сжатие. Следовательно, 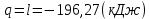 Ответ: V2=0,085239 м3, l=q=-196,27 кДж. Задача 6.8 Воздух в количестве 1 кг при температуре t=24℃. и начальном давлении р1=0,1 МПа сжимается адиабатно до конечного давления р2=1 МПа. Определить конечный объем, конечную температуру и затрачиваемую работу. Решение: Из соотношения параметров в адиабатном процессе находим 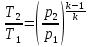 Отсюда конечная температура равна: 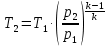 Принимая k=1,4 получаем: 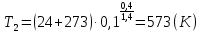 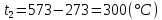 Затраченная работа 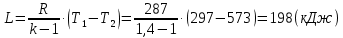 Конечный объем определяется из уравнения состояния 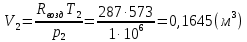 Ответ: V2=0,1645 м3, T2=300 ͦС, L=198 кДж. Задача 6.9 Адиабатным сжатием повысили температуру воздуха в двигателе так, что она стала равной температуре воспламенения нефти; объем при этом уменьшился в 14 раз. Определить конечную температуру и конечное давление воздуха, если р1=0,09 МПа и t1=110℃.. Решение: Конечную температуру определяем по формуле, учитывая показатель адиабаты воздуха k=1,4:   Конечное давление при адиабатическом процессе равно:  Ответ: T2=827  , p2=3,61 МПа. , p2=3,61 МПа.Задача 6.10 Из сосуда, содержащего углекислоту при давлении p=1,6 МПа и температуре t=110℃, вытекает 2/3 содержимого. Вычислить конечное давление и температуру, если в процессе истечения не происходит теплообмена со средой (k принять равным 1,28). Решение: Если из сосуда вытекает 2/3 содержимого, то удельный объем оставшейся в сосуде углекислоты возрастает втрое. Поэтому: 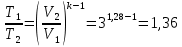 Отсюда получаем 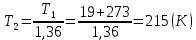 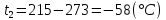 Конечное давление равно: 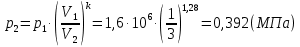 Ответ: t2=-58 ͦС , p2=0,392 МПа. Задача 6.11 Воздух в количестве 1 кг при р1=0,5 МПа и t1=108℃ , расширяется политропно до давления р2=0,1 МПа. Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенной теплоты и полученную работу, если показатель политропы m = 1,2. Решение: Определим начальный объем воздуха: 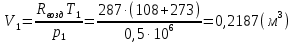 Конечный объем воздуха равен: 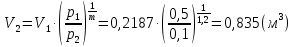 Конечную температуру проще всего получить из характеристического уравнения 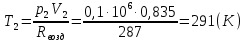 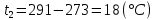 Величина работы 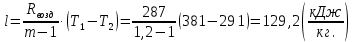 Изменение внутренней энергии находим по общей для всех процессов формуле: 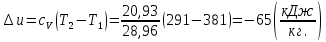 Количество теплоты, сообщенной воздуху 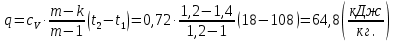 Нетрудно видеть, что в этом процессе внешняя работа совершается за счет подведенной теплоты и уменьшения внутренней энергии. Исходя из этого можно проверить полученные результаты следующим образом: 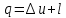 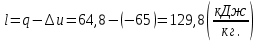 Ответ: ∆u=-65 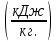 , q=64,8 , q=64,8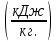 , l=129,2 , l=129,2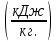 Задача 6.12 Воздух массой 1,5 кг сжимают политропно от р1=0,09 МПа и t1=24℃до р2=1 МПа; температура при этом повышается до t2=108℃.. Определить показатель политропы, конечный объем, затраченную работу и количество отведенной теплоты. Решение: Зависимости между начальными и конечными параметрами политропного процесса: 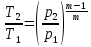 Отсюда найдем показатель политропы m: 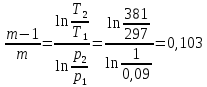 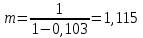 Конечный объем находим из характеристического уравнения: 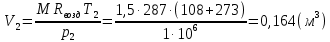 Затраченная работа равна: 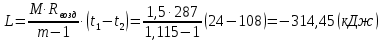 Количество отведенной теплоты: 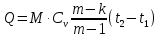 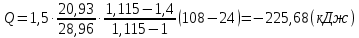 Ответ: m=1,115, V2=0,164 м3, L=-314,45 кДж, Q=-225,68 кДж. |
