философия. практическая работа. Задача 1 Имеются следующие данные о работе промышленных предприятий одной отрасли за год
 Скачать 209.86 Kb. Скачать 209.86 Kb.
|
Рассчитаем для каждой группы проценты выполнения плана.Полученные результаты поместим в таблицу.
Вывод: С увеличением стоимости основных средств выпуск продукции возрастает.Задача 8 Поставки молока и молочных продуктов в торговую сеть города за отчетный период характеризуются следующими данными:
Определить выполнение плана поставки: по каждому продукту; по всем продуктам в условно-натуральном измерении (в пересчете на молоко). Решение: 1) Определим выполнение плана поставки по каждому продукту. Молоко: 805 : 820 100 = 98,2% Сливочное масло: 24 : 21 100 = 114,3% Плавленые сыры: 16 : 13 100 = 123,1% Рассчитаем объем выпуска молочной продукции в пересчете на молоко по плану. Молоко: 820 Сливочное масло: 21 23 = 483 Плавленые сыры: 13 4,2 = 54,6  Итого: 820 + 483 + 54,6 = 1357,6. Итого: 820 + 483 + 54,6 = 1357,6.Рассчитаем фактический объем выпуска молочной продукции в пересчете на молоко. Молоко: 805 Сливочное масло: 24 23 = 552 Плавленые сыры: 16 4,2 = 67,2  Итого: 805 + 552 + 67,2 = 1424,2. Итого: 805 + 552 + 67,2 = 1424,2.Определим степень выполнения задания по выпуску продукции. 1424,2 : 1357,6 100 = 104,9% Вывод: Выпуск молочной продукции по сравнению с планом возрос на 4,9%. Задача 15 Определить установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:
Решение: Среднюю установленную продолжительность трудового дня производственного рабочего по заводу в целом найдем по формуле средней арифметической взвешенной. 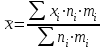 , где xi – продолжительность смены,ni – количество смен,mi – число рабочих в смену. , где xi – продолжительность смены,ni – количество смен,mi – число рабочих в смену.Получаем: 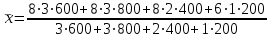 = 41200 : 5200 = 7,923 7,9 ч. = 41200 : 5200 = 7,923 7,9 ч.Задача 22 Имеются следующие данные о рабочем стаже у работающих одного из подразделений предприятия (в годах): 8, 5, 4, 6, 8, 12, 3, 14, 4, 7, 8, 9, 10, 12, 3, 4, 5, 3, 2, 2, 4, 7, 10, 15, 2, 3, 12, 3, 4, 6, 8, 2, 13, 9, 3, 8, 10, 4, 5, 8, 10, 6, 7, 9, 12, 10, 15, 8, 3, 4, 6, 2, 1, 5, 7, 3, 5, 4, 8, 7. Требуется: ранжировать ряд, построить интервальный ряд распределения, вычислить средний стаж работы, колеблемость стажа, моду и медиану для ранжированного и интервального рядов. Решение: Запишем данные в виде таблицы.
Располагая данные о рабочем стаже в порядке возрастания, получаем ранжированный ряд.
Обозначим исследуемый признак через х. Определим размах варьирования признака х. Составим сгруппированный статистический ряд распределения. Количество интервалов примем равным 5. Выделим следующие интервалы:
Подсчитаем количество вариантов признака (частоты) в каждом интервале. Вычислим относительные частоты, разделив частоты в интервале на общую сумму частот. Вычислим середины интервалов, сложив начало и конец интервала и разделив результат на 2. Получим следующий интервальный ряд распределения.
Определим по построенному интервальному ряду моду и медиану. Модальный интервал – это интервал с наибольшей частотой, т.е. «3 – 6». Значение моды определим по формуле: 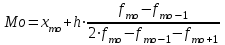 где 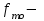 частота в модальном интервале, частота в модальном интервале, 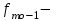 частота в интервале, предшествующем модальному, частота в интервале, предшествующем модальному, 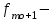 частота в интервале, следующим за модальным, частота в интервале, следующим за модальным, 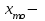 нижняя граница модального интервала, h - величина модального интервала. нижняя граница модального интервала, h - величина модального интервала.В данном случае: 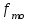 = 17, = 17, 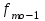 = 14, = 14, 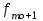 = 16, = 16, 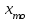 = 3, h = 3. = 3, h = 3. Получим: 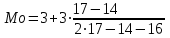 = 5,25 лет. = 5,25 лет.Медианный интервал – это интервал, в котором значение накопленной частоты достигает значения, равного половине суммы частот 60 : 2 = 30. Таким образом, медианным является интервал «3 – 6». Значение медианы определим по формуле: 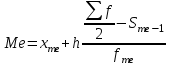 , , где 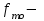 частота медианного интервала, частота медианного интервала, 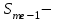 накопленная частота в интервале, предшествующем медианному, накопленная частота в интервале, предшествующем медианному, 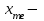 нижняя граница медианного интервала, h - величина медианного интервала. нижняя граница медианного интервала, h - величина медианного интервала. В данном случае: 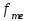 = 17, = 17, 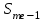 = 14, = 14, 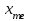 = 3, h = 3. = 3, h = 3.Получим: 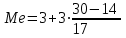 = 5,82 лет. = 5,82 лет.Выборочную среднюю найдем по формуле: 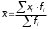 , где xi – варианты, fi – частоты. , где xi – варианты, fi – частоты. Выборочную дисперсию найдем по формуле: 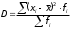 Используя данные расчетной таблицы, получаем: 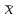 = 366 : 60 = 6,1 лет. = 366 : 60 = 6,1 лет.Дисперсия: 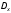 = 764,4 : 60 = 12,74. = 764,4 : 60 = 12,74.Вычислим среднее квадратическое отклонение 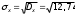 = 3,57. = 3,57.Вычислим коэффициент вариации: 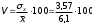 = 58,5%. = 58,5%.Вычислим величину среднего стажа по несгруппированным данным: 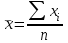 = 397 : 60 = 6,62 лет. = 397 : 60 = 6,62 лет.Вычислим по несгруппированным данным значения моды и медианы. Мода дискретного ряда – это величина, встречающаяся в данной совокупности чаще других. Такой величиной являются значения 3, 4 и 8. Медиана дискретного ряда – это величина, стоящая в середине ранжированного ряда. Поскольку ряд включает в себя 60 значений, то медианой будет являться среднее арифметическое значений, стоящих на 30-й и 31-й позициях, т.е. медианой является число 6. |
