философия. практическая работа. Задача 1 Имеются следующие данные о работе промышленных предприятий одной отрасли за год
 Скачать 209.86 Kb. Скачать 209.86 Kb.
|
|
Задача 29 Выпуск продукции по предприятию в неизменных отпускных ценах составил:
Требуется определить абсолютный прирост, темпы роста и прироста (базисные и цепные), абсолютное значение одного процента прироста, средний темп прироста, средний уровень ряда. Произвести аналитическое выравнивание ряда динамики (по прямой) и построить его графическое изображение. Решение: Определим цепные, базисные и средние показатели анализа ряда динамики. Абсолютные приросты вычислим по формуле At = yt - y0 (по базисной схеме) и at = yt – yt-1 (по цепной схеме). Темпы роста вычислим по формуле 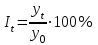 (по базисной схеме) (по базисной схеме)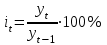 (по цепной схеме). (по цепной схеме). Темпы прироста вычислим по формуле 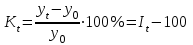 (по базисной схеме), (по базисной схеме), 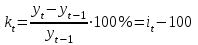 (по цепной схеме). (по цепной схеме).Полученные значения поместим в таблицу.
Вычислим средний уровень ряда. 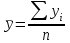 = 1120 : 7 = 160 млн. руб. = 1120 : 7 = 160 млн. руб.Определим среднегодовые абсолютный прирост, темпы роста и прироста. 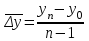 = (210 – 100) : (7 1) = 18,3 млн. руб. = (210 – 100) : (7 1) = 18,3 млн. руб.Вычислим средние темпы роста и прироста. 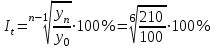 = 113,2% = 113,2%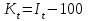 = 113,2 100 = 13,2% = 113,2 100 = 13,2%Произведем аналитическое выравнивание уровней ряда динамики. По виду графика предположим, что зависимость описывается уравнением прямой: y = at + b. Для определения параметров 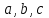 составим систему уравнений составим систему уравнений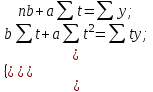 Составим вспомогательную таблицу.
Подставим полученные значения в систему уравнений. 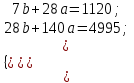 Решая эту систему уравнений, получаем: a = 18,39; b = 86,43. Уравнение прямой имеет вид: y = 18,39t+ 86,43. Рассчитаем по полученному уравнению выровненные уровни ряда динамики рассчитаем среднюю ошибку аппроксимации.
Построим графическое изображение исходного ряда и выравненных уровней. 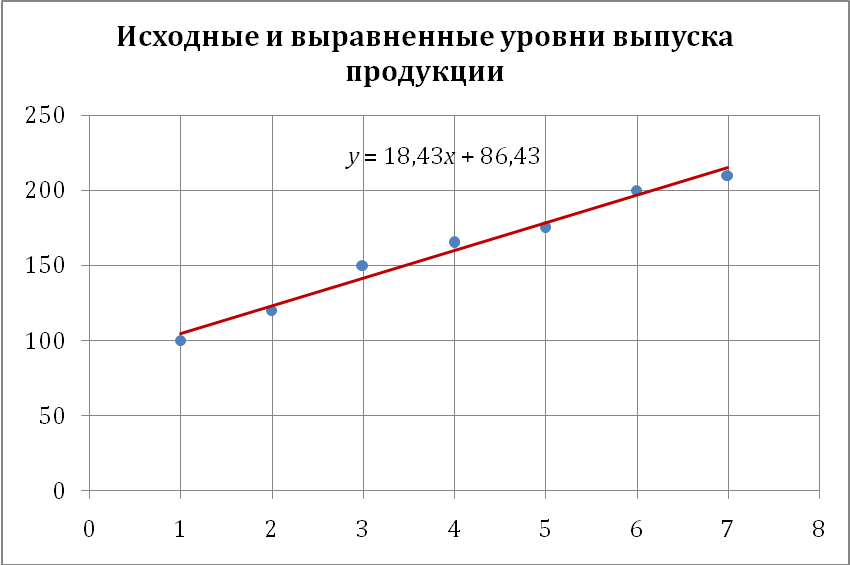 Задача 36 Вычислить по нижеследующим данным сводный агрегатный индекс себестоимости тонны продукции завода и тождественные ему среднеарифметический и среднегармонический индексы.
Определить сумму снижения (повышения) общей величины затрат на производство за счет изменения объема изготовленной продукции и себестоимости тонны продукции. Решение: Вычислим индивидуальные индексы себестоимости: 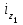 = 7,2 : 8,0 = 0,9; = 7,2 : 8,0 = 0,9;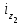 = 3,6 : 4,0 = 0,9. = 3,6 : 4,0 = 0,9.Определим общий индекс себестоимости. 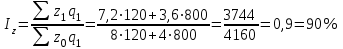 Вычислим общий индекс себестоимости по формуле среднегармонического индекса. 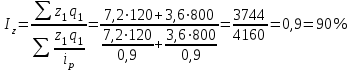 Вычислим общий индекс себестоимости по формуле среднеарифметического индекса. 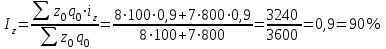 Определим общий индекс физического объема. 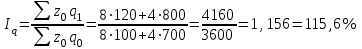 Общее изменение затрат составило: Z =Z1 –Z0 = 3744 – 3600 = 144 тыс. руб. В том числе за счет изменения: а) физического объема продукции: Z(q) = Z0 ( 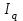 – 1) = 3600 (1,156 – 1) = 560 тыс. р. – 1) = 3600 (1,156 – 1) = 560 тыс. р.б) себестоимости: Z(z) = Z0 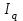 ( (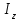 – 1) = 3600 1,156 (0.9 – 1) = -416 тыс. р. – 1) = 3600 1,156 (0.9 – 1) = -416 тыс. р.Выводы: Себестоимость в целом снизилась на 10%, что привело к уменьшению затрат на 416 тыс. р.; физический объем продукции возрос на 15,6%, что привело к увеличению затрат на 560 тыс. р. Общее увеличение затрат составило 144 тыс. р.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||