Статистика Ангелина. Задача 1 Имеются следующие данные об обороте и среднесписочной численности работников двадцати торговых предприятий

• Название: Задача 1 Имеются следующие данные об обороте и среднесписочной численности работников двадцати торговых предприятий
• Дата: 23.05.2022
• Размер: 107.47 Kb.
• Имя файла: Статистика Ангелина.docx
• Тип: Задача; #545630

Задача 1

Имеются следующие данные об обороте и среднесписочной численности работников двадцати торговых предприятий:

№ п/п	Оборот, тыс. р.	Среднесписочная численность работников, чел.
1	1313	5
2	311	2
3	1644	4
4	327	2
5	1615	6
6	679	5
7	649	3
8	1023	5
9	892	4
10	1654	5
11	1402	6
12	1146	4
13	578	3
14	734	5
15	875	4
16	508	2
17	1110	4
18	935	3
19	1711	6
20	484	2

С целью выявления зависимости между объемом оборота и средней выработкой на одного работника произведите группировку предприятий по размеру оборота, образовав четыре группы с равными интервалами. В каждой группе и по итогу в целом подсчитайте:

1) количество предприятий;

2) объем оборота – всего в среднем на одно предприятие;

3) среднесписочное число работников – всего и в среднем на одно предприятие;

4) среднюю выработку (оборот на одного работника).

Результаты группировки оформите в разработочной и групповой таблицах. Сделайте выводы.

Решение:

Для выявления зависимости между размером торговой площади и объемом оборота магазинов произведем группировку магазинов по торговой площади, разбив совокупность на четыре группы с равными интервалами.



d – величина интервала;

n – число групп



I – 311-661

II – 661-1011

III – 1011-1361

IV –1361-1711

№ группы	Интервал	Оборот, тыс.р	Среднесписочная численность работников, чел.
I	311-661	311	2
		327	2
		649	3
		578	3
		508	2
		484	2
		2857	14
II	661-1011	679	5
		892	4
		734	5
		875	4
		935	3
		4115	21
III	1011-1361	1313	5
		1023	5
		1146	4
		1110	4
		4592	18
IV	1361-1711	1644	4
		1615	6
		1654	5
		1402	6
		1711	6
		8026	27

№	Интервал	Кол-во предприятий		Оборот, тыс.руб.				Среднесписочная численность работников, чел.
				всего		в среднем		всего		в среднем
I	311-661	6		2857		476,2		14		2
II	661-1011	5		4115		823		21		4
III	1011-1361	4		4592		1148		18		5
IV	1361-1711	5		8026		1605,2		27		5
Итого			20		19590		4052,4		80		16

19590/80=244,875 тыс.р./1 чел.

Вывод: группировка показала наличие и направление зависимости оборота в зависимости от среднесписочной численности работников – с увеличением численности работников на 1 человека также растет среднее значение оборота на 1 предприятие, т.е. увеличение факторного признака влечет за собой увеличение результативного признака.

Задача 12

Данные о численности населения области на начало года (тыс. чел.):

Год	Численность населения, всего	В том числе
		городского	сельского
1-й	2890	1810	1080
2-й	2960	1890	1070
3-й	3130	2065	1065
4-й	3100	2043	1057

Определите:

1) относительные величины структуры (долю городского и сельского населения в общей численности по годам);

2) относительные величины координации (число городского населения на 100 человек сельского);

3) относительные величины динамики численности всего населения в процентах к его численности по первому году.

Решение:

1) Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%):

, где m_i- объем исследуемой части совокупности, M – общий объем исследуемой совокупности.

Для 1 года: ОВС = 1810/2890*100% = 62,63%

ОВС = 1080/2890*100% = 37,37%

Для 2 года: ОВС = 1890/2960*100% = 63,85%

ОВС = 1070/2960*100% = 36,15%

Для 3 года: ОВС = 2065/3130*100% = 65,97%

ОВС = 1065/3130*100% = 34,03%

Для 4 года: ОВС = 2033/3100*100% = 65,58%

ОВС = 1067/3100*100% = 34,42%

2) Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнен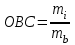ия (%):

, где m_i- одна из частей исследуемой совокупности, m_b- часть совокупности, которая является базой сравнения.

В нашем случае, базой сравнения является численность сельского населения, значит:

Для 1 года ОВК = 1810/1180*100% 168 человек (На 100 жителей сельского населения приходится 168 городского);

Для 2 года ОВК = 1890/1070*100% 177 человек;

Для 3 года ОВК = 2065/1065*100% 194 человек;

Для 4 года ОВК = 2033/1067*100% 191 человек;

3) Относительная величина динамики (ОВД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате получаем коэффициент роста, который выражается кратным отношением. При исчислении этой величины в процентах, (результат умножается на 100) получаем темп роста. Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста-ОВД_б ), так и с переменным базовым уровнем (цепные темпы роста - ОВД_ц)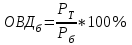



где Р_Т - уровень текущий; Р_б - уровень базисный;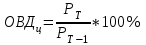



где Р_Т - уровень текущий; Р_Т-1 - уровень, предшествующий текущему;

По условию задачи, рассчитываем ОВД, исходя из численности 1 года, следовательно считаем, тогда:

Для 2 года = 2960/2890*100% = 102,4 % (темп роста населения за второй год увеличился на 2,4 %);

Для 3 года = 3130/2890 = 108,3% (темп роста населения за второй год увеличился на 8,3 %);

Для 4 года = 3100/2890 = 107,3% (темп роста населения за второй год увеличился на 7,3 %).

Задача 35

Данные о производстве яиц в хозяйствах всех категорий области:

Год	Произведено яиц, млн шт.
2007	722
2008	790
2009	896
2010	972
2011	1002

Определите:

1) вид динамического ряда;

2) средний уровень динамического ряда;

3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;

4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.

Результаты расчетов представьте в таблице. Изобразите динамический ряд на графике. Сделайте выводы.

Выполните экстраполяцию уровней динамического ряда на предстоящие два года:

1) по уравнению тренда;

2) с помощью среднего абсолютного прироста;

3) с помощью среднего темпа роста.

Решение:

Имеем интервальный динамический ряд, в котором каждый интервал равен одному году.

Формулы для расчета показателей ряда динамики следующие.

Абсолютный прирост по годам (цепной) и к базисному году, соответственно, равен: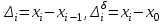



Темп роста по годам и к базисному году, соответственно, равен:



Темп прироста по годам и к базисному году, соответственно, равен:



Между цепными и базисными показателями динамики существует определенная связь:

- сумма абсолютных приростов с переменной базой дает общий прирост за исследуемый период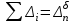

- произведение всех темпов роста по годам равно темпу роста последнего результата к базисному году:

Результаты расчета приведены в таблице.

Год	Произведено яиц, млн шт.	Абсолютный прирост, млн.шт		Темпы роста, %			Темпы прироста, %			Абс. значение 1% прироста
		цепной	к базисному году		цепной	к базисному году		цепной	к базисному году
2007	722	-	-		-	-		-	-		-
2008	790	68	68		109,4	109,4		9,42	9,42		0,7
2009	896	106	174		113,4	124,1		13,42	14,68		0,8
2010	972	76	250		108,5	134,6		8,48	10,53		0,9
2011	1002	30	280		103,1	138,8		3,09	4,16		1,0
Итого	4382	+280	772

Среднегодовой абсолютный прирост определим по формуле:

млн.шт.

Среднегодовые темпы роста и прироста:

или 108,5%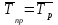

=108,5-100 = 8,5%,

то есть ежегодно уровни ряда возрастали в среднем на 8,5%.

Представим динамический ряд на графике: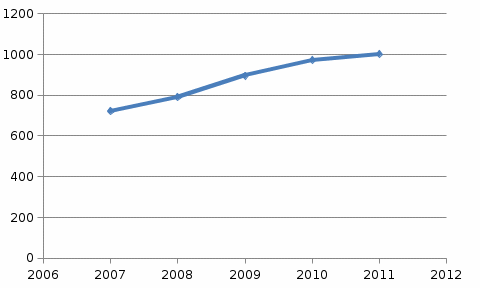

Рис.1. Динамика роста производства яиц в хозяйствах всех категорий области за 2007 -2011 гг.
Вывод: объем производства яиц за 4 года вырос на 280 млн. шт. Среднегодовой абсолютный прирост производства яиц составил 70 млн. шт. или 8,5%. На графике так же виден рост производства яиц.

Задача 47

Оборот и изменение цен в магазине за два периода:

Товарные группы	Оборот, тыс. р.		Изменение цен в отчетном периоде по сравнению с базисным, %
	базисный период	отчетный период
А	100	110	+ 10
Б	90	100	+ 5
В	70	70	Без изменения

Определите:

1) индивидуальные и общий индексы цен;

2) общие индексы оборота в действующих и сопоставимых ценах;

3) абсолютную сумму переплат населения в связи с изменением цен. Покажите взаимосвязь индексов. Сделайте выводы.

Решение:

Для проведения необходимых расчетов построим дополнительную таблицу:

Группа товаров	оборот тыс.р.		Изменение цен в отчетном периоде по сравнению с базисным, %	Цена базисного периода, усл.ед., q0	Цена отчетного периода, усл.ед., q1
	Базисный период	Отчетный период
1	100	110	+10	1	1,1
2	90	100	+5	1	1,05
3	70	70	0	1	1,0
Итого	260	280

1. Общий индекс оборота в фактических ценах равен: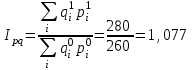




Определим Индекс оборота в сопоставимых ценах:


Общий индекс цен: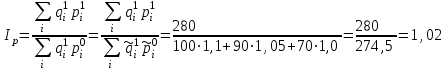


Итак, общий индекс цен составил 1,256, то есть в отчетном периоде по сравнению с базисным общий уровень цен всей реализованной продукции увеличился на 25,6%.

Взаимосвязь между индексами: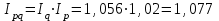



2) Абсолютное изменение оборота, в том числе вследствие изменения физического объема оборота и цен.

Из таблицы видно, что оборот всех трех видов продукции в отчетном периоде по сравнению с базисным увеличилась на 20 тыс. руб. 280-260)

Изменение оборота вследствие изменения физического объема оборота и цен рассчитаем по формулам

а) Изменение цен

тыс.руб.

б) Изменение физического объема товарооборота

тыс.р.

Вывод. оборот в отчетном периоде по сравнению с базисным увеличилась на 20 тыс.р. Его изменение было вызвано изменениями в объемах оборота(+14,5тыс.р.) и за счет непосредственного изменения уровня цен(+5,5тыс.р.). Таким образом, на изменение оборота может оказывать влияние несколько факторов.

Задача 65

Данные о движении кадров производственно-ремонтного предприятия за два года:

Показатели	Базисный год	Отчетный год
Численность работников на начало года	315	308
Принято работников	25	21
Уволено работников	32	29
В том числе:
по собственному желанию	6	2
по сокращению штатов	12	16
на пенсию, по инвалидности, по призыву в армию	10	8
за нарушение трудовой дисциплины, ввиду несоответствия занимаемой должности	4	3

Определите численность работников на конец каждого года, абсолютные и относительные показатели движения кадров за каждый год (коэффициенты оборота по приему, увольнению, необходимого оборота и текучести кадров). Дайте оценку изменения интенсивности движения работников. Сделайте выводы.
Решение:

Численность работников на конец базисного года = 315+25-32 = 308 чел.

Численность работников на конец отчетного года = 308+21-29 = 300 чел.

Абсолютные показатели движения:

- Оборот по приему кадров: Оп₀ = 25; Оп₁= 21.

- Оборот по увольнению: Оу₀ = 32; Оу₁ = 29.

- Общий оборот: Опу₀ = 25+32 = 57; Опу₁= 21+29 = 50.

- Оборот по увольнению необходимый: Ону₀ = 12+10 = 22; Ону₁ = 16+8 = 24.

- Оборот по увольнению излишний: Оту₀ = 5+5 = 10; Оту₁ = 2+3 = 5.

- Средняя списочная численность: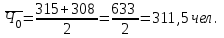





Относительные показатели движения:

- Коэффициенты приема:







- Коэффициенты увольнения: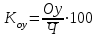







- Коэффициенты общего оборота: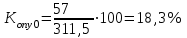







- Коэффициенты необходимого оборота: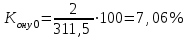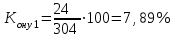







- Коэффициенты излишнего оборота: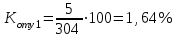







Средняя списочная численность работников в отчетном периоде по сравнению с базисным уменьшилась в том числе за счет уменьшения коэффициентов приема, а также за счет наличия излишнего оборота по увольнению, то есть текучесть кадров увеличилась.

Задача 80

Имеются следующие данные по экономике за год, млрд. р.:

Расходы на конечное потребление:

- домашних хозяйств 1352

- государственных учреждений 572

-некоммерческих организаций,

обслуживающих домашние хозяйства 60

Валовое накопление:

- основного капитала 524

- прирост запасов материальных оборотных средств 98

Экспорт товаров и услуг 640

Импорт товаров и услуг 561

Определите валовой внутренний продукт методом конечного использования.

Решение:

Валовый внутренний продукт определим, просуммировав сумму конечного потребления, валового национального сбережения и сальдо экспорта-импорта.

ВВП=1352+572+60+(524+98)+(640-561)=2685 млрд. р.

Вывод: валовой внутренний продукт равен 2685 млрд.руб.

Задача 96

Имеются следующие данные по торговым предприятиям:

Предприятия	Оборот на ноябрь, тыс. руб.	Товарные запасы на 1 ноября, тыс. р.			Норматив товарных запасов в днях
		в торговой сети	в том числе товары сезонного хранения	кроме того, товары в пути
Первое	150	56	-	4	9
Второе	450	334	10	6	25

Определите:

1) товарные запасы текущего хранения;

2) товарные запасы в днях;

3) отклонения товарных запасов от норматива в днях и в сумме.

Сделайте выводы.

Решение:

1) товарные запасы текущего хранения:





2) товарные запасы в днях:





3) отклонения товарных запасов от норматива в днях и в сумме:



Д=30 дней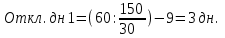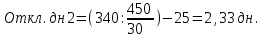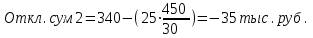











<sub>Таким образом,

по 1 предприятию: товарные запасы текущего хранения – 0,4; товарные запасы в днях – 12; отклонения товарных запасов от норматива в днях – 3 дн., в сумме – 15 тыс.руб.

по 2 предприятию: товарные запасы текущего хранения – 0,76; товарные запасы в днях – 22,7; отклонения товарных запасов от норматива в днях – 2,33 дн., в сумме – (-35) тыс.руб.</sub>

Задача 129

Имеются следующие данные о кредитах коммерческого банка:

Квартал	Среднеквартальная ставка по кредитам, % годовых	Объем выданных кредитов, млн р.
I	18	280
II	16	366
III	15	349
IV	17	329

Рассчитайте среднюю процентную ставку по кредитам банка. Укажите, какую формулу средней использовали.

Решение: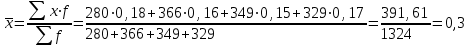



Используя формулу средней арифметической взвешенной определили среднюю процентную ставку по выданным кредитам коммерческого банка. Она составила 30%.

Ответ: 30%

Список литературы

1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1995.

2. Ефимова М.Р. Практикум по общей теории статистики: учебное пособие. – М.: Финансы и статистика, 2003.

3. Практикум по теории статистики: Учебное пособие / Под ред. Р.А. Шмойловой. – М: Финансы и статистика, 1999.

4. Курс социально-экономической статистики: Учебник / Под ред. проф. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.