|
|
произведение высших порядков. Задача 1 Найти производную второго порядка функции Решение
Производные высших порядков
Задача 1:
|
Найти производную второго порядка функции
|
Решение:
|
Согласно определению, вторая производная - это первая производная от первой производной, то есть
Поэтому сначала найдем производную первого порядка от заданной функции согласно правилам дифференцирования и используя таблицу производных:
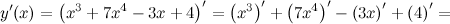
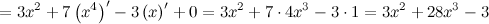
Теперь найдем производную от производной первого порядка. Это будет искомая производная второго порядка:
|
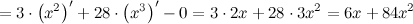
Ответ:
|
|
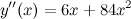
Задача 2:
|
Найти  , если 
|
Решение:
|
Находим первую производную как производную произведения, тогда имеем:
Вторую производную находим как производную от первой производной:
Искомое значение:
|
Ответ:
|
|
Задача 3:
|
Найти производную  -го порядка функции
|
Решение:
|
Будем последовательно находить производные первого, второго, третьего и так далее порядков заданной функции для того, чтобы установить закономерность, которую можно будет обобщить на -ую производную.
Производную первого порядка находим как производную частного:
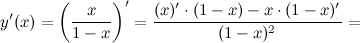
Здесь выражение 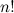 называется факториалом числа (читается "эн факториал"). Факториал числа равен произведению чисел от одного до , то есть
Производная второго порядка есть первая производная от первой производной, то есть
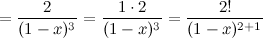
Производная третьего порядка:
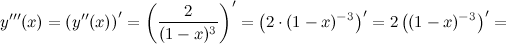
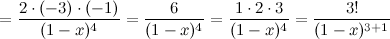
Четвертая производная:
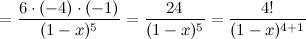
Заметим закономерность: в числителе стоит факториал числа, которое равно порядку производной, а в знаменателе выражение 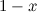 в степени на единицу больше, чем порядок производной, то есть
|
Ответ:
|
|
Задача 4:
|
Найти производную пятого порядка функции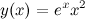 
|
Решение:
|
В силу того, что заданная функция есть произведение двух функций  и 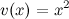 , то для нахождения требуемой производной применим формулу Лейбница:
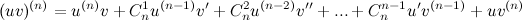
Найдем все производные, находящиеся в правой части указанного равенства и посчитаем коэффициенты при слагаемых. -ая производная функции равна:
Найдем последовательно производные функции :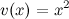
Итак, можем сделать вывод, что  для 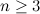 . Тогда формула Лейбница для заданной функции немного упростится (исчезнут слагаемые, которые содержат производную функции 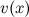 , начиная с третьего порядка):
Вычислим теперь оставшиеся коэффициенты  :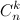
Тогда
Так как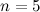 
|
Ответ:
|
| |
|
|
Скачать 123 Kb.