задачи термо. Задача 1 Определить линейную плотность теплового потока для трубки парового котла
 Скачать 50.03 Kb.
|
|
Задача 1 Определить линейную плотность теплового потока для трубки парового котла (λ1 = 50 Вт/(м К)), если внутренний диаметр паропровода dвн = 36 мм, а наружный dнар = 44 мм. Наружная сторона стенки омывается дымовыми газами с температурой tж1 = 920 °С, а внутри движется вода с температурой tж2 = 240 °С. Снаружи труба покрыта слоем сажи (λс = 0,07 Вт/(м К)) толщиной 1,5 мм, а с внутренней стороны - слоем накипи (λн = 0,15 Вт/(м К)) толщиной 2,5 мм. Коэффициент теплоотдачи от дымовых газов к стенке трубки α1 = 220 Вт/(м2 К), а со стороны воды α2= 2500 Вт/(м2 К). Определить также температуры на поверхностях трубки, сажи и накипи. Как изменится линейная плотность теплового потока для «чистой» трубки (без сажи и накипи) при прочих неизменных условиях. Изобразить график изменения температуры по толщине слоев стенки трубки, сажи и накипи в пограничных слоях. Линейный коэффициент теплопередачи от дымовых газов к воде 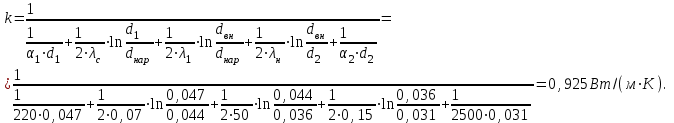 где d1, = dнар + 2 · δс = 0,044 + 2 · 0,0015 = 0,047 м; d2, = dвн- 2 · δн = 0,036 - 2 · 0,0025 = 0,031 м. Линейная плотность теплового потока q = k1 · π · (tж1 - tж2) = 0,925 · 3,14 · (920 - 240)= 1976 Вт/м. Температура: - на поверхности сажи 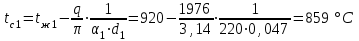 ;- на наружной поверхности трубки 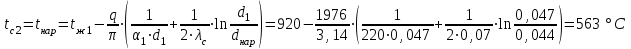 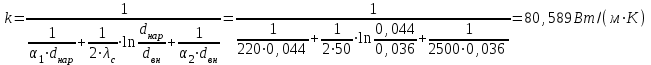 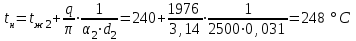 . 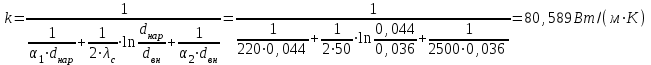q = k1 · π · (tж1 - tж2) = 8,589 · 3,14 · (920 - 240) = 18348 Вт/м. 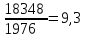 раза.Результаты расчета приведены в таблице:
Задача 2 Определить время нагрева пластины толщиной 2δ =100 мм до заданной температуры поверхности пластины tw = 89 °С, если толщина пластины во много раз меньше её ширины и длины. Найти также среднюю по массе температуру пластины. Исходные данные: - материал пластины - сталь; - коэффициент теплопроводности пластины λ = 40 Вт/(м · К); - удельная теплоемкость Ср = 520 Дж/(кг · К); - плотность ρ = 7700 кг/м3; - одинаковая по толщине начальная температура пластины tо = 30°С; - среда, в которую помещена пластина - масло; - температура среды (поддерживается постоянной) tж=120°С; - коэффициент теплоотдачи от среды к пластине α = 150 Вт/(м2 · К). Рассматривается симметричная задача: Критерий Био 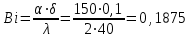 .Критерий Фурье 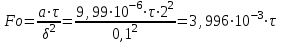 где а - температуропроводность материала пластины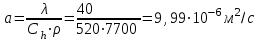 Принимаем Fо > 0,3 и ограничиваемся только первым членом ряда, т.е n=1. Температура на поверхности пластины определяется по формуле 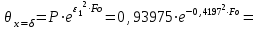 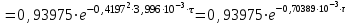 где Р = 0,93975 и ε1 = 0,4197 - коэффициенты для расчета нагревания пластины толщиной 2δ, [1, таблица 2-1]. 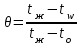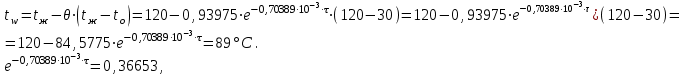Из соотношения  находим искомую температуру откуда находим время нагрева поверхности пластины до заданной температуры поверхности tw = 89 °С τ =1426 с = 23,765 мин. Проверяем критерий Фурье 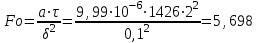 ,т.к.Fо > 0,3, то расчет выполнен верно. Средняя безразмерная температура по толщине пластины, т.к. Fо>0,3, то определяется по формуле: 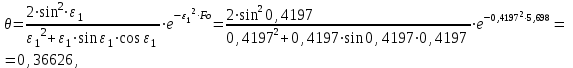 тогда средняя температура по толщине пластины 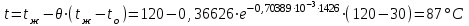 .Задача 3 Определяем режим стекания конденсата: Z=(g*l3/ν2)1/3*λж*∆t/(r*νж*ρж), где νж, ρж, λж – свойства конденсата при t = (tn + tc)/2; tn – температура пара; tc – температура стенки; r – теплота конденсации водяного пара при Р = 0,0042 МПа. При Р = 0,1 МПа: tn = 1000С; r = 2257кДж/кг. При t = (tn + tc)/2 = (100+80)/2 = 900С для воды: - коэффициент кинематической вязкости: νж = 0,326*10-6 м2/с; - коэффициент теплопроводности: λ ж = 68*10-2 Вт/(м·К); -плотность: ρж = 965,3 кг/м3; -критерий Прандтля при t = 900C: Prn = 1,95; -критерий Прандтля при tc = 800C: Prc = 2,21; Z = [9,81*3,53/(0,326*10-6)2]1/3*68*10-2 *(100 – 80)/(2257*103*0,326*10-6 *965,3) Z = 2992 > 2300 – режим стекания плёнки конденсата турбулентный . 2.Число Рейнольдса при турбулентном режиме стекания плёнки конденсата: Re = [89+0,024*(Prn/Prc)0,25*Prn0,5*(Z-2300)]4/3 Re=[89 + 0,024*(1,95/2,21)0,25*1,950,5*(2992 - 2300)]4/3 = 536,5. 3.Коэффициент теплоотдачи: α = Re* r*νж*ρж/(∆t*h) = 536,5*2257*103*0,326*10-6*965,3/(20*3,5) = 5444 Вт/(м2*К). 4.Мощность теплового потока, отводимого трубой при конденсации пара: Q = α*(tп - tс)*F = α*(tп - tс)*π*d*l = 5444*(100 – 80)*3,14*0,02*3,5 = 23932 Вт. |