Курсовая. Теплотехника_Задачи 1-10_Вариант 13_доработка. Задача 1 Определить тепловой поток q вт, проходящий через плоскую многослойную стенку, имеющую поверхность f 94 м
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Задача 1 Определить тепловой поток Q Вт, проходящий через плоскую многослойную стенку, имеющую поверхность F = 94 м2, а также найти температуру на границе слоев, если известно, что стенка состоит из слоя шамота толщиной δ1 = 0,46 м и слоя тепловой изоляции толщиной σ2 = 0,25 м; коэффициенты теплопроводности слоев соответственно λ1 = 0,84 Вт/(м*К) и λ2 = 0,28 Вт/(м*К); температура внутренней поверхности стенки t1 = 1395°С, температура наружной поверхности t3 = 80°С. Как изменится величина теплового потока, если слой тепловой изоляции будет убран, а температура на наружной поверхности стенки увеличится до значения t2 = 90°С. Решение: Термическое сопротивление слоя шамота: 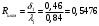 м2·К/Вт м2·К/ВтТермическое сопротивление слоя тепловой изоляции: 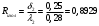 м2·К/Вт. м2·К/Вт.Суммарное термическое сопротивление плоской двухслойной стенки: 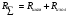 м2·К/Вт м2·К/Вт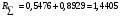 м2·К/Вт. м2·К/Вт.Плотность теплового потока через плоскую двухслойную стенку из закона Определяем плотность теплового потока через двухслойную стенку по формуле 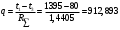 Вт/м2. Вт/м2.Для определения теплового потока, проходящего через стенку при стационарном тепловом состоянии, необходимо его плотность q умножить на поверхность плоской стенки. Тепловой поток по формуле 𝑄 = 𝑞∙𝐹 = 912,893 ∙ 94 = 85812 Вт. Найдем температуру на границе слоев, 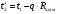 . .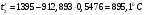 или 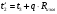 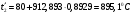 Если слой тепловой изоляции будет убран, а температура на наружной по-верхности стенки увеличится до значения t2= 90°С, величина теплового потока 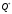 составит. составит.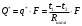 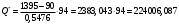 Вт = 224 кВт. Вт = 224 кВт.т.е. увеличится в 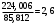 раза. раза.Ответ: тепловой поток 𝑄 = 85812 Вт; температура на границе слоев 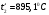 ; ;тепловой поток без слоя изоляции 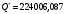 Вт = 224 кВт, Вт = 224 кВт, увеличится в 2,6. «Параметры состояния» Задача 2 Какой объем занимает 1 кг азота при температуре 810С и давлении 0,17 МПа. Решение: Молярная масса азота равна 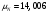 кг/кмоль. кг/кмоль.Объем (удельный) 1 кг азота при заданной температуре и давлении найдем из уравнения Менделеева-Клапейрона: 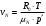 где 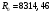 Дж/(кмоль·К) – универсальная газовая постоянная, Дж/(кмоль·К) – универсальная газовая постоянная, 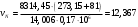 м2⁄кг. м2⁄кг.Ответ: удельный объем азота равен 12,367 м2⁄кг. Задача 3 Во сколько раз объем определенной массы газа при Т1 = -190С меньше, чем при Т2 = 170С, если давление в обоих случаях одинаковое? Решение: При постоянном давлении объем газа изменяется по уравнению: 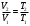 . .Следовательно, 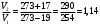 . .Объем определенной массы газа при Т1 = -190С меньше, чем при Т2 = 170С, в 1,14 раза. Задача 4 Определить массу 5 м3 водорода, 5 м3 кислорода и 5 м3 углекислоты при давлении 5 бар и температуре 81 0С. Решение: Молярная масса водорода, кислорода и углекислого газа, соответственно, равна 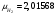 кг/кмоль. кг/кмоль.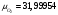 кг/кмоль. кг/кмоль.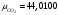 кг/кмоль. кг/кмоль.Масса V, м3 газа при заданной температуре и давлении найдем из уравнения Менделеева-Клапейрона: 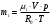 , ,где 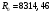 Дж/(кмоль·К) - универсальная газовая постоянная. Дж/(кмоль·К) - универсальная газовая постоянная. Если объем газа, температура и давление одинаковы, можно записать: 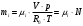 где N – количество киломолей газа. В нашем случае 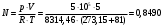 кмоль. кмоль.Тогда масса водорода 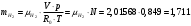 кг. кг.масса кислорода 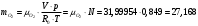 кг. кг.масса углекислого газа 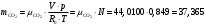 кг. кг.Ответ: масса водорода 1,711 кг; масса кислорода 27,168 кг; масса углекислого газа 37,365 кг. Задача 5 Баллон с кислородом емкостью 21 л находится под давлением 7 Мпа при 130С. После расходования части кислорода давление понизилось на 5,5 Мпа, а температура упала до 70С. Определить массу израсходованного кислорода. Решение: Молярная масса кислорода равна 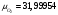 кг/кмоль. кг/кмоль.Начальную массу кислорода m1 в объеме V при заданной начальной температуре t1 и давлении p1 найдем из уравнения Менделеева-Клапейрона: 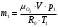 , ,где 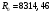 Дж/(кмоль·К) - универсальная газовая постоянная; Дж/(кмоль·К) - универсальная газовая постоянная; 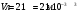 - объем емкости с кислородом. - объем емкости с кислородом. Тогда: 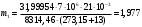 кг кгМассу кислорода m2 после того, как часть его была израсходована, найдем аналогично: 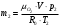 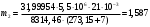 кг кгМасса израсходованного кислорода составляет: 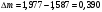 кг = 390 г. кг = 390 г.Ответ: масса израсходованного кислорода составляет 0,39 кг или 390 г. Задача 6 В котельной электрической станции за 20 ч работы сожжены 60 т каменного угля, имеющего теплоту сгорания 28900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 19% тепла, полученного при сгорании. Решение: Количество тепла, превращенного в электрическую энергию за 20 ч работы, Q = 60・1000・28900・0,19 = 3,29・108 кДж. Эквивалентная ему электрическая энергия или работа 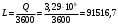 кВт ч. кВт ч.Следовательно, средняя электрическая мощность станции  кВт. кВт.Задача 7 В закрытом сосуде заключен газ при разряжении 49 мм.рт.ст. и температуре 800С. Показания барометра – 760 мм рт.ст. до какой температуры нужно охладить газ, чтобы разряжение стало равным 100 мм рт.ст? Решение: Изохорным называют процесс, протекающий при неизменном объеме рабочего тела. Так как процесс происходит при V = соnst, то зависимость между конечными и начальными параметрами (закон Шарля):  . .Согласно формуле получаем:  , отсюда , отсюда K = 54,70С. K = 54,70С.Ответ: газ нужно охладить до температуры 54,70С. \ Задача 8 1 кг воздуха при давлении P1 = 5,1 бар и температуре 1110С расширяется политропно до давления P2 =1,756 бар. Определить конечное состояние воздуха, изменение внутренней энергии, количество внутренней энергии, количество подведенного тепла и полученную работу, если показатель политропы равен 1,2. Решение: Температура воздуха в конце политропного расширения может быть найдена из уравнения политропного процесса: 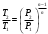 Откуда, 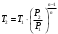 . .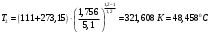 Объем 1 кг воздуха в начале процесса расширения найдем из уравнения Менделеева-Клапейрона: 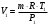 где R = 287 Дж/(кг·К) – газовая постоянная воздуха; тогда 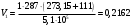 м3/кг. м3/кг.Аналогично объем 1 кг воздуха в конце процесса расширения: 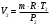 где R = 287 Дж/(кг·К) – газовая постоянная воздуха; тогда 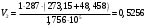 м3. м3.Иначе, из уравнения политропного процесса: 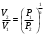 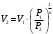 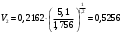 м3. м3.результат такой же. Изменение внутренней энергии U в политропном процессе: 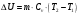 где cv - удельная изохорная теплоемкость воздуха: 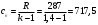 Дж/ (кг·K). Дж/ (кг·K).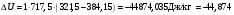 кДж/ кг. кДж/ кг.Изменение внутренней энергии отрицательно, т.к. воздух в процессе охлаждается. Количество подведенного тепла Q в политропном процессе: 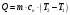 где 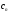 - удельная теплоемкость политропного процесса, находится по формуле: - удельная теплоемкость политропного процесса, находится по формуле: 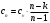 , ,где k = 1,4 – показатель адиабаты воздуха; тогда: 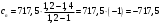 Дж/ (кг·K). Дж/ (кг·K).Теплота политропного процесса: 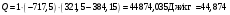 кДж/ кг. кДж/ кг.т.о., в данном политропном процессе 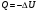 . .Теплота положительна, следовательно, заданный процесс расширения протекает с внешним подводом теплоты. Полученная работа расширения в политропном процессе: 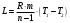 . .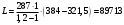 Дж/ кг = 89,7 кДж/ кг. Дж/ кг = 89,7 кДж/ кг.Работа положительна, т.к. процесс идет с увеличением объеме рабочего тела. Иначе, из первого начала термодинамики: 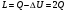 . .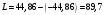 кДж/ кг. кДж/ кг.результат такой же. Ответ: температура в конце расширения 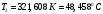 ; ; начальный 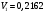 м3 и конечный объем м3 и конечный объем 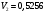 м3; м3;работа расширения 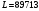 Дж/ кг = 89,7 кДж/ кг; Дж/ кг = 89,7 кДж/ кг; подведенная теплота 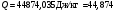 кДж/ кг; кДж/ кг; изменение внутренней энергии воздуха  кДж/ кг. кДж/ кг.Задача 9 «Цикл Карно. Круговые процессы. Компрессоры» Определить расход воды на охлаждение воздуха в рубашке двухступенчатого компрессора производительностью 9,34 м3/мин в промежуточном и концевом холодильниках, если в холодильниках воздух охлаждается до начально температуры, а вода нагревается на 150С. Воздух перед компрессором имеет давление Р1= 1,01 бар и температуру t1= 90С, сжатие воздуха в компрессоре происходит политропно (дать объяснение этому) (n=1,3) до конечного давления Р2 = 8,54 бар. Решение: Количество тепла, отводимого в рубашке компрессора: от 1 кг воздуха -  от G кг воздуха - Q = q G . Количество тепла, отводимого в промежуточном и концевом холодильниках: от 1 кг воздуха –  от G кг воздуха - Qхол = qхол · G . Массовую производительность компрессора определяем из характеристического уравнения:  кг/мин кг/минЗначение газовой постоянной для воздуха берем из таблицы (приложение 1). Rвоз = 287 Дж/(кг·К) Промежуточное давление – уравнение:  бар. бар.Температура в конце сжатия – уравнение:  К = 87,80С. К = 87,80С.Здесь z = 2 (двухступенчатый компрессор). Количество тепла, отводимого в рубашке компрессора,   кДж /мин. кДж /мин.Количество тепла, отводимого в промежуточном и концевом холодильниках,   кДж /мин. кДж /мин.Здесь формула для вычисления теплоемкости идеального газа:  . .Расход охлаждающей воды  кг/мин кг/минЗдесь  кДж/(кг・К) - теплоемкость воды на линии насыщения. кДж/(кг・К) - теплоемкость воды на линии насыщения. Задача 10 «Водяной пар» На получение пара давлением Р = 59 атм затрачено тепла 401 ккал/кг. Определить состояние пара и его плотность, если пар получается из воды с температурой С = 1500С. Решение: Энтальпия воды при температуре 150°С (по табл. Д.1 приложения 2) составляет 632,2 кДж/кг. Зависимость удельной изобарной теплоемкости воды и водянного пара от давления 5,98 Мпа и температуры 1500С: Сp = 4,186 кДж/(кг・К). Теплота, затрачиваемая на получение пара q = Сp・Q = 4,186・401 = 1721,5 кДж/кг. Энтальпия пара hx = h’ + q = 632,2 + 401×4,186 = 2353,7 кДж/ кг. Характеристики водяного пара при давлении 59 aт (5,98 МПа) получаем интерполяцией (табл. Д.2 приложения 4): h’=1212,6 кДж/кг; h’’=2784,6 кДж/кг; r =1572,0 кДж/кг; ’’ = 30,7 кг/м3. Сравнивая энтальпию полученного пара с энтальпией сухого пара, устанавливаем, что пар влажный. Степень сухости пара определяем исходя из уравнения:  Плотность полученного пара  кг/м3. кг/м3.Список использованной литературы 1 Сборник задач по технической термодинамике и теплопередаче / Под ред. Б.Н. Юдаева. – М.: Высш. школа, 1964. – 372 с. 2 Рабинович О.М. Сборник задач по технической термодинамике. – М.: Машиностроение, 1969. – 376 с. 3 Кириллин В.А., Шейндмин А.Е., Шпильрайн Э.Э. Задачник по технической термодинамике. – М.: Госэнергоиздат, 1957. – 256 с. 4 Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. – Л.: Химия, 1970. – 624 с. 5 Болгарский А.В., Голдобеев В.И., Идиатуллин Н.С., Толкачев Д.Ф. Сборник задач по термодинамике и теплопередаче. – М.: Высш. школа, 1972.- 304 с. 6 Дементий Л.В., Кузнецов А.А., Менафова Ю.В. Сборник задач по технической термодинамике и теплопередаче. - Краматорск: ДГМА, 2002. - 260 с.Приложение 1  Приложение 2 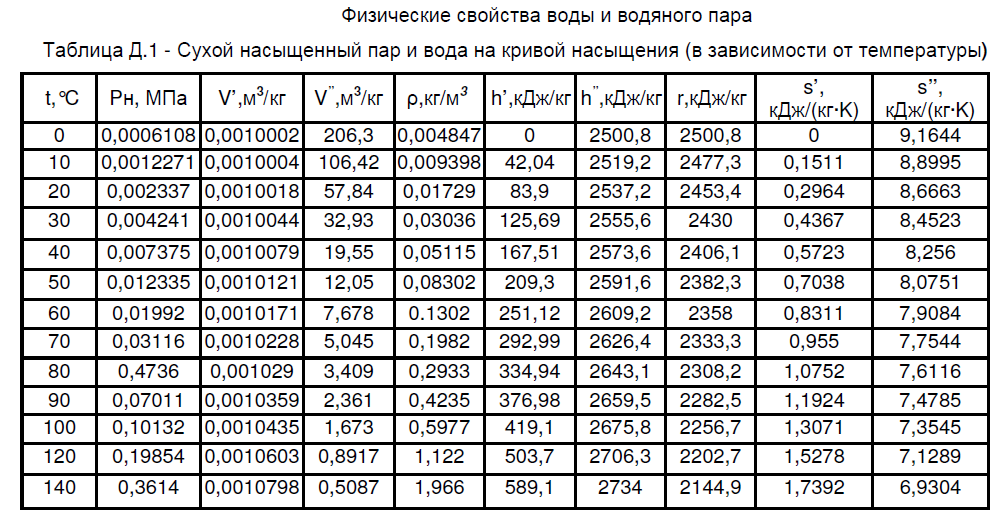 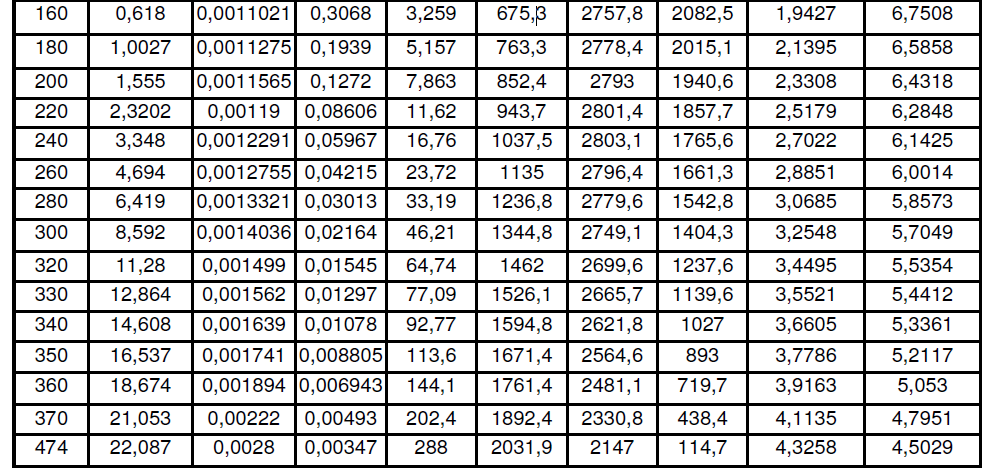 Приложение 2 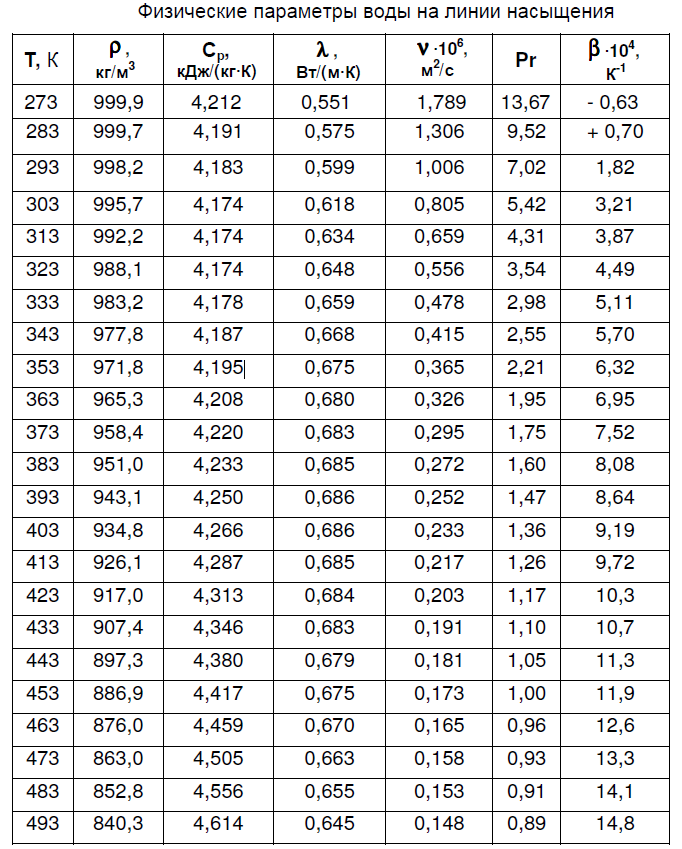 Приложение 4 Таблица Д.2 - Сухой насыщенный пар и вода на кривой насыщения (в зависимости от давления) 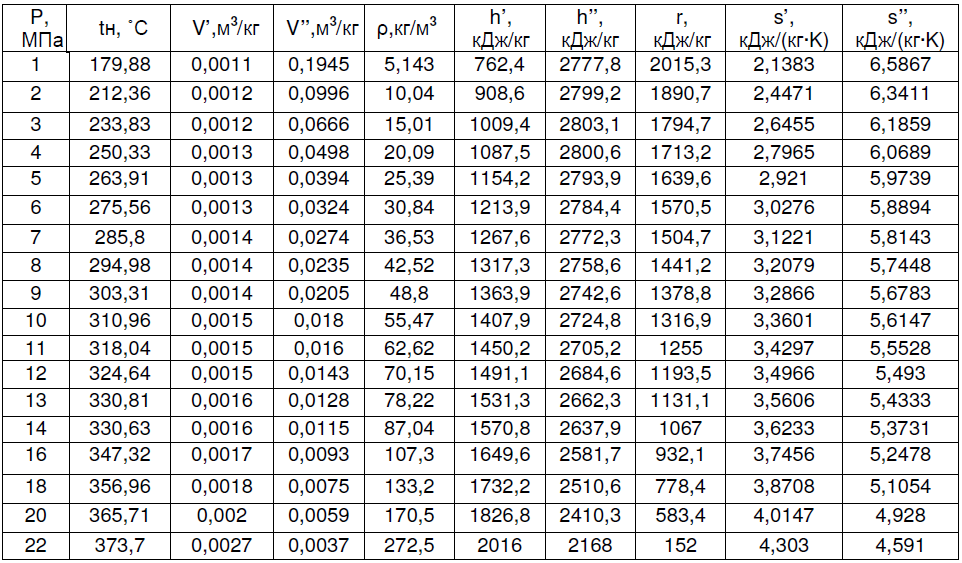 |
