ргз ферма. Задача 1 по дисциплине Основы строительной механики Тема работы Расчет статически неопределимой рамы на прочность студент гр. Агс202
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Расчётно-графическая задача №1 по дисциплине Основы строительной механики Тема работы: Расчет статически неопределимой рамы на прочность Выполнил: студент гр. АГС-20-2 ________________/Сахапова Л.А./ Оценка: ______________ Дата: ________________ Проверил: профессор каф. механики ______________/Насонов М.Ю./ Санкт-Петербург 2022 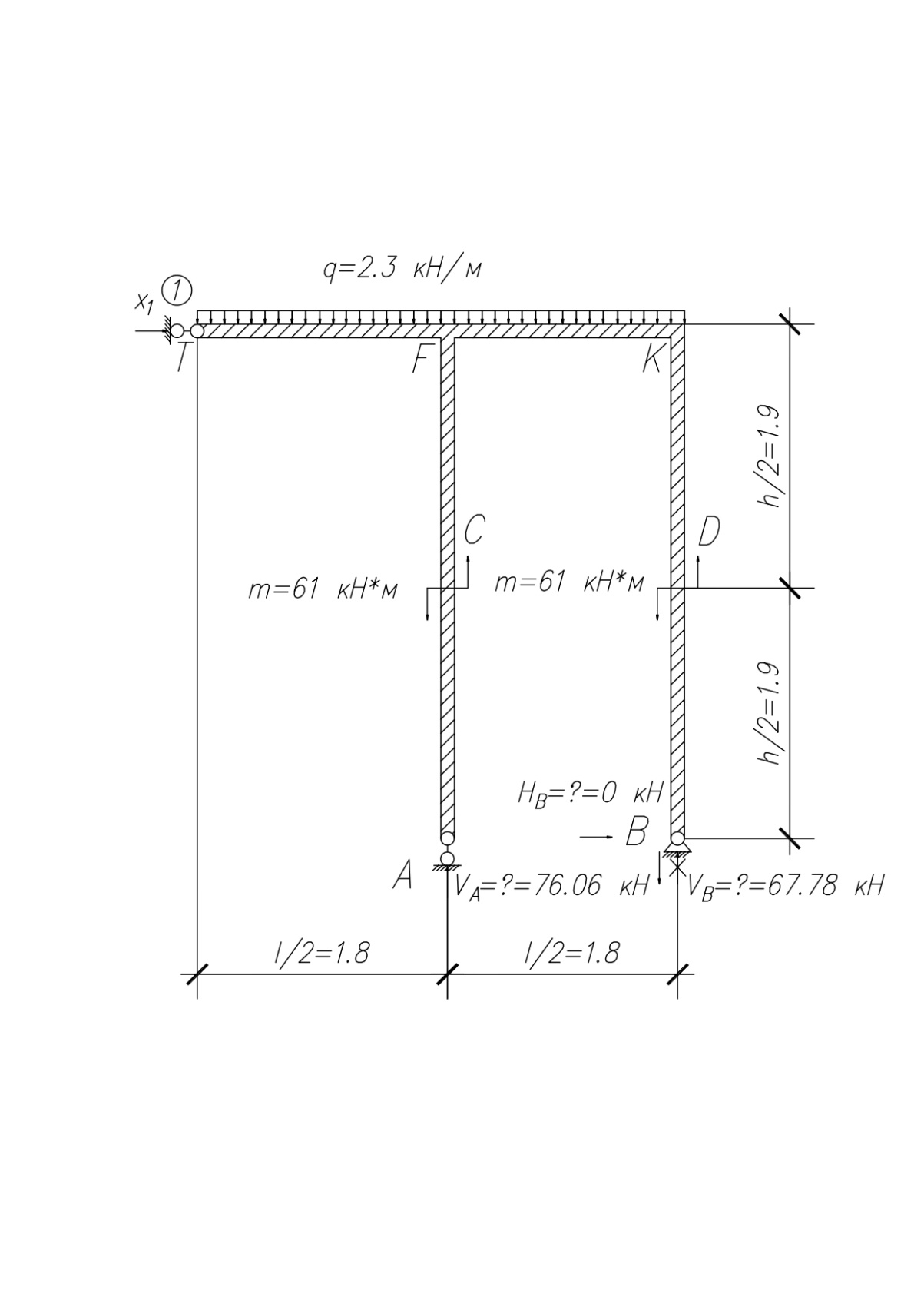 Дано: см. рис. Дано: см. рис.Материал: сталь ВСТ3СП5 R = 240 МПа Задание: Подобрать двутавровое сечение, исходя из условий прочности Решение: Раскрытие статической неопределимости рамы А. Предварительные действия Определим степень статической неопределимости рамы 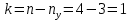 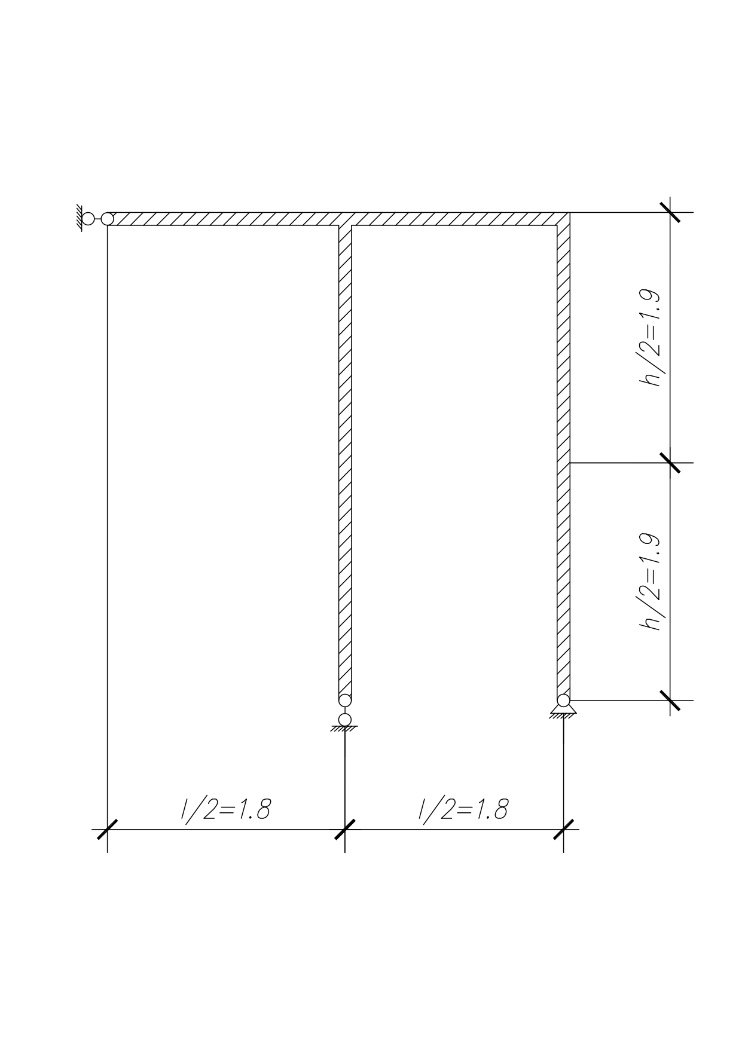 Степень статической неопределимости рамы равна 1 Степень статической неопределимости рамы равна 1Для того, чтобы найти силу x1 необходимо к 3 уравнениям статики добавить 1 уравнение совместности деформации Создадим основную систему 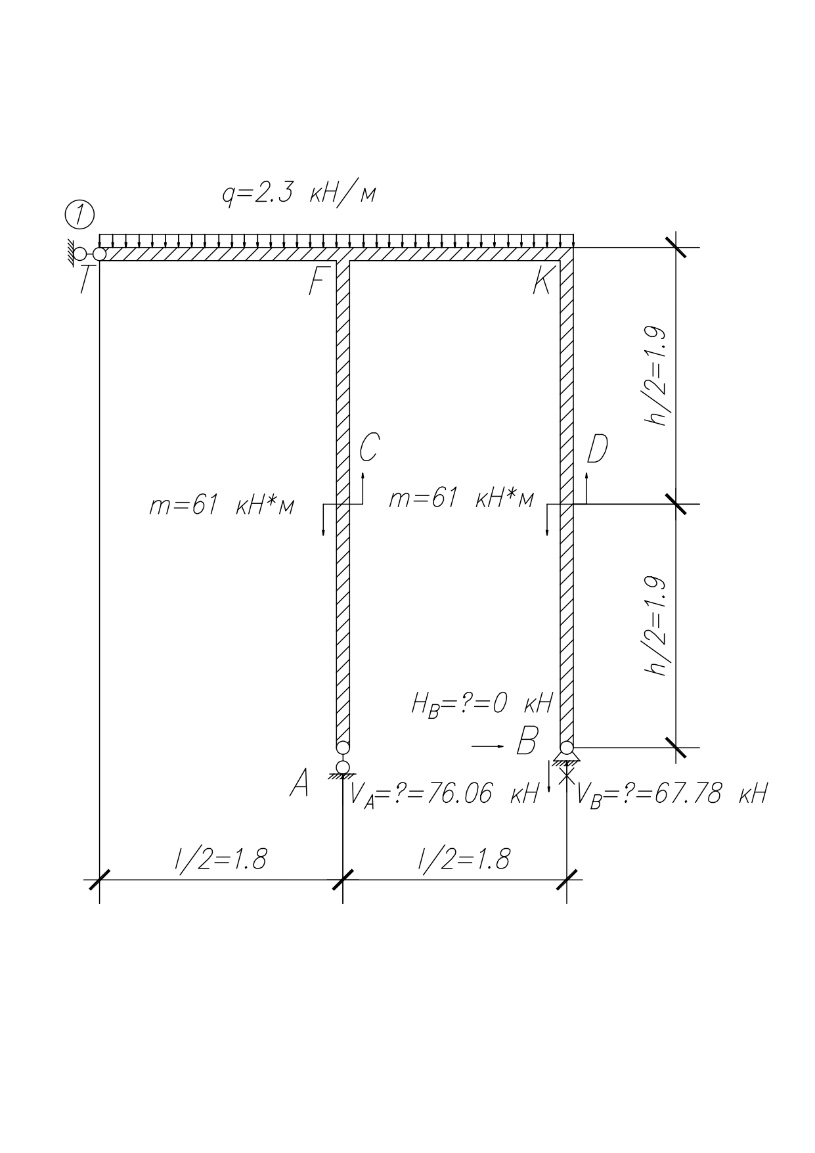 Создадим эквивалентную систему Создадим эквивалентную систему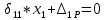 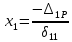 Б. Определим перемещение 1 точки от внешней нагрузки 1. Определим опорные реакции а) ∑x = 0 → HB →+ тм ←– HB – 4.4q = 0 HB – 30.8 = 0 HB = 30.8 кН ⊕ б) Определим опорную реакцию VA ∑mB = 0 → VA +⟲ тм ⟳ – - VA * 4.4 + P *2.2 + q * 4.4 * 2.2 +q* 4.4 * 2.2 = 0 - VA * 4.4 + 20 *2.2 + 7 * 4.4 * 2.2 +7* 4.4 * 2.2 = 0 VA = + 40.8 кН ⊕ в) Определим опорную реакцию VB ∑mA = 0 → VB +⟲ тм ⟳ – + VB * 4.4 + HB * 2.2 – P * 2.2 – q * 4.4 * 2.2 = 0 + VB * 4.4 + 30.8 * 2.2 – 20 *2.2 – 7 *4.4 * 2.2 = 0 VB = 10 кН ⊕ г) Выполним проверку Ⅰ ∑y = 0 ↑+ тм ↓– – P – q * 4.4 + VB + VA = – 20 – 7 * 4.4 + 40.8 + 10 = 0 д) Выполним проверку ⅠⅠ ∑mM = 0 +⟲ тм ⟳ – – VA *3.3 + P * 1.1 + q *4.4 *1.1 – HB *2.2 + VB *1.1 = 0 – 40.8 *3.3 + 20 * 1.1 + 7 *4.4 *1.1 – 30.8 *2.2 + 10 *1.1 = 0 0 = 0 2. Построим эпюры QP и MP 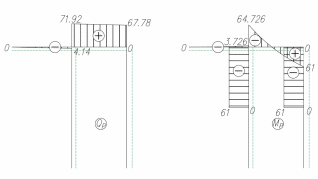 3. Проверим правильность построения эпюры MP по методу вырезания узлов 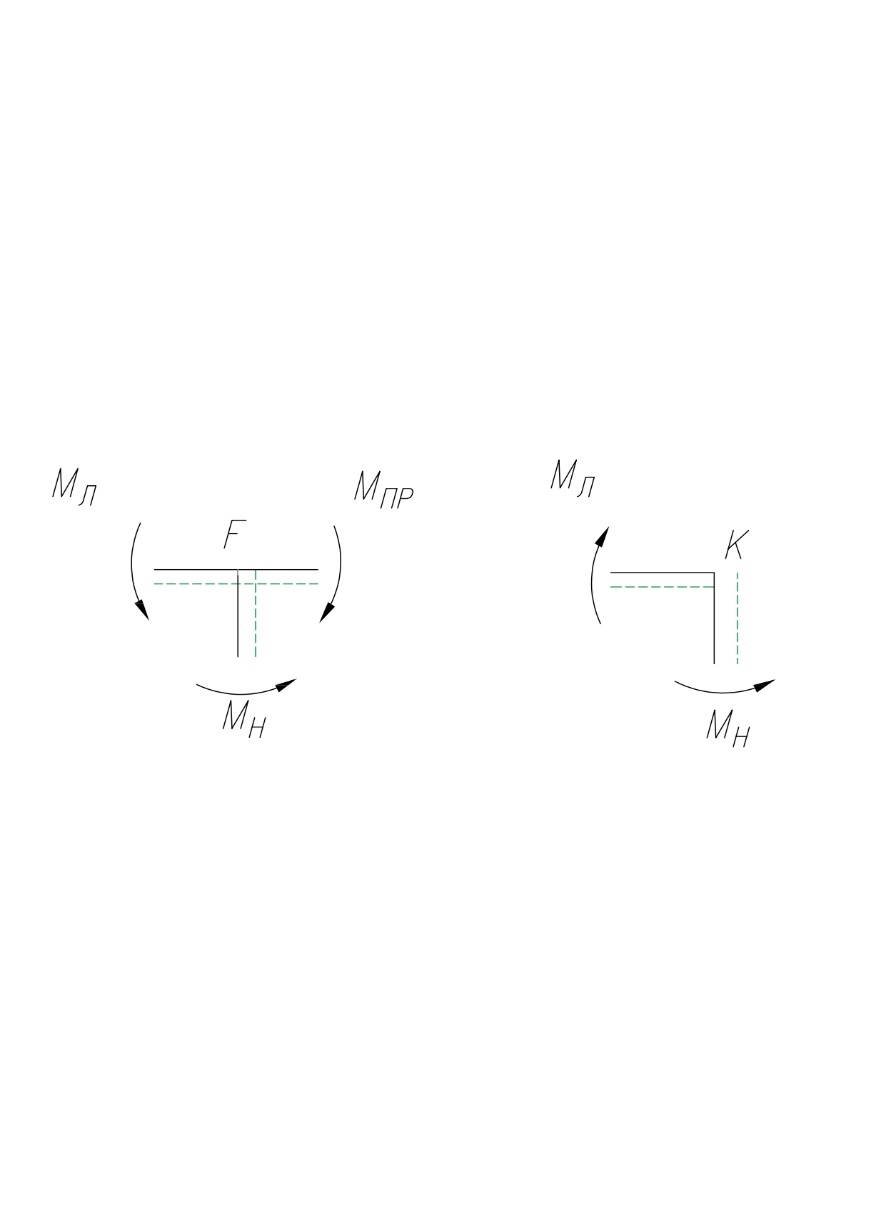 Узел C ∑mF = 0 +⟲ тм ⟳ – + 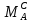 - - 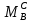 + + 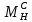 = – 15,4 + 15,4 + 0 = 0 = – 15,4 + 15,4 + 0 = 0Вывод: узел C находится в статическом равновесии 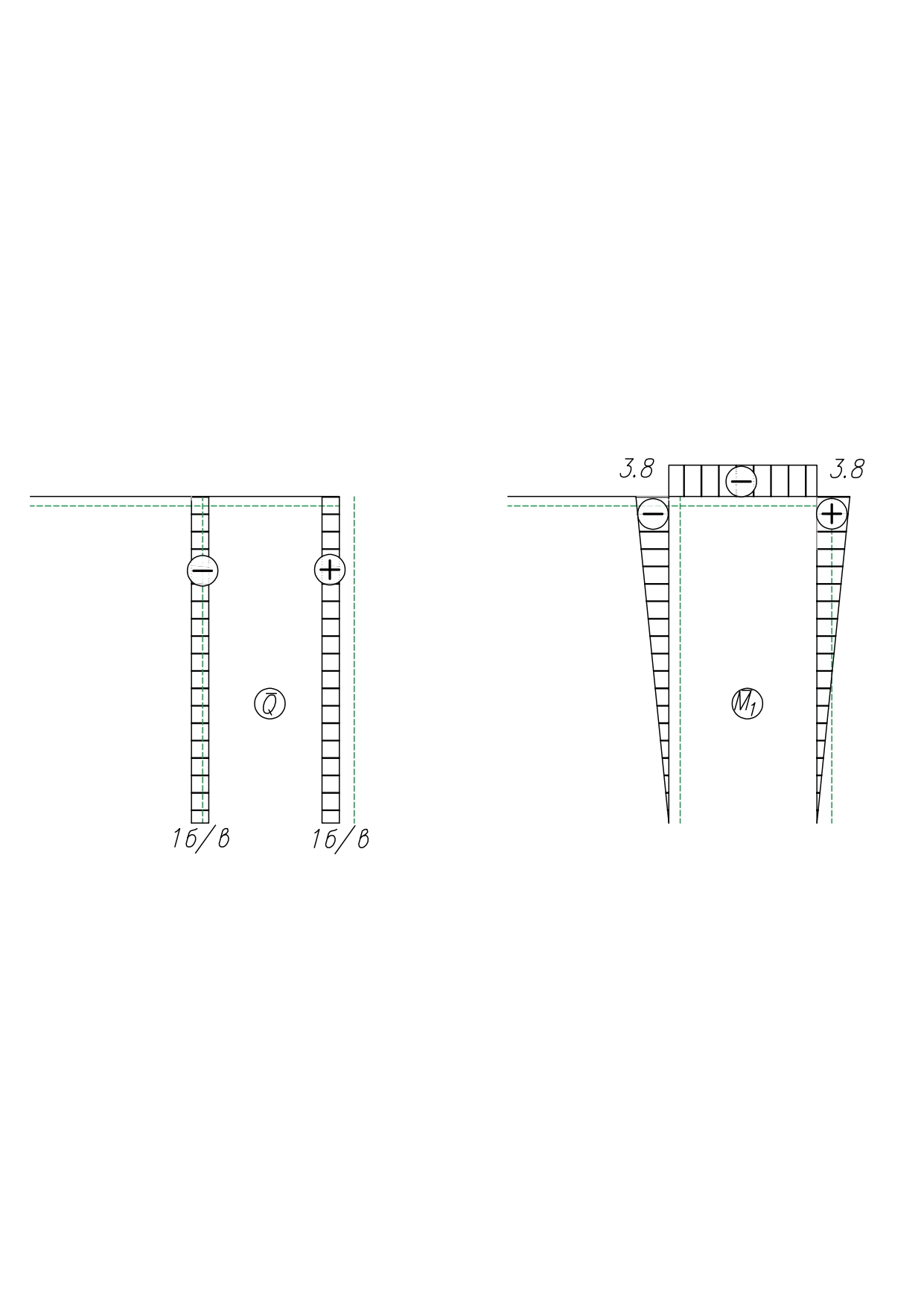 Построим эпюры Q и M от единичной нагрузки Построим эпюры Q и M от единичной нагрузки а) Определим опорные реакции 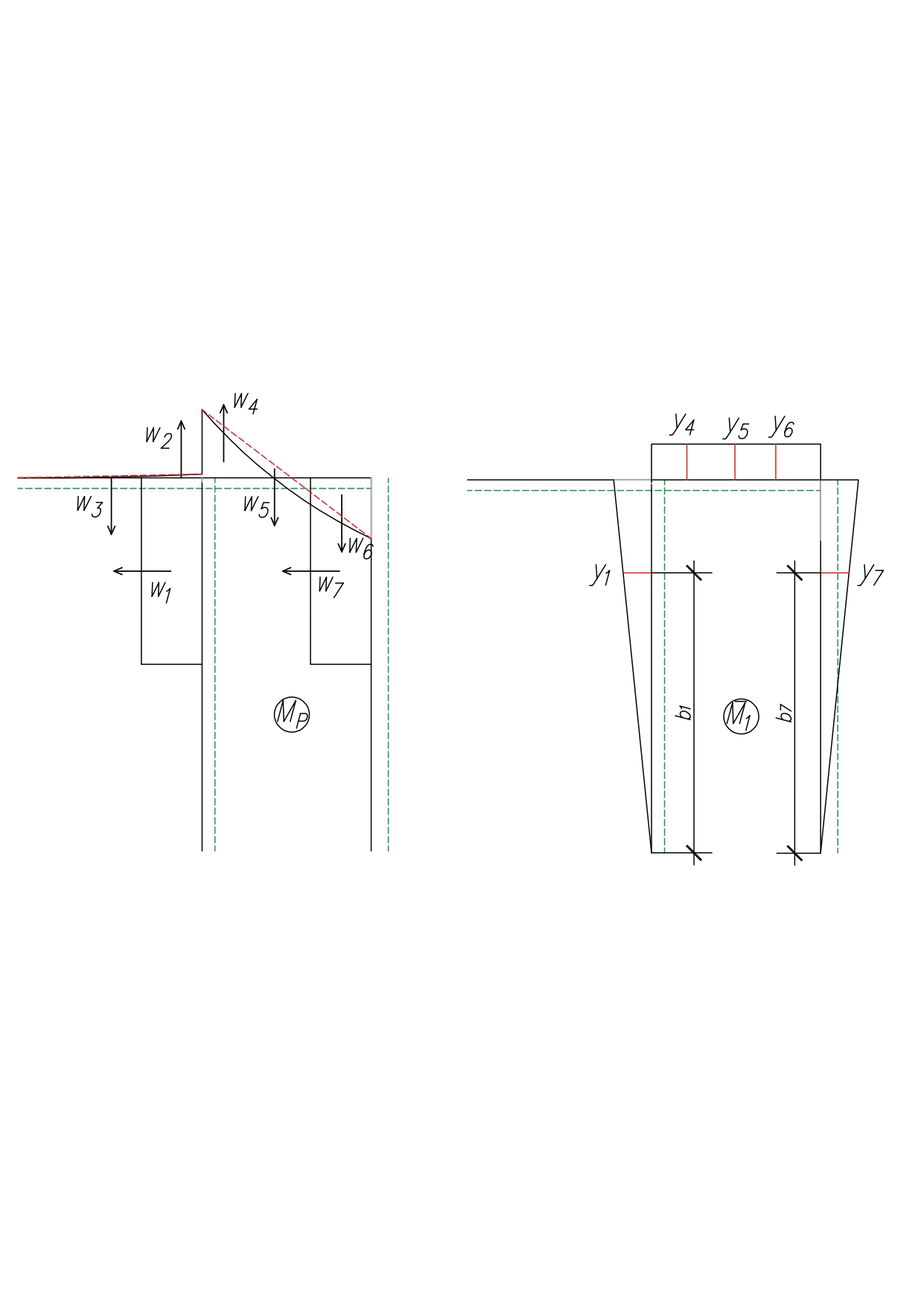 б) Построим эпюры Q и M б) Построим эпюры Q и M Определим перемещение точки 1 от внешней нагрузки а) Определим площади простых фигур 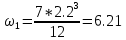 кН*м2 = кН*м2 = 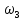 = = 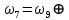 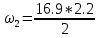 = 18.59 кН*м2 ⊖ = 18.59 кН*м2 ⊖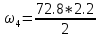 = 80.08 кН*м2 ⊕ = 80.08 кН*м2 ⊕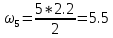 кН*м2 ⊕ кН*м2 ⊕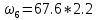 = 149.16 кН*м2 ⊕ = 149.16 кН*м2 ⊕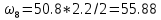 кН*м2 ⊕ кН*м2 ⊕б) Определим ординаты единичной эпюры 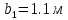 м ⊕ м ⊕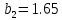 м ⊕ м ⊕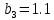 м ⊖ м ⊖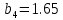 м ⊖ м ⊖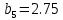 м ⊖ м ⊖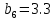 м ⊖ м ⊖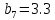 м ⊖ м ⊖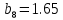 м ⊕ м ⊕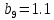 м ⊕ м ⊕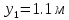 м ⊕ м ⊕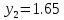 м ⊕ м ⊕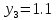 м ⊖ м ⊖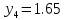 м ⊖ м ⊖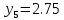 м ⊖ м ⊖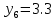 м ⊖ м ⊖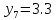 м ⊖ м ⊖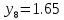 м ⊕ м ⊕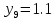 м ⊕ м ⊕в) Определим перемещение точки 1 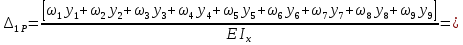 = 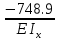 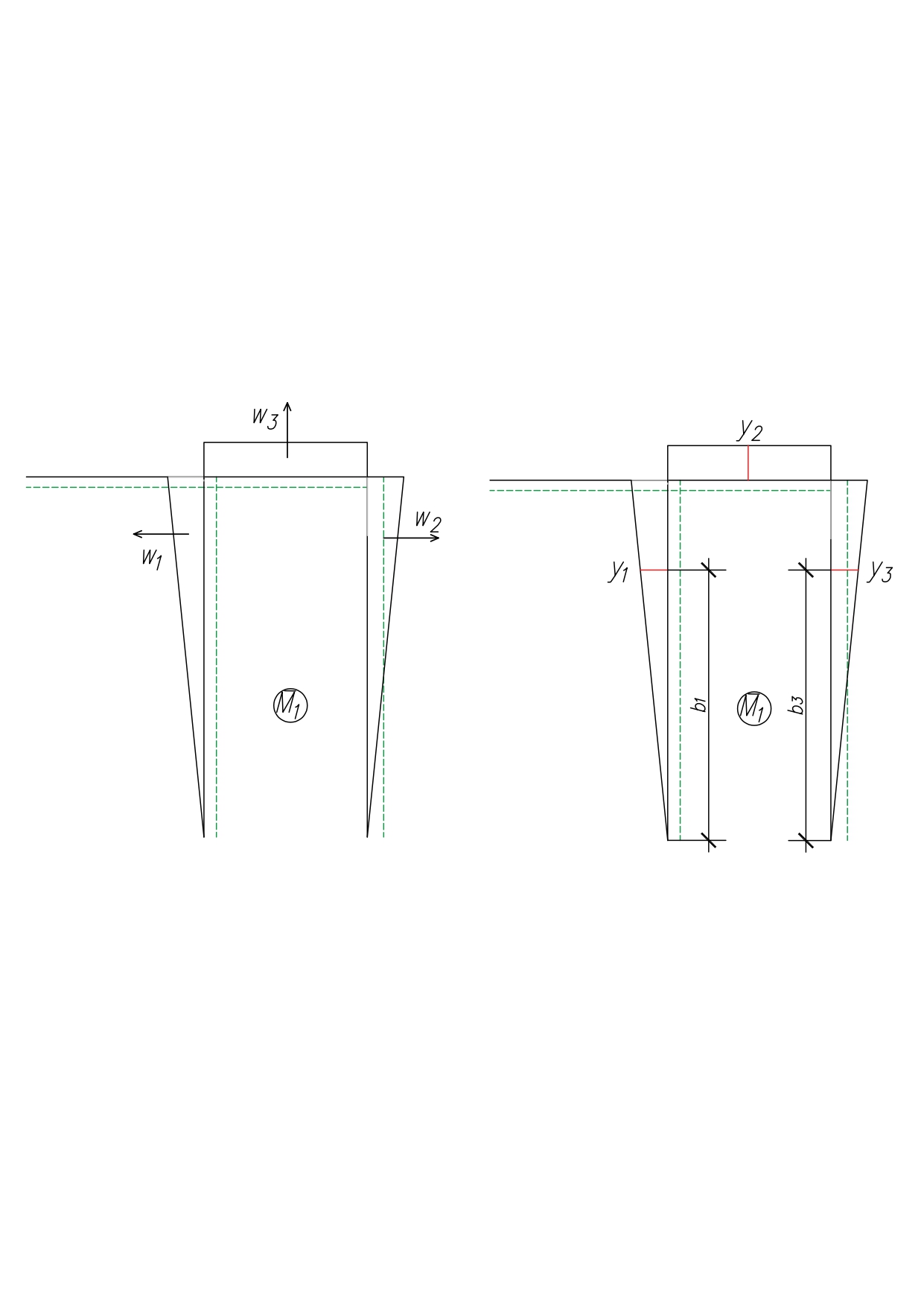 а) Определим площади простых фигур грузовой эпюры 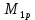 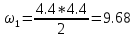 м2 ⊖ м2 ⊖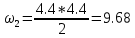 м2 ⊕ м2 ⊕б) Определим ординаты единичной эпюры 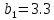 м м 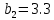 м м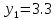 м ⊖ м ⊖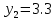 м ⊕ м ⊕ в) Определим перемещение точки 1 от единичной силы 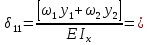 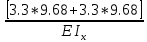 = = 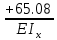 ⊕ ⊕Определим неизвестную силу 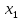 , возникающую в лишней связи , возникающую в лишней связи 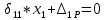 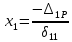 = = 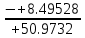 = - 0.17 кН = - 0.17 кНЗнак «-» показывает, что предположение о направлении действия силы 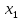 было неверным было невернымРасчет статические определимой рамы 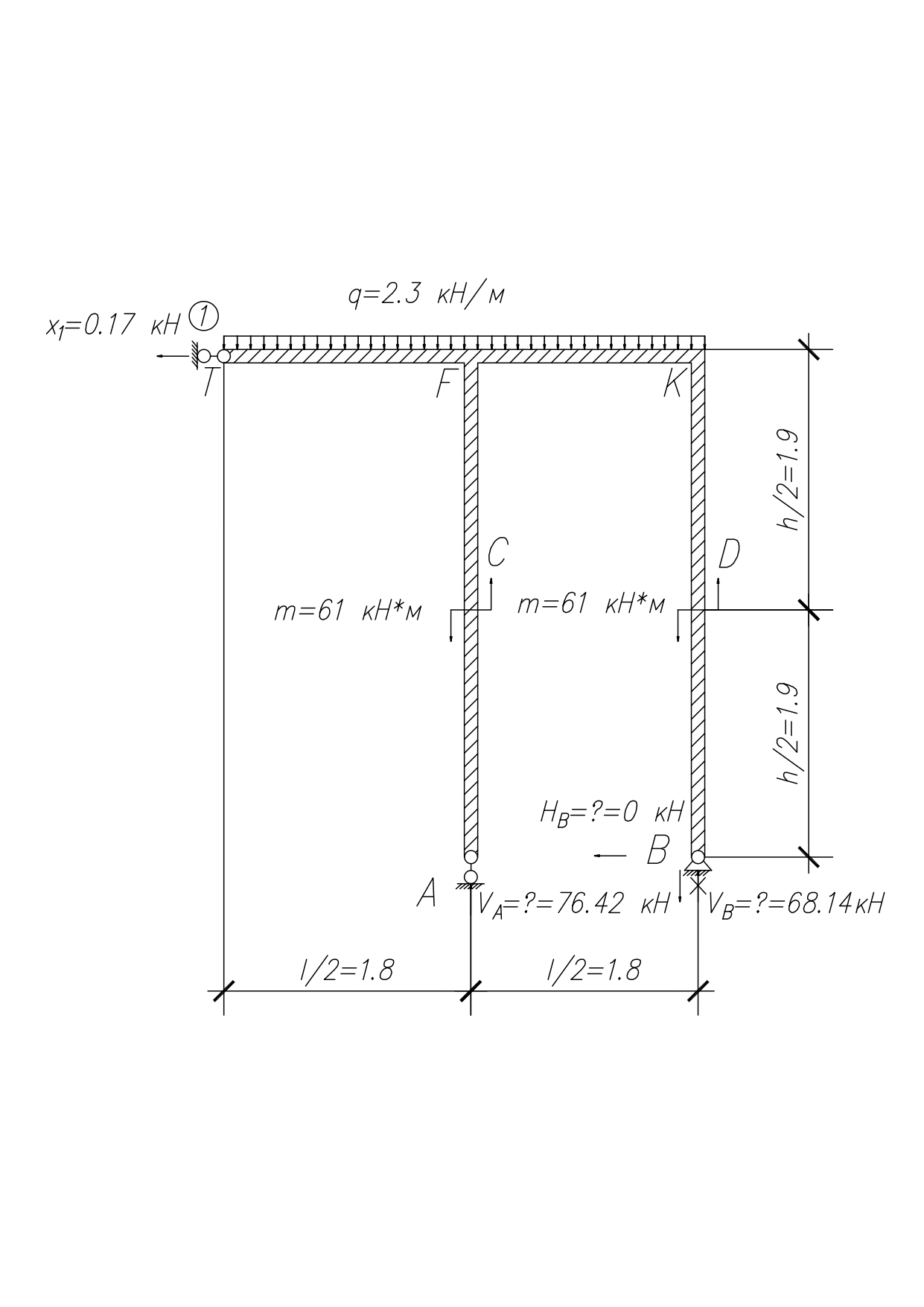 А. Построим эпюры внутренних усилий А. Построим эпюры внутренних усилий1. Определим опорные реакции а) Определим опорную реакцию VB ∑mA = 0 → VB +⟲ тм ⟳ – + VB * 1.8 + m1 + m2 - [q * 1.8] * 0.9 + [q * 1.8] * 0.9 + x1* 3.8 = 0 + VB * 1.8 + 61 + 61 - [2.3 * 1.8] * 0.9 + [2.3 * 1.8] * 0.9 + 0.17 * 3.8 = 0 + VB * 1.8 + 61 + 61 – 3.726 + 3.726 + 0.646 = 0 + VB * 1.8 = - 122.646 + VB = 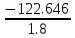 + VB = - 68.14 кН VB = 68.14 кН ⊖ б) Определим опорную реакцию VA ∑mB = 0 → VA +⟲ тм ⟳ – - VA * 1.8 + m1 + m2 + [q * 3.6] * 1.8 + x1* 3.8 = 0 - VA * 1.8 + 61 + 61 + [2.3 * 3.6] * 1.8 + 1.7 * 3.8 = 0 - VA * 1.8 + 61 + 61 + 14.904 + 0.646 = 0 - VA * 1.8 = - 137.55 + VA = 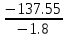 + VA = + 76.42 кН VA = 76.42 кН ⊕ в) ∑x = 0 → HB →+ тм ←– HB – x1 = 0 HB = x1 HB = 0.17 кН ⊕ г) Выполним проверку Ⅰ ∑y = 0 ↑+ тм ↓– - VB – [q * 3,6] + VA = - 2.3 * 3.6 – 68.14 + 76.42 = 0 д) Выполним проверку ⅠⅠ ∑mM = 0 +⟲ тм ⟳ – + VA * 0.9 + m1 + m2 + [q * 0.9] * 0.45 - [q * 2.7] * 1.35 - VB * 2.7 - HB * 3.8 = + 76.42 * 0.9 + 61 + 61 + [2.3 * 0.9] * 0.45 - [2.3 * 2.7] * 1.35 – 68.14 * 2.7 – 0.17 * 3.8 = + 68.778 + 61 + 61 + 0.9315 – 8.3835 – 183.978 – 0.646 = 0 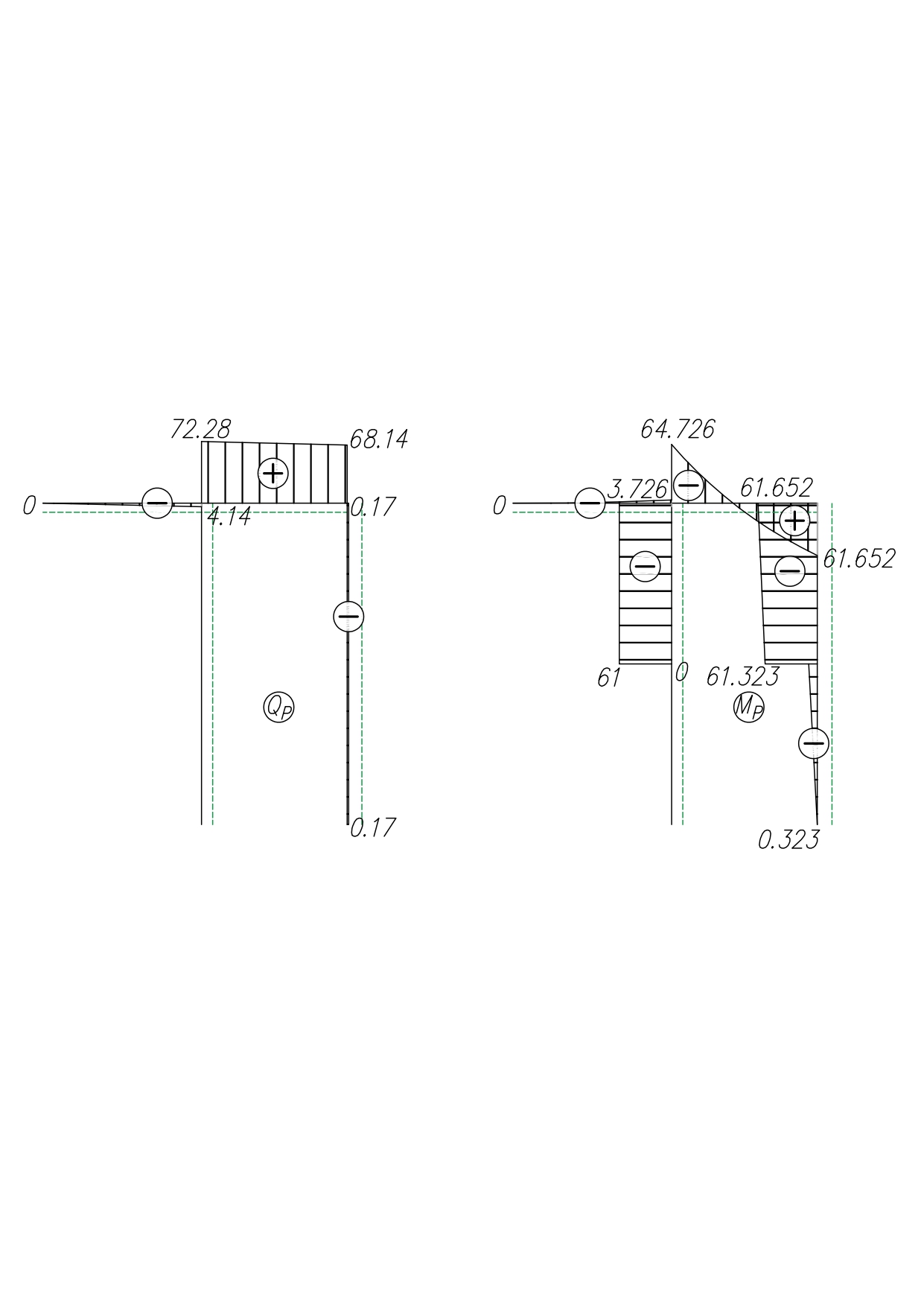 2. Построим эпюры внутренних усилий 2. Построим эпюры внутренних усилий 3. Проверим правильность построения эпюры M методом вырезания узлов 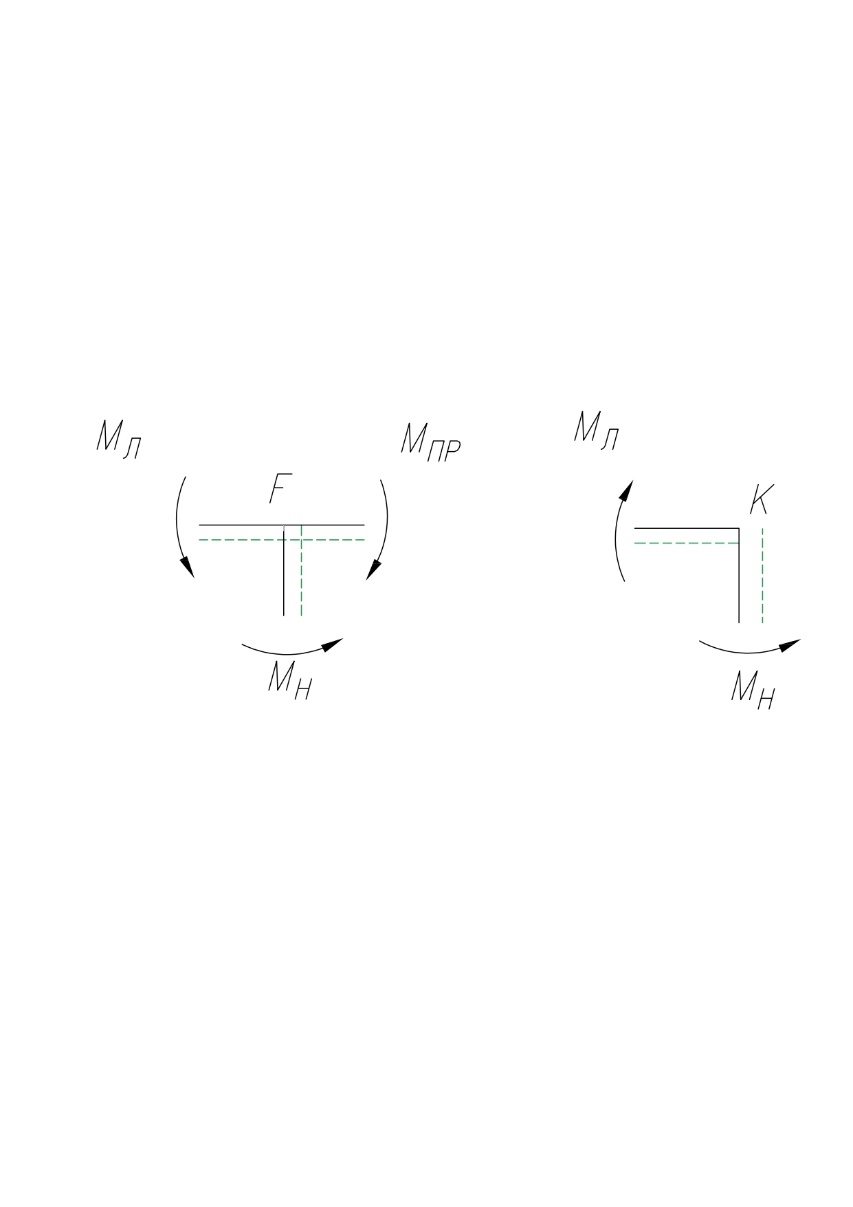 Узел F ∑mF = 0 +⟲ тм ⟳ – + 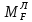 - - 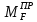 + + 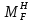 = + 3,726 + 61 – 64,726 = 0 = + 3,726 + 61 – 64,726 = 0Узел K ∑mK = 0 +⟲ тм ⟳ – - 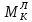 + + 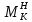 = + 61.652 – 61.652 = 0 = + 61.652 – 61.652 = 0Вывод: узлы F и K находятся в статическом равновесии 4 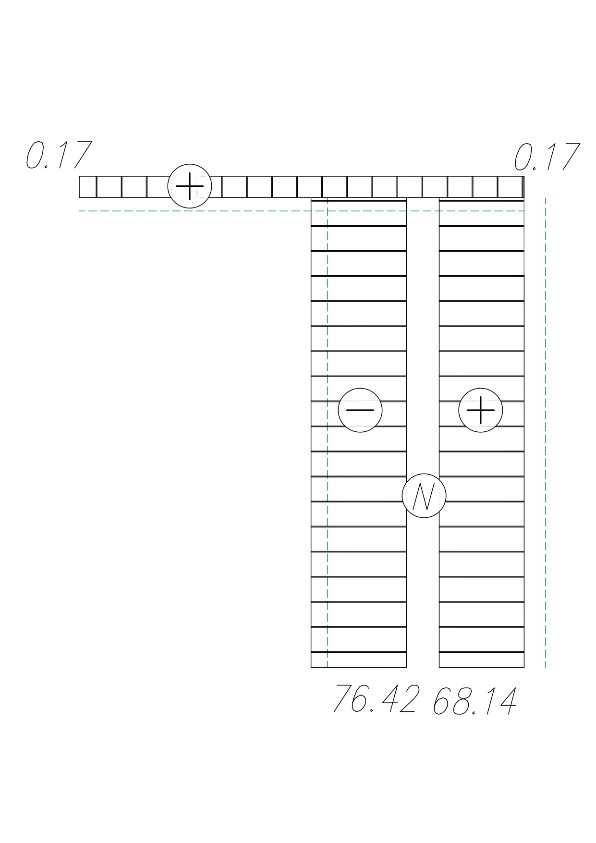 . Проверим правильность построения эпюры Q и N методом вырезания узлов . Проверим правильность построения эпюры Q и N методом вырезания узловУзел F ∑x = 0 →+ тм ←– - Nпр + Nл = - 0.17 + 0.17 = 0 ∑y = 0 ↑+ тм ↓– - Qпр – Qл + Nл = - 4.14 – 72.28 + 76.42 = 0 Узел K ∑x = 0 →+ тм ←– - 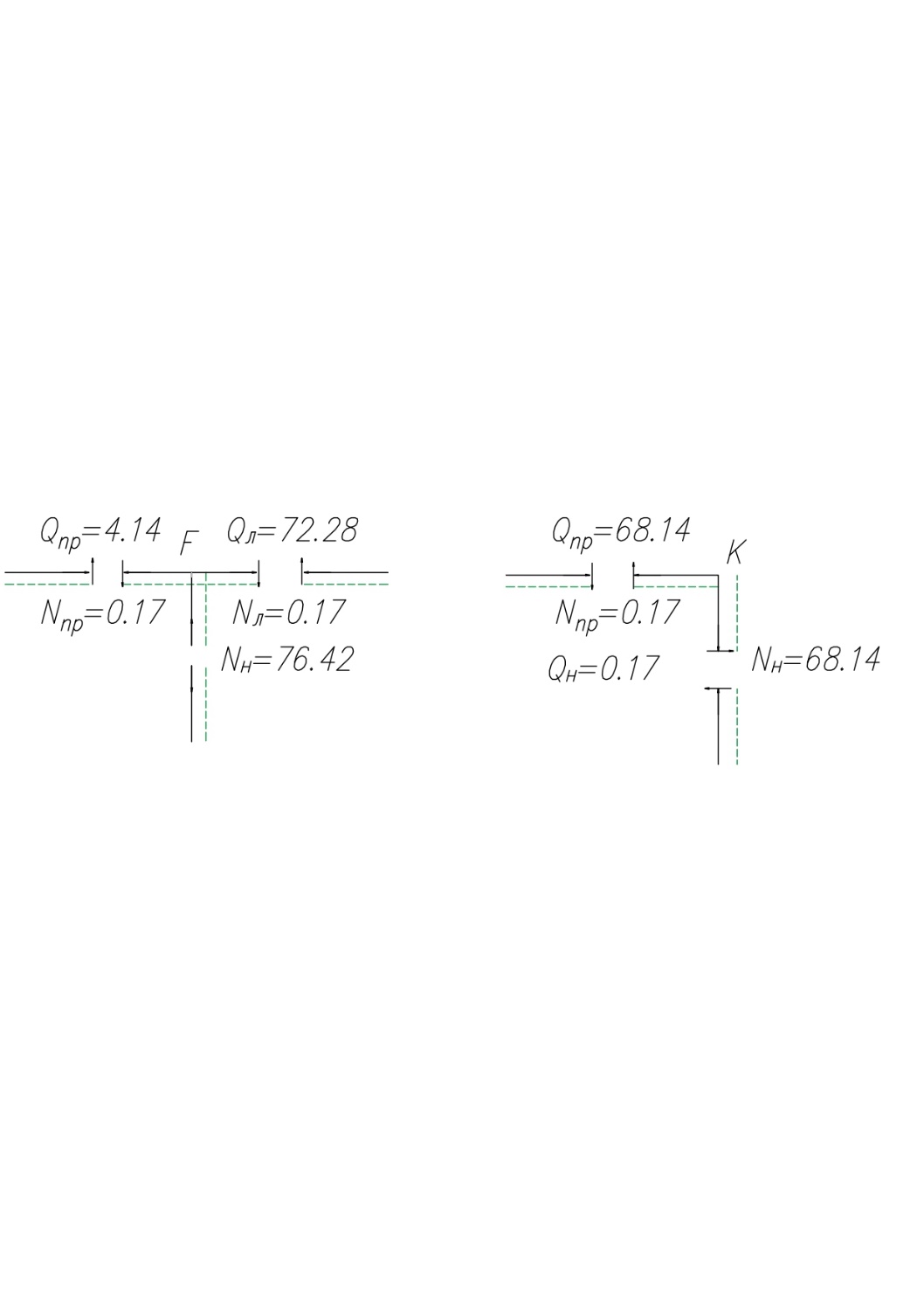 Nпр + Qн = - 0.17 + 0.17 = 0 Nпр + Qн = - 0.17 + 0.17 = 0 ∑y = 0 ↑+ тм ↓– + Qпр – Nн = + 68.14 – 68.14 = 0 5. Определим точность нахождения силы x1 при помощи определения перемещения точки 1 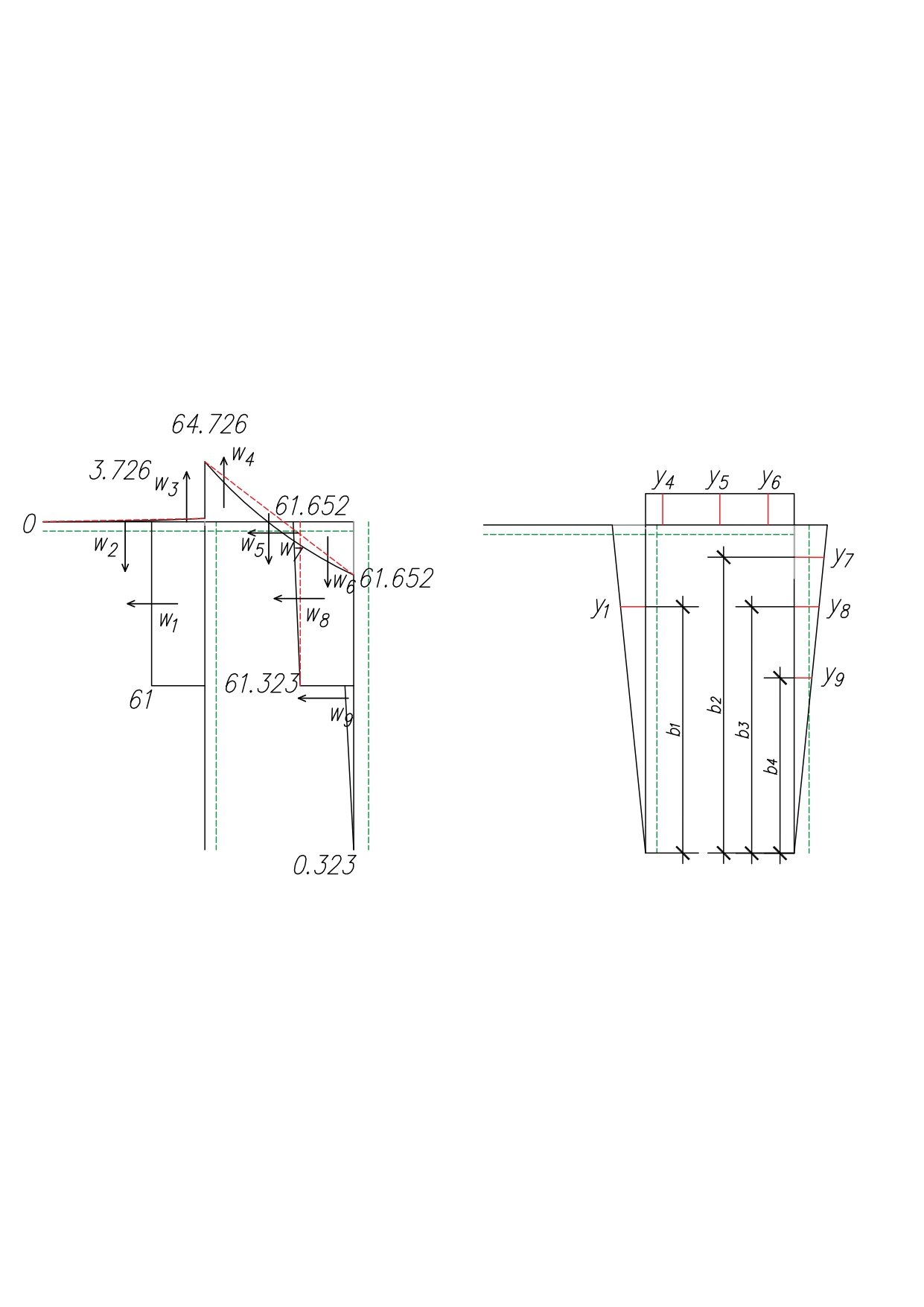 а) Определим площади простых фигур 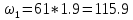 кН*м2 ⊖ кН*м2 ⊖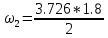 = 3.3534 кН*м2 ⊖ = 3.3534 кН*м2 ⊖ кН*м2 ⊕ кН*м2 ⊕ = 58.2534 кН*м2 ⊖ = 58.2534 кН*м2 ⊖ кН*м2 ⊕ кН*м2 ⊕ = 55.4868 кН*м2 ⊕ = 55.4868 кН*м2 ⊕ кН*м2 ⊖ кН*м2 ⊖ кН*м2 ⊖ кН*м2 ⊖ кН*м2 ⊖ кН*м2 ⊖б) Определим ординаты единичной эпюры  м м 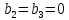 м м 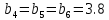 м м 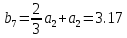 м м 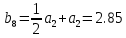 м м  м м  м ⊖ м ⊖ м м  м ⊖ м ⊖  м ⊕ м ⊕  м ⊕ м ⊕  м ⊕ м ⊕ в) Определим перемещение точки 1  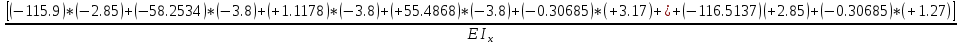 = = 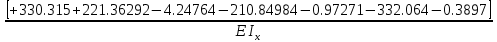 = = 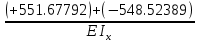 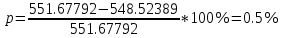 6. Подбор и проверка сечения а) Подберем двутавр по максимальному изгибающему моменту Mизг = 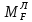 = 64.726 кН*м = 64.726*100 кН*см ⊖ = 64.726 кН*м = 64.726*100 кН*см ⊖а) σ = 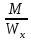 ≤ R ≤ R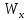 = = 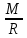 = = 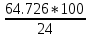 = 269.69 см3 = 269.69 см3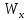 = 269.69 см3 → сортамент → № 20Б3 = 269.69 см3 → сортамент → № 20Б3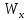 = 274.3 см3 = 274.3 см3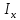 = 2852.62 см4 = 2852.62 см4S = 8 мм = 0.8 см = b 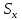 = 158.46 см3 = 158.46 см3h = 208 мм = 20.8 см F = 40.24 см2 б) Проверим подобранное сечение по нормальным напряжениям - первое сечение Максимальный изгибающий момент и соответствующая ему продольная сила Mизг = 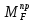 = 64.726 кН*м = 64.726*100 кН*см ⊖ = 64.726 кН*м = 64.726*100 кН*см ⊖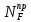 = 0.17 кН ⊕ = 0.17 кН ⊕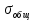 = =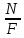 + + 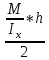 = = 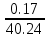 + + 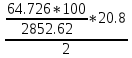 = 23.602 кН/см2 = 236.02 МПа < R = 240 МПа = 23.602 кН/см2 = 236.02 МПа < R = 240 МПа - второе сечение Максимальная продольная сила и соответствующий ему изгибающий момент Mизг = 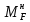 = 61 кН*м = 61*100 кН*см ⊖ = 61 кН*м = 61*100 кН*см ⊖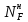 = 76.42 кН ⊖ = 76.42 кН ⊖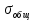 = =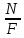 + + 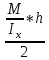 = = 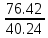 + + 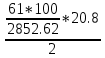 = 24.138 кН/см2 = 241.38 МПа > R = 240 МПа = 24.138 кН/см2 = 241.38 МПа > R = 240 МПа в) Проверим подобранное сечение по касательным напряжениям Qmax = 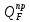 = 72.28 кН ⊕ = 72.28 кН ⊕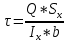 = = 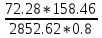 = 5.02 кН/см2 = 50.2 МПа ˂ = 5.02 кН/см2 = 50.2 МПа ˂ 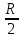 = [τ] = 120 МПа = [τ] = 120 МПаПолная проверка прочности: Для полной проверки прочности необходимо выбрать несколько сечений рамы, которых должна быть достаточно большая продольная сила, достаточно большой изгибающий момент и достаточно большая поперечная сила. В учебных целях выберем одно сечение 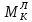 = 61.652 кН*м = 61.652*100 кН*см ⊕ = 61.652 кН*м = 61.652*100 кН*см ⊕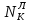 = 0.17 кН ⊕ = 0.17 кН ⊕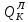 = 68.14 кН ⊕ = 68.14 кН ⊕- определим нормальные напряжения, действующие в точке 7 от продольной силы 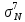 = =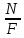 = = 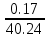 = 0.004 кН/см2 = 0.04 МПа ⊕ = 0.004 кН/см2 = 0.04 МПа ⊕ - определим нормальные напряжения в точке 7 от изгибающих моментов t = 12 мм = 1.2 см 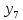 = = 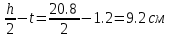 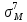 = =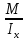 * *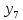 = = 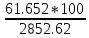 * 9.2 = 19.89 кН/см2 = 198.9 МПа ⊕ * 9.2 = 19.89 кН/см2 = 198.9 МПа ⊕- определим общее напряжение в точке 7 от продольной силы и изгибающего момента 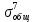 = =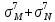 = = 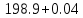 = 198.94 МПа ⊕ = 198.94 МПа ⊕- определим касательные напряжения, действующие в точке 7 Определим статический момент, отсеченной части сечения, для точки 7 относительно нейтральной оси 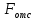 = =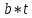 = = 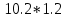 = 12.24 см2 = 12.24 см2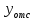 = =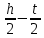 = = 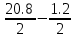 = 9.8 см = 9.8 см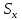 = = 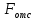 * * 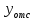 = 12.24 * 9.8 = 119.952 см3 = 12.24 * 9.8 = 119.952 см3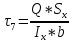 = = 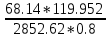 = 3.58 кН/см2 = 35.8 МПа ⊕ = 3.58 кН/см2 = 35.8 МПа ⊕ - рассмотрим элементарный параллелепипед, вырезанный вокруг точки 7 Рассчитаем прочность элементарного параллелепипеда - определим положение главных площадок 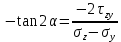 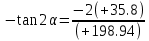 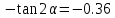 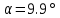 Знак ⊕ показывает, что наклонные площадки необходимо повернуть против часовой стрелке для того, чтобы они стали главными - определим направление действия главных напряжений - определим числовые значения главных напряжений 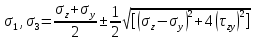 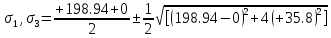 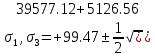 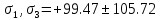 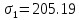 ⊕ ⊕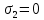 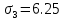 ⊖ ⊖Определим эквивалентные напряжения по 3 теории прочности, т.к. материал сталь пластичный материал и главные экстремальные нормальные напряжения имеют разные знаки 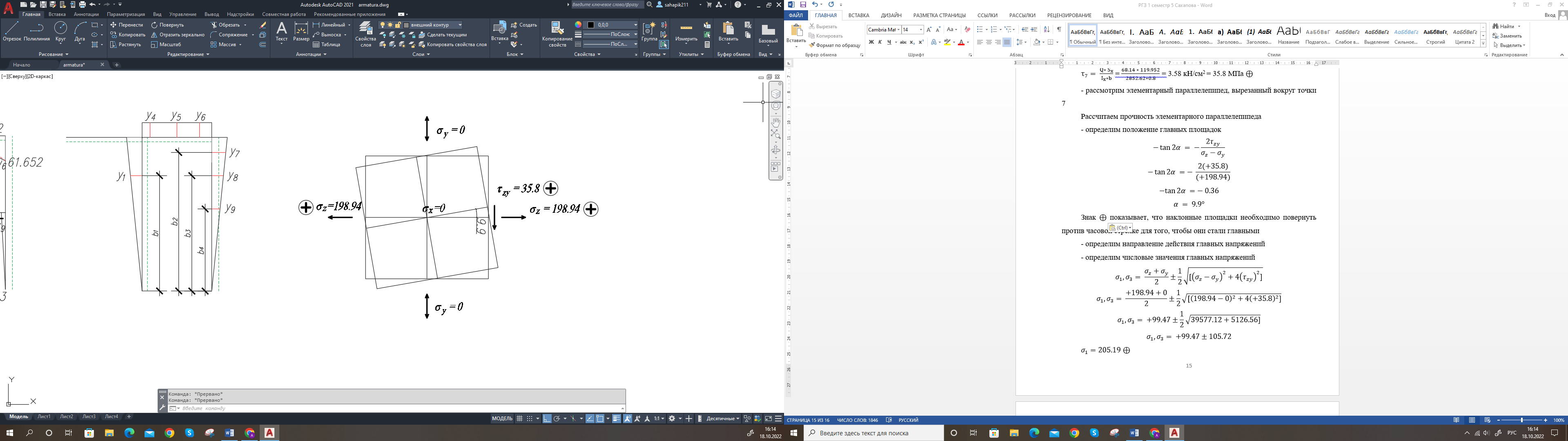 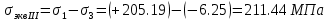 - Проверим прочность элементарного параллелепипеда по эквивалентным напряжениям 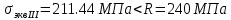 - Найдем положение экстремальных площадок, на которых действует экстремальные касательные напряжения - Определим направление действия экстремальных касательных напряжений - Определим численные значения экстремальных касательных напряжений 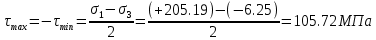 - Проверим прочность элементарного параллелепипеда по экстремальным напряжениям 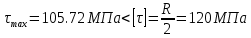 Вывод: условия прочности по нормальным и касательным напряжениям удовлетворяются. Окончательно принимаем двутавр №20Б3 |
