Задачи на максимизацию прибыли и минимизацию убытков в условиях. Задача 1 Постановка задачи
 Скачать 32.25 Kb. Скачать 32.25 Kb.
|
|
Задачи на максимизацию прибыли и минимизацию убытков в условиях совершенной конкуренции Задача 1 Постановка задачи: Используя данные таблицы, определите оптимальный объем производства фирмы – совершенного конкурента, если цена реализации данного товара 30 у. е.:
Технология решения задачи: В условиях совершенной конкуренции условием максимизации прибыли является МС = Р, поэтому необходимо определить МС. Продолжим таблицу.
МС = Р при объеме 10 ед. – это оптимальный объем производства. Ответ: 10 ед. продукции. Задача 2 Постановка задачи: Определите, какой объем лучше выпускать предприятию, продающему товар по цене, равной 15 у. е., и имеющему следующие затраты на производство и реализацию продукции (см. таблицу). Определите максимальную прибыль.
Технология решения задачи: Для решения задачи надо определить предельные затраты и сравнить их с ценой (см. таблицу, расположенную ниже). При объеме производства равном 1 ед., а также при объеме, равном 7 ед. продукции, выполняется условие совершенной конкуренции МС = Р. Но прежде чем сделать вывод об оптимальном объеме производства, надо подсчитать прибыль, а до этого общую выручку.
Из таблицы видно, что при данной цене товара нет оптимального объема, т. к. производство убыточно, но убытки минимальны, когда МС = Р, поэтому предприятию следует выпускать именно этот объем производства, чтобы минимизировать убытки. Ответ: Q = 7 ед. Задача 3 Постановка задачи: Объем выпуска фирмы в условиях совершенной конкуренции 100 т, цена товара 2 тыс. у. е., общие издержки (100 т) составляют 130 тыс. у. е. Определите общую прибыль фирмы. Технология решения задачи: определяем общую выручку TR = 100 * 2 = 200 тыс. у. е. и сравниваем ее с общими затратами: 200 – 130 = 70 тыс. у. е. Ответ: 70 тыс. у. е. Задача 4 Постановка задачи: Функция общих затрат фирмы имеет вид 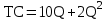 . Фирма реализует продукцию на совершенно конкурентном рынке по цене 170 $. Определите, какую прибыль получит фирма? . Фирма реализует продукцию на совершенно конкурентном рынке по цене 170 $. Определите, какую прибыль получит фирма?Технология решения задачи: Найдем предельные издержки: 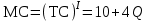 . В условиях совершенной конкуренции МС = Р, 10 + 4 Q = 170, отсюда Q = 40 ед. . В условиях совершенной конкуренции МС = Р, 10 + 4 Q = 170, отсюда Q = 40 ед. Затем необходимо подсчитать общую выручку: TR (40) = 40 * 170 = 6800 $ и общие затраты: TC = 10 * 40 + 2 * 1600 = 3600 $. Теперь можно определить общую прибыль: TPr = 6800 – 3600 = 3200 $. Ответ: 3200 $. Задача 5 Постановка задачи: Общие издержки фирмы, совершенного конкурента, определяются формулой ТС = 10 Q2 + 24 Q + 88. Оптимальным для фирмы является производство 16 ед. продукции. Определите, какая цена установилась на рынке. Технология решения задачи: Оптимальный объем производства фирмы-конкурента определяется, исходя из условия МС=Р, поэтому необходимо найти МС 16-й ед. продукции. 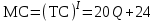 , MC (16) = 20 * 16 + 24 = 344 у. е. , MC (16) = 20 * 16 + 24 = 344 у. е. Ответ: 344 у. е. Задача 6 Постановка задачи: В краткосрочный период конкурентная фирма производит 100 ед. товара Х при средних постоянных затратах 5 $ и продает их по цене 30 $ за штуку. Как изменится прибыль предприятия, если средние переменные затраты снизились с 20 до 10 $, а цена не изменилась. Технология решения задачи: Сначала определяется первоначальная прибыль. Для этого рассчитываются общая выручка: TR = 30 * 100 = 3000 $ и общие затраты: ТС = (5 + 20) * 100 = 2500 $. Отсюда общая прибыль равна 3000 – 2500 = 500 $. Затем подсчитываются новые общие издержки: TC = (5 + 10) * 100 = 1500 $. Следовательно, общая прибыль будет равна 3000 – 1500 = 1500 $. Прибыль выросла в 3 раза. Ответ: увеличится с 500 до 1500 $ , т. е. в 3 раза. Задача 7 Постановка задачи: Используя данные таблицы, определите, ниже какого уровня должна опуститься цена, чтобы фирма – совершенный конкурент прекратила производство в коротком периоде?
Технология решения задачи: Предприятие в условиях совершенной конкуренции прекращает производство продукции, если цена падает ниже средних переменных затрат, поэтому надо рассчитать средние, средние постоянные и средние переменные затраты. Сделаем это в таблице:
Самое меньшее значение средних переменных затрат 3 у. е., следовательно, падение цены ниже 3 у. е. приведет к свертыванию производства совершенным конкурентом. Ответ: ниже 3 у. е. Задача 8 Постановка задачи: Спрос на продукцию конкурентной отрасли 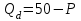 , а предложение , а предложение 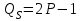 . Если у одной фирмы отрасли восходящий участок кривой предельных издержек . Если у одной фирмы отрасли восходящий участок кривой предельных издержек МС = 3Q + 5, то при каких цене и объеме производства фирма будет максимизировать прибыль? Технология решения задачи: Из равенства спроса и предложения определяется рыночная цена: 50 – Р = 2Р – 1, Р = 17. Оптимальный объем производства фирмы-конкурента определяется, исходя из условия МС = Р, 3Q + 5 = 17, Q = 4. Ответ: P = 17 у. е., Q = 4 ед. |
