Задание. Задание 1. Задача 1 Построить комплексные чертежи точек а (15,30,0), в (25,20,15), с (25,10,15 ), d (15, 30,20)
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
Практическое задание 1 Модуль 1. Методы проецирования Модуль 2. Задание плоскости на чертеже Задание Решить графические задачи по темам: 1.1. Методы проецирования. 1.2. Метод Монжа. 1.3. Трехкартинный комплексный чертеж точки – задача 1. 1.4. Задание прямой на комплексном чертеже – задача 2. 2.1. Задание плоскости на чертеже – задачи 3, 4. 2.2. Задание поверхности на чертеже. 2.3. Задание линейчатых поверхностей – задачи 5, 6, 7. 2.4. Задание поверхностей вращения – задачи 8, 9. 2.5. Прямой геликоид – задача 10. Задача 1 Построить комплексные чертежи точек: А (15,30,0), В (25,20,15), С (25,10,15), D (15, 30,20). 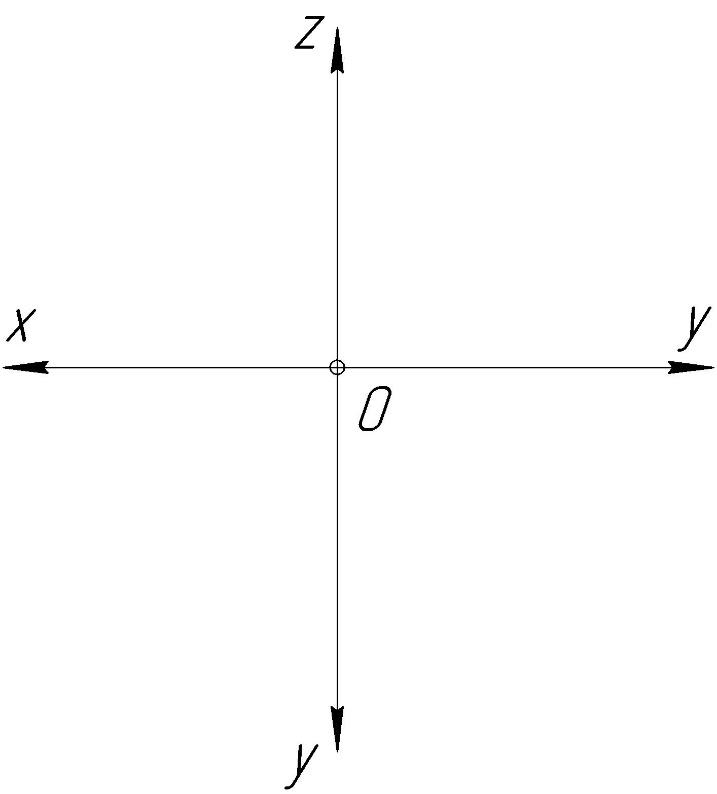 Задача 2 Построить горизонтальную проекцию отрезка АВ, если = 30 (угол наклона к П2 ), В дальше от П2 , чем А. 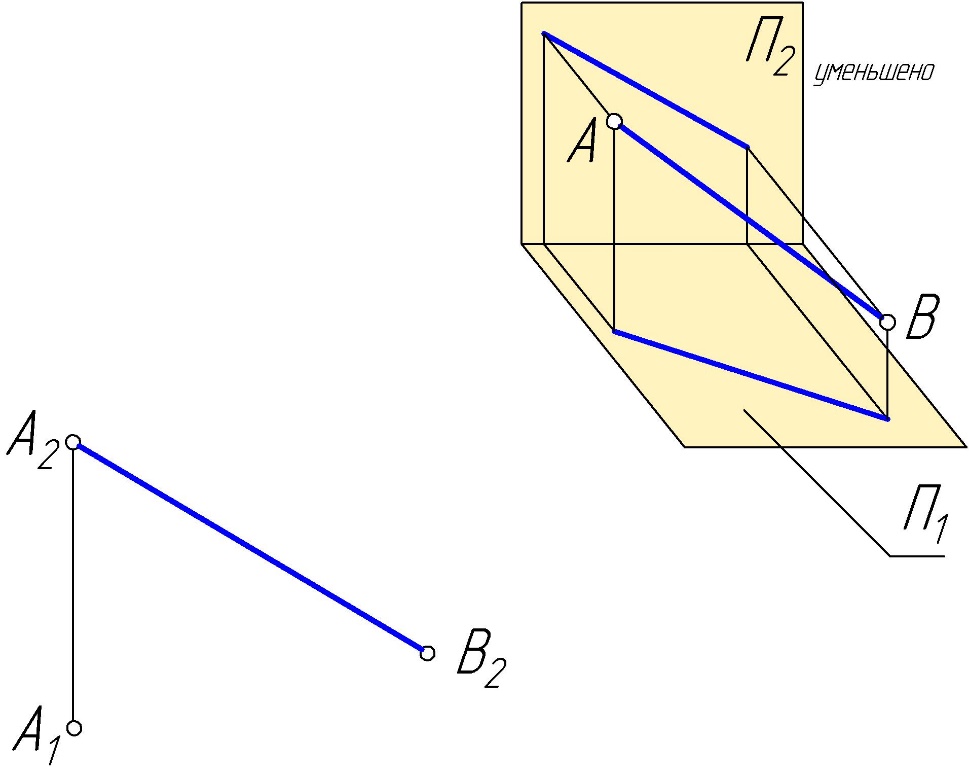 Задача 3 Плоскость задана двумя параллельными прямыми m // n. Треугольник DEF(D1 E1F1) принадлежит . Найти фронтальную проекцию треугольника DEF. 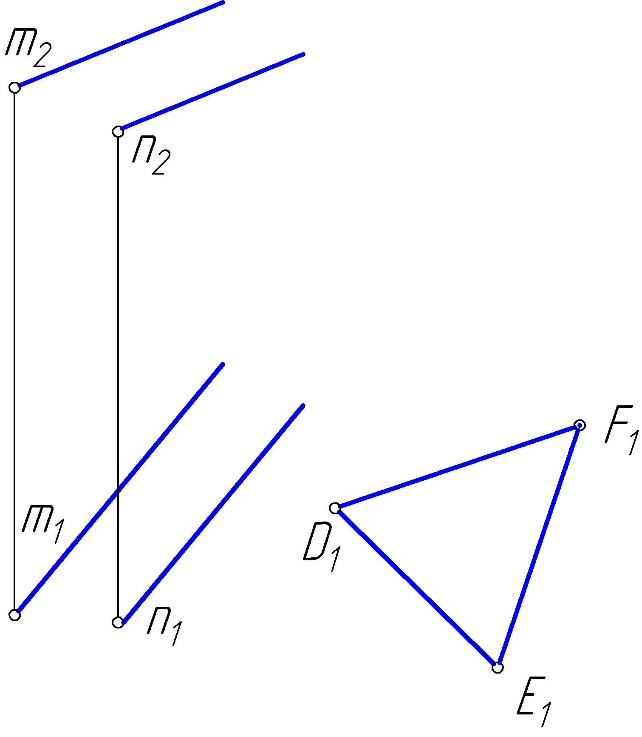 Задача 4 Достроить горизонтальную проекцию плоскости (KLM), если плоскость (АВС) // (KLM). 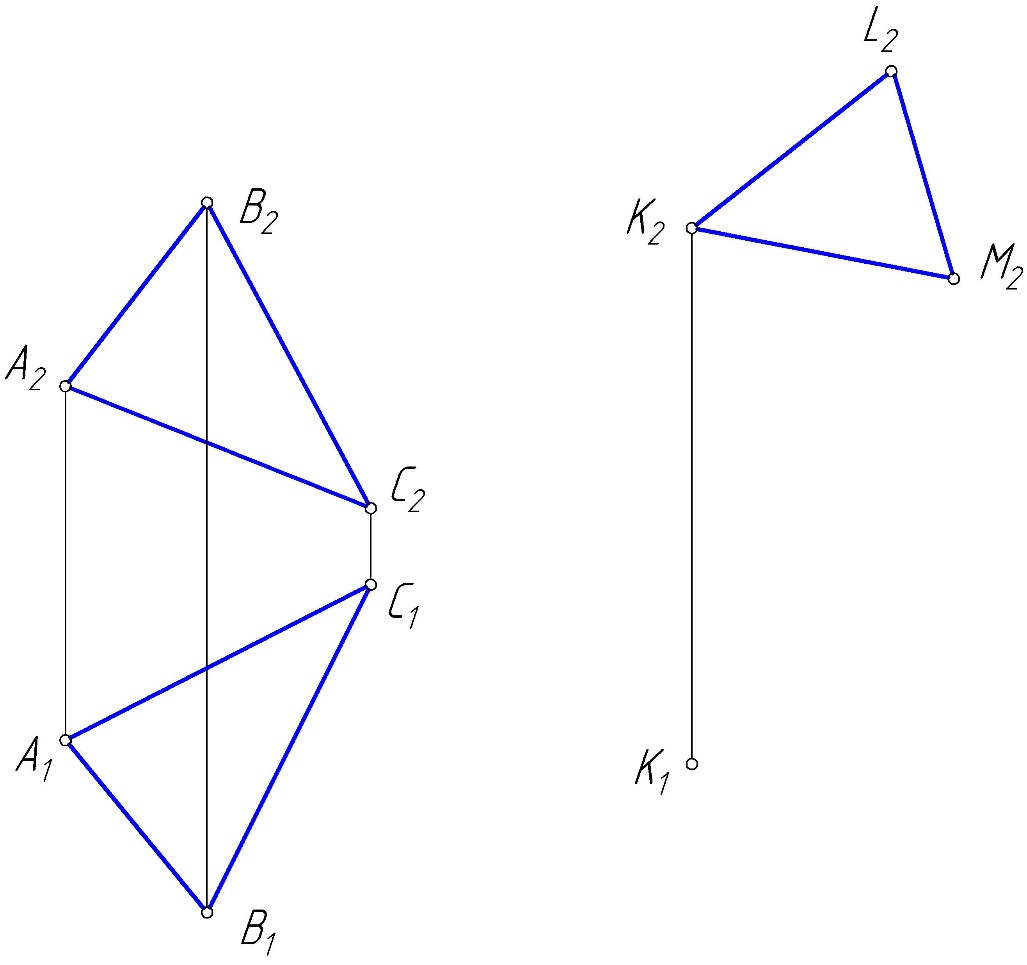 Задача 5 Построить проекции пирамидальной поверхности (1,2,3,S)и недостающие проекции точек А(А2), В(В1), А1, В2 = ?Записать алгоритмическую часть определителя поверхности (закон каркаса). 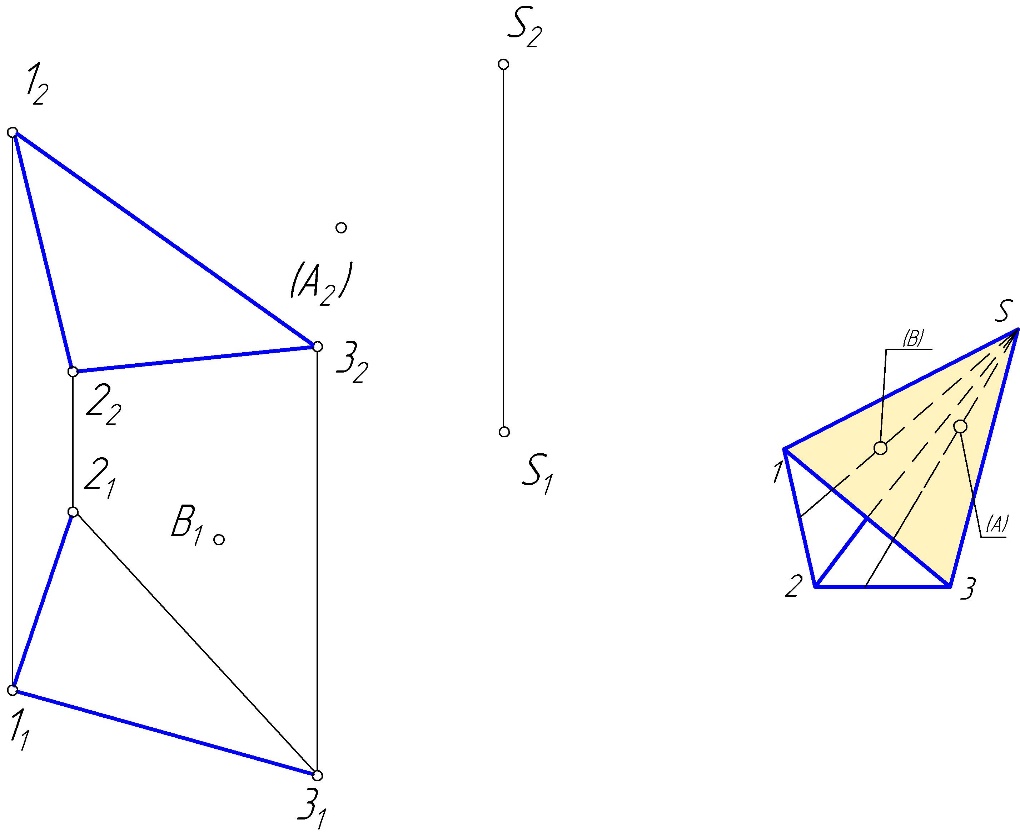 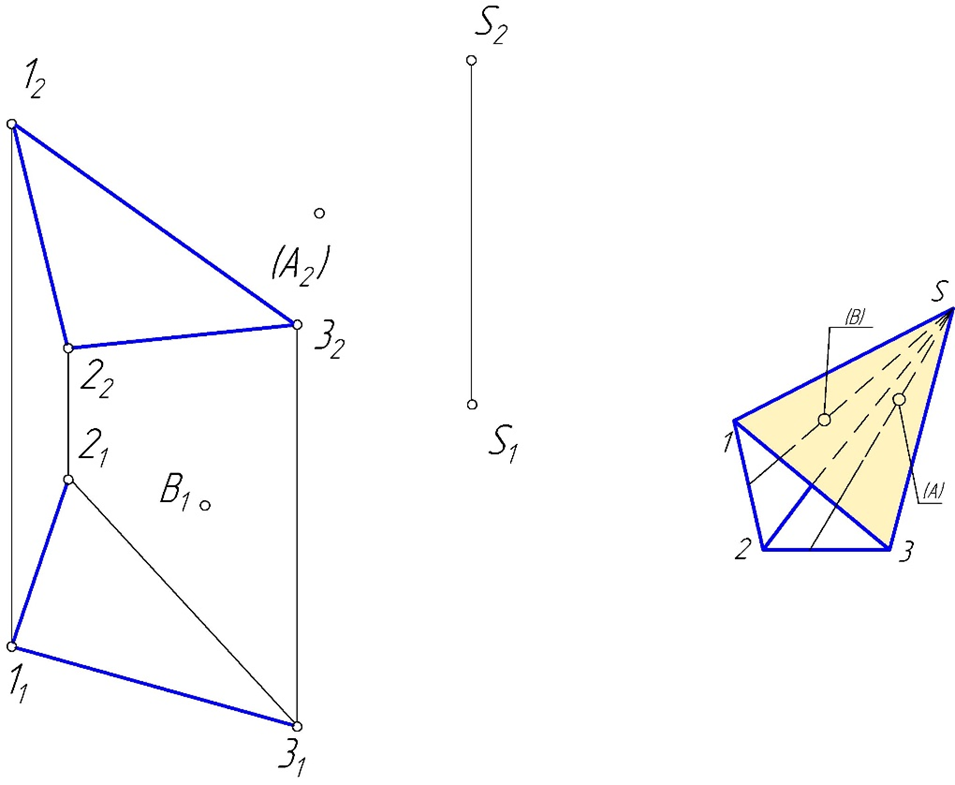 Задача 6 Построить проекции цилиндрической поверхности (m, s), высота h = 40 мм. Достроить недостающую проекцию линии l(l2). l1 = ? Записать алгоритмическую часть определителя поверхности (закон каркаса). 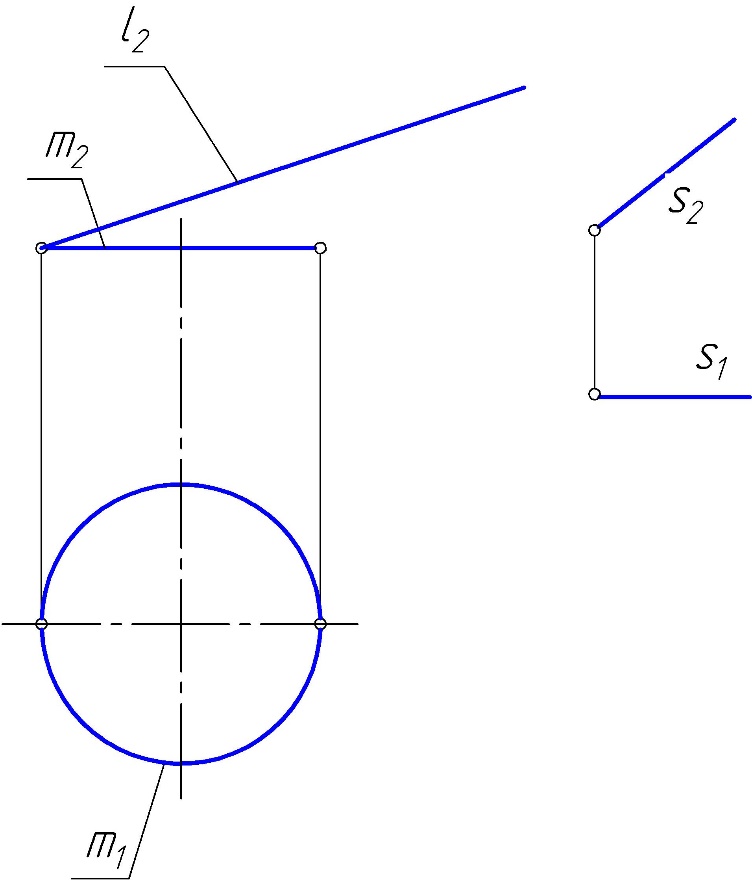 Задача 7 Построить проекции гиперболического параболоида (n,m,)и недостающую проекцию линииb(b2), b1 = ?– плоскость параллелизма. Записать алгоритмическую часть определителя поверхности (закон каркаса). 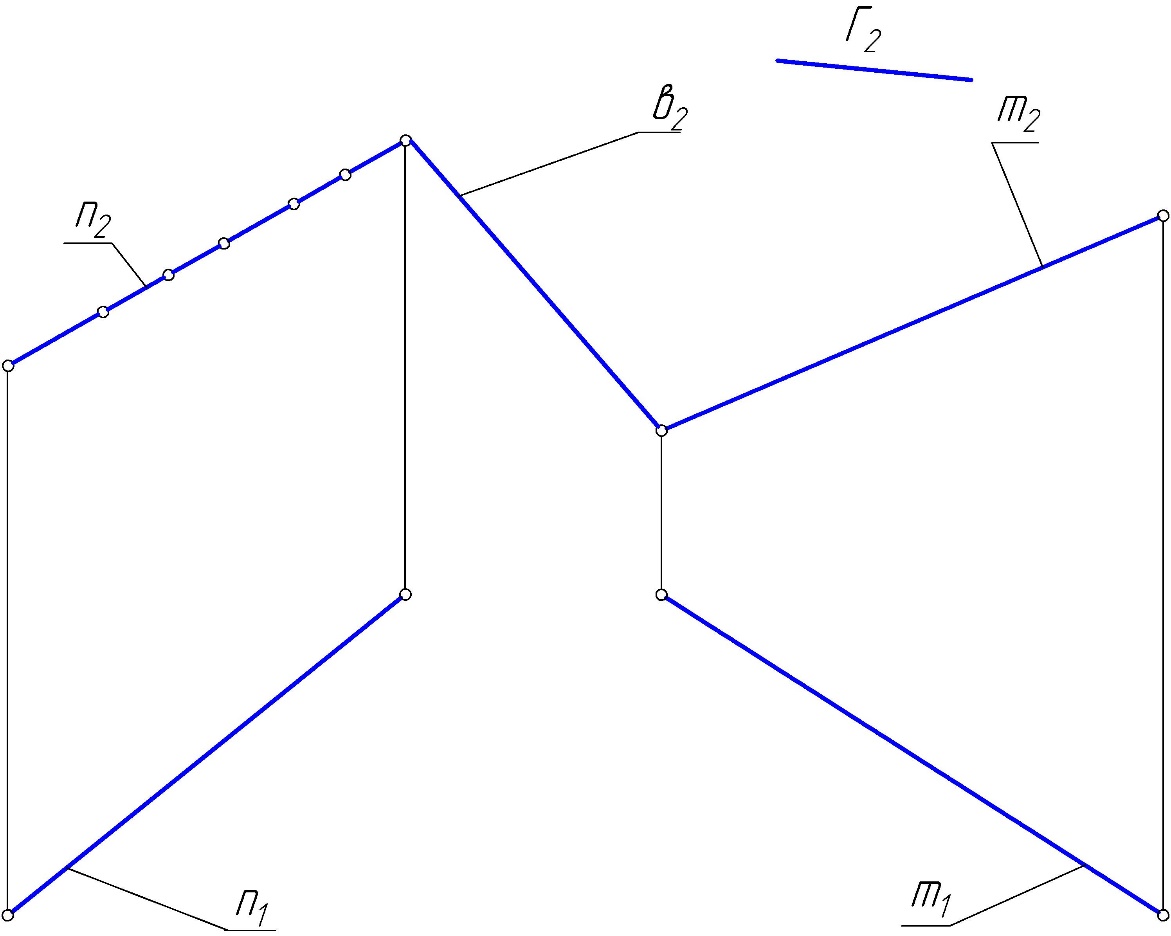 Задача 8 Задана сфера (i,l). Построить недостающие проекции линии n(n2), принадлежащие . n1, n3 = ? Записать алгоритмическую часть определителя поверхности (закон каркаса). 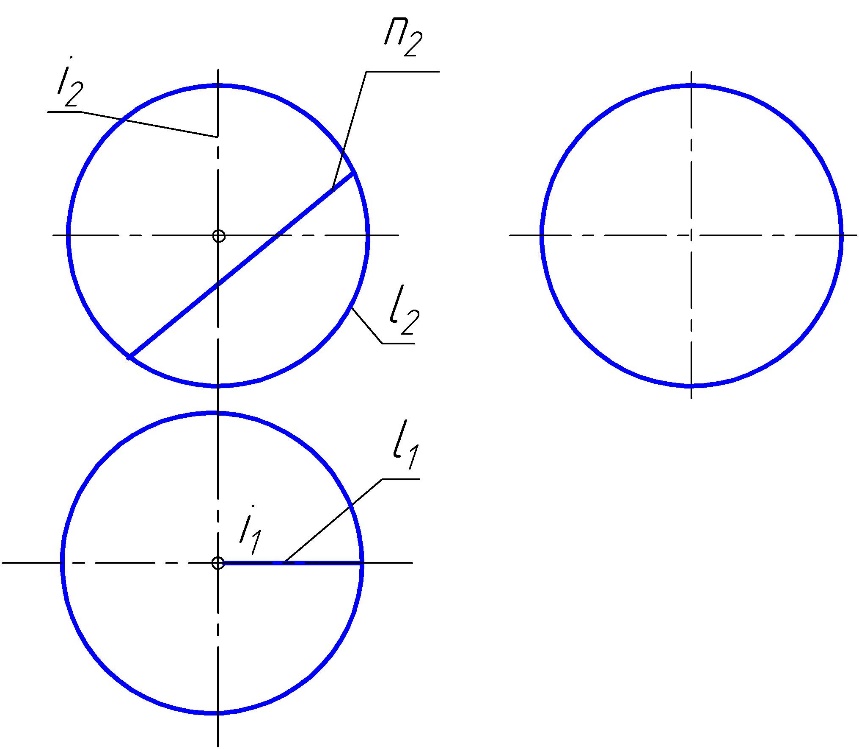 Задача 9 Построить проекции поверхности однополостного гиперболоида вращения (i,l). Точки А(А2), В(В1), . Найти недостающие проекции точек А и В. А1 = ? В2 = ? Записать алгоритмическую часть определителя поверхности (закон каркаса). 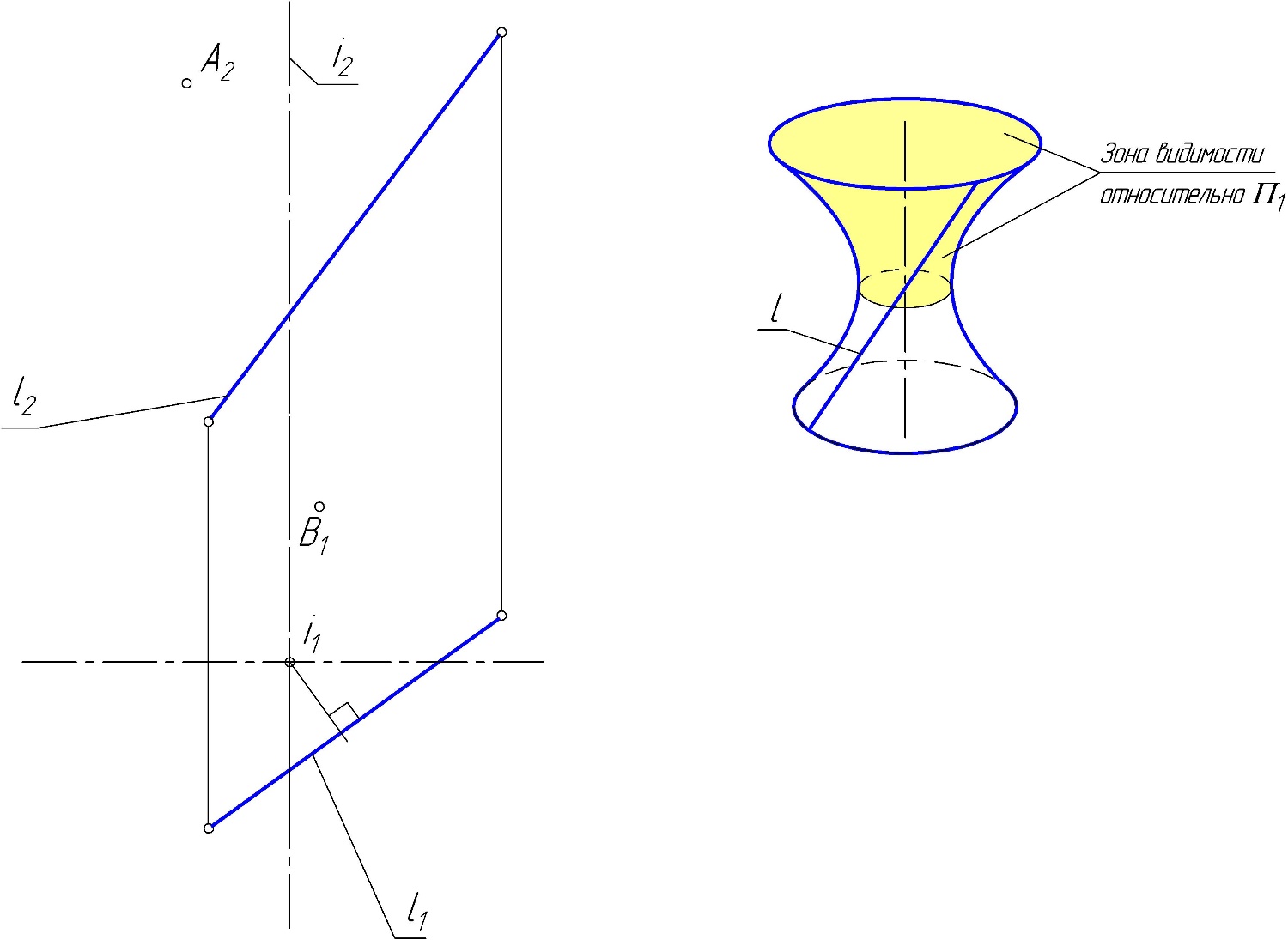 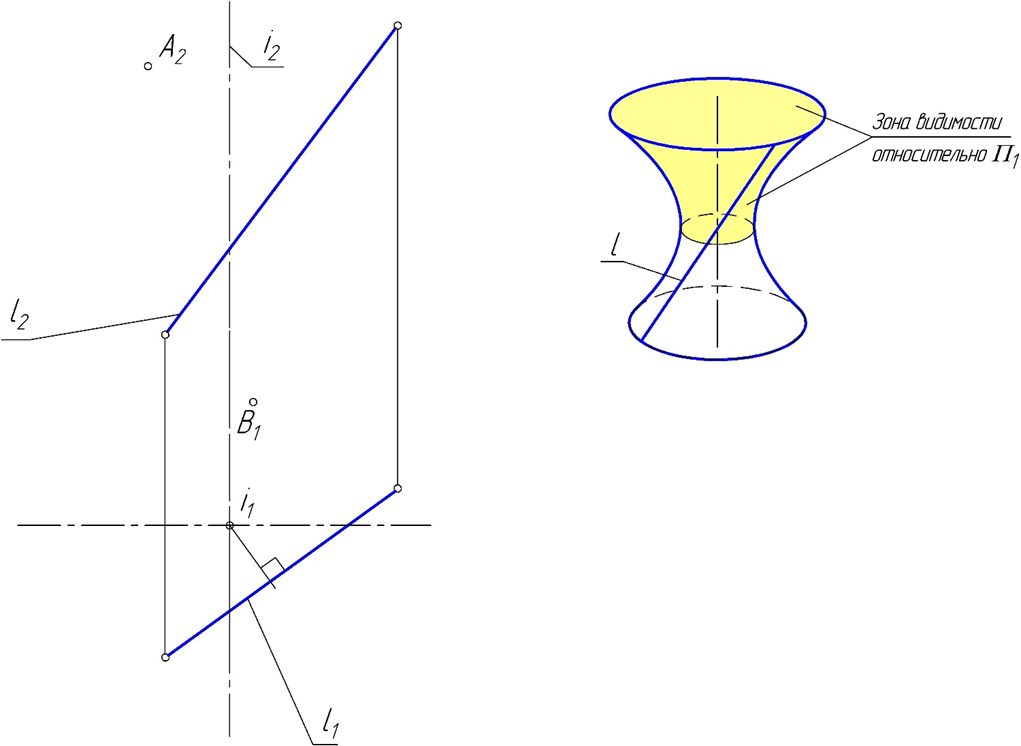 Задача 10 Построить проекции прямого геликоида (i,m) и недостающую проекцию линии n(n2). n1= ? Записать алгоритмическую часть определителя поверхности (закон каркаса). 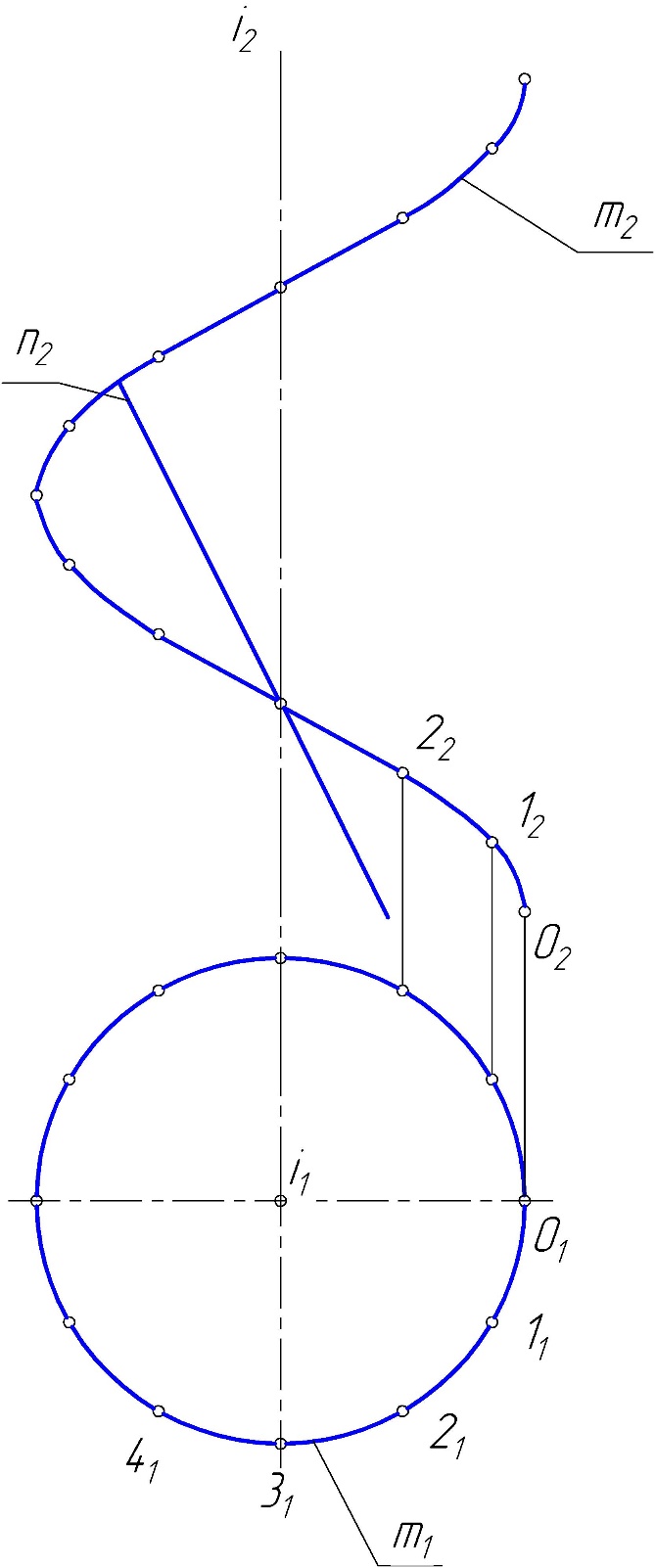 Рекомендации по выполнению задания 1) Для выполнения практического задания 1 необходимо распечатать условия задач 1–10 на листах формата А4 (8 страниц). 2) Используя графическое и текстовое условия, выполнить вручную графическое решение задач 1–10 на распечатанных листах. 3) Оформленные страницы сфотографировать или отсканировать, на проверку прислать файлы в формате рисунка (jpg, png). |
