Расчет линейной электрической цепи при несинусоидальных напряжениях и токах. КР3_046. Задача 1 Расчет линейной электрической цепи при несинусоидальных напряжениях и токах
 Скачать 489 Kb.
|
|
Задача №1 Расчет линейной электрической цепи при несинусоидальных напряжениях и токах На рис. 1 показана цепь с источником периодической несинусоидальной ЭДС. График функции  изображен на рис. 2. Амплитуда ЭДС, угловая частота первой гармоники и параметры цепи даны в табл. 1.Для расчета данной цепи необходимо: Разложить аналитически в ряд Фурье заданную периодическую несинусоидальную ЭДС , ограничившись вычислением первых трех гармоник; написать уравнение мгновенного значения ЭДС.Определить действующее значение несинусоидальной ЭДС, заданной графиком на рис. 2. Вычислить действующее значение тока на неразветвленном участке цепи и записать закон его изменения  с учетом указанных выше членов разложения в ряд Фурье.Построить график тока на неразветвленном участке цепи. На графике показать первые три гармоники и суммарную кривую, полученную в результате графического сложения отдельных гармоник. Определить активную, реактивную, полную мощности цепи. 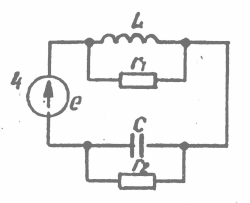 Рис. 1. Схема цепи 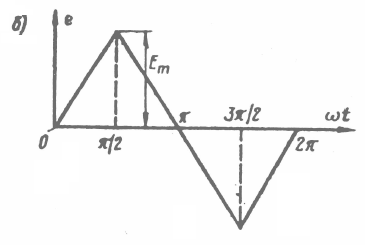 Рис. 2. Форма кривой ЭДС Дано:  В,  рад/с,  Ом,  Ом,  мГн,  мкФ.Решение 1. Исходная функция ЭДС 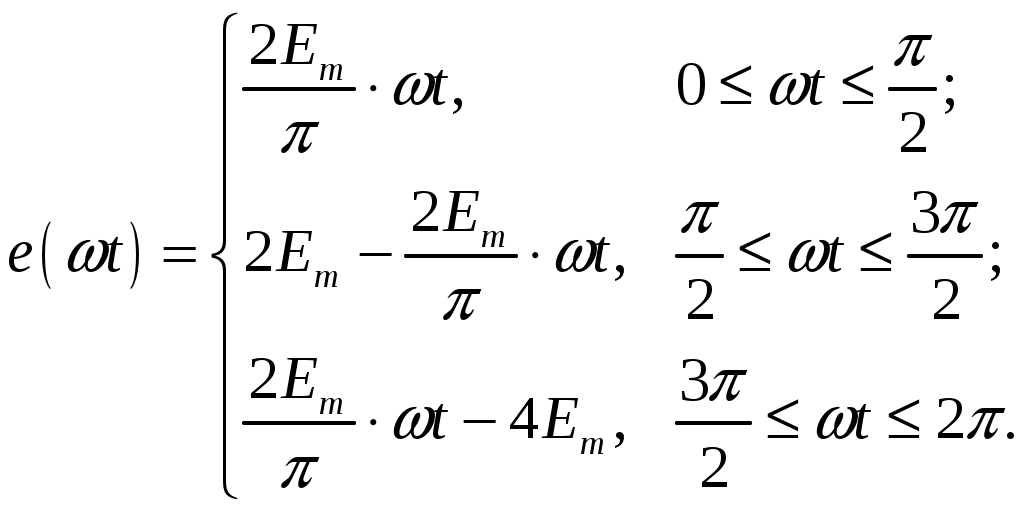 .Разложим в ряд Фурье заданную периодическую несинусоидальную ЭДС, ограничившись первыми тремя гармониками:  .Мгновенное значение ЭДС: 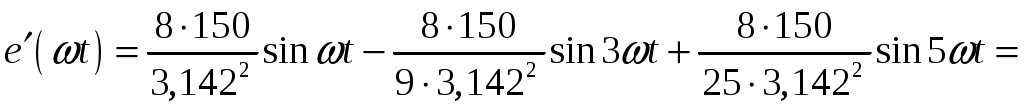  В.2. Действующее значение несинусоидальной ЭДС 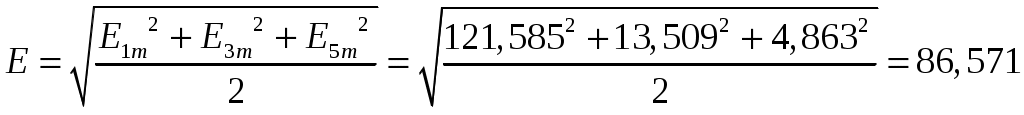 В.3. Определим ток в цепи отдельно для каждой гармонической составляющей. Для основной гармоники (K=1) индуктивное и емкостное сопротивления:  Ом, Ом.Комплексное сопротивление цепи 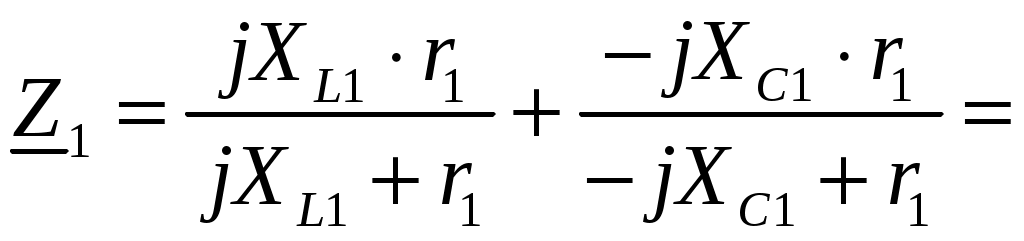 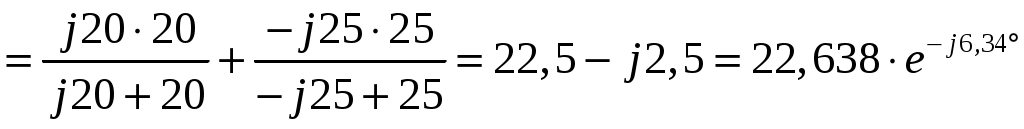 Ом.Комплекс действующего значения входной ЭДС 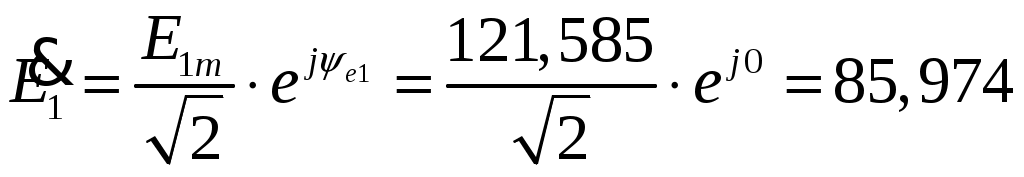 В.Комплекс действующего значения ток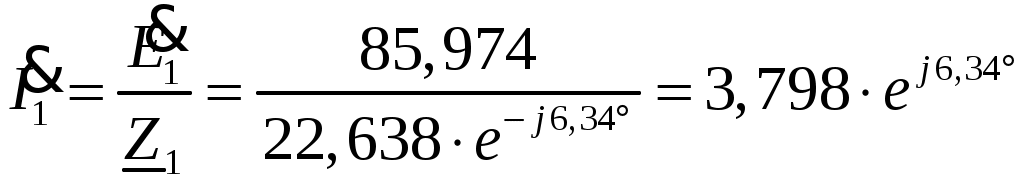а  А.Мгновенное значение первой гармоники тока   А.Для третьей гармоники (K=3) индуктивное и емкостное сопротивления:  Ом, Ом.Комплексное сопротивление цепи 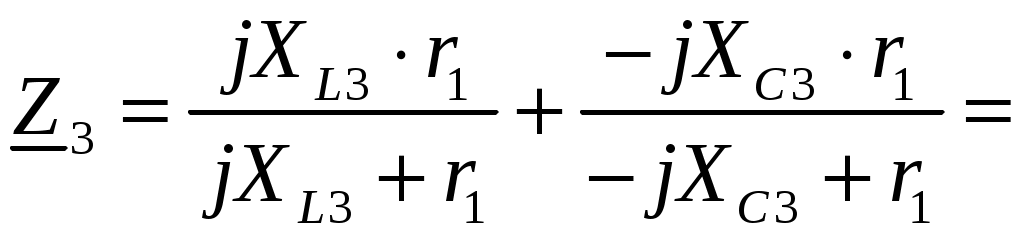 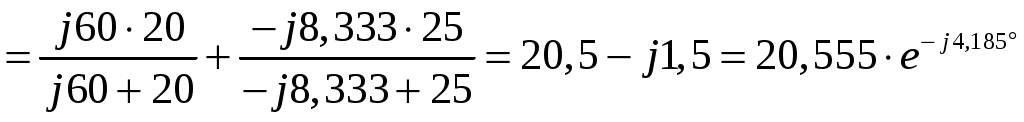 Ом.Комплекс действующего значения входной ЭДС 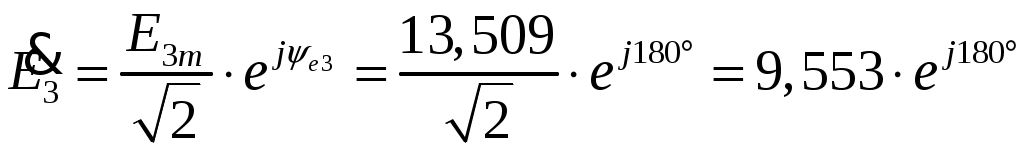 В.Комплекс действующего значения ток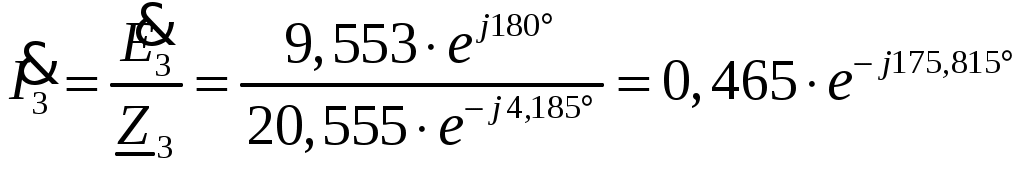а  А.Мгновенное значение третьей гармоники тока   А.Для пятой гармоники (K=5) индуктивное и емкостное сопротивления:  Ом, Ом.Комплексное сопротивление цепи 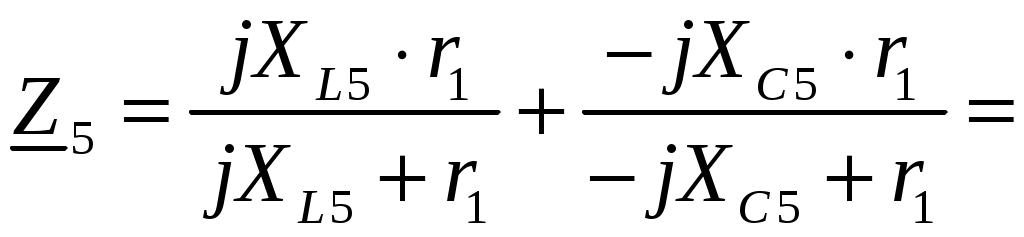 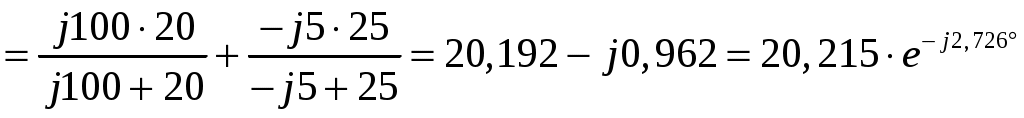 Ом.Комплекс действующего значения входной ЭДС 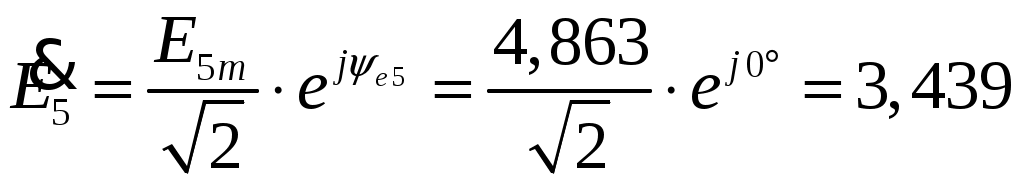 В.Комплекс действующего значения ток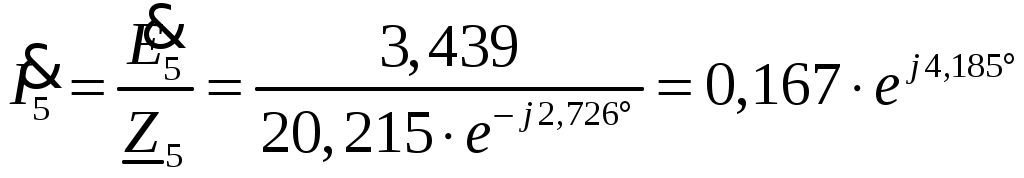а  А.Мгновенное значение пятой гармоники тока   А.Действующее значение тока на неразветвленном участке цепи  А.Мгновенное значение тока    А.4. Построим график тока на неразветвленном участке цепи и его отдельных гармоник: 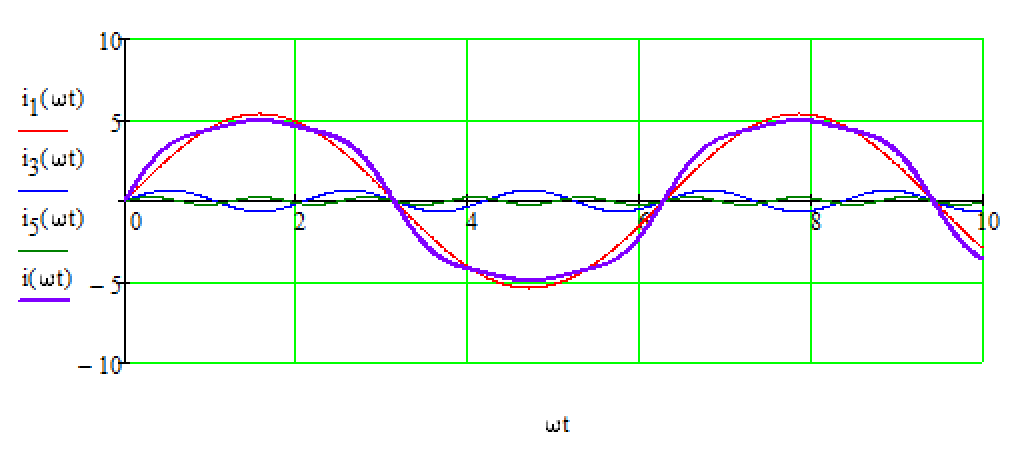 5. Активная мощность цепи    Вт.Реактивная мощность цепи    Вт.Полная мощность цепи  В·А.Задача №2 Расчет переходных процессов в линейных цепях с сосредоточенными параметрами при постоянной ЭДС источника питания В электрической цепи (рис. 3) в результате коммутации возникает переходный процесс. Параметры цепи приведены в табл. 2, постоянная ЭДС источника  В.Определить закон изменения во времени тока 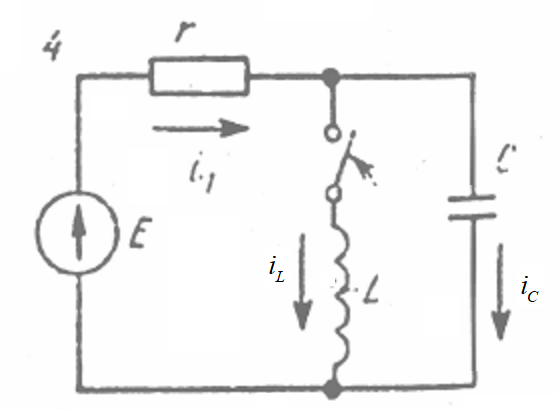 и построить его график. Рис. 3. Схема цепи Дано:  Ом,  Гн,  мкФ.Решение Классический метод 1. Расчет режима до коммутации (контакты разомкнуты). Токи в ветвях цепи:  , .Напряжение на конденсаторе  В.По первому закону коммутации  .По второму закону коммутации  В.2. Расчет принужденного режима после коммутации (контакты замкнуты). Токи в ветвях цепи:  , А.3. Расчет искомого тока и его производной для момента коммутации (t=0). По законам Кирхгофа составляем уравнения для схемы после коммутации:  , (1) , (2) . (3)Из уравнения (3) 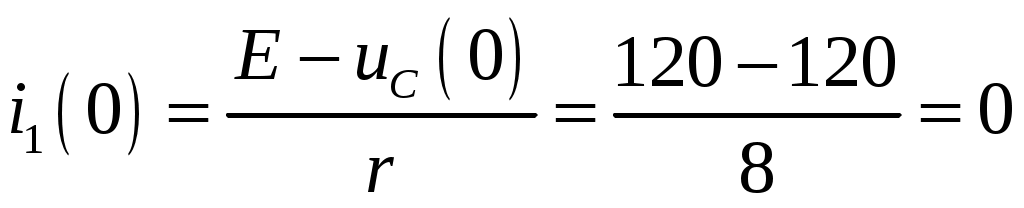 .Из уравнения (1)  .Продифференцируем уравнение (3): 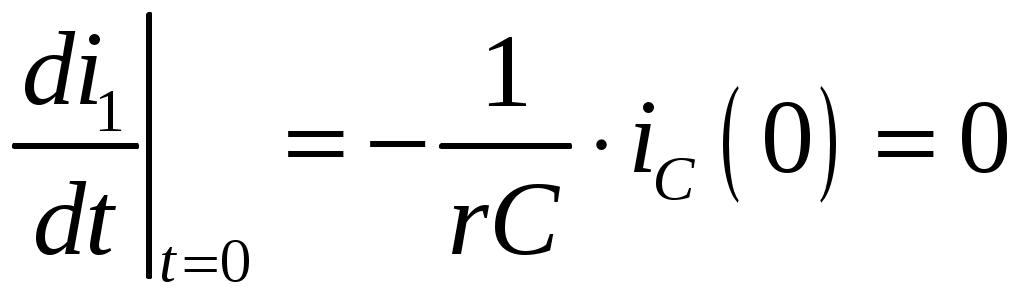 , .4. Определение корней характеристического уравнения. Входное сопротивление для схемы после коммутации в операторной форме приравняем нулю: 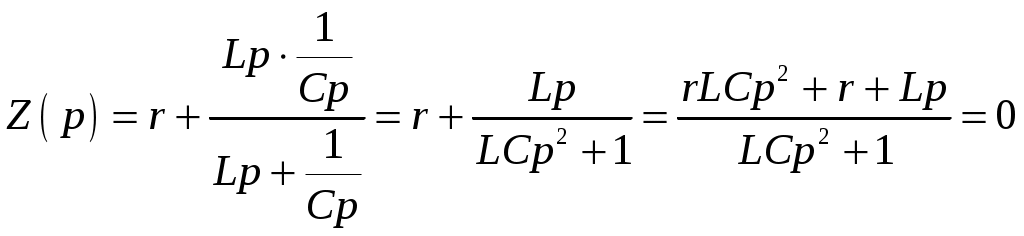 .Характеристическое уравнение  , .Это уравнение имеет два корня 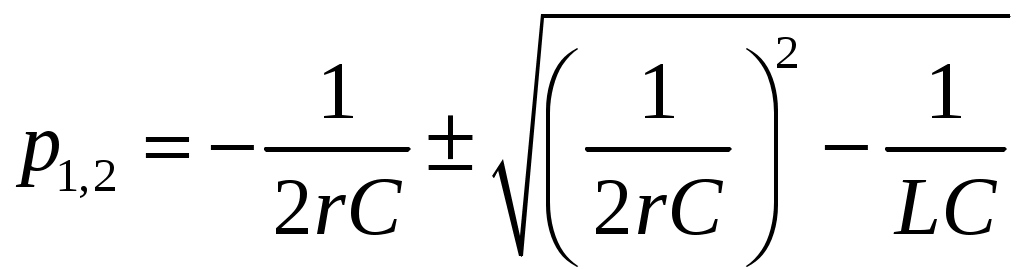 .После подстановки численных значений заданных величин получаем:  1/с, 1/с.Поскольку корни вещественные, отрицательные и разные, режим будет апериодическим, свободная составляющая тока запишется в виде  .5. Определение постоянных интегрирования и закона изменения во времени искомого тока. Переходный ток на неразветвленном участке цепи  .Производная этого тока  .Находим значения тока и его производной для момента времени t=0: 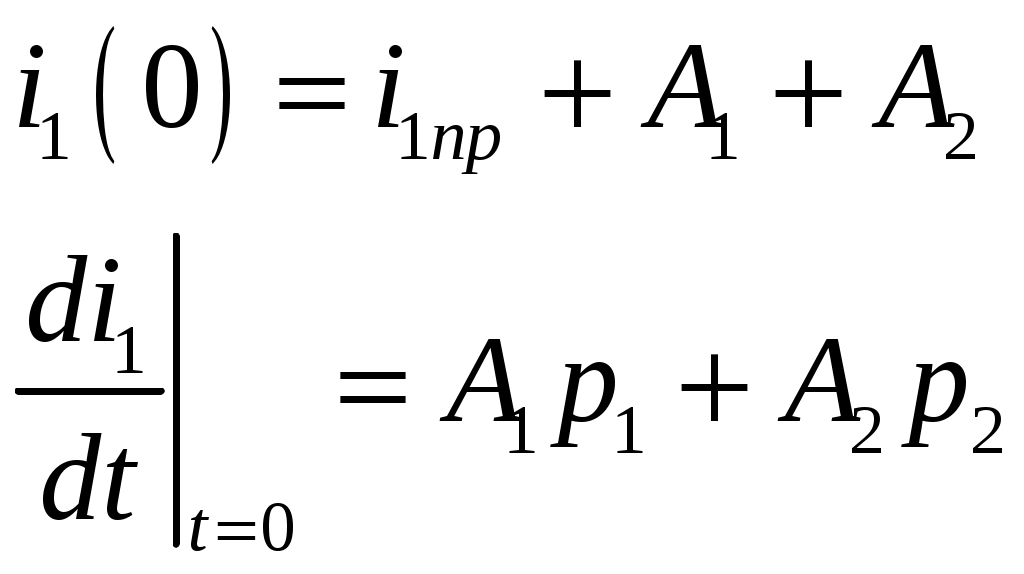 После подстановки численных значений получим систему уравнений: 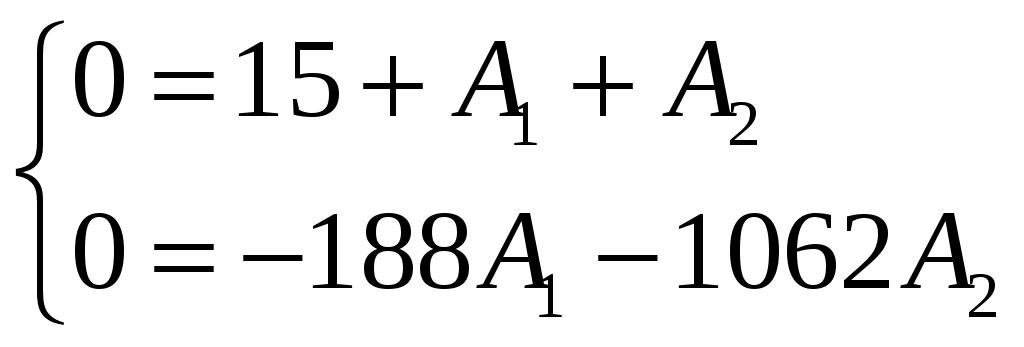 Решая эту систему уравнений, находим:  А, А.Таким образом, искомый ток  А.Строим график тока: 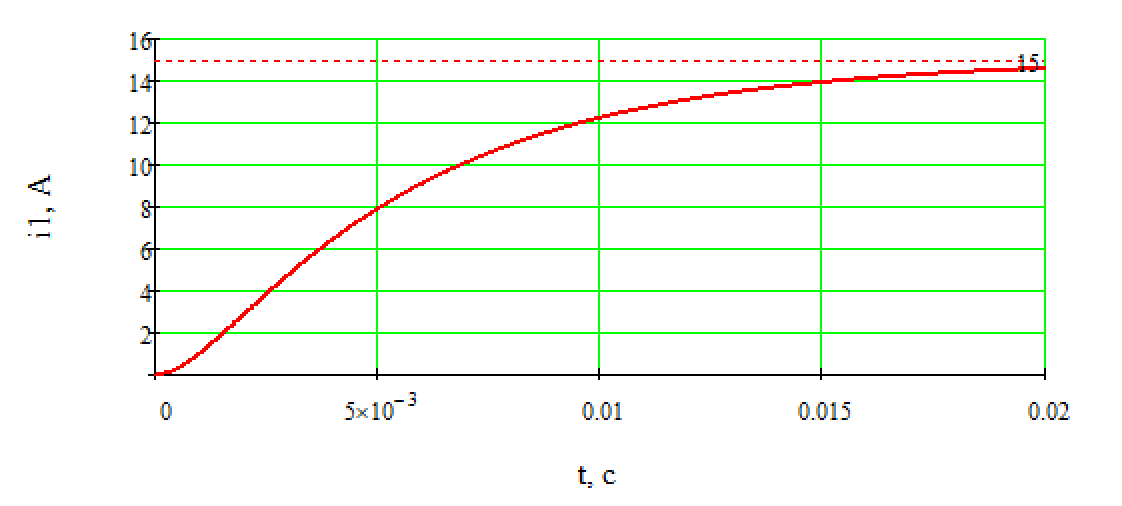 Рис. 4. График искомого тока Операторный метод Начальные условия переходного процесса в электрической цепи определены в первом пункте расчета классическим методом: 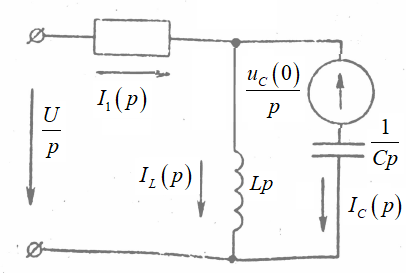,  В. С учетом этого составляем операторную схему замещения цепи (рис. 5) и записываем для нее уравнения по законам Кирхгофа: Рис. 5. Операторная схема замещения 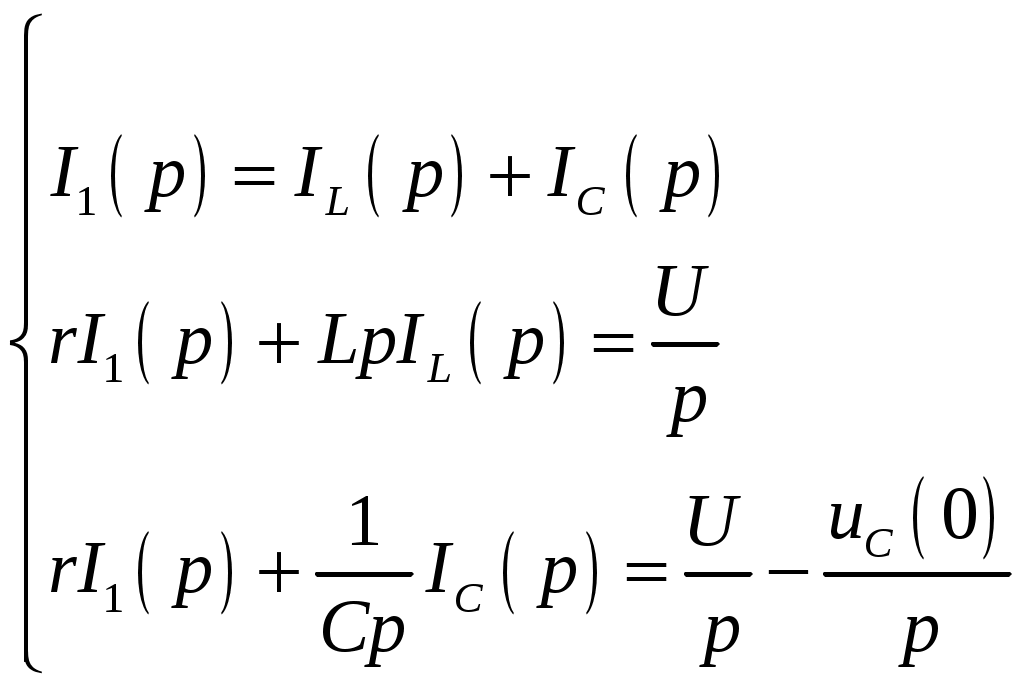 Решив эту систему относительно тока 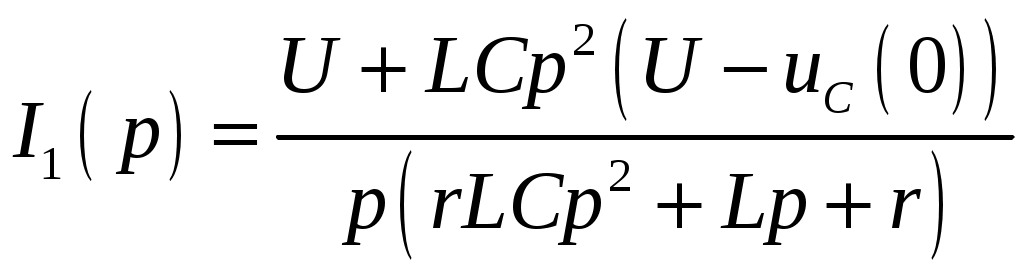 , получим: .После подстановки числовых значений получим: 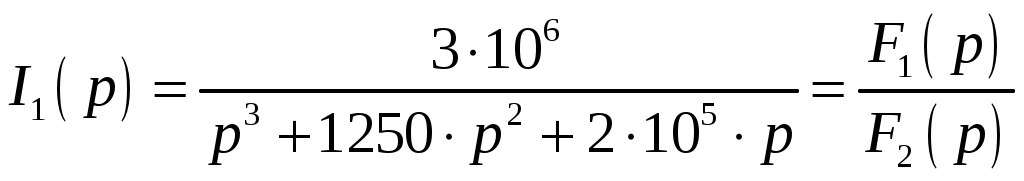 .Для нахождения оригинала определим корни знаменателя, для чего приравняем его к нулю:  , ,  1/с,  1/с.Так как знаменатель имеет три корня, то сумма в формуле разложения состоит из трех слагаемых: 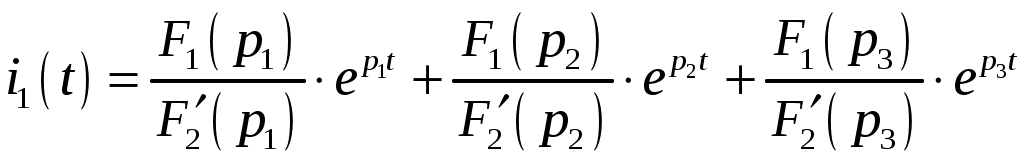 .Числители слагаемых:  .Производная знаменателя:  .Знаменатели слагаемых:  , , .Подставим полученные значения в формулу теоремы разложения: 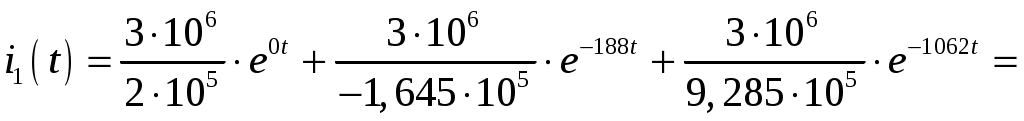  А. |