КР Вариант 4. Задача 1 Рассчитайте температуру плавления меди по шкале Фаренгейта, если по шкале Кельвина она равна 1356 К

• Название: Задача 1 Рассчитайте температуру плавления меди по шкале Фаренгейта, если по шкале Кельвина она равна 1356 К
• Дата: 07.02.2022
• Размер: 66.81 Kb.
• Имя файла: КР Вариант 4.docx
• Тип: Задача; #354223

Задача 1
Рассчитайте температуру плавления меди по шкале Фаренгейта, если по шкале Кельвина она равна 1356 К.
Решение

Шкала Фаренгейта это температурная шкала, 1 градус которой (1°F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F.

Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением:

t °С = 5/9· (t °F - 32), (1)

то есть изменение температуры на 1 °F соответствует изменению на 5/9 °С.

Температуру плавления меди по шкале Кельвина равна 1356 К, а по шкале Цельсия 1356К - 273,16К = 1082,84 °С.

Значит, по шкале Фаренгейта температура плавления меди будет равна из формулы (1):
t °F =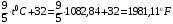

Задача 2
Камень массой 1,2 кг падает с высоты h=14 м на землю. Определить вызванное этим процессом изменение энтропии системы камень-земля. Температура камня и окружающей среды равна t=20˚С.
Решение
Падение камня - процесс необратимый.

Изменение энтропии ΔS в этом процессе можно найти, используя первое начало термодинамики:

ΔQ = ΔU+A, (1)

где ΔU – изменение внутренней энергии; A – работа.

Так как ΔQ = T·ΔS, то T·ΔS=ΔU+A. (2)

По условию задачи температура, а следовательно, и внутренняя энергия не изменяются (ΔU=0).

Работа A равна изменению потенциальной энергии системы камень - Земля:

A = ΔEпот = m·g·h. (3)

Поэтому T·ΔS = m·g·h,

Отсюда: ΔS =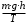

Подставим численные значения:

Задача 3
Определить потерю работоспособности, происходящую в тепловыделяющем элементе атомного реактора, где выделяющееся в процессе ядерной реакции тепло поглощается водой, протекающей при давлении 100 кГ/см². Вода нагревается от t₁=190°C до t₂=280°С. Температура тепловыделяющего элемента постоянна по его высоте и равна t₃=380° С. Расчёт потери вести на Q=100 ккал переданного тепла. Температура окружающей среды tcp=20°C. Считать, что тепловые потери отсутствуют.
Решение
Потеря работоспособности равна T₀·ΔS, где ΔS - изменение энтропии системы.

При этом ΔS = ΔS₁ + ΔS₂, где ΔS₁ - изменение энтропии тепловыделяющего элемента, ΔS₂ - изменение энтропии воды в процессе ее нагревания.

Эти изменения равны: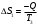

, (1)

Подставим в формулу (1) численные значения величин предварительно преобразовав их в системе СИ. Q=100 ккал = 419 кДж.

T₃ = t₃ + 273,16 К = 380° С +273,16 К = 653,16 К.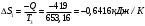



, (2)

где т - масса воды, поглотившая 419 кДж тепла, 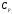- изобарная теплоемкость воды, равная 4,19 кДж/кг·К.

Масса воды равна:



Тогда вычислим ΔS₂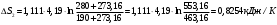



Увеличение энтропии системы

ΔS = ΔS₁ + ΔS₂ = - 0,6416+0,8254 =0,1838 кДж/К.

Потеря работоспособности

ΔL = T₀·ΔS = 293· 0,1838 = 53,85 кДж.

Задача 4
Определить излучательную способность поверхности Солнца, если известно, что его температура равна 6000˚С и условия излучения близки к излучению абсолютно чёрного тела. Вычислить длину волны, на которую приходится максимум спектральной плотности излучения.
Решение

Лучистый поток, излучаемый с единицы поверхности по всем направлениям сферического пространства_: называется плотностью потока излучения. Поток излучения и плотность потока излучения содержат лучи различных длин волн, поэтому такой вид излучения является интегральным. В соответствие с законом Стефана-Больцмана плотность теплового потока излучения от абсолютно черного тела определяется формулой: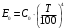

, (1)

где 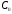= 5,7 Вт/(м²·К⁴) - коэффициент излучения абсолютно черного тела; Т- абсолютная температура тела, К

Считая условия излучения Солнца близкими к излучению абсолютно черного тела, определяем плотность теплового потока излучения от Солнца.

Абсолютная температура в Кельвинах:

Т = 273,16+t = 273,16 + 6000 = 6273,16 К



Из справочных данных диаметр Солнца составляет d=1,392·10⁹ м.

Вычисляем площадь поверхности сферы:

, (2)



Определяем излучательную способность поверхности Солнца:

, (3)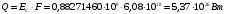


Связь между длиной волны, при которой будет наблюдаться максимум спектральной плотности излучения и абсолютной температурой тела определяется законом Вина:



следовательно




Задача 5
В паросборнике находится водяной пар. Определить массу водяного пара, если объём паросборника V=6,06 м³ , а удельный объём пара =20,2 см³/г.
Решение
Удельный объем вещества (м³/кг) – величина, равная отношению
объема тела к его массе:

, (1)
Выразим удельный объём пара =20,2 см³/г в системе СИ:

=20,2 см³/г = 20200 м³/кг

Массу пара выразим из формулы (1), откуда следует, что: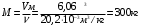