СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ_Вариант 66. Задача 1 Стальной стержень переменного сечения находится под действием двух продольных сил, приложенных по оси стержня (рис. 1, табл. 1)

• Название: Задача 1 Стальной стержень переменного сечения находится под действием двух продольных сил, приложенных по оси стержня (рис. 1, табл. 1)
• Дата: 07.04.2021
• Размер: 205 Kb.
• Имя файла: СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ_Вариант 66.doc
• Тип: Задача; #192389

Вариант 66 (схема 6, строка 6)

Задача 1

Стальной стержень переменного сечения находится под действием двух продольных сил, приложенных по оси стержня (рис.1, табл.1).

Построить эпюры поперечных сил, напряжений и перемещений. Весом самого стержня пренебречь.

При расчете можно принимать: площадь сечения А=10 см² , длина участков а=с=1м, b=2м, модуль упругости при растяжении для стали МПа, силы F₁ и F₂ направлены вниз, а F₃ и F₄ – вверх.

Величина	Вариант	Точка приложения
	6
A10-4, М2	10
a, м	1
b, м	2
c, м	1
F2, кН	100	М
F4, кН	200	К

При расчете можно принимать модуль упругости при
растяжении для стали 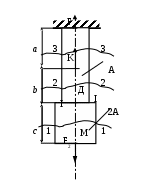МН/м² .



Решение:

Верхний конец стержня жестко заделан. Нижний конец свободен. Разбиваем стержень на свободные участки начиная со свободного конца. Границами участков являются сечения к которым приложены внешние силы или в которых изменяются размеры поперечного сечения стержня.

Пользуясь методом сечений, определяем значения внутренних продольных сил в сечениях стержня. Поскольку нижний конец не закреплен, удобнее начинать с него, не определяя реакции заделки стержня.

Рассмотрим сечение на участке МД. Составим уравнение проекций на ось у: , откуда кН.

На участке МД имеет место растяжения.

Проводим сечение на участке ДК. По аналогии записываем уравнение проекций на ось у: , откуда кН.

Продольная сила положительна, следовательно, на участке ДК имеет место растяжение.

Проводим сечение на участке КН. Записываем уравнение проекций на ось у: , откуда кН.

Продольная сила отрицательна, следовательно, третий участок сжат.

Зная продольную силу на каждом участке, определим значения нормальных напряжений. Имея ввиду, что А₁=2А=20см²=0,0020м², А₂=А=10см²=0,0010м², А₃=А=10см²=0,0010м²,

МПа (растяжение)

МПа (растяжение)

МПа (сжатие)

По найденным значениям 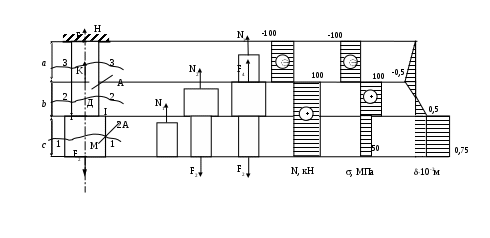и строим эпюры. Для этого проводим две базовые прямые, параллельные оси стержня. Считая прямые за нулевые линии, откладываем вправо и влево от них соответственно положительные и отрицательные значения и .


Определим полное удлинение стержня

, подставляя числовые значения, получим

м=0,75мм

Перемещения в сечениях

м

м

м


Задача 3.1

Для заданной схемы балки (рис. 5) требуется написать выражения поперечных сил и изгибающих моментов для каждого участка в общем виде, построить эпюры Q и М, найти максимальный момент М_max и подобрать стальную балку двутаврового поперечного сечения при [] = 160 МПа. Данные взять из табл. 3.1.

Варианты	Данные величины
	а, м	b, м	l,м	Изгибающий момент М, кН*м	Сосредо- точенная сила F, кН	Равномерно распределенная нагрузка q, kH/м
6	3,2	4,4	13	10	13	7

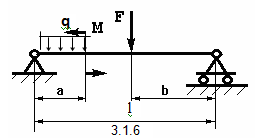Решение:

Определяем опорные реакции. Так как горизонтальная нагрузка отсутствует, то опора А имеет только вертикальную реакцию R_А. составляем уравнения равновесия. Распределенную нагрузку заменяем равнодействующей 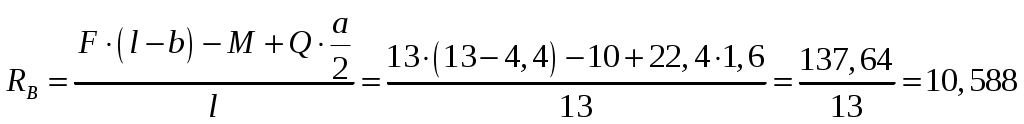кН.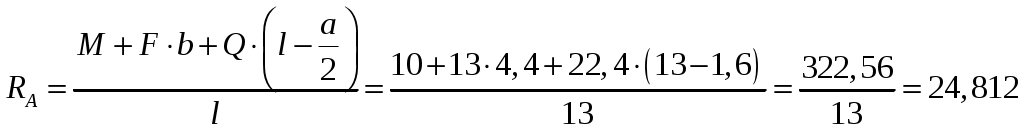

, ,

кН,

, ,

кН.

Для проверки правильности определения опорных реакций составим уравнение проекций внешних сил на ось Y.

, .
2. Построение эпюр Q и М.

Для построения эпюр внутренних усилий воспользуемся методом сечений и следующим правилом знаков.

Если внешняя сила слева от сечения направлена вверх, то она создает положительную поперечную силу и положительный изги­бающий момент. Внешняя сила справа от сечения, направленная вниз, создает положительную поперечную силу и отрицательный из­гибающий момент.

Если внешний сосредоточенный момент слева от сечения на­правлен по часовой стрелке, то он создает положительный изгибаю­щий момент. Внешний сосредоточенный момент справа от сечения, направленный против часовой стрелки, создает положительный из­гибающий момент.

Рассмотрим первый участок: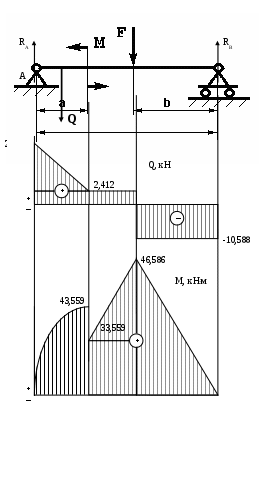



кН

кН,

кН

кНм

кНм, кНм,



Рассмотрим второй участок:



кН

кНм

кНм,

кНм,

Рассмотрим третий участок (идем от правого края):



кН

кНм

кНм, кНм,

После построения эпюр проверяем их правильность. На эпюре Q в месте приложения сосредоточенных сил наблюдаем скачек на величину и в направлении этих сил.

На эпюре М там, где приложен сосредоточенный момент имеет место скачек на величину и в направлении этого момента. Там, где приложена сосредоточенная сила, на эпюре моментов прямая меняет угол наклона.

По эпюре моментов определяем максимальное значение изгибающего момента М_mах = 46,586 кНм.

Из условия прочности по нормальным напряжениям



Вычислим м³ = 291 см³.

По сортаменту прокатной стали, выбираем двутавр № 24а см³.
ЛИТЕРАТУРА

1. 
   Вереина Л. И. Краснов М. М. Техническая механика. Учебник для студентов учреждений среднего профессионального образования. М.: Академия, 2010.- 288 с.;
   
2. 
   Олофинская В. П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий. Учебное пособие, 2-е издание. Профессиональное образование.: Инфра-М, Форум, 2011.-349 с.;
   
3. 
   Сетков В. И. Сборник задач по технической механике. Учеб. Пособие для студентов учреждений среднего профессионального образования – 2-е изд., М.: Академия, 2010. - 224 с.;
   
4. 
   Эрдеди А. А. Теоретическая механика. Сопротивление материалов. Учебное пособие для СПО. М.: Академия, 2009. – 320 с.;
   
5. 
   Кривошапко С. Н., Копнов В. А. Сопротивление материалов. Руководство для решения задач и выполнения лабораторных и расчетно-графических работ. Высшая школа, 2009. – 243 с.