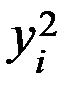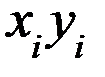Методы математического анализа. Задача 1 в результате некоторого тестирования 20 испытуемых была получена следующая выборка 5, 7, 9, 4, 7, 5, 4, 4, 9, 7, 5, 4, 5, 4, 5, 5, Ранжировать ряд.
 Скачать 225.25 Kb.
|
|
Задача 1 В результате некоторого тестирования 20 испытуемых была получена следующая выборка: 5, 7, 9, 4, 7, 5, 4, 4, 9, 7, 5, 4, 5, 4, 5, 5, . . .  1 Ранжировать ряд. 2 Записать вариационный ряд, учитывая значение варианты 6. 3 Найти относительные частоты. 4 Построить графическую иллюстрацию ряда.  5 Найти числовые характеристики (моду, медиану, средне выборочное значение, размах, дисперсию, среднеквадратическое отклонение, коэффицент вариации).Решение: Имеем выборку объема N = 25. Построим ранжированный (в порядке возрастания) ряд вариант с соответствующими им частотами. Для этого сначала ранжируем варианты выборки. Получаем: 2, 3, 3, 4, 4, 4, 5, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10, 10, 11, 11. Подсчитав количество повторений каждой варианты, получим требуемый дискретный вариационный ряд распределения выборки с. в. X:
Полигоном частот называют ломанную, отрезки который соединяют точки (X1, N1), (X2, N2), …, (Xk, Nk). Д 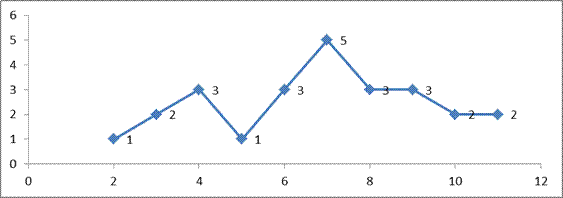 ля построения полигона частот на оси абсцисс откладывают варианты Xi, а на оси ординат – соответствующие им Ni. Точки (Xi, Ni) соединяют отрезками прямых и получают полигон частот: Для определения частостей вариант нужно вычислить для каждой варианты отношение Ni/N = WI, где N = 25 – объем выборки. Получаем вариационный ряд вариант с соответствующими им частостями:
Статистической функцией распределения  называется относительная частота (частность) того, что признак примет значение, меньшее заданного  , т. е. Запишем значения статистической (эмпирической) функции распределения в аналитическом виде: 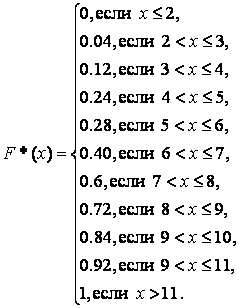 Ее график имеет вид: 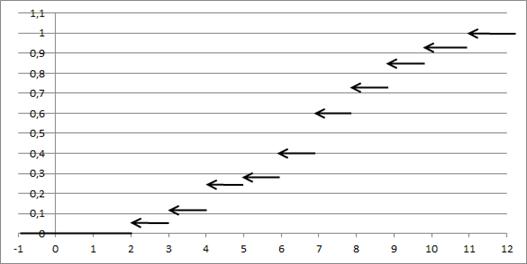 Определим выборочную среднюю: 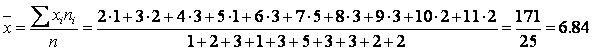 .Вычислим дисперсию: 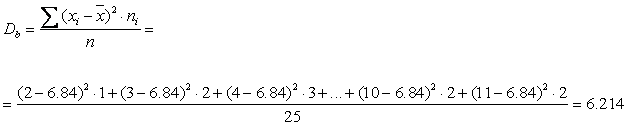 Медианой  вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений: Модой  называется варианта, которой соответствует наибольшая частота: Задача 2 Автоконцерн утверждает, что доля автомобилей с несрабатывающими подушками безопасности не превосходит 4. В партии объемом 170 машин оказалось 8 автомобилей которые не прошли краш-тест. Не противоречит ли это утверждению производителя? Доверительная вероятность 0,95. Решение: Доля автомобилей, не прошедших тест ω=10200=0,05 Средняя ошибка выборки для автомашин, не прошедших тест ∆ω=ω(1-ω)n=0,05(1-0,05)200=0,05∙0,95200=0,0002375=0,0154 μω=tω∙∆ω Значение определяем по таблице распределения Лапласа: Φt=γ2=0,992=0,495;t=2,58 μω=tω∙∆ω=0,0154∙2,58=0,039732 Таким образом, имеем: 0,05-0,039732≤ω≤0,05+0,039732; 0,010268≤ω≤0,089732 Средняя ошибка выборки для доли автомобилей, не прошедших тест, с вероятностью 0,99 находится в пределах от 0,010268 до 0,089732, что говорит о том, что не противоречит утверждению производителя. Задача 3 Проводились испытания новых подгузников. В эксперименте участвовали 1300 мальчиков и 1330 девочек. У 170 мальчиков и 165 девочек наблюдались аллергические реакции. Можно ли утверждать, что аллергические реакции от новых подгузников у девочек возникают не чаще, чем у мальчиков? Доверительная вероятность равна 0,99. Решение: Пусть р1 – процент аллергических реакций от новых подгузников у девочек, р2 –процент аллергических реакций у мальчиков. Введем нулевую гипотезу на уровне значимости : Н0: р1 = р2 при конкурирующей гипотезе Н1: р1> р2 Критическое значение двусторонней критической области найдём из соотношения . В данном случае: По таблице функций Лапласа определяем При нулевая гипотеза принимается, а при – отвергается: Вычислим наблюдаемое значение критерия по формуле: где m1=115;n1=1900;m2=120;n2=1800 Подставляем значения: Uнабл=1151900-1201800115+1201900+18001-115+1201900+180011900+11800 = =115∙18-120∙191900∙1823537001-235370018+191900∙18=-2101900∙182353700∙34653700∙371900∙18= =-7190∙62353700∙3465100∙11900∙18=-7190∙6∙11000∙235∙346537∙19∙18=-7114100∙64,35= =-71,14∙8,022≈-0,765 Так как U набл=0,765<1,96=uкр, то полученное значение попало в область принятия гипотезы, о том что аллергеческие реакции у девочек возникают не чаще чем у мальчиков. Задача 4 Два человека дегустируют 10 сортов кофе. Каждый из них расположил эти сорта в порядке убывания предпочтений.
Есть ли какая-нибудь связь между этими результатами? Доверительная вероятность 0,99. Решение: Два человека дегустируют 10 сортов кофе. Каждый из них расположил эти сорта в порядке убывания предпочтений (второй и третий столбцы). Есть ли какая-нибудь разница между этими результатами? Доверительная вероятность р=95%.
Заполним таблицу:
d- это разность между значениями дегустаторов для одного и того же сорта чая, то есть 4-й столбец – это разность 2-го и 3-го столбцов. Каждое число 4-го столбца возводим в квадрат и результат записываем в 5-й столбец. В последней строке указана сумма чисел 5-го столбца. Гипотеза Н0: между результатами этих исследований нет связи, они несогласованны друг с другом. Гипотеза Н1: между результатами этих исследований существует связь.  Это граничная точкаРанговый коэффициент корреляции Спирмена:  Статистика  Гипотезу Н0 отвергаем и принимаем гипотезу Н1 на уровне значимости 5%. Между результатами исследований существует некая связь. Задача 5 Даны измерения двух случайных величин:
Задание: 1 Построить корреляционное поле XY. 2 Вычислить коэффициент корреляции между X и Y, сделать вывод. 3 Найти уравнение линейной регрессии и построить его на корреляционном поле. 4 Доказать (или опровергнуть) гипотезу о равенстве нулю генерального коэффициента корреляции.Решение: 1) Выборочный коэффициент корреляции: 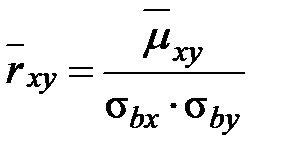 =  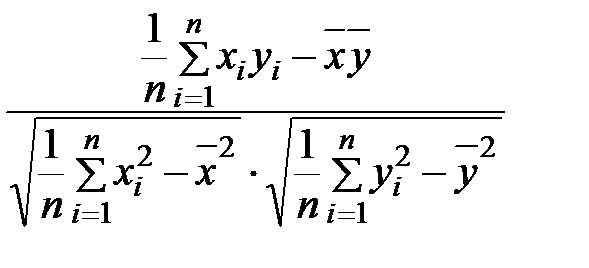;2) линейное уравнение регрессии Y на X : 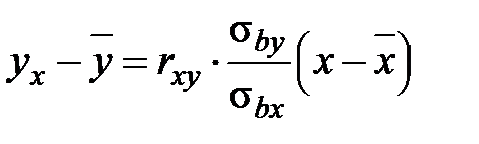 ,где 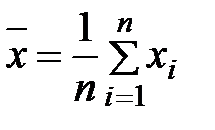 ,  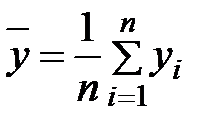 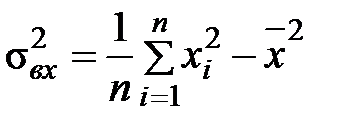,  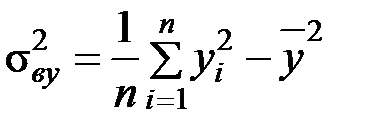,  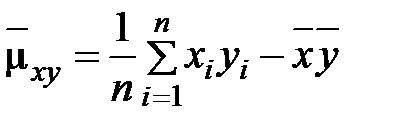.Проведем необходимые вычисления, для чего составим расчетную таблицу:
Тогда получаем: 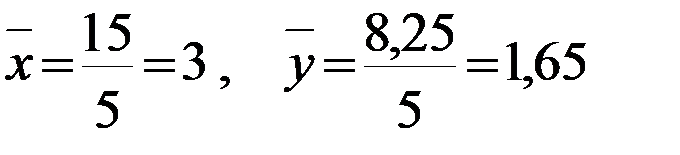 , 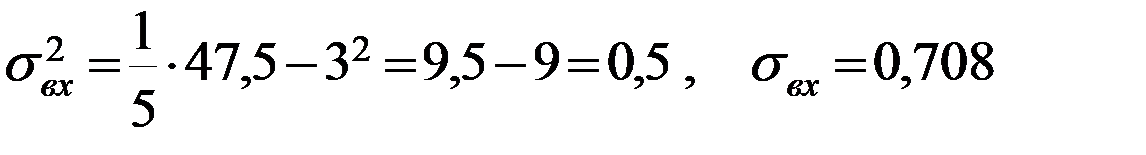 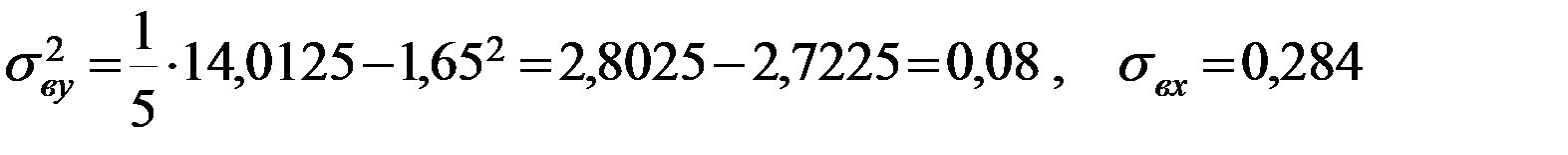, ,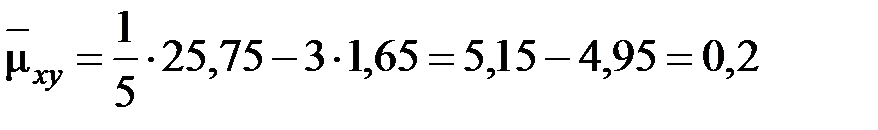 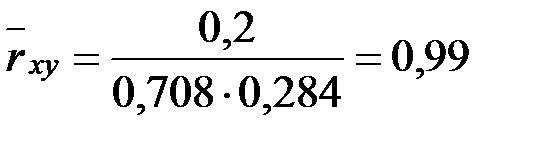.Запишем уравнение линейной регрессии Y на X :   ,  |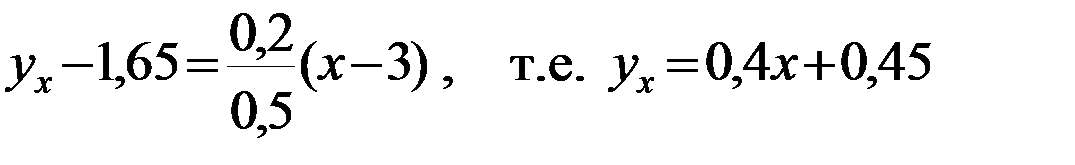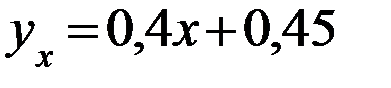
